Determination of Dynamic Properties of Fine-Grained Soils at High Cyclic Strains
Abstract
1. Introduction
2. Study Area
3. Material and Methods
3.1. Soil Description
3.2. Testing Apparatus
3.3. Testing Procedure
4. Results and Discussion
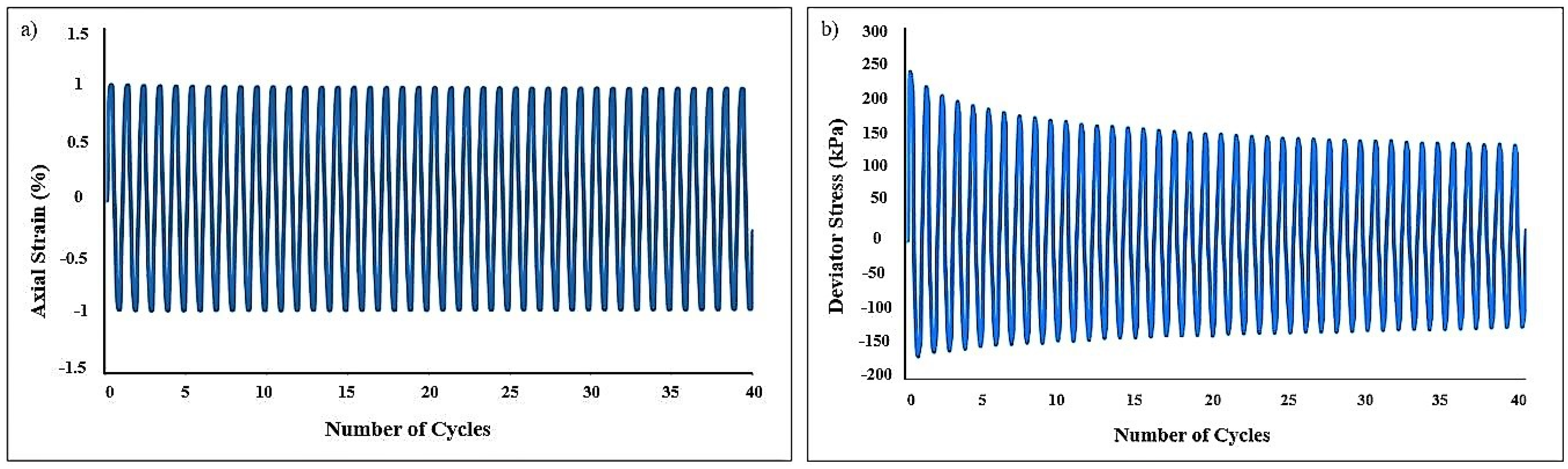
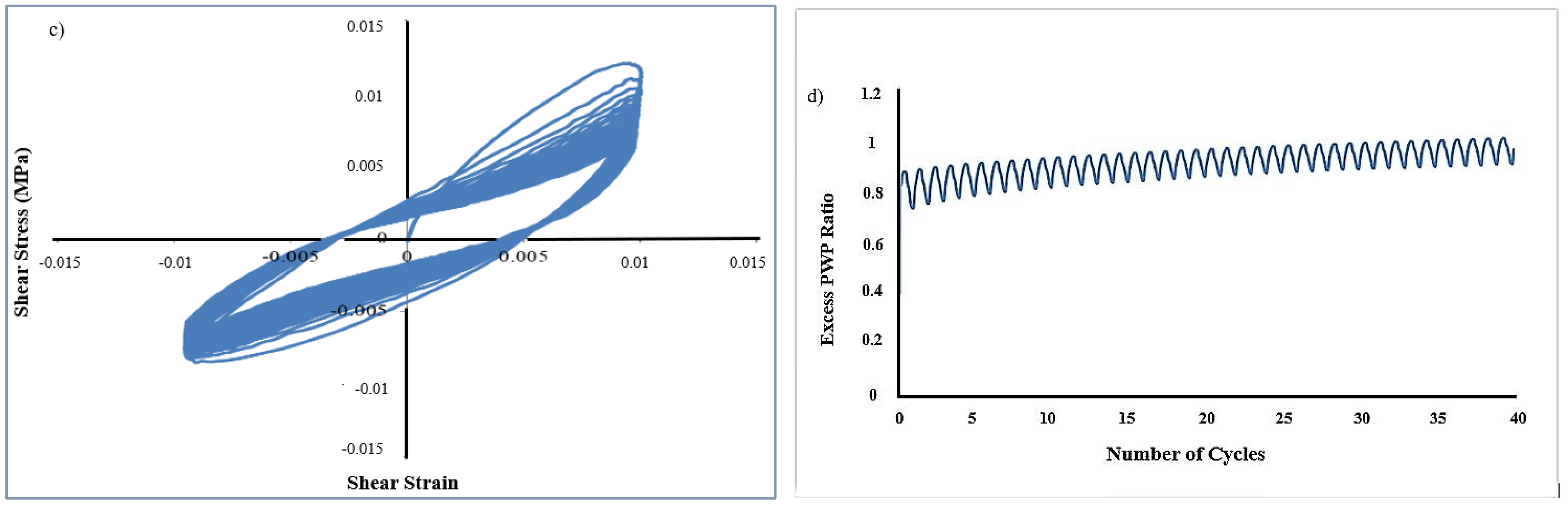
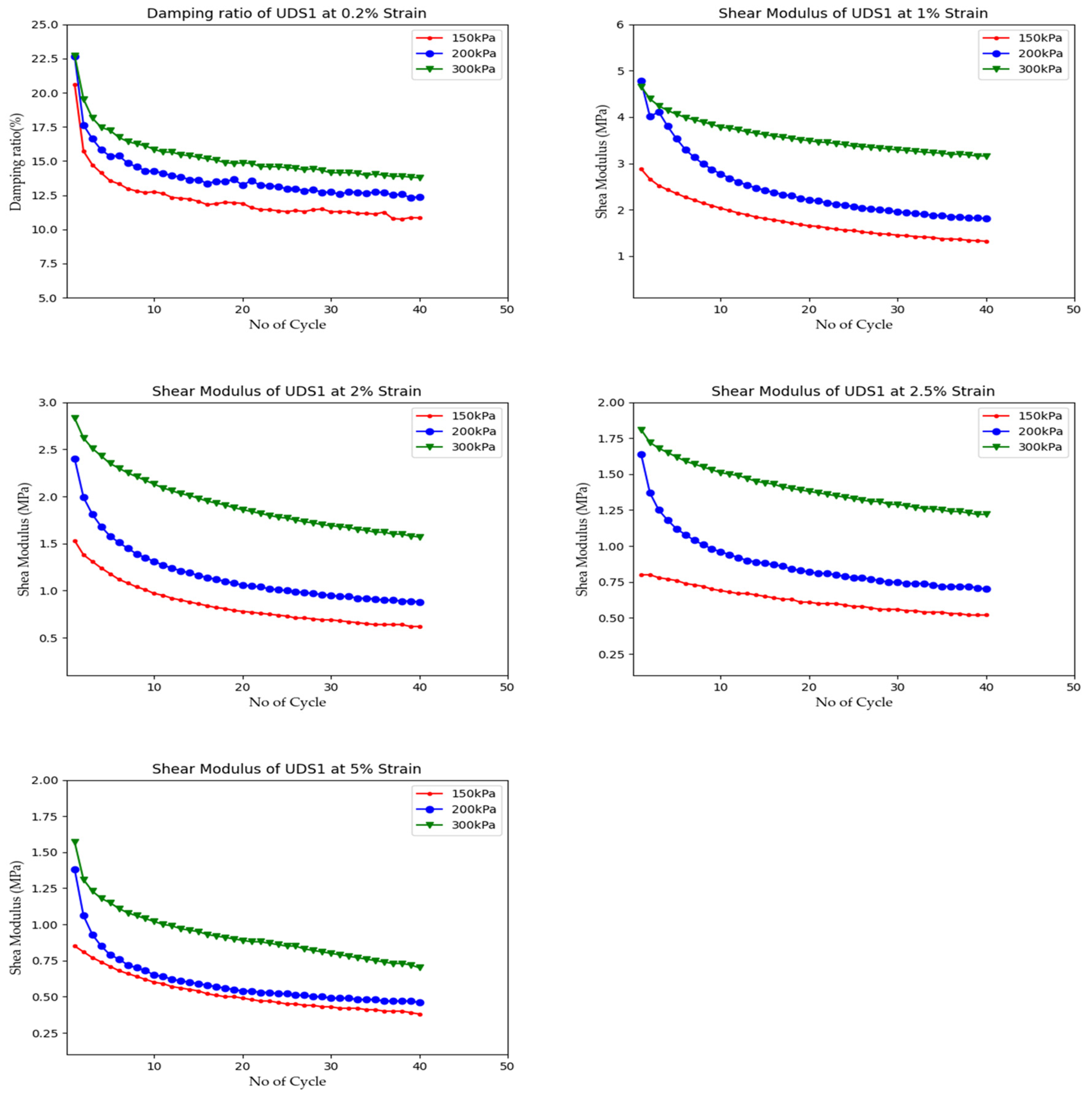
4.1. Undrained Cyclic Shear
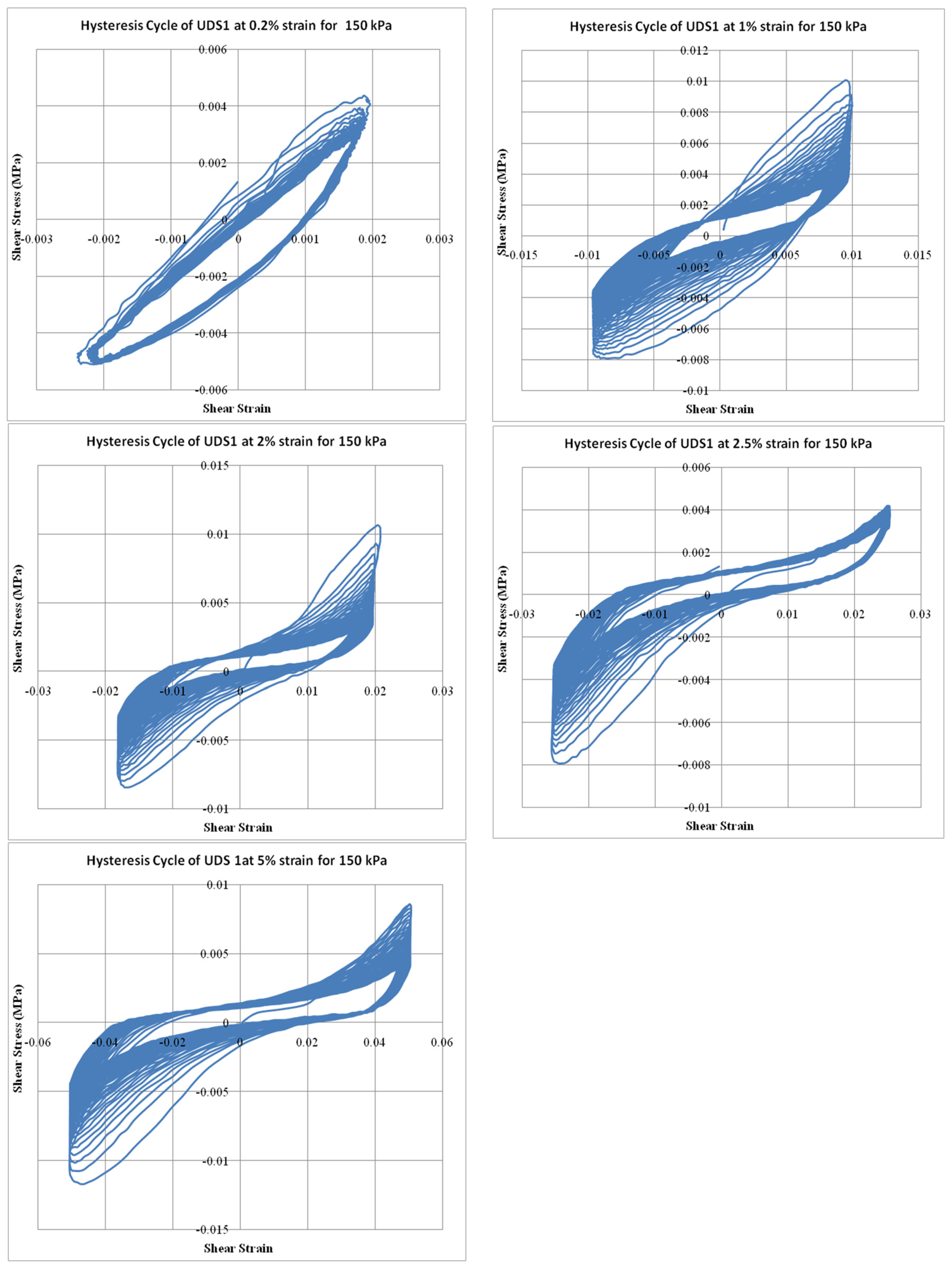
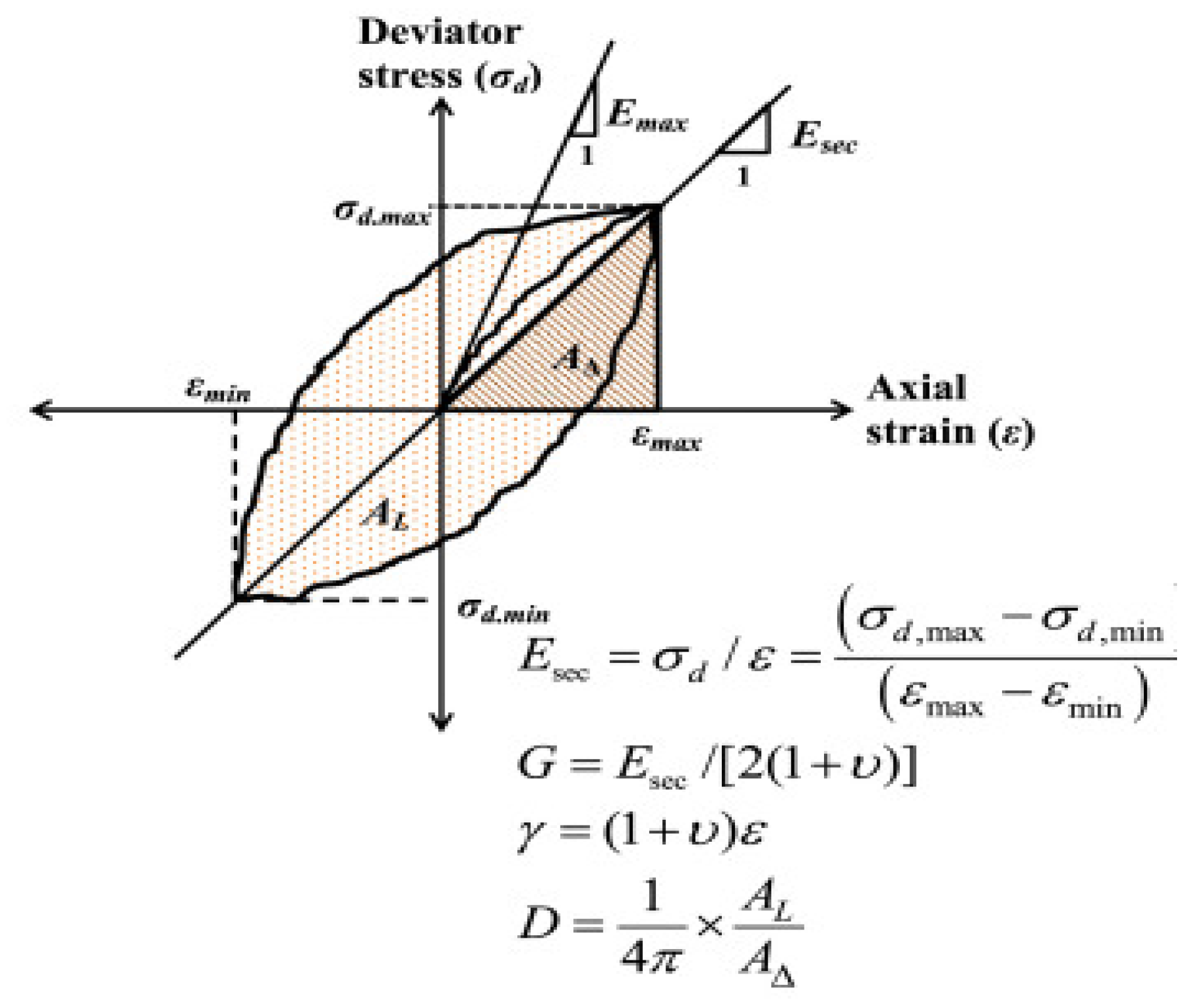
4.2. Shear Modulus and Damping Ratio
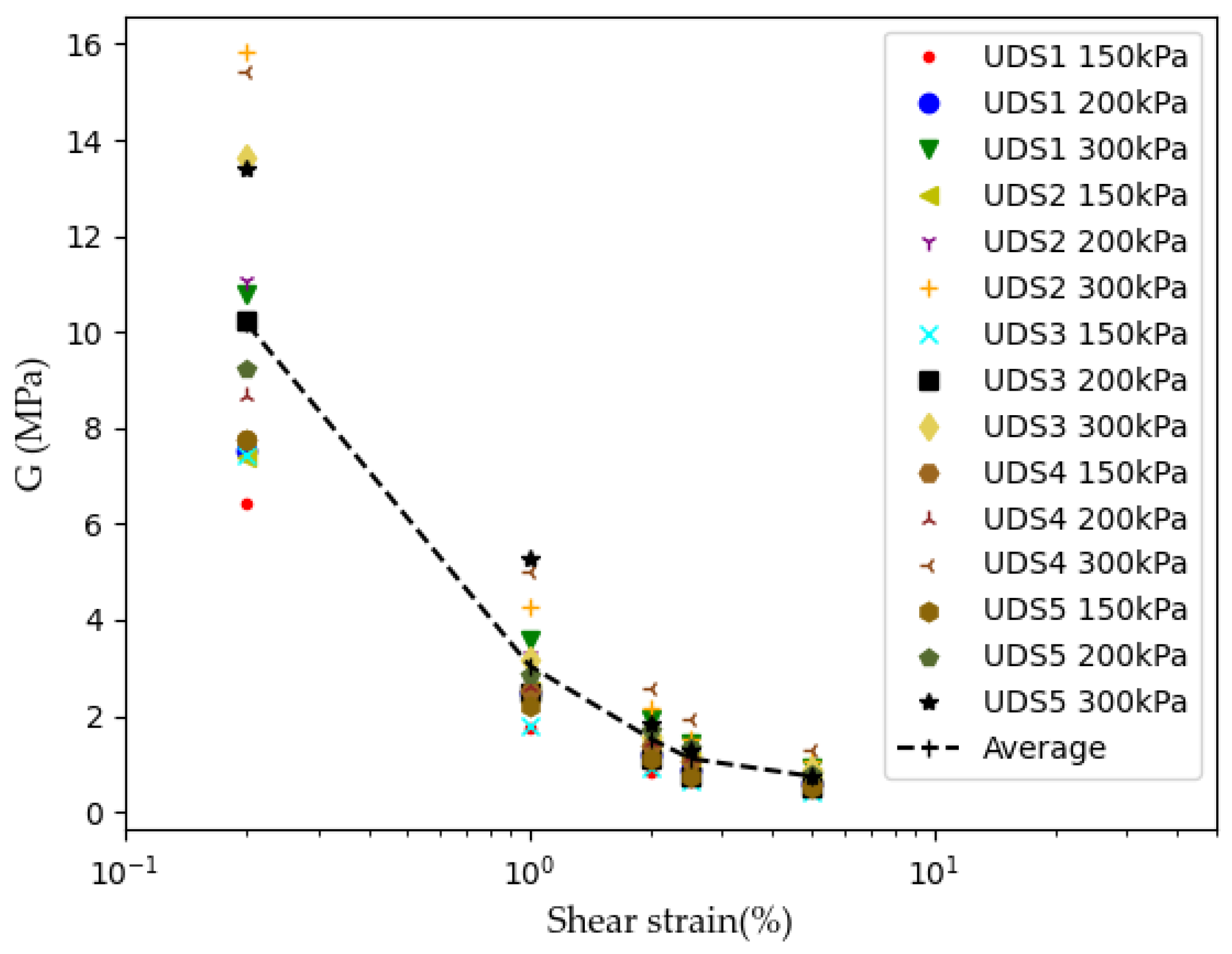
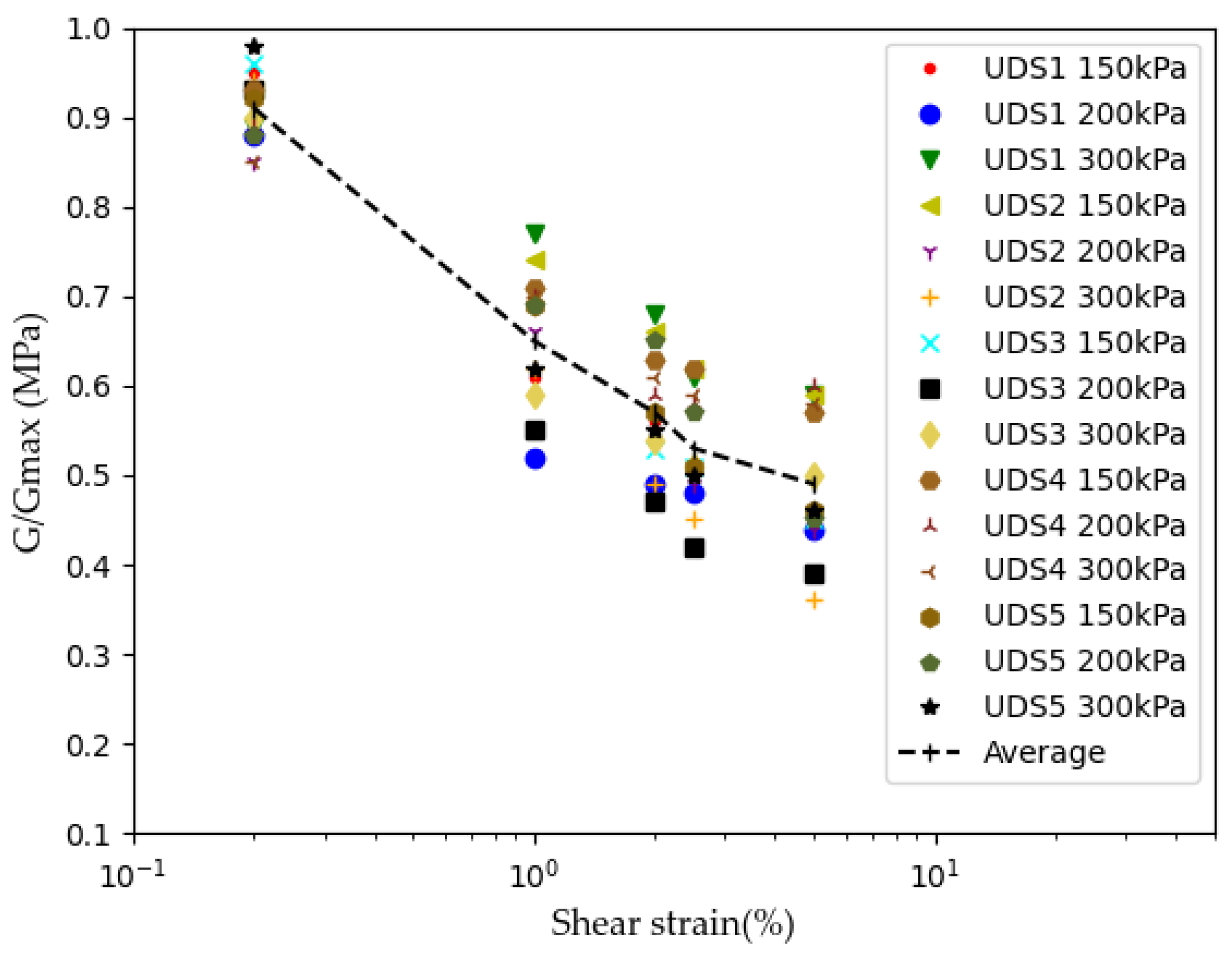
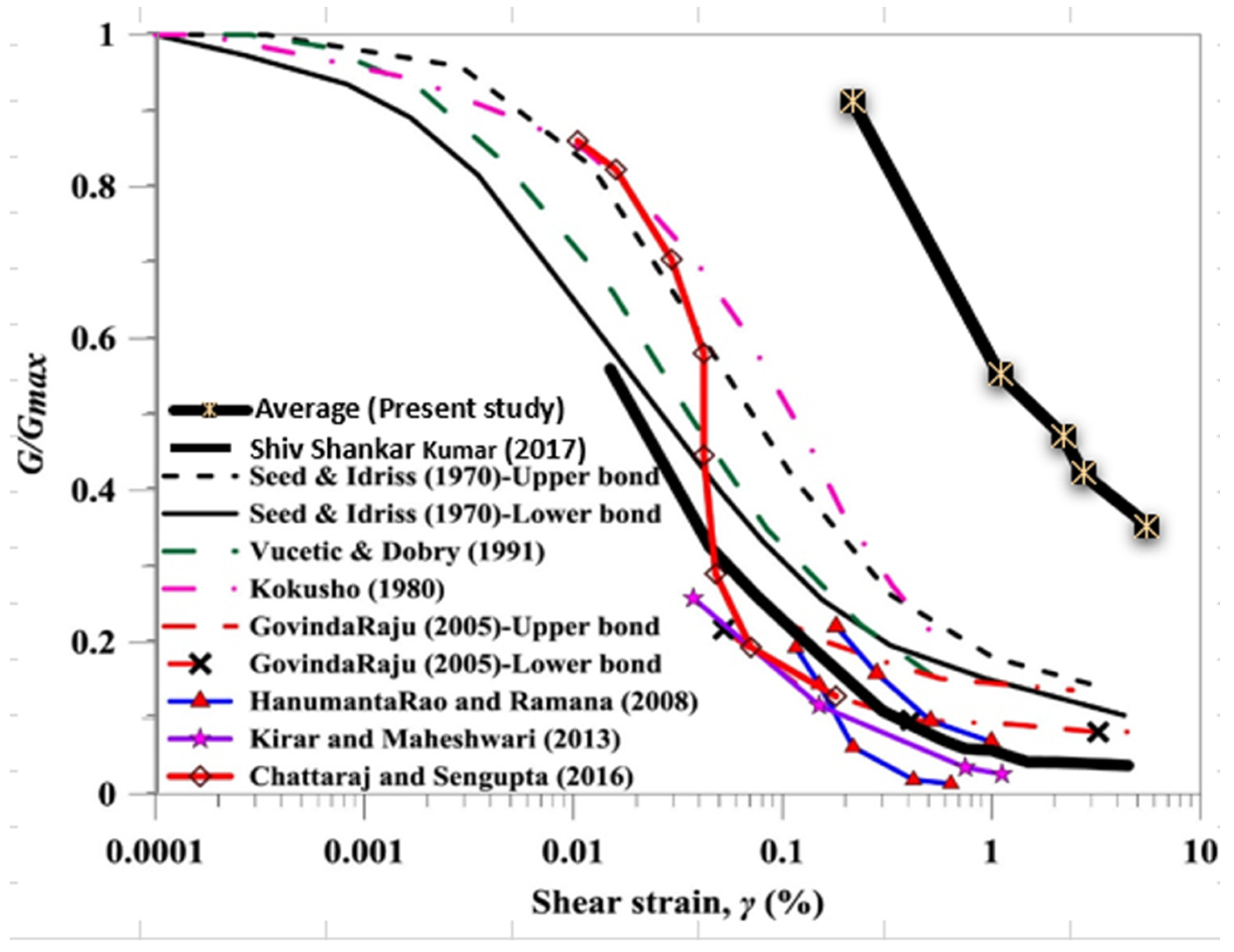
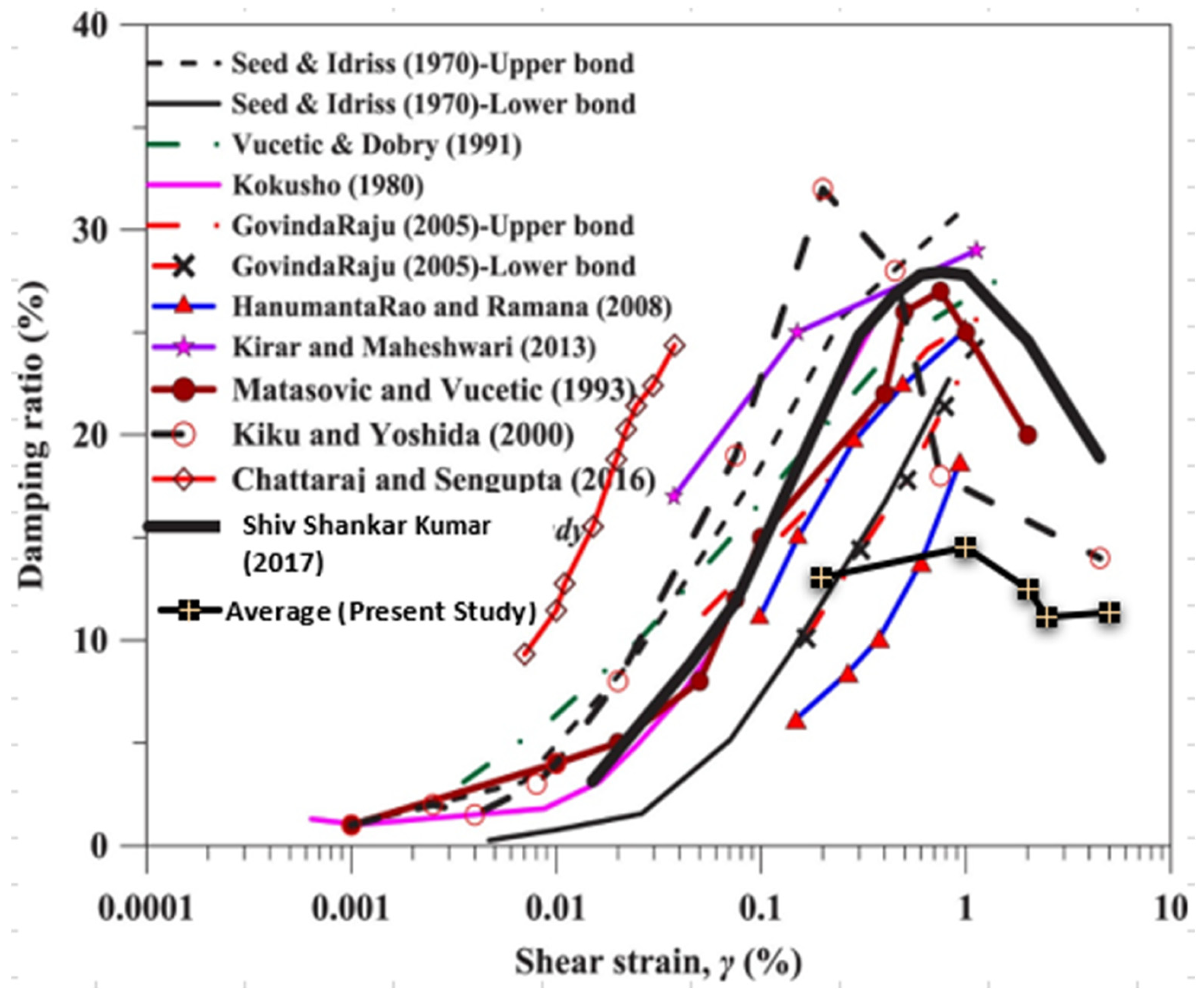
4.3. Effect of Shear Strain on SM and DR
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Celebi, M.; Prince, J.; Dietel, C.; Onate, M.; Chavez, G. The culprit in Mexico City—Amplification of motions. Earthq. Spectra 1987, 3, 315–328. [Google Scholar] [CrossRef]
- Neagu, C.; Arion, C. Dynamic laboratory investigation for soil seismic response. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; Volume 15, pp. 1–7. [Google Scholar]
- Vucetic, M.; Dobry, R. Effect of soil plasticity on cyclic response. J. Geotech. Eng. 1991, 117, 89–107. [Google Scholar] [CrossRef]
- Villacreses, J.P.; Caicedo, B.; Caro, S.; Yépez, F. A novel procedure to determine shear dynamic modulus and damping ratio for partial saturated compacted fine-grained soils. Soil Dyn. Earthq. Eng. 2020, 131, 106029. [Google Scholar] [CrossRef]
- Sitharam, T.G.; GovindaRaju, L.; Murthy, S.B. Evaluation of liquefaction potential and dynamic properties of silty sand using cyclic triaxial testing. Geotech. Test. J. 2004, 27, 1–7. [Google Scholar]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2001. [Google Scholar]
- Roblee, C.; Chiou, B. A proposed geoindex model for design selection of non-linear properties for site response analyses. In International Workshop on Uncertainties in Nonlinear Soil Properties and Their Impact on Modeling Dynamic Soil Response; PEER Headquarters: Sacramento, CA, USA, 2004. [Google Scholar]
- Kumar, S.S.; Krishna, A.M.; Dey, A. Evaluation of dynamic properties of sandy soil at high cyclic strains. Soil Dyn. Earthq. Eng. 2017, 99, 157–167. [Google Scholar] [CrossRef]
- Dinesh, S.V.; Sitharam, T.G.; Vinod, J.S. Dynamic properties and liquefaction behaviour of granular materials using discrete element method. Curr. Sci. 2004, 87, 1379–1387. [Google Scholar]
- Mohtar, C.S.E.; Drnevich, V.P.; Santagata, M.; Bobet, A. Combined resonant column and cyclic triaxial tests for measuring undrained shear modulus reduction of sand with plastic fines. Geotech. Test. J. 2013, 36, 1–9. [Google Scholar] [CrossRef]
- Okur, D.V.; Ansal, A. Stiffness degradation of natural fine grained soils during cyclic loading. Soil Dyn. Earthq. Eng. 2007, 27, 843–854. [Google Scholar] [CrossRef]
- Rienzo, F.; Oreste, P.; Pelizza, S. Subsurface geological-geotechnical modeling to sustain underground civil planning. Eng. Geol. 2008, 96, 187–204. [Google Scholar] [CrossRef]
- Aloisio, A.; Totani, F.; Totani, G. Experimental dispersion curves of non-penetrable soils from direct dynamic measurements using the seismic dilatometer (SDMT). Soil Dyn. Earthq. Eng. 2021, 143, 106616. [Google Scholar] [CrossRef]
- Tafili, M.; Duque, J.; Ochmański, M.; Mašín, D.; Wichtmann, T. Numerical inspection of Miner’s rule and drained cyclic preloading effects on fine-grained soils. Comput. Geotech. 2023, 156, 105310. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Hall, W.J., Ed.; Prentice Hall: London, UK, 1996. [Google Scholar]
- Ansal, A.M.; Iyisan, R.; Yildirim, H.T. The cyclic behaviour of soils and effects of geotechnical factors in microzonation. Soil Dyn. Earthq. Eng. 2001, 21, 445–452. [Google Scholar] [CrossRef]
- Cao, Y.L.; Law, K.T. Energy dissipation and dynamic behaviour of clay under cyclic loading. Can. Geotech. J. 1992, 29, 103–111. [Google Scholar] [CrossRef]
- Gaitán-Serrano, J.F.; Ortiz-Pulido, M.P.; Camacho-Tauta, J.F. Shear modulus reduction curves of guayuriba sand by cyclic triaxial and bender element tests. In Proceedings of the Third International Conference on GEOMATE, Nagoya, Japan, 13–15 November 2013; pp. 1–6. [Google Scholar]
- Konrad, J.M.; Wagg, B.T. Undrained cyclic loading of anisotropically consolidated clayey silts. J. Geotech. Eng. 1993, 119, 929–949. [Google Scholar] [CrossRef]
- Li, L.L.; Dan, H.B.; Wang, L.Z. Undrained behavior of natural marine clay under cyclic loading. Ocean. Eng. 1996, 38, 1792–1805. [Google Scholar] [CrossRef]
- O’Reilly, M.P.; Brown, S.F.; Overy, R.F. Cyclic loading of silty clay with drainage periods. J. Geotech. Eng. 1991, 117, 354–362. [Google Scholar] [CrossRef]
- Thirugnanasampanther, S. Cyclic Behaviour and Dynamic Properties of Soils Under Simple Shear Loading. Ph.D. Thesis, University of East London, London, UK, 2016. [Google Scholar]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Measurement and parameter effects. J. Soil Mech. Found. 1972, 98, 603–624. [Google Scholar] [CrossRef]
- Ishihara, K. Liquefaction and flow failure during earthquakes. Geotechnique 1993, 43, 351–415. [Google Scholar] [CrossRef]
- Seed, H.B.; Robert, T.; Wong, I.; Idriss, M.; Tokimatsu, K. Moduli and Factors for Dynamic Analyses of Cohesion Less Soils; University of California: Berkeley, CA, USA, 1984. [Google Scholar]
- Brennan, A.J.; Thusyanthan, N.I.; Madabhushi, S.P.G. Evaluation of shear modulus and damping in dynamic centrifuge tests. J. Geotech. Geoenviron. Eng. 2005, 131, 1488–1497. [Google Scholar] [CrossRef]
- Kiku, H.; Yoshida, N. Dynamic deformation property tests at large strains. Earthq. Eng. 2000, 1748, 1–13. [Google Scholar]
- Hussain, A.; Yeat, R.S. Active faulting in the southern Peshawar basin, Pakistan. Geol. Bull. Univ. Peshawar 2002, 35, 113–124. [Google Scholar]
- Janjuhah, H.T.; Ishfaque, M.; Mehmood, M.I.; Kontakiotis, G.; Shahzad, S.M.; Zarkogiannis, S.D. Integrated Underground Mining Hazard Assessment, Management, Environmental Monitoring, and Policy Control in Pakistan. Sustainability 2021, 13, 13505. [Google Scholar] [CrossRef]
- Yasir, M.; Ahmed, W.; Islam, I.; Sajid, M.; Janjuhah, H.T.; Kontakiotis, G. Composition, Texture, and Weathering Controls on the Physical and Strength Properties of Selected Intrusive Igneous Rocks from Northern Pakistan. Geosciences 2022, 12, 273. [Google Scholar] [CrossRef]
- Bilal, A.; Mughal, M.S.; Janjuhah, H.T.; Ali, J.; Niaz, A.; Kontakiotis, G.; Antonarakou, A.; Usman, M.; Hussain, S.A.; Yang, R. Petrography and Provenance of the Sub-Himalayan Kuldana Formation: Implications for Tectonic Setting and Palaeoclimatic Conditions. Minerals 2022, 12, 794. [Google Scholar] [CrossRef]
- Mateen, A.; Wahid, A.; Janjuhah, H.T.; Mughal, M.S.; Ali, S.H.; Siddiqui, N.A.; Shafique, M.A.; Koumoutsakou, O.; Kontakiotis, G. Petrographic and Geochemical Analysis of Indus Sediments: Implications for Placer Gold Deposits, Peshawar Basin, NW Himalaya, Pakistan. Minerals 2022, 12, 1059. [Google Scholar] [CrossRef]
- Zaheer, M.; Khan, M.R.; Mughal, M.S.; Janjuhah, H.T.; Makri, P.; Kontakiotis, G. Petrography and Lithofacies of the Siwalik Group in the Core of Hazara-Kashmir Syntaxis: Implications for Middle Stage Himalayan Orogeny and Paleoclimatic Conditions. Minerals 2022, 12, 1055. [Google Scholar] [CrossRef]
- Khwaja, A.A.; Jan, M.Q. The 8 October 2005 Muzaffarabad earthquake: Preliminary seismological investigations and probabilistic estimation of peak ground accelerations. Curr. Sci. 2008, 1158–1166. [Google Scholar]
- Seed, H.B.; Idriss, K.M. Soil moduli and damping factors for dynamic response analyses. Report No. EERC 70-10. Earthq. Eng. Res. Cent. 1970. [Google Scholar]
- Shafiee, A.; Ghate, R. Shear Modulus and Damping Ratio in Aggregate-Clay Mixtures: An Experimental Study Versus ANNs Prediction. J. Appl. Sci. 2008, 8, 3068–3082. [Google Scholar] [CrossRef]
- Ghayoomi, M.; Suprunenko, G.; Mirshekari, M. Cyclic Triaxial Test to Measure Strain-Dependent Shear Modulus of Unsaturated Sand. Int. J. Geomech. 2017, 17, 11. [Google Scholar] [CrossRef]
- Kokusho, T. Cyclic Triaxial Test of Dynamic Soil Properties for Wide Strain Range. Soils Found. 1980, 20, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Govindaraju, L. Liquefaction and Dynamic Properties of Sandy Soils. Unpublished. Ph.D. Thesis, Department of Civil Engineering, Indian Institute of Science, Bangalore, India, 2005. [Google Scholar]
- Hanumantharao, C.; Ramana, G.V. Dynamic soil properties for microzonation of Delhi, India. J. Earth Syst. Sci. 2008, 117, 719–730. [Google Scholar] [CrossRef]
- Chattaraj, R.; Sengupta, A. Liquefaction potential and strain dependent dynamic properties of Kasai River sand. Soil Dyn. Earthq. Eng. 2016, 90, 467–475. [Google Scholar] [CrossRef]
- Kirar, B.; Maheshwari, B.K. Effects of Silt Content on Dynamic Properties of Solani Sand. In Proceedings of the 7th Conference of the International Conference on Case Histories in Geotechnical Engineering, Chicago, IL, USA, 29 April–4 May 2013. [Google Scholar]
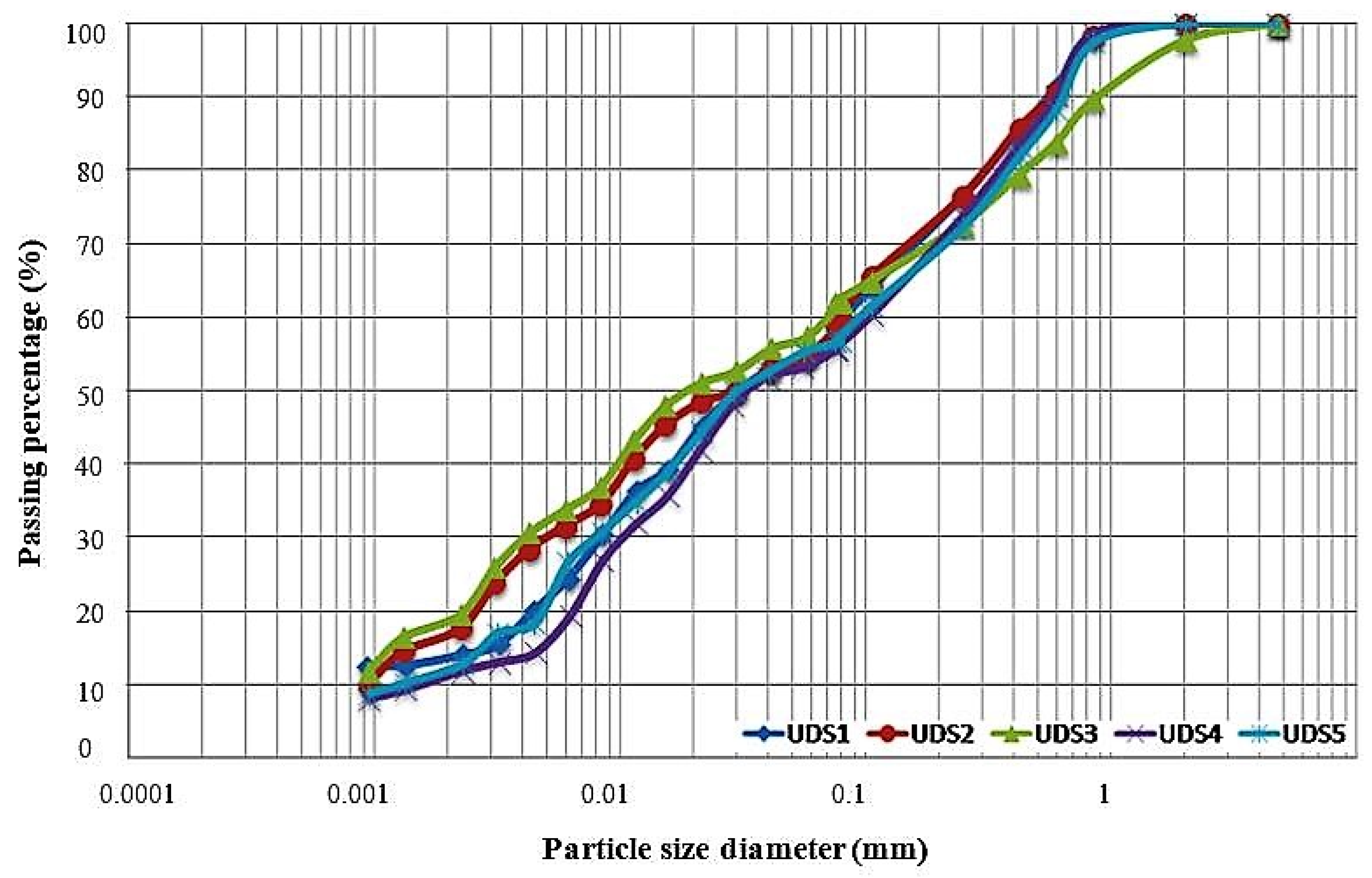



| Sample | Moisture Content (%) | Specific Gravity | Liquid Limit (LL)(%) | Plastic Limit (PL)(%) | Plasticity Index LL-PL | Passing Percentage No. 200 | Group Symbol | Soil Type |
|---|---|---|---|---|---|---|---|---|
| UDS1 | 14.8 | 2.68 | 22.9 | 17.19 | 5.71 | 58.6 | CL-ML | Sandy Silty Clay |
| UDS2 | 15.8 | 2.70 | 23.67 | 16.7 | 6.97 | 59.3 | CL-ML | Sandy Silty Clay |
| UDS3 | 15.9 | 2.72 | 21.7 | 17.3 | 4.4 | 62.1 | CL-ML | Sandy Silty Clay |
| UDS4 | 11.6 | 2.69 | 26.08 | 22.03 | 4.05 | 55.6 | CL-ML | Sandy Silty Clay |
| UDS5 | 12.3 | 2.69 | 29.7 | 24.4 | 5.3 | 56.7 | CL-ML | Sandy Silty Clay |
| Sample | Confining Pressure, kPa | Strains % | |
|---|---|---|---|
| UDS1 | UDS1a | 150 | 0.2, 1, 2, 2.5 and 5 |
| UDS1b | 200 | ||
| UDS1c | 300 | ||
| UDS2 | UDS2a | 150 | 0.2, 1, 2, 2.5 and 5 |
| UDS2b | 200 | ||
| UDS2c | 300 | ||
| UDS3 | UDS3a | 150 | 0.2, 1, 2, 2.5 and 5 |
| UDS3b | 200 | ||
| UDS3c | 300 | ||
| UDS4 | UDS4a | 150 | 0.2, 1, 2, 2.5 and 5 |
| UDS4b | 200 | ||
| UDS4c | 300 | ||
| UDS5 | UDS5a | 150 | 0.2, 1, 2, 2.5 and 5 |
| UDS5b | 200 | ||
| UDS5c | 300 | ||
| G(Avg.) | Gmax | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strains(%) | 0.2 | 1 | 2 | 2.5 | 5 | 0.2 | 1 | 2 | 2.5 | 5 |
| UDS1 | 6.43 | 1.77 | 0.85 | 0.63 | 0.52 | 6.76 | 2.88 | 1.53 | 1.23 | 1.20 |
| UDS2 | 7.40 | 2.52 | 1.43 | 1.08 | 0.76 | 7.95 | 3.39 | 2.16 | 1.73 | 1.29 |
| UDS3 | 7.46 | 1.81 | 0.94 | 0.67 | 0.40 | 7.81 | 3.32 | 1.76 | 1.30 | 0.90 |
| UDS4 | 7.75 | 2.51 | 1.40 | 1.04 | 0.57 | 8.36 | 3.52 | 2.21 | 1.68 | 0.99 |
| UDS5 | 7.78 | 2.23 | 1.11 | 0.75 | 0.51 | 8.43 | 3.23 | 1.93 | 1.47 | 1.11 |
| UDS1 | 7.52 | 2.47 | 1.18 | 0.89 | 0.61 | 8.59 | 4.78 | 2.40 | 1.83 | 1.38 |
| UDS2 | 11.08 | 3.28 | 1.57 | 1.11 | 0.82 | 13.00 | 5.01 | 2.90 | 2.25 | 1.85 |
| UDS3 | 10.25 | 2.47 | 1.11 | 0.72 | 0.50 | 11.05 | 4.49 | 2.37 | 1.70 | 1.29 |
| UDS4 | 8.68 | 2.62 | 1.47 | 1.15 | 0.78 | 9.74 | 3.73 | 2.47 | 1.99 | 1.31 |
| UDS5 | 9.24 | 2.85 | 1.72 | 1.34 | 0.80 | 10.53 | 4.11 | 2.64 | 2.35 | 1.78 |
| UDS1 | 10.81 | 3.57 | 1.93 | 1.41 | 0.93 | 12.19 | 4.66 | 2.83 | 2.31 | 1.57 |
| UDS2 | 15.82 | 4.26 | 2.15 | 1.54 | 1.07 | 16.89 | 6.88 | 4.34 | 3.43 | 2.96 |
| UDS3 | 13.65 | 3.15 | 1.57 | 1.13 | 0.86 | 15.16 | 5.38 | 2.88 | 2.20 | 1.74 |
| UDS4 | 15.43 | 5.02 | 2.56 | 1.92 | 1.30 | 18.18 | 7.19 | 4.23 | 3.27 | 2.23 |
| UDS5 | 13.40 | 5.27 | 1.84 | 1.29 | 0.72 | 13.72 | 8.52 | 3.35 | 2.58 | 1.56 |
| Strains(%) | 0.2 | 1 | 2 | 2.5 | 5 |
|---|---|---|---|---|---|
| 150 kPa | |||||
| UDS1 | 12.40 | 13.24 | 11.05 | 10.41 | 11.27 |
| UDS2 | 13.19 | 14.43 | 12.70 | 11.12 | 10.47 |
| UDS3 | 12.22 | 13.54 | 11.59 | 10.09 | 9.23 |
| UDS4 | 12.21 | 14.01 | 12.47 | 11.07 | 11.06 |
| UDS5 | 13.20 | 15.30 | 12.67 | 10.88 | 10.82 |
| 200 kPa | |||||
| UDS1 | 9.84 | 14.47 | 13.42 | 13.43 | 15.76 |
| UDS2 | 13.63 | 14.73 | 12.08 | 10.34 | 9.59 |
| UDS3 | 13.85 | 14.26 | 11.31 | 9.74 | 9.73 |
| UDS4 | 13.45 | 14.37 | 12.81 | 11.51 | 11.72 |
| UDS5 | 13.76 | 13.92 | 12.34 | 11.31 | 11.62 |
| 300 kPa | |||||
| UDS1 | 12.97 | 15.61 | 14.41 | 13.04 | 13.17 |
| UDS2 | 13.78 | 14.87 | 12.73 | 11.23 | 11.80 |
| UDS3 | 15.33 | 15.25 | 11.97 | 9.92 | 9.41 |
| UDS4 | 12.68 | 14.53 | 13.29 | 12.65 | 14.77 |
| UDS5 | 12.79 | 15.36 | 12.42 | 10.87 | 10.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.S.A.; Asif, A.R.; Ahmed, W.; Islam, I.; Waseem, M.; Janjuhah, H.T.; Kontakiotis, G. Determination of Dynamic Properties of Fine-Grained Soils at High Cyclic Strains. Geosciences 2023, 13, 204. https://doi.org/10.3390/geosciences13070204
Shah SSA, Asif AR, Ahmed W, Islam I, Waseem M, Janjuhah HT, Kontakiotis G. Determination of Dynamic Properties of Fine-Grained Soils at High Cyclic Strains. Geosciences. 2023; 13(7):204. https://doi.org/10.3390/geosciences13070204
Chicago/Turabian StyleShah, Syed Samran Ali, Abdul Rahim Asif, Waqas Ahmed, Ihtisham Islam, Muhammad Waseem, Hammad Tariq Janjuhah, and George Kontakiotis. 2023. "Determination of Dynamic Properties of Fine-Grained Soils at High Cyclic Strains" Geosciences 13, no. 7: 204. https://doi.org/10.3390/geosciences13070204
APA StyleShah, S. S. A., Asif, A. R., Ahmed, W., Islam, I., Waseem, M., Janjuhah, H. T., & Kontakiotis, G. (2023). Determination of Dynamic Properties of Fine-Grained Soils at High Cyclic Strains. Geosciences, 13(7), 204. https://doi.org/10.3390/geosciences13070204










