Abstract
This work presents an analysis of data obtained through unique laboratory experiments on hydraulic fracturing. In the experiments, sufficiently large artificial samples were used to model a reservoir. Thus, it was possible to simulate several wells simultaneously, given that hydraulic fracture was initiated in one of them. In addition, the setup construction provided a true triaxial stress–strain state. The setup allowed us to investigate parameters that are difficult to access in real conditions. The data processing based on six laboratory experiments on hydraulic fracturing showed discrepancies between the values of the minimum stresses calculated from the fracture closure pressure and the actual values known based on the experimental conditions. There was also a discrepancy between the theoretical values of the fracture breakdown pressure and those obtained through the experiments. This paper examines phenomena such as backstress as the main reasons for this discrepancy. Backstress is stress acting on the walls of a fracture or well and is caused by the filtered hydraulic fracturing fluid. The authors demonstrated that by taking into account this phenomenon, one can significantly reduce the differences between calculated and experimental values. Therefore, the authors call for the careful use of the standard theory when determining the stress state in real fields.
1. Introduction
The hydraulic fracturing process involves fracture initiation in the oil-saturated reservoir, induced by pumping pressurized fluid into the reservoir through a specially drilled well. The interaction of the expanding fracture with the surrounding rock remains of interest to researchers.
Numerous papers describe studies of hydraulic fracture propagation using both of the earliest two-dimensional models [1,2,3,4], which are still popular, and three-dimensional models [5,6,7,8]. Fracture initiation and propagation are influenced by stress distribution in the reservoir under development [9,10,11]. To carry out hydraulic fracturing correctly, it is important to know the principal stresses acting on the undeformed formation [12]. Therefore, there are various methods used to determine these values using the analysis of borehole data. Some methods are based on the analysis of the pressure–time dependence function obtained from the well during mini-hydraulic fracturing of the base.
In addition to the impacts of the tectonic stresses on hydraulic fracture initiation and propagation, fracturing fluid filtration and formation poroelasticity may affect fracturing. The main objective of our study was to evaluate the impacts of the poroelastic effects on the estimation of the minimum horizontal stress and formation breakdown pressure.
The previous works [13,14,15,16,17,18,19] considered the influence of the poroelastic effect on the development of hydraulic fracturing and associated processes. These studies analyzed whether poroelastic stresses resulting from the diffusion of hydraulic fracturing fluid pressure into the surrounding permeable formation (backstress) affect the fracture dimensions, the process of propagation, and the stress distribution. The authors of [17,18,19] undertook analytical backstress value determination, showing a decrease in the fracture length and increase in the fracture width due to the backstress effect using numerical simulations. The studies in [20,21,22] analyzed the influence of the backstress effect on the mini-mum confining pressure, assumed to be equal to the fracture closure pressure. The studies in [23,24] investigated the impact of the backstress effect on the value of formation breakdown pressure.
However, it is impossible to observe fracture shape modifications in the real field. It is also complicated to estimate the stress–strain state in the near-wellbore or near-fracture zone in the real field under development. There are studies that present the different approaches to hydraulic fracturing modeling considering the backstress effect. In these studies, there is no comparison of the computer simulation results with the experimental models. The current study presents an analysis of the results of a series of unique laboratory experiments on hydraulic fracturing. The main advantage of these experiments is that we knew the exact initial stress–strain state of the sample. Moreover, it was possible to conduct classical well tests based on records of pressure changes in the well. The main contribution of this work is that it allows one to estimate the backstress impact on the stress field realized in the model sample. In the course of this work, the backstress values were estimated analytically. It was concluded that the backstress effect significantly influences fracture initiation and the existing stress distribution in the undeformed formation near the wellbore and fracture zone. Thus, the consideration of backstress diminishes the discrepancy between the theoretically calculated values of minimum principal stress and pressure and the known values from the borehole data and conditions of the laboratory experiments.
2. Laboratory Experiments on Hydraulic Fracturing
To investigate the process of hydraulic fracturing, a series of laboratory experiments were conducted. Figure 1 shows the unique setup used to simulate the process of fracture formation in the area of the well into which the fluid is injected [25]. This experimental setup differs from the usual equipment designed for testing cores or cubic samples and intended for experiments with samples in disk form, which allow one to measure the pore pressure distribution through the sample. The setup design consists of two steel disks with a wide ring between them. The lower disk and the ring wall, as a whole form, a working chamber with the following dimensions: diameter—43 cm, height—6.6 cm. The model sample of the formation is separated from the upper disk of the setup with a rubber membrane. In this study, the setup is considered as a layered medium, i.e., a permeable layer, in which fracture propagation occurs, surrounded by the impermeable walls of the setup.
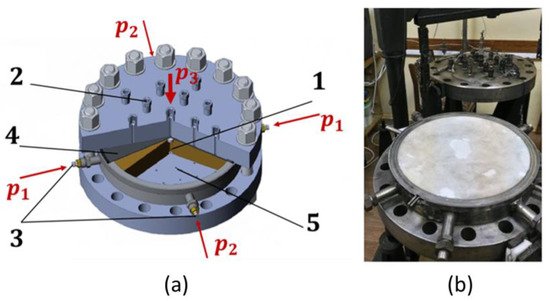
Figure 1.
A schematic illustration of the experimental setup (a) (P1, P2, and P3—the loads applied to the model sample in the experiment; 1—central borehole, 2—vertical pressure port, 3—horizontal pressure ports, 4—rubber membrane, 5—pore-pressure-metering ports). An actual photo of the setup (b).
The central well is a brass tube (diameter 16 mm) hermetically inserted into the lower disk cover of the setup and sealed with a screw plug at the upper end. The tube has a vertical slot in the middle part, into which a thin brass gauze folded in half is inserted. The brass gauze serves as a seed for the fracture. The size of the gauze petals is 8x8 mm. The tube can rotate freely around the vertical axis so that it is possible to orient the fracture perforation in a given direction. The construction of the setup allows one to simulate two types of hydraulic fractures: vertical fractures (along the vertical well) and horizontal fractures (perpendicular to the well). This study focuses on vertical experimental hydraulic fractures.
The modeling materials and fluids were selected in such a way that the propagation of the hydraulic fracture in the laboratory experiment was similar to its propagation in a real field. Similarity criteria were used to achieve similarity between the processes in laboratory and real-world models [25,26]. A mineral oil and mixture of gypsum and cement are the most suitable materials for modeling fracturing fluid and formation. The essential characteristics of the modeling material are Young’s modulus E = 4 × 109 Pa, Poisson’s ratio ν = 0.25, porosity φ = 0.4, permeability k = 2 × 10−15 m2, and the fracturing fluid, characterized by viscosity µ = 0.12 Pa·s.
The laboratory experiments on hydraulic fracturing included several conditional stages. Initially, a modeling material is poured into the working chamber of the experimental setup. The dimensions of the working chamber determine the dimensions of the model sample. The resulting porous sample is saturated with a solution of gypsum in water. Therefore, there is an initial pore pressure P0 in the model sample. After that, the setup is closed, the model sample is loaded, and the fracturing fluid, or more precisely, the mineral oil, is injected into the preliminary prepared well at a constant flow rate. As a result, a hydraulic fracture is formed. Hydraulic fracturing was carried out after a stable pore pressure distribution in the sample was established.
The lithostatic pressure in the reservoir model is simulated by filling the gap between the top disk cover and the rubber membrane with water under constant pressure. Horizontal loading on the model sample is carried out by pumping gas or fluid into flat copper chambers located along the inner surfaces of the ring wall of the working chamber.
It is important to note that the horizontal stresses used in further calculations are the calculated horizontal stresses σmin* acting on the central region of the sample. They consider the applied horizontal loads and the friction between the model sample and the metal covers. The authors conducted a three-dimensional geomechanical simulation of the stress distribution in the model sample stresses with all the boundary conditions determined from the experimental data. As a result, the correct stress–strain state, specifically the principle minimum stress acting on the sample [5], was determined. The authors simulated the sample itself and the lower disk of the installation in the simulator (Figure 1). Two horizontal loads, P1 and P2, were uniformly applied to the lateral surface of the sample in perpendicular directions. The vertical load P3 was also uniformly applied to the upper surface of the sample. The lower base of the installation was fixed in all directions. At the contact plane between the model sample and the lower cover disk, the dry friction was established with the coefficient. The coefficient of friction was taken as the standard for the metal–rock interaction. The calculated minimum stress is uniform in the central region of the sample, which is important for understanding the processes taking place in the experiment. Since there is friction between the sample and the bottom of the installation, the values of the main horizontal stresses depend on the vertical load and significantly exceed the values of the horizontal loads.
A series of six laboratory experiments on hydraulic fracturing were carried out. As a result, vertical fractures were formed. The obtained curves have a characteristic pattern [27]. Provided that the fluid is pumped at a constant rate, there is an approximately linear increase in pressure over time until it comes close to the peak. The subsequent non-linearity corresponds to the first appearance of leaks, which can also be considered as the moment of fracture initiation. The point of maximum pressure on the graph corresponds to the moment of fracture formation. Thereafter, there is a pressure drop to a value called the fracture propagation pressure. There is a further rapid pressure drop to the fracture closure pressure after terminating the fluid injection into the well. Thus, experimental formation breakdown pressures were determined from these pressure curves.
The results of experimental data processing are shown in Table 1. This table contains some characteristics for each experiment, such as the fluid injection rate Q, the initial pore pressure in the model sample P0, the vertical and horizontal loads P1, P2, and P3, the minimum stress σmin* acting uniformly on the central region of the model sample, and the formation breakdown pressure FBP.

Table 1.
The principal characteristics of the laboratory experiments on hydraulic fracturing.
3. Methods
The main objects of study are the borehole, the area near the borehole, and the stress field in this area before, during, and after hydraulic fracturing.
The theoretical estimation of some values promotes the investigation of the real stress field in the formation. The evaluation of parameters such as the formation breakdown pressure and the minimum stress acting on the formation was the main aim of this work. In the course of the study, the experimental data were analyzed.
3.1. The Minimum Formation Stress Estimation
According to the commonly accepted theory [28], the fracture closure pressure is equal to the minimum tectonic stress.
In order to examine this theory using the experimental data, additional processing of the experimental data was conducted. For our study, we used a method of fracture closure pressure calculation based on the pressure variations described in Nordgren [3] and Nolte [29]. This method is based on a comparison of the pressure behavior, the first pressure derivative, and a semi-logarithmic pressure derivative depending on the G-function [30,31].
According to the G-function method, the moment of fracture closure is identified using three curves, namely, the pressure curve, the curve of the first derivative of pressure versus G-function (∂p/∂G), and the semilog derivative of pressure versus G-function (∂p/∂(ln(G) = G∂p/∂G). Since this method was applied to data obtained during the period after the fluid injection shut-in, we assumed that the fluid filters into the reservoir at a constant rate. Consequently, a semi-logarithmic derivative curve before the moment of fracture closure behaves in the manner of a straight line passing through the origin of the coordinates [32], and the moment of fracture closure is defined as the deviation of the semi-logarithmic pressure derivative curve from the straight line passing through the origin of the coordinates. The accuracy of the identification of the closure moment obtained from the semi-logarithmic curve is verified based on whether or not the first pressure derivative curve has a horizontal part at this moment, which, in turn, corresponds to the second derivative of pressure versus G-function, being equal to zero, and may look like a local extremum or an inflection point on the curve of dependence of the first pressure derivative on the G-function. As the G-function method is based on the assumptions that the rate of fluid flow in a reservoir is constant and the surface area of edges remains unchanged during fracture closure, which is not always true, it results in a deviation of the semi-logarithmic derivative curve from the straight line. The curve can deviate up or down from the straight line, depending on the kind of assumption failure.
We used the G-function method to process the obtained time dependencies of pressure (Figure 2), i.e., we plotted the pressure curves, the first pressure derivative, and semilog pressure derivative depending on G-function. The first peak after the ISIP point on the first derivative and semilog derivative curves corresponds to the influence of injection shut-in and was not taken into account. Based on the characteristic behavior of the curves described above, we determined the pressure and the time of fracture closure, shown in the graphs with the vertical dashed yellow line.
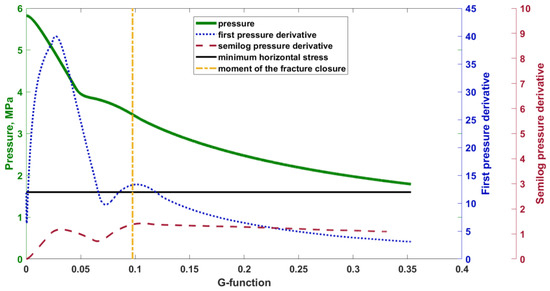
Figure 2.
Curves of different pressure functions depending on the G-function, resulting from the processing of the data obtained during a laboratory experiment on the formation of a vertical fracture.
The results of the theoretical estimation is presented in Table 2.

Table 2.
A comparison of the experimentally obtained and theoretically calculated values of the minimum principle stress.
The estimates of fracture closure pressure given in Table 2 are not equal to the minimum stress in the sample, which contradicts the general theory [28]. However, this assumption of equality applies only to ideal impermeable and homogeneous rocks, while for permeable rocks, some additional effects on the media should be considered.
3.2. Formation Breakdown Pressure Estimation
There are several approaches for estimating the hydraulic formation breakdown pressure [21,24,33]. Since the object of investigation is the near-wellbore stress field, it is necessary to mathematically interpret the distribution of the horizontal stresses around the circular wellbore. For this purpose, the classical Kirsch problem [34] solution for stress concentration around a circular hole [35] is used. This distribution is written for a formation with pore pressure P0, fracturing fluid pressure Pw, and in situ horizontal stresses SH and Sh acting far from the well. Note that for poroelastic medium effective stresses σH and σh, one uses the Terzaghi representation (σH = SH − P0, σh = Sh − P0). Compressive stresses are considered as positive hereafter, SH ≥ Sh. The effective stresses σrr, σθθ, and τrθ form around the circular hole with an inner pressure of Pw in a plane subjected to biaxial compression with SH and Sh, and the pore pressure P0 corresponds to a state in the vicinity of an ideal vertical well. The effective stresses σrr, σθθ, and τrθ have the form in the polar coordinate system, represented by the equation below.
Here, r and ϑ are coordinates in a polar coordinate system with the origin coinciding with the center of the borehole, ϑ is the angle from the location to SH; and R is the radius of the borehole.
A part of the classical Kirsch problem solution was used in [24] to check the stress state at the borehole wall for the case of r = R. In the framework of that study, the equation for breakdown pressure estimation was derived. The equation for σθθ was rewritten (Equation (2)) considering the fact that the fracture initiates and propagates perpendicular to the direction of action of the minimum main stress (ϑ = 0°). It was also assumed that the fracture initiation occurs whenever the minimum principal stress becomes tensile and its modulus exceeds the uniaxial tensile strength of the rock mass UTS:
where Pw* corresponds to pressure in the well resulting in fracture initiation or fracture breakdown pressure FBP, α is Biot’s coefficient, and ν is Poisson’s ratio. A rearrangement of Equation (2) leads to the following breakdown pressure equation:
For further calculations of the breakdown pressure, knowledge of the material characteristics is essential. The modeling material used in the series of six laboratory experiments on vertical hydraulic fracture formation was a mixture of gypsum and cement saturated with a gypsum solution in water. Since the modeling material was not a substance with standard characteristics, there was a need to estimate the single-axis tensile strength (UTS) of this compound. The method used for UTS determination is presented below.
According to some sources [36,37,38,39], the UTS value can be determined by identifying the reopening pressure of the hydraulic fracture. These studies asserted that it is not necessary to overcome the tensile strength of the medium in the course of repeated fracturing, because the fracture already exists. Therefore, repeated fracturing is considered to be another applicable method for determining the tensile strength by subtracting the breakdown pressure of the reopened fracture from the breakdown pressure of the primary fracture (Figure 3). Since the observed effects in the near-well zone are the same in both stages of the experimental series, the determined values of formation breakdown pressure and fracture reopening pressure will include the backstress effect. Backstress is taken into account in both pressure values, but when subtracting these values from one another, backstress is reduced.
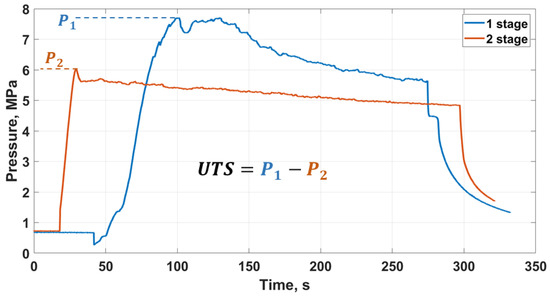
Figure 3.
The dependence of pressure on time in a well with hydraulic fracturing for the primary and repeated hydraulic fracturing.
In the framework of this study, two two-stage experiments were conducted to determine the UTS value. The first stage was a standard laboratory experiment on hydraulic fracturing, as described above. The second stage involved re-conducting hydraulic fracturing to expand the existing fracture. The loading parameters of the samples and the results of the tensile strength calculations are shown in Table 3.

Table 3.
Results of the tensile strength, defined using two-stage laboratory experiments on hydraulic fracturing.
The corrected tensile strength value is 2.07 MPa. This tensile strength value was used in further calculations, as it was considered to be more accurate under the conditions of hydraulic fracturing.
The theoretical calculations of the formation breakdown pressure obtained using Equation (3) are presented in Table 4.

Table 4.
A comparison of the experimentally obtained and theoretically calculated values of the hydraulic formation breakdown pressure.
As can be seen from the comparison of the experimental and calculated values of the formation breakdown pressure, the discrepancy in the values is significant. The possible influence of the experimental setup design on the laboratory measurements of the formation breakdown pressure was investigated. The adjusted values of the minimum stress acting on the model sample were obtained through the model reservoir simulation.
4. Modified Methods: Considering the Backstress Effect
Since, in both cases, the theoretical estimations differ from the experimental values, the authors suggest considering the effect of the reverse stress acting on the model sample due to the filtration of fracturing fluid from the well into the model sample. In some sources, this effect is called backstress [15,16,17,18,19,20,21,22].
Several studies [19,40,41,42] describe recent investigations of backstress influence on the development of a hydraulic fracture. In these studies, the concept of backstress is presented as additional compressive stress acting to close the fracture by increasing the pore pressure of the fluid in the vicinity of the hydraulic fracture. This additional stress appears in the fractured formation due to the filtration of fracturing fluid from the closed fracture into the near wellbore region. The circular layer around the well on which the backstress effect is acting can be quite thin (Figure 4). The analysis of its size and evolution during fluid filtration deserves specific study. However, in this study, we assume that all the estimations are made in this thin area.
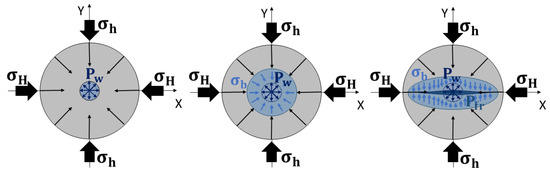
Figure 4.
Schematic illustration of the near-wellbore area where the backstress effect appears due to fluid leakage from the well or closed fracture.
It is possible to estimate the zone into which the fracturing fluid is leaked. Figure 5 illustrates the fracturing fluid leakage into the model sample in one of the laboratory experiments (top view). The borehole in the model sample in which the hydraulic fracture formed is shown in the right part of the picture. The model sample was divided in the direction of fracture growth. Thus, the lower boundary of the area, highlighted with a mint-green line, corresponds to the fracture. The mint-green line outlines the area of fluid filtration during hydraulic fracturing. The further penetration of the fracturing fluid occurred after the hydraulic fracturing.

Figure 5.
Illustration of fracturing fluid leakage into the model sample in one of the laboratory experiments.
However, during the time period in which the minimum tectonic stress and fracture pressure of the formation are estimated, the volume of fracturing fluid is mainly concentrated in the near-well zone. Additionally, the backstress effect is considered in this area.
Some works [21,42] have provided a simplified formula for the backstress calculations in cases characterized by longer times for stationary mode establishment:
where α—Biot’s coefficient (α = 0.7), ν —Poisson’s ratio (ν = 0.25), and Pfr—the average pressure in the fracture at the moment of injection termination.
The hydrodynamic issue of flow in the fracture and filtration in the formation was not considered, since the study mainly aimed to assess the backstress effect on the fracture closure pressure. Therefore, the pressure in the fracture is considered to be constant and equal to the mean value of the pressure in the borehole (at the center of the model sample) and the pressure at the tip of the fracture. We registered the pressure change in the well over time. The pressure at the tip is considered to be equal to the fracture closure pressure.
Equation (4) is proposed for the case of one permeable layer representing a hydrocarbon reservoir between two impermeable layers preventing the fracturing fluid from filtrating into upper and lower layers [20,21,22].
4.1. The Minimum Stress Estimation
Considering the backstress effect, Equation (1), for minimum principle stress estimation, is represented as follows:
The application of Equation (4) to backstress calculations in Equation (5) is considered to be correct, since the laboratory experimental setup can be represented as a layered medium, where the model material acts as a permeable layer and the steel upper and lower covers act as impermeable layers of the medium surrounding the permeable one. It is important to note that some papers [21,43,44] have proved that for the vertical fracture model, the backstress value is calculated using the formula in Equation (4) if the reservoir has impermeable boundaries on both sides.
4.2. The Formation Breakdown Pressure Estimation
As can be seen from Equation (2), Haimson, in the theory of breakdown pressure estimation, already considered the so-called backstress. Initially, in his studies, Haimson observed the similarity between the theories of thermoelasticity and poroelasticity. More precisely, Haimson observed similarity between the classical Kirsch problem solution for stress concentration around a circular hole [35] and the solution to the issue of stress distribution in the formation due to the heating of an infinite cylinder. The term for backstress in the theory of poroelasticity was introduced, similar to the term for the initial heating of an object in the theory of thermoelasticity [45].
The term that was proposed by Haimson is written for an infinite cylinder. We suggest doubling this value, because in laboratory conditions, we have a cylinder with exact dimensions that is surrounded by an impermeable material.
Additionally, in Haimson’s approach to the formation breakdown pressure estimation, one ignores the possibility of the influence of changing pore pressure on the well wall. In order to take this effect into consideration, Schmitt proposed rewriting the Terzaghi equations for effective stresses in the following form: σH = SH − βP0, σh = Sh − βP0, SH ≥ Sh, where β—pore pressure coefficient (0 ≤ β ≤ 1).
Thus, Equation (4) has the following form:
A rearrangement of Equation (4) leads to the following form of the breakdown pressure equation:
5. Results
5.1. The Minimum Principal Sample Stress Estimation
The data presented in Table 5 confirm the assumption that the discrepancy in the theoretical (σmin*) and experimental (Pcl) values of minimum horizontal stress is due to an additional effect. The backstress effect, taken into consideration here, decreased the observed deviation.

Table 5.
A comparison of the experimentally obtained and theoretically calculated values of the minimum principal stress.
To analyze how backstress influences hydraulic fracture closure, we compared the minimum stress values calculated in each experiment with and without taking account of backstress, with the fracture closure pressure, according to the commonly accepted theory, being equal to the minimum stress in the sample σmin* (Figure 6).
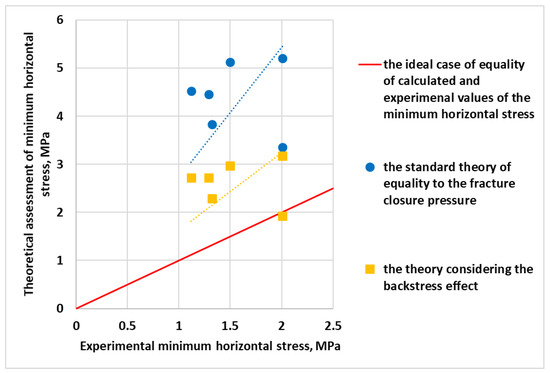
Figure 6.
Comparison of the results of calculations of the minimum horizontal stress using different approaches for theoretical estimation.
As can be seen from the results of the comparison, the backstress effect, which we considered when calculating the minimum horizontal stress, reduces the discrepancy in the experimental and theoretical data. The obtained estimates prove that the modified theory for minimum horizontal stress determination considering the backstress effect is more appropriate.
5.2. Formation Breakdown Pressure Estimation
The data presented in Table 6 show that the discrepancy in the theoretical and experimental values of the minimum horizontal stress is due to an additional effect. The backstress effect, taken into consideration here, decreased the observed deviation in the values. The results of the theoretical estimates of formation breakdown pressure are presented in Table 6.

Table 6.
Experimental values of formation breakdown pressure and theoretical estimates made for different boundary conditions (UTS = 2.7 MPa).
Figure 7 shows that the best results are obtained using the modified theory. The joint consideration of the backstress effect [24] and the modified expressions for effective stresses [23] for a material with vanishing porosity had a significant impact on the resulting theoretical estimations of the fracture breakdown pressure. The use of the adjusted uniaxial tensile strength also contributes to a reduction in the difference between the theoretically calculated values of the formation breakdown pressure and the experimental ones, although the previous two modifications contribute the most to the results.
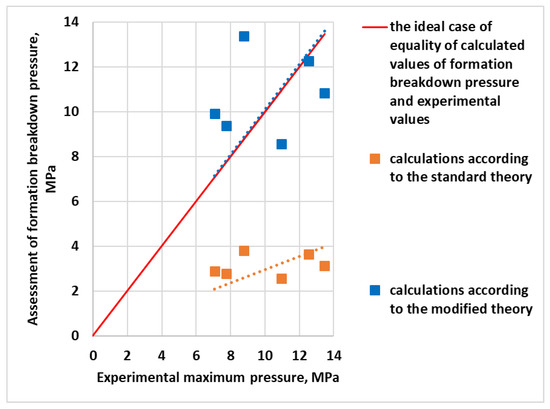
Figure 7.
Comparison of the results of calculations of the maximum pressure using different approaches for theoretical estimation.
6. Discussion
Considering the modification introduced into the standard theory of formation breakdown pressure estimation, a parameter of vanishing porosity was proposed. IT was claimed that parameter β depends on rock porosity; it was suggested to be close to unity for highly porous rocks and to vanish for rocks with vanishing porosity. According to our understanding, this parameter can be altered due to the redistribution of fluid in the rock mass surrounding the well: the filtration of highly viscous hydraulic fracturing fluid into the medium surrounding the well reduces the effective porosity and permeability after the replacement of the reservoir fluid with a fracturing fluid with a lower viscosity. Tensile failure occurs near the wellbore, and when this layer has a non-zero size, the effective stresses determined by the parameter β must be used in the tensile failure law. This leads to an increase in the effective stresses and a corresponding increase in the pressure in the well required to initiate tensile failure.
Figure 8 shows the influence of parameter β on the formation breakdown pressure. The latest theory shows the best level of agreement with the experimental data at β = 0.35. The variation in parameter β shows that the FBP value tends to increase when the porosity of the material decreases. The modeling material’s porosity is quite high (about 40%) in the laboratory experiments, but when filling the impacted zone with the fracturing fluid, the porosity becomes lower. The mean value of the resulting vanishing porosity parameter was chosen.
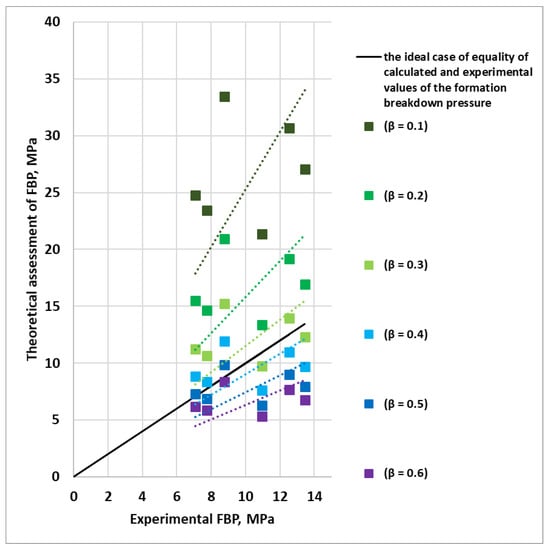
Figure 8.
Comparison of the results of calculations of the fracture breakdown pressure using different approaches for theoretical estimation.
Figure 8 shows that the material characteristics can significantly affect the effective stresses realized in the formation and the resulting value of the formation breakdown pressure. Consequently, the use of the pore pressure coefficient β can be considered as a fairly reasonable step.
In this part of the study, we estimated the possible impact of a “poro-effect” of backstress on hydraulic fracture initiation and propagation in laboratory experiments. However, it is essential to note that the initial and boundary conditions in the laboratory experiments were similar. There is a need to investigate the impacts of additional different loading conditions on the processes in the model sample during hydraulic fracturing for more accurate calculations.
7. Conclusions
This study considered the standard theories based on theoretical estimations of two different values: the minimum horizontal stress and the formation breakdown pressure. The methods were applied to laboratory data obtained through experiments on hydraulic fracturing. The comparison of the experimental values with the obtained calculations confirmed the accuracy of these approaches. Both approaches showed a notable discrepancy between the theoretical and experimental data.
The authors of the study suggest that this discrepancy appears due to side effects in the model sample with the hydraulic fracture. In particular, the backstress effect was considered. This effect can be represented as additional compressive stress appearing in the near-wellbore region due to the filtration of fracturing fluid from the well or the closed fracture into the surrounding area.
Consideration of the backstress effect when calculating the minimum horizontal stress and the formation breakdown pressure significantly reduced the observed discrepancy in the experimental and theoretically calculated values. The analysis of the obtained estimates proves that these modifications markedly impact the resulting calculations. This is justified by the fact that the processes under investigation here occur in a region saturated with filtered fluid. Thus, side effects associated with fluid filtration should be taken into consideration.
Author Contributions
Supervision, conceptualization, S.B.T.; methodology, supervision, resources, writing—review and editing, M.A.T.; methodology, data curation, validation, formal analysis, resources, writing—original draft preparation, visualization, E.V.N.; investigation, methodology, data curation, E.V.Z. and P.E.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out within the scope of state assignment by the Ministry of Science and Higher Education of the Russian Federation (theme No 122032900167-1).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Perkins, T.K.; Kern, L.R. Widths of Hydraulic Fractures. September 1. Soc. Pet. Eng. 1961, 10, 937–949. [Google Scholar] [CrossRef]
- Khristianovic, S.A.; Zheltov, Y.P. Formation of vertical fractures by means of highly viscous liquid. In World Petroleum Congress Proceedings; OnePetro: Richardson, TX, USA, 1955; pp. 579–586. [Google Scholar]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Borisov, V.; Ivanov, A.; Kritskiy, B.; Menshov, I.; Ramazanov, M.; Savenkov, E. Fully coupled numerical simulation techniques for 3D hydraulic fracturing. J. Phys. Conf. Ser. 2018, 1141, 012085. [Google Scholar] [CrossRef]
- Adachia, J.; Siebritsb, E.; Peircec, A.; Desrochesd, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Gravouil, A.; Moës, N.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets—Part II: Level set update. Int. J. Numer. Methods Eng. 2002, 53, 2569–2586. [Google Scholar] [CrossRef]
- Moes, N.; Gravouil, A.; Belytschko, T. Extended finite element and level set methods for non-planar 3D crack growth. In IUTAM Symposium on Computational Mechanics of Solid Materials at Large Strains; Springer: Dordrecht, The Netherlands, 2003; Volume 108. [Google Scholar] [CrossRef]
- Afanasyev, I.S.; Nikitin, A.N.; Latypov, I.D.; Haidar, A.M.; Borisov, G.A. Hydrofracturing crack geometry prediction. Oil Ind. J. 2009, 11, 62–66. [Google Scholar]
- Berchenko, I.E.; Detournay, E. Deviation of hydraulic fractures through poroelastic stress changes induced by fluid injection and pumping. Int. J. Rock Mech. Min. Sci. 1997, 34, 1009–1019. [Google Scholar] [CrossRef]
- Hagoort, J.; Weatherill, B.; Settari, A. Modeling the Propagation of Waterflood-Induced Hydraulic Fractures. Soc. Pet. Eng. J. 1980, 20, 293–303. [Google Scholar] [CrossRef]
- Zoback; Mastin, L.G.; Barton, C.A. In-situ stress measurements in deep boreholes using hydraulic fracturing, wellbore breakouts, and stonely wave polarization. In Proceedings of the ISRM International Symposium, Stockholm, Sweden, 31 August–3 September 1986. [Google Scholar]
- Papanastasiou, P. The influence of plasticity in hydraulic fracturing. Int. J. Fract. 1997, 84, 61–79. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. The influence of the cohesive process zone in hydraulic fracturing modelling. Int. J. Fract. 2011, 167, 33–45. [Google Scholar] [CrossRef]
- Linkov, A. On decaying influence of initial conditions in the problem of hydraulic fracturing. Dokl. Phys. 2016, 16, 351–353. [Google Scholar] [CrossRef]
- Gladkov, I.O.; Linkov, A.M. Solution of a Plane Hydrofracture Problem with Stress Contrast. J. Appl. Mech. Tech. Phys. 2018, 59, 341–351. [Google Scholar] [CrossRef]
- Kovalyshen, Y. Fluid-Driven Fracture in Poroelastic Medium. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2010. [Google Scholar]
- Kovalyshen, Y.; Detounay, E. Propagation of a Semi-Infinite Hydraulic Fracture in a Poroelastic Medium. In Proceedings of the Fifth Biot Conference on Poromechanics, Vienna, Austria, 10–12 July 2013. [Google Scholar]
- Baykin, A.N.; Golovin, S.V. Modelling of hydraulic fracture propagation in inhomogeneous poroelastic medium. J. Phys. Conf. Ser. 2016, 722, 012003. [Google Scholar] [CrossRef]
- Cleary, M.P. Analysis of mechanisms and procedures for producing favourable shapes of hydraulic fractures. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 21–24 September 1980. [Google Scholar]
- Detournay, E.; Cheng, A.-D.; Roegiers, J.-C.; McLennan, J.D. Poroelasticity considerations in in situ stress determination by hydraulic fracturing. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 507–513. [Google Scholar] [CrossRef]
- Detournay, E. Analysis and Design Methods || Fundamentals of Poroelasticity. Geology 1993, 113–171. [Google Scholar] [CrossRef]
- Schmitt, D.R.; Zoback, M.D. Poroelastic effects in the determination of the maximum horizontal principal stress in hydraulic fracturing tests—A proposed breakdown equation employing a modified effective stress relation for tensile failure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 499–506. [Google Scholar] [CrossRef]
- Haimson, B.C.; Fairhurst, C. In-situ stress determination at great depth by means of hydraulic fracturing. In Proceedings of the The 11th US Symposium on Rock Mechanics (USRMS), Berkeley, CA, USA, 16–19 June 1969. [Google Scholar]
- Trimonova, M.; Baryshnikov, N.; Zenchenko, E.; Zenchenko, P.; Turuntaev, S. The Study of the Unstable Fracure Propagation in the Injection Well: Numerical and Laboratory Modeling. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 16–18 October 2017; OnePetro: Richardson, TX, USA, 2017. [Google Scholar]
- De Pater, C.J.; Cleary, M.P.; Quinn, T.S.; Barr, D.T.; Johnson, D.E.; Weijers, L. Experimental verification of dimensional analysis for hydraulic fracturing. SPE Prod. Facil. 1994, 9, 230–238. [Google Scholar] [CrossRef]
- Gaarenstroom, L.; Tromp, R.A.J.; De Jong, M.; Brandenburg, A.M. Overpressures in the Central North Sea: Implications for trap integrity and drilling safety. Geol. Soc. Lond. Pet. Geol. Conf. Ser. 1993, 4, 1305–1313. [Google Scholar] [CrossRef]
- Hickman, S.H.; Zoback, M.D. The interpretation of hydraulic fracturing pressure-time data for in situ stress determinations. In Proceedings Workshop on Hydraulic Fracturing Rock Stress Measurements; Citeseer: University Park, PA, USA, 1981; pp. 103–127. [Google Scholar]
- Nolte, K.G. Determination of fracture parameters from fracturing pressure decline. In Proceedings of the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 23–26 September 1979. [Google Scholar]
- Barree, R.D. Applications of pre-frac injection/falloff tests in fissured reservoirs-field examples. In Proceedings of the SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 5–8 April 1998. [Google Scholar]
- Barree, R.D.; Barree, V.L.; Craig, D. Holistic fracture diagnostics. In Proceedings of the Rocky Mountain Oil & Gas Technology Symposium, Denver, CO, USA, 16–18 August 2007. [Google Scholar]
- Castillo, J.L. Modified Fracture Pressure Decline Analysis Including Pressure-Dependent Leakoff. In Proceedings of the SPE/DOE Joint Symposium on Low Permeability Reservoirs, Denver, CO, USA, 18–19 May 1987. [Google Scholar]
- Zhang, J.; Yin, S. Fracture gradient prediction: An overview and an improved method. Pet. Sci. 2017, 14, 720–730. [Google Scholar] [CrossRef]
- Kirsh, E.G. Die Theorie der Elastizitat und die Bedurfnisse der Festigkeitslehre. Zantralblatt Verlin Dtsch. Ing. 1898, 42, 797–807. [Google Scholar]
- Paterson, M.S. Experimental Rock Deformation: The Brittle Field; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Rutqvist, J.; Tsang, C.-F.; Stephansson, O. Uncertainty in the maximum principal stress estimated from hydraulic fracturing measurements due to the presence of the induced fracture. Int. J. Rock Mech. Min. Sci. 2000, 37, 107–120. [Google Scholar] [CrossRef]
- Zhang, J.; Roegiers, J.C. Discussion on “Integrating borehole-breakout dimensions, strength criteria, and leak-off test results, to constrain the state of stress across the Chelungpu Fault, Taiwan”. Tectonophysics 2010, 492, 295–298. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Wolff, R.G.; Keys, W.S.; Shuter, E. Hydraulic fracturing to determine the regional in situ stress field, Piceance Basin, Colorado. Geol. Soc. Am. Bull. 1976, 87, 250–258. [Google Scholar] [CrossRef]
- Zoback, M.D.; Rummel, F.; Jung, R.; Raleigh, C.B. Laboratory hydraulic fracturing experiments in intact and pre-fractured rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1977, 14, 49–58. [Google Scholar] [CrossRef]
- Baykin, A.N.; Golovin, S.V. Non-symmetry of a hydraulic fracture due to the inhomogeneity of the reservoir. arXiv 2016, arXiv:161009471. [Google Scholar]
- Baykin, A.N.; Golovin, S.V. Application of the fully coupled planar 3D poroelastic hydraulic fracturing model to the analysis of the permeability contrast impact on fracture propagation. Rock. Mech. Rock. Eng. 2018, 51, 3205–3217. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.H.-D. Plane strain analysis of a stationary hydraulic fracture in a poroelastic medium. Int. J. Solids Struct. 1991, 27, 1645–1662. [Google Scholar] [CrossRef]
- Vandamme, L.M.; Roegiers, J.-C. Poroelasticity in hydraulic fracturing simulators. J. Pet. Technol. 1990, 42, 1199–1203. [Google Scholar] [CrossRef]
- Boone, T.J.; Detournay, E. Response of a vertical hydraulic fracture intersecting a poroelastic formation bounded by semi-infinite impermeable elastic layers. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 189–197. [Google Scholar] [CrossRef]
- Nowacki, W. Thermoelasticity, 2nd ed.; Pergamon: Oxford, UK, 1986. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).