Abstract
Recent studies have shown that giant landslides correlate with climatic variations. However, the precise processes involved in this phenomenon need to be better defined. This study investigates the causes of giant landslides using a modeling approach. Here, I show that the effect of meteoric water infiltration could be distinguished from that of the sea level rise in triggering paleo-landslides. It is possible to identify the cause of coastal paleo-landslides based on the age of occurrence and comparison with climatic signals when glacial maxima are wetter than during interglacial periods, as in Polynesia and East Equatorial Africa, but not in other cases (Caribbean, Indonesia). The role of pore-pressure variations and sea water loading variations is discussed. The interaction between the relative sea level rise, pre-existing relief and deep weak structure due to the presence of highly weathered lavas may trigger the conditions for a large landslide. Highly weathered lavas have very low friction angles in volcanic islands. When volcanoes are still active, pressure fluctuations in the magma chamber caused by sea level lowering are expected to play a significant role in the destabilization of the relief. Competing processes in real cases make it difficult to distinguish between these processes.
1. Introduction
Landslides are one of the main processes that destroy relief and displace material. A dramatic example is the catastrophic Vajont landslide in Italy in 1963 in relation to water-level rise and rainfall increase [1]. Catastrophic landslides are often expected in areas of active seismicity [2] or in the context of significant volcanic activity [3,4]. Volcano slopes are a major concern in terms of civil engineering monitoring and risk prevention because important cities are built on potentially unstable slopes. In the case of active seismicity, the acceleration of the ground surface and subsurface may generate slope destabilization. From a theoretical perspective, the slope stability depends strongly on the mechanical properties of the rocks [5], on the geometry of weakness zones, on the loading and stress conditions [2,6,7,8,9] and on the presence of fluids [1,10,11,12]. In volcanic areas, the interaction between magma reservoirs, magma intrusions, and pre-existing faults influences the deformation of volcanic surfaces [13,14,15] and could generate landslides. Phreatomagmatic processes [16], pore pressure increases due to precipitation [17], and rift zone intrusions [13] are thought to influence slope instability on volcanic edifices. The study of coastal volcanism and volcanic islands is essential to a better understanding of volcanic edifices’ growth, their dismantling mechanism and their activity [18]. Fundamental destabilization processes have been observed in context, such as in Mount Etna, where the slide occurred in response to the loading of the edifice on a weak basement [19], highlighting the significant role of gravitational spreading and sliding on volcanic edifices [20].
From a practical perspective, the present-day slope stability conditions of a volcanic edifice are influenced by factors such as its past eruptive history, possible landslides, faults and fractures, and alteration by fluid circulation, which could have created significant heterogeneities. Such heterogeneities may hide weaknesses and the potential occurrence of slope instabilities [21,22]. Thus the long geological history of old volcanic edifices is expected to produce complex geometries that are often difficult to understand in detail. A complex volcano can be defined by a succession of different eruptive phases that contribute to the building, destroying and re-building parts of the volcano again (Figure 1). On the flanks of volcanoes and in their internal structure, the rocks may consist of fresh or weathered massive lavas, tephra-fall deposits, ignimbrites or low cemented pyroclasts, among other rocks. This study focuses on volcano slope instabilities caused by non-eruptive processes. The volcano could be active or inactive, and the rocks composing the volcano are affected by phreatic activity (i.e., hot water and gas circulation) that would have weakened their mechanical properties. The eruptive history of a volcano, as well as the nature of the constituent rocks of its flanks, must be carefully considered when assessing the slope stability of volcanoes from a geotechnical perspective. These complex scenarios could lead to unfavorable conditions for the stability of the present-day slope and difficulties in taking the spatial heterogeneity of the mechanical parameters into account (Figure 1).
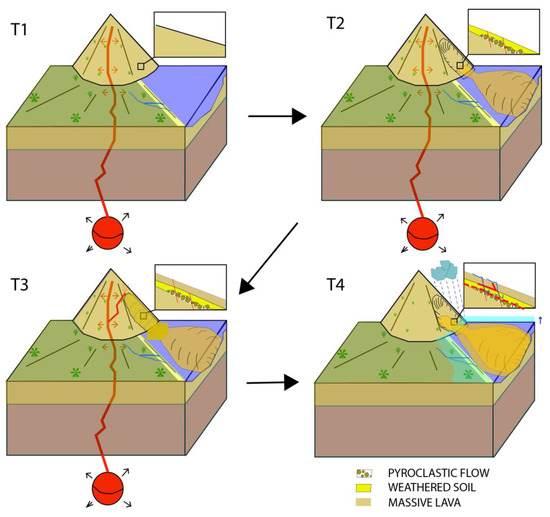
Figure 1.
Complex evolution of volcanic edifices and locations of deep weakness zone, (T1) Young volcanic edifice composed of massive lavas, (T2) Volcanic edifice after a giant landslide caused by a volcanic process, where pyroclastic flows, as well as soil and lava weathering, occur, (T3) Filling of the landslide scar by thick volcanic lavas above the pyroclastic debris and the weathered soils, (T4) Deep rooting of the landslide into the weakness zone favored by meteoric water infiltration and/or sea level loading in the case of an old and complex volcano and/or the presence of deeply incised canyons.
It has been suggested that giant landslides could be correlated with climatic variations [16]. Some studies assume that giant landslides may have occurred during periods of a low stand [23], while others suggest that high stands or sea level rise are more favorable for causing slope instability [24]. This issue remains controversial and poorly studied, despite the expected sea level rise associated with climate warming.
The role of climatic conditions in triggering giant landslides on volcanoes is investigated in this study. The possible occurrence of a giant landslide on a volcano in relation to climatic variations is investigated from a theoretical perspective. The processes favoring instability that are discussed in this study are (i) Sea water loading with relative sea level rise, (ii) Pore pressure changes related to climatic variation, (iii) Rock and soil weathering, (iv) Weakness zone geometries, (v) Pressure fluctuations of the magma reservoir caused by sea level unloading.
2. Method
2.1. Slope Stability Model
In order to analyze the causes of stress that may trigger a giant landslide and to discuss the stability of a given relief, a 2D model was implemented. Two different geometries of the landslide were implemented to compare the role of the geometry of a weakness zone on the theoretical stability of a volcanic edifice. The first geometry (Figure 2A) is based on the Cullman wedge model [25]. Basically, a balance is achieved between the weight of the expected landslide and the resistance force generated by the rock properties [26]. The resistance shear stress along the sliding surface is given by τc = σn tanϕ + C until the landslide occurs, where σn is the normal stress, ϕ is the friction angle of the slope-forming material, and C is the cohesion, and could be used to describe bedded rocks [27]. Considering the angle for which the effective cohesion is maximized for a value equal to β/2 + ϕ/2, it is assumed that θ = β/2 + ϕ/2 [25,28]. This model allows us to calculate the maximum stable height for a simple geometry (Figure 2A):
where H is the maximum stable height of the slope, β is the hillslope gradient, ρr is the bulk rock density, and g is the gravitational acceleration. This model has been widely used in geomorphological studies to predict the maximum unfailed height of slopes [25]. In the theoretical calculation, vertical loading, pore pressure increase and volcanic rock properties with depth are included. Including the pore pressure U and considering the load of the sea water column of thickness Hm with a bulk density of the water ρm, the following can be obtained:
H = 4C·sin β cos ϕ/(ρr g[1 − cos (β − ϕ)])
H2 − 4 H (C sin β cos ϕ − U sin ϕ cos β)/(ρr g [1 − cos (β − ϕ)]) + ρm Hm2/ρr = 0
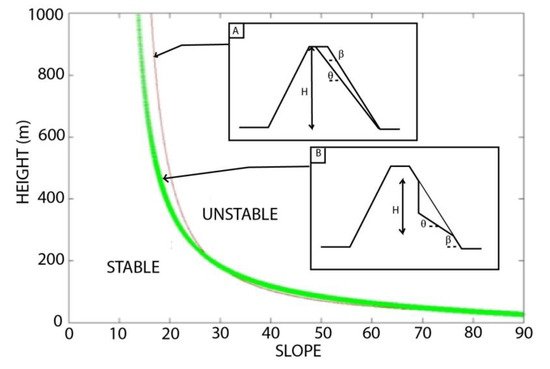
Figure 2.
Effect of the initial slope β on the maximum stable relief H for two different landslide geometries. (A) Cullman wedge model, (B) concave geometry model. ρc = 3000 kgm−3, C = 1 MPa, ϕ = 100.
Equation (2) allows us to estimate the geometry of the maximum stable relief (height and slope) immediately before the collapse, as well as the geometry of the landslide. The thickness of the sea water column considered could include sea level variations related to Quaternary climate variations, but also the relative sea level rise due to subsidence.
Using the same method, it is also possible to calculate the maximum stable height for a second kind of landslide geometry (Figure 2B, concave geometry model) using the following equation:
where H1 can be calculated by resolving the following equation:
H = H1 + H1 cos β sin (β/2 + ϕ/2)/sin (β/2 − ϕ/2)
H12 − 4H1 (C cos ϕ − U sin ϕ)/(ρr g[sin β – sin ϕ])
+ ρm Hm2 sin (β/2 − ϕ/2)/(ρr sin β cos β/2 + ϕ/2) = 0
+ ρm Hm2 sin (β/2 − ϕ/2)/(ρr sin β cos β/2 + ϕ/2) = 0
This study focuses on the role of pore pressure, water loading and mechanical properties of rocks on slope stability. Geotechnical approaches are also useful to evaluate the safety factor FS = resisting forces/driving forces ≈ [τ × S]/[ρr V g sin θ] when the slope is destabilized only by its own weight [6,24,29].
2.2. Mechanical Properties of Volcanic Rocks
There are at least two ways to estimate the effective mechanical properties of rocks in a given geological context. The first method is to use experimental data that describe the mechanical behavior of a rock close to that of the studied area. The second is to propose hypotheses about the causes of failure (i.e., gravity, pore pressure, ground acceleration, eruption) and to estimate the effective values of the mechanical parameters that triggered the observed failure. Here, we verify that the mechanical properties of the rocks estimated using a modeling approach are not in contradiction with experimental data for volcanic rocks.
The parameterization of the model was conducted, assuming that the relief was close to critical stability. The effective mechanical properties of the rocks of the volcanic edifice considered in this numerical experiment were calibrated using some characteristics of a giant landslide that occurred in Tahiti 872 kyrs ago [30,31,32,33]. However, the investigation presented in this study is purely theoretical, and the geometries, as well as the rock heterogeneity, do not represent a real case.
The relief was assumed to have a total height of ~4500 m with an initial slope β of 8–12°. Two different geometries were tested to estimate the maximum stable relief H as a function of the initial slope (Figure 2). The effect of the precise geometry (Cullman wedge model vs. concave geometry model) of the landslide on the critical values of height and the initial slope of the stable relief is not negligible (Figure 2), but this study does not focus on the precise geometry of landslides.
The mechanical properties of volcanic rocks are strongly dependent on their alteration [34] and stress loading. The cohesion and angle of friction were estimated by Rodriguez-Losada et al. [5] for different volcanic rocks under different slope heights. Cohesion C can be obtained using the equation C = kHl, where H is the slope height, and k and l are coefficients determined experimentally for different volcanic rocks [5]. For weathered, massive lavas, k = 0.04 and l varies from 0.41 to 0.60. For weakly cemented pyroclasts, k = 0.05 and l = 0.5. The angle of friction ϕ could also be estimated using the equation ϕ = a ln(H) + b, where a and b are obtained experimentally. Rodriguez-Losada et al. [5] showed that very low friction angles of <13° are obtained at depths >1000 m for low cemented pyroclasts (a = 6; b = 54). A volcanic edifice composed of low cemented pyroclasts has cohesion values between 0.5 and 1 MPa at depths of 1500–3000 m (Figure 3A). At this depth, a theoretical volcanic edifice with weakly cemented pyroclasts has friction angles between 6° and 10° (Figure 3B).
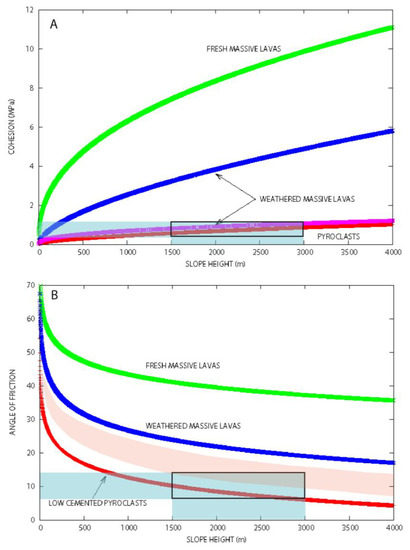
Figure 3.
Effect of depth on mechanical properties. (A) Cohesion for low cemented pyroclasts (k = 0.05; l = 0.5) and fresh (k = 0.37; l = 0.60) and weathered (k = 0.04; l = 0.41 and 0.60) massive lavas, (B) Angle of friction for low cemented pyroclasts (a = 6; b = 54) and fresh (a = 5.6; b = 82) and weathered (a = 7; b = 75) massive lavas.
2.3. Modeling Hydroclimatic Variations
In this study, sea level loading and pore pressure were simulated as a function of climate evolution. The water column loading considered was estimated using a proxy. Sea level is known to change almost simultaneously with δ18O variation [35,36]. A δ18O curve [37] was used to simulate climate forcing. This curve was recalibrated to simulate Quaternary sea level variations reaching an amplitude of 120 m.
Hydroclimatic variations are also caused by Milankovitch astronomic cycles and can be simulated using insolation or δ18O curves [38]. In this study, it is assumed that more humid conditions are capable of causing an increase in the effective pore pressure. The purpose of this assumption is to discuss the timing of potential giant landslides in relation to Quaternary climatic conditions (i.e., precipitation rates). The time required for the water to flow from the surface to a depth of 4.5 km was estimated to be ~150 days in Oregon [39]. In the model, the propagation is considered instantaneous, which is justified on a long time scale (>1 kyr). The amplitude of the variation of the pore pressure ΔP due to water infiltration into the crust is 0.01 MPa at Mt. Hood [39] and 2 MPa on the south flank of Kilauea volcano [17]. In this study, different values for the pore pressure variation were tested in the case where sea level effects are dominant (0 < ΔP < 0.125 MPa) and in the case where pore pressure processes are dominant (0 < ΔP < 0.5 MPa).
2.4. Pressure Variation in the Magma Reservoir
The loading fluctuation caused by sea level variation is ΔLSL(t) = gρm Hm(t).
Sea water unloading, which causes a decrease in lithostatic pressure at depth, enhances magma production [40]. Decompression favors partial melting of the mantle and magma release. The magma production rate DF/Dt at constant entropy S can be estimated as [40,41]:
where PM is the magma reservoir pressure, F is the melt fraction, t is the time, and U is the mean mantle upwelling rate.
DF/Dt = (δF/δPM)S (dPM/dt − U·▽PM)
The magma pressure variation δΔPM/dt can be considered as a function of the seawater unloading variation δΔLSL/dt under adiabatic conditions and for very high viscosity (i.e., ηc=1023 Pa.s) of the crustal rocks. In this case, δΔPM/dt = −δΔLSL/dt.
When the viscous response is not negligible (ηc < 1022 Pa.s; [40]), the equation is δΔPM/dt +ΔPM (Ec/ηc) = −δΔLSL/dt, where Ec is the elastic modulus, and a delay of ~10 kyr after the forcing by sea water unloading is expected.
3. Results
The current question that we attempt to answer focuses on the thresholds and conditions that favor slope instability for volcanic edifices in relation to climate variations.
3.1. Influence of Water Column Loading on Slope Stability
Considering a simple geometry for the expected landslide (Figure 2A, Cullman wedge geometry), the role of sea level variation on slope stability was estimated using Equation (1). As a volcanic island subsides, there is an increase in relative sea level, consequently, an increase in water loading on the slope, which could be significant, enough to trigger a potential landslide.
Under the Cullman wedge geometry condition, an increase in loading by a water column of 120 m causes a slight decrease in the stability height (Figure 4C). The more the increase in water loading, the less the stability. Irrespective of the geometry of the sliding mass, the maximum height of the stable relief is affected by the increase in the loading by a water column of 400 m. A water column increase of 400 m is reached in less than 1 Myr for a moderate subsidence rate (~0.25 mm/yr) contemporaneously with a sea level high of +120 m during an interglacial period. In this case, slope instabilities are observed on higher slopes (>25°) but also on smaller slopes (Figure 4). The role of sea water loading could trigger landslides of smaller dimensions (150–300 m) for higher slopes (25–30°, Figure 4C, dark gray square).
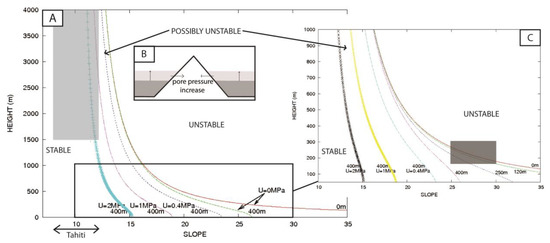
Figure 4.
(A) Effect of increasing pore pressure and sea water loading on the relief stability. The light gray area represents the field where a theoretically stable relief changes to an unstable relief when submitted to an increase in the sea water column loading between 0 and 400 m and an increase in pore-water pressure between 0 MPa and 2 MPa. (B) Schematic representation of the effect of subsidence. (C) The details are as follows: a relief of ~200 m with a slope of 25° < β < 30° could be affected by water loading (dark gray square). ρc = 3000 kgm−3, C = 1 MPa, ϕ = 10° and the geometry of the landslide is identical to those presented in Figure 2A.
3.2. Influence of the Pore Pressure on Slope Stability
Our model suggests that a significant effect of the pore pressure increase on the height of the stable relief could occur (Figure 4). The pore pressure increase significantly reduces the stability of the relief. As expected, the higher the pore pressure is, the lower the maximum height H before the giant landslide occurs. If the pore pressure increases by more than 1 MPa, the slope stability is significantly reduced (Figure 4A,B). A relief of more than 1500 m, with a slope of ~12°, could be affected by landslides under these conditions. Depending on the initial relief H, a pore pressure increase of 1 MPa could cause instabilities of more than 1000 m.
3.3. Competing Influence of Sea Level Loading vs. Pore Pressure Variations over Time on Slope Stability
In this study, the influence of sea level loading and pore pressure variations over time was modeled in relation to meteoric water infiltration. The variation over time of the maximum height H of a volcanic edifice before the occurrence of a giant landslide is shown in Figure 5. The maximum stable height depends on the sea level and on the pore pressure value. Taking into account that the maximum sea level fluctuation during the last million years is ~120 m, and that the amplitude and the timing of the loading are known (Figure 5B), the variation in the maximum stable height H of a theoretical volcano before a giant landslide occurs was calculated. The absolute value of the maximum stable height H depends strongly on the mechanical properties of the rocks and the slope. This issue is not discussed in this study because the focus of this study is on the variation of stability caused by the climatic evolutions.
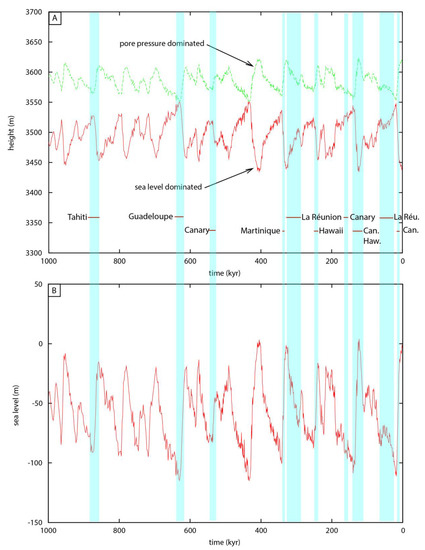
Figure 5.
(A) Maximum height H before the landslide occurred. The geometry of the island is shown in Figure 4. The effects of sea level loading and pore pressure are simulated. The sea water loading depends on the variation in sea level, while the effect of the pore pressure depends on the fluctuation in precipitation. In the first case (sea level-dominated), the pore pressure is considered to range between 0 and 125 kPa depending on the climatic variation. In the second case (pore pressure-dominated), the pore pressure is assumed to range between 0 and 500 kPa depending on the climatic variation. The absolute values of H are indicative, and only the trends are interpreted in this study. g = 9.81 ms−2, C = 1 MPa, ϕ = 10°, ρ = 2800 kg/m−3, β = 7°, and a subsidence rate of 0.25 mm/yr are considered. (B) Simulated sea level variations during the last million years using the δ18O curve of Lisiecki and Raymo [37]. The light blue lines represent the giant landslides on volcanoes during the last 1 Ma of Table 1.
If sea water loading is the main process influencing landslides, then the higher the sea level is, the lower the stability will be. The maximum height H is expected to decrease as the sea level rises (Figure 5). With all other parameters being equal, the maximum stable height H of a volcanic edifice during interglacial periods is 50 m higher than during glacial periods considering the sea water loading is the main parameter influencing the system.
In the specific case of Polynesian climatic variation, where the climate is more humid during glacial maxima [42], as simulated here, the giant landslides generated by a pore pressure increase are expected to occur during glacial periods (Figure 5A). In the specific case of the Polynesian volcanic edifice, the period when the landslides are expected (i.e., the time when the maximum stable height H before a giant landslide is expected to occur) is different when the dominant process triggering the landslide is sea level loading or pore pressure loading (Figure 5A).
The influence of sea level unloading on magma reservoir pressure increases at depth is better correlated than the sea level loading with the occurrence of giant landslides (Figure 5). This may indicate that, in many cases, the volcanoes were active (i.e., a magma reservoir was present at depth). If this process was the cause of the giant landslides, the viscosity of the crust was very high in many cases, except for La Réunion (290–320 kyr; [37]), the Canary Islands (134 ± 6; [3]) and Hawaii (127 ± 10; [43]), where a delay is observed with low sea level. The effect of sea level unloading influence on magma pressure rise is contemporaneous with the effect of pore pressure rise caused by meteoric water infiltration in Polynesia and East Africa (i.e., where precipitation increases during glacial periods).
4. Discussion
4.1. Rock Weathering and Slope Instability
Volcanic edifices are composed of massive lavas as well as non-massive lava, scoria, ash falls and pyroclastic flows, among others. These volcanic products can be highly weathered by the humid climate when they are exposed for thousands or millions of years. Laboratory experiments on weathered, massive lavas show that cohesion can be low (0.8–1 MPa) at depths ranging from 1500 m to 3000 m (Figure 3A).
The angle of friction of weathered, massive lavas is estimated from laboratory experiments [5] to range between 23° and 19° (Figure 3B). Lavas that have been extremely altered by rain and fluid circulation at depth for thousands of years are expected to have mechanical properties lower than those of fresh volcanic rocks. Furthermore, the effective mechanical properties (C and ϕ) of fractured and faulted reliefs are lower than those used for triaxial experiments on unfractured rocks. Effective mechanical properties consider the heterogeneities present in old and complex volcanic edifices, including low-cemented pyroclast and weathered soils. Soil layers can be observed trapped between volcanic lava flows or lava deposits [44]. These soils are expected to have reduced mechanical properties. A sliding bed with distributed soft and hard rock is a fundamental factor underlying translational landslides [21]. The model has been calibrated to be compatible with past giant landslide events (~1500–3000 m thick, initial slope β~8–12°, cohesion C of 0.3–1 MPa, Figure 2), such as the event that occurred in Tahiti, Society Archipelago (Figure 2) [32,33]. The values used here correspond to highly weathered rocks of an old and fractured volcanic edifice or low-cemented pyroclasts that could be interlayered at depth.
Rock mechanical properties C and ϕ decrease over time when exposed to weathering. The more weathering that occurs, the greater the decrease in C and ϕ. During humid periods, this decrease is greater than during dry periods (Figure 6A). In contrast, diagenetic processes are expected to improve the mechanical properties of rocks (Figure 6B). As pressure increases at depth, porosity and connectivity may decrease. In addition, mineralization at depth can also improve rock cohesion in certain cases.
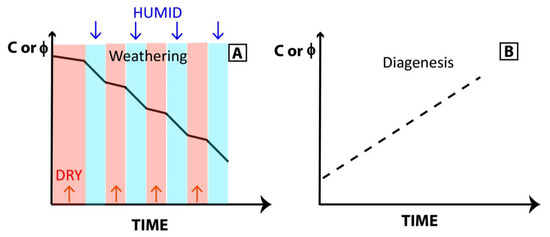
Figure 6.
Influence on the mechanical rock properties C and ϕ of (A) Weathering (B) Diagenesis.
4.2. Weakness Zones and Geological Inheritance
The construction of volcanoes is often polygenic, and numerous heterogeneities exist on polygenic volcanic edifices [45], but also on monogenetic ones due to variations in eruptive dynamism. The complex and long volcano-tectonic history of long-lived volcanic edifices may explain why numerous fractures and significant weathering are observed. The highly fractured and heterogeneous material (basaltic flows and volcanic breccia) of volcanic edifices are often complex and difficult to model in detail at all scales. Layers of weathered soils interlayered between lavas flows can also be observed [44], as well as pyroclastic deposits. Low friction angle values were estimated or used in various studies for weak structures, effective rock properties, or faults [6,25,46,47,48].
Studies using theoretical models simplify the complexity of the real world [49]. The effective mechanical properties implemented in modeling differ from experimental properties in the laboratory. Pre-existing zones of weakness at depth are present in many volcanic edifices but are different in each case. The real geometry of a specific volcanic edifice or a specific landslide is not the aim of this study. A general flat isosceles trapezoid model is considered. This model does not permit us to forecast exactly when a large landslide will occur, but only to discuss the possibility of distinguishing the influence of meteoric water infiltration from sea water loading/unloading using climatic correlation from a theoretical perspective.
4.3. Sea Level Variation Effect on Landslides and Volcanic Activity
The role of sea level rise in triggering landslides has been suggested in the case of the Vajont landslide (1963, Italy) [1,7]. As the sea level rises, (i) Water loading increases (ii) Water infiltrates the rocks. The loading caused by sea level rises could cause slope instability if the slope is close to equilibrium immediately prior to the rise in sea level. Furthermore, a sea level rise may cause erosion at the base of the cliff, which could promote cliff retreat, rock fall and landslides [50]. However, the effect of loading forces on the base of a slope can also favor slope stability. A vertical loading force at the base of the volcano can cause an increase in stability by counteracting the potential movements of the relief. In other words, when the sea level drops at the base of a slope, it could favor instability (Figure 7A). This result is suggested by the decrease of the safety factor FS as the loading decreases. When a significant loading is above the center of mass of the potential landslide, it causes the destabilization of the slope by triggering rock failure (Figure 7B).
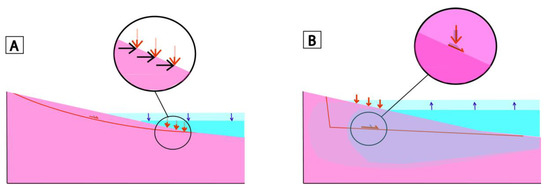
Figure 7.
Influence of the sea level variation with respect to the position of the center of mass of the potential sliding area: (A) Slope instability caused by sea level lowering when the load is located at the base of the slope, (B) slope instability caused by a sea level rise above the center of mass with seawater infiltration.
Giant landslides in volcanic areas appear to be correlated with climatic variations [23]. Fluctuation in sea level loading is one of the potential causes of giant landslides [12]. However, indirect interactions are also possible in volcanic areas. The unloading associated with sea level lowering could change the pressure on the magma reservoir [40]. A decrease in pressure has implications as magma flows into and out of the reservoir. If the connection to the deeper magma source remains open, one consequence is an increased rate of replenishment with primitive magma [51]. In addition, reduced load allows the eruption of denser magma that would otherwise be trapped at shallow depths [52].
The potential interaction between sea level changes and landslides, as well as landslides and volcanic eruptions [53], could cause difficulties in interpretation. If the magma reservoir is shallow, a landslide could cause dike intrusion, but if the magma reservoir is deeper, dike intrusion after a landslide is more difficult.
4.4. Pore Pressure Variation
Another process that can cause landslides is pore pressure increase. Fluids are known to be a triggering and driving factor for landslides [11]. Various mechanisms could explain a pore pressure increase of ~1 MPa. First, a significant amount of water must enter the system. For example, unsaturated rocks of porosity n in an area of volume V could become saturated if a significant volume nV infiltrates. The volume of water could be higher if a dense fracture network exists. Meteoric water infiltration at a depth of 1000 m under lithostatic pressure could cause an increase in pore pressure. An increase of more than 1 MPa in the pore pressure at depth due to meteoric water is not unrealistic and has been proposed in previous studies (e.g., [17]).
An alternative mechanism that could also lead to a significant increase in pore pressure is the progressive collapse of the base of the volcanic edifice. In this scenario, the slow creep of the edifice on a pre-existing weak structure can locally trigger overpressure conditions that reach high pressures [8]. In a volcanic context, hydrothermal processes are also expected to play a role in the pore pressure increase and rock weathering at depth.
The pore pressure can change in relation to meteoric water infiltration in highly fractured rocks. In this case, meteoric water infiltration increases as the precipitation rate increases. Consequently, climatic variations are expected to influence the pore pressure variations in highly fractured rocks. The correlation between climatic variations and giant landslides may be caused by pore pressure increases at depth.
4.5. Climate Variation and Correlation with Giant Landslides
Precipitation increased during glacial maxima in Polynesia [42], Mexico [54], and eastern equatorial Africa [55] but decreased in NW Europe [56], the Caribbean [57] and Indonesia [58,59].
When humid conditions occurred during warmer phases, the potential effect of water infiltration on pore pressure acted to increase instability during warmer interglacial periods, similar to sea level loading. In this case, interglacial phases are expected to cause more slope instability. However, it is difficult to distinguish the influence of sea level loading from meteoric water infiltration at depth on giant paleo-landslides in this case.
In contrast, when precipitation increased during glacial maxima, the effects of sea level loading and depth water infiltration on giant paleo-landslides were not simultaneous. In this case, it is theoretically possible to discriminate the process that plays the main role in triggering giant landslides. For instance, in Polynesia, increased meteoric water infiltration occurred during glacial maxima and may have increased slope instability during glacial maxima, whereas sea level rise caused slope instability during interglacials (Figure 5A). The age of giant landslides (Table 1) may be a good argument for distinguishing between these two processes, but only in Polynesia, Mexico or eastern equatorial Africa, and not in NW Europe, the Caribbean or Indonesia.
In this study, I suggest that a climatic origin of landslides is possible, even if a volcano is extinct, if there are pre-existing weakness zones at depth that cause low effective cohesion and internal friction. Seismic or volcanic processes are not necessarily directly responsible for giant landslides, although these processes may have played a role in creating weak zones in these areas in the past. In 70% of cases, giant landslides occurred when the sea level was rising, regardless of the precipitation rate. Because of the potential delay caused by viscous processes (i.e., 10 kyr of delay for a viscosity less than 1022 Pa.s), it could also be correlated with the magma chamber unloading due to sea level lowering. This result could be influenced by the data set considered, and further studies on giant landslides on volcanic islands would improve this interpretation.

Table 1.
Giant landslide ages in volcanic areas during the last 1 Ma.
Table 1.
Giant landslide ages in volcanic areas during the last 1 Ma.
| Volcano | Age (ka) | References |
|---|---|---|
| Canary Islands (El Hierro, El Golfo) | 10–17 | [60] |
| La Réunion | 20–68 | [61] |
| Hawaii (Alika phase 1) | 112 | [43] |
| Hawaii (Alika phase 2) | 127 ± 10 | [43] |
| Canary Islands (El Hierro, El Golfo) | 134 ± 6 | [3] |
| Hawaii (Southern Lanai) | 135 | [62] |
| Canary Islands (Tenerife) | 150–170 | [63] [64] |
| Hawaii (Southern Lanai) | 240 | [62] |
| La Réunion | 290–320 | [61] |
| Martinique | 337 ± 5 | [65] |
| Canary Islands (La Palma) | 537 ± 8 | [66] [67] |
| Guadeloupe | 629 ± 13 | [68] |
| Hawaii (Haleakala, Hana) | 860 | [69] |
| Tahiti-Nui (north) | 872 ± 10 | [30] |
4.6. Discussion of Giant Landslides Real Cases
This theoretical study allows us to describe the causes of giant landslides more precisely and could be used to discuss real cases. For the first time, the reason why all giant landslides caused by climate variation do not occur during interglacial maximum could be explained. For example, the Tahiti volcano (Society Archipelago, French Polynesia, Pacific Ocean) is a shield volcano, extinct since 230 kyr, with a mean slope of 6–10°, subsiding at a rate of 0.39–0.15 mm/yr (e.g., [33]). At least two major listric discontinuities caused by two giant landslides that occurred 872 ± 10 kyrs ago and 850–650 kyrs B.P. have been described at a depth > 1000 m [30,32,33]. In the South Pacific, glacial periods of time are wetter than interglacial ones. The Tahiti giant landslide, dated at 872 ± 10 kyrs B.P., could have been triggered by a pore pressure increase because it occurred during a glacial period (Figure 5). Nevertheless, if it occurred during the warming phase, the landslide could have been triggered by the sea water unloading that caused a magma reservoir pressure increase with a delay of several thousand years. A more accurate age is necessary to propose a unique interpretation of the Tahiti giant landslide.
La Réunion volcano (i.e., Piton de la Fournaise) is an active shield volcano, composed of basaltic lavas, formed from solidified lava flows accumulated over hundreds of thousands of years, and located in the Indian Ocean above a hot spot. Several landslides occurred on La Réunion volcano slopes at 290–320 kyr and 20–68 kyr B.P. [61]. The eastern flank of the volcano is unstable and is in the initial stages of failure. In La Réunion, heavy precipitations are known in the present day and also during the interglacial time. The past giant landslides that occurred at 290–320 kyr and 20–68 kyr B.P. during cooling periods of times (Figure 5) could have been triggered by sea water unloading, causing magma reservoir pressure increase with a delay of several thousand years.
The Guadeloupe volcano (i.e., La Soufrière), Lesser Antilles, in the Caribbean, is an active stratovolcano [68] composed of lavas flows, debris flows, pyroclastics gathering ash, pumice, and scoria deposits [34]. It is 1467 m high, and. several eruptions, as well as landslides, have been described. The main landslide is 629 ± 13 kyrs old [68]. Concerning the Guadeloupe landslides, they occurred during a glacial phase or during the warming phase (Figure 5). The glacial phases are drier in the Caribbean and exclude pore pressure increases. If it occurred during the glacial phase, the potential cause of the Guadeloupe giant landslide is the magma reservoir pressure increase associated with sea water unloading. Nevertheless, if the giant landslide occurred during the warming phase, the causes could be the sea level loading increase or/and the water infiltration increase. The stratovolcano of La Martinique (i.e., Montagne Pelée), Lesser Antilles, in the Caribbean, which occurred 337 ± 5 kyrs ago [65] during the glacial phase or during the warming phase (Figure 5) has the same potential causes.
4.7. Small Landslides vs. Giant Landslides
The size of the expected landslide depends on the initial slope of the relief. Locally, as in a deeply incised canyon of volcanic islands, significant slopes can be observed. In the case of a significant slope (>25°), the critical value for the height of the stable relief is less than 300 m (Figure 4C). Consequently, smaller landslides can be triggered locally. When rotational landslides occur, significant slopes develop in the upstream part. The resulting relief may be close to the instability conditions that favor the development of new landslides and other retrogressive erosion processes. It can be difficult to distinguish the relief associated with numerous “small” landslides from that caused by giant landslides [32,70].
Erosion and repetition of small landslides could gradually reduce the loading. As previously shown, loading affects the maximum height expected before a landslide occurs. Reducing the load increases the maximum height before a landslide occurs and thus reduces the potential occurrence of a landslide. Consequently, the potential occurrence of a giant landslide could be reduced by the occurrence of small landslides and relief erosion. Previous studies have shown that the probability of small landslides occurring is higher than that of giant landslides (e.g., [9]). Nevertheless, giant landslides have also been described, suggesting that there are specific conditions that favor giant landslides.
5. Conclusions
The probability of a large landslide on an old volcanic edifice in an area where no recent volcanic and/or seismic activities have been observed in the last thousand years is not null. Large landslides caused by non-volcanic processes could occur on old volcanic islands (>200 kyrs). In fact, our modeling suggests that a large landslide (>1500 m deep) could occur due to an increase in pore pressure (~0.5 MPa) or sea level variation. These processes could be discriminated against in areas where glacial maxima are wetter than interglacial periods, but not in the other cases, based only on temporal correlation. This finding is also a consequence of the mechanical properties of highly weathered or fractured volcanic rocks in weakness zones (low cohesion < 1 MPa, and angle of friction < 13°) at depth in old weathered volcanic edifices. Sea level unloading can be responsible for giant landslides, which cause pressure increases in the magma reservoirs at depth and magma release. When the viscous response of the magma reservoir is not negligible (ηc < 1022 Pa.s), a delay of 10 kyrs could occur. During the last million years, several giant landslides in tropical areas have been correlated with sea level unloading during glacial periods of uplift, suggesting that this effect is a driving mechanism in many cases.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The three anonymous reviewers are acknowledged for their suggestions and the time dedicated to the review process. The academic editor is also acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Muller-Salzburg, L. The Vajont catastrophe—A personnal review. Eng. Geol. 1987, 24, 423–444. [Google Scholar] [CrossRef]
- Keefer, D.K. The importance of earthquake-induced landslides to long-term slope erosion and slope-failure hazards in seismically active regions. Geomorphology 1994, 10, 265–284. [Google Scholar] [CrossRef]
- Carracedo, J.C.; Day, S.J.; Guillou, H.; Pérez Torrado, F.J. Giant Quaternary landslides in the evolution of La Palma and El Hierro, Canary Islands. J. Volcanol. Geotherm. Res. 1999, 94, 169–190. [Google Scholar] [CrossRef]
- Blahüt, J.; Balek, J.; Klimeš, J.; Rowberry, M.; Kusák, M.; Kalina, J. A comprehensive global database of giant landslides on volcanic islands. Landslides 2019, 16, 2045–2052. [Google Scholar] [CrossRef]
- Rodriguez-Losada, J.A.; Hernandez-Gutérrez, L.E.; Olalla, C.; Perucho, A.; Serrano, A.; Eff-Darwich, A. Geomechanical parameters of intact rocks and rock masses from the Canary Islands: Implications on their flank stability. J. Volcanol. Geotherm. Res. 2009, 182, 67–75. [Google Scholar] [CrossRef]
- Cala, M.; Flisiak, J. Slope stability with FLAC and limit equilibrium methods. In FLAC and Numerical Modeling in Geomechanics; Billaux, D., Rachez, X., Detournay, C., Hart, R., Eds.; Balkema: Rotterdam, The Netherlands, 2001; pp. 111–114. [Google Scholar]
- Kilburn, C.R.J.; Petley, D.N. Forecasting giant, catastrophic slope collapse: Lessons from Vajont, Northern Italy. Geomorphology 2003, 54, 21–32. [Google Scholar] [CrossRef]
- Veveakis, E.; Vardoulakis, I.; Di Toro, G. Thermoporomechanics of creeping landslides: The 1963 Vaiont slide, northern Italy. J. Geophys. Res. 2007, 112, F03026. [Google Scholar] [CrossRef]
- Urgeles, R.; Camerlinghi, A. Submarine landslides of the Mediterrranean Sea: Trigger mechanisms, dynamics, and frequency-magnitude distribution. J. Geophys. Res. 2013, 118, 2600–2618. [Google Scholar] [CrossRef]
- Crozier, M.J. Deciphering the effect of climate change on landsliding activity: A review. Geomorphology 2010, in press. [Google Scholar] [CrossRef]
- Cappa, F.; Guglielmi, Y.; Viseur, S.; Garambois, S. Deep fluids can facilitate rupture of slow-moving giant landslides as a result of stress transfer and frictional weakening. Geophys. Res. Lett. 2014, 41, 61–66. [Google Scholar] [CrossRef]
- Aslan, G.; De Michele, M.; Raucoules, D.; Bernardie, S.; Cakir, Z. Transient motion of the largest landslide on earth, modulated by hydrological forces. Sci. Rep. 2021, 11, 10407. [Google Scholar] [CrossRef]
- Le Corvec, N.; Walter, T.R. Volcano spreading and fault interaction influenced by rift zone intrusions: Insights from analogue experiments analyzed with digital image correlation technique. J. Volcanol. Geotherm. Res. 2009, 183, 170–182. [Google Scholar] [CrossRef]
- Gargani, J.; Geoffroy, L.; Gac, S.; Cravoisier, S. Fault slip and Coulomb stress variations around a pressured magma reservoir: Consequences on seismicity and magma intrusion. Terra Nova 2006, 18, 403–411. [Google Scholar] [CrossRef]
- Hampel, A.; Hetzel, R. Slip reversals on active normal faults related to the inflation and deflation of magma chambers: Numerical modeling with application to the Yellowstone-Teton region. Geophys. Res. Lett. 2008, 35, L07301. [Google Scholar] [CrossRef]
- McMurtry, G.M.; Watts, P.; Fryer, G.J.; Smith, J.R.; Imamura, F. Giant landslides, mega-tsunamis, and paleo-sea level in the Hawaiian Islands. Mar. Geol. 2004, 203, 219–233. [Google Scholar] [CrossRef]
- Cervelli, P.; Segall, P.; Johnson, K.; Lisowski, M.; Miklius, A. Sudden aseismic fault slip on the south flank of Kilauea volcano. Nature 2002, 415, 1014–1018. [Google Scholar] [CrossRef]
- De Ritis, R.; Passaro, S.; Pensa, A. Editorial for Special Issue “Present and Past Submarine Volcanic Activity (1)”. Geosciences 2022, 12, 458. [Google Scholar] [CrossRef]
- Nicolosi, I.; Caracciolo, F.; Branca, S.; Ventura, G.; Chiappini, M. Volcanic conduit migration over a basement landslide at Mount Etna (Italy). Sci. Rep. 2014, 4, 5293. [Google Scholar] [CrossRef]
- Murray, J.B.; van Wyke de Vries, B. Basement sliding and the formation of fault systems on Mt. Etna volcano. J. Volcanol. Geotherm. Res. 2022, 428, 107573. [Google Scholar] [CrossRef]
- Du, Y.; Xie, M.; Jia, J. Stepped settlement: A possible mechanism for translational, landslides. Catena 2019, 187, 104365. [Google Scholar] [CrossRef]
- Du, Y.; Chen, C. Data Mining for Landslide Genetic Mechanism Analysis in the Yunnan Province of China. Geotech. Geol. Eng. 2022, 40, 5631–5642. [Google Scholar] [CrossRef]
- Quidelleur, X.; Hildenbrand, A.; Samper, A. Causal link between Quaternary paleoclimatic changes and volcanic islands evolution. Geophys. Res. Lett. 2008, 35, L02303. [Google Scholar] [CrossRef]
- Gargani, J.; Bache, F.; Jouannic, G.; Gorini, C. Slope destabilization during the Messinian Salinity Crisis. Geomorphology 2014, 213, 128–138. [Google Scholar] [CrossRef]
- Bigot-Cornier, F.; Montgomery, D.R. Valles Marineris landslides: Evidence for a strength limit to Martian relief? Earth Planet. Sci. Lett. 2007, 260, 179–186. [Google Scholar] [CrossRef]
- Du, Y.; Xie, M.-W.; Jiang, Y.-J.; Li, B.; Chicas, S. Experimental Rock Stability Assessment Using the Frozen–Thawing Test. Rock Mech. Rock Eng. 2017, 50, 1049–1053. [Google Scholar] [CrossRef]
- Zhang, L.; Niu, F.; Liu, M.; Wang, Z.; Wang, J.; Dong, T. Fracture characteristics and anisotropic strength criterion of bedded sandstone. Front. Earth Sci. 2022, 10, 879332. [Google Scholar] [CrossRef]
- Champel, B.; van der Beck, P.; Mugnier, J.-L.; Leturny, P. Growth and lateral propagation of fault-related folds in the Siwaliks of western Nepal: Rates, mechanisms, and geomorphic signature. J. Geophys. Res. 2002, 107, 2111. [Google Scholar] [CrossRef]
- Hürlimann, M.; Garcia-Piera, J.O.; Ledesma, A. Causes and mobility of large volcanic landslides: Application to Tenerife, Canary Islands. J. Volcanol. Geotherm. Res. 2000, 103, 121–134. [Google Scholar] [CrossRef]
- Hildenbrand, A.; Gillot, P.-Y.; Le Roy, I. Volcano-tectonic and geochemical evolution of an oceanic intra-plate volcano: Tahiti-Nui (French Polynesia). Earth Planet. Sci. Lett. 2004, 217, 349–365. [Google Scholar] [CrossRef]
- Hildenbrand, A.; Gillot, P.-Y.; Marlin, C. Geomorphological study of long-term erosion on a tropical volcanic ocean island: Tahiti-Nui (French Polynesia). Geomorphology 2008, 93, 460–481. [Google Scholar] [CrossRef]
- Gargani, J. Modelling the mobility and dynamics of a large Tahitian landslide using runout distance. Geomorphology 2020, 370, 107354. [Google Scholar] [CrossRef]
- Gargani, J. Isostatic Adjustment, Vertical Motion Rate Variation and Potential Detection of Past Abrupt Mass Unloading. Geosciences 2022, 12, 302. [Google Scholar] [CrossRef]
- Navelot, V.; Géraud, Y.; Favier, A.; Diraison, M.; Corsini, M.; Lardeaux, J.-M.; Verati, C.; Mercier de Lépinay, J.; Legendre, L.; Beauchamps, G. Petrophysical properties of volcanic rocks and impacts of hydrothermal alteration in the Guadeloupe Archipelago (West Indies). J. Volcanol. Geotherm. Res. 2018, 360, 1–21. [Google Scholar] [CrossRef]
- Gargani, J.; Rigollet, C. Mediterranean Sea level variations during the Messinian Salinity Crisis. Geophys. Res. Lett. 2007, 34, L10405. [Google Scholar] [CrossRef]
- Gargani, J.; Moretti, I.; Letouzey, J. Evaporite accumulation during the Messinian Salinity Crisis: The Suez Rift Case. Geophysical Research Letters 2008, 35, L02401. [Google Scholar] [CrossRef]
- Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic 18O records. Paleoceanography 2005, 20, 1003. [Google Scholar]
- Gargani, J.; Stab, O.; Cojan, I.; Brulhet, J. Modelling the long-term fluvial erosion of the river Somme during the last million years. Terra Nova 2006, 18, 118–129. [Google Scholar] [CrossRef]
- Saar, M.O.; Manga, M. Seismicity induced by seasonal groundwater recharge at Mt. Hood, Oregon. Earth Planet. Sci. Lett. 2003, 214, 605–618. [Google Scholar] [CrossRef]
- Sternai, P.; Caricchi, L.; Garcia-Castellanos, D.; Jolivet, L.; Sheldrake, T.E.; Castelltort, S. Magmatic pulse driven by sea-level changes associated with the Messinian salinity crisis. Nat. Geosci. 2017, 10, 783–787. [Google Scholar] [CrossRef]
- Jull, M.; McKenzie, D. The effect of deglaciation on mantle melting beneath Iceland. J. Geophys. Res. 1996, 101, 21815–21828. [Google Scholar] [CrossRef]
- Saez, A.; Valero-Garces, B.L.; Giralt, S.; Moreno, A.; Bao, R.; Pueyo, J.J.; Hernandez, A.; Casas, D. Glacial Holocene slimate changes in SE Pacific. The Raraku Lake sedimentary record (Easter Island, 27°S). Quat. Sci. Rev. 2009, 28, 2743–2759. [Google Scholar] [CrossRef]
- McMurtry, G.M.; Herrero-Bervera, E.; Cremer, M.; Resig, J.; Sherman, C.; Smith, J.R.; Torresan, M.E. Stratigraphic constraints on the timing and emplacement of the Alika 2 giant Hawaiian submarine landslide. J. Volcanol. Geotherm. Res. 1999, 94, 35–58. [Google Scholar] [CrossRef]
- Hevia-Cruz, F.; Hildenbrand, A.; Sheldon, N. Enhanced Weathering of Volcanic Islands during Glacial-Interglacial Transitions: Insights from Well-Dated Paleosols Spanning the Last Million Year in Sao Miguel Island, Eastern Azores; Conférence “Climat et impacts”: Orsay, France, 2022. [Google Scholar]
- Hildenbrand, A.; Gillot, P.-Y.; Bonneville, A. Offshore evidence for a huge landslide of the northern flank of Tahiti-Nui (French Polynesia). Geochem. Geophys. Geosystems 2006, 7, Q03006. [Google Scholar] [CrossRef]
- Got, J.-L.; Monteiller, V.; Monteux, J.; Hassani, R.; Okubo, P. Deformation and rupture of the oceanic crust may control growth of Hawaiian volcanoes. Nature 2008, 451, 453–456. [Google Scholar] [CrossRef] [PubMed]
- Egholm, D.L.; Clausen, O.R.; Sandiford, M.; Kristensen, M.B.; Korstgard, J.A. The mechanics of clay smearing along fault. Geology 2008, 36, 787–790. [Google Scholar] [CrossRef]
- Abers, G.A. Slip on shallow-dipping normal faults. Geology 2009, 37, 767–768. [Google Scholar] [CrossRef]
- Gargani, J. Poincaré, le Hasard et L’étude des Systèmes Complexes; L’Harmattan: Paris, France, 2012; 124p. [Google Scholar]
- Ye, F.Y.; Barriot, J.P.; Carretier, S. Initiation and recession of the fluvial knickpoints of the Island of Tahiti (French Polynesia). Geomorphology 2013, 186, 162–173. [Google Scholar] [CrossRef]
- Pinel, V.; Jaupart, C. The effect of edifice load on magma ascent beneath a volcano. Philos. R. Soc. London Ser. A 2000, 358, 1515–1532. [Google Scholar] [CrossRef]
- Pinel, V.; Jaupart, C. Magma chamber behavior beneath a volcanic edifice. J. Geophys. Res. 2003, 108, 2072. [Google Scholar] [CrossRef]
- Longpré, M.A.; Troll, V.R.; Walter, T.R.; Hansteen, T.H. Volcanic and geochemical evolution of the Teno massif, Tenerife, Canary Islands: Some repercussions of giant landslides on ocean island magmatism. Geochem. Geophys. Geosyst. 2009, 10, Q12017. [Google Scholar] [CrossRef]
- Ganeshram, R.S.; Pedersen, T.F. Glacial-interglacial variability in upwelling and bioproductivity off NW Mexiso: Implications for Quaternary paleoclimate. Paleoceanography 1998, 13, 634–645. [Google Scholar] [CrossRef]
- Chiang, J.C.H. The Tropics of Paleoclimate. Ann. Rev. Earth Planet. Sci. 2009, 37, 263–297. [Google Scholar] [CrossRef]
- Guiot, J.; Pons, A.; de Beaulieu, J.L.; Reille, M. A 140000 year continental climate reconstruction from two European pollen records. Nature 1989, 338, 309–313. [Google Scholar] [CrossRef]
- Curtis, J.H.; Brenner, M.; Hodell, D.A. Climate change in the circum-Caribbean (Late Pleistocene to Present) and implications for Regional Biogeography. In Biogeography of the West Indies; Charles, A.W., Florence, E.S., Eds.; CRC Press: Boca Raton, FL, USA, 2001; 608p. [Google Scholar] [CrossRef]
- Costa, K.M.; Russel, J.M.; Vogel, H.; Bijaksana, S. Hydrological connectivity and mixing of Lake Towati, Indonesia in response to paleoclimatic changes over the last 60,000 years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2015, 417, 467–475. [Google Scholar] [CrossRef]
- Russell, J.M.; Vogel, H.; Konecky, B.L.; King, J.W. Glacial forcing of central Indonesian hydroclimate since 80000 yr B.P. Proc. Natl. Acad. Sci. USA 2014, 111, 5100–5105. [Google Scholar] [CrossRef]
- Gee, M.J.; Watts, A.B.; Masson, D.G.; Mitchell, N.C. Landslides and the evolution of El Hierro in the Canary Islands. Mar. Geol. 2001, 177, 271–293. [Google Scholar] [CrossRef]
- Lenat, J.F.; Labazuy, P. Growth and collapse of the Reunion Island volcanoes. Bull. Volcanol. 2008, 70, 717–742. [Google Scholar]
- Rubin, K.H.; Fletcher, C.H., III; Sherman, C. Fossiliferous Lanai deposits formed by multiple events rather than a single giant tsunami. Nature 2000, 408, 675–681. [Google Scholar] [CrossRef]
- Hunt, J.E.; Wynn, R.B.; Masson, D.G.; Talling, P.J.; Teagle, D.A.H. Sedimentological and geochemical evidence for multistage failure of volcanic island landslides: A case study from Icod landslide on north Tenerife, Canary Islands. Geochem. Geophys. Geosystems 2011, 12, Q12007. [Google Scholar] [CrossRef]
- Masson, D.G.; Watts, A.B.; Gee, M.J.R.; Urgeles, R.; Mitchell, N.C.; Le Bas, T.P.; Canals, M. Slope failures on the flanks of the western Canary Islands. Earth-Sci. Rev. 2002, 57, 1–35. [Google Scholar] [CrossRef]
- Quidelleur, X.; Samper, A.; Boudon, G.; Le Friant, A.; Komorowski, J.C. Radiometric dating of large volume flank collapses in the Lesser Antilles Arc. Eos Trans. AGU 2004, 85. [Google Scholar]
- Guillou, H.; Carracedo, J.C.; Duncan, R.A. K-Ar, 40Ar/39Arages and magnetostratigraphy of Brunhes and Matuyama lava sequencesfrom La Palma Island. J. Volcanol. Geotherm. Res. 2001, 106, 175–194. [Google Scholar] [CrossRef]
- Groom, S.; Barfod, D.N.; Millar, I.; Downes, H. The Cumbre Nueva collapse (La Palma, Canary Islands): New age determinations and evidence of an isotopic excursion. J. Volcanol. Geotherm. Res. 2022, 433, 107708. [Google Scholar] [CrossRef]
- Samper, A.; Quidelleur, X.; Lahitte, P.; Mollex, D. Timing ofeffusive volcanism and collapse events within an oceanic arc island:Basse Terre, Guadeloupe archipelago (Lesser Antilles Arc). Earth Planet. Sci. Lett. 2007, 258, 175–191. [Google Scholar] [CrossRef]
- Moore, J.G.; Clague, D.A. Volcano growth and evolution of the island of Hawaii. Geol. Soc. Am. Bull. 1992, 104, 1471–1484. [Google Scholar] [CrossRef]
- Gargani, J. Relative sea level and abrupt mass unloading in Barbados during the Holocene. Geomorphology 2022, 413, 108353. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).