Next Article in Journal
On the Annual and Semi-Annual Components of Variations in Extent of Arctic and Antarctic Sea-Ice
Previous Article in Journal
Full Waveform Inversion Based on an Asymptotic Solution of Helmholtz Equation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 13
Issue 1
10.3390/geosciences13010020
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Seepage-Induced Pore Pressure Variations Beneath an Earthen Levee Measured with a Novel Seismic Tool

by
Daniel Locci-Lopez
* and
Juan M. Lorenzo
Department of Geology and Geophysics, Louisiana State University, Baton Rouge, LA 70803-4101, USA
*
Author to whom correspondence should be addressed.
Geosciences 2023, 13(1), 20; https://doi.org/10.3390/geosciences13010020
Submission received: 13 December 2022 / Revised: 8 January 2023 / Accepted: 9 January 2023 / Published: 12 January 2023
(This article belongs to the Section Geophysics)
Browse Figures
Review Reports Versions Notes

Abstract

:
Shear-wave seismic reflection velocity-versus-depth models can complement our understanding of seepage pore pressure variations beneath earthen levees at locations between geotechnical sites. The seasonal variations of water level in the Mississippi River create pore pressure changes in the adjacent hydraulically connected aquifer on the protected side of artificial levees. Time-lapse shear-wave velocity analysis or repetition of seismic acquisition over an area is a non-invasive method that can detect seasonal pore pressure variations in shallow (<40 m) aquifers. The seismic reflection patterns during the seasonal pore pressure variations of the river show a distinctive change in the velocity semblance analysis, which is translated as a change in the average stress carried by the grain-to-grain contact, or simply the effective pressure. The seismic data show a greater variation of up to +140/−40 m/s or +700/−150 kPa in the confined aquifer zone, compared with the leaky confined aquifer zone of up to +46/−48 m/s or +140/−80 kPa. These relative effective pressure characteristics allow us to distinguish between confined and leaky aquifers and can be an optional approach for pressure prediction in floodplains along levees without the need to drill borings in the area to measure piezometric data.

1. Introduction

Agricultural, industrial, and urban landscapes protected by adjacent dikes or levees encourage further development and population growth. Just in the United States, ~55% of the population lives next to flood-prone zones that are protected by levees or dikes [1,2]. However, climate change is increasing flooding events near coasts and rivers [3]. It is expected that river and coastal storm flooding will cause urban property damage of over USD 700 thousand million annually by 2030 around the world [4].
Lands adjacent to the levee can be damaged through heaving during high water levels or flood events. Where there is a low-permeability surface layer across the flood plain, an increase in pore pressure in the more-permeable substratum can weaken and break the overlying low-permeability layer, and allow water to move to the surface, creating local flooding [5]. Pore pressure in the substratum increases with the level of the river when it is hydraulically connected to the stream bed [6] (Figure 1b).
Artificial levees in the Lower Mississippi River Valley (LMRV) serve as flood prevention structures that control and maintain in place the natural lateral accretion of the river over time. These earthen levees provide safety to major urban cities (e.g., Kansas City, St. Louis, Memphis, Vicksburg, Baton Rouge, and New Orleans) in the United States during seasonal flooding events [9]. The seasonal hydraulic head fluctuations in the Mississippi River incorporate pore pressure changes in the hydraulically connected aquifer below the protected side of artificial levees [8,10,11,12].
Currently, few options exist to monitor seepage pressure or piezometric head under levees induced by high water levels in a river. The most common method is using a piezometer in a well that measures the pressure head of groundwater at a single location [13,14]. Under special circumstances, when the water pressure head exceeds the surface elevation of the well, a flow meter is used to measure the rate of water relieved from the subsurface [15].
Floodplain sediments are heterogeneous at the meter-scale and depending on the geological history of the river, the facies composition and architecture can change laterally and vertically. Multiple well piezometers across an area can monitor the water pressure of a formation but normally do not provide the necessary laterally continuous data [16] at the meter-scale. Analytical and finite-difference modeling using piezometric data are useful methods to predict inter-well changes, but these techniques will always be limited by the existence of observation wells at either single or multiple locations.
Near-surface seismic analysis has the potential to monitor the structural integrity of levees as well as dams during their lifetime [17]. Time-lapse seismic studies can monitor changes of near-surface properties, including groundwater level variations [18,19,20,21], water saturation changes [22,23,24,25,26] chemical and weathering effects [27,28,29,30], permafrost thaw [31], deep fluid storage dynamics [32,33] and Critical Zone interactions [34].
Although it remains under-used in the geotechnical field, near-surface seismic analysis is a non-invasive method that can be correlated to underground water pore pressure. In particular, shear-wave (S) seismic velocities can potentially improve predictions in the water pore pressure regime at close intervals (~0.5 m), such as in floodplains adjacent to levees. The oil and gas industry regularly monitors changes in reservoir pressure and saturation via time-lapse seismic analysis [35,36,37]. Repeated 3D CMP (Common Mid-Point) seismic reflection volumes are acquired in the same location over time using compressional-wave (P) sources with vertical and/or horizontal component geophones. Pressure and fluid saturation changes in the reservoir result in changes to the elastic properties of the rock framework, such as the bulk and shear modulus that can be detected under favorable circumstances using P- and S-wave velocities from seismic data [37]. If reservoir pore pressure declines because of depletion, effective pressure should increase, as well as the seismic velocity. On the other hand, if reservoir pore pressure increases from injection, effective pressure would decrease together with the seismic velocity.
Laboratory experiments show that P-wave and S-wave velocities increase as the effective pressure of the media also increases [2,38,39,40,41,42].
Confining pressure ( P c ) also increases with the weight of the overlying sediments [43]. However, in water-saturated unconsolidated media, pore fluid pressure ( P p ) lowers the stress at grain-to-grain contacts and is also known as the effective pressure, ( P e ), where α is an effective-stress coefficient whose value is assumed to be one in unconsolidated sediments [44].
P e = P c − α P p .
Small changes in pore pressure can result in large variations in the shear-wave velocity (VS) because if the media approaches critical porosity, the shear strength, or rigidity of the media, will approach zero [45]. P-wave seismic velocities are sensitive to changes in the bulk and shear moduli. In contrast, S-wave seismic velocities are mainly sensitive to the shear modulus or rigidity of the media [37]. Because the bulk modulus of water is large relative to the unconsolidated sediment framework, the bulk moduli and P-wave velocities of water saturated samples are strongly dependent on porosity [46]. In general, sediment VS values are more sensitive to pore pressure than P-wave velocities [45].
Experimental field seismic data could be used to corroborate the results from laboratory experiments [2,45,47,48,49,50,51,52] and develop a methodology that is adequate to monitor and characterize effective pressure with seismic velocity variations.
In particular, time-lapse analysis or repetition of seismic acquisition over an area has the potential to demonstrate the sensitivity of seismic velocity values to pressure changes in the subsurface. Pressure changes caused by the Mississippi river seasonal hydraulic head variations could be captured by VS variations. Changes in the observed RMS (Root Mean Square) reflection hyperbola can be converted into interval velocity (VINT) or formation velocity. By using a power regression of laboratory data [2], we can convert VINT to effective pressure. Further verification of these results can be confirmed by comparison with empirical power-curve results of [45] and analytical models of Walton [53] and Lee [54].
To further investigate the pressure regime changes in an aquifer induced by the seasonal hydraulic head variations on the Mississippi River, we designed a seismic field experiment on the protected side of an artificial levee of the Mississippi River. Between May 2019 and August 2021, at our study area we conducted horizontal-component shear-wave (SH) seismic surveys focused on characterizing the aquifer that is hydraulically connected to the Mississippi River (Figure 2). We performed the experiments across both a confined aquifer and leaky confined aquifer during high (13.5 m), low (6 m) and intermediate (8 and 10 m) river water levels (stages). If during a high river stage, the layer above the aquifer is permeable enough to leak, we expect that the observed horizontal-component shear-wave seismic velocity (VSH) changes in the aquifer will be insignificant. However, if the layer above the aquifer remains sealed, then we expect changes in the estimated VSH values.
We also compare the predicted effective pressure variations from the seismic data against a stress distribution diagram that uses the local boring data and a transient pore pressure fluid flow model [8]. The effective pressure difference between low and high stage, or the differential effective pressure allow us to compare the seismic data results with the modeled stress distribution diagram.

2. Geological and Geotechnical Setting of the Study Area

A suitable floodplain zone lies 25 m from the Mississippi River on the western edge of Louisiana State University in Baton Rouge, and at the northernmost point of the Duncan Point Bar (Figure 1a). We chose this site because it is publicly accessible for investigation and is historically prone to under-the-levee seepage and flooding [12]. During high stages in the Mississippi River, the building at the study location experiences seepage in its basement. As well, during high stages, water seeps through cracks in the cement road of the adjacent parking lot located to its east (Figure 2).
At this site, the soil structure appears to be similar to a standard levee section as defined by [55] (Figure 1b), a sandy alluvium that ranges from 25 to 45 m in thickness overlain by a lower-permeability top layer that varies between 1.5 to 37.5 m in thickness. To implement pressure relief wells and reduce pressure in the low-permeability surface layer (Figure 3), engineering boring logs were collected at 10 drilled wells. These logs help characterize the subsurface surrounding the building and include visual classifications and grain size laboratory analysis of sediment samples drilled. Despite the installation of five pressure-relief wells in the area, flooding continues and the conditions in and around the building have not improved. Based on boring logs, the upper 10 m of the subsurface appear highly heterogeneous in composition (sand, silt, and clay) and variable in thickness. The tops of some of buried sandy/silt ridges lie within 1 to 3 m of the ground surface in some locations [12]. The general trend interpreted from the boring logs finds a top stratum that varies in thickness between 3 m and 10 m and is composed of a combination of fine sand, silt, and clay. The natural levee blanket is composed of silt with 5–20% clay, high-plasticity clay, and lean clay with the remaining soils composed of lean clays and sandy silts [56,57]. The logs show a general increase in the silt content relative to the clay, from east to west (away from the river), which suggests that the general hydraulic conductivity may also increase with distance from the river (Figure 3).
Based on the laboratory results from the 10 borings, the upper blanket is relatively impervious and has a calculated average saturated hydraulic conductivity of 1.8 × 10−6 cm/s, but is lower than in previous studies of 3.2 × 10−5 cm/s [57,58] in the Duncan Point bar. This upper blanket thins and ruptures towards the landside, thus weakening the lower-permeability top stratum between the high hydraulic conductivity sands and the surface [58,59]. The coarser-grained units below the natural levee blanket are hydraulically connected to the Mississippi river [60], and field borings show approximately 50 m of higher hydraulic conductivity sands (5–20 × 10−2 cm/s) which comprise the aquifer [57,58].
The upper 40 m of sediments at our study area share the near-surface sedimentary facies common throughout the LMRV (Figure 3), which contains Holocene point bar channel deposits and associated abandoned channels [12,61]. Point bar sedimentary sequences are the product of the river’s lateral accretion over time, developing highly vertical and horizontal heterogeneous soils in terms of grain size and composition [12,61]. The upper 10-m section of Mississippi point bars is often composed of interbedded sands, silts, and clays with preservation of the original accretionary dip angle and represents the inclination of the inner bank of the river channel bend [62]. Point bar facies trends generally fine upward because of the variation in current strength in the channel, even though this relationship is not always the case. Silty and sandy ridges are laid down during high stages on the stream, and silty and clayey deposits are laid down in swale depressions during falling river stages [63]. The variations in the interbedded zone or Inclined Heterolithic Strata (IHS) are attributed to the scroll bar topography [64]. The lower section of the point bar is characterized by trough cross-bedded sandy strata [65] that are generally more homogenous in lithology with coarser grain size than the upper section [66]. Cliff face exposures of a maximum of 6 m in the Duncan Point bar, Louisiana, show laminated beds of silty clays with an angle of 7° degrees perpendicular to the river, and ripple-drift laminations of fine sand and silt [67].

3. Methods

3.1. Seismic Field Methods and Data Processing

We aim to acquire seismic data during the lowest- and highest-possible river stage as well as during an intermediate stage to confirm the estimated velocity trends. Seismic surveys conducted during the high and low river stages use the shoot-through/split-spread acquisition geometry (Table 1) with moving source and fixed geophones method [68] in order to maximize fold and signal-to-noise ratio. We resurvey the same lines during an intermediate river stage (Table 2) to confirm that velocity values are also intermediate between those seen at the other two stages. For the intermediate-stage survey, we use a single-fold but more efficient and quicker pseudowalkaway acquisition geometry (PWA) [69]. We move the source a distance equal to the geophone array length (24 m) to provide lateral continuous seismic returns while expediting the data acquisition [70]. We aim to detect S-wave velocity variations caused by pressure changes in the skeletal matrix of the soils during seasonal river level fluctuations (Figure 4).
We placed one seismic line on the west side of the building, 25 m east of the toe of the artificial levee (Figure 2). At this location, the engineering boring logs (Figure 3) indicate a thicker (~8 to 14 m) upper impervious levee blanket, and there is no strong evidence of cracks or water leakage at the surface. We consider this area to contain the confined aquifer. We placed another seismic line over a potentially leaky, confined aquifer on the east side of the building, 355 m of the toe of the levee. At this location, engineering logs from nearby wells (6 and 10) (Figure 3) show a thinner (~3 to 5 m) levee blanket above the aquifer.
During the surveys, we generate a (SH) seismic source signal by horizontally striking a steel I-beam at right angles to the direction of the survey line. The I-beam is rotated 90 degrees so that its edges can be firmly planted in the ground and further held down by the weight of the operator. We use the horizontal-component data [74,75] to derive standard common midpoint (CMP) seismic profiles [76] (Figure 5). S-wave reflection seismic analysis is less common than seismic refraction tomography or surface wave dispersion analysis for extracting S-wave velocities in the near-surface. S-waves provide higher vertical resolution than P-waves due to their slower velocities, resulting in a smaller wavelength [75,77,78,79]. The S-waves are more sensitive to lithological contrasts and do not produce significant frequency-dependent attenuation and dispersion due to fluid saturation. By using this technique, we are able to investigate the shallow subsurface between 10 and 40 m depths.
The VSH profiles in this study provide laterally continuous CMP data with a horizontal resolution of 0.5 m (Figure 6 and Figure 7). The vertical resolution is ~10 m for the first 40 m in the VSH profiles, and it is defined by the higher confidence points in the semblance analysis. In order to reduce the likelihood of contamination by converted SH-to-P-waves, we make two recordings of each seismic gather. That is, we strike the shear-source plate twice, from two directions at 180 degrees from each other and at right angles to the seismic line. Differencing these data sets with normal and reverse polarity helps remove any converted modes and enhances SH reflections at the top and within the aquifer.
Open-source signal analysis tools [71] and an accompanying graphical user interface [80] facilitate data processing and help improve the seismic interpretation by increasing the signal-to-noise ratio and enhancing seismic reflectors from the top and interior of the aquifer. For the shoot-through/split-spread geometry data, the CMP fold is maximum in the middle and decreases linearly toward the end and start of the profile (Figure 5). Higher fold leads to more accurate velocity analyses. By comparison, the shotpoint gathers collected using PWA geometry (Figure 2) have a fold of 1.
Love (surface) waves, partly interfere with the earlier near-surface SH reflected wave arrivals [81] and are difficult to separate. We choose to remove or mute (Table 1) the cone of surface wave cone at the top of each shot gather to increase the signal-to-noise ratio. A mean starting value for the apparent surface wave propagation velocity is ~115 m/s. From this initial value, we test a range of f-k (frequency-wave number) filter dips and best remove the coherent surface-wave noise (Table 1), highlighting the reflections. We reapply the mute to remove any residual noise from the surface waves cone.
For each CMP-SH seismic data gather, we can derive an estimate of VSH within individual layers, or interval velocity (VINT; Figure 8) through an analysis of the RMS velocity (VRMS) of seismic reflection hyperbola originating at top and bottom of each layer. We select the best VRMS (SH) versus-time values from the output of a standard semblance velocity analysis [72] (Figure 8). In a semblance display, high-values of the contoured velocity spectra (VRMS) [71,72] highlight the best statistical match of hyperbolic arrivals detected within the data. The uncertainty range of the contoured high-value velocity spectra (VRMS) in the semblance analysis have a mean of 28 m/s and standard deviation = ±7 m/s.
From the juxtaposition of VINT-versus-depth, we generate 2D VINT profiles for the analysis results of velocity-versus-depth for each CMP gather. To make the visual interpretation easier, we use the kriging interpolation method [82] to generate (Figure 6 and Figure 7). We repeat the process for low stage and high stage sections and generate a low stage minus high stage profile.
The kriging interpolation is one of the most flexible and accurate gridding methods when the sample points are not constant intervals, such as the semblance analysis velocity picking that depends on the resolvability of the seismic reflectors. The high lateral resolution (0.5 m) of the CMP gathers interpolated with the kriging method serves as a quality control and compensates for clustered data by giving less weight to the cluster in the overall prediction. The nodes in the grid are based on the known data points neighboring the node; therefore, each data point is weighted by its distance away from the node. This results in laterally smoother shear-wave profiles (Figure 6 and Figure 7) that minimize the strong lateral variations caused by noise and compensate for the lower vertical resolution (10 m).

3.2. Predictions of Effective Pressure from S-Wave Velocity

Several studies highlighted the empirical relationships of effective pressure and S-wave velocity [45,46,50,83], and determined that in unconsolidated dry and water-saturated laboratory sand samples, S-wave velocity data can be approximated by power–law relationships.
The meter-scale heterogeneous nature of the point bar sediments and the uncertainty of the variations of the physical properties (e.g., clay content) in the area makes the empirical model better suited to the study, since theoretical models such as Walton [53] and Lee [54] are constrained by many variables that are not available in the drilled borings. By using available laboratory data [2,50] we create an empirical power–law trend curve that can directly predict effective pressure ( P e ) from seismically acquired VS in unconsolidated sands. We use Pe values from 0.05 to 50 MPa to fit the power–law curve to the data (Figure 9):
P e = 0.0000007413 ( V s ) 3.5   ( coefficient   of   correlation   R 2 = 0.95 ) .
To verify the relationship (Equation (2)), we compare the power-curve trend (Figure 9) to well-stablished theoretical models that can predict effective pressure from VS in unconsolidated sands, such as Walton [53] and Lee [54].
The predicted effective pressure values from Walton [53] and Lee [54] agree well with the measured effective pressure values from Prasad [50] and Zimmer [2]. Both theoretical results are almost identical to the power–law curve (Equation (2)) for VS from 200 m/s to 600 m/s (Figure 9a) but show a noticeable difference at velocities greater than 600 m/s (Figure 9a). The curve by Lee [54] for over 600 m/s follows more closely the power–law curve from Prasad [50] and Zimmer [2]’s data, showing an improvement over the whole range. However, we are working in the first 40 m using VS as low as 100 m/s, and there is a lot of uncertainty in the VS and effective pressure relationship for less than 200 m/s. Therefore, by extrapolating Prasad [50] and Zimmer [2]’s power–law data (Figure 9b), we can address these low-velocity zones (less than 200 m/s).
We use Equation (2) to convert the VSH profiles (Figure 6 and Figure 7) to effective pressure (Figure 10 and Figure 11).

3.3. Differential Pore Pressure

By applying the same relationship (1) for low and high river stages:
P e   h i g h = P c − P p   h i g h   and   P e   l o w = P c − P p   l o w .
Then, subtracting
P e   l o w − P e   h i g h = ( P c − P p l o w ) − ( P c − P p h i g h )
Therefore,
P e   l o w − P e   h i g h = P p h i g h   − P p l o w .
Simplified,
Δ P e = − Δ P p
where Δ P e is the differential effective pressure of low river stage ( P e   l o w ) minus high river stage ( P e   h i g h ), and Δ P p is the differential pore pressure of low river stage ( P p   l o w ) minus high river stage ( P p   h i g h ). An increase in differential effective pressure from low minus high stages results in a decrease in differential pore pressure (Equation (3)).

3.4. Fluid Flow Pressure Model and Stress Distribution Diagram to Predict Effective Pressure

In order to evaluate the possible significance of observed changes in the seismic velocity values, we develop a seasonal stress distribution diagram of the first 40 m of the floodplain sediments. We predict the hydraulic head or pore pressure as a function of distance from the intersection of the river bottom and the aquifer. We use Equation (4) from Ozkan et al. [8] to create a transient fluid flow model (Figure 12b,c) by incorporating the boring laboratory data (Figure 12a) and the river stages from the Mississippi River (Figure 4). The available boring laboratory data have visual classifications and grain size laboratory analysis of sediment samples drilled, unit weight (γ), and hydraulic conductivity values. The borings do not have pressure measurements with varying water levels on the Mississippi River. The borings indicate a range from 5 to 15 m of thickness of the upper low-permeability layer in the area (Figure 12a). We choose 10 m conservatively.
The stress distribution diagram uses the local boring data with the sediment’s unit weight for the upper lower permeability layer and the higher permeability substratum. The fluid flow pressure model with varying river water levels (Table 2) incorporates the pore pressure into the stress distribution diagram.
Varying water levels in the river during a flood causes varying flow velocities in the subsurface, inducing a transient fluid flow system [84]. Observations on water wells near tidal water bodies show sinusoidal fluctuations of hydraulic head levels responding to periodic changes on the water stage [85]. To this end, river water level variations are defined by boundary conditions expressed by sinusoidal head functions that can predict underseepage pressure at different times and distances on the protected side of the levee during a flood cycle [6,85,86,87,88].
The solution to determine time-dependent hydraulic head development beneath the levee as a response to the stage fluctuations observed in the river is [8]:
h 1 x , t = H 0 erfc x 2 S T t + Im h x , t
where H 0 = initial hydraulic head applied to the aquifer; h 1 = rise or fall of hydraulic head in the aquifer above a horizontal datum; x = distance from aquifer river intersection; t   = time; T   = aquifer transmissivity; S = aquifer storage coefficient, and Im h x , t is the imaginary part of the function h x , t (Figure 12b,c).
We create two scenarios to simulate and capture the minimum and maximum possible stress changes during varying river water levels. Both scenarios share the same layering thickness and unit weights. The only property that actively changes with varying river water levels is the pore pressure, which affects the effective pressure. In this case, we calculate the pore pressure at 25 m from the levee toe at low stage (6 m) and high stage (13.5 m).
Inclusion of pore pressure in the stress distribution diagram (Figure 13), results in a constant differential effective pressure change with depth.

3.5. Comparison of Seismic Data and Stress Model

To compare the seismic field data results and the modeled stress distribution diagram, we plot their respective differential effective pressure with depth (Figure 14). The stress distribution diagram shows a constant differential effective pressure of 70 kPa from 10 to 40 m. However, the differential effective pressure from the seismic data shows a non-constant differential pressure with increasing depth for both east and west sides of the building (Figure 2).
On the west side of the building in our study area, where the confined aquifer is located, the velocity values for a central CMP are higher with depth in the low stage than the high stage (Figure 15a). The PWA survey during the intermediate stage maintains velocity values within the low and high stage velocity values. On the east side, where the leaky confined aquifer is located, there is not a distinguishable difference in velocity values with depth during the low, intermediate, and high stages (Figure 15b).

4. Results

Observed VSH variations are more easily explained if we interpret that, during high river stage, the lower permeability layer above the aquifer maintains its pore pressure. In this manner, increases or decreases in the grain particle-to-particle contact pressure can trigger a corresponding decrease or increase in the observed VSH seismic data. Semblance velocity analysis-derived models of reflected seismic arrivals (SH) at the seismic acquisition sites show higher velocity values with depth in the low stage than the high stage in the area where the confined aquifer is located (Figure 15a). The PWA survey results show that during the intermediate stage, velocity values lie between those observed at low and high stages (Figure 15a). The differential VSH profile shows a variation of up to +140/−40 m/s in the confined aquifer zone (Figure 6c).
In contrast, we interpret the observed VSH variations where the “leaky” confined aquifer is located to indicate that the same lower permeability layer above the aquifer does not maintain its pore pressure during high river stage. There is not a significant difference in velocity values with depth between the low, intermediate, and high stages (Figure 15b). The grain particle-to-particle contact pressure does not change enough to create a significant velocity variation during varying river stages. The differential S-wave seismic velocity profile shows a variation of up to +46/−48 m/s in the leaky confined aquifer zone (Figure 7c).
Effective pressure estimates (Figure 10 and Figure 11) derived from the VSH profiles (Figure 6 and Figure 7) confirm the initial identification of the confined and leaky confined aquifer zones. The profiles show a variation of up to +700/−150 kPa in the confined aquifer zone (Figure 10c) with an increase in differential effective pressure with depth; whereas the leaky confined aquifer zone shows a variation of up to +140/−80 kPa (Figure 11c) with a decrease in differential effective pressure first, and around 30 m there is an increase.
Multiple characteristics in the known geology predict a significant physical change at the base of the Holocene sediments. We observed a general increase in all the VSH data (Figure 6 and Figure 7) around 30 m in depth, which probably represents the Holocene–Pleistocene contact [89]. This contact is characterized by a change from fine-grained flood basin sediments to coarse-grained braided stream sediments [56,61]. This transition is characterized by decrease in water content; a distinctive stiffening of soil consistency; a decrease in rate of penetration of sampling devices; an increase in soil strength; and the occurrence of calcareous concretions [89].
The difference between the low and high effective pressure profiles from the seismic data (Figure 10c and Figure 11c) serves as a direct comparison with the differential effective pressure from the stress distribution diagram (Figure 13c). The differential effective pressure derived from the seismic data shows a non-constant pressure change with increasing depth for both east and west sides of the study area building (Figure 14). However, the stress distribution diagram shows a constant differential effective pressure of 70 kPa with depth (Figure 14).

5. Discussion

The closely spaced CMP samples (Figure 6 and Figure 7) are useful because they provide laterally continuous data to assess the pressure changes in the floodplain sediments. Piezometers can monitor water pressure in the aquifer below low-permeability surface layer but do not provide the necessary laterally continuous data at the meter-scale. S-wave seismic velocities can sense effective pressure changes in the aquifer continuously throughout the length of the acquisition survey. For example, the VSH data show a difference between low and high river stages which is representative of a relative change in effective pressure.
The seismic reflection technique can offer higher horizontal resolution (0.5 m) than seismic refraction tomography or surface wave dispersion analysis for extracting S-wave velocities in the near-surface (<40 m). Even though surface wave dispersion analysis is one of the most used methods for soil site investigations, the horizontal resolution is limited to 10 m where VS is less than 500 m/s for depths shallower than 30 m [90]. The vertical resolution for the surface wave dispersion method can be higher depending on the phase velocity and highest frequency available [91], but is known to decrease with depth as the surface waves sample deeper material and are limited to the length of the surface wave with depth [90]. The seismic reflection data is only able to image the subsurface below around 10 m in depth and cover our target zone (>10 m but less than 40 m). This limitation of seismic reflection imaging is because of the presence of surface waves, which are typically muted or filtered out as noise during reflection processing.
In the semblance velocity analysis, seismic reflectors in a single shot-gather can be difficult to identify with the noise that overlaps or obscures the reflection hyperbolas. This noise is from the surface waves at shallower intervals or contamination from external sources in urban areas (cars, people walking, etc.). A way to increase signal-to-noise ratio in the semblance analysis is by increasing the fold with a shoot-through/split-spread acquisition geometry. The highest fold is at the middle of the survey and decreases towards the edges. Having a higher fold means that the probability of having the same hyperbolic events velocity-corrected to be flat at an equal time is higher. In other words, the best statistical match of hyperbolic arrivals is detected within the data. Therefore, in Figure 8 the higher semblance values represent the highest confidence points. After flattening the CMP gathers with the correct VRMS, the stacking or sum process of the traces ensure that we reduce the uncertainty of external unwanted noise. The stacking procedure of gathers with high fold is one of the biggest noise suppressants. As a rule of thumb, we picked the high-value of the contoured velocity spectra (VRMS) with increasing velocity to avoid possible multiples being mixed in the analysis. Therefore, the fold can be seen as a measure to reduce uncertainty in the data; the higher the fold, the less the uncertainty. In addition, we incorporate the uncertainty range of the contoured high-value velocity spectra (VRMS) in the semblance analysis, which have a mean of 28 m/s and a standard deviation = ± 7 m/s. That is, how much velocity estimates can change depending on the picked VRMS in the semblance plot.
SH data confirms that with increasing distance from the levee, the aquifer transitions from a confined aquifer to a leaky confined aquifer (Figure 2). At a distance of 25 m east of the toe of the artificial levee (Figure 2), the post-stack seismic CMP profile on the west side of the building (Figure 5a) shows dipping point bar sediment layers with strong continuous seismic reflectors. By contrast, the post-stack CMP profile at 355 m from the levee and east of the study area building (Figure 5b), shows seismic reflectors with noticeable discontinuities interpreted as possible cracks. Preferential water flow paths could exist in these discontinuous features permitting upward flow through the natural blanket [57].
The limitation of using S-wave seismic post-stack data is that seismic reflectors are not resolved above 10 m, limiting the seismic interpretation of the upper, lower-permeability top stratum. Love (surface) waves partly interfere with the earlier near-surface SH reflected wave arrivals and are difficult to separate. For example, Figure 5a shows several dipping layers from A’ to A, specifically at ~10 m in depth, and in the horizontal distance from 30 m to 48 m, the dipping reflector signal-to-noise ratio starts to decrease. This results in the first picked velocity in the semblance analysis plot (velocity vs. time) from 30 m to 48 m to be a higher time with respect to the zone from 1 m to 30 m on the CMP gathers, therefore causing a lower-velocity zone, as seen in Figure 6 (from 30 to 48 m).
The higher effective pressure observed during low river stage (Figure 10 and Figure 11) could be result of the interparticle stresses such as soil suction stress [51,92]. For example, Shen, Crane, Lorenzo, and White [51] showed that soil suction stress can be as high as 700 kPa in clay, and 1.5 kPa in sand. Confining pressure becomes more influential than interparticle stresses at depths greater than 0.1 m in sand and 100 m in clay. During the high river stage, the layer above the confined aquifer must remain impervious so that the pore pressure changes in the aquifer can decrease the particle-to-particle contact effective pressure and reduce S-wave velocity sensed by the seismic data. This scenario causes the biggest variation in differential effective pressure between low and high river stages, suggesting that the pore water pressure is maintained in the confined aquifer. The effective pressure from the seismic data shows a greater variation of up to +700/−150 kPa in the confined aquifer zone (Figure 10c), compared with the leaky confined aquifer zone of up to +140/−80 kPa (Figure 11c).
The lower variation of differential effective pressure in the interpreted leaky confined aquifer (Figure 11c) may be the result of insufficient pore pressure building up in the aquifer. One possible explanation for this phenomenon is that during high river stages, there is upward leakage of water through preferential flow paths made by cracks in the upper impermeable layer that does not trigger a sufficient change in S-wave seismic velocities between low and high river stages. An alternative interpretation is that the pore pressure is not enough to trigger a decrease in S-wave seismic velocities at a distance of 355 m from the Mississippi River levee. However, by modeling the pore pressure decrease with distance from the levee toe (Figure 12c) using Equation (4), we found that the pore pressure during low stage and high stage are the same at 2000 m from the levee toe. Therefore, at 355 m the pore pressure from the Mississippi River should be maintained and be similar as at a distance of 25 m. An upward leakage of water through preferential flow paths made by cracks could be the mechanism that does not allow a sufficient change in S-wave seismic velocities during high stage.
The uncertainty in the kriging-interpolated datasets between the confined and leaky aquifers (VSH and effective pressure profiles) is compared by calculating the standard deviation of the gridded differential profiles independently. In the confined aquifer differential profiles (Figure 6c and Figure 10c), there is a higher standard deviation of ±54 m/s or 101 kPa in comparison with the leaky aquifer differential profiles (Figure 7c and Figure 11c) with a standard deviation of ±24 m/s or ±50 kPa. The confined aquifer shows a higher dispersion of VSH or effective pressure values than the leaky aquifer. In other words, the lower variation of VSH or effective pressure in the leaky confined aquifer may be the result of insufficient pore pressure building up in the aquifer, as compared with the confined aquifer.
The effective pressure models created from the S-wave seismic acquisition can change depending on the power–law relationship used (Figure 9). The powerline trend that uses all the available samples is the most conservative curve since it is backed up by most of the data available on natural sands [2,50]. There are no available measurements of effective pressure and shear-wave velocity in the study area (Duncan Point). Prasad [50] and Zimmer [2]’s measurements were made in a controlled laboratory setting with sand samples from different regions. For example, Zimmer (2003) used an experimental apparatus constructed to measure compressional- and shear-wave velocities at ultrasonic frequencies through unconsolidated sediment samples at pressures from 0.1 MPa and 20 MPa. Walton [53] and Lee [54]’s theoretical models are within the same trend of the resulting power-curve from the plotted data (Figure 9). The strong lateral heterogeneity in floodplain sediments makes clay content difficult to predict regardless of the number of borings in the area. Clay content can drastically change the S-wave velocity and pressure relationship (Figure 9b). This is demonstrated by other empirical power-curve results from [45], which use both clean sands and sand packs that have 8% clay by weight (Figure 9b). The incorporation of as much as 8% of clay in the clean sands bind the loose sand grains, thereby increasing the S-wave velocity at a given pressure [45].

6. Conclusions

In our study area, floodplain sediments are heterogeneous at the meter-scale with changes in facies composition and architecture. The seasonal variations in the water level of the Mississippi River create pore pressure changes in the adjacent hydraulically connected aquifer on the protected side of artificial levees.
Time-lapse S-wave velocity analysis or repetition of seismic acquisition over an area demonstrated to be an effective method to detect seasonal pressure variations in shallow (<40 m) aquifers. We performed a seismic field experiment on the protected side of an artificial levee of the Mississippi River to investigate the pressure regime changes in an aquifer induced by the seasonal hydraulic head variations on the Mississippi River.
Pressure changes caused by the river seasonal hydraulic head variations were captured by S-wave velocities variations caused by hyperbolic seismic reflections changes for the same event at different times of the year. In the semblance velocity analysis, a change in the reflection hyperbola represents a change in seismic velocity.
The seismic reflection patterns during high, intermediate, and low river seasonal variations show a distinctive change in the velocity semblance analysis, which is translated as a change in the average stress carried by the grain-to-grain contact, or simply the effective pressure. We performed the time-lapse seismic experiments at 25 m and 355 m from the levee toe. The west side of the study area closer to the river has a thicker (~8 to 14 m) upper impervious confining layer than the east side (~3 to 5 m), which contains a leaky confined aquifer. The seismic data show a greater variation of up to +140/−40 m/s or +700/−150 kPa in the confined aquifer zone, compared with the leaky confined aquifer zone of up to +46/−48 m/s or +140/−80 kPa.
Higher water levels in the Mississippi River increase the pore pressure in the confined aquifer of the floodplain area, and this pore pressure increase can be translated as a decrease in the S-wave velocities from the seismic reflection surveys or effective pressure. In the scenario of the leaky confined aquifer, there is upward leakage of water through preferential flow paths made by cracks in the upper impermeable layer not triggering a sufficient change in S-wave seismic velocities between low and high river stages.
These relative effective pressure characteristics allow us to distinguish between confined and leaky aquifers, and can be an optional approach for pressure prediction in floodplains along the levees without the need to drill borings in the area to measure piezometric data.
However, future investigations may still benefit from the integration of VSH data and effective pressure measurements with depth in field conditions to calibrate the differential effective pressure trends from both the seismic data and the stress model. While laboratory results are an effective approach to obtain controlled effective pressure and seismic velocity measurements, field data can be used to estimate effective pressure from VSH in absolute units rather than relative.

Author Contributions

Conceptualization, D.L.-L. and J.M.L.; Methodology, D.L.-L. and J.M.L.; Software, D.L.-L. and J.M.L.; Validation, D.L.-L. and J.M.L.; Formal analysis, D.L.-L. and J.M.L.; Investigation, D.L.-L. and J.M.L.; Resources, J.M.L.; Data curation, D.L.-L.; Writing—original draft, D.L.-L.; Writing—review & editing, D.L.-L. and J.M.L.; Visualization, D.L.-L.; Supervision, J.M.L.; Project administration, J.M.L.; Funding acquisition, D.L.-L. and J.M.L.. All authors have read and agreed to the published version of the manuscript.

Funding

Work in this study by D.L. was supported by a SEG 2020 Near-Surface Research Award program, a 2021 American Association of Petroleum Geologists Foundation Grants-in-Aid Program (Ike Crumbly Minorities in Energy Grant), a 2020 Debra and James Anderson Superior Graduate Scholarship, a 2019 and 2020 Applied Depositional Geosystems (ADG) Fellowship, a 2019 and 2021 Houston Energy and L.P. Graduate Student Scholarship, and a 2021 USGS Water Resources Research Act Program (Project ID 2020LA032B to J.M.L).

Data Availability Statement

The data used in this study are presented within the body of the article and may also be obtained by contacting the corresponding author.

Acknowledgments

Many people contributed to the development of this research. F. Tsai generously provided boring descriptions. A. Omale, F. Tsai’s graduate students, and P. Bart’s 2019 Seismic Stratigraphy class provided field support during the acquisition of the seismic data. The LSU School of Veterinary Medicine facilitated access to their grounds during the survey acquisition.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Boyd, E. Assessing the Benefits of Levees: An Economic Assessment of US Counties with Levees; Levees.org: New Orleans, LA, USA, 2009. [Google Scholar]
  2. Zimmer, M.A. Seismic Velocities in Unconsolidated Sands: Measurements of Pressure, Sorting, and Compaction Effects; Stanford University: Stanford, CA, USA, 2004. [Google Scholar]
  3. Schiermeier, Q. Increased flood risk linked to global warming. Nature 2011, 470, 316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Ward, P.J.; Winsemius, H.C.; Kuzma, S.; Bierkens, M.F.; Bouwman, A.; De Moel, H.; Loaiza, A.D.; Eilander, D.; Englhardt, J.; Erkens, G. Aqueduct floods methodology. World Resour. Inst. 2020, 1–28. Available online: https://www.wri.org/research/aqueduct-floods-methodology (accessed on 12 December 2022).
  5. Cola, S.; Girardi, V.; Bersan, S.; Simonini, P.; Schenato, L.; De Polo, F. An optical fiber-based monitoring system to study the seepage flow below the landside toe of a river levee. J. Civ. Struct. Health Monit. 2021, 11, 691–705. [Google Scholar] [CrossRef]
  6. Cooper, H.H.; Rorabaugh, M.I. Ground-water movements and bank storage due to flood stages in surface streams. U.S.G.P.O. 1963, ill, 343–366. [Google Scholar]
  7. Heinrich, P.; Autin, W. Baton Rouge 30 X 60 Minute Geologic Quadrangle: Louisiana Geological Survey; Louisiana Geological Survey: Baton Rouge, LA, USA, 2000. [Google Scholar]
  8. Ozkan, S.; Adrian, D.D.; Sills, G.L.; Singh, V.P. Transient Head Development due to Flood Induced Seepage under Levees. J. Geotech. Geoenvironmental Eng. 2008, 134, 781–789. [Google Scholar] [CrossRef]
  9. USACE. The Mississippi River & Tributaries Project: History of the Lower Mississippi River Levee System; Mississippi River Commission: Vicksburg, MS, USA, 2007. [Google Scholar]
  10. Fisk, H.N. Geological Investigation of the Alluvial Valley of the Lower Mississippi River, 170; Mississippi River Commission: Vicksburg, MS, USA, 1944. [Google Scholar]
  11. Meyer, R.R.; Turcan, A.N. Geology and Ground-water Resources of the Baton Rouge Area, Louisiana; US Government Printing Office: Washington, DC, USA, 1955. [Google Scholar]
  12. Turnbull, W.; Mansur, C. Underseepage and its control: A symposium: Investigation of underseepage-Mississippi River levees. Trans. Am. Soc. Civ. Eng. 1961, 126, 1429–1481. [Google Scholar] [CrossRef]
  13. Dunnicliff, J. Geotechnical Instrumentation for Monitoring Field Performance; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
  14. Van Der Kamp, G. Methods for determining the in situ hydraulic conductivity of shallow aquitards—An overview. Hydrogeol. J. 2001, 9, 5–16. [Google Scholar] [CrossRef]
  15. Mansur, C.I.; Postol, G.; Salley, J.R. Performance of Relief Well Systems along Mississippi River Levees. J. Geotech. Geoenviron. Eng. 2000, 126, 727–738. [Google Scholar] [CrossRef]
  16. Zhu, L.; Gong, H.; Chen, Y.; Li, X.; Chang, X.; Cui, Y. Improved estimation of hydraulic conductivity by combining stochastically simulated hydrofacies with geophysical data. Sci. Rep. 2016, 6, 22224. [Google Scholar] [CrossRef] [Green Version]
  17. Lorenzo, J.; Doll, W. Levees and Dams: Advances in Geophysical Monitoring and Characterization; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
  18. Ivanov, J.; Miller, R.D.; Ballard, R.F., Jr.; Dunbar, J.B.; Smullen, S. Time-lapse seismic study of levees in southern Texas. In SEG Technical Program Expanded Abstracts 2005; Society of Exploration Geophysicists: Houston, TX, USA, 2005; pp. 1121–1124. [Google Scholar]
  19. Ivanov, J.; Miller, R.D.; Stimac, N.; Ballard, R.F., Jr.; Dunbar, J.B.; Smullen, S. Time-lapse seismic study of levees in southern New Mexico. In SEG Technical Program Expanded Abstracts 2006; Society of Exploration Geophysicists: New Orleans, LA, USA, 2006; pp. 3255–3259. [Google Scholar]
  20. Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; J. Wiley Hoboken: Hoboken, NJ, USA, 2004. [Google Scholar]
  21. Pasquet, S.; Bodet, L.; Bergamo, P.; Guérin, R.; Martin, R.; Mourgues, R.; Tournat, V. Small-scale seismic monitoring of varying water levels in granular media. Vadose Zone J. 2016, 15, 1–14. [Google Scholar] [CrossRef]
  22. Cameron, A.; Knapp, C. A new approach to predict hydrogeological parameters using shear waves from multichannel analysis of surface waves method. In Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems, Denver, CO, USA, 20–24 March 2009; p. 475. [Google Scholar]
  23. Grelle, G.; Guadagno, F.M. Seismic refraction methodology for groundwater level determination: “Water seismic index”. J. Appl. Geophys. 2009, 68, 301–320. [Google Scholar] [CrossRef]
  24. Konstantaki, L.; Carpentier, S.; Garofalo, F.; Bergamo, P.; Socco, L. Determining hydrological and soil mechanical parameters from multichannel surface-wave analysis across the Alpine Fault at Inchbonnie, New Zealand. Near Surf. Geophys. 2013, 11, 435–448. [Google Scholar] [CrossRef]
  25. Pasquet, S.; Holbrook, W.; Carr, B.; Sims, K. Geophysical imaging of shallow degassing in a Yellowstone hydrothermal system. Geophys. Res. Lett. 2016, 43, 12027–12035. [Google Scholar] [CrossRef]
  26. Pride, S.R. Relationships between seismic and hydrological properties. In Hydrogeophysics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 253–290. [Google Scholar]
  27. Bergamo, P.; Dashwood, B.; Uhlemann, S.; Swift, R.; Chambers, J.E.; Gunn, D.A.; Donohue, S. Time-lapse monitoring of fluid-induced geophysical property variations within an unstable earthwork using P-wave refraction. Geophysics 2016, 81, EN17–EN27. [Google Scholar] [CrossRef] [Green Version]
  28. Bergamo, P.; Socco, L.V. P-and S-wave velocity models of shallow dry sand formations from surface wave multimodal inversionVP and VS model of dry sand with SW. Geophysics 2016, 81, R197–R209. [Google Scholar] [CrossRef]
  29. Ikeda, T.; Tsuji, T.; Takanashi, M.; Kurosawa, I.; Nakatsukasa, M.; Kato, A.; Worth, K.; White, D.; Roberts, B. Temporal variation of the shallow subsurface at the Aquistore CO2 storage site associated with environmental influences using a continuous and controlled seismic source. J. Geophys. Res. Solid Earth 2017, 122, 2859–2872. [Google Scholar] [CrossRef]
  30. Lu, Z. Feasibility of using a seismic surface wave method to study seasonal and weather effects on shallow surface soils. J. Environ. Eng. Geophys. 2014, 19, 71–85. [Google Scholar] [CrossRef]
  31. Ajo-Franklin, J.; Dou, S.; Daley, T.; Freifeld, B.; Robertson, M.; Ulrich, C.; Wood, T.; Eckblaw, I.; Lindsey, N.; Martin, E. Time-lapse surface wave monitoring of permafrost thaw using distributed acoustic sensing and a permanent automated seismic source. In Proceedings of the 2017 SEG International Exposition and Annual Meeting, Houston, TX, USA, 27 September 2017. [Google Scholar]
  32. Arts, R.; Eiken, O.; Chadwick, A.; Zweigel, P.; Van der Meer, L.; Zinszner, B. Monitoring of CO2 injected at Sleipner using time lapse seismic data. In Proceedings of the Greenhouse Gas Control Technologies-6th International Conference, Kyoto, Japan, 1–4 October 2002; pp. 347–352. [Google Scholar]
  33. Chadwick, A.; Williams, G.; Delepine, N.; Clochard, V.; Labat, K.; Sturton, S.; Buddensiek, M.-L.; Dillen, M.; Nickel, M.; Lima, A.L.; et al. Quantitative analysis of time-lapse seismic monitoring data at the Sleipner CO2 storage operation. Lead. Edge 2010, 29, 170–177. [Google Scholar] [CrossRef] [Green Version]
  34. St. Clair, J.; Moon, S.; Holbrook, W.; Perron, J.; Riebe, C.; Martel, S.; Carr, B.; Harman, C.; Singha, K.; deB. Richter, D. Geophysical imaging reveals topographic stress control of bedrock weathering. Science 2015, 350, 534–538. [Google Scholar] [CrossRef] [Green Version]
  35. Landrø, M. Discrimination between pressure and fluid saturation changes from time-lapse seismic data. Geophysics 2001, 66, 836–844. [Google Scholar] [CrossRef]
  36. Lumley, D.E. Time-lapse seismic reservoir monitoring. Geophysics 2001, 66, 50–53. [Google Scholar] [CrossRef]
  37. Johnston, D.H. Practical Applications of Time-Lapse Seismic Data; Society of Exploration Geophysicists: Houston, TX, USA, 2013. [Google Scholar] [CrossRef]
  38. Domenico, S. Effect of brine-gas mixture on velocity in an unconsolidated sand reservoir. Log Anal. 1977, 18. [Google Scholar] [CrossRef]
  39. Estes, C.; Mavko, G.; Yin, H.; Cadoret, T. Measurements of velocity, porosity, and permeability on unconsolidated granular materials. SRB Annu. Rep. B 1994, 55, G1-1–G1-9. [Google Scholar]
  40. Prasad, M.; Meissner, R. Attenuation mechanisms in sands: Laboratory versus theoretical (Biot) data. Geophysics 1992, 57, 710–719. [Google Scholar] [CrossRef] [Green Version]
  41. Robertson, P.; Sasitharan, S.; Cunning, J.; Sego, D. Shear-wave velocity to evaluate in-situ state of Ottawa sand. J. Geotech. Eng. 1995, 121, 262–273. [Google Scholar] [CrossRef]
  42. Yin, H. Acoustic Velocity and Attenuation of Rocks: Isotropy, Intrinsic Anisotropy, and Stress-induced Anisotropy; Stanford University: Stanford, CA, USA, 1993. [Google Scholar]
  43. Hofmann, R.; Xu, X.; Batzle, M.; Prasad, M.; Furre, A.-K.; Pillitteri, A. Effective pressure or what is the effect of pressure? Lead. Edge 2005, 24, 1256–1260. [Google Scholar] [CrossRef]
  44. Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1943. [Google Scholar]
  45. Huffman, A.R.; Castagna, J.P. The petrophysical basis for shallow-water flow prediction using multicomponent seismic data. Lead. Edge 2001, 20, 1030–1052. [Google Scholar] [CrossRef]
  46. Zimmer, M.A.; Prasad, M.; Mavko, G.; Nur, A. Seismic velocities of unconsolidated sands: Part 1—Pressure trends from 0.1 to 20 MPa. Geophysics 2007, 72, E1–E13. [Google Scholar] [CrossRef]
  47. Castagna, J.P. Petrophysical imaging using AVO. Lead. Edge 1993, 12, 172–178. [Google Scholar] [CrossRef]
  48. Eberhart-Phillips, D.; Han, D.-H.; Zoback, M. Empirical relationships among seismic velocity, effective pressure, porosity, and clay content in sandstone. Geophysics 1989, 54, 82–89. [Google Scholar] [CrossRef]
  49. Lee, M.W. Predicting S-Wave Velocities for Unconsolidated Sediments at Low Effective Pressure; U. S. Geological Survey: Denver, CO, USA, 2010. [Google Scholar]
  50. Prasad, M. Acoustic measurements in unconsolidated sands at low effective pressure and overpressure detection. Geophysics 2002, 67, 405–412. [Google Scholar] [CrossRef]
  51. Shen, J.; Crane, J.M.; Lorenzo, J.M.; White, C.D. Seismic velocity prediction in shallow (<30 m) partially saturated, unconsolidated sediments using effective medium theory. J. Environ. Eng. Geophys. 2016, 21, 67–78. [Google Scholar]
  52. Velea, D.; Shields, F.D.; Sabatier, J.M. Elastic wave velocities in partially saturated Ottawa sand: Experimental results and modeling. Soil Sci. Soc. Am. J. 2000, 64, 1226–1234. [Google Scholar] [CrossRef]
  53. Walton, K. The effective elastic moduli of a random packing of spheres. J. Mech. Phys. Solids 1987, 35, 213–226. [Google Scholar] [CrossRef]
  54. Lee, M.W. A simple method of predicting S-wave velocity. Geophysics 2006, 71, F161–F164. [Google Scholar] [CrossRef]
  55. USACE. Design and Construction of Levees: In Engineering and Design Manuals; Dept. of the Army: Washington, DC, USA, 2000. [Google Scholar]
  56. Kolb, C.; Van Lopik, J. Geology of the Mississippi River Deltaic Plain, Southeastern Louisiana: US Army Corps of Engineers; Technical Report 2; Waterways Experiment Station: Vicksburg, MS, USA, 1958. [Google Scholar]
  57. Jafari, N.H.; Cadigan, J.A.; Stark, T.D.; Woodward, M.L. Phreatic Surface Migration through an Unsaturated Levee Embankment. J. Geotech. Geoenvironmental Eng. 2019, 145, 11. [Google Scholar] [CrossRef]
  58. Woodward, M. Mississippi River Levees LSU-Duncan Point Seepage Study; Rep. No. ITEM M-227.5 to 217.1-L; U.S. Army Corps of Engineers: Washington, DC, USA, 1992. [Google Scholar]
  59. DeHaan, H.; Stamper, J.; Walters, B. Mississippi River and Tributaries System 2011 Post-Flood Report: Documenting the 2011 Flood, the Corps’ Response, and the Performance of the MR&T System; U.S. Army Corps of Engineers Digital Library: Vicksburg, MS, USA, 2012. [Google Scholar]
  60. Fisk, H.N. Geological Investigation of the Atchafalaya Basin and the Problem of Mississippi River Diversion; Waterways Experiment Station: Vicksburg, MS, USA, 1952. [Google Scholar]
  61. Saucier, R.T. Geomorphology and Quaternary Geologic History of the Lower Mississippi Valley; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1994; Volume 1. [Google Scholar]
  62. Thomas, R.G.; Smith, D.G.; Wood, J.M.; Visser, J.; Calverley-Range, E.A.; Koster, E.H. Inclined heterolithic stratification—Terminology, description, interpretation and significance. Sediment. Geol. 1987, 53, 123–179. [Google Scholar] [CrossRef]
  63. Saucier, R.T. Geological Investigation of the Mississippi River Area, Artonish to Donaldsville, La; Waterways Experiment Station: Vicksburg, MS, USA, 1969. [Google Scholar]
  64. Gibling, M.; Rust, B. Alluvial ridge-and-swale topography: A case study from the Morien Group of Atlantic Canada. Alluv. Sediment. 1993, 17, 133–150. [Google Scholar]
  65. Allen, J. The classification of cross-stratified units. With notes on their origin. Sedimentology 1963, 2, 93–114. [Google Scholar] [CrossRef]
  66. McGowen, J.; Garner, L. Physiographic Features and Stratification Types of Coarse-Grained Pointbars: Modern and Ancient Examples 1. Sedimentology 1970, 14, 77–111. [Google Scholar] [CrossRef]
  67. Davies, D.K. Sedimentary structures and subfacies of a Mississippi River point bar. J. Geol. 1966, 74, 234–239. [Google Scholar] [CrossRef]
  68. Evans, B.J. A Handbook for Seismic Data Acquisition in Exploration; Society of Exploration Geophysicists: Houston, TX, USA, 1997. [Google Scholar] [CrossRef]
  69. Vincent, P.D.; Steeples, D.W.; Tsoflias, G.P.; Sloan, S.D. Two approaches to noise tests. In SEG Technical Program Expanded Abstracts 2005; Society of Exploration Geophysicists: Houston, TX, USA, 2005; pp. 1180–1183. [Google Scholar]
  70. Lorenzo, J.M.; Hicks, J.; Vera, E.E. Integrated seismic and cone penetration test observations at a distressed earthen levee: Marrero, Louisiana, U.S.A. Eng. Geol. 2014, 168, 59–68. [Google Scholar] [CrossRef]
  71. Stockwell, J.W., Jr. The CWP/SU: Seismic Un∗ x package. Comput. Geosci. 1999, 25, 415–419. [Google Scholar] [CrossRef]
  72. Taner, M.T.; Koehler, F. Velocity spectra—Digital computer derivation applications of velocity functions. Geophysics 1969, 34, 859–881. [Google Scholar] [CrossRef]
  73. Stolt, R.H. Migration by Fourier transform. Geophysics 1978, 43, 23–48. [Google Scholar] [CrossRef]
  74. Helbig, K. Shear-waves—What they are and how they can be used. Shear-Wave Explor. Ed. SN Domen. SH Danbom Geophys. Dev. Ser. 1986, 1, 19–36. [Google Scholar]
  75. Stümpel, H.; Kähler, S.; Meissner, R.; Milkereit, B. The use of seismic shear waves and compressional waves for lithological problems of shallow sediments. Geophys. Prospect. 1984, 32, 662–675. [Google Scholar] [CrossRef]
  76. Liner, C.L. Elements of 3D Seismology; Society of Exploration Geophysicists: Tulsa, OK, USA, 2016. [Google Scholar]
  77. Sheriff, R.E. Geophysical Methods; Prentice Hall: Hoboken, NJ, USA, 1989. [Google Scholar]
  78. Jarvis, K.D.; Knight, R.J. Aquifer heterogeneity from SH-wave seismic impedance inversion. Geophysics 2002, 67, 1548–1557. [Google Scholar] [CrossRef]
  79. Harris, J.B. Hammer-impact SH-wave seismic reflection methods in neotectonic investigations: General observations and case histories from the Mississippi Embayment, USA. J. Earth Sci. 2009, 20, 513–525. [Google Scholar] [CrossRef]
  80. Lorenzo, J.M.; Rousset, D.; Senechal, G. L_SU (V0. 3.9): A graphical user interface useful for building seismic flows from Seismic Unix. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2019; p. NS21A-10. [Google Scholar]
  81. Miller, R.D.; Xia, J.; Park, C.B. Love waves: A menace to shallow shear wave reflection surveying. In SEG Technical Program Expanded Abstracts 2001; Society of Exploration Geophysicists: San Antonio, LA, USA, 2001; pp. 1377–1380. [Google Scholar]
  82. Hammah, R.; Curran, J. Geostatistics in geotechnical engineering: Fad or empowering? GeoCongress 2006, 2006, 1–5. [Google Scholar]
  83. Fam, M.; Santhamarian, J. A study of consolidation using mechanical and electromagnetic waves. Geotechnique 1997, 47, 203–219. [Google Scholar] [CrossRef]
  84. Peter, P. Canal and River Levees. Dev. Geotech. Eng. 1982, 29, 249–253. [Google Scholar]
  85. Ferris, J.G. Cyclic Fluctuations of Water Level as a Basis for Determining Aquifer Transmissibility; US Geological Survey: Washington, DC, USA, 1952. [Google Scholar]
  86. Pinder, G.F.; Bredehoeft, J.D.; Cooper, H.H., Jr. Determination of aquifer diffusivity from aquifer response to fluctuations in river stage. Water Resour. Res. 1969, 5, 850–855. [Google Scholar] [CrossRef]
  87. Hall, F.R.; Moench, A.F. Application of the convolution equation to stream-aquifer relationships. Water Resour. Res. 1972, 8, 487–493. [Google Scholar] [CrossRef]
  88. Ozkan, S.; Adrian, D.D. Analytical Construction of Transient Flow Nets in Homogeneous and Isotropic Flow Medium. J. Geotech. Geoenvironmental Eng. 2008, 134, 888–893. [Google Scholar] [CrossRef]
  89. Heinrich, P.; Paulsell, R.; Milner, R.; Snead, J.; Peele, H. Investigation and GIS Development of the Buried Holocene-Pleistocene Surface in the Louisiana Coastal Plain; Louisiana State University, Louisiana Geological Survey: Baton Rouge, LA, USA, 2015. [Google Scholar]
  90. Park, C.B. MASW horizontal resolution in 2D shear-velocity (Vs) mapping. Open-File Rep. Lawrence Kans. Geol. Surv. 2005, 36, 1–11. [Google Scholar]
  91. Ivanov, J.; Miller, R.D.; Feigenbaum, D.; Morton, S.L.; Peterie, S.L.; Dunbar, J.B. Revisiting levees in southern Texas using Love-wave multichannel analysis of surface waves with the high-resolution linear Radon transform. Interpretation 2017, 5, T287–T298. [Google Scholar] [CrossRef]
  92. Lu, N.; Likos, W. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
Geosciences 13 00020 g001 550
Figure 1. (a) Regional location and sedimentary setting. The study area (black box) along the northern Gulf of Mexico Coast, USA, lies west of the city of Baton Rouge, Louisiana (right insets). Mapped surface sedimentary facies [7] are expected to represent near-surface (0–40 m) sediments. (b) Schematic view of confined flow under a levee (adapted from [8]).
Figure 1. (a) Regional location and sedimentary setting. The study area (black box) along the northern Gulf of Mexico Coast, USA, lies west of the city of Baton Rouge, Louisiana (right insets). Mapped surface sedimentary facies [7] are expected to represent near-surface (0–40 m) sediments. (b) Schematic view of confined flow under a levee (adapted from [8]).
Geosciences 13 00020 g001
Geosciences 13 00020 g002 550
Figure 2. Study area. Seismic and geotechnical data shown in this paper were collected on the eastern side of the artificial levee at the LSU Veterinary School. CMP (common Mid-Point) and PWA (pseudowalkaway) acquisition surveys are denoted with solid lines. Surveys A-A’ and B-B’ were acquired on the west side of the LSU School of Veterinary Medicine building. Surveys C-C’ and D-D’ were acquired on the east side of the building. We use data from ten (10) geotechnical wells (numbered black circles) that include laboratory physical properties (Figure 3). The rectangle with dashed lines is the parking lot east of the Veterinary school with visible surface cracks with water leaks during the high river stage.
Figure 2. Study area. Seismic and geotechnical data shown in this paper were collected on the eastern side of the artificial levee at the LSU Veterinary School. CMP (common Mid-Point) and PWA (pseudowalkaway) acquisition surveys are denoted with solid lines. Surveys A-A’ and B-B’ were acquired on the west side of the LSU School of Veterinary Medicine building. Surveys C-C’ and D-D’ were acquired on the east side of the building. We use data from ten (10) geotechnical wells (numbered black circles) that include laboratory physical properties (Figure 3). The rectangle with dashed lines is the parking lot east of the Veterinary school with visible surface cracks with water leaks during the high river stage.
Geosciences 13 00020 g002
Geosciences 13 00020 g003 550
Figure 3. Ten borings were conducted along the periphery of the LSU School of Veterinary Science building in 1979 (courtesy of a private firm). We group the soil descriptions into three dominant sediment types: clay, silt, or sand.
Figure 3. Ten borings were conducted along the periphery of the LSU School of Veterinary Science building in 1979 (courtesy of a private firm). We group the soil descriptions into three dominant sediment types: clay, silt, or sand.
Geosciences 13 00020 g003
Geosciences 13 00020 g004 550
Figure 4. River water stages from January 2019 to November 2022. Monitoring location USGS 07374000 Mississippi River at Baton Rouge, LA. Black circles indicate seismic acquisition dates with their respective river stages in the Vet. School grounds. The blue curve is the river stage, the red line is the maximum recorded river stage, the yellow line is the lowest recorded river stage, and the green line is the national weather service flood stage.
Figure 4. River water stages from January 2019 to November 2022. Monitoring location USGS 07374000 Mississippi River at Baton Rouge, LA. Black circles indicate seismic acquisition dates with their respective river stages in the Vet. School grounds. The blue curve is the river stage, the red line is the maximum recorded river stage, the yellow line is the lowest recorded river stage, and the green line is the national weather service flood stage.
Geosciences 13 00020 g004
Geosciences 13 00020 g005 550
Figure 5. (a) West CMP shear-wave seismic reflection profile (A-A’) at 25 m from levee toe. (b) East CMP shear-wave seismic reflection profile (C-C’) at 355 m from levee toe. Rectangles with dashed lines represent the zone where the velocity analysis has a usable fold. Solid interpreted lines represent continuous seismic reflectors. Dashed lines represent cracks.
Figure 5. (a) West CMP shear-wave seismic reflection profile (A-A’) at 25 m from levee toe. (b) East CMP shear-wave seismic reflection profile (C-C’) at 355 m from levee toe. Rectangles with dashed lines represent the zone where the velocity analysis has a usable fold. Solid interpreted lines represent continuous seismic reflectors. Dashed lines represent cracks.
Geosciences 13 00020 g005
Geosciences 13 00020 g006 550
Figure 6. West side (25 m from levee toe) shear-wave seismic profiles. Kriging-interpolated CMP-based interval velocities during (a) low and (b) high river stages, and the (c) differential shear-wave velocity. Mean = 35.5 m/s and standard deviation = ± 54 m/s.
Figure 6. West side (25 m from levee toe) shear-wave seismic profiles. Kriging-interpolated CMP-based interval velocities during (a) low and (b) high river stages, and the (c) differential shear-wave velocity. Mean = 35.5 m/s and standard deviation = ± 54 m/s.
Geosciences 13 00020 g006
Geosciences 13 00020 g007 550
Figure 7. East side (355 m from levee toe) shear-wave seismic profiles. Kriging-interpolated CMP-based interval velocities during (a) low and (b) high river stages, and (c) the differential shear-wave velocity. Mean = 2 m/s and standard deviation = ±24 m/s.
Figure 7. East side (355 m from levee toe) shear-wave seismic profiles. Kriging-interpolated CMP-based interval velocities during (a) low and (b) high river stages, and (c) the differential shear-wave velocity. Mean = 2 m/s and standard deviation = ±24 m/s.
Geosciences 13 00020 g007
Geosciences 13 00020 g008 550
Figure 8. Semblance analysis of shear-wave seismic data during low (a), middle (b), and high (c) stages. The middle-stage analysis uses a PWA survey and the low and high stages use a CMP data set. The solid lines represent trends with the highest semblance points. On the right of the semblance plot is the seismic reflection sorted by CMP.
Figure 8. Semblance analysis of shear-wave seismic data during low (a), middle (b), and high (c) stages. The middle-stage analysis uses a PWA survey and the low and high stages use a CMP data set. The solid lines represent trends with the highest semblance points. On the right of the semblance plot is the seismic reflection sorted by CMP.
Geosciences 13 00020 g008
Geosciences 13 00020 g009 550
Figure 9. Effective pressure vs. shear-wave velocity plots with Walton [53] and Lee [54] theoretical models, and empirical power-curve results from Huffman and Castagna [45], which use both clean sands and sand packs that have 8% clay by weight. (a) A plot in MPa with the full range of laboratory data from Prasad [50] and Zimmer [2], and (b) a plot in kPa for the range of effective pressure and velocity of interest in this study.
Figure 9. Effective pressure vs. shear-wave velocity plots with Walton [53] and Lee [54] theoretical models, and empirical power-curve results from Huffman and Castagna [45], which use both clean sands and sand packs that have 8% clay by weight. (a) A plot in MPa with the full range of laboratory data from Prasad [50] and Zimmer [2], and (b) a plot in kPa for the range of effective pressure and velocity of interest in this study.
Geosciences 13 00020 g009
Geosciences 13 00020 g010 550
Figure 10. West side (25 m from levee toe) effective pressure profiles. Kriging-interpolated CMP interval velocities converted to effective pressure in kPa during (a) low and (b) high river stages, and the (c) differential effective pressure. Mean = 101 kPa and standard deviation = ±274 kPa.
Figure 10. West side (25 m from levee toe) effective pressure profiles. Kriging-interpolated CMP interval velocities converted to effective pressure in kPa during (a) low and (b) high river stages, and the (c) differential effective pressure. Mean = 101 kPa and standard deviation = ±274 kPa.
Geosciences 13 00020 g010
Geosciences 13 00020 g011 550
Figure 11. East side (355 m from levee toe) effective pressure profiles. Kriging-interpolated CMP interval velocities converted to effective pressure in kPa during (a) low and (b) high river stages, and the (c) differential effective pressure. Mean = 18 kPa and standard deviation = ±50 kPa.
Figure 11. East side (355 m from levee toe) effective pressure profiles. Kriging-interpolated CMP interval velocities converted to effective pressure in kPa during (a) low and (b) high river stages, and the (c) differential effective pressure. Mean = 18 kPa and standard deviation = ±50 kPa.
Geosciences 13 00020 g011
Geosciences 13 00020 g012 550
Figure 12. (a) Typical levee section with selected parameters from the boring laboratory data to use in the transient fluid flow model created in Wolfram Mathematica. Boring laboratory data include unit weight values (γ) and thickness of upper lower permeability clay layer, and higher permeability substratum. Resulting transient fluid flow model with the duration of a flooding event during minimum (6 m) and maximum (13.5 m) river stages in time (b) and distance from the levee toe (c).
Figure 12. (a) Typical levee section with selected parameters from the boring laboratory data to use in the transient fluid flow model created in Wolfram Mathematica. Boring laboratory data include unit weight values (γ) and thickness of upper lower permeability clay layer, and higher permeability substratum. Resulting transient fluid flow model with the duration of a flooding event during minimum (6 m) and maximum (13.5 m) river stages in time (b) and distance from the levee toe (c).
Geosciences 13 00020 g012
Geosciences 13 00020 g013 550
Figure 13. Stress distribution diagrams from borings and transient fluid flow model for confining pressure (a), pore pressure (b), and effective pressure (c) during low (6 m) and high river stages (13.5 m).
Figure 13. Stress distribution diagrams from borings and transient fluid flow model for confining pressure (a), pore pressure (b), and effective pressure (c) during low (6 m) and high river stages (13.5 m).
Geosciences 13 00020 g013
Geosciences 13 00020 g014 550
Figure 14. Comparison of differential effective pressure from the stress distribution diagram derived (Figure 13c) and from differential effective pressure from the shear-wave seismic velocity data (Figure 10c and Figure 11c).
Figure 14. Comparison of differential effective pressure from the stress distribution diagram derived (Figure 13c) and from differential effective pressure from the shear-wave seismic velocity data (Figure 10c and Figure 11c).
Geosciences 13 00020 g014
Geosciences 13 00020 g015 550
Figure 15. Comparison of shear-wave seismic velocities during low and high river stages using a central CMP and during mid-river stage using the PWA data on (a) the east side of Vet. School (25 m from levee toe) and (b) west side (355 m from levee toe).
Figure 15. Comparison of shear-wave seismic velocities during low and high river stages using a central CMP and during mid-river stage using the PWA data on (a) the east side of Vet. School (25 m from levee toe) and (b) west side (355 m from levee toe).
Geosciences 13 00020 g015
Table
Table 1. Equipment, their accuracy, and seismic algorithms used to collect and display the seismic data.
Table 1. Equipment, their accuracy, and seismic algorithms used to collect and display the seismic data.
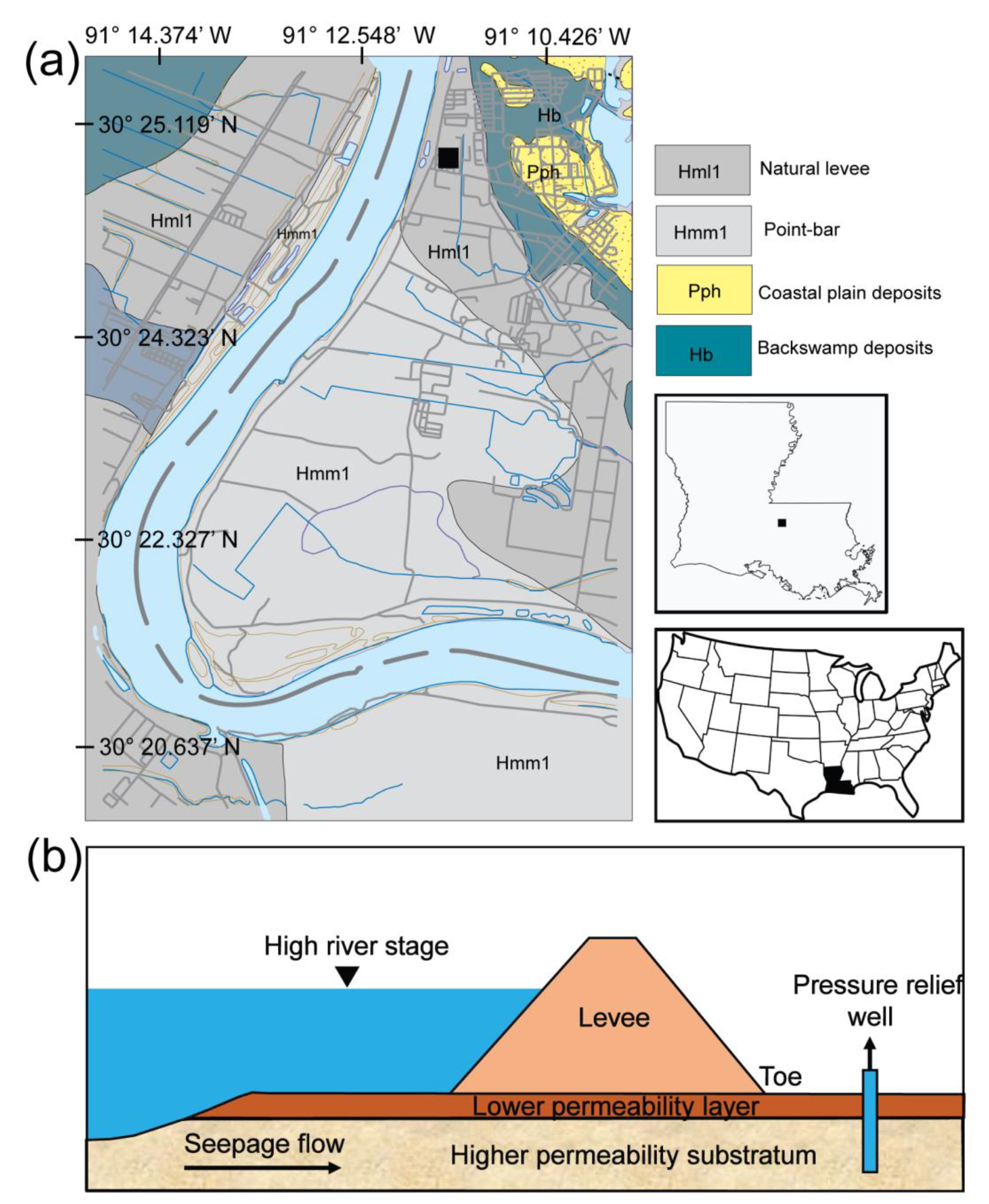
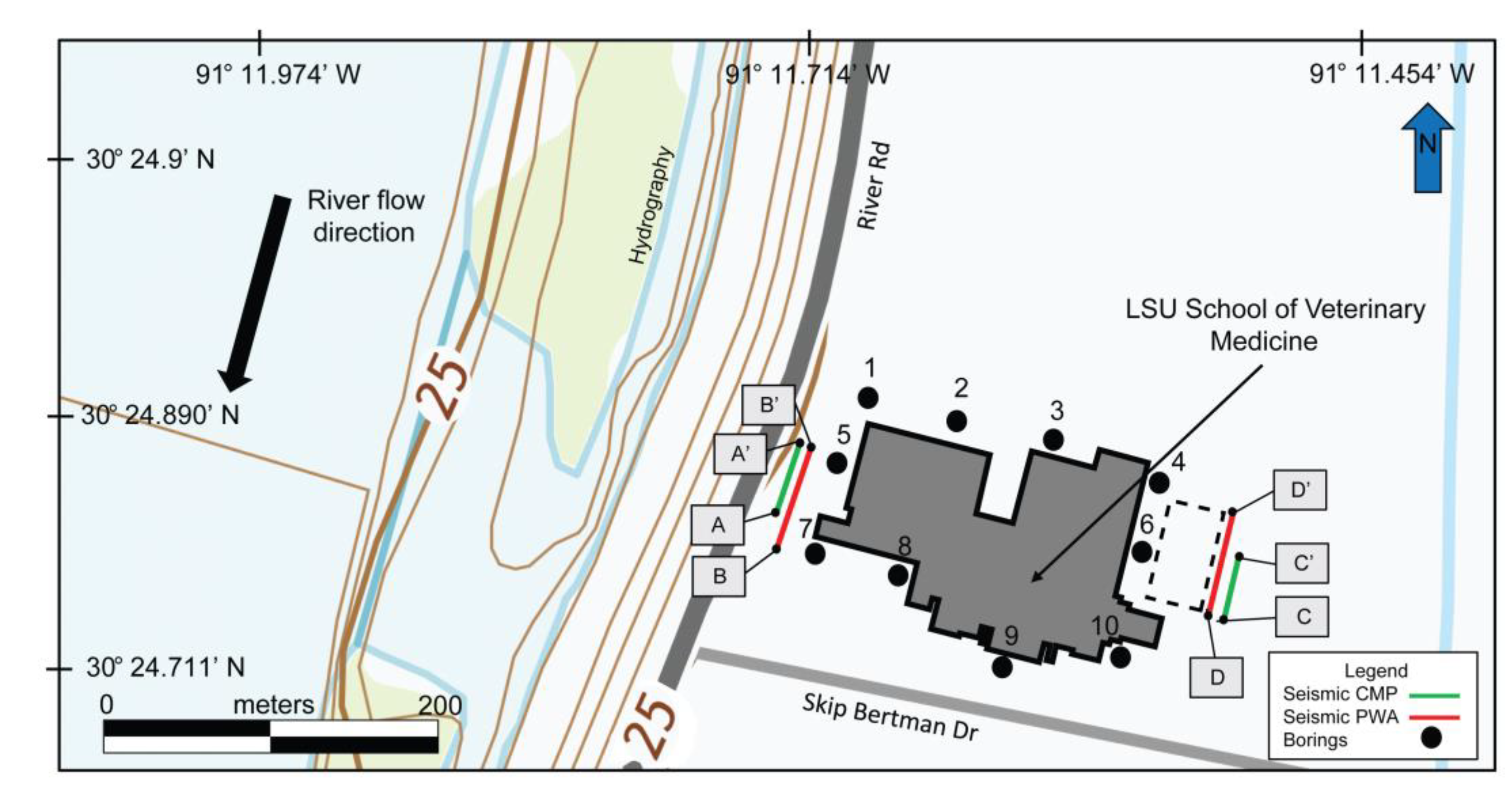
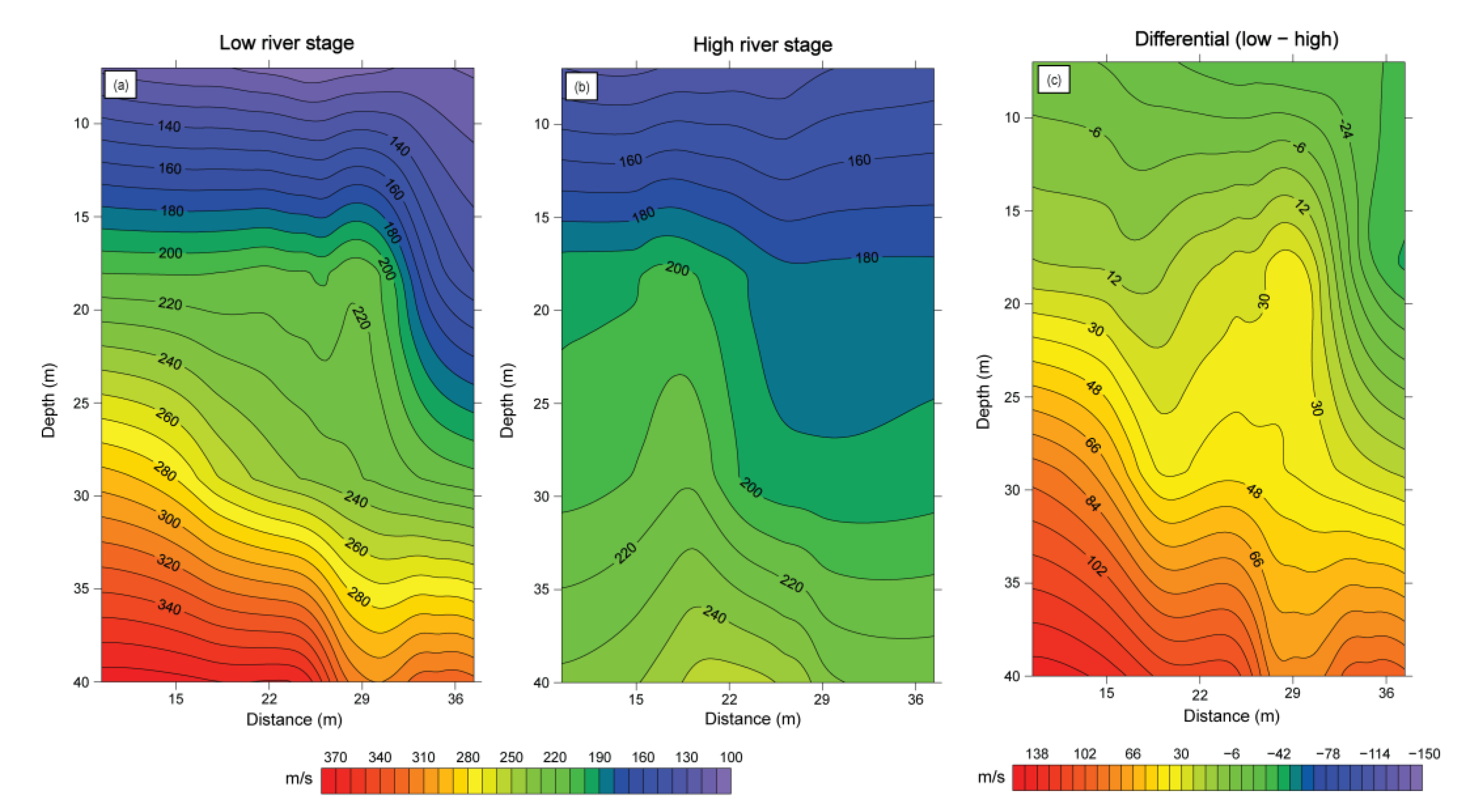
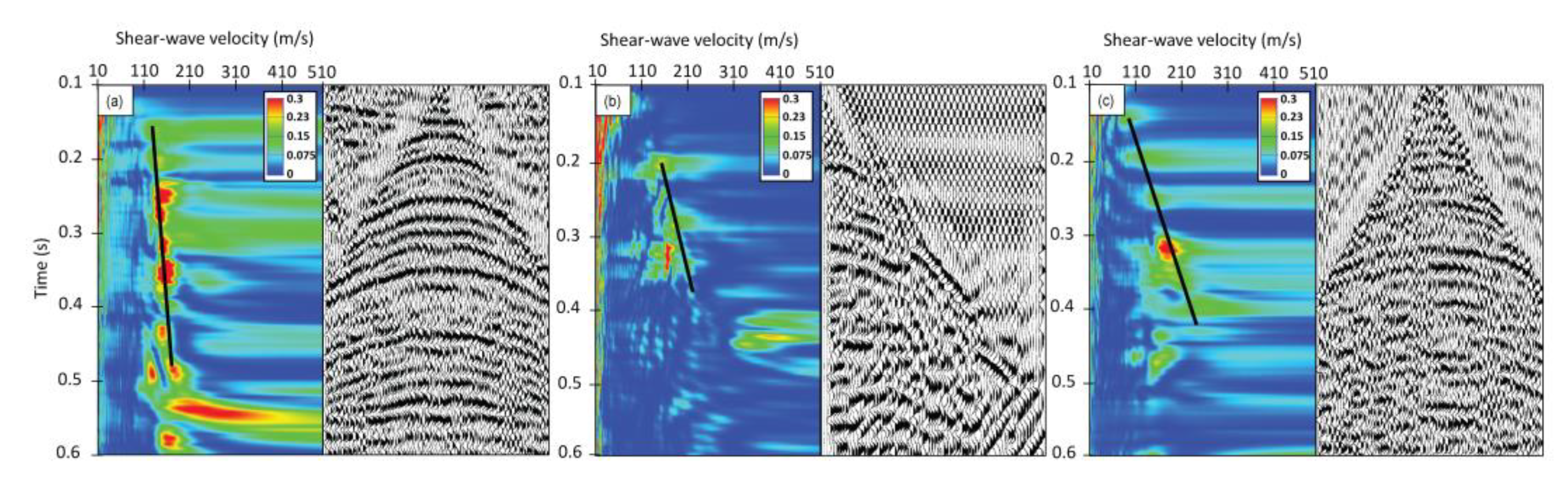
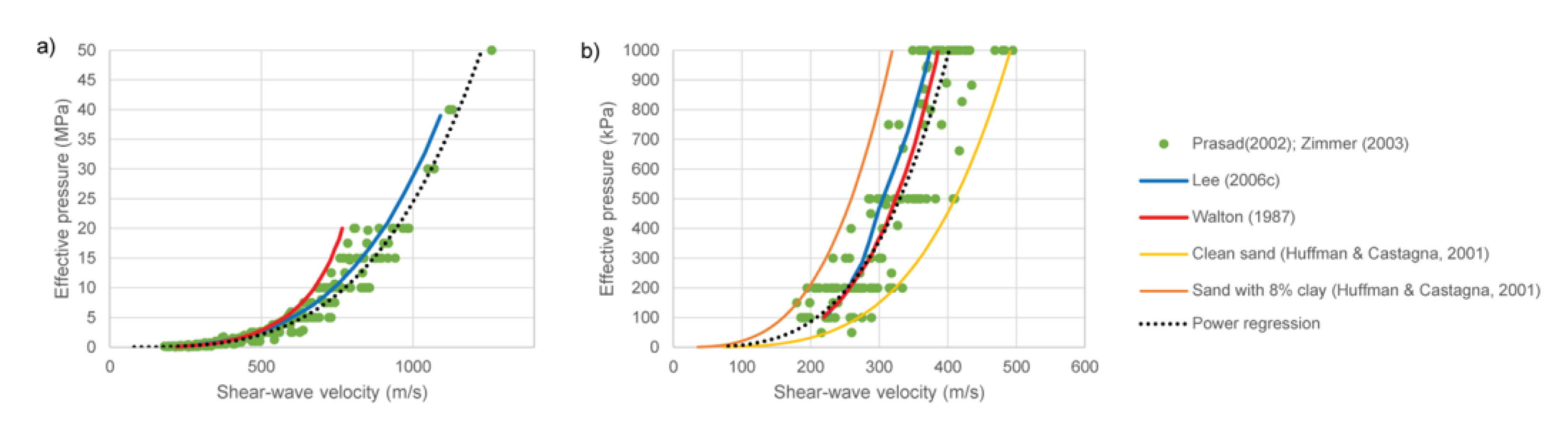
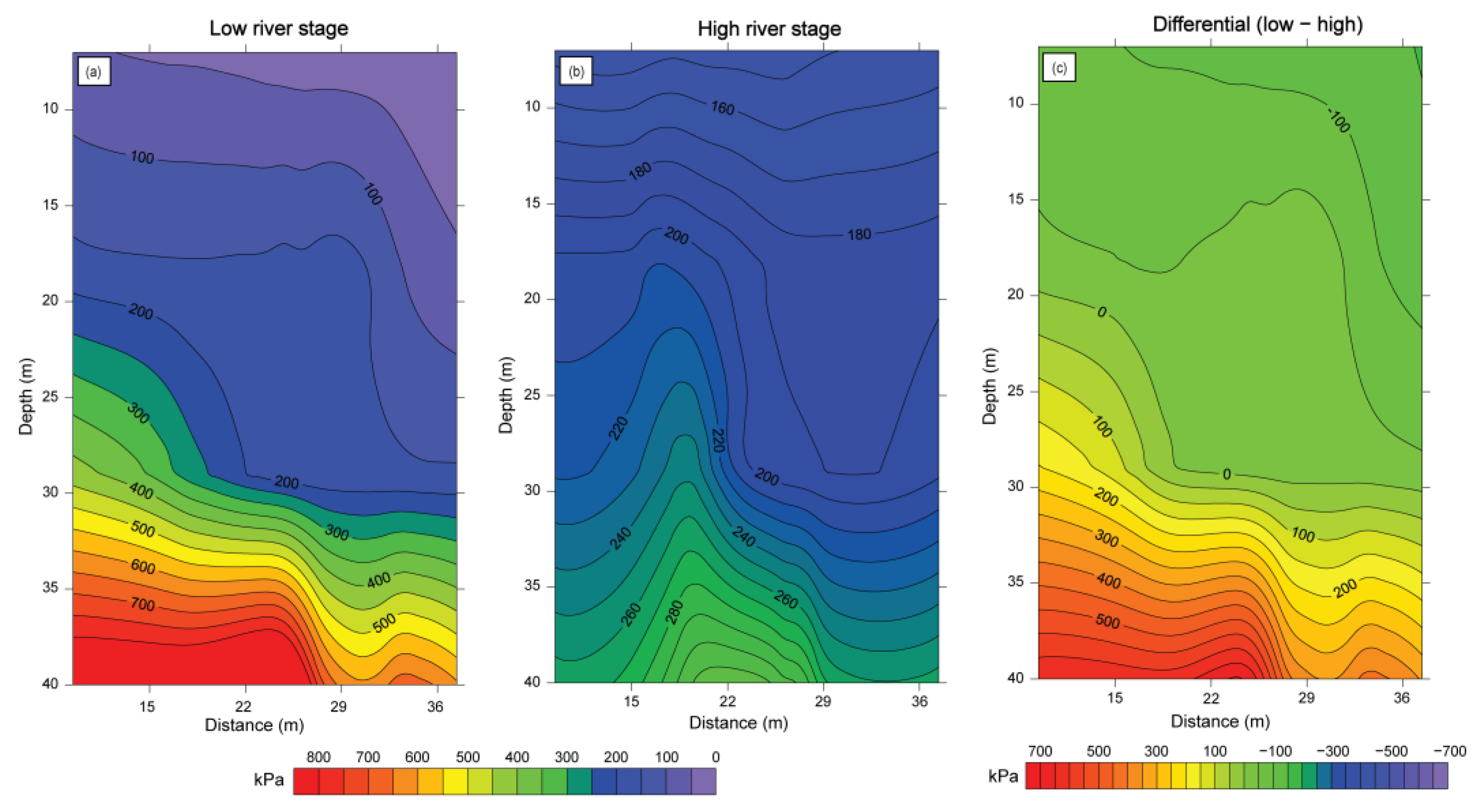
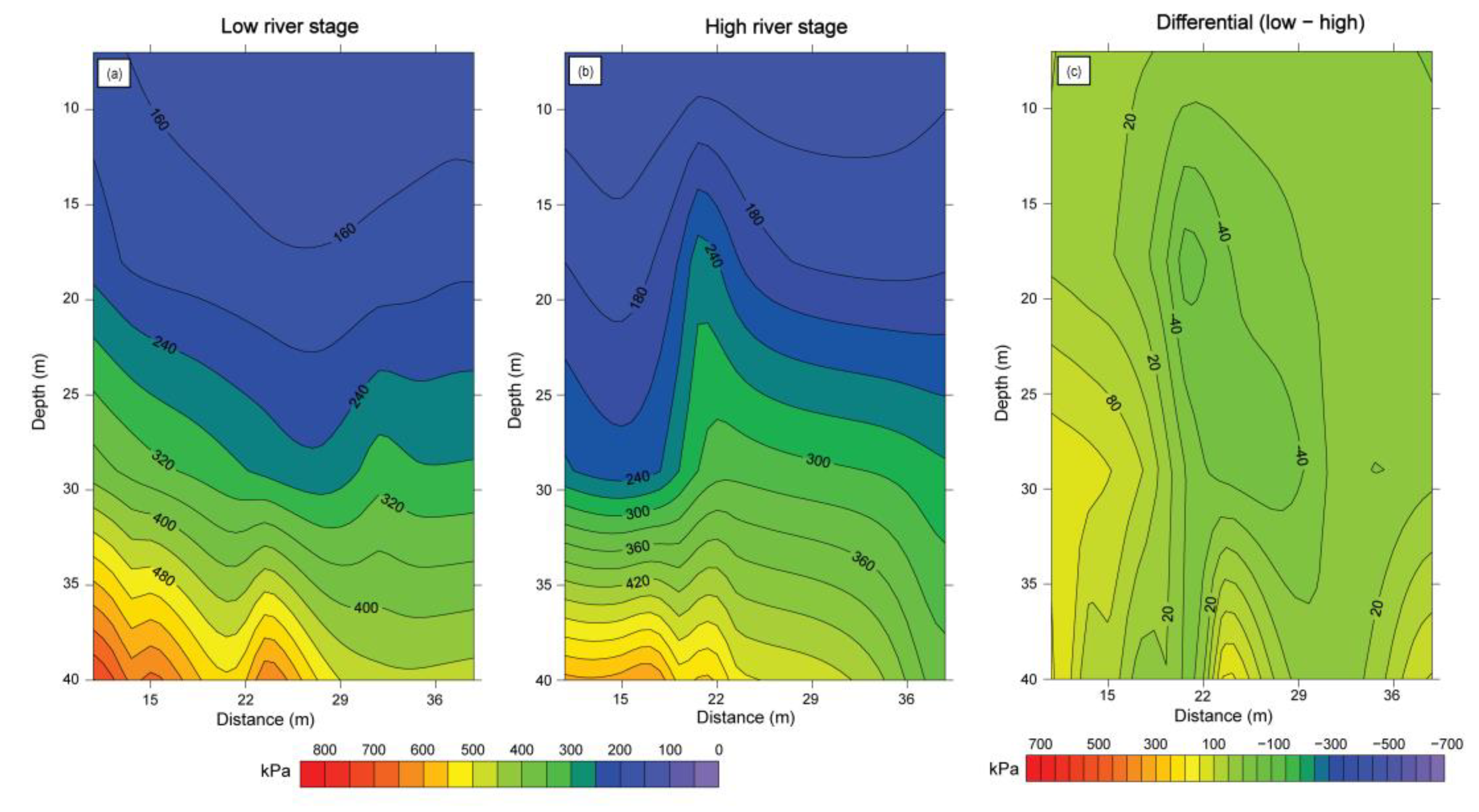
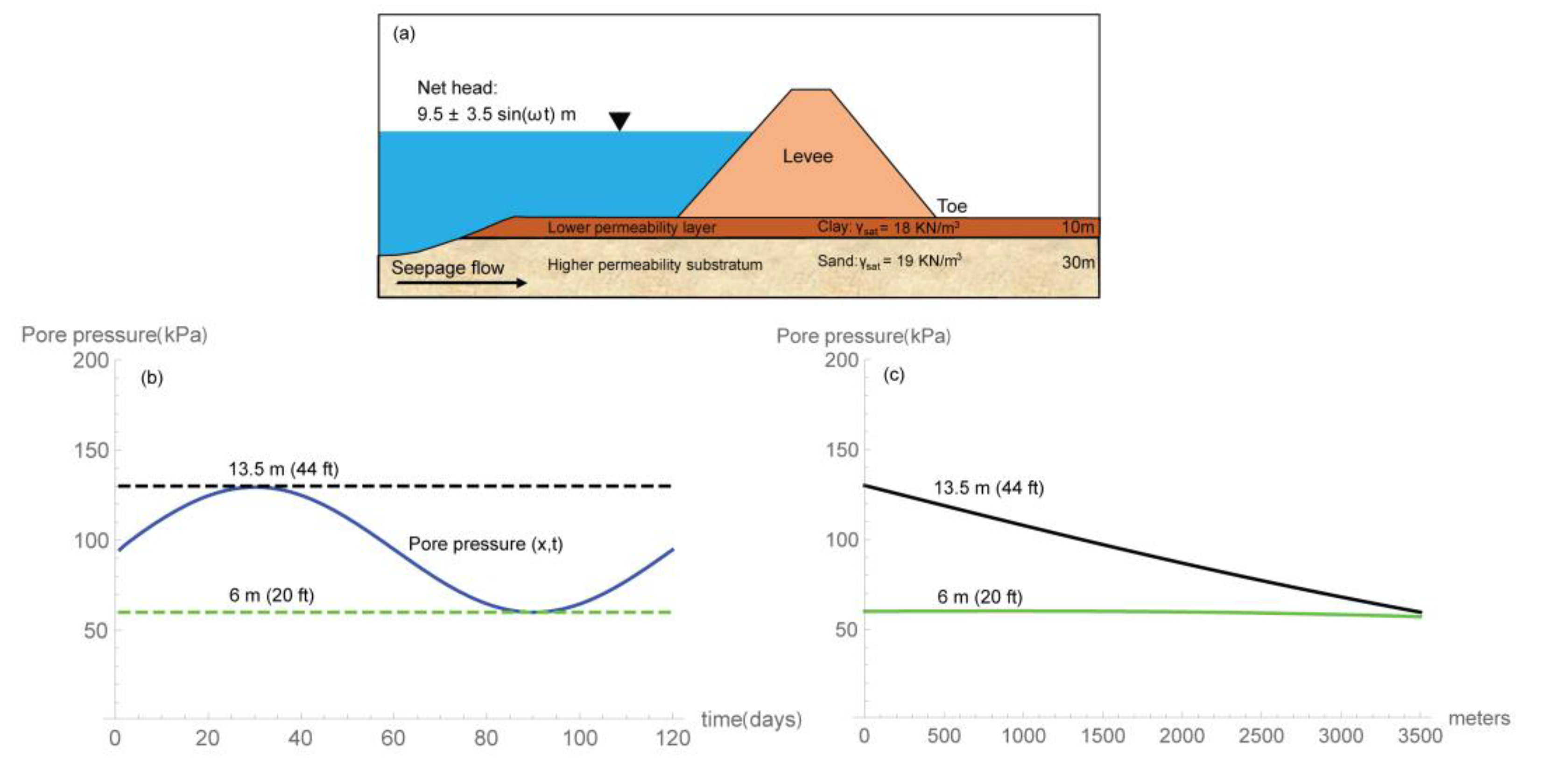
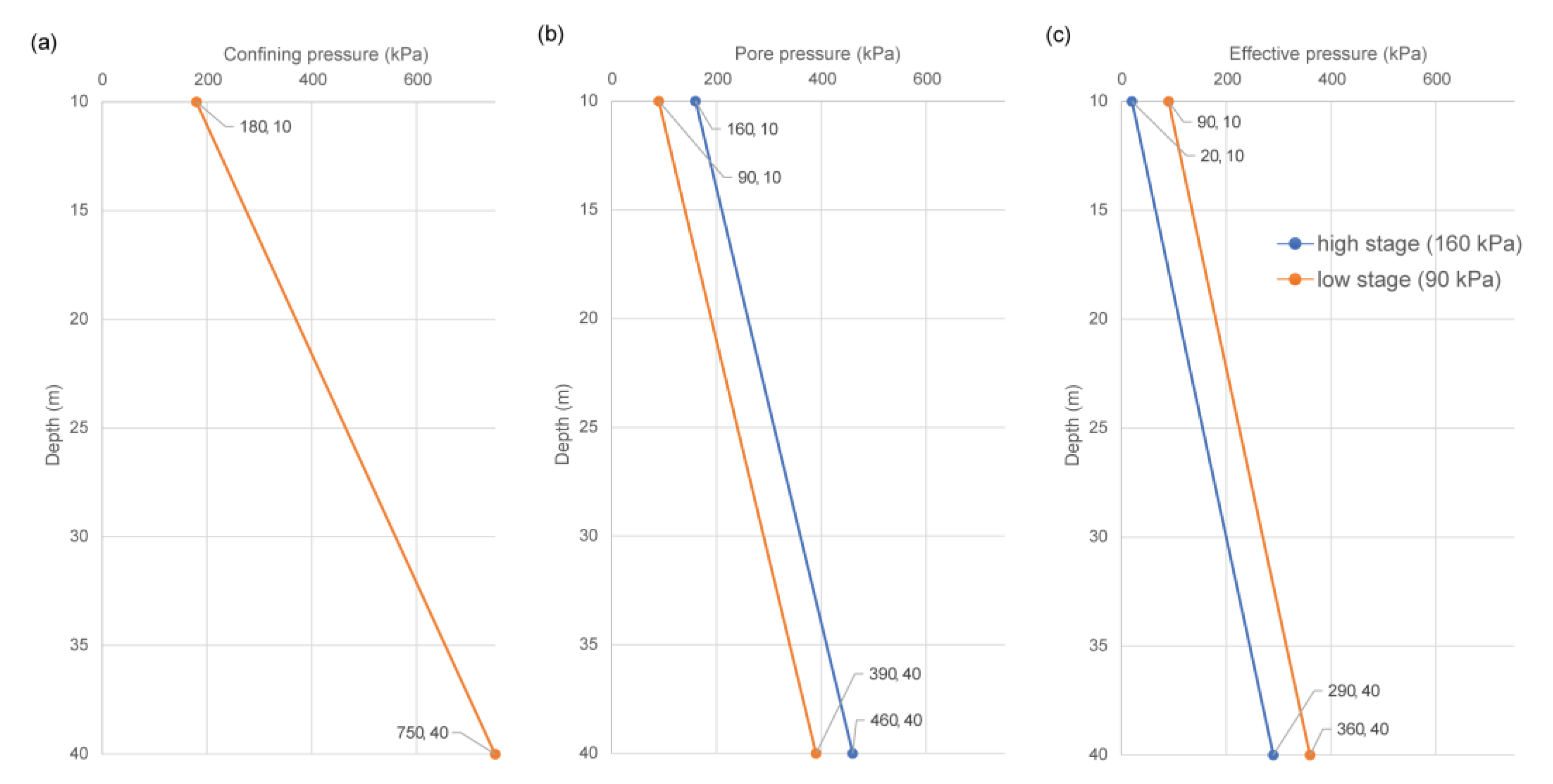
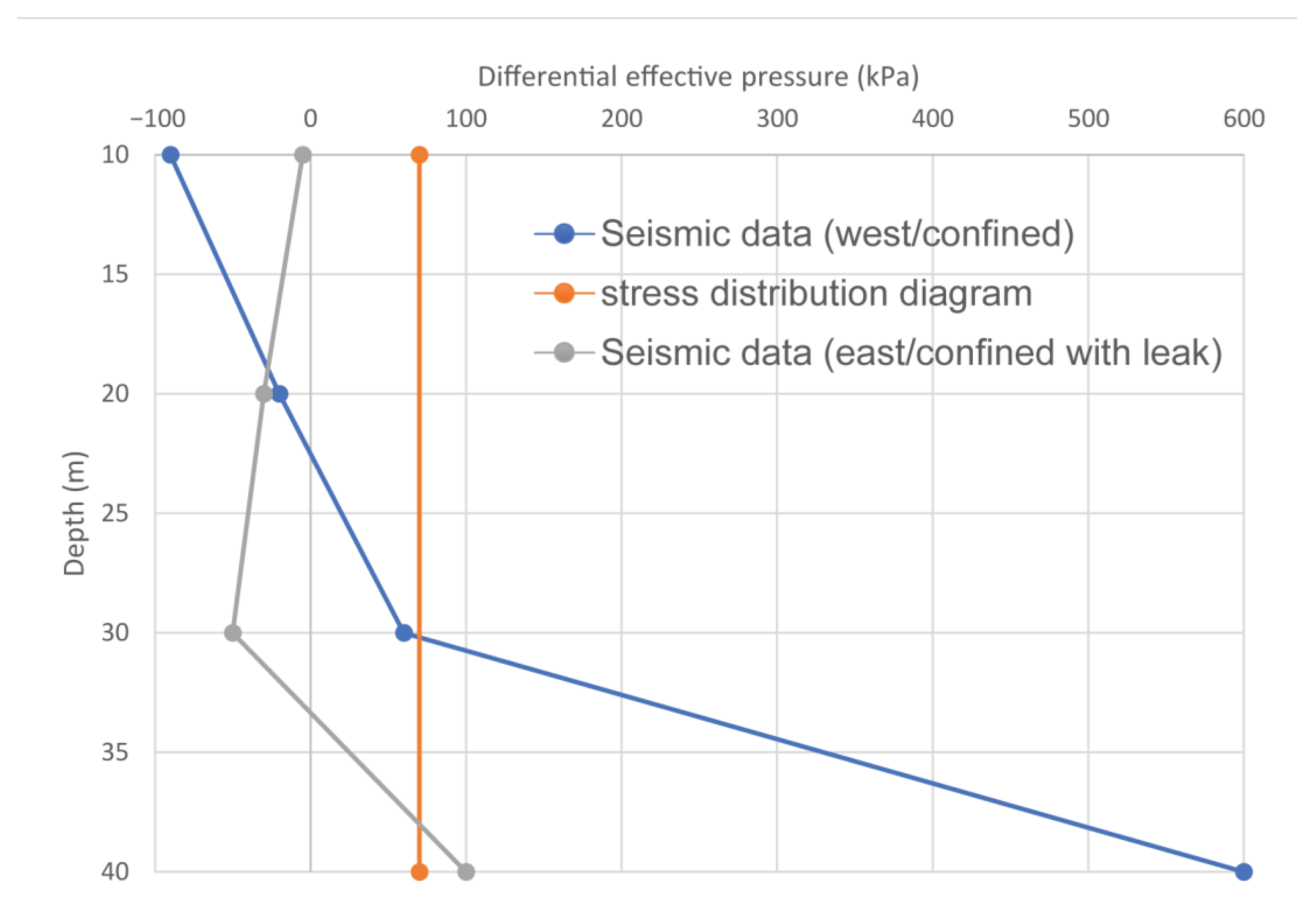
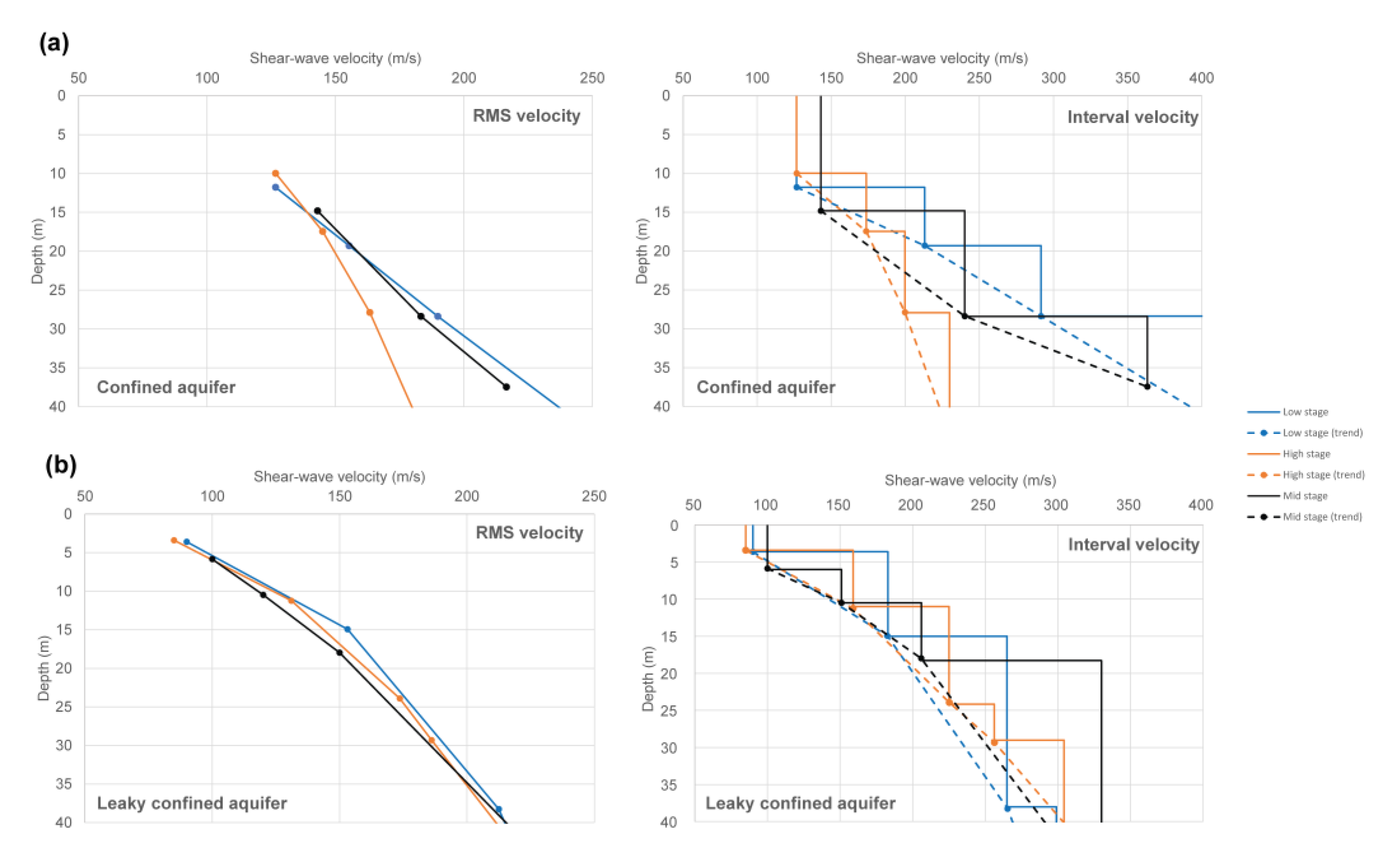
Seismic Data AcquisitionDescription
Geophone separation1 m
Source–receiver offset1–72 m for PWA, 1–48 m for CMP
PWA survey detailsPWA survey used a fixed array of 24 geophones (1- spacing) with equally spaced seismic sources every 24 m [68,69,70].
Geophones4.5 Hz horizontal component
Seismograph24-Channel, 24-bit resolution, DAQlink4 Seismic Source.
Seismograph take out cablesTwo twenty-four (24) take-out cables linked in series for a total of forty-eight (48) channels controlled by Rota-Long-Switch.
Sample rate, record length, Nyquist frequency1000 S/s, 2 s, 500 Hz
Seismic sourceHorizontal blows: I beam ~13.6 kg (30-lb), each head of the “I” is ~15.25 cm (6″) wide by ~28 cm (11″) long using ~4.5 kg (10-lb) sledgehammer.
Seismic data processing flow
Data reformatFrom SEG-Y to Seismic Unix format [71]
SH-wave enhancementPolarity subtraction from opposite blow directions.
GeometryOffset and CMP creation based on field notes and loaded to headers.
Automatic Gain Control (AGC)50 ms window
Band-pass filteringZero-phase, sine-squared tapered filter with corner frequencies at 30, 35, 60, 90 (Hz).
Top muteSurface wave removal on each shot gather
f-k filterTo remove surface waves that were missed on top mute or overlaid reflection events with reject slopes.
Slope values: 0,6,7,13,14,20 and −20, −14, −13, −7, −6,0.
Top mute (secondary)Surface wave removal on each shot gather
Spiking DeconvolutionSpiking deconvolution is used to increase the signal density of the wavelet.
Normal moveout and stackingThe velocity analysis result is used to correct for normal moveout of seismic reflectors and stack the data to produce a post-stack image [72].
MigrationStolt post-stack migration [73] to correct dipping events to true subsurface position and collapse diffractions.
Table
Table 2. Acquisition survey dates with their respective river stages.
Table 2. Acquisition survey dates with their respective river stages.
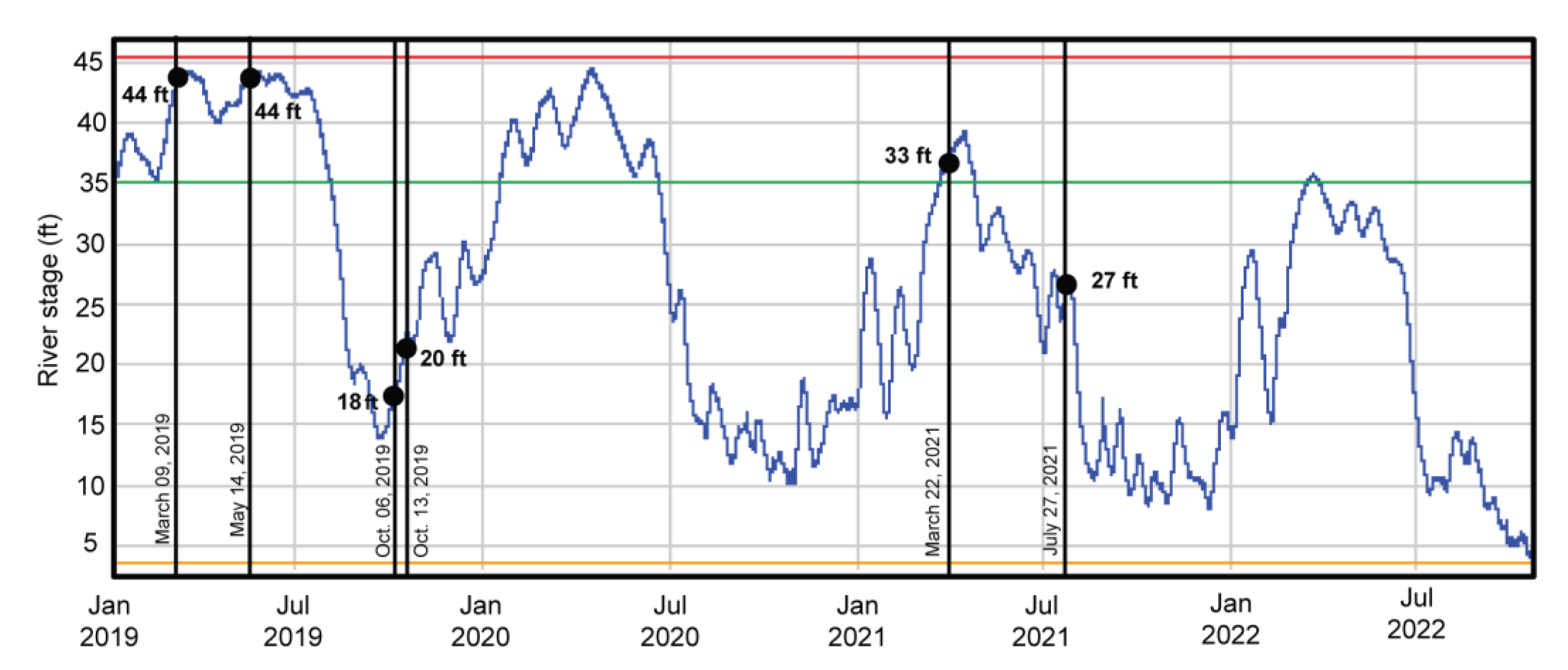
SurveyRiver Stage (ft)River Stage (m)Date
Seismic east (C-C’)44 (high)13.5 (high)9 March 2019
Seismic east (C-C’)18 (low)5 (low)6 October 2019
Seismic west (A-A’)44 (high)13.5 (high)14 May 2019
Seismic west (A-A’)20 (low)6 (low)13 October 2019
PWA Seismic east (D-D’) 33 (intermediate)10 (intermediate)22 March 2021
PWA Seismic west (B-B’) 27 (intermediate)8 (intermediate)27 July 2021
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Locci-Lopez, D.; Lorenzo, J.M. Seepage-Induced Pore Pressure Variations Beneath an Earthen Levee Measured with a Novel Seismic Tool. Geosciences 2023, 13, 20. https://doi.org/10.3390/geosciences13010020

AMA Style

Locci-Lopez D, Lorenzo JM. Seepage-Induced Pore Pressure Variations Beneath an Earthen Levee Measured with a Novel Seismic Tool. Geosciences. 2023; 13(1):20. https://doi.org/10.3390/geosciences13010020

Chicago/Turabian Style

Locci-Lopez, Daniel, and Juan M. Lorenzo. 2023. "Seepage-Induced Pore Pressure Variations Beneath an Earthen Levee Measured with a Novel Seismic Tool" Geosciences 13, no. 1: 20. https://doi.org/10.3390/geosciences13010020

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop