Abstract
The scale-dependent transport of Saharan dust aerosols by African easterly waves (AEWs) is examined analytically and numerically. The analytical analysis shows that the meridional and vertical wave transports of dust are modulated by the Doppler-shifted frequency, , and the wave growth rate, , both of which are functions of the zonal wave scale. The analytical analysis predicts that the AEW dust transports, which are driven by the Reynolds stresses acting on the mean dust gradients, are largest for the twin limits: , which corresponds to flow near a critical surface, a local effect; and , which corresponds to the slowest growing waves, a global effect. The numerical analysis is carried out with the Weather Research and Forecasting (WRF) model, which is radiatively coupled to the dust field. The model simulations are based on an AEW spectrum consistent with observations. The simulations agree with the theoretical predictions: the slowest growing waves have the strongest transports, which are as much as ~40% larger than the transports of the fastest growing wave. Although the transports are highly scale-dependent, largely due to the scale dependence of , the location of the critical surface and thus the location of the maximum dust transports are not.
1. Introduction
Saharan dust storms are among the most striking natural events on Earth. Born of land-atmosphere interaction, the storms emerge from complex processes that involve dust emission by an array of wind systems, which range from small-scale turbulent diffusion to synoptic-scale circulations [1,2]. Among the wind systems are African easterly waves (AEWs), which are the signature synoptic-scale circulation over North Africa during boreal summer [3,4,5].
The AEWs are manifestations of the barotropic-baroclinic instability of the African easterly jet, which sits in midtroposphere and is positioned along ~15° N [4,6]. The AEWs emerge every 2–6 days and propagate westward along two tracks; one north and the other south of the AEJ. The north track AEWs extend into the Sahara Desert where they contribute to the episodic emission of dust, which can coalesce into synoptic-scale plumes that feedback onto the AEWs to enhance their strength [7,8,9,10,11,12,13,14,15]. The AEWs, in turn, transport the dust to regions far from their desert origin.
The study of Saharan dust transport spans more than a half century [15,16,17]. Carlson and Prospero [16] is among the earliest studies to document the connection between Saharan dust and AEWs. Based on data collected during the 1969 BOMEX field experiment, Carlson and Prospero [16] showed that the dust plumes and the AEWs were coupled, evidenced by their common frequency, zonal spatial scale, and westward speed. Subsequent observational and modeling studies have further corroborated the connection between AEWs and the emission and transport of Saharan dust [15,17,18,19].
Nathan et al. [20] combined a theoretical framework with numerical simulations in order to expose the physical and dynamical processes that control the zonal-mean transports of Saharan dust during the initial growth phase of AEWs. The theoretical framework was built on a linear conservation equation for the eddy dust field, which yielded analytical expressions for the meridional and vertical dust transports. The expressions showed explicitly the dependence of the transports on the background distribution of zonal-mean wind and dust. The framework predicted that the dust transports would be largest in regions where background dust gradients are large near a critical surface (a critical surface is defined by the locus of points where the background zonal wind matches the phase speed of the wave). The theoretical prediction agreed with the numerical simulations, which were carried out with a mechanistic version of the WRF model coupled to an interactive dust model. The simulations showed, based on climatologically representative distributions of background wind and dust, that the meridional and vertical transports of dust are largest at ~18° N and ~800 hPa, a region within the Sahel where the background dust gradients are large near a critical surface.
Grogan and Nathan [21] extended Nathan et al. [20] by examining two cases: active transports, in which the dust is radiatively coupled to the circulation; and passive transports, in which the dust is radiatively decoupled from the circulation. Employing an analytical analysis to assist in the interpretation of the WRF-dust model simulations, Grogan and Nathan [21] showed that whether the dust transports are largest for the radiatively passive or radiatively active case depends on the growth rate of the AEWs, and that the meridional dust transports dominate in the passive case, while the vertical dust transports dominate in the active case.
Nathan et al. [20] and Grogan and Nathan [21] both focused on the dust transports associated with the fastest growing AEW. Focusing on this wave was motivated by the principle that in an initial wave spectrum, it is the fastest growing wave that will first emerge and thus will be the most physically relevant. This linear selection principle is at the heart of linear instability theory [22].
Intuitively, one would expect that the fastest growing AEWs would also be the most effective transporters of Saharan dust. But as will show both analytically and numerically, the linear selection principle does not apply to dust transports; that is, the fastest growing AEWs are actually the least effective transporters of dust, while the slowest growing AEWs are the most effective.
The analytical and numerical analyses presented in the following two sections pivot on two questions. What is the relative importance of critical surfaces and wave growth to the dust transports? For what zonal wave scales are the eddy transports maximized?
2. Analytical Analysis
This section exposes the physics that controls the scale-dependent transports of Saharan dust, which will aid in the interpretation of the numerical simulations shown in Section 3.
The dust transport vector can be written as [20]:
where and represent, respectively, the dust transports (dust fluxes) in the meridional and vertical directions. The overbar denotes a zonal average and the primes denote perturbations (waves), where , , and represent the perturbation meridional wind, vertical wind, and dust mass mixing ratio.
As shown by Nathan et al. [20], the linear conservation equation for the perturbation dust field can be written as:
This equation states that local time changes in the dust concentration are due to advection of the eddy dust by the zonal-mean background current; meridional and vertical advection of zonal-mean dust by the eddy wind field; and sources and sinks of dust, For the analytical analysis, we only consider sinks of eddy dust, which include, for example, dry deposition and gravitational settling. For the analysis, we choose the simple form, , where D > 0 is a constant dust depletion rate.
To understand how the critical surface and wave growth rate combine to affect the eddy dust transports, it is instructive to first examine how they combine to affect the dust concentration. To do so, we assume that the eddy fields, which represent the AEWs, have normal mode solutions of the form:
where the amplitude moduli (eigenfunctions), , , and , which are functions of latitude (y) and height (z), depend on the (complex) eigenfrequency, is the frequency and is the growth rate, where is the complex phase speed and is the real (dimensional) zonal wavenumber, which is inversely proportional to wavelength (wave scale). The asterisk denotes the complex conjugate of the preceding term.
Insertion of Equation (3) into Equation (2) yields:
where
is the Doppler-shifted frequency.
Equation (4) states that the eddy dust concentration, is controlled by the product between a modulator and the advective transport of zonal-mean dust by the wave field. The modulator is a function of the Doppler shifted frequency, , wave growth rate, and the depletion rate, D. Because is a function of the zonal-mean background wind, which varies with latitude and height, its effect on is local. In contrast, the effect of on is global, i.e., is independent of latitude and height, so that changes in will affect the dust concentration throughout the domain. The local versus global effects of and will manifest in the dust transports.
If , , and D are small, say, , where , a parameter setting that corresponds to weakly damped, slowly growing waves near a critical surface, then the eddy dust concentration must be large, i.e., , in order to balance the advective transport of the mean dust field by the wave. If , it follows that , a singular limit that yields unrealistically large dust concentrations. The singularity is removed, however, if D = O(1), or if additional physics, such as nonlinearity, are included in the problem. Even if additional physics are included, will still be locally large in the twin limit , a fact that is reflected in the dust transports shown next and in the numerical simulations shown in Section 3.2.
Expressions for the meridional and vertical dust transports are obtained by multiplying Equation (4) by (), rearranging terms, and then zonally averaging; the result is:
As discussed in Grogan and Nathan [21], the dust transports are driven by the Reynolds stresses that act on the zonal-mean dust gradients in both directions. Consistent with the analysis of the dust concentration presented above, the modulation of the transports is largest for the twin limits: , which corresponds to flow near a critical surface, a local effect; and , which corresponds to the slowest growing waves, a global effect. Equations (6) and (7) also show that for a given and , the transports will be largest where the background dust gradients are largest.
3. Numerical Analysis
3.1. Model
This section describes the WRF-dust model, the spatial distributions for the zonal-mean background wind and dust fields, the wave spectrum to be examined, and the solution procedure for the numerical simulations.
3.1.1. Weather Research and Forecasting Dust Model (WRF-Dust)
The scale-dependent transports of Saharan mineral dust aerosols are examined through a series of numerical experiments conducted with a mechanistic version of the WRF-dust model. The model is described in detail in Grogan et al. [12] and thus is only summarized here. The model couples the Weather Research and Forecasting (WRF) model (version 3.7) to an online dust model developed by Chen et al. [23]. The dust model, which is built around 12 dust particle sizes whose radii range from 0.15 µm to 5.00 µm, accounts for the advection and sedimentation of dust. Each particle size is governed by its own conservation equation. The dust field is radiatively coupled to the dynamics by incorporating their aerosol optical properties―extinction, single scattering albedo and asymmetric parameter―into the NASA Goddard Space Flight Center (GSFC) radiative transfer mode. The GSFC radiation model accounts for the dust absorption and scattering of solar and terrestrial radiation, as well as the dust absorption of radiation emitted by other constituents [24,25]. To isolate the direct radiative effects of the dust, boundary layer microphysics, cumulus parameterization, planetary boundary layer, and land surface processes are deactivated.
The model domain is a global channel that projects onto a cylindrical-equidistant grid. The horizontal resolution is 0.5° and the boundary conditions are zonally periodic and symmetric at the channel sidewalls (40° N and 10° S). There are 50 levels in the vertical, which extend from the surface up to 100 hPa; no-slip conditions are applied at the top and bottom (horizontal) boundaries. A 30-min hyper diffusion is imposed on the horizontal wind fields. To eliminate any spurious reflections that might occur at the upper boundary, a Rayleigh damping layer is imposed at the top boundary for the wind and temperature fields. The additional damping has no consequential effect on the growth rates or structures of the waves.
3.1.2. Background Wind and Dust Fields
The background wind and dust distributions to be used in the numerical simulations are chosen consistent with observations and are shown in Figure 1. The zonal-mean background easterly jet is the same used by Grogan et al. [12]: the initial basic state wind is symmetric in latitude, asymmetric in height, and centered at 15° N and 650 hPa, with a maximum wind speed of 15 As shown by Grogan et al. [12], this background jet is barotropically and baroclinically unstable to synoptic-scale disturbances (AEWs).
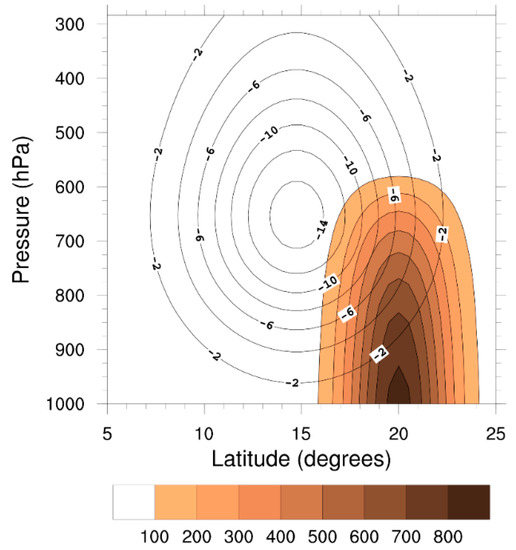
Figure 1.
Basic state zonal wind (solid; contour interval: 2 ms−1) and basic state dust mass mixing ratio for the sum of the 12 dust particle sizes (color; interval: 100 µg kg−1).
The background dust distribution is a meridionally symmetric Gaussian distribution with a half width at half maximum of ~2.5°. The dust plume is centered at 20° N, which positions the bulk of the plume in the latitude belt that contains the largest dust emissions [26]. The dust mixing ratios are then scaled so that the maximum aerosol optical depth (AOD) equals 1.0 at the center of the plume. This maximum AOD corresponds to a maximum dust concentration of 841 µg kg−1, given the plume height and the log-normally distributed particle size distribution. This amount of dust loading is comparable to observed AODs, but is conservative considering that during intense dust emissions the AOD can reach values as large as 4.0 [27].
3.1.3. AEW Spectrum
AEWs span a wide range of zonal scales [28,29,30,31]. Gu et al. [30], for example, used a five-year daily rainfall dataset from the Tropical Rainfall Measuring Mission (TRMM) to calculate the spectral power of AEWs. They found that the largest power approximately resides in the zonal wavenumber range, k = 8 to k = 14, where k, the nondimensional zonal wavenumber, is related to the dimensional zonal wavenumber, , by ; , where is the radius of Earth and is latitude, and is the dimensional wavelength. Hsieh and Cook [31] used a realistic regional climate model to calculate the spectral power of AEWs and also found that the power is largest in the same approximate wavenumber range as Gu et al. [30]. Based on these studies, the transports to be shown in Section 3.2 will be calculated for .
3.1.4. Solution Procedure
The transports associated with each zonal wavenumber in the range k = 8 to k = 14 are calculated following the three-step procedure described in Grogan et al. [12]. Step 1: A wave perturbation of fixed wavenumber is superimposed onto the background wind field shown in Figure 1. The initial amplitude of the perturbation is chosen sufficiently small (~10−4 m s−1) such that during the initial growth phase the wave is controlled by the linear dynamics of the system, i.e., the zonally averaged wave fluxes do not produce any appreciable changes in the zonally averaged background flow. Step 2: The model is integrated forward in time until the domain-averaged wave energy achieves exponential growth to an accuracy of 10−3 for at least 12 h. The wave energy is computed using the meteorological fields from the WRF-dust model, which are output every 4 h for three-dimensional wind, temperature, pressure, geopotential height, dust mixing ratios, and heating rates. Step 3: Once exponential growth is attained, a Fast-Fourier transform algorithm is used to obtain the spatial structures for the eddy wind, temperature and dust fields, which are then scaled to produce a peak meridional wind of 5 m s−1. The growth rate, frequency and transports are then calculated based on the wave structures.
3.2. Results
The analytical analysis shown in Section 2 underscores the importance of the Doppler-shifted frequency, , and the growth rate, , in modulating the dust transports. Figure 2 shows the scale dependence of these two terms. The growth rate peaks at k = 12 (), though the difference between the k = 12 growth rate and that of its immediate neighbors, k = 10 and k = 13, is small, only ~0.02%. However, the difference between the k = 12 growth rate and that of the slowest growing k = 8 wave is large, ~65.2%.
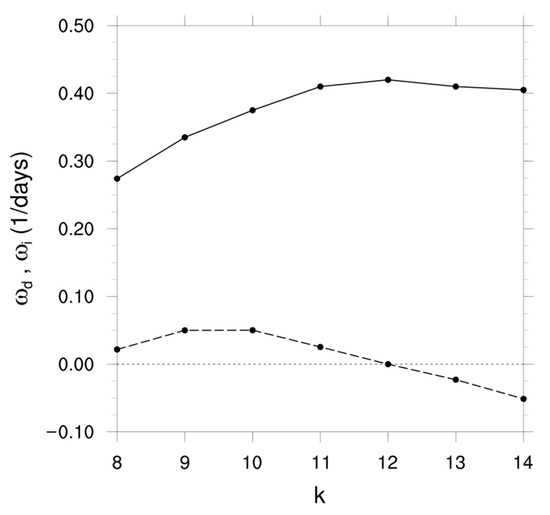
Figure 2.
The variation of growth rate, (solid line), and Doppler-shifted frequency, (dashed line), as a function of nondimensional zonal wavenumber, k, where has been calculated at 18° N, 780 hPa, which corresponds to the location of the fastest growing (k = 12) wave critical surface.
To examine the variation of the Doppler-shifted frequency, , as a function of zonal wavenumber, k, we choose = 8.41 m/s, such that for the k = 12 wave. This value of fixes the location of the k = 12 critical surface. Therefore, the extent to which for a particular k departs from zero is a measure of how sensitive the location of the critical surface is to changes in k. Figure 2 shows that the maximum departure of from the k = 12 wave is ~0.05 d−1 for waves k = 9, 10 and 14. This means that the location of the critical surface and thus the location of maximum dust transports are relatively insensitive to changes in zonal wave scale. In comparison, ranges from 0.27 d−1 (k = 8) to 0.42 d−1 (k = 12), a range of 0.15 d−1, which is about a factor 3 larger than the range of variation of .
To aid in the interpretation of the dust transports, we begin with an analysis of the vertical structures of and for k = 8, 10, 12 and 14. The structures are shown in Figure 3 at 18° N, which is the latitude along which is largest. Each k shares three commonalities. First, the maximum in is located at ~800 hPa. Second, the structure of the field tilts eastward with height, a configuration that is consistent with an amplifying AEW [5]. For geostrophic flow , so that the dust transports will be largest 90° west of the trough, consistent with the analysis of dust-coupled waves by Grogan and Thorncroft [15]. Third, for each k, and are ~180° out of phase at ~800 hPa, so that where . Thus the transports are down the background dust gradient. As shown in the analytical analysis by Nathan et al. [20], and later in this study, near (18° N, 800 hPa) the maximum in coincides with the critical surface, . It is in this region where the analytical analysis presented in Section 2 predicts a local maximum in the dust transports, which can be inferred from the phasing and magnitudes of the vertical structures shown in Figure 3, i.e., the strongest meridional winds coincide with the highest dust concentrations.
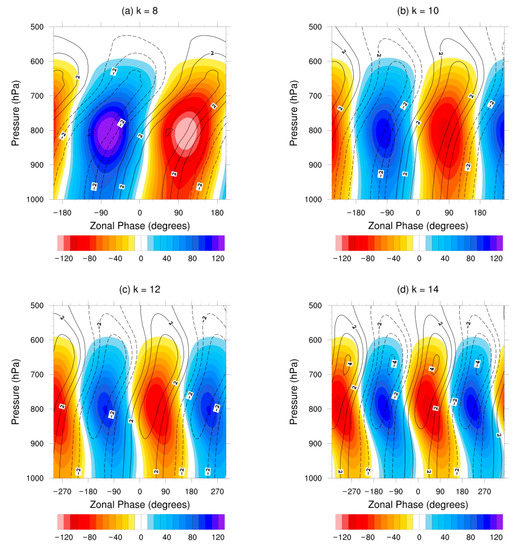
Figure 3.
Vertical structures of (colors; μg kg−1) and (solid/dashed contours correspond to positive/negative values; ms−1) at 18° N for (a) k = 8, (b) k = 10, (c) k = 12, and (d) k = 14. On the horizontal axis, the zonal phase angle is relative to the AEW scale; 360° of zonal phase corresponds to one AEW wavelength. For example, for the k = 8 wave, 8° of zonal phase is 1° of longitude. Each plot shows 50° of longitude.
The differences between the vertical structures for the different AEW zonal scales are most evident in the magnitude of , which decreases as k increases (cf. Figure 3a–d). The eddy dust field is largest for the slowest largest growing k = 8 wave, which was predicted by Equation (4), i.e., for the twin limits and , must become large in order to balance the advective transport of the background dust by the wave.
The vertical structures of and as a function of k, which have similar properties as the structures shown in Figure 3, are shown in Figure 4. For each k, and are in phase at ~800 hPa, so that where . Thus the strongest vertical wind coincides with the maximum dust concentration, so that the vertical dust transports are down the background dust gradient, irrespective of wave scale. The maximum vertical wind speed (~0.008 ms−1) is about the same for each k, but the maximum dust concentration decreases as k increases, as in Figure 5.
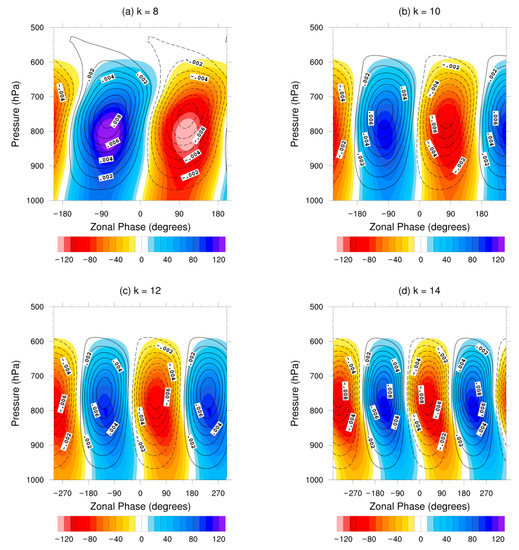
Figure 4.
Vertical structures of (colors; μg kg−1) and (solid/dashed contours correspond to positive/negative values; ms−1) at 18° N for (a) k = 8, (b) k = 10, (c) k = 12, and (d) k = 14. On the horizontal axis, the scale for the zonal phase angle is the same as in Figure 3.

Figure 5.
Meridional dust transports (×10−6 kg m−2s−1) for (a) k = 8, (b) k = 10, (c) k = 12, and (d) k = 14. Overlaid are the critical surface (bold contour) and the maximum meridional background dust gradient (dashed vertical line).
Figure 5 shows as a function of k. For each k, the meridional dust transports are directed southward south of the background dust maximum, which is located at 20° N (see Figure 1), and northward north of the maximum. For all waves, the maximum southward transports are near (18° N, 800 hPa), i.e., in the region where the maximum in the background meridional dust gradient (dashed vertical line) coincides with the critical surface (bold contour). The slowest growing k = 8 wave has the largest transports while the fastest growing k = 12 wave has the smallest transports, in agreement with the analytical prediction given in Section 2. Both north and south of the dust maximum, the vertical extent of the transports uniformly decreases as k increases. For example, for k = 8, the transports extend to the surface, whereas for k = 14, the transports only become significant above ~950 hPa.
Figure 6 shows as a function of k, which has similar properties as the meridional dust transports shown in Figure 5. For each k, the vertical dust transports are directed upward both north and south of the background dust maximum. Like the meridional dust transports, irrespective of wave scale, the vertical transports are largest where the maximum in the meridional dust gradient coincides with the critical surface. The slowest growing k = 8 wave has the largest transports and the fastest growing k = 12 wave the smallest. In addition, the vertical extent of the transports decreases as the zonal wavenumber increases (compare, for example, Figure 6a and Figure 6d).

Figure 6.
As for Figure 5, but for the vertical dust transports (×10−9 kg m−2s−1). (a) k = 8, (b) k = 10, (c) k = 12, and (d) k = 14.
Figure 7 shows the variations of the maximum in the meridional and vertical dust transports as a function of k. In agreement with the analytical analysis presented in Section 2, the transport curves are an approximate mirror image of the growth rate curve shown in Figure 2. The transports are largest for the slowest growing k = 8 and k = 14 waves and smallest for the fastest growing k = 11 and k = 12 waves. For example, () is ~30% (40%) larger for k = 8 than for k = 12.
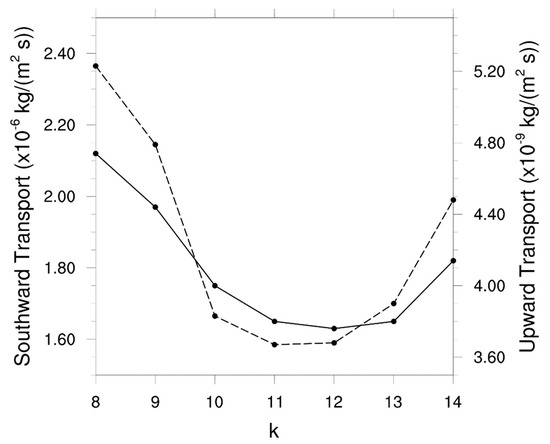
Figure 7.
Southward transports (solid; left axis) and upward transports (dashed; right axis) at the intersection of the critical surface and maximum meridional basic-state dust gradient, as a function of nondimensional zonal wavenumber, k.
4. Conclusions and Discussion
We have examined the scale-dependent transport of Saharan mineral dust aerosols during the initial growth phase of AEWs using analytical and numerical analyses. The analytical analysis, which was based on a conservation equation for the perturbation dust field, yielded explicit expressions for the zonal-mean dust transports in the meridional and vertical directions, the same expressions derived in Grogan and Nathan [21]. Their study, however, focused on the difference between radiatively active and radiatively passive dust transports by AEWs, not on the scale dependence of the transports.
Our analysis shows that the meridional and vertical wave transports of dust are modulated by the Doppler-shifted frequency, , and the wave growth rate, , both of which are functions of the zonal wave scale. The analytical analysis shows that the AEW dust transports, which are driven by the Reynolds stresses acting on the mean dust gradients, are largest for the twin limits: , which corresponds to flow near a critical surface, a local effect; and , which corresponds to the slowest growing waves, a global effect.
This unexpected and non-intuitive result, i.e., the slowest growing waves, not the fastest growing waves, are the most effective transporters of dust, agrees with the numerical simulations carried out with a mechanistic version of the WRF model, which was coupled to an interactive dust model. The linear simulations, which modeled the initial growth phase of the dust-modified AEWs, were based on a climatologically representative background state, one that was comprised of a zonal-mean jet and a zonal-mean dust distribution. The AEW spectrum whose transports were examined were chosen consistent with observations, which show that the most power resides in zonal wavenumbers [28,29,30]. The simulations show that the maximum meridional (vertical) dust transport associated with the slowest growing k = 8 wave is ~30% (~40%) larger than the fastest growing k = 12 wave. In addition, the numerical simulations show that as k increases, the vertical extent of the transports decreases. Although the transports and their spatial structures are highly scale dependent, largely due to the scale dependence of (see Figure 2), the location of the critical surface and thus the location of the maximum dust transports are not.
The above results were obtained for an unstable, zonally uniform background jet. The individual waves that develop on such a jet do not interact with each other during their initial growth phase. Moreover, in a zonally uniform jet, the wave scale remains constant as the wave moves downstream. In contrast, in a zonally nonuniform jet, the disturbance is comprised of a wave packet whose amplitude and zonal scale will be modulated as it moves through the jet [5,10,32].
For example, Bercos-Hickey et al. [10] used a comprehensive version of the WRF model, which was radiatively coupled to an interactive dust model, to examine the dust-modified dynamics of the AEJ-AEW system for a single summer (July–September 2006). They showed that in the dust-free simulations, as the AEWs moved through the jet, the zonal wavelengths expanded from ~2800 km to ~3200 km, an increase of ~15%. In the case of dust-coupled AEWs, the zonal wavelengths expanded from ~2800 km to ~3400 km, an increase of ~20%. To the extent that our results can be applied locally to a zonally varying jet, we would expect changes in the downstream transports of dust due to changes in the zonal scale of the dust-modulated AEWs. To address precisely how zonal variations in the background fields would affect the scale-dependent transports of dust would require an extension of the theory presented here and more realistic numerical simulations.
In addition to considering the effects of zonal variations on the transports, another important extension would be to examine the scale-dependent transports over the life cycles of the AEWs, which have been shown to evolve over four stages: initial growth; nonlinear stabilization; peak amplitude, and long-time equilibration [13,33]. As shown by Grogan et al. [13] in a zonally-averaged framework, as the dust-modified waves emerge from the initial growth phase and enter into the nonlinear stabilization phase, several dynamical processes will combine to affect the waves. For example, the dust-modified heat and momentum fluxes will stabilize the jet, altering both its structure and location. The stabilization of the jet will slow the wave growth, thus reducing its effective growth rate. Given our analytical analysis and linear WRF-dust model simulations, a reduction in the effective growth rate alone would be expected to further enhance the dust transports globally. As the wave continues to grow, albeit more slowly, it will continue to alter the jet. The alteration of the jet will affect the Doppler-shifted frequency and thus the location of the critical surface, which, as we have shown, is a key determinant in the location of maximum dust transports.
As the wave grows to finite amplitude, the nonlinear stabilization phase will eventually transition to the peak amplitude phase. This is when the wave reaches its largest amplitude, which, as shown by Grogan et al. [13], is enhanced by the eddy dust-heating effects. A larger wave amplitude might be expected to strengthen the dust transports, since the transports depend on the momentum fluxes, which are proportional to the square of the wave amplitude. But as Equations (6) and (7) make clear, the transports depend on the product between the momentum fluxes and the background dust gradients. As shown by Nathan et al. [20] and in this study, during the growing phase of the waves, the dust transports erode the background dust gradients. Thus the net dust transports will depend on the competition between the tendency of larger wave amplitudes (larger momentum fluxes) to strengthen the transports and the tendency of the waves to reduce the background dust gradients and thus weaken the transports.
In the context of this study, the central question is how might the zonal wave scale affect the dust transports beyond the initial growth phase. We have shown that during the initial growth phase it is the slowest growing waves that are the most effective transporters of Saharan dust by AEWs. But will this hold as the waves grow to finite amplitude? One might surmise that for an initial wave packet it will be the fastest growing wave that will achieve the largest amplitude and thus will eventually become the most effective transporter of the dust. This may not be the case, however. Studies have shown that through wave-wave interactions, the slowest growing waves can achieve a larger amplitude than the fastest growing waves [34,35,36,37]. It is conceivable, then, that the slowest growing waves, which we have shown dominate the transports during the initial growth phase, may continue to dominate the transports as they grow to finite amplitude. This, of course, will require further study.
Author Contributions
Conceptualization, T.R.N. and D.F.P.G.; methodology, T.R.N.; software and numerical simulation, D.F.P.G.; validation, T.R.N. and D.F.P.G.; formal analysis, T.R.N.; writing—original draft preparation and writing, T.R.N.; review and editing, T.R.N. and D.F.P.G.; visualization, D.F.P.G.; funding acquisition, T.R.N. and D.F.P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Science Foundation, NSF Grant 1624414-0 (TRN) and NSF Grant 2108233 (DFPG).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Model output data will be made available upon request.
Acknowledgments
We acknowledge high-performance computing support from Cheyenne (doi:10.5065/D6RX99HX), which is provided by NCAR’s Computational and Information Systems Laboratory.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Cuesta, J.; Marsham, J.H.; Parker, D.J.; Flamant, C. Dynamical mechanisms controlling the vertical redistribution of dust and the thermodynamic structure of the West Saharan atmospheric boundary layer during summer. Atmos. Sci. Let. 2009, 10, 34–42. [Google Scholar] [CrossRef]
- Knippertz, P.; Todd, M.C. Mineral dust aerosols over the Sahara: Meteorological controls on emission and transport and implications for modeling. Rev. Geophys. 2012, 50, 1007. [Google Scholar] [CrossRef]
- Carlson, T.N. Some remarks on African disturbances and their progress over the tropical Atlantic. Mon. Weather Rev. 1969, 97, 716–726. [Google Scholar] [CrossRef]
- Burpee, R.W. The origin and structure of easterly waves in the lower troposphere of North Africa. J. Atmos. Sci. 1972, 29, 77–90. [Google Scholar] [CrossRef]
- Reed, R.J.; Hollingsworth, A.; Heckley, W.A.; Delsol, F. An evaluation of the performance of the ECMWF Operational System in analyzing and forecasting easterly wave disturbances over Africa and the Tropical Atlantic. Mon. Weather Rev. 1988, 116, 824–865. [Google Scholar] [CrossRef]
- Pytharoulis, I.; Thorncroft, C.D. The low-level structure of African easterly waves in 1995. Mon. Weather Rev. 1999, 127, 2266–2280. [Google Scholar] [CrossRef]
- Jones, C.; Mahowald, N.; Luo, C. Observational evidence of African desert dust intensification of easterly waves. Geophys. Res. Lett. 2004, 31, L17208. [Google Scholar] [CrossRef]
- Ma, P.-L.; Zhang, K.; Shi, J.J.; Matsui, T.; Arking, A. Direct radiative effect of mineral dust on the development of African easterly waves. J. App. Meteor. Clim. 2012, 51, 2090–2104. [Google Scholar] [CrossRef]
- Hosseinpour, F.; Wilcox, E.M. Aerosol interactions with African/Atlantic climate dynamics. Environ. Res. Lett. 2014, 9, 075004. [Google Scholar] [CrossRef]
- Bercos-Hickey, E.; Nathan, T.R.; Chen, S.-H. Saharan Dust and the African Easterly Jet-African Easterly Wave System: Structure, Location, and Energetics. Q. J. Roy. Meteor. Soc. 2017, 143, 2797–2808. [Google Scholar] [CrossRef] [Green Version]
- Bercos-Hickey, E.; Nathan, T.R.; Chen, S.-H. Effects of Saharan dust aerosols and West African precipitation on the energetics of African easterly waves. J. Atmos. Sci. 2022, 79, 1911–1926. [Google Scholar] [CrossRef]
- Grogan, D.F.P.; Nathan, T.R.; Chen, S.-H. Effects of Saharan Dust on the Linear Dynamics of African Easterly Waves. J. Atmos. Sci. 2016, 73, 891–911. [Google Scholar] [CrossRef]
- Grogan, D.F.P.; Nathan, T.R.; Chen, S.-H. Saharan Dust and the Nonlinear Evolution of the African Easterly Jet–African Easterly Wave System. J. Atmos. Sci. 2017, 74, 27–47. [Google Scholar] [CrossRef]
- Nathan, T.R.; Grogan, D.F.P.; Chen, S.-H. Subcritical destabilization of African easterly waves by Saharan mineral dust. J. Atmos. Sci. 2017, 74, 1039–1055. [Google Scholar] [CrossRef]
- Grogan, D.F.P.; Thorncroft, C.D. The characteristics of African easterly waves coupled to Saharan mineral dust aerosols. Q. J. R. Meteorol. Soc. 2019, 145, 1130–1146. [Google Scholar] [CrossRef]
- Carlson, T.N.; Prospero, J.M. The large-scale movement of Saharan air outbreaks over the northern equatorial Atlantic. J. Appl. Meteor. 1972, 11, 283–297. [Google Scholar] [CrossRef]
- Jones, C.; Mahowald, N.; Luo, C. The role of easterly waves on African desert dust transport. J. Climate 2003, 16, 3617–3628. [Google Scholar] [CrossRef]
- Karyampudi, V.M.; Carlson, T.N. Analysis and numerical simulations of the Saharan air layer and its effect on easterly wave disturbances. J. Atmos. Sci. 1988, 45, 3102–3136. [Google Scholar] [CrossRef]
- Knippertz, P.; Todd, M.C. The central west Saharan dust hot spot and its relation to African easterly waves and extratropical disturbances. J. Geophys. Res. 2010, 115, D12117. [Google Scholar] [CrossRef]
- Nathan, T.R.; Grogan, D.F.P.; Chen, S.-H. Saharan dust transport during the incipient growth phase of African easterly waves. Geosciences 2019, 9, 388. [Google Scholar] [CrossRef] [Green Version]
- Grogan, D.F.P.; Nathan, T.R. Passive versus active transport of Saharan dust aerosols on African easterly waves. Atmosphere 2021, 12, 1509. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: New York, NY, USA, 1987. [Google Scholar]
- Chen, S.-H.; Liu, Y.-C.; Nathan, T.R.; Davis, C.; Torn, R.; Sowa, N.; Cheng, C.-T.; Chen, J.-P. Modeling the effects of dust-radiative forcing on the movement of Hurricane Helene (2006). Q. J. R. Meteorol. Soc. 2015, 141, 2563–2570. [Google Scholar] [CrossRef]
- Chou, M.D.; Suarez, M.J. A solar radiation parameterization for atmospheric studies. NASA Tech. Memo. 1999, 15, 104606. [Google Scholar]
- Chou, M.D.; Suarez, M.J.; Liang, X.Z.; Yan, M.M.H. A thermal infrared radiation parameterization for Atmospheric Studies. NASA Tech. Memo. 2001, 19, 104606. [Google Scholar]
- Engelstaedter, S.; Washington, R. Atmospheric controls on the annual cycle of North African dust. J. Geophys. Res. 2007, 112, D03103. [Google Scholar] [CrossRef]
- Kocha, C.; Lafore, J.-P.; Tulet, P.; Seity, Y. High-resolution simulation of major West African dust-storm: Comparison with observations and investigation of dust impact. Quart. J. Roy. Meteor. Soc. 2012, 138, 455–470. [Google Scholar] [CrossRef]
- Burpee, R.W. Some features of synoptic-scale waves based on a compositing analysis of GATE data. Mon. Weather Rev. 1975, 103, 921–925. [Google Scholar] [CrossRef]
- Reed, R.J.; Norquist, D.C.; Recker, E.E. The structure and properties of African wave disturbances as observed during phase III of GATE. Mon. Weather Rev. 1977, 105, 317–333. [Google Scholar] [CrossRef]
- Gu, G.; Adler, R.F.; Huffman, G.J.; Curtis, S. Summer synoptic-scale waves over West Africa observed by TRMM. Geophys. Res. Lett. 2003, 30, 1729. [Google Scholar] [CrossRef]
- Hsieh, J.-S.; Cook, K.H. A study of the energetics of African easterly waves using a regional climate model. J. Atmos. Sci. 2007, 64, 421–440. [Google Scholar] [CrossRef]
- Nathan, T.R. Nonlinear spatial baroclinic instability in slowly varying zonal flow. Dyn. Atmos. Oceans 1997, 27, 81–90. [Google Scholar] [CrossRef]
- Thorncroft, C.D.; Hoskins, B.J. An idealized study of African easterly waves. II: A nonlinear view. Q. J. R. Meteorol. Soc. 1994, 120, 983–1015. [Google Scholar] [CrossRef]
- Hart, J.E. Wavenumber selection in nonlinear baroclinic instability. J. Atmos. Sci. 1981, 38, 400–408. [Google Scholar] [CrossRef]
- Appleby, J.C. Selection of baroclinic waves. Q. J. R. Meteorol. Soc. 1988, 114, 1173–1179. [Google Scholar] [CrossRef]
- Nathan, T.R. Finite amplitude interactions between unstable baroclinic waves and resonant topographic waves. J. Atmos. Sci. 1988, 45, 1052–1071. [Google Scholar] [CrossRef]
- Nathan, T.R. On the role of dissipation in the finite amplitude interactions between forced and free baroclinic waves. Geophys. Astrophys. Fluid Dyn. 1989, 45, 113–130. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).