GEOENT: A Toolbox for Calculating Directional Geological Entropy
Abstract
:1. Introduction
2. Materials and Methods
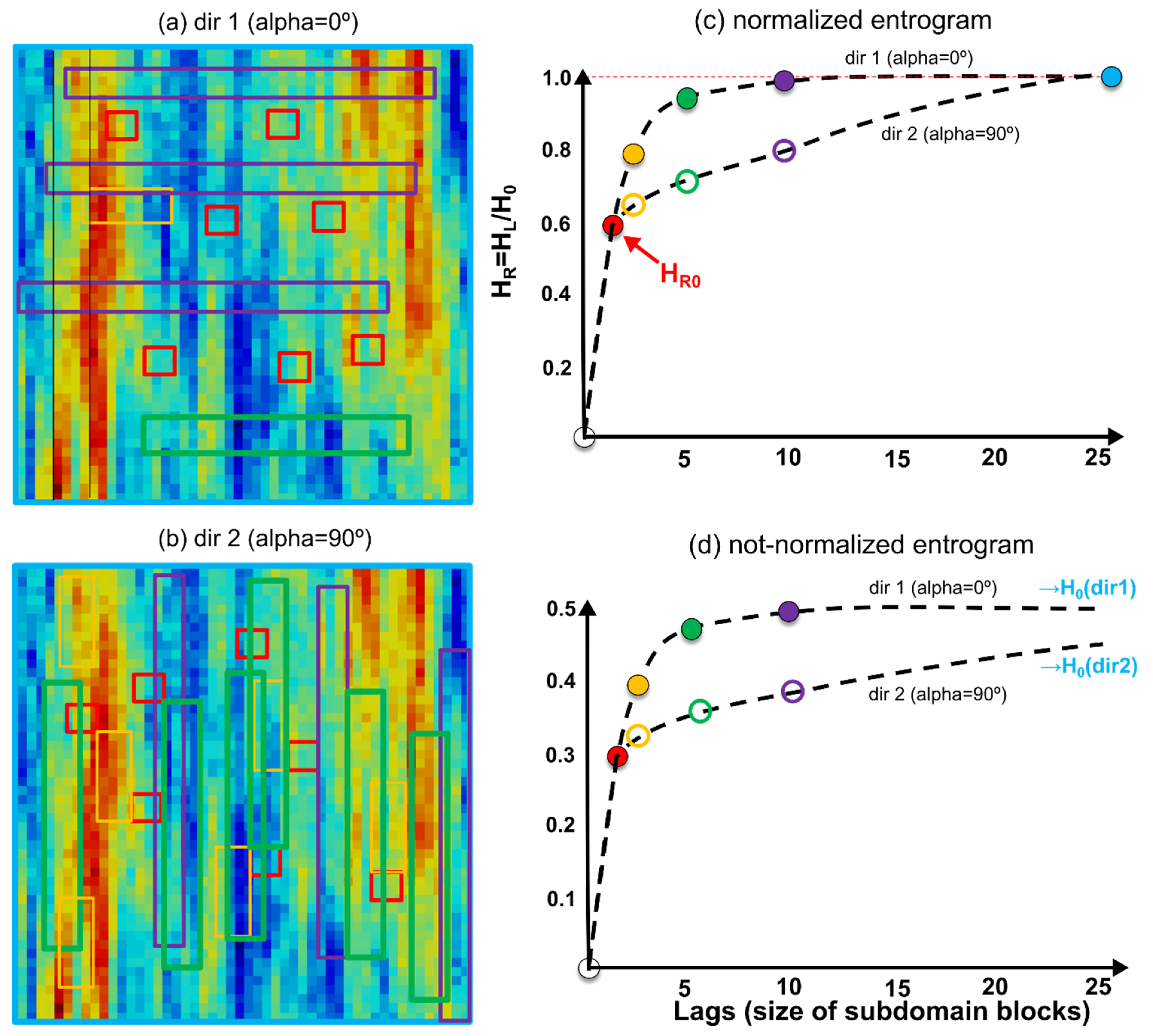
2.1. Mathematical Definition of Directional Entrograms
2.2. Implementation in GEOENT
3. Application of GEOENT to Representative Datasets
3.1. Illustrative Example
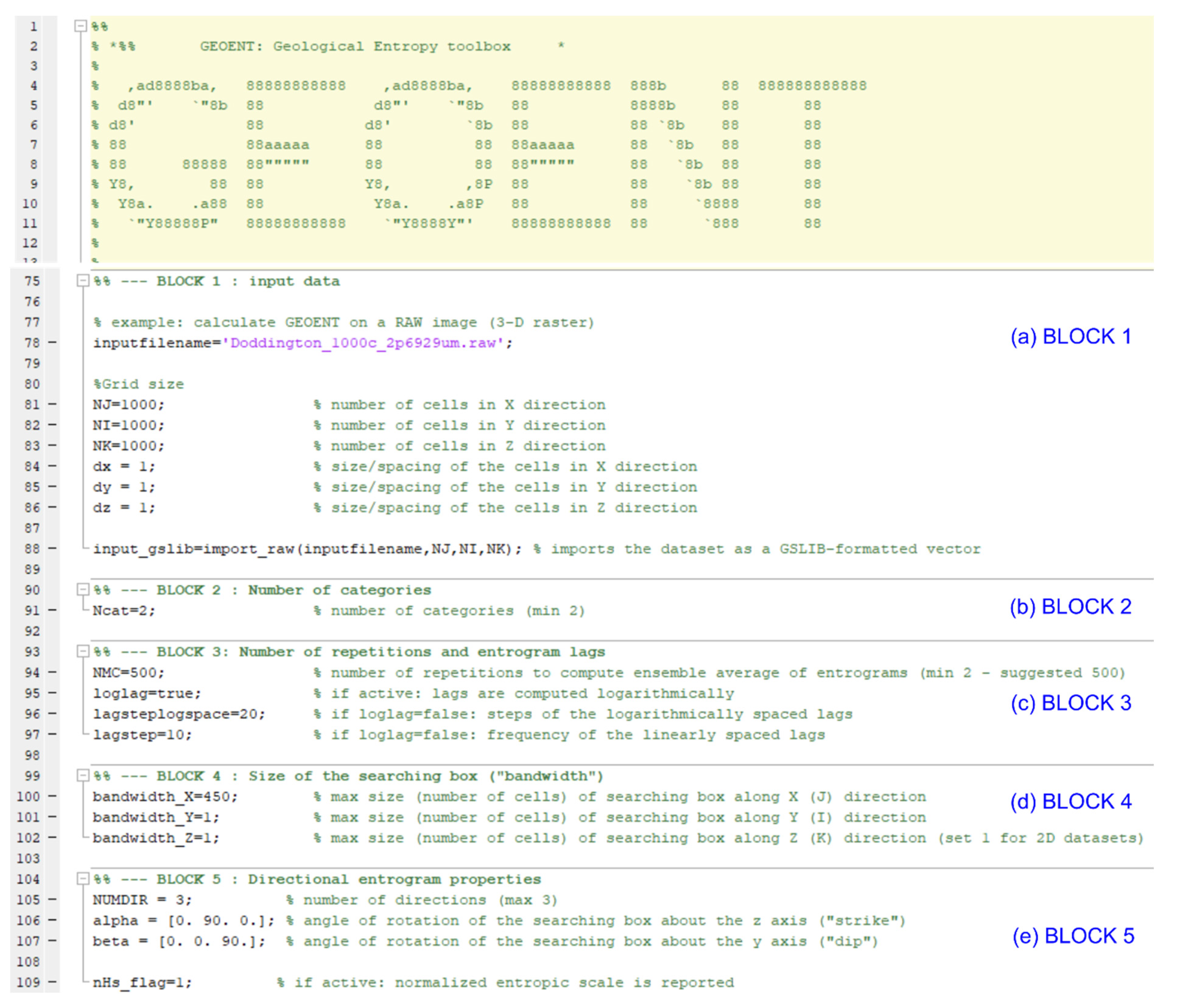
- In Block 1, NJ = 300; NI = 300; NK = 300; dx = 1; dy = 1; dz = 1 (corresponding to the specific directions of this dataset). Since the dataset was already saved as a GSLIB format, it was directly imported into MATLAB without format transformation;
- In Block 2, Ncat = 5, such that the continuous variable distribution is binned into five categories;
- In Block 3, NMC = 500, such that the number of repetitions to compute the ensemble averages of entrograms in each direction is 500; loglag = true, such that lags are computed logarithmically; lagsteplogspace = 20, which is the number of steps of the logarithmically spaced lags;
- In Block 4, bandwidth_X = 300, bandwidth_Y = 1, and bandwidth_Z = 1, such that the maximum size (number of voxels) of the searching box is 300 × 1 × 1 over X, Y, and Z when the strike and dip angles ‘alpha’ and ‘beta’ are = 0° and = 0°, respectively;
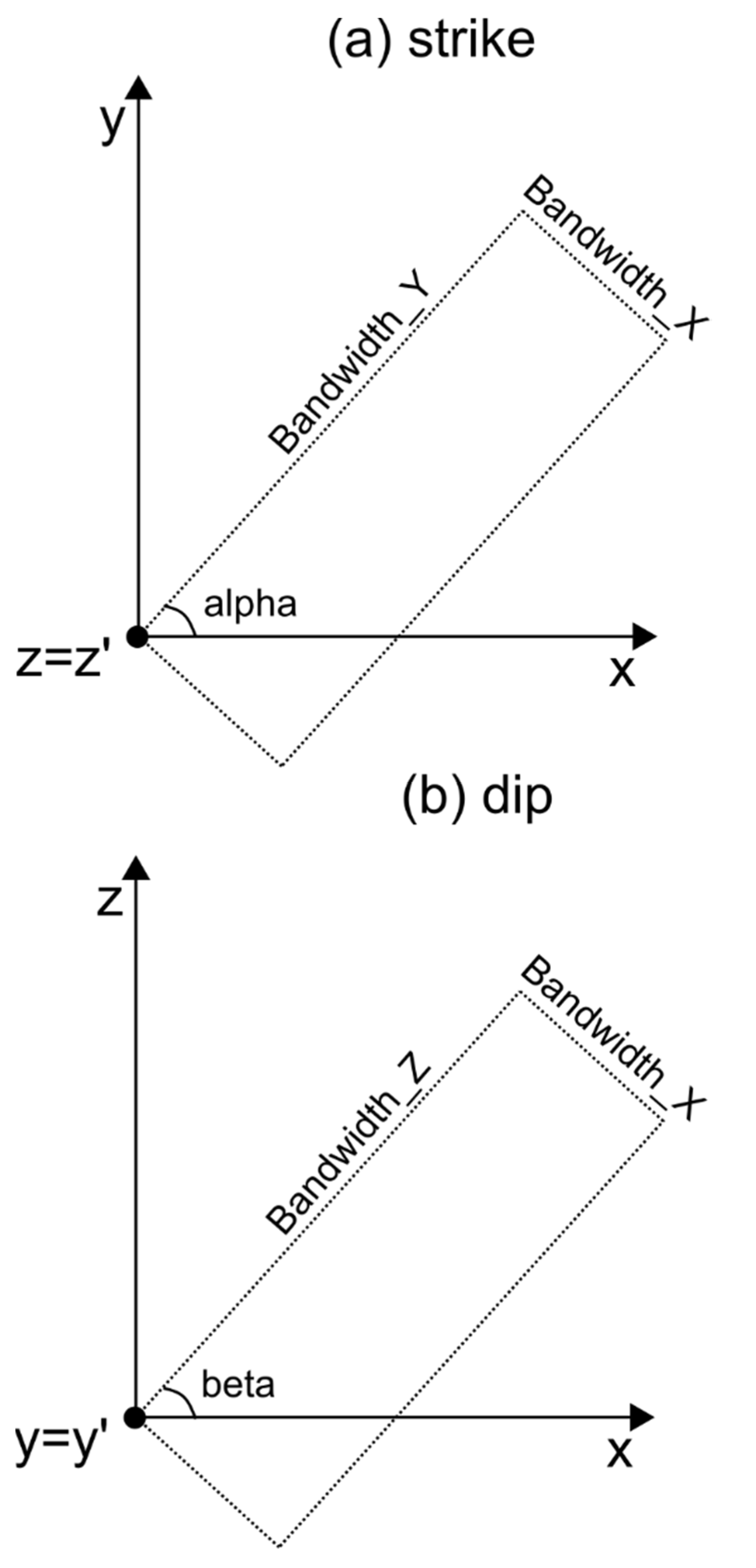
- In Block 45, NUMDIR = 3, such that we compute three directional entrograms, each one defined by the directions specified by ‘alpha’ and ‘beta’ angles. We also set alpha = {0. 90. 0.} and beta = {0. 0. 90.}, such that the first entrogram is oriented over the x direction, the second entrogram is oriented over the y axis, and the third entrogram is oriented over the z direction. We finally set nHs_flag = 1, after which normalised entrograms were plotted.
3.2. Two-Dimensional (2D) Training Images
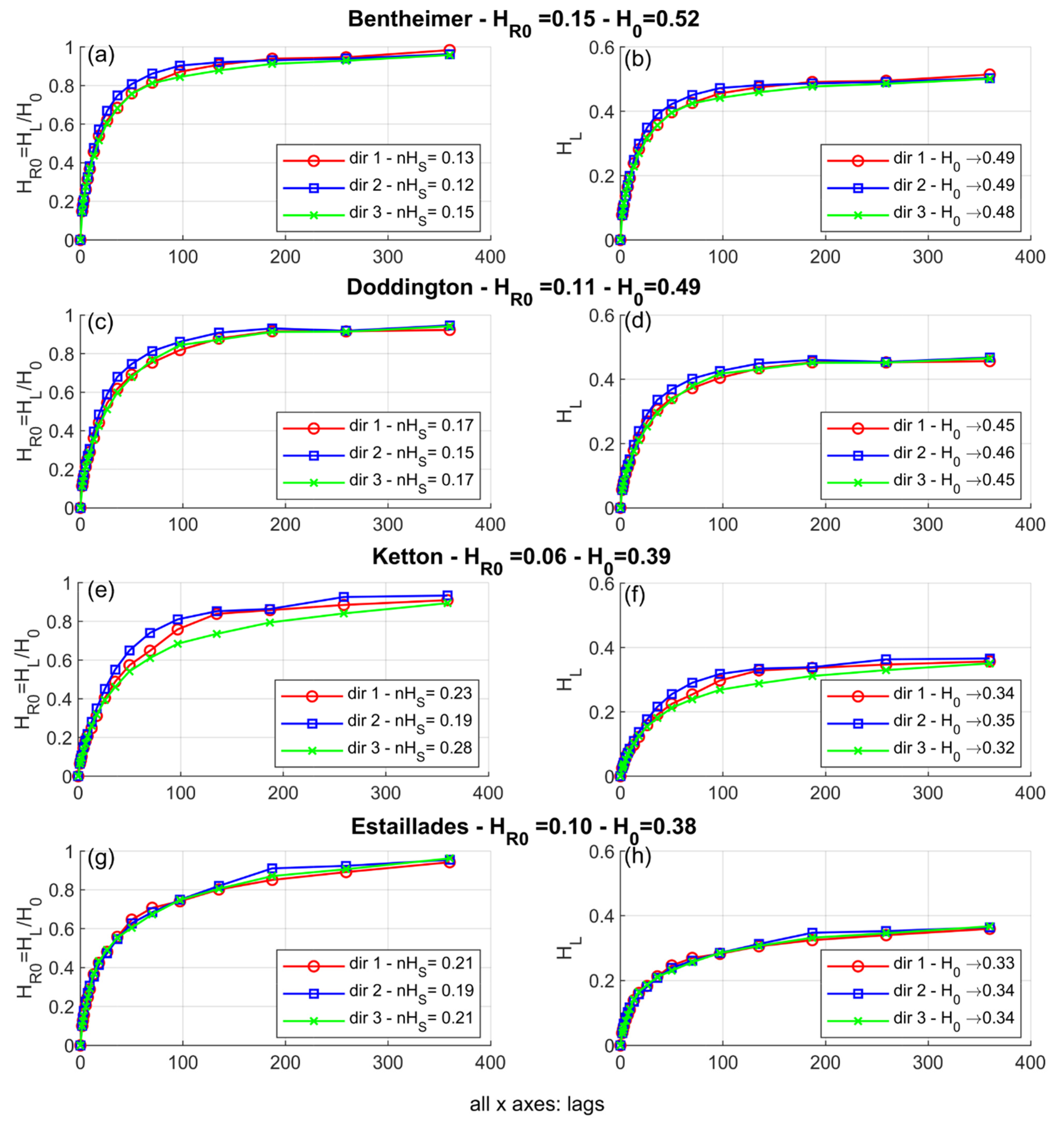
3.3. Three-Dimensional (3D) X-ray Microtomography Images
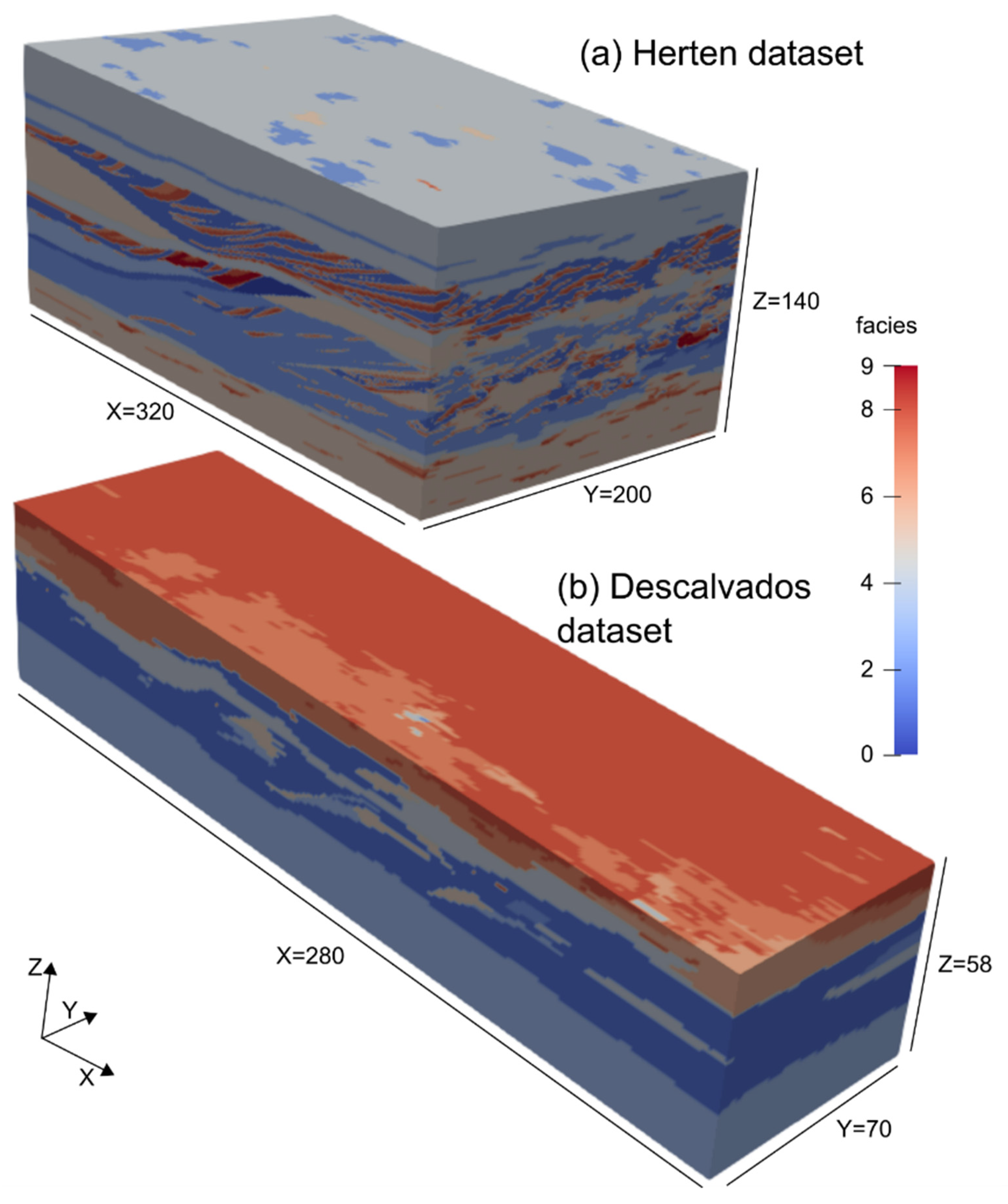
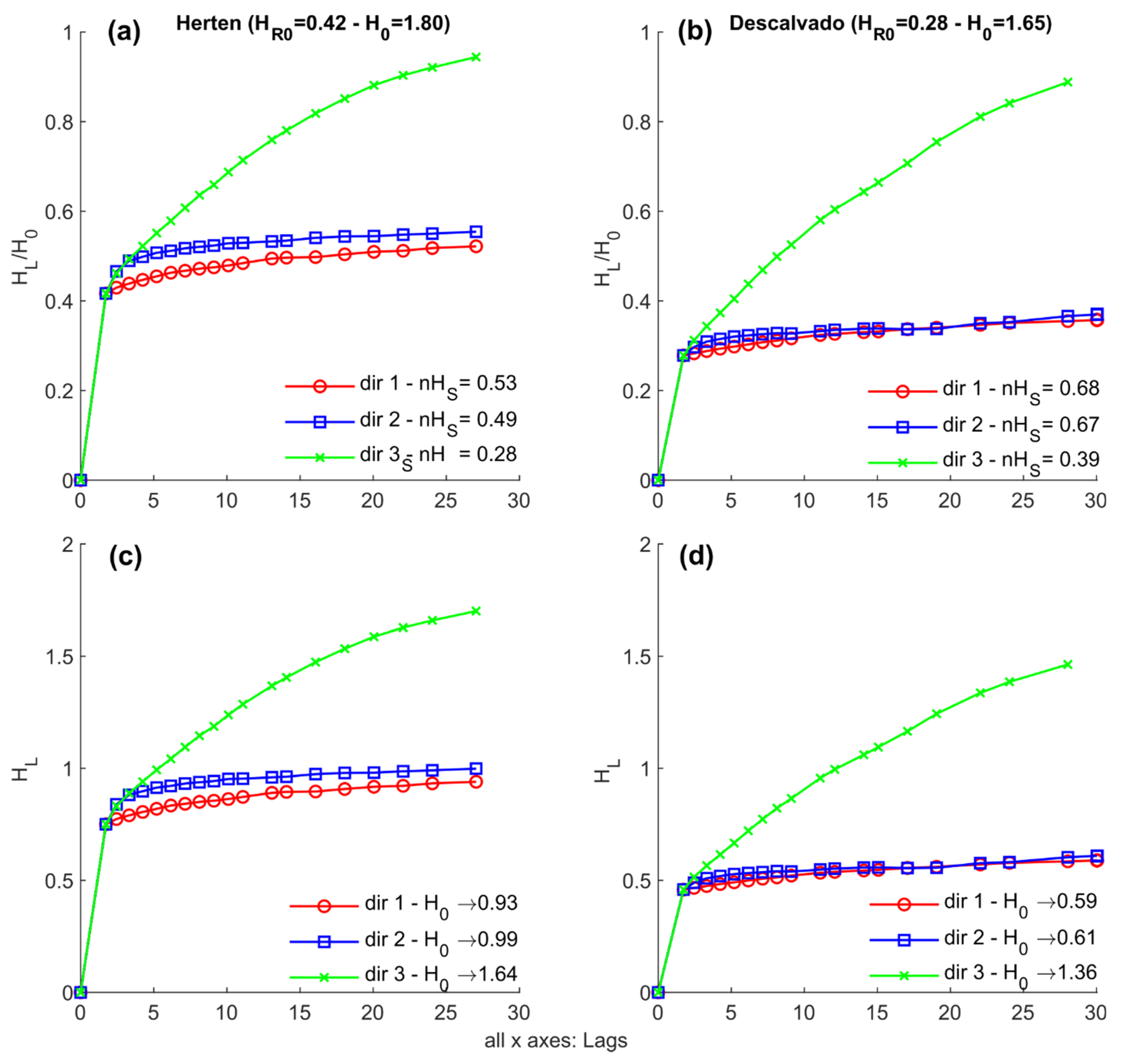
3.4. Three-Dimensional (3D) Aquifer Analogues
- The Descalvado aquifer, described as a moderately heterogeneous fluvial–aeolian deposit of the upper part of the Pirambóia Formation (Triassic) of south-eastern Brazil [44].
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Shannon Information Entropy
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Schug, J.; Schuller, W.-P.; Kappen, C.; Salbaum, J.M.; Bucan, M.; Stoeckert, C.J. Promoter Features Related to Tissue Specificity as Measured by Shannon Entropy. Genome Biol. 2005, 6, R33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kress, G.; Van Leeuwen, T. Reading Images: The Grammar of Visual Design; Routledge: London, UK, 2020. [Google Scholar]
- Zhou, R.; Cai, R.; Tong, G. Applications of Entropy in Finance: A Review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C.; Wang, W. A New Image Encryption Algorithm Based on Chaos and Secure Hash SHA-256. Entropy 2018, 20, 716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Journel, A.G.; Deutsch, C.V. Entropy and Spatial Disorder. Math. Geol. 1993, 25, 329–355. [Google Scholar] [CrossRef]
- Christakos, G. A Bayesian/Maximum-Entropy View to the Spatial Estimation Problem. Math. Geol. 1990, 22, 763–777. [Google Scholar] [CrossRef]
- Naimi, B.; Hamm, N.A.S.; Groen, T.A.; Skidmore, A.K.; Toxopeus, A.G.; Alibakhshi, S. ELSA: Entropy-Based Local Indicator of Spatial Association. Spat. Stat. 2019, 29, 66–88. [Google Scholar] [CrossRef]
- Pham, T.D. GeoEntropy: A Measure of Complexity and Similarity. Pattern Recognit. 2010, 43, 887–896. [Google Scholar] [CrossRef]
- Thiesen, S.; Vieira, D.M.; Mälicke, M.; Loritz, R.; Wellmann, J.F.; Ehret, U. Histogram via Entropy Reduction (HER): An Information-Theoretic Alternative for Geostatistics. Hydrol. Earth Syst. Sci. 2020, 24, 4523–4540. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon Entropy Measure with Statistical Tests for Image Randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef] [Green Version]
- Batty, M.; Morphet, R.; Masucci, P.; Stanilov, K. Entropy, Complexity, and Spatial Information. J. Geogr. Syst. 2014, 16, 363–385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wellmann, J.F.; Regenauer-Lieb, K. Uncertainties Have a Meaning: Information Entropy as a Quality Measure for 3-D Geological Models. Tectonophysics 2012, 526–529, 207–216. [Google Scholar] [CrossRef]
- Bianchi, M.; Pedretti, D. Geological Entropy and Solute Transport in Heterogeneous Porous Media. Water Resour. Res. 2017, 53, 4691–4708. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, M.; Pedretti, D. An Entrogram-Based Approach to Describe Spatial Heterogeneity with Applications to Solute Transport in Porous Media. Water Resour. Res. 2018, 54, 4432–4448. [Google Scholar] [CrossRef]
- Pedretti, D. Heterogeneity-Controlled Uncertain Optimization of Pump-and-Treat Systems Explained through Geological Entropy. Int. J. Geomath. 2020, 11, 22. [Google Scholar] [CrossRef]
- Pedretti, D.; Bianchi, M. Preliminary Results from the Use of Entrograms to Describe Transport in Fractured Media. Acque Sotter. Ital. J. Groundw. 2019, 8. [Google Scholar] [CrossRef]
- Ye, Z.; Jiang, Q.; Yao, C.; Liu, Y.; Cheng, A.; Huang, S.; Liu, Y. The Parabolic Variational Inequalities for Variably Saturated Water Flow in Heterogeneous Fracture Networks. Geofluids 2018, 2018, 9062569. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.; Fan, X.; Zhang, J.; Sheng, J.; Chen, Y.; Fan, Q.; Qin, H. Evaluation of Connectivity Characteristics on the Permeability of Two-Dimensional Fracture Networks Using Geological Entropy. Water Resour. Res. 2021, 57, e2020WR029289. [Google Scholar] [CrossRef]
- Bijeljic, B.; Mostaghimi, P.; Blunt, M.J. Insights into Non-Fickian Solute Transport in Carbonates: Insights into Non-Fickian Solute Transport in Carbonates. Water Resour. Res. 2013, 49, 2714–2728. [Google Scholar] [CrossRef] [Green Version]
- Berkowitz, B.; Scher, H. On Characterization of Anomalous Dispersion in Porous and Fractured Media. Water Resour. Res. 1995, 31, 1461–1466. [Google Scholar] [CrossRef]
- Hyman, J.D.; Aldrich, G.; Viswanathan, H.; Makedonska, N.; Karra, S. Fracture Size and Transmissivity Correlations: Implications for Transport Simulations in Sparse Three-Dimensional Discrete Fracture Networks Following a Truncated Power Law Distribution of Fracture Size. Water Resour. Res. 2016, 52, 6472–6489. [Google Scholar] [CrossRef]
- Koltermann, C.E.; Gorelick, S. Heterogeneity in Sedimentary Deposits: A Review of Structure-Imitating, Process-Imitating, and Descriptive Approaches. Water Resour. Res. 1996, 32, 2617–2658. [Google Scholar] [CrossRef]
- Scheibe, T.D. Characterization of the Spatial Structuring of Natural Porous Media and Its Impacts on Subsurface Flow and Transport. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1993. [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide; Oxford University Press: Oxford, UK, 1998; ISBN 978-0-19-510015-0. [Google Scholar]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS. A User’s Guide; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Comunian, A.; Renard, P.; Straubhaar, J.; Bayer, P. Three-Dimensional High Resolution Fluvio-Glacial Aquifer Analog—Part 2: Geostatistical Modeling. J. Hydrol. 2011, 405, 10–23. [Google Scholar] [CrossRef] [Green Version]
- Maharaja, A. TiGenerator: Object-Based Training Image Generator. Comput. Geosci. 2008, 34, 1753–1761. [Google Scholar] [CrossRef]
- Strebelle, S. Conditional Simulation of Complex Geological Structures Using Multiple-Point Statistics. Math. Geol. 2002, 34, 1–21. [Google Scholar] [CrossRef]
- Flannery, B.P.; Deckman, H.W.; Roberge, W.G.; D’Amico, K.L. Three-Dimensional X-Ray Microtomography. Science 1987, 237, 1439–1444. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-Scale Imaging and Modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Le Gros, M.A.; McDermott, G.; Larabell, C.A. X-Ray Tomography of Whole Cells. Curr. Opin. Struct. Biol. 2005, 15, 593–600. [Google Scholar] [CrossRef]
- Otten, W.; Pajor, R.; Schmidt, S.; Baveye, P.C.; Hague, R.; Falconer, R.E. Combining X-Ray CT and 3D Printing Technology to Produce Microcosms with Replicable, Complex Pore Geometries. Soil Biol. Biochem. 2012, 51, 53–55. [Google Scholar] [CrossRef] [Green Version]
- Reijonen, H.M. Benefits of Applying X-Ray Computed Tomography in Bentonite Based Material Research Focussed on Geological Disposal of Radioactive Waste. Env. Sci. Pollut. Res. 2020, 15, 38407–38421. [Google Scholar] [CrossRef] [Green Version]
- Sayab, M.; Suuronen, J.-P.; Hölttä, P.; Aerden, D.; Lahtinen, R.; Kallonen, A.P. High-Resolution X-Ray Computed Microtomography: A Holistic Approach to Metamorphic Fabric Analyses. Geology 2015, 43, 55–58. [Google Scholar] [CrossRef]
- Yang, Y.; Tao, L.; Iglauer, S.; Hejazi, S.H.; Yao, J.; Zhang, W.; Zhang, K. Quantitative Statistical Evaluation of Micro Residual Oil after Polymer Flooding Based on X-Ray Micro Computed-Tomography Scanning. Energy Fuels 2020, 34, 10762–10772. [Google Scholar] [CrossRef]
- Alhashmi, Z.; Blunt, M.J.; Bijeljic, B. The Impact of Pore Structure Heterogeneity, Transport, and Reaction Conditions on Fluid–Fluid Reaction Rate Studied on Images of Pore Space. Transp. Porous. Med. 2016, 115, 215–237. [Google Scholar] [CrossRef] [Green Version]
- Andrew, M.; Bijeljic, B.; Blunt, M.J. Pore-Scale Imaging of Trapped Supercritical Carbon Dioxide in Sandstones and Carbonates. Int. J. Greenh. Gas Control 2014, 22, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Honari, A.; Bijeljic, B.; Johns, M.L.; May, E.F. Enhanced Gas Recovery with CO2 Sequestration: The Effect of Medium Heterogeneity on the Dispersion of Supercritical CO2–CH4. Int. J. Greenh. Gas Control 2015, 39, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Mosser, L.; Dubrule, O.; Blunt, M.J. Reconstruction of Three-Dimensional Porous Media Using Generative Adversarial Neural Networks. Phys. Rev. E 2017, 96, 043309. [Google Scholar] [CrossRef] [Green Version]
- Bayer, P.; Comunian, A.; Höyng, D.; Mariethoz, G. High Resolution Multi-Facies Realizations of Sedimentary Reservoir and Aquifer Analogs. Sci. Data 2015, 2, 150033. [Google Scholar] [CrossRef] [Green Version]
- Bayer, P.; Huggenberger, P.; Renard, P.; Comunian, A. Three-Dimensional High Resolution Fluvio-Glacial Aquifer Analog: Part 1: Field Study. J. Hydrol. 2011, 405, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Pringle, J.K.; Westerman, A.R.; Clark, J.D.; Drinkwater, N.J.; Gardiner, A.R. 3D High-Resolution Digital Models of Outcrop Analogue Study Sites to Constrain Reservoir Model Uncertainty: An Example from Alport Castles, Derbyshire, UK. Pet. Geosci. 2004, 10, 343–352. [Google Scholar] [CrossRef]
- Höyng, D.; D’Affonseca, F.M.; Bayer, P.; de Oliveira, E.G.; Perinotto, J.A.J.; Reis, F.; Weiß, H.; Grathwohl, P. High-Resolution Aquifer Analog of Fluvial–Aeolian Sediments of the Guarani Aquifer System. Env. Earth Sci. 2014, 71, 3081–3094. [Google Scholar] [CrossRef]
- Höyng, D.; Prommer, H.; Blum, P.; Grathwohl, P.; Mazo D’Affonseca, F. Evolution of Carbon Isotope Signatures during Reactive Transport of Hydrocarbons in Heterogeneous Aquifers. J. Contam. Hydrol. 2015, 174, 10–27. [Google Scholar] [CrossRef] [PubMed]
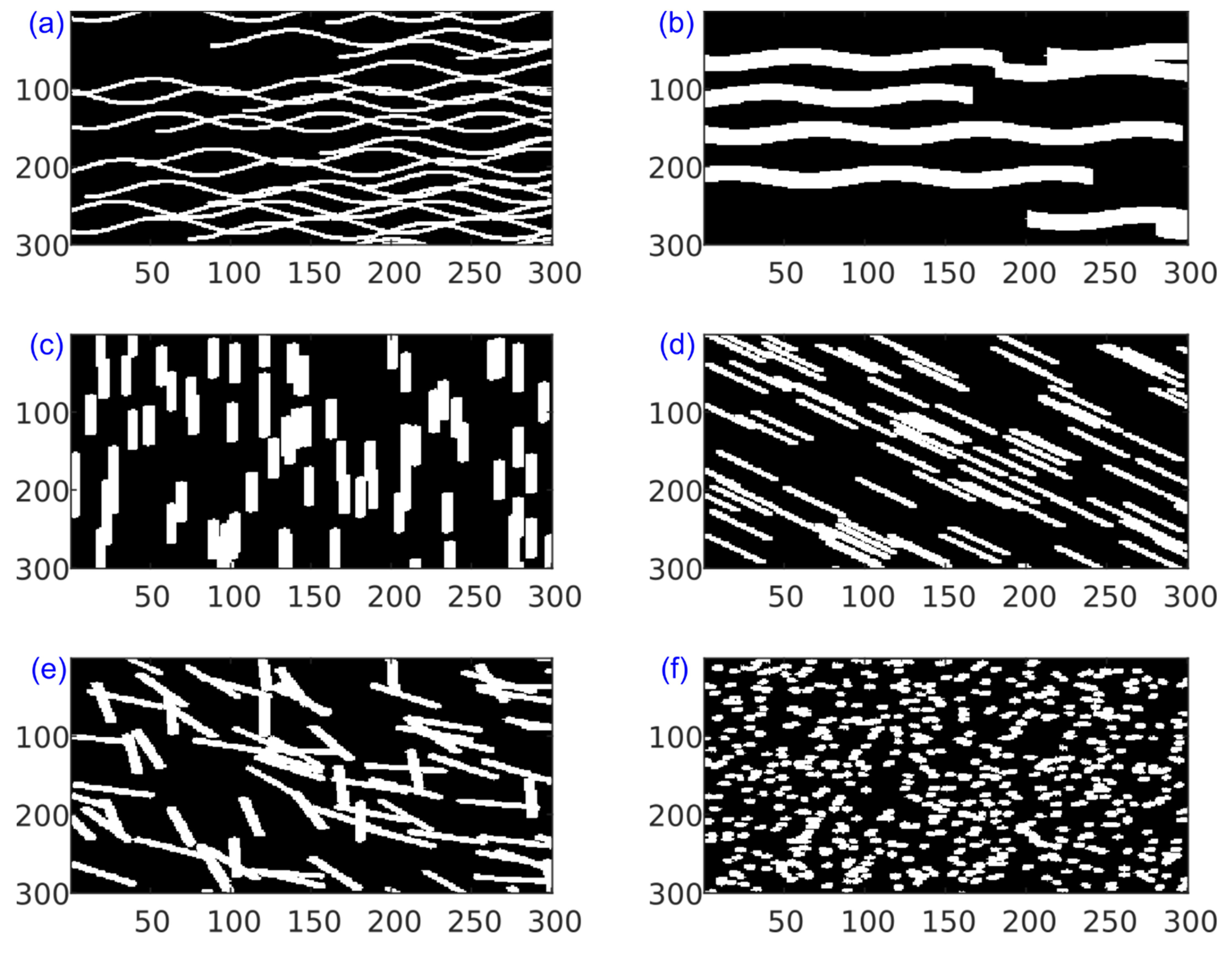
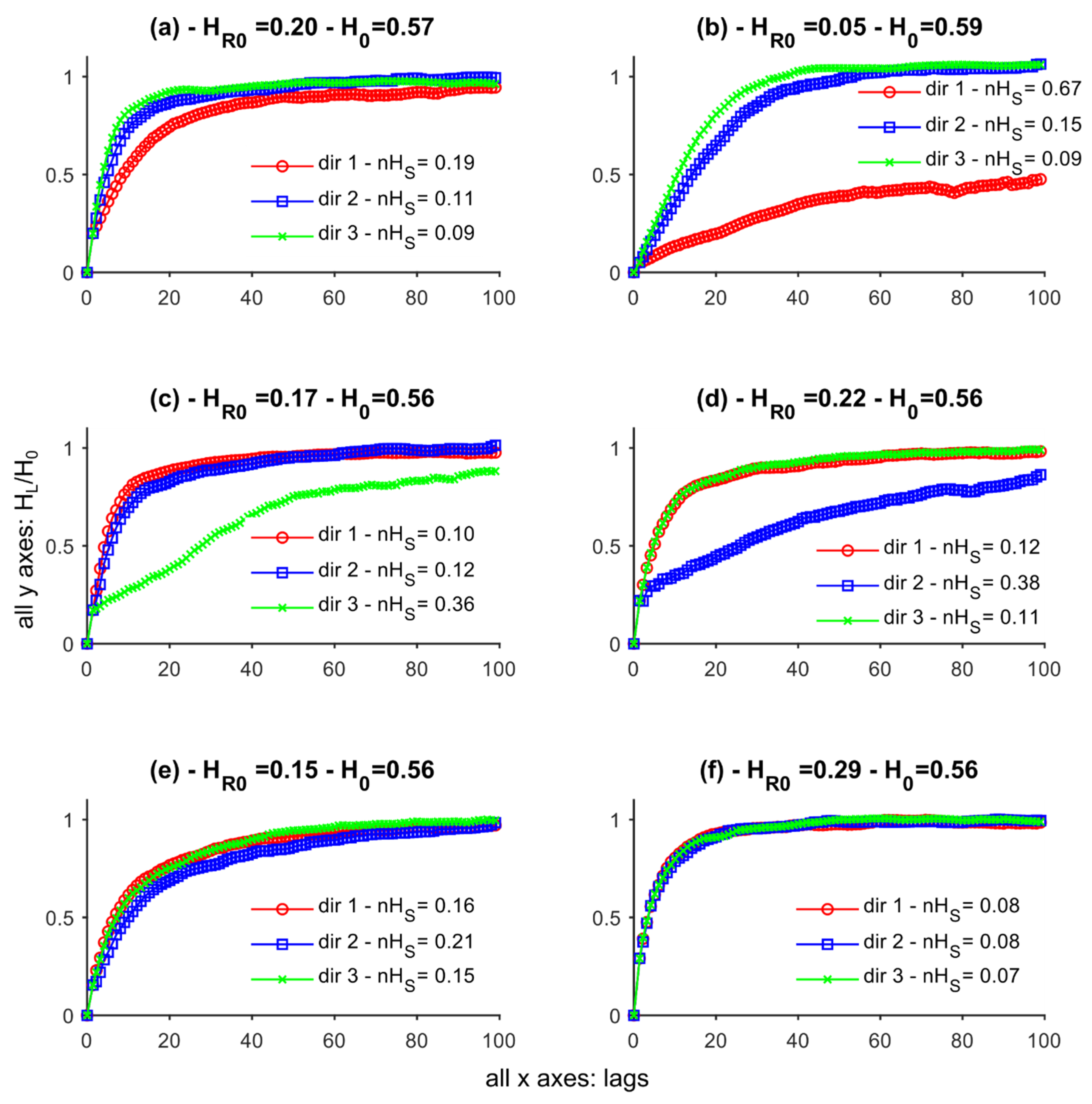


| Image | Length | Width | Orientation | Amplitude | Wavelength |
|---|---|---|---|---|---|
| (a) | 300 | 5 | 90 | 5 | 100 |
| (b) | 300 | 20 | 90 | 5 | 100 |
| (c) | 50 | 5 | 0 | 1 | 1 |
| (d) | 50 | 5 | 135 | 1 | 1 |
| (e) | 50 | 5 | 135 {90;180} | 1 | 100 |
| (f) | 5 | 5 | 90 {45;135} | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedretti, D.; Bianchi, M. GEOENT: A Toolbox for Calculating Directional Geological Entropy. Geosciences 2022, 12, 206. https://doi.org/10.3390/geosciences12050206
Pedretti D, Bianchi M. GEOENT: A Toolbox for Calculating Directional Geological Entropy. Geosciences. 2022; 12(5):206. https://doi.org/10.3390/geosciences12050206
Chicago/Turabian StylePedretti, Daniele, and Marco Bianchi. 2022. "GEOENT: A Toolbox for Calculating Directional Geological Entropy" Geosciences 12, no. 5: 206. https://doi.org/10.3390/geosciences12050206
APA StylePedretti, D., & Bianchi, M. (2022). GEOENT: A Toolbox for Calculating Directional Geological Entropy. Geosciences, 12(5), 206. https://doi.org/10.3390/geosciences12050206







