Numerical Modelling Challenges in Rock Engineering with Special Consideration of Open Pit to Underground Mine Interaction
Abstract
:1. Introduction
2. Fundamental Questions about Numerical Analysis of Rock Engineering Problems
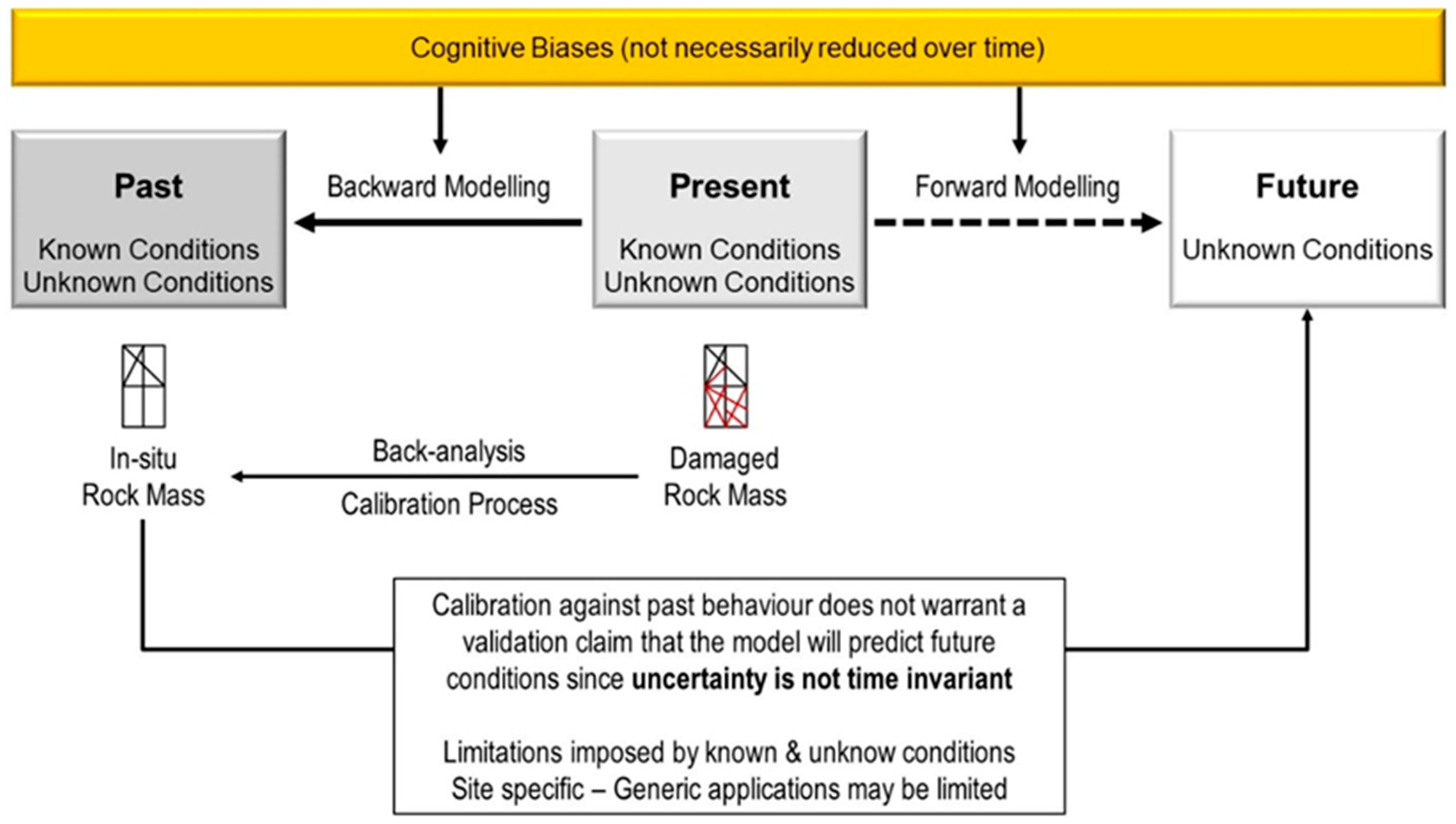
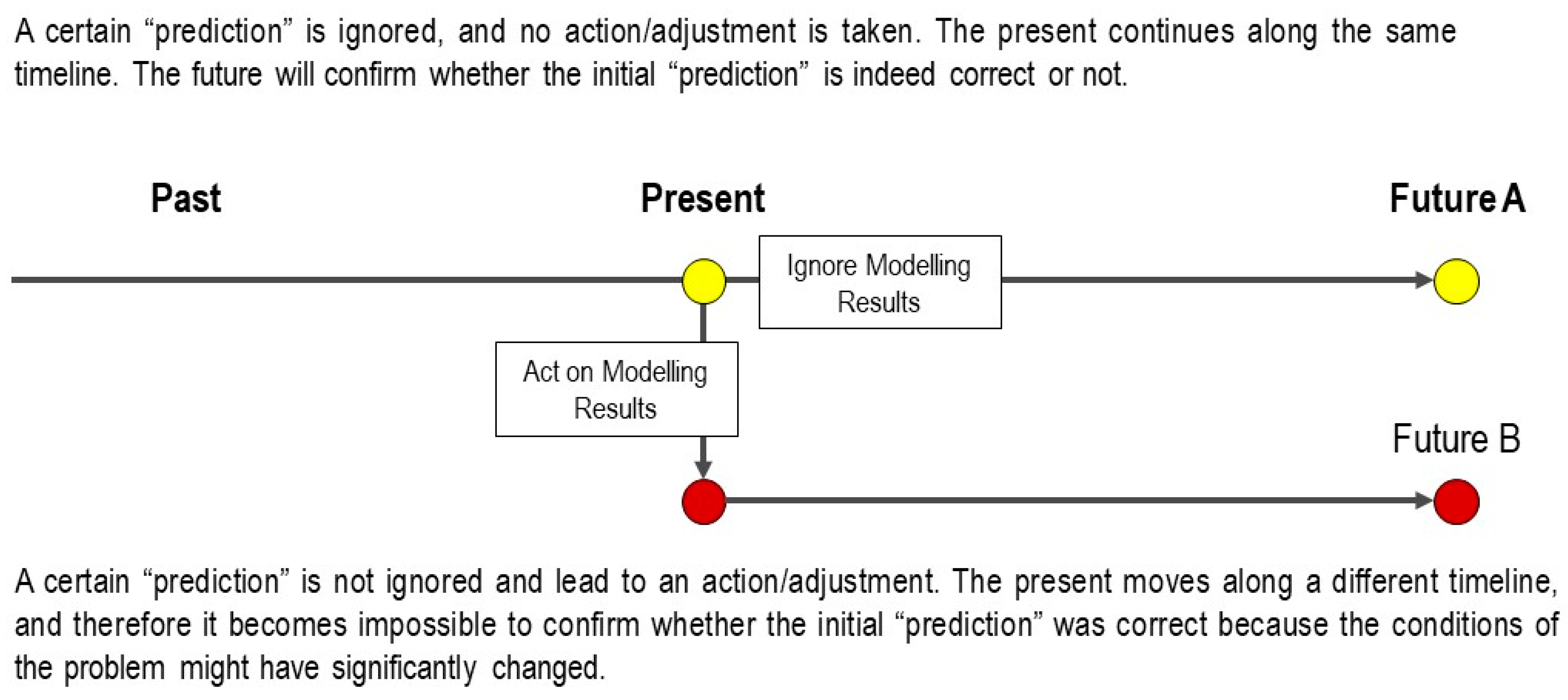
2.1. Are Numerical Models Capable of Predicting the Future?
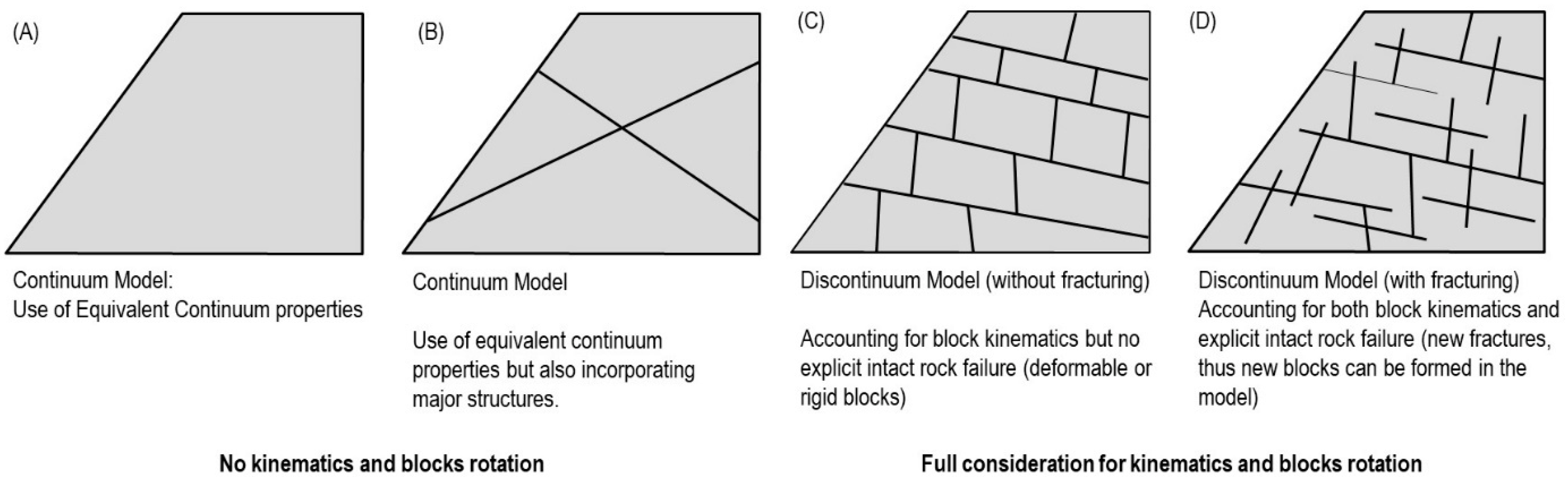
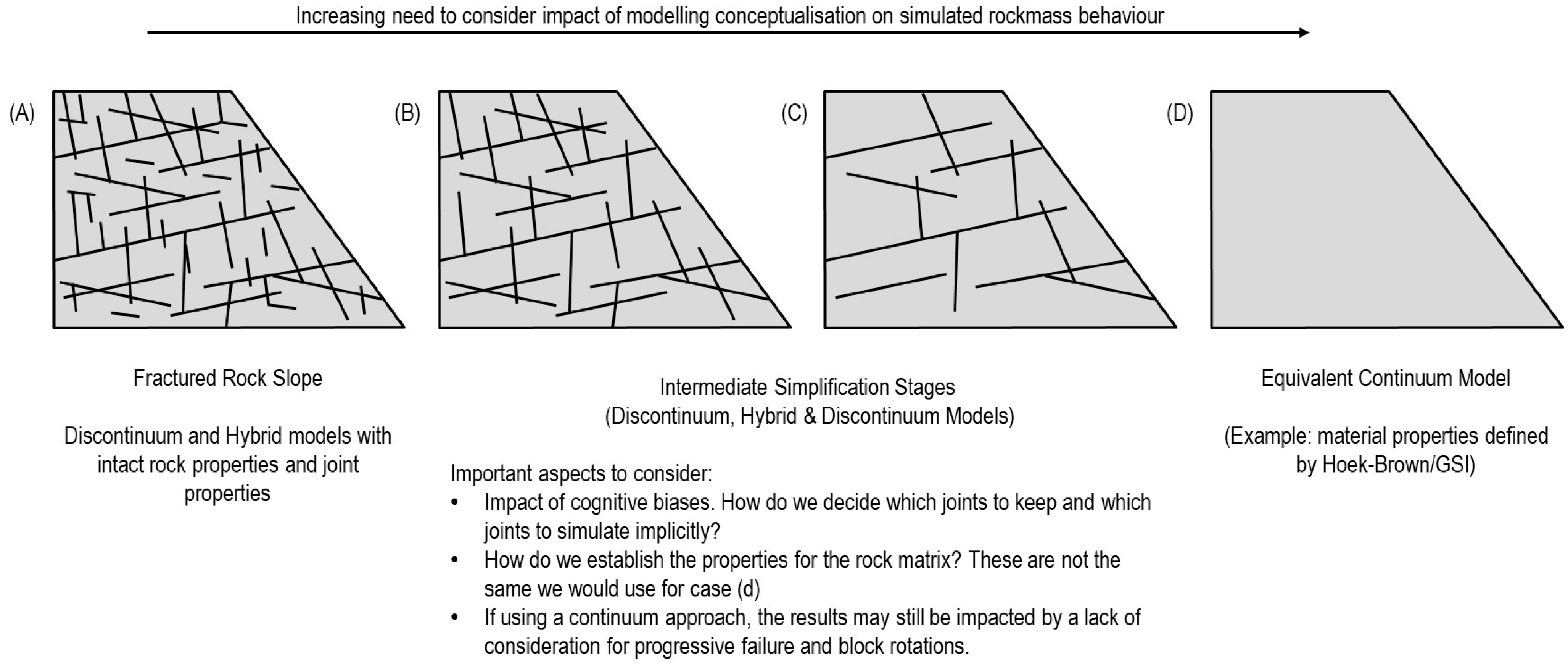
2.2. Continuum and Discontinuum Modelling
- Continuum methods: Boundary Element Method (BEM), Finite Element Method (FEM), and Finite Difference Method (FDM);
- Discontinuum methods: Discrete Elements Method (DEM), Discontinuous Deformation Analysis (DDA), and Discrete Fracture Network Method (DFN);
- Hybrid models: Hybrid BEM/DEM, Hybrid FEM/BEM, Hybrid FEM/DEM (FDEM), and other hybrid models.
- How do we reduce the impact of cognitive biases, that is, how do we decide which joints to keep and which joints to simulate implicitly?
- How do we establish the properties for the rock matrix since those cannot be the same as an equivalent continuum model?
- If using a continuum approach, will the results be impacted by a lack of consideration for progressive failure and block rotations?
2.3. Difficult Questions and Considerations about Numerical Modelling
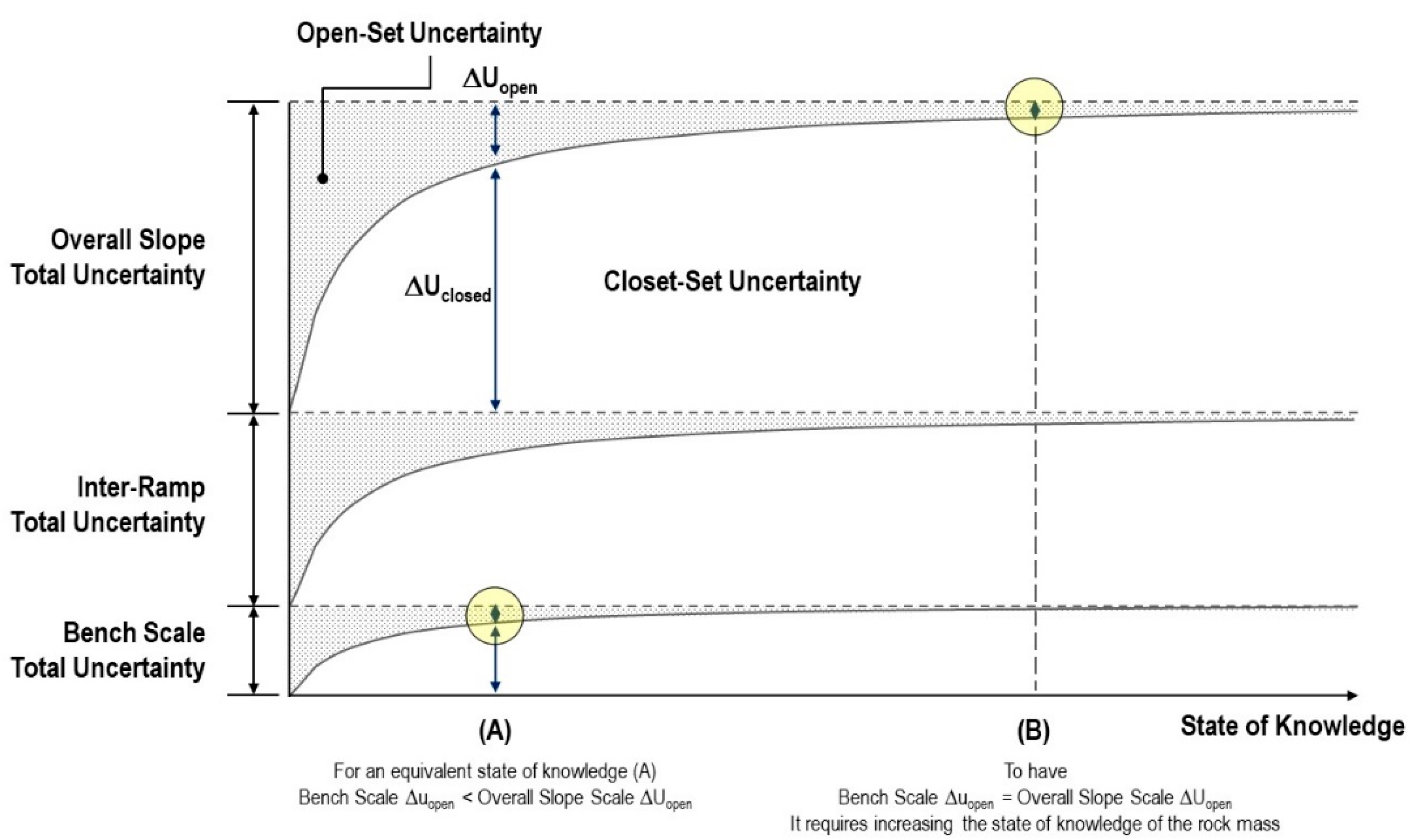
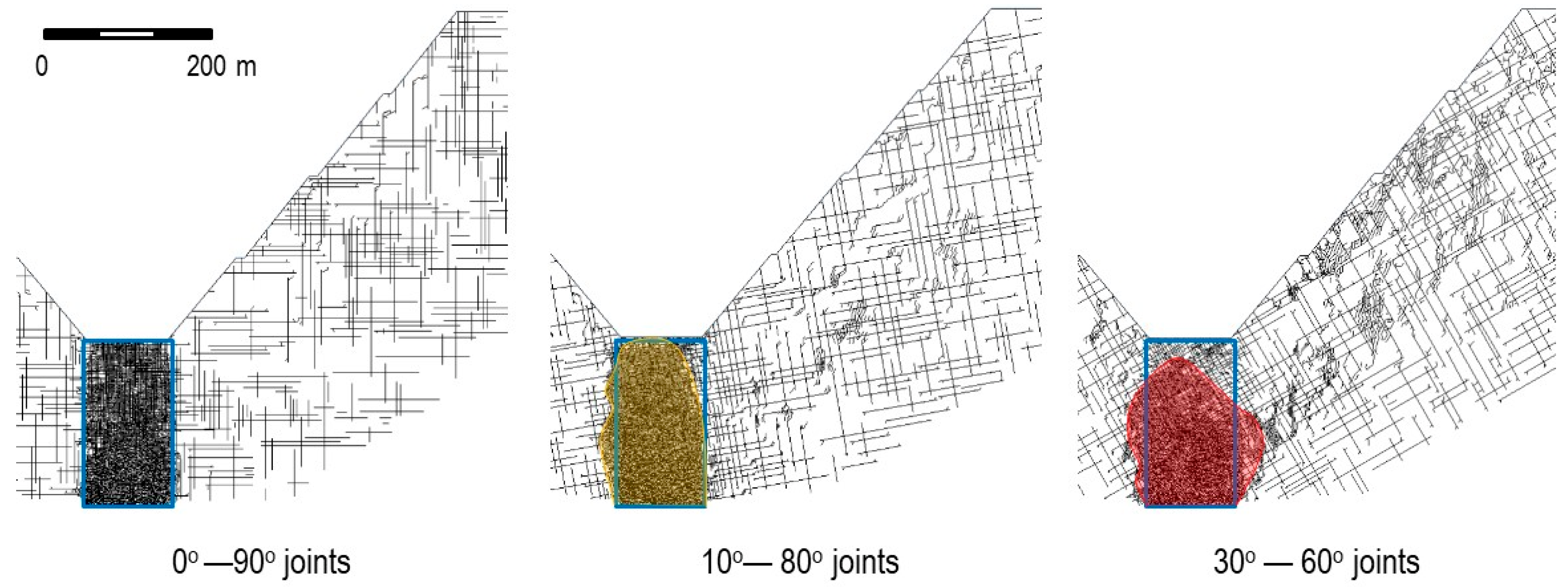
2.4. Model Scale: Why “Go Big or Go Home” Is Not the Ideal Slogan for Modelling Rock Engineering Problems
3. Examples of Future Modelling Challenges: Analysis of Pit-to-Cave Transition
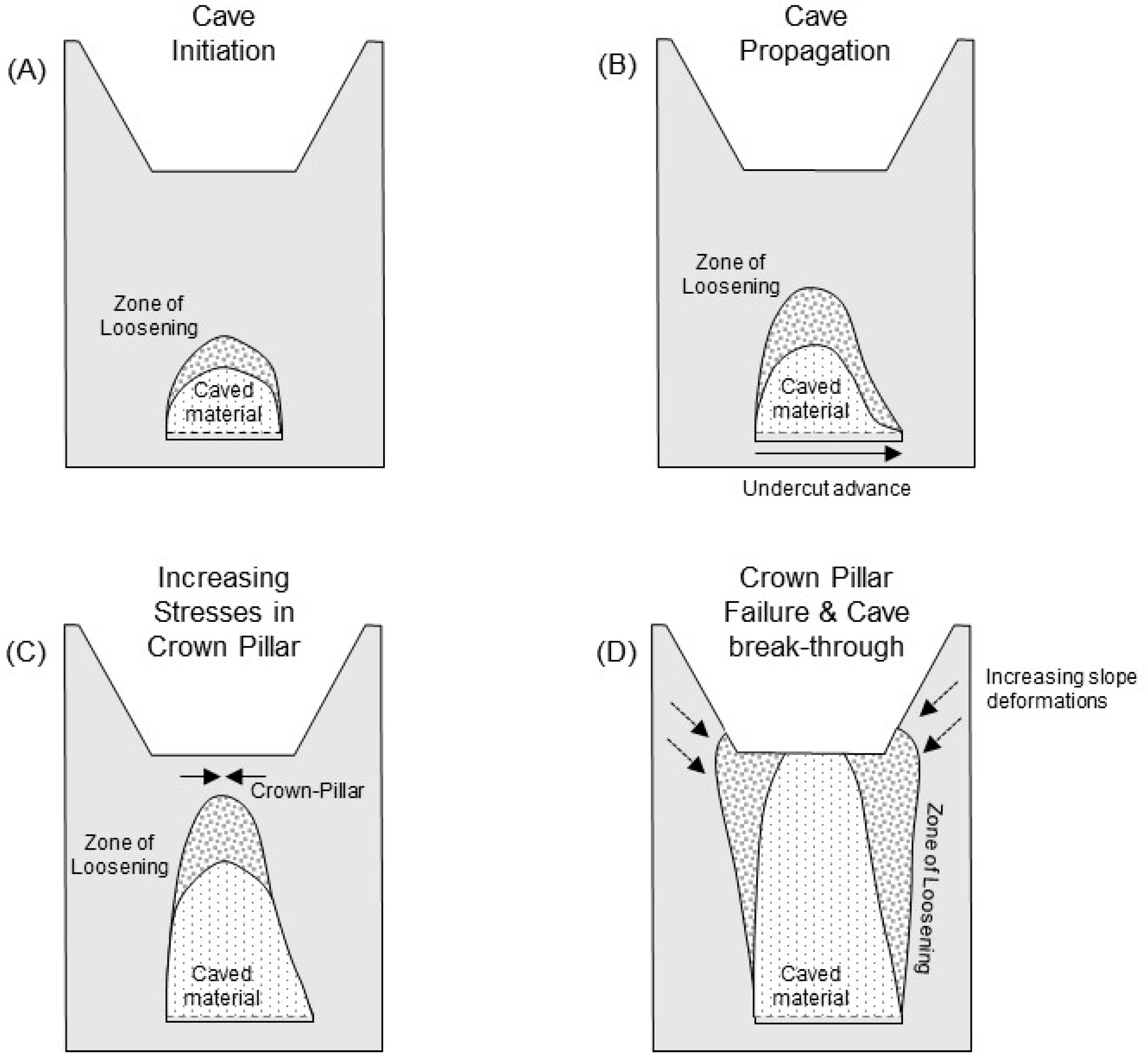
3.1. Slope Failure and Caving Mechanisms
- Kinematic: sliding, toppling, wedges due to joints and structures;
- Composite: a combination of stress-induced failure and sliding, rotation along pre-existing structures;
- Circular/quasi-circular/rotational: through very weak and altered rock masses and waste dumps.
3.2. Hybrid FDEM Examples
3.2.1. Model Setup
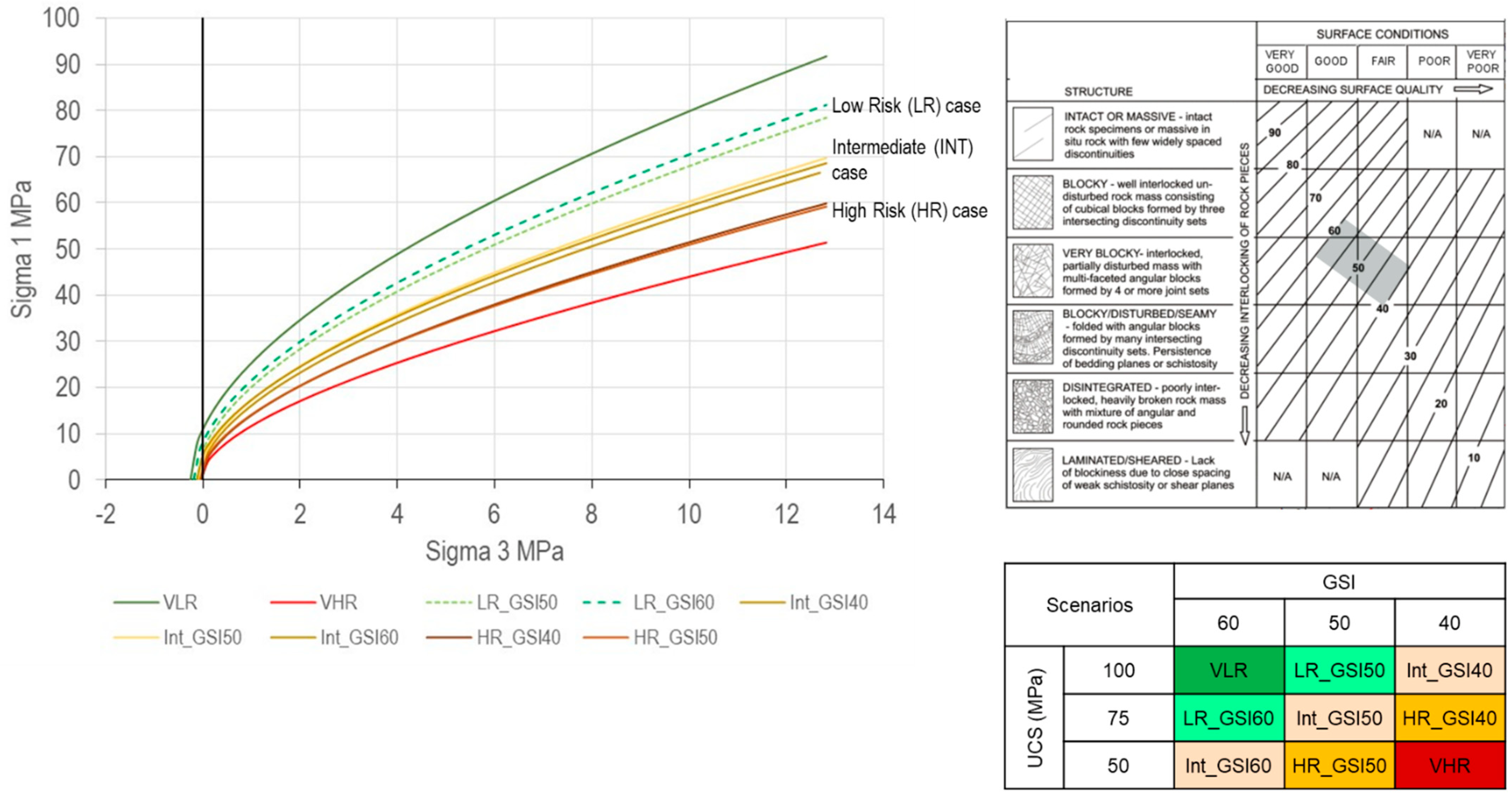
3.2.2. Material Parameters
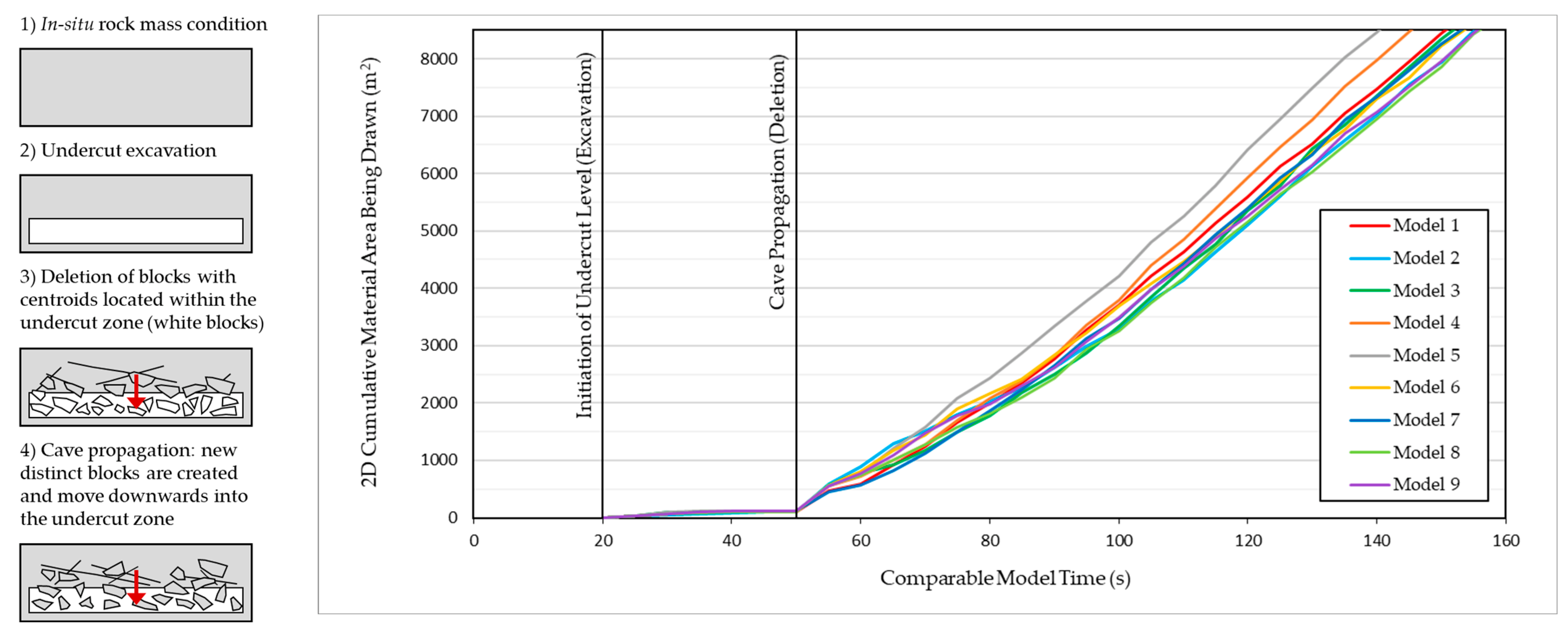
3.2.3. Simulation of Pit Excavation, Undercut Initiation, and Production
3.2.4. Results
4. Discussion and Conclusions
- Method and Approach:
- 2D models offer the opportunity to complete a relatively substantial number of preliminary models to understand the relevance of modelling parameters, geological setting, and mining strategy. However, 2D models are limited in terms of simulating what effectively are 3D problems (e.g., slope and cave mining), and they should only be considered as part of a toolbox approach and not as a unique solution;
- Selection of constitutive models for materials and their application at different zones of interest can significantly impact results. Model simplification should only be done with care and thought and with the justification that the simplification process will not invalidate the results. This limitation extends to 2D and 3D models alike;
- Emphasis should be on the choices that each modeler makes to be able to use their numerical models within the scope of their purpose and represent realistic outcomes. For example, the conceptual FDEM models presented in this paper investigated different simplification decisions, whether focusing on geological or modelling specific parameters, and are included to show the significance of these decisions on the use and interpretation of the results.
- Geological Setting and Data Confidence:
- d.
- In our particular case, the existence of a fault extending from the left flank of the undercut level increased the deformation observed in the slope above and, subsequently, the cave propagation was affected. Without confidence in the structural setting, confidence in the numerical models is significantly reduced;
- e.
- Depending on the model purpose, the inclusion of a discrete fracture network could be considered non-negotiable due to the impact on both the mechanisms of interaction between mining areas and the magnitude of deformation experienced in the models. Without carefully considering anisotropic effects, certain modelling results may be invalidated;
- f.
- The numerical models are based on a simplification of a complicated geological setting. This limitation is common to many 2D and 3D models used in the industry. There is the tendency to assign the same GSI ratings to large domains in both 2D and 3D models, which is clearly a non-realistic assumption since rock masses are inherently variable.
- Model Calibration and Validation:
- g.
- Each of the models presented a different shape of caved material, and because the cave shapes remain unknown at the pre-feasibility and feasibility level, it further raises the issue of validating forward modelling results that represent conditions many years in the future. This limitation is not specific to the FDEM models presented in this paper and it extends to all forward models, whether 2D or 3D;
- h.
- In general terms, and not limited to the FDEM models presented herein, deformations are generally measured on the surface of an excavation. Therefore, matching deformations rather than the failure mechanisms is not a condition sufficient to state that a particular model is calibrated and validated;
- i.
- Models may be realistic, but it is important to recognize the difference between “realistic” and “reality”. Models by definitions simplify reality; furthermore, it may be possible for two different models to simulate the same realistic behavior using different modelling approaches (e.g., continuum vs. discontinuum). Thus, calibrated parameters may not transfer easily between different modelling scenarios and between different geological settings.
Author Contributions
Funding
Conflicts of Interest
References
- Eberhardt, E.; Woo, K.; Stead, D.; Elmo, D. Transitioning from Open Pit to Underground Mass Mining: Meeting the Rock Engineering Challenges of Going Deeper. In Proceedings of the 2015 International Symposium on Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015. [Google Scholar]
- Araneda, O. Codelco: Present, future and excellence in projects. In Proceedings of the 8th International Conference & Exhibition on Mass Mining (MassMin2020), Santiago, Chile, 9–11 December 2020. [Google Scholar] [CrossRef]
- Whittle, D.; Brazil, M.; Grossman, P.; Rubinstein, J.; Thomas, D. Combined optimisation of an open-pit mine outline and the transition depth to underground mining. Eur. J. Oper. Res. 2018, 268, 624–634. [Google Scholar] [CrossRef]
- Vyazmensky, A. Numerical Modelling of Surface Subsidence Associated with Block Cave Mining Using a Finite Element/Discrete Element Approach. Ph.D. Thesis, Simon Fraser University, Vancouver, BC, Canada, 2008. [Google Scholar]
- Elmo, D.; Vyazmensky, A.; Stead, D.; Rance, J. Numerical analysis of pit wall deformation induced by block-caving mining: A combined FEM/DEM DFN synthetic rock mass approach. In Proceedings of the 5th International Conference and Exhibition on Mass Mining (MassMin2008), Luleå, Sweden, 9–11 June 2008. [Google Scholar]
- Elmo, D.; Rogers, S.; Beddoes, R.; Catalan, A. An integrated finite/discrete element method discrete fracture network synthetic rock mass approach for the modelling of surface subsidence associated with panel cave mining at the Cadia East underground project. In Proceedings of the 2nd International Symposium on Block and Sublevel Caving (Caving 2010), Perth, Australia, 20–22 April 2010. [Google Scholar] [CrossRef]
- Sainsbury, D.; Sainsbury, B. Three-dimensional analysis of pit slope stability in anisotropic rock masses. In Proceedings of the 2013 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering (Slope Stability 2013), Brisbane, Australia, 25–27 September 2013. [Google Scholar] [CrossRef]
- Beck, D.; Pfitzner, M. Interaction between deep block caves and existing, overlying caves or large open pits. In Proceedings of the 5th International Conference and Exhibition on Mass Mining (MassMin2008), Luleå, Sweden, 9–11 June 2008. [Google Scholar]
- Beck, D.; Sharrock, G.; Capes, G. A Coupled DFE-Newtonian Cellular Automata Cave Initiation, Propagation And Induced Seismicity. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Borges, J. On exactitude in science. Los Anales de Buenos Aires 1946, 3. [Google Scholar] [CrossRef]
- Barton, N. Continuum or discontinuum: GSI or JRC. Invited keynote lecture. In Proceedings of the Geotechnical Challenges in Mining, Tunnelling and Underground Structures (ICGCMTU2021), Malaysia (On-Line Conference), 20–21 December 2021. [Google Scholar]
- Elmo, D.; Stead, D. The Role of Behavioural Factors and Cognitive Biases in Rock Engineering. Rock Mech. Rock Eng. 2021, 54, 2109–2128. [Google Scholar] [CrossRef]
- Read, J.; Stacey, P. Guidelines for Open Pit Slope Design; CSIRO Publishing: Melbourne, Victoria, Autralia, 2009. [Google Scholar] [CrossRef] [Green Version]
- Taleb, N. The Black Swan: The Impact of the Highly Improbable; Random House Publishing Group: New York, NY, USA, 2010. [Google Scholar]
- Ross, I.; Stewart, C. Issues with transitioning from open pits to underground caving mines. In Proceedings of the 8th International Conference & Exhibition on Mass Mining (MassMin2020), Santiago, Chile, 9–11 December 2020. [Google Scholar] [CrossRef]
- Elmo, D. Evaluation of a Hybrid FEM/DEM Approach for Determination of Rock Mass Strength Using a Combination of Discontinuity Mapping and Fracture Mechanics Modelling, with Particular Emphasis on Modelling of Jointed Pillars. Ph.D. Thesis, Camborne School of Mines. University of Exeter, Exeter, UK, 2006. [Google Scholar]
- Elmo, D.; Stead, D. Chapter 23: Applications of fracture mechanics to rock slopes. In Rock Mechanics and Engineering Volume 3: Analysis, Modeling & Design, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; Volume 3. [Google Scholar] [CrossRef]
- Jing, J. A review of techniques, advances, and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Coggan, J.; Stead, D. Numerical modelling of the effects of weak mudstone on tunnel roof behaviour. In Proceedings of the 58th Canadian Geotechnical Conference, Saskatoon, SK, Canada, 18–21 September 2005. [Google Scholar]
- Singh, R.; Sun, G. Fracture Mechanics Applied to Slope Stability Analysis. International Symposium on Surface Mining Future Concepts; University of Nottingham: Nottingham, UK, 1989. [Google Scholar]
- Scavia, C.; Castelli, M. Analysis of the propagation of natural discontinuities in rock bridges. In Proceedings of the ISRM International Symposium EUROCK 96, Turin, Italy, 2–5 September 1996. [Google Scholar]
- Hajiabdolmajid, V. Mobilization of Strength in Brittle Failure of Rock. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2001. [Google Scholar]
- Spreafico, M. Gravitational Instability in Heterogeneous Rock Slabs in Valmarecchia: Long-Term Evolution and Mitigation Strategies. Ph.D. Thesis, University of Bologna, Bologna, Italy, 2015. [Google Scholar]
- Christianson, M.; Board, M.; Rigby, D. UDEC simulation of triaxial testing of lithophysal tuff. In Proceedings of the 41st U.S. Symposium on Rock Mechanics, Golden, CO, USA, 17–21 June 2006. [Google Scholar]
- Alzo’ubi, A. The Effect of Tensile Strength on the Stability of Rock Slopes. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2009. [Google Scholar]
- Havaej, M.; Stead, D.; Eberhardt, E.; Fisher, B. Characterization of bi-planar and ploughing failure mechanisms in footwall slopes using numerical modelling. Eng. Geol. 2014, 178, 109–120. [Google Scholar] [CrossRef]
- Potyondy, D.; Cundall, P. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Pierce, M.; Cundall, P.; Potyondy, D. A synthetic rock mass model for jointed rock. In Proceedings of the 1st Canada-US Rock Mechanics Symposium, Vancouver, BC, Canada, 27–31 May 2007. [Google Scholar]
- Sholtès, L.; Donzé, F. A DEM analysis of step-path failure in jointed rock slopes. C. R. Mec. 2015, 343, 155–165. [Google Scholar] [CrossRef]
- Jiang. M.; Jiang, T.; Crosta, G.; Shi, Z.; Chen, H.; Zhang, N. Modeling failure of jointed rock slope with two main joint sets using a novel DEM bond contact model. Eng. Geol. 2015, 193, 79–96. [Google Scholar] [CrossRef]
- Kahneman, D. Thinking, Fast and Slow; Penguin Books: London, UK, 2011. [Google Scholar]
- Karimi Sharif, L.; Elmo, D.; Stead, D. Improving DFN-geomechanical model integration using a novel automated approach. Comput. Geotech. 2019, 105, 228–248. [Google Scholar] [CrossRef]
- Brummer, R. The transition from open pit to underground mining: An unsual slope failure mechanism at Palabora. In Proceedings of the International Symposium on Stability of Rock Slopes in Open Pit Mining and Civil Engineering, Cape Town, South Africa, 3–6 April 2006. [Google Scholar]
- Sainsbury, B.; Pierce, M.; Mas Ivars, D. Analysis of Caving Behaviour Using a Synthetic Rock Mass Ubiquitous Joint Rock Mass Modelling Technique. In Proceedings of the First Southern Hemisphere International Rock Mechanics Symposium, Perth, Australia, 16–19 September 2008. [Google Scholar] [CrossRef]
- Sainsbury, D.; Sainsbury, B.; Paetzold, H.-D.; Lourens, P.; Vakili, A. Caving-induced subsidence behaviour of lift 1 at the Palabora block cave mine. In Proceedings of the 7th International Conference and Exhibition on Mass Mining (MassMin 2016), Sydney, Australia, 9–11 May 2016. [Google Scholar]
- Vyazmensky, A.; Stead, D.; Elmo, D.; Moss, A. Numerical Analysis of Block Caving-Induced Instability in Large Open Pit Slopes: A Finite Element/Discrete Element Approach. Rock Mech. Rock Eng. 2010, 43, 21–39. [Google Scholar] [CrossRef]
- Woo, K.; Eberhardt, E.; Rabus, B.; Stead, D.; Vyazmensky, A. Integration of field characterisation, mine production and InSAR monitoring data to constrain and calibrate 3-D numerical modelling of block caving-induced subsidence. Int. J. Rock Mech. Min. 2012, 53, 166–178. [Google Scholar] [CrossRef]
- Elmo, D.; Vyazmensky, A.; Stead, D.; Rogers, S. Applications of a finite discrete element approach to model block cave mining. In Innovative Numerical Modelling in Geomechanics; CRC Press: Boca Raton, FL, USA, 2012; pp. 355–371. [Google Scholar] [CrossRef]
- Makridakis, S.; Hibon, M.; Moser, C. Accuracy of Forecasting: An Empirical Investigation. J. R. Stat. Soc. 1979, 142, 97. [Google Scholar] [CrossRef]
- Hammah, R.; Curran, J. It is better to be approximately right than precisely wrong: Why simple models work in mining geomechanics. In Proceedings of the International Workshop on Numerical Modeling for Underground Mine Excavation Design, Asheville, NC, USA, 28 June 2009. [Google Scholar]
- Stead, D.; Coggan, J.; Elmo, D.; Yan, M. Modelling Brittle Fracture in Rock Slopes Experience Gained and Lessons Learned. In Proceedings of the 2007 International Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering, Perth, Australia, 12–14 September 2007. [Google Scholar] [CrossRef]
- Flores, G.; Catalan, A. A transition from a large open pit into a novel ‘macroblock variant’ block caving geometry at Chuquicamata mine, Codelco Chile. J. Rock Mech. Geotech. Eng. 2019, 11, 549–561. [Google Scholar] [CrossRef]
- Campbell, R.; Mardiansyah, F.; Banda, H.; Tshisens, J.; Griffiths, C.; Beck, D. Early experiences from the Grasberg block cave: A rock mechanics perspective. In Proceedings of the 8th International Conference & Exhibition on Mass Mining (MassMin2020), Santiago, Chile, 9–11 December 2020. [Google Scholar] [CrossRef]
- Ginting, A.; Widijanto, E.; Yuniar, A. Grasberg open pit to Grasberg Block Cave transition water management plan. In Proceedings of the 8th International Conference & Exhibition on Mass Mining (MassMin2020), Santiago, Chile, 9–11 December 2020. [Google Scholar]
- Flores, G.; Karzulovic, A. Geotechnical Guidelines for a Transition from Open Pit to Underground Mining. Main Activity 2: Geotechnical Guidelines Caving Propagation. International Caving Study II Task 4 Technical Report. July 2003. [Google Scholar]
- Flores, G.; Karzulovic, A. Geotechnical Guidelines for a Transition from Open Pit to Underground Mining. Main Activity 2: Geotechnical Guidelines Geotechnical Characterization. International Caving Study II Task 4 Technical Report. May 2003. [Google Scholar]
- Flores, G.; Karzulovic, A. Geotechnical Guidelines for a Transition from Open Pit to Underground Mining. Principal Activity 2: Geotechnical Guidelines Surface Crown Pillar; International Caving Study II Task 4 Technical Report; 04. International Caving Study II Task 4 Technical Report. April 2003. [Google Scholar]
- Wellman, E.; Nicholas, D.; Branon, C. Geomechanics considerations in the Grasberg pit to block cave transition. In Proceedings of the 5th International Conference and Exhibition on Mass Mining (MassMin2008), Luleå, Sweden, 9–11 June 2008. [Google Scholar]
- Moss, A. MINE 507: Block Caving Systems; Lecture Notes; University of British Columbia: Vancouver, BC, Canada, 2021. [Google Scholar]
- Hamman, E.; Cowan, M.; Venter, J.; de Souza, J. Considerations for open pit to underground transition interaction. In Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Perth, Australia, 12–14 May 2020. [Google Scholar] [CrossRef]
- Baczynski, N. Stepsim4 ‘Step-Path’ Method for Slope Risks. In Proceedings of the ISRM International Symposium, Melbourne, Australia, 19–24 November 2000. ISRM-IS-2000-429. [Google Scholar]
- Brown, E. Block Caving Geomechanics; Issue 3 of JKMRC monograph series in mining and mineral processing; Julius Kruttschnitt Mineral Research Centre; The University of Queensland: Indooroopilly, Australia, 2003. [Google Scholar]
- Sainsbury, B. A Model for Cave Propagation and Subsidence Assessment in Jointed Rock Masses. Ph.D. Thesis, The University of New South Wales, Sydney, New South Wales, Australia, 2012. [Google Scholar]
- Rockfield, Elfen. Rockfield Software Ltd.: Swansea, UK, 2022. Available online: https://www.rockfieldglobal.com (accessed on 17 February 2022).
- Pine, R.; Owen, D.; Coggan, J.; Rance, J. A new discrete fracture modelling approach for rock masses. Géotechnique 2007, 57, 757–766. [Google Scholar] [CrossRef]
- Owen, D.; Feng, Y.; de Souza Neto, E.; Cottrell, M.; Wang, F.; Andrade Pires, F.; Yu, J. The modelling of multi-fracturing solids and particulate media: Modelling of multi-fracturing solids. Int. J. Numer. Meth. Engng. 2004, 60, 317–339. [Google Scholar] [CrossRef]
- Hoek, E.; Diederichs, M. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Zhang, Z. An empirical relation between mode I fracture toughness and the tensile strength of rock. Int. J. Rock Mech. Min. 2002, 39, 401–406. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]

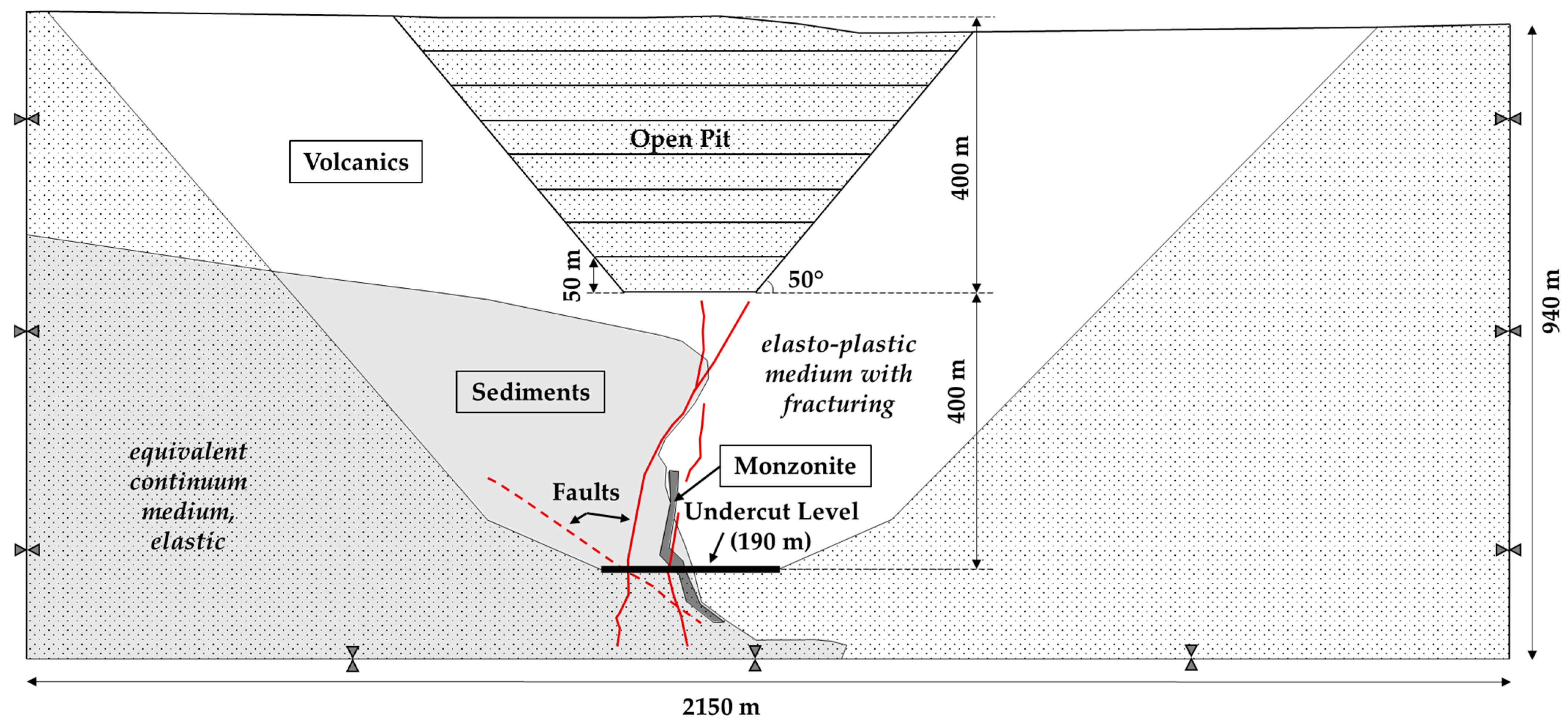

| Project Stage | |||||
|---|---|---|---|---|---|
| Project Level Status | Conceptual | Prefeasibility | Feasibility | Design and Construction | Operations |
| Geotechnical Characterization | Regional data compilation | Local scale data compilation and assessment | Ongoing collection of new local scale data | Improvement of database and 3D model | Continued refinement and maintenance of database and 3D model |
| Target levels of data confidence for each model | |||||
| Geology | >50% | 50–70% | 65–85% | 80–90% | >90% |
| Structural | >20% | 40–50% | 45–70% | 60–75% | >75% |
| Hydrogeological | >20% | 30–50% | 40–65% | 60–75% | >75% |
| Rock mass | >30% | 40–65% | 60–75% | 70–80% | >80% |
| Geotechnical | >30% | 40–60% | 50–75% | 65–85% | >80% |
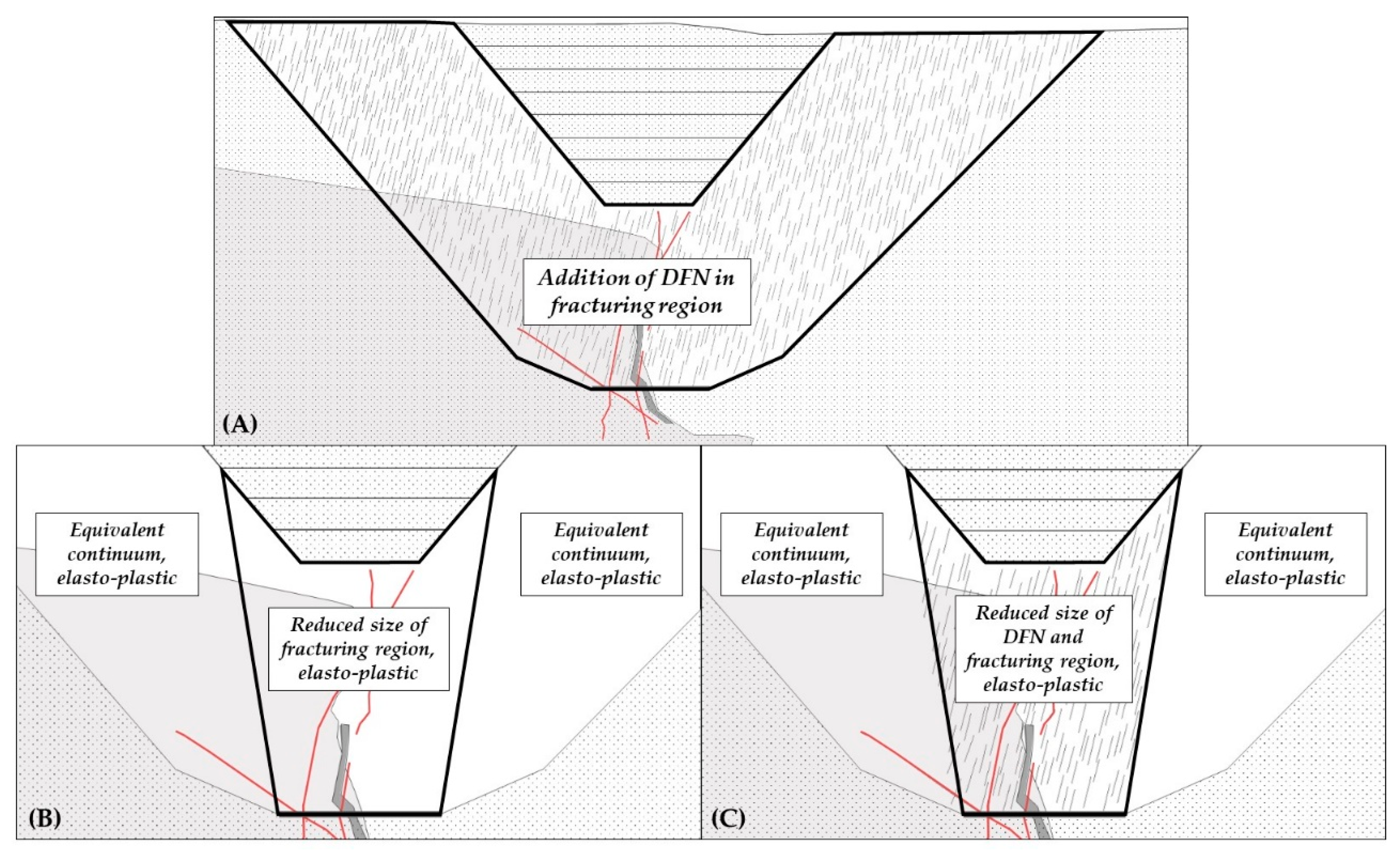
| Model No. | Description |
|---|---|
| 1 | Base case pit-to-cave transition. |
| 2 | Undercut level initiation on left side and reversed draw sequencing. |
| 3 | Symmetric draw sequence. |
| 4 | Fault to the left of the undercut level removed. |
| 5 | Symmetric draw sequence, fault to the left of the undercut level removed. |
| 6 | Discrete fabric structures introduced in fracturing region with coupled DFN model. |
| 7 | Reduced size of fracturing region. |
| 8 | Discrete fabric structures introduced in fracturing region with coupled DFN model of reduced size. |
| 9 | No open pit. |
| Parameter | Unit | Value | Source | ||
|---|---|---|---|---|---|
| Volcanics | Sediments | Monzonite | |||
| Intact | |||||
| UCS, σci | MPa | 121 | 99 | 123 | Lab value |
| Young’s Modulus, Ei | GPa | 67.7 | 68.0 | 65.0 | Lab value |
| Hoek–Brown material constant, mi | - | 18.9 | 12.0 | 19.7 | Lab value |
| Tensile strength, σt | MPa | 6.4 | 8.3 | 6.2 | Generalized Hoek–Brown |
| Poisson’s ratio, ν | - | 0.27 | 0.28 | 0.26 | Lab value |
| Rock mass | |||||
| GSI | - | 63 | 48 | 78 | Field estimate |
| Young’s Modulus, Erm | GPa | 38.6 | 17.8 | 55.3 | Generalized Hoek–Diederichs [57] |
| Density, ρ | kg m−3 | 2880 | 2880 | 2880 | Lab value |
| Tensile strength, σtm | MPa | 3.0 | 2.3 | 4.1 | Mohr–Coulomb Criteria |
| Cohesion, c | MPa | 4.1 | 2.5 | 6.2 | Generalized Hoek–Brown |
| Friction, φ | degrees | 49.8 | 40.0 | 53.7 | Generalized Hoek–Brown |
| Fracture energy, Gf | J m−2 | 12.8 | 21.0 | 12.7 | [58] |
| Dilation, ψ | degrees | 6 | 5 | 13 | [59] |
| Discontinuities | Faults | Joints and newly generated fractures | |||
| Fracture cohesion, c | MPa | 0.6 | 0 | Lab value | |
| Fracture friction, φ | degrees | 17 | 31 | Lab value | |
| Normal stiffness, kn | GPa m−1 | 5 | 5 | [16] | |
| Shear stiffness, ks | GPa m−1 | 0.5 | 0.5 | [16,54] | |
| Stress level | |||||
| In situ stress ratio, K | - | 2 | Conceptual | ||
| Stage | Duration (s) | Number of Stages | Time Step Control Data | |||
|---|---|---|---|---|---|---|
| Initial Time Step (s) | Max Time Step (s) | Max Change (%) | Factor of Critical Timestep | |||
| Equilibrium | 2 | 1 | 1e-5 | 1 | 101 | 0.75 |
| Pit Excavation | 2 | 8 | ||||
| Post-pit Equilibrium | 2 | 1 | ||||
| Undercut Excavation | 5 | 3–5 | ||||
| Initial Cave Propagation | 5 | 1 | ||||
| Active Cave Propagation (with deletion) | 10–30 | 9 | ||||
| Purpose of Model (Test) | Related Models 1 | Description of Results |
|---|---|---|
| Direction of undercut level excavation and draw | 2, 3, 5 | Mine design parameters, such as the direction of the draw, do not significantly impact the magnitude of deformation observed in the left pit wall relative to other scenarios. Reversed draw (No. 2) resulted in the development of a tension crack in a similar location, while the slope deformation decreased, despite an increased HOD. The symmetric draw resulted in a tension crack forming lower in the pit wall. Cave shapes with reversed and symmetrical draws were more centralized, while the base case model showed propagation skewed to the left despite the deformation of the left slope pushing the cave to the right. The effect of the slope deformation pushing the cave development to the right can be seen in model No. 3 due to the symmetrical draw. Reversed draw required a longer model run time to extract the same amount of material, while symmetric draw negligibly impacted the run time. |
| Fault connection between pit and cave | 4, 5 | The pit wall deformation decreased significantly in the absence of the fault providing a connection between the pit walls and undercut level. The formation of tension cracks still occurred to release strain due to the deformation in the left pit wall from dilation at the contact of the stiff volcanics overlying the softer sedimentary units. Symmetric draw sequencing affected both the model run time and the HOD at a greater rate without the fault present. Cave shapes were more centralized due to the decrease in deformation, similar to the shape of the developed caves in the models with reversed and symmetric draws (No. 2 and 3). |
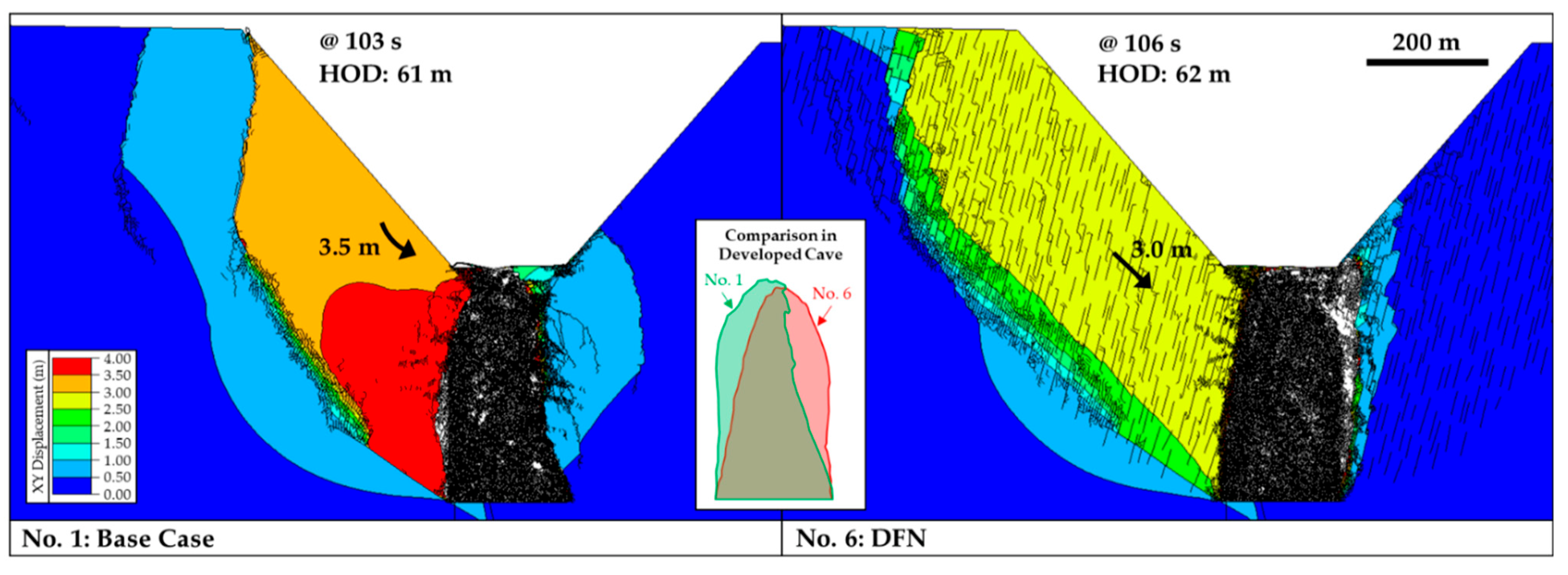
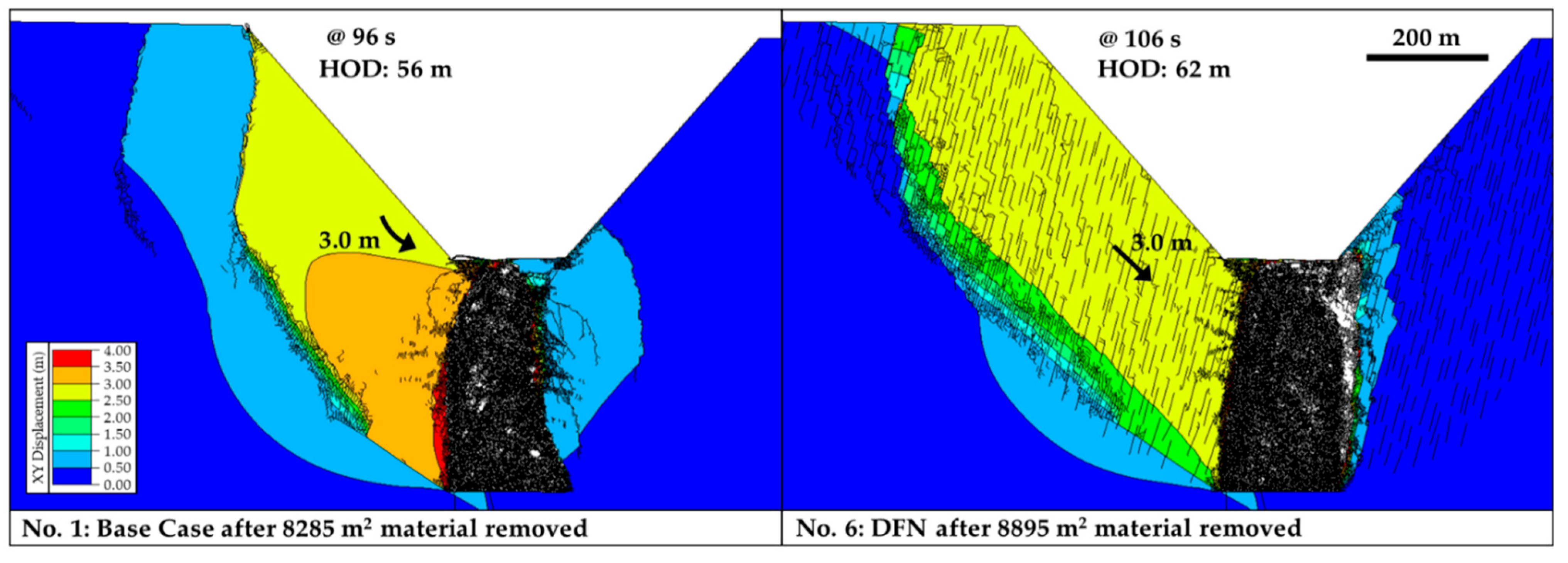
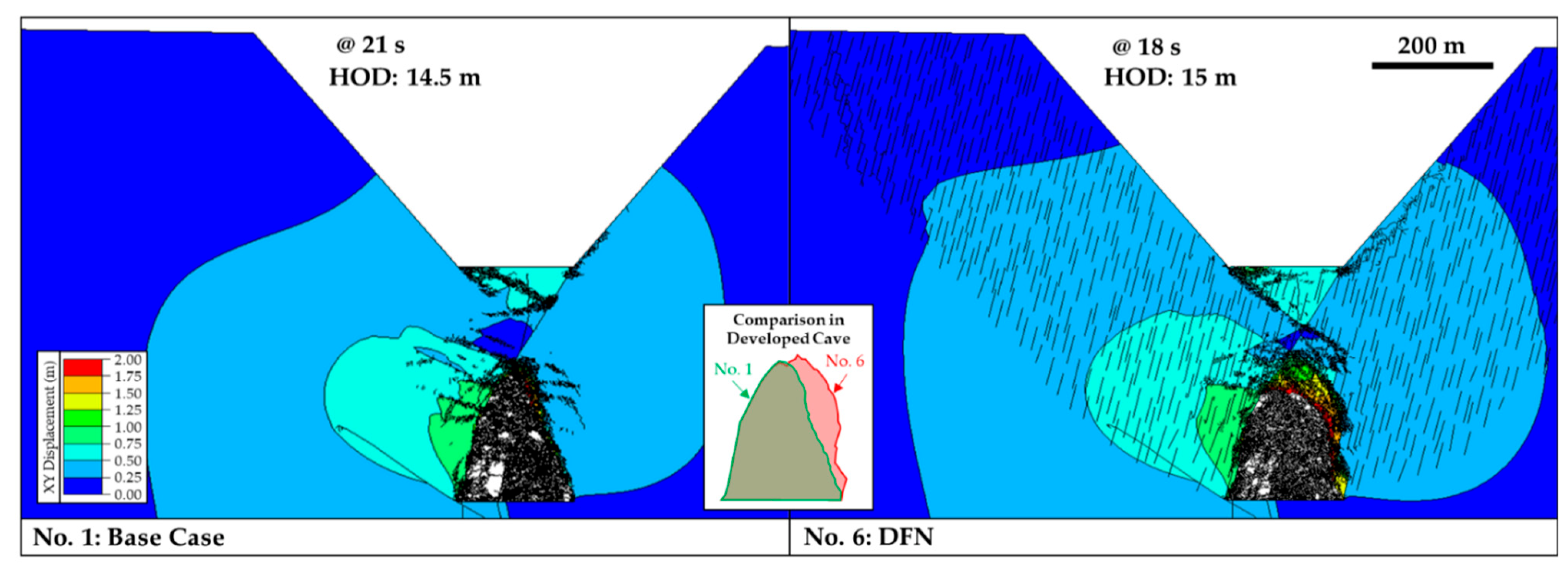
| Inclusion of DFN | 6, 8 | Inclusion of a DFN within the full fracturing zone (No. 6) resulted in a decrease in the deformation within the pit wall but an increase in the deformation on the crest due to the connection between the fault on the left side of the undercut level and surface through the joint network. Cave propagation is influenced by the orientation of the DFN fabric. Model No. 1 (no DFN) shows the equivalent deformation to No. 6 (with DFN) along the pit slope, but the deformation is achieved for smaller HOD (Figure 14). Note that the DFN includes fractures with sizes of ~50 m and spacings of ~10–15 m, and therefore it does not impact the assigned GSI values. However, the anisotropy effect on the models is significant regarding the deformation mechanism, magnitude of deformation behind the pit crest, and the cave development shape. In model No. 8, where the fracturing area and DFN area were reduced, the deformation magnitudes at the right pit toe are doubled. |
| Scale of fracturing regions | 7, 8 | Limiting the fracturing region to the cave area alone removes the mechanisms of deformation associated with the pit-to-cave transition; however, as seen in No. 7, it has the equivalent effect of removing the fault at the left side of the UCL. HOD for No. 7 was more comparable to the model without the open pit (No. 9). A noticeable change in the shape of the developed cave on the left side could be attributed to the decrease in deformation pushing the cave to the right near the pit toe. The inclusion of the DFN in the smaller fracturing area resulted in less change between cave shape and HOD (comparing No. 8 to No. 6), which may indicate that the inclusion of the DFN can better capture caving characteristics even with limiting fracturing to the cave area. However, the deformation magnitudes are different on either toe of the slope, and the impact of the fault on the left of the UCL is neglected. |
| Caving without an open pit | 9 | There is no significant effect of the pit on the cave propagation rate or shape, despite a slight increase in HOD in No. 9. While no equivalent model to No. 9 has been run with a DFN included, it is expected that the confinement would result in less impact from the fabric anisotropy. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shapka-Fels, T.; Elmo, D. Numerical Modelling Challenges in Rock Engineering with Special Consideration of Open Pit to Underground Mine Interaction. Geosciences 2022, 12, 199. https://doi.org/10.3390/geosciences12050199
Shapka-Fels T, Elmo D. Numerical Modelling Challenges in Rock Engineering with Special Consideration of Open Pit to Underground Mine Interaction. Geosciences. 2022; 12(5):199. https://doi.org/10.3390/geosciences12050199
Chicago/Turabian StyleShapka-Fels, Tia, and Davide Elmo. 2022. "Numerical Modelling Challenges in Rock Engineering with Special Consideration of Open Pit to Underground Mine Interaction" Geosciences 12, no. 5: 199. https://doi.org/10.3390/geosciences12050199
APA StyleShapka-Fels, T., & Elmo, D. (2022). Numerical Modelling Challenges in Rock Engineering with Special Consideration of Open Pit to Underground Mine Interaction. Geosciences, 12(5), 199. https://doi.org/10.3390/geosciences12050199







