Effect of Boulder Size on Debris Flow Impact Pressure Using a CFD-DEM Numerical Model
Abstract
:1. Introduction
2. Methods and Parameters
2.1. CFD-DEM Numerical Approach
2.2. Physical and Mechanical Parameters of the Model
3. Results
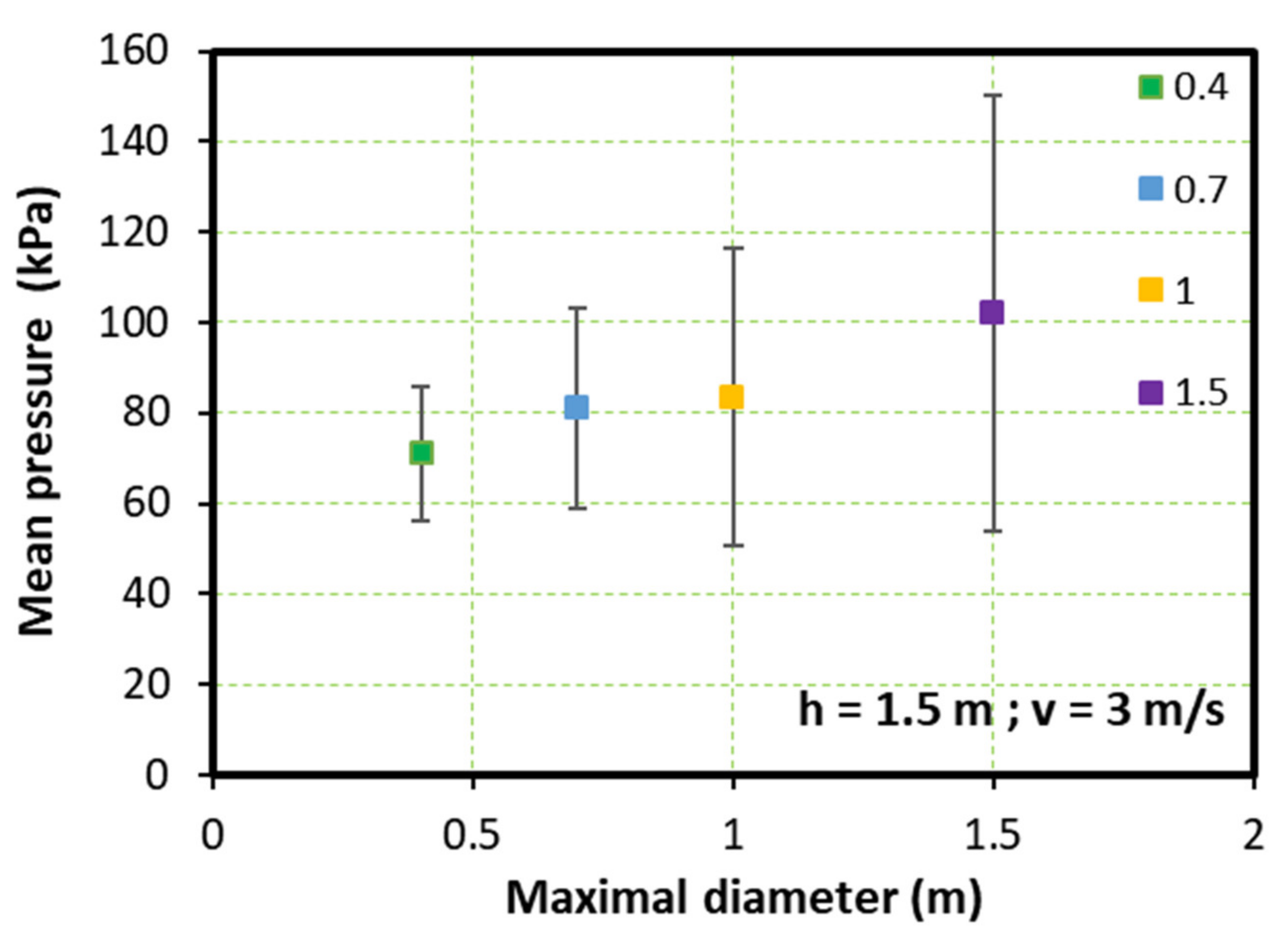
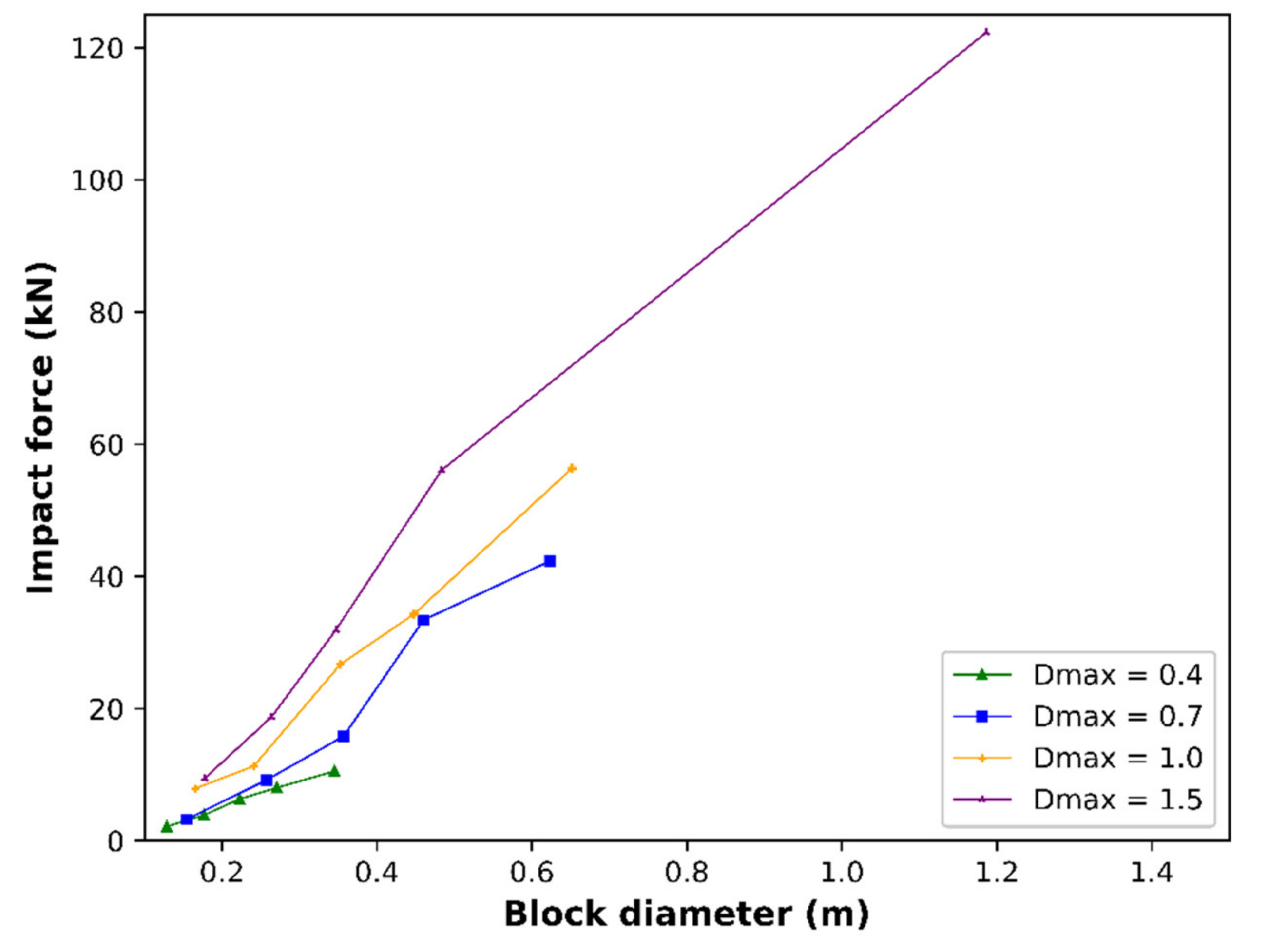
3.1. Effect of the Block Size
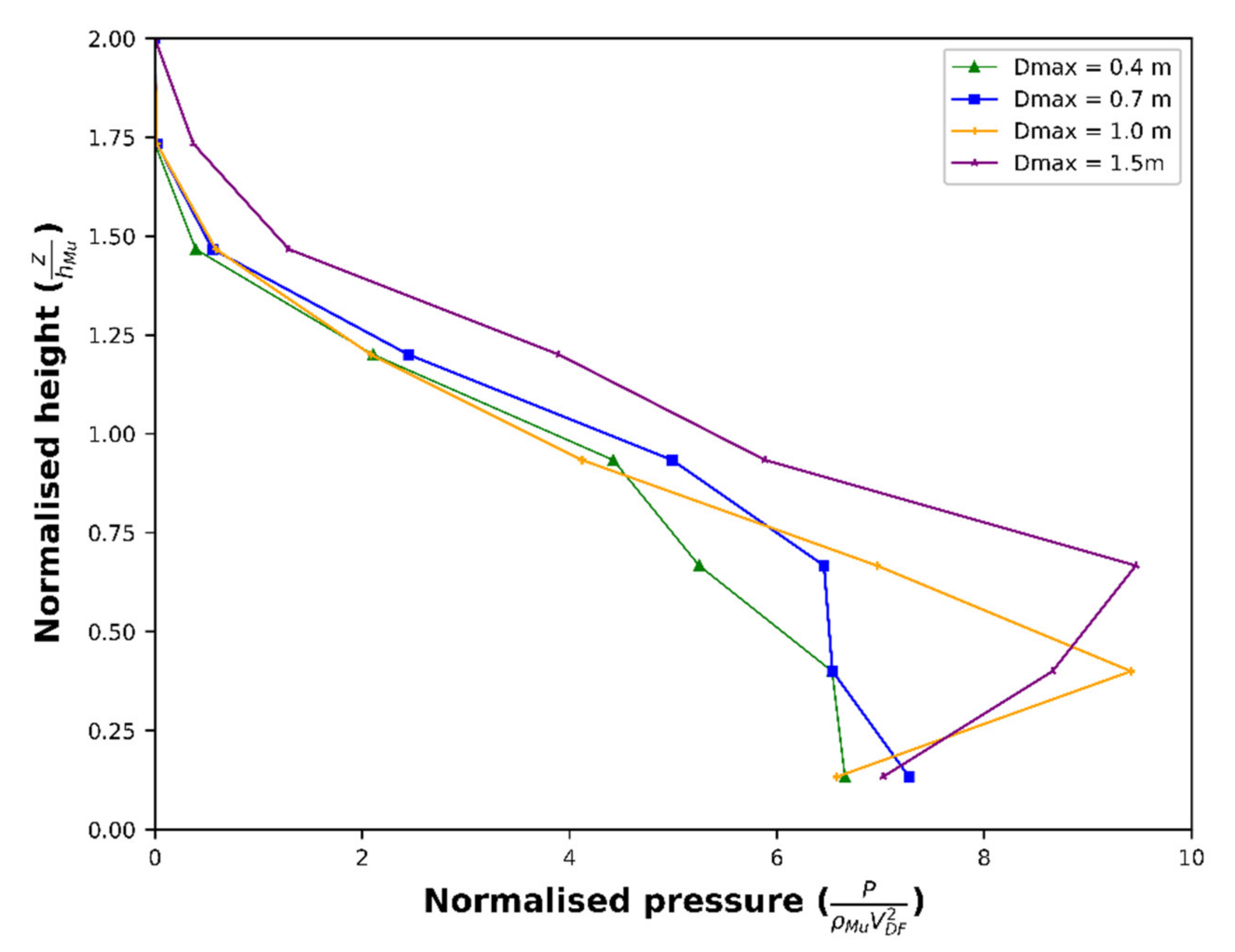
- To estimate the total pressure, the pressure applied by the blocks on the obstacles were measured and added to the effect of the fluid phase through hydrostatic pressure. The mean total pressure was calculated between t = 9 s and t = 12 s.
- The pressure was normalized to the density of the DF and the velocity () with ρ = 1867 kg/m3 and v = 3 m/s. We noted .
- The height was normalized to the flow height in cases without obstacles.
3.2. Influence of Individual Impacts on the Structure
4. Discussion
5. Conclusions
- The CFD-DEM model provides a precise average pressure value as a function of the flow height, the flow velocity and the block size.
- The effect of the block size on the impact pressure is that the highest maximum impact pressures resulted from coarser particle size distributions. There is a cumulative effect of a high number of collisions on the impact pressure on the obstacle.
- The same flow, with given macroscopic characteristics (height, velocity, density), induces different impact pressures depending on the particle size distribution of the blocks transported and affects the distribution of the individual contact forces on the obstacle.
- When the grain size distribution is spread out towards larger diameters, the temporal variation in the pressure applied on the obstacle increases. Furthermore, blocks of a given size imply greater contact forces when the maximum block size is greater. The biggest blocks also affect the impact forces of the smallest blocks; therefore, they can also exert stronger forces on the pillar.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thouret, J.; Antoine, S.; Magill, C.; Ollier, C. Lahars and debris flows: Characteristics and impacts. Earth-Sci. Rev. 2020, 201, 103003. [Google Scholar] [CrossRef]
- Franco, R.D.V.; Thouret, J.C.; Delaite, G.; Van Westen, C.; Sheridan, M.F.; Siebe, C.; Mariño, J.; Souriot, T.; Stinton, A. Mapping and assessing volcanic and flood hazards and risks, with emphasis on lahars, in Arequipa, Peru. Spec. Pap. Geol. Soc. Am. 2010, 464, 265–280. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.M.; Chen, H.X. Two-dimensional simulation of debris flow impact pressures on buildings. Eng. Geol. 2017, 226, 236–244. [Google Scholar] [CrossRef]
- Jalayer, F.; Aronica, G.T.; Recupero, A.; Carozza, S.; Manfredi, G. Debris flow damage incurred to buildings: An in situ back analysis. J. Flood Risk Manag. 2018, 11, S646–S662. [Google Scholar] [CrossRef]
- Papathoma-Köhle, M.; Kappes, M.; Keiler, M.; Glade, T. Physical vulnerability assessment for alpine hazards: State of the art and future needs. Nat. Hazards 2011, 58, 645–680. [Google Scholar] [CrossRef]
- Kelfoun, K.; Druitt, T.H. Numerical modeling of the emplacement of Socompa rock avalanche, Chile. J. Geophys. Res. Solid Earth 2005, 110, 1–13. [Google Scholar] [CrossRef]
- O’ Brien, J.S.; Julien, P.Y.; Fullerton, W.T. Two-dimensional water flood and mudflood simultion. J. Hydraul. Eng. 1993, 119, 244–261. [Google Scholar] [CrossRef]
- Schilling, S.P. LAHARZ: GIS Programs for Automated Delineation of Lahar Hazard Zones; U.S. Geological Survey Open-File Report. 1998. Available online: https://pubs.er.usgs.gov/publication/ofr98638 (accessed on 15 March 2022).
- Thouret, J.C.; Enjolras, G.; Martelli, K.; Santoni, O.; Luque, J.A.; Nagata, M.; Arguedas, A.; MacEdo, L. Combining criteria for delineating lahar-and flash-flood-prone hazard and risk zones for the city of Arequipa, Peru. Nat. Hazards Earth Syst. Sci. 2013, 13, 339–360. [Google Scholar] [CrossRef]
- Horton, P.; Jaboyedoff, M.; Rudaz, B.; Zimmermann, M. Flow-R, a model for susceptibility mapping of debris flows and other gravitational hazards at a regional scale. Nat. Hazards Earth Syst. Sci. 2013, 13, 869–885. [Google Scholar] [CrossRef] [Green Version]
- Scheidl, C.; Rickenmann, D. TopFlowDF-A simple gis based model to simulate debris-flow runout on the fan. In Proceedings of the 5th International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, Padua, Italy, 14–17 June 2011; pp. 253–262. [Google Scholar] [CrossRef]
- Pitman, E.B.; Long, L.E. A two-fluid model for avalanche and debris flows. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 363, 1573–1601. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, H.; Dai, Z.; Xu, Q.; Liu, F.; Sawada, K.; Moriguchi, S.; Yashima, A. SPH-based numerical simulation of catastrophic debris flows after the 2008 Wenchuan earthquake. Bull. Eng. Geol. Environ. 2015, 74, 1137–1151. [Google Scholar] [CrossRef]
- Teufelsbauer, H.; Wang, Y.; Pudasaini, S.P.; Borja, R.I.; Wu, W. DEM simulation of impact force exerted by granular flow on rigid structures. Acta Geotech. 2011, 6, 119–133. [Google Scholar] [CrossRef]
- Leonardi, A.; Wittel, F.K.; Mendoza, M.; Vetter, R.; Herrmann, H.J. Particle-Fluid-Structure Interaction for Debris Flow Impact on Flexible Barriers. Comput. Civ. Infrastruct. Eng. 2016, 31, 323–333. [Google Scholar] [CrossRef] [Green Version]
- Shen, W.; Zhao, T.; Zhao, J.; Dai, F.; Zhou, G.G.D. Quantifying the impact of dry debris flow against a rigid barrier by DEM analyses. Eng. Geol. 2018, 241, 86–96. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. SPH model for fluid—Structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Teufelsbauer, H.; Wang, Y.; Chiou, M.C.; Wu, W. Flow-obstacle interaction in rapid granular avalanches: DEM simulation and comparison with experiment. Granul. Matter 2009, 11, 209–220. [Google Scholar] [CrossRef]
- Albaba, A.; Schwarz, M.; Wendeler, C.; Loup, B.; Dorren, L. Numerical modeling using an elastoplastic-adhesive discrete element code for simulating hillslope debris flows and calibration against field experiments. Nat. Hazards Earth Syst. Sci. 2019, 19, 2339–2358. [Google Scholar] [CrossRef] [Green Version]
- Proske, D.; Suda, J.; Hübl, J. Debris flow impact estimation for breakers. Georisk 2011, 5, 143–155. [Google Scholar] [CrossRef]
- Papathoma-Köhle, M.; Gems, B.; Sturm, M.; Fuchs, S. Matrices, curves and indicators: A review of approaches to assess physical vulnerability to debris flows. Earth-Sci. Rev. 2017, 171, 272–288. [Google Scholar] [CrossRef]
- Mead, S.R.; Magill, C.; Lemiale, V.; Thouret, J.C.; Prakash, M. Examining the impact of lahars on buildings using numerical modelling. Nat. Hazards Earth Syst. Sci. 2017, 17, 703–719. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Choi, C.E.; Liu, L.H.D.; Ng, C.W.W. Effects of particle size of mono-disperse granular flows impacting a rigid barrier. Nat. Hazards 2018, 91, 1179–1201. [Google Scholar] [CrossRef]
- Chehade, R.; Chevalier, B.; Dedecker, F.; Breul, P.; Thouret, J.C. Discrete modelling of debris flows for evaluating impacts on structures. Bull. Eng. Geol. Environ. 2021, 80, 6629–6645. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Itasca. Particle Flow Code 5.0 Documentation. 2016. Available online: https://geomatlab.com/itasca/pfc5.0help/source/index.html (accessed on 15 March 2022).
- Zhao, T.; Houlsby, G.T.; Utili, S. Investigation of granular batch sedimentation via DEM–CFD coupling. Granul. Matter 2014, 16, 921–932. [Google Scholar] [CrossRef]
- Zhao, L.; He, J.W.; Yu, Z.X.; Liu, Y.P.; Zhou, Z.H.; Chan, S.L. Coupled numerical simulation of a flexible barrier impacted by debris flow with boulders in front. Landslides 2020, 17, 2723–2736. [Google Scholar] [CrossRef]
- Hu, K.; Wei, F.; Li, Y. Real-time measurement and preliminary analysis of debris-flow impact force at Jiangjia Ravine, China. Earth Surf. Process. Landf. 2011, 36, 1268–1278. [Google Scholar] [CrossRef]
- Poudyal, S.; Choi, C.E.; Song, D.; Zhou, G.G.D.; Yune, C.Y.; Cui, Y.; Leonardi, A.; Busslinger, M.; Wendeler, C.; Piton, G.; et al. Review of the mechanisms of debris-flow impact against barriers. In Proceedings of the Seventh International Conference on Debris-Flow Hazards Mitigation, Golden, CO, USA, 10–13 June 2019; pp. 1027–1034. [Google Scholar]
- Bardou, E.; Ancey, C.; Bonnard, C.; Vulliet, L. Classification of debris-flow deposits for hazard assessment in alpine areas. In Proceedings of the 3th International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, Davos, Switzerland, 10–12 September 2003; Available online: http://infoscience.epfl.ch/record/94551 (accessed on 15 March 2022).
- Martelli, K. The physical vulnerability of urban areas facing the threat of inundation from lahars and flash floods: Application to the case study of Arequipa, Peru. PhD Thesis, Université Blaise Pascal-Clermont-Ferrand II, Clermont-Ferrand, France, 2013. [Google Scholar]
- Kang, H.; Kim, Y. The physical vulnerability of different types of building structure to debris flow events. Nat. Hazards 2016, 80, 1475–1493. [Google Scholar] [CrossRef]
- Lo, W.C.; Tsao, T.C.; Hsu, C.H. Building vulnerability to debris flows in Taiwan: A preliminary study. Nat. Hazards 2012, 64, 2107–2128. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Li, X.; Xu, Q. Physical vulnerability models for assessing building damage by debris flows. Eng. Geol. 2018, 247, 145–158. [Google Scholar] [CrossRef]
- Fuchs, S.; Keiler, M.; Ortlepp, R.; Schinke, R.; Papathoma-Köhle, M. Recent advances in vulnerability assessment for the built environment exposed to torrential hazards: Challenges and the way forward. J. Hydrol. 2019, 575, 587–595. [Google Scholar] [CrossRef]
- Quan Luna, B.; Blahut, J.; Van Westen, C.J.; Sterlacchini, S.; Van Asch, T.W.J.; Akbas, S.O. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef] [Green Version]
- Trujillo-Vela, M.G.; Galindo-Torres, S.A.; Zhang, X.; Ramos-Cañón, A.M.; Escobar-Vargas, J.A. Smooth particle hydrodynamics and discrete element method coupling scheme for the simulation of debris flows. Comput. Geotech. 2020, 125, 103669. [Google Scholar] [CrossRef]
- Lei, Y.; Cui, P.; Zeng, C.; Guo, Y. An empirical mode decomposition-based signal process method for two-phase debris flow impact. Landslides 2018, 15, 297–307. [Google Scholar] [CrossRef]
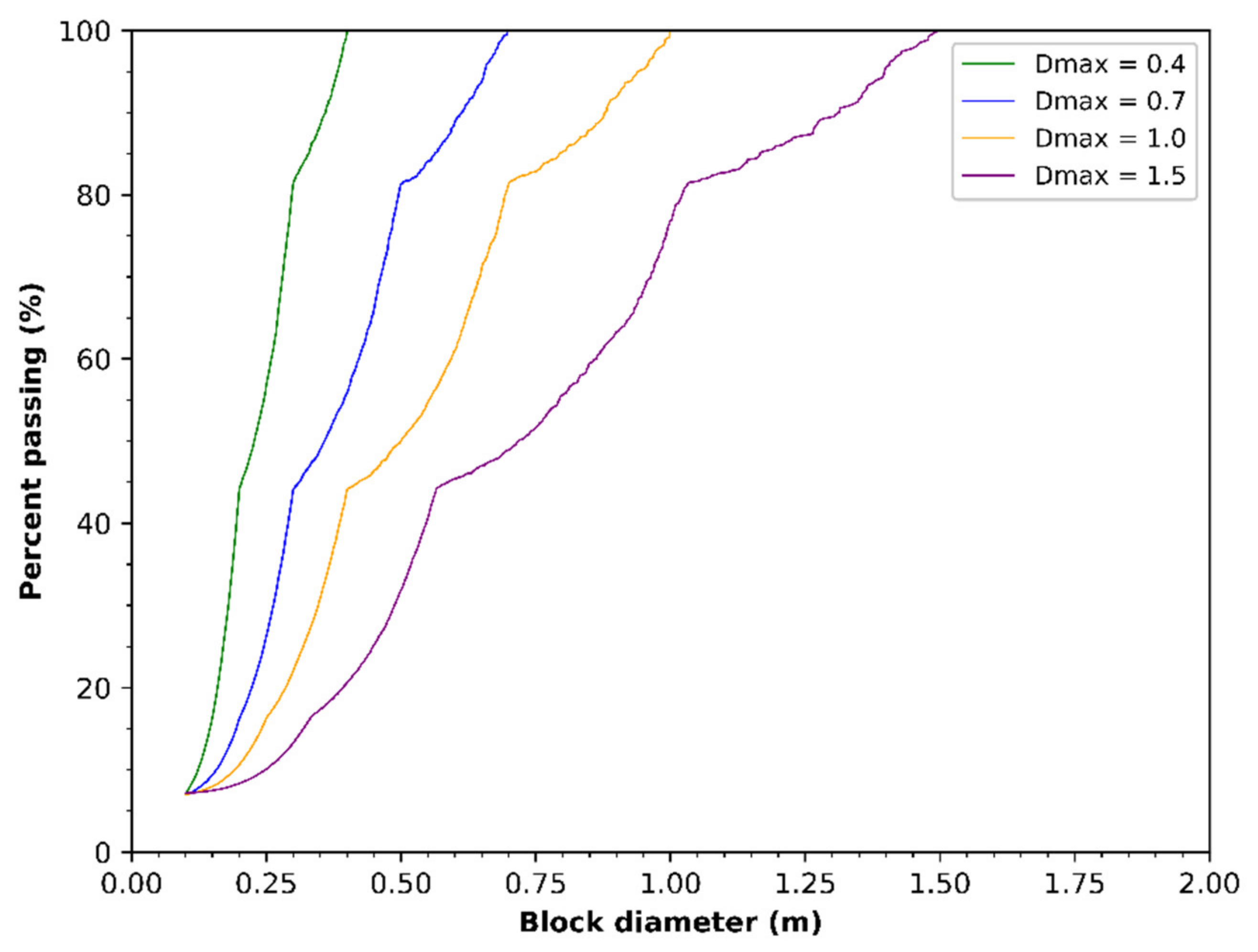
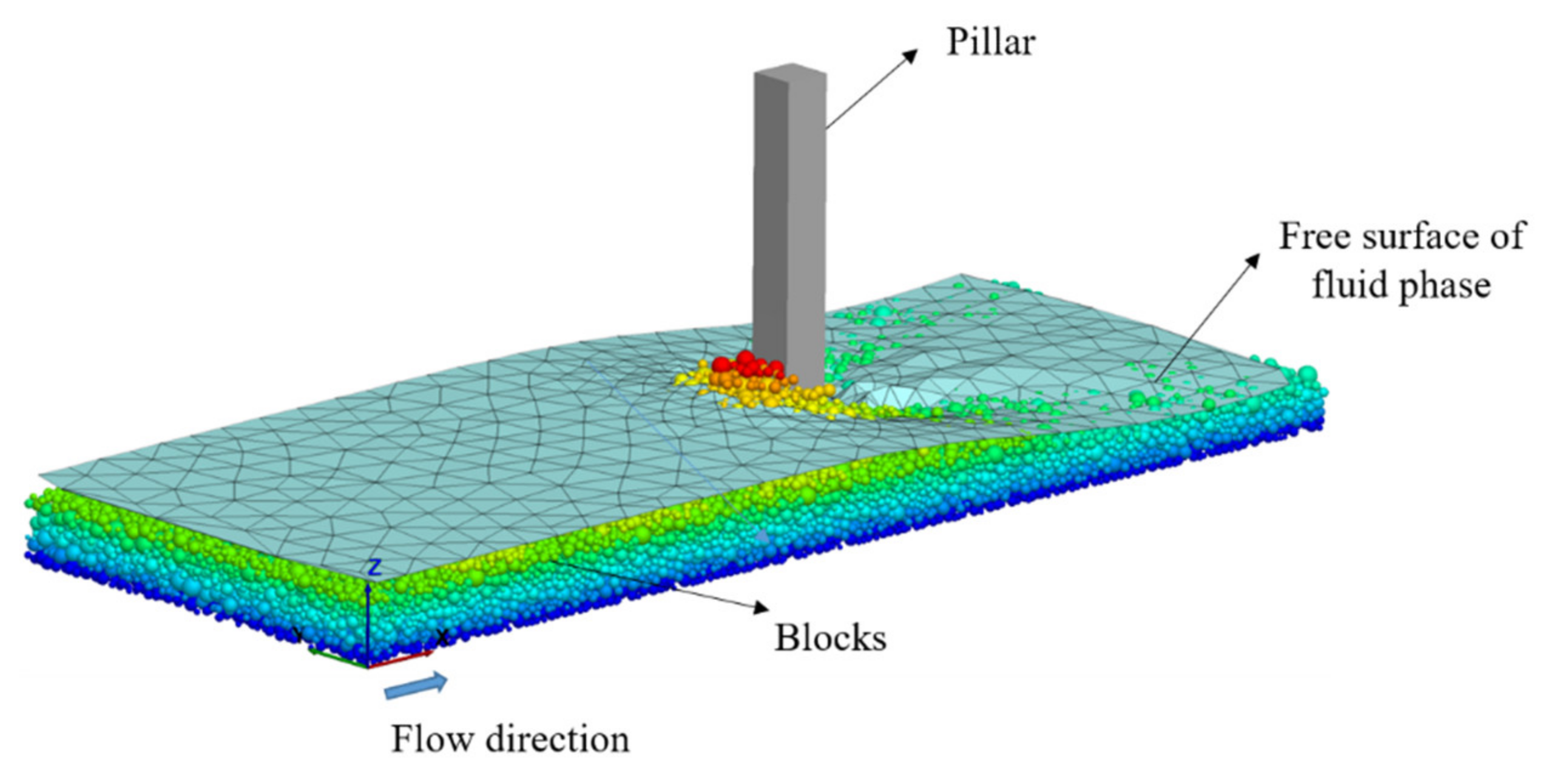
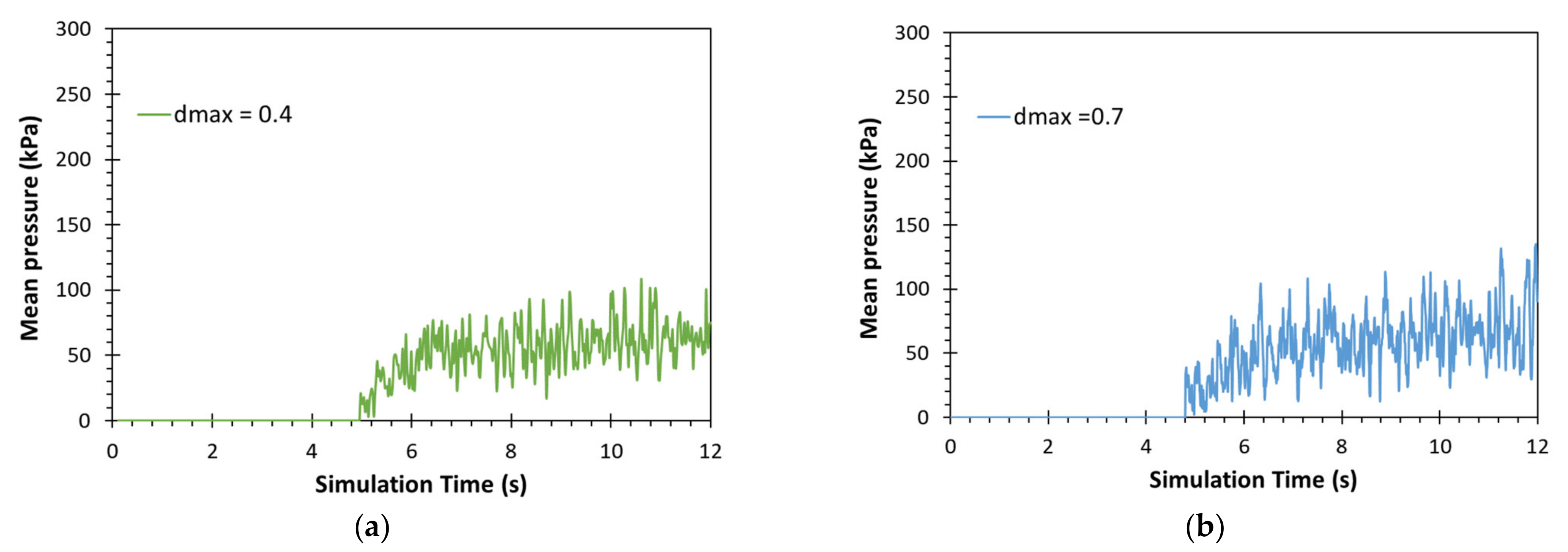

| Solid Fraction | Apparent Density | Flow Rate |
|---|---|---|
| 55% | 1867 kg/m3 | 40 m3/s |
| Shape | Block Size | Porosity | Flow Height | Flow Velocity | Froude Number |
|---|---|---|---|---|---|
| Sphere | = 0.1 m = 0.4 m | 0.45 | 1.5 m | 3.00 m/s | 0.78 |
| Normal Stiffness | Tangential Stiffness | Rolling Resistance | Friction Coefficient | Fluid Density | Block Density | Fluid Viscosity |
|---|---|---|---|---|---|---|
| 107 N/m | 5 × 106 N/m | 0.2 | 0.4 | 1100 kg/m3 | 2500 kg/m3 | 0.048 Pa.s |
| Intensity | Vulnerability Function | Case Study Example |
|---|---|---|
| Height h (m) | h = 1.5; V1 = 0.272 | |
| Velocity v (m/s) | v = 3 m/s; V2 = 0.179 | |
| Impact pressure p (kPa) | p = 72 kPa; V3 = 0.489 |
| h (m) | v (m/s) | dmax (m) | Pmoy (kPa) | V3 |
|---|---|---|---|---|
| 1.5 | 3 | 0.4 | 72 | 0.489 |
| 0.7 | 81 | 0.568 | ||
| 1 | 83.5 | 0.587 | ||
| 1.5 | 102 | 0.710 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chehade, R.; Chevalier, B.; Dedecker, F.; Breul, P.; Thouret, J.-C. Effect of Boulder Size on Debris Flow Impact Pressure Using a CFD-DEM Numerical Model. Geosciences 2022, 12, 188. https://doi.org/10.3390/geosciences12050188
Chehade R, Chevalier B, Dedecker F, Breul P, Thouret J-C. Effect of Boulder Size on Debris Flow Impact Pressure Using a CFD-DEM Numerical Model. Geosciences. 2022; 12(5):188. https://doi.org/10.3390/geosciences12050188
Chicago/Turabian StyleChehade, Rime, Bastien Chevalier, Fabian Dedecker, Pierre Breul, and Jean-Claude Thouret. 2022. "Effect of Boulder Size on Debris Flow Impact Pressure Using a CFD-DEM Numerical Model" Geosciences 12, no. 5: 188. https://doi.org/10.3390/geosciences12050188
APA StyleChehade, R., Chevalier, B., Dedecker, F., Breul, P., & Thouret, J.-C. (2022). Effect of Boulder Size on Debris Flow Impact Pressure Using a CFD-DEM Numerical Model. Geosciences, 12(5), 188. https://doi.org/10.3390/geosciences12050188






