Effect of Freezing-Thawing Cycles on the Elastic Waves’ Properties of Rocks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Tested Rocks
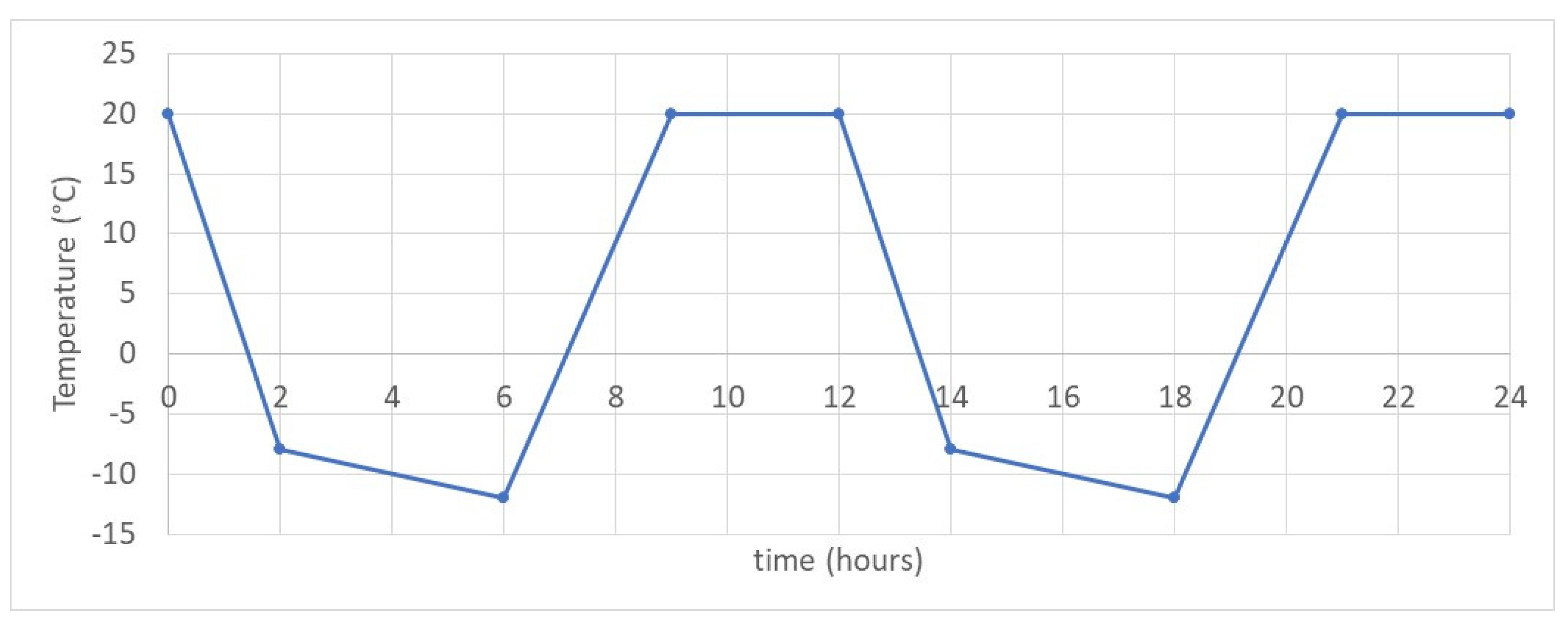
2.2. Experimental Device
- An electric pulse generator that can generate P-wave, and two S-waves, S1 and S2, perpendicular to one another;
- A transmitter and a receiver for P- and S-waves;
- A transducer used to control the force applied by the pump on the test; the contact is systematically obtained under a 2 kN load to be strictly reproductible and to be able to compare results.
2.3. Signal Processing
3. Results
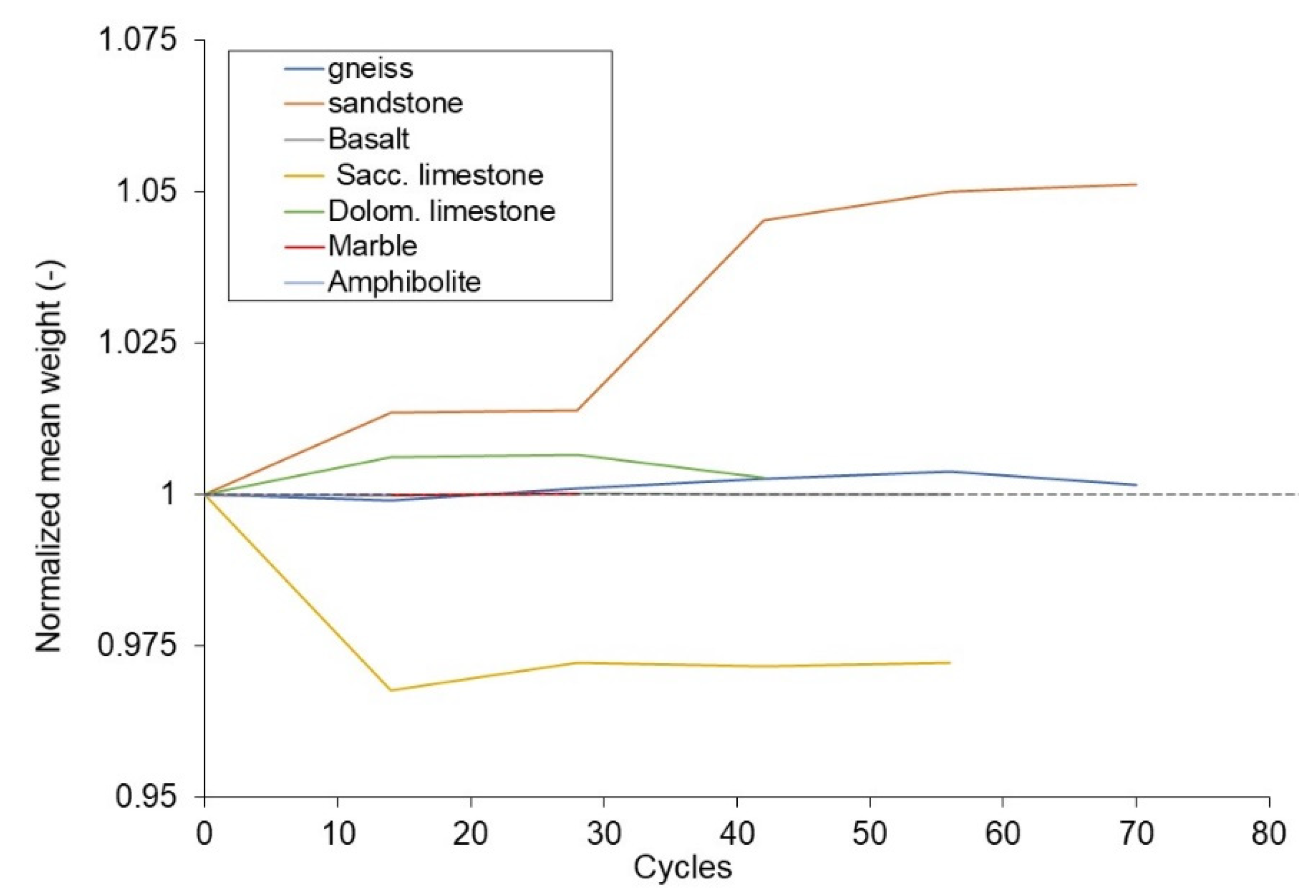
3.1. Macroscopic Observations and Evolution of the Weight of the Samples
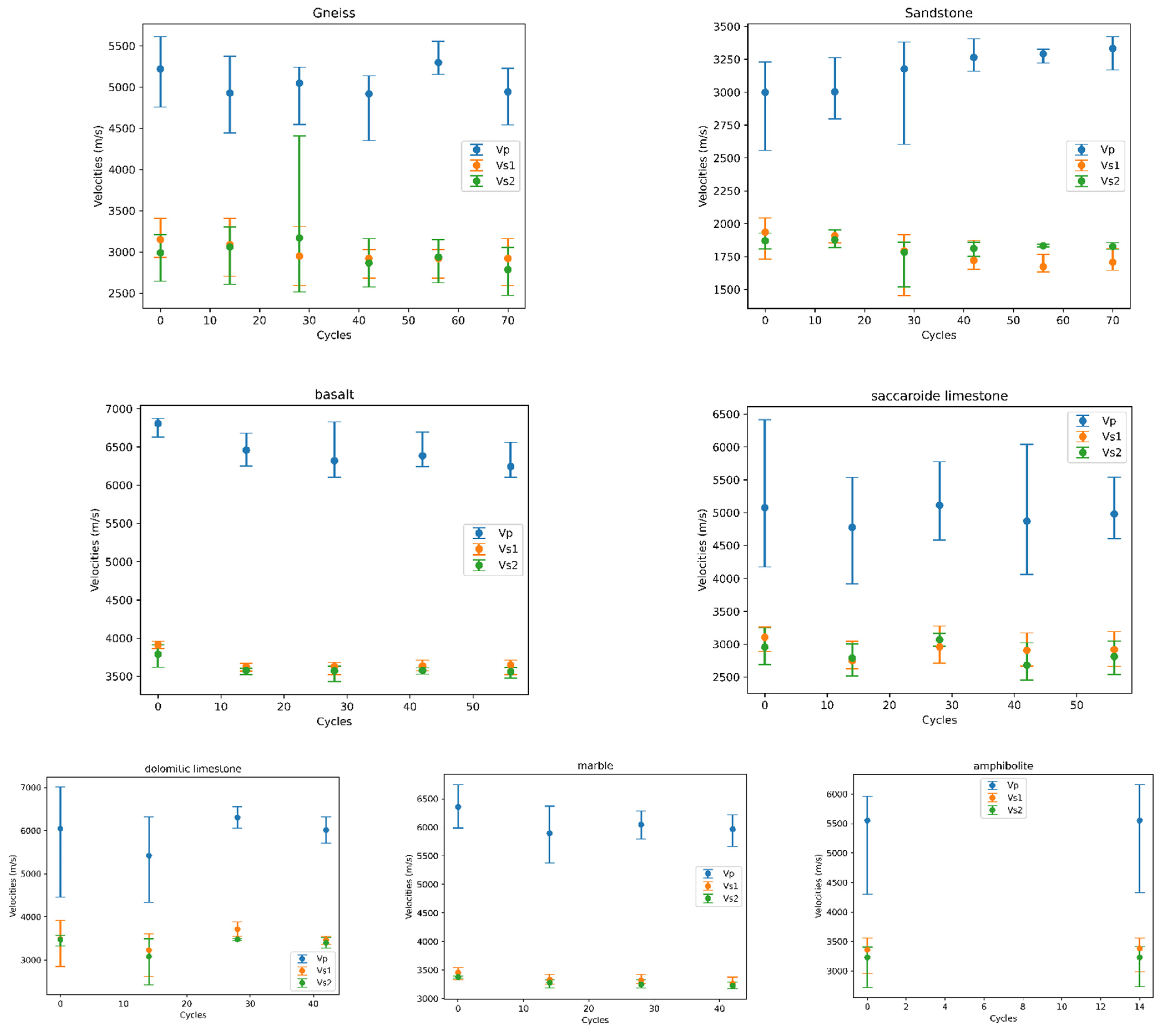
3.2. Velocities of Elastic Waves
3.2.1. General Evolution
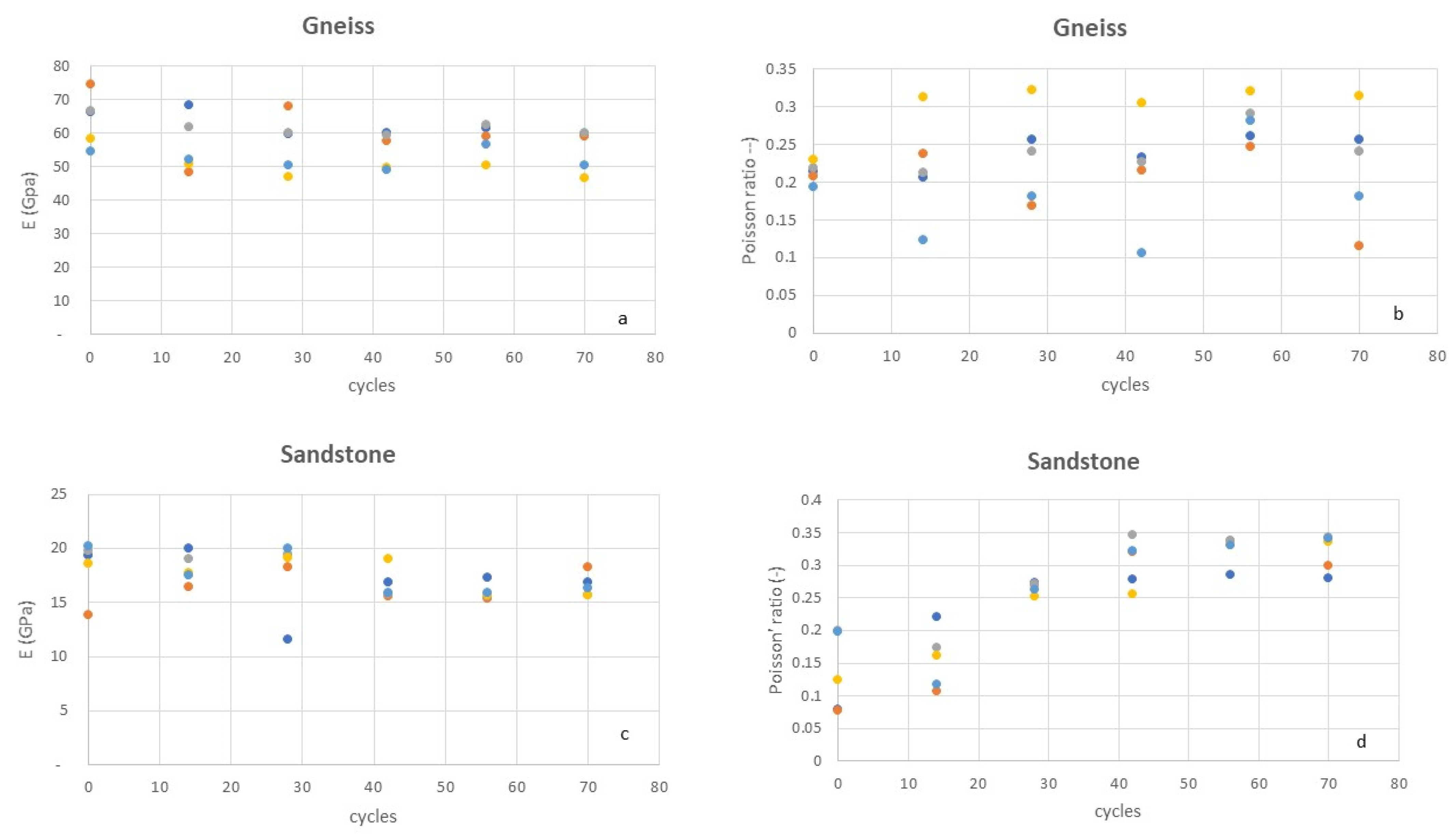
3.2.2. Dynamic Elastic Modulus and Poisson Ratio
3.2.3. Evolution of Vp/Vs Ratio
3.2.4. Evolution of Vs1/Vs2 Ratio
3.3. Frequency Analysis
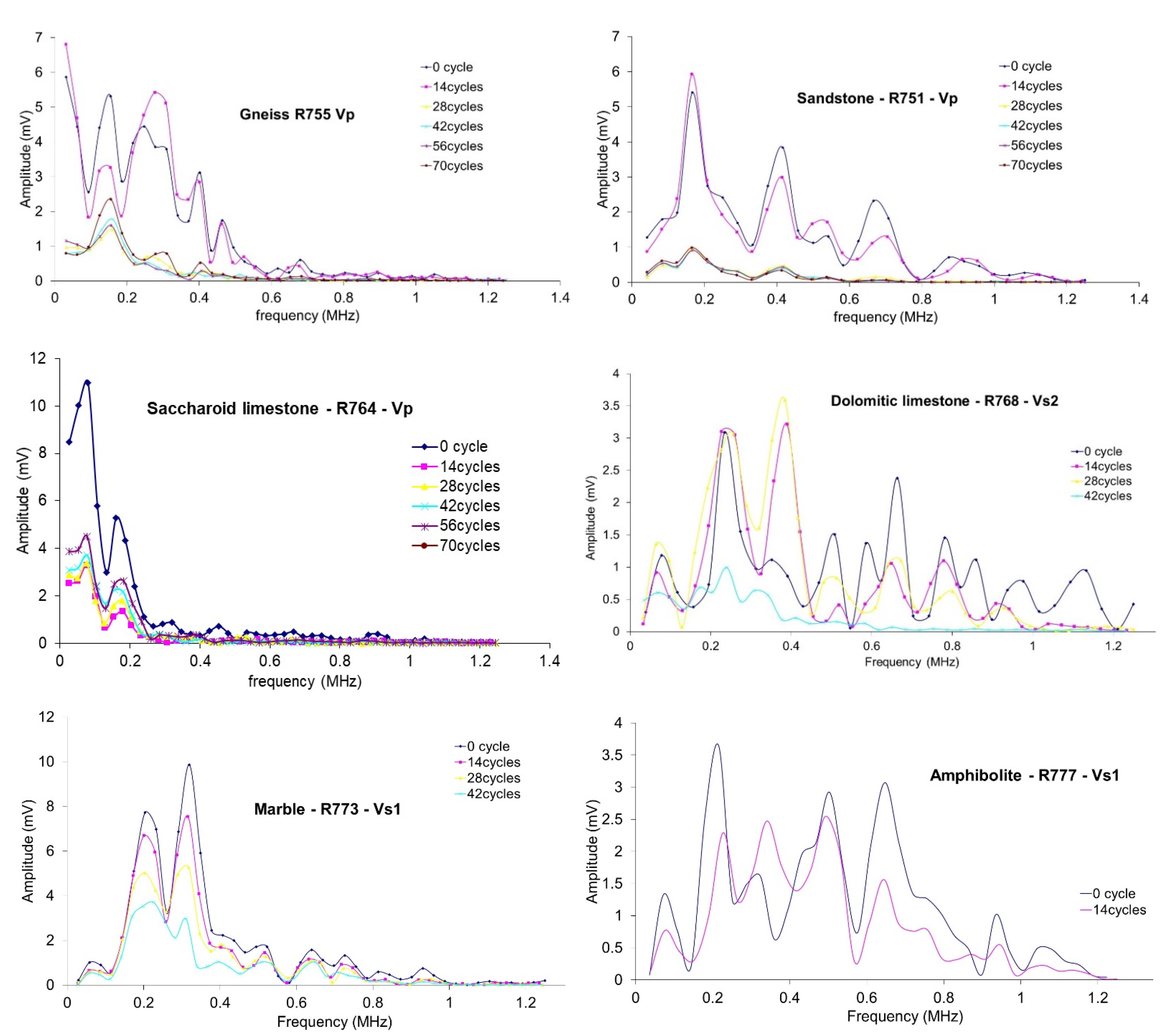
3.3.1. Observations on the Evolution of Spectrum Amplitude
- Sandstone: Evolution of the frequency is the same regardless of the type of waves P, S1 and S2. Sandstone has very large and comparable amplitudes for 0 and 14 cycles, and very small (and comparable) amplitude afterwards;
- Basalt and dolomitic limestone: When FT cycles increase, a regular decrease of the Vp amplitudes is observed. “Regular” means that after each set of 14 cycles, Vp amplitude decreases. This decrease is also observed on Vs1 and Vs1 but less regular (i.e., globally, amplitude of n cycles is superior to amplitude of (n + 14) cycles, but it can be not true punctually);
- Marble: when FT cycles increase a regular decrease of the Vp, Vs1 and Vs2 amplitudes is obtained;
- Amphibolite: it seems to behave as marble but with only two curves (0 and 14 cycles) it is difficult to conclude on a trend;
- Gneiss and saccharoidal limestone: No global trend is observed on all samples. Moreover, 3/5 gneiss samples behave as sandstone but the other two do not.
3.3.2. Observations on the Evolution of Spectrum Frequencies
3.4. Spectral Energies
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Samples Weight (g) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cycle | Samples | Gneiss | Sandstone | Basalt | Saccharoidal Limestone. | Dolomitic Limestone. | Marble | Amphibolite |
| 0 | 1 | 464.37 | 379.37 | 509.68 | 278.85 | 659.85 | 1520.01 | 538.12 |
| 2 | 450.51 | 375.31 | 509.89 | 265.98 | 654.71 | 1538.91 | 517.79 | |
| 3 | 493.71 | 372.07 | 498.21 | 276.17 | 675.24 | 1527.66 | 638.60 | |
| 4 | 497.91 | 372.08 | 491.84 | 283.93 | 984.14 | 1529.34 | 616.44 | |
| 5 | 498.33 | 377.19 | 496.07 | 253.65 | 992.97 | 626.98 | ||
| mean | 480.97 | 375.20 | 501.14 | 271.72 | 793.38 | 1528.98 | 587.59 | |
| 14 | 1 | 463.92 | 383.41 | 509.70 | 270.44 | 663.00 | 1520.01 | 538.13 |
| 2 | 450.09 | 380.66 | 509.93 | 261.25 | 660.68 | 1538.91 | 517.82 | |
| 3 | 493.10 | 375.81 | 498.20 | 274.36 | 677.14 | 1527.66 | 638.61 | |
| 4 | 497.46 | 377.82 | 491.81 | 263.14 | 990.84 | 1529.34 | 616.48 | |
| 5 | 497.73 | 383.72 | 495.73 | 999.76 | 627.01 | |||
| mean | 480.46 | 380.28 | 501.07 | 267.30 | 798.28 | 1528.98 | 587.61 | |
| 28 | 1 | 464.86 | 384.46 | 509.81 | 271.67 | 662.65 | 1519.93 | |
| 2 | 450.99 | 380.65 | 509.99 | 263.14 | 661.39 | 1539.14 | ||
| 3 | 494.30 | 375.95 | 498.52 | 276.11 | 676.57 | 1527.70 | ||
| 4 | 498.47 | 377.87 | 491.98 | 263.34 | 991.52 | 1529.89 | ||
| 5 | 498.79 | 383.18 | 495.95 | 1000.76 | ||||
| mean | 481.48 | 380.42 | 501.25 | 268.57 | 798.58 | 1529.17 | ||
| 42 | 1 | 465.64 | 396.01 | 509.72 | 271.73 | 662.54 | ||
| 2 | 451.65 | 391.58 | 509.92 | 262.24 | ||||
| 3 | 494.87 | 388.48 | 498.28 | 276.24 | 676.30 | |||
| 4 | 498.95 | 389.72 | 491.81 | 263.34 | ||||
| 5 | 499.94 | 395.13 | 495.76 | |||||
| mean | 482.21 | 392.18 | 501.10 | 268.39 | 669.42 | |||
| 56 | 1 | 465.47 | 398.44 | 509.64 | 271.16 | |||
| 2 | 451.79 | 393.24 | 509.83 | 262.45 | ||||
| 3 | 497.81 | 390.28 | 498.72 | 276.61 | ||||
| 4 | 499.16 | 391.46 | 491.72 | 263.98 | ||||
| 5 | 499.82 | 396.28 | 495.63 | |||||
| mean | 482.81 | 393.94 | 501.11 | 268.55 | ||||
| 70 | 1 | 464.68 | 399.23 | |||||
| 2 | 450.72 | 393.67 | ||||||
| 3 | 494.72 | 390.69 | ||||||
| 4 | 499.07 | 391.51 | ||||||
| 5 | 499.59 | 396.88 | ||||||
| mean | 481.76 | 394.40 | ||||||
References
- Hall, K. Evidence for freeze-thaw events and their implications for rock weathering in northern Canada. Earth Surf. Process. Landf. 2004, 29, 43–57. [Google Scholar] [CrossRef]
- Hallet, B. Why do freezing rocks break? Science 2006, 314, 1092–1093. [Google Scholar] [CrossRef]
- Draebing, D.; Krautblatter, M. The Efficacy of Frost Weathering Processes in Alpine Rockwalls. Geophys. Res. Lett. 2019, 46, 6516–6524. [Google Scholar] [CrossRef]
- Eppes, M.C.; Hancock, G.S.; Kiessling, S.; Moser, F. Rates of subcritical cracking and long-term rock erosion. Geology 2018, 46, 951–954. [Google Scholar] [CrossRef]
- Ravanel, L.; Magnin, F.; Deline, P. Impacts of the 2003 and 2015 summer heatwaves on permafrost-affected rock-walls in the Mont Blanc massif. Sci. Total Environ. 2017, 609, 132–143. [Google Scholar] [CrossRef]
- Magnin, F.; Westermann, S.; Pogliotti, P.; Ravanel, L.; Deline, P.; Malet, E. Snow control on active layer thickness in steep alpine rock walls (Aiguille du Midi, 3842 m a.s.l., Mont Blanc massif). Catena 2017, 149, 648–662. [Google Scholar] [CrossRef]
- Deprez, M.; de Kock, T.; de Schutter, G.; Cnudde, V. A review on freeze-thaw action and weathering of rocks. Earth-Sci. Rev. 2020, 203, 103143. [Google Scholar] [CrossRef]
- Liping, W.; Ning, L.; Jilin, Q.; Yanzhe, T.; Shuanhai, X. A study on the physical index change and triaxial compression test of intact hard rock subjected to freeze-thaw cycles. Cold Reg. Sci. Technol. 2019, 160, 39–47. [Google Scholar] [CrossRef]
- Draebing, D.; Krautblatter, M. P-wave velocity changes in freezing hard low-porosity rocks: A laboratory-based time-average model. Cryosph. Discuss. 2012, 6, 1163–1174. [Google Scholar] [CrossRef]
- Villarraga, C.J.; Gasc-Barbier, M.; Vaunat, J.; Darrozes, J. The effect of thermal cycles on limestone mechanical degradation. Int. J. Rock Mech. Min. Sci. 2018, 109, 115–123. [Google Scholar] [CrossRef]
- Fortin, J.; Schubnel, A.; Guéguen, Y. Elastic wave velocities and permeability evolution during compaction of Bleurswiller sandstone. Int. J. Rock Mech. Min. Sci. 2005, 42, 873–889. [Google Scholar] [CrossRef]
- Fortin, J.; Gasc-barbier, M.; Merrien-soukatchoff, V. Comportement des roches en température. In Thermomécanique Des Roches; Gasc-Barbier, M., Merrien-Soukatchoff, V., Berest, P., Eds.; Presses des Mines: Paris, Frence, 2018. [Google Scholar]
- Vagnon, F.; Colombero, C.; Colombo, F.; Comina, C.; Ferrero, A.M.; Mandrone, G.; Vinciguerra, S.C. Effects of thermal treatment on physical and mechanical properties of Valdieri Marble—NW Italy. Int. J. Rock Mech. Min. Sci. 2019, 116, 75–86. [Google Scholar] [CrossRef]
- Vagnon, F.; Colombero, C.; Comina, C.; Ferrero, A.M.; Mandrone, G.; Missagia, R.; Vinciguerra, S.C. Relating physical properties to temperature-induced damage in carbonate rocks. Geotech. Lett. 2021, 11, 1–11. [Google Scholar] [CrossRef]
- Martínez-Martínez, J.; Benavente, D.; Gomez-Heras, M.; Marco-Castaño, L.; García-Del-Cura, M.Á. Non-linear decay of building stones during freeze-thaw weathering processes. Constr. Build. Mater. 2013, 38, 443–454. [Google Scholar] [CrossRef]
- Gueguen, Y.; Palciauskas, V. Introduction to the Physics of Rocks; Pricetown University Press: Pricetown, UK, 1994. [Google Scholar]
- Lama, R.D.; Vutukuri, V.S. Handbook on Mechanical Properties of Rocks, 2nd ed.; Trans Tech Publications: Clausthal, Germany, 1978. [Google Scholar]
- Lliboutry, L. le fluage de la glace. La Houille Blanche 1970, 56, 489–492. [Google Scholar] [CrossRef] [Green Version]
- Gunzburger, Y.; Merrien-Soukatchoff, V.; Guglielmi, Y. Influence of daily surface temperature fluctuations on rock slope stability: Case study of the Rochers de Valabres slope (France). Int. J. Rock Mech. Min. Sci. 2005, 42, 331–349. [Google Scholar] [CrossRef]
- Merrien-Soukatchoff, V.; Clément, C.; Senfaute, G.; Gunzburger, Y. Monitoring of a potential rockfall zone: The case of ‘Rochers de Valabres’ site. In Proceedings of the International Conference on Landslide Risk Management, Vancouver, BC, Canada, 31 May–3 June 2005; pp. 416–422. [Google Scholar]
- Clément, C.; Merrien-Soukatchoff, V.; Dünner, C.; Gunzburger, Y. Stress measurement by overcoring at shallow depths in a rock slope: The scattering of input data and results. Rock Mech. Rock Eng. 2009, 42, 585–609. [Google Scholar] [CrossRef]
- Hoek, E. Rock Mechanics Laboratory Testing in the Context of a Consulting Engineering Organization. Int. J. Rock Mech. Min. Sci. 1977, 14, 93–101. [Google Scholar] [CrossRef]
- Zharikov, A.V.; Pek, A.A.; Lebedev, E.B.; Dorfman, A.M.; Zebrin, S.R. The effects of water fluid at temperatures up to 850 °C and pressure of 300 MPa on porosity and permeability of amphibolite. Phys. Earth Planet. Inter. 1993, 76, 219–227. [Google Scholar] [CrossRef]
- Gasc-Barbier, M.; Hoang, T.T.N.; Marache, A.; Sulem, J.; Riss, J. Morphological and mechanical analysis of natural marble joints submitted to shear tests. J. Rock Mech. Geotech. Eng. 2012, 4, 296–311. [Google Scholar] [CrossRef]
- Gasc-Barbier, M.; Virely, D.; Guittard, J.; Merrien-Soukatchoff, V. Different approaches to fracturation of marble rock—The case study of the St Beat tunnel (French Pyrenees). In Proceedings of the International Society for Rock Mechanics, Liege, Belgium, 9–12 May 2006; pp. 619–623. [Google Scholar] [CrossRef]
- Afnor—French Standard. NF P94-411—Rock—Determination of the Ultrasonic Waves Velocity in Laboratory—Transmission Method. 2002. Available online: www.afnor.fr (accessed on 21 January 2022).
- Afnor—European Standard. NF EN 12371—Natural Stone Test Methods—Determination of Frost Resistance. 2010. Available online: www.afnor.fr (accessed on 21 January 2022).
- Wanatabe, T.; Sassa, K. Velocity and Amplitude of P-Waves Transmitted through Fractured zones composed of Multiple Thin Low-velocity Layers. Int. J. Rock Mech. Min. Sci. Geomech. 1995, 32, 313–324. [Google Scholar] [CrossRef]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Denis, A.; Panet, M.; Tourenq, C. Rock identification by means of continuity index. In Proceedings of the 4th International Congress on Rock Mechanics, Montreux, Suisse, 2–8 September 1979; p. 125. [Google Scholar]
- Klimis, N. Geothechnical characterization of a thermal cracked marble. In Proceedings of the 7th International Congress on Rock Mechanics, Aachen, Deutschland, 16–20 September 1991; pp. 353–361, ISBN 90 5410 0141. [Google Scholar]
- Aubert, J.E.; Gasc-Barbier, M. Hardening of clayey soil blocks during freezing and thawing cycles. Appl. Clay Sci. 2012, 65–66, 1–5. [Google Scholar] [CrossRef]
- Yu, G.; Vozoff, K.; Durney, D.W. Effects of confining pressure and water saturation on ultrasonic compressional wave velocities in coals. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 515–522. [Google Scholar] [CrossRef]
- Martınez-Martinez, J.; Benavente, D.; Ordonez, S.; Garcıa-del-Cura, M.A. Multivariate statistical techniques for evaluating the effects of brecciated rock fabric on ultrasonic wave propagation. Int. J. Rock Mech. Min. Sci. 2008, 45, 609–620. [Google Scholar] [CrossRef]



| Density Kg/m3 | Porosity % | UCS MPa | E GPa | |
|---|---|---|---|---|
| Gneiss | 2.65 × 103 | 1.1–3.3 | 25–110 | 7–20 |
| Sandstone | 2.15 × 103 | 13.7 | 55.5 (dry) | 15 |
| Basalt | 2.97 × 103 | |||
| Saccharoidallimestone | 2.56 × 103 | |||
| Dolomitic limestone | 2.74 × 103 | 1–4 | ||
| Marble | 2.70 × 103 | 0.3 | 70–90 | 60–70 |
| amphibolite | 2.74 × 103 | 1.2 | 100–250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasc-Barbier, M.; Merrien-Soukatchoff, V. Effect of Freezing-Thawing Cycles on the Elastic Waves’ Properties of Rocks. Geosciences 2022, 12, 103. https://doi.org/10.3390/geosciences12030103
Gasc-Barbier M, Merrien-Soukatchoff V. Effect of Freezing-Thawing Cycles on the Elastic Waves’ Properties of Rocks. Geosciences. 2022; 12(3):103. https://doi.org/10.3390/geosciences12030103
Chicago/Turabian StyleGasc-Barbier, Muriel, and Véronique Merrien-Soukatchoff. 2022. "Effect of Freezing-Thawing Cycles on the Elastic Waves’ Properties of Rocks" Geosciences 12, no. 3: 103. https://doi.org/10.3390/geosciences12030103
APA StyleGasc-Barbier, M., & Merrien-Soukatchoff, V. (2022). Effect of Freezing-Thawing Cycles on the Elastic Waves’ Properties of Rocks. Geosciences, 12(3), 103. https://doi.org/10.3390/geosciences12030103






