Vs30 Structure of Almeria City (SE Spain) Using SPAC and MASW Methods and Proxy Correlations
Abstract
1. Introduction
2. Study Area and Geological Setting
2.1. Almeria City
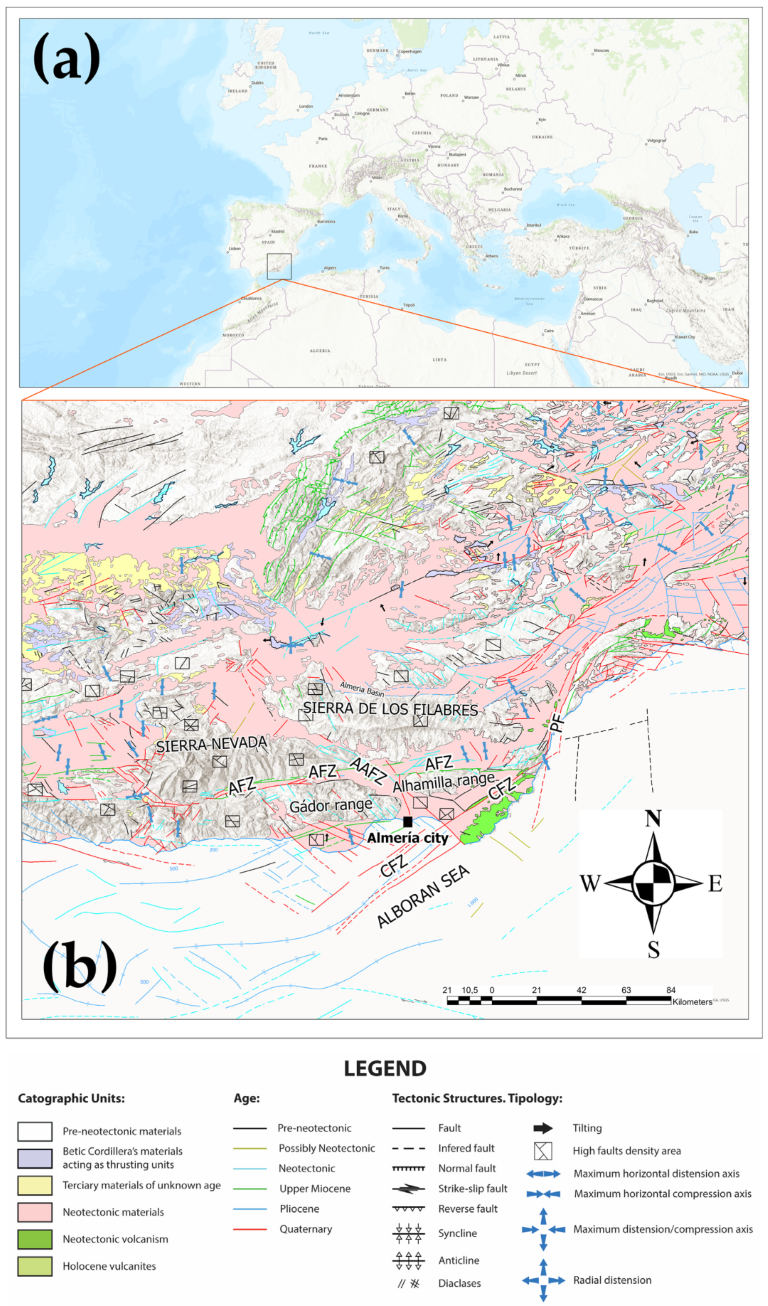
2.2. Neotectonics of the Almeria Area
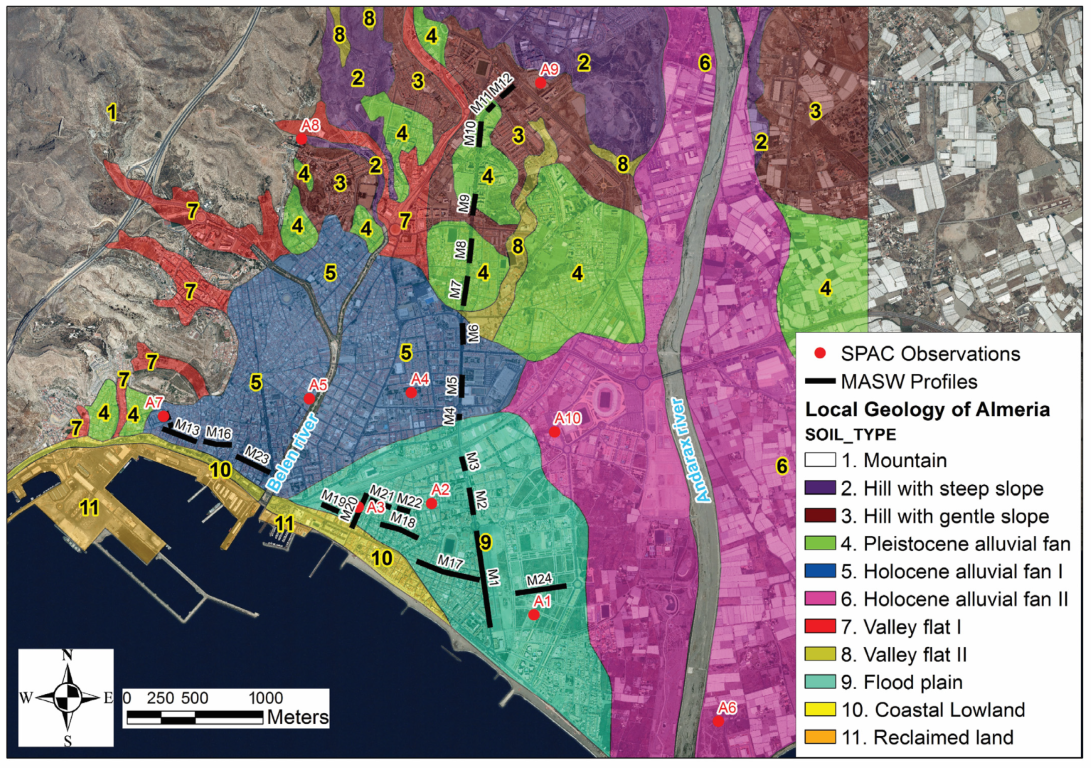
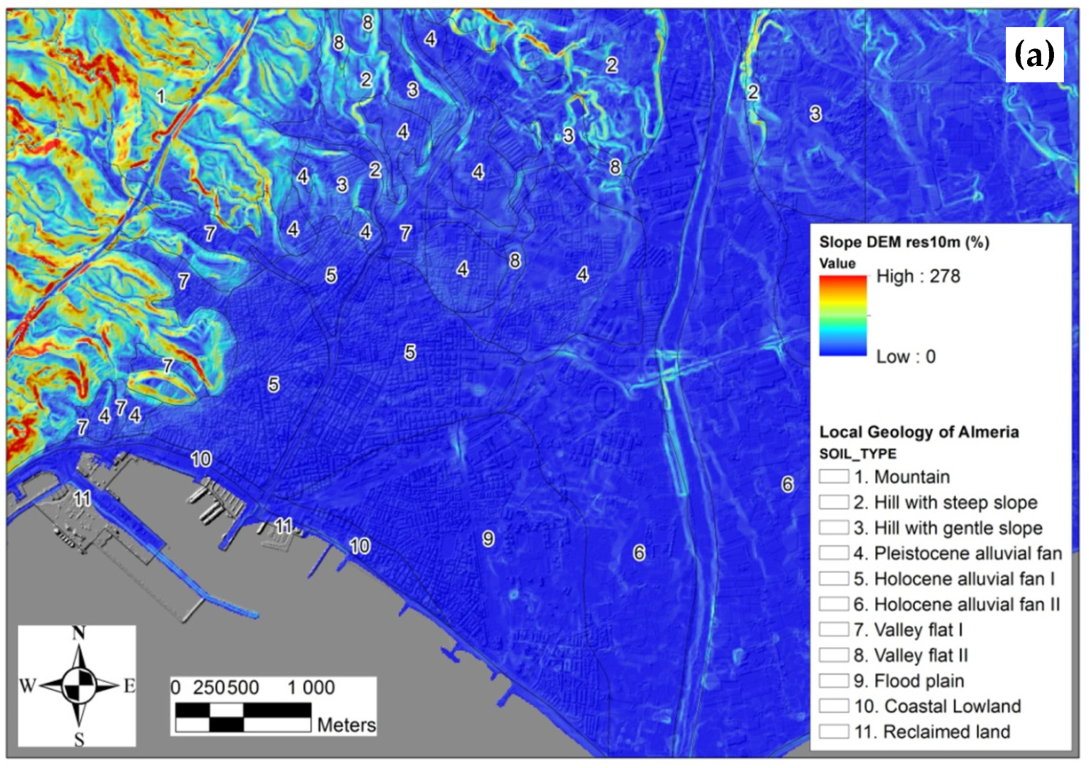
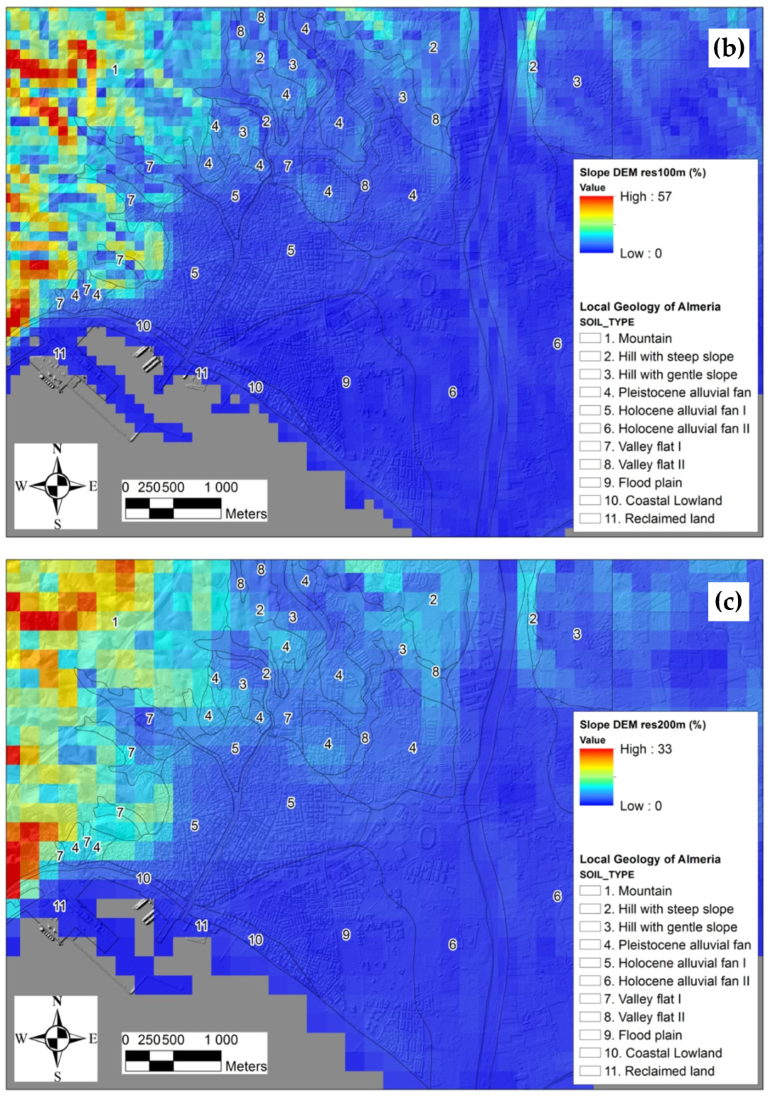
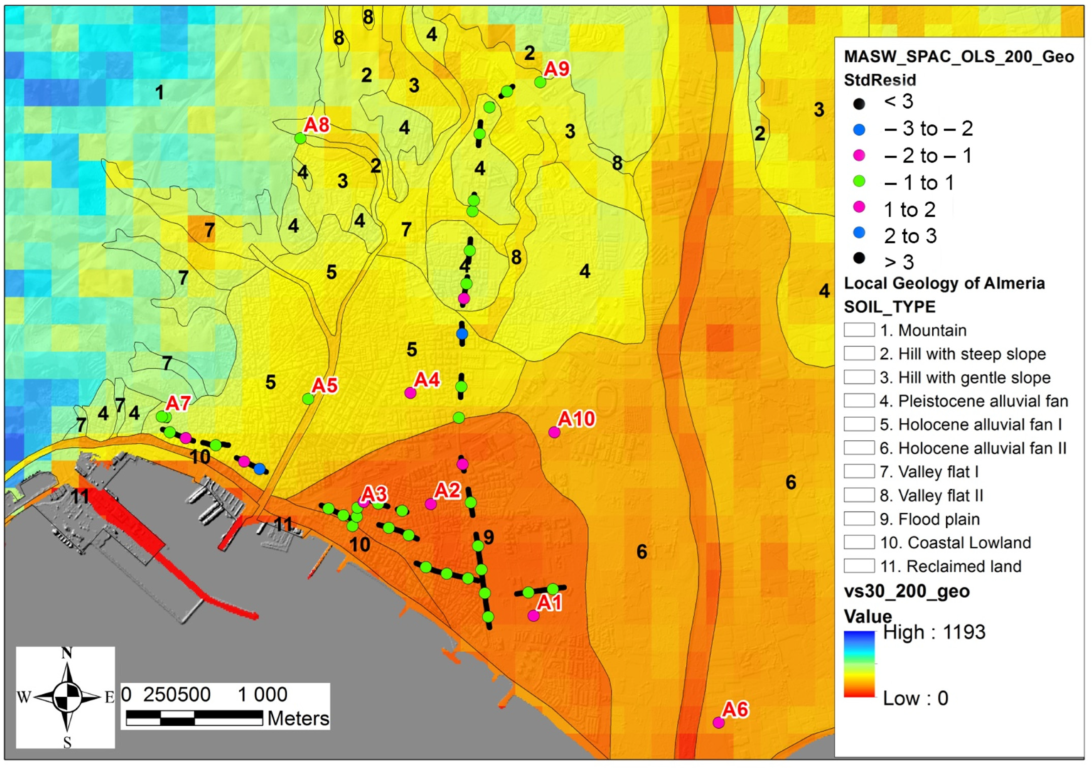
2.3. Local Geology of Almeria City
3. Methodology
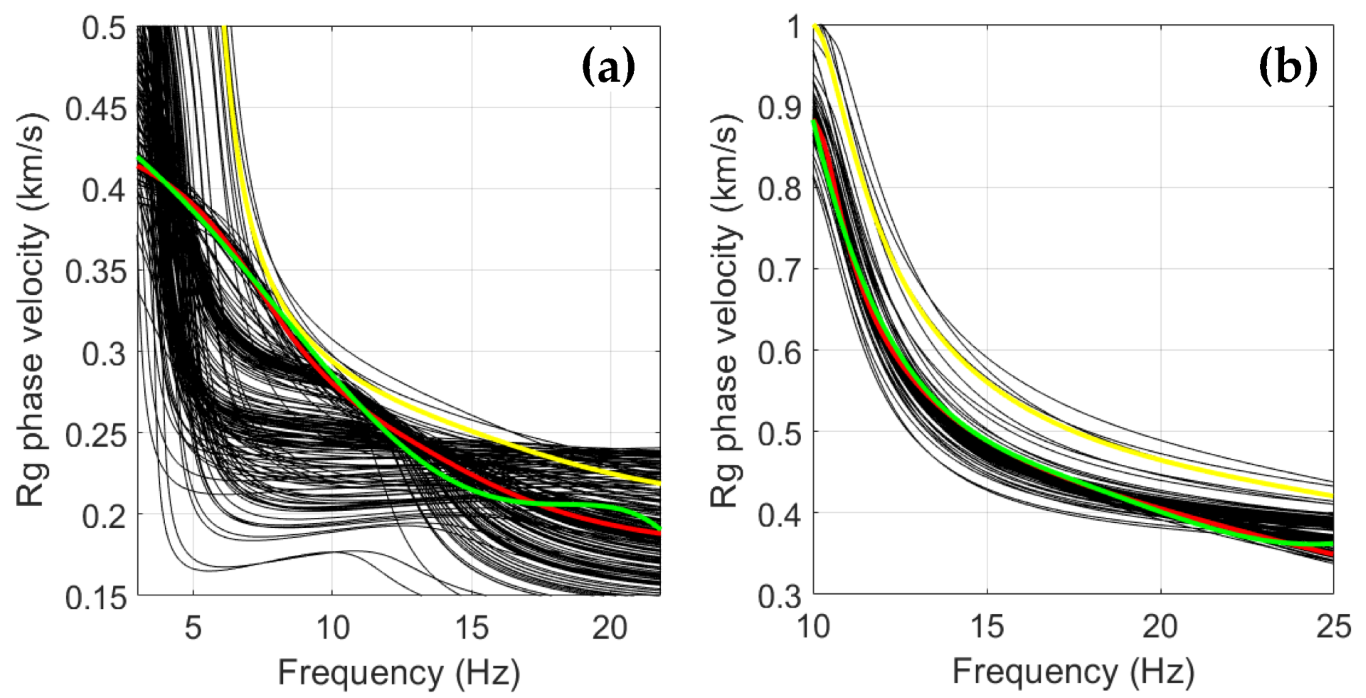
3.1. SPAC Method
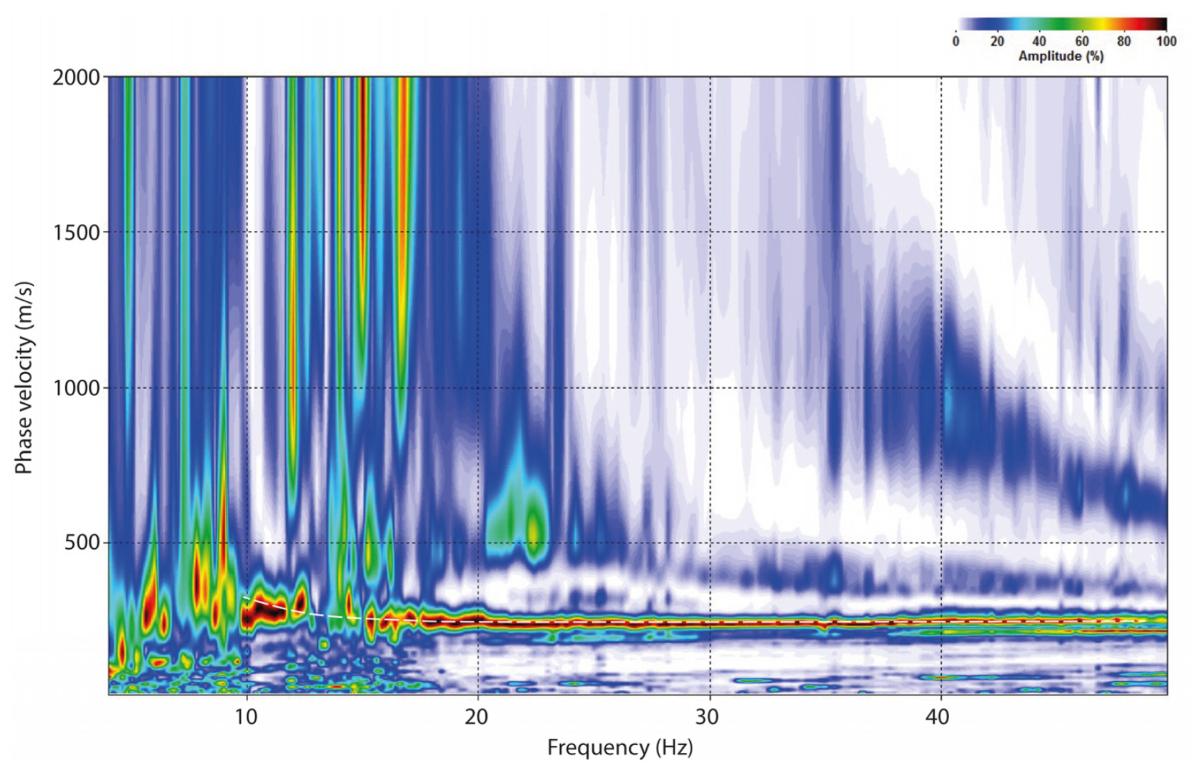
3.2. MASW Method
3.3. Topographic Slope Method
4. Results
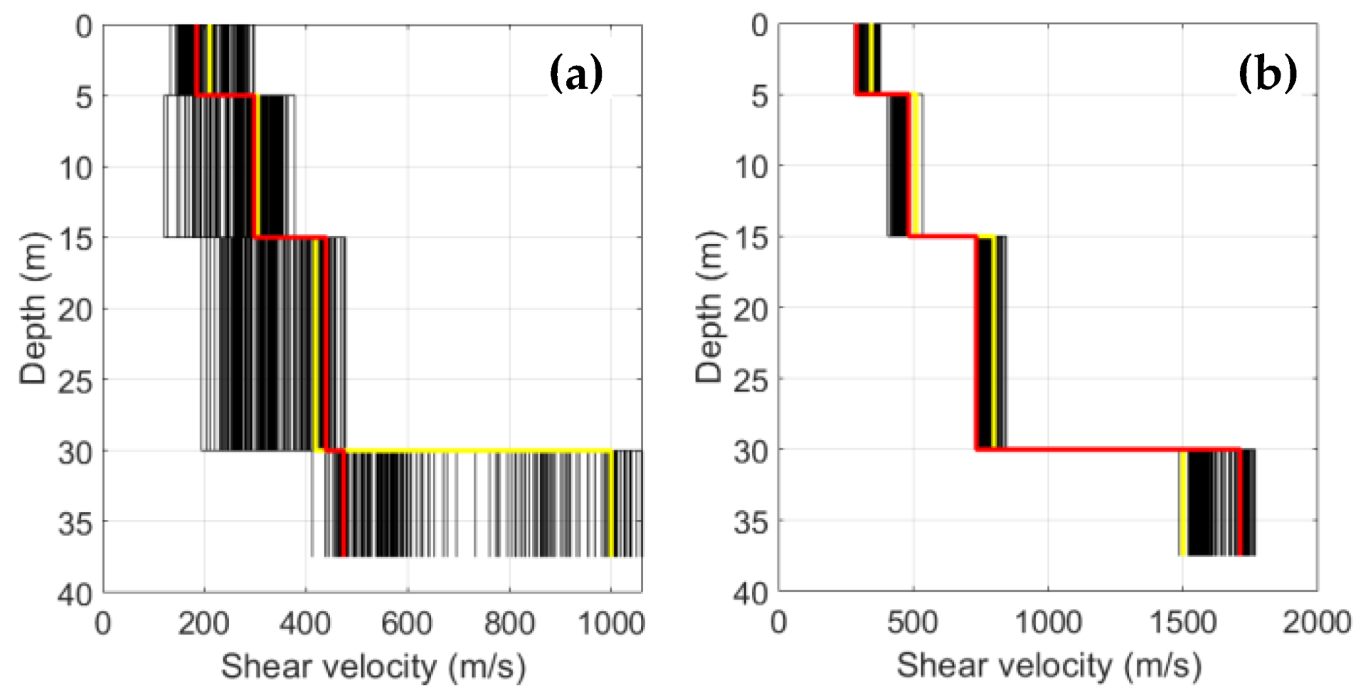
4.1. SPAC-Based Vs30 Values
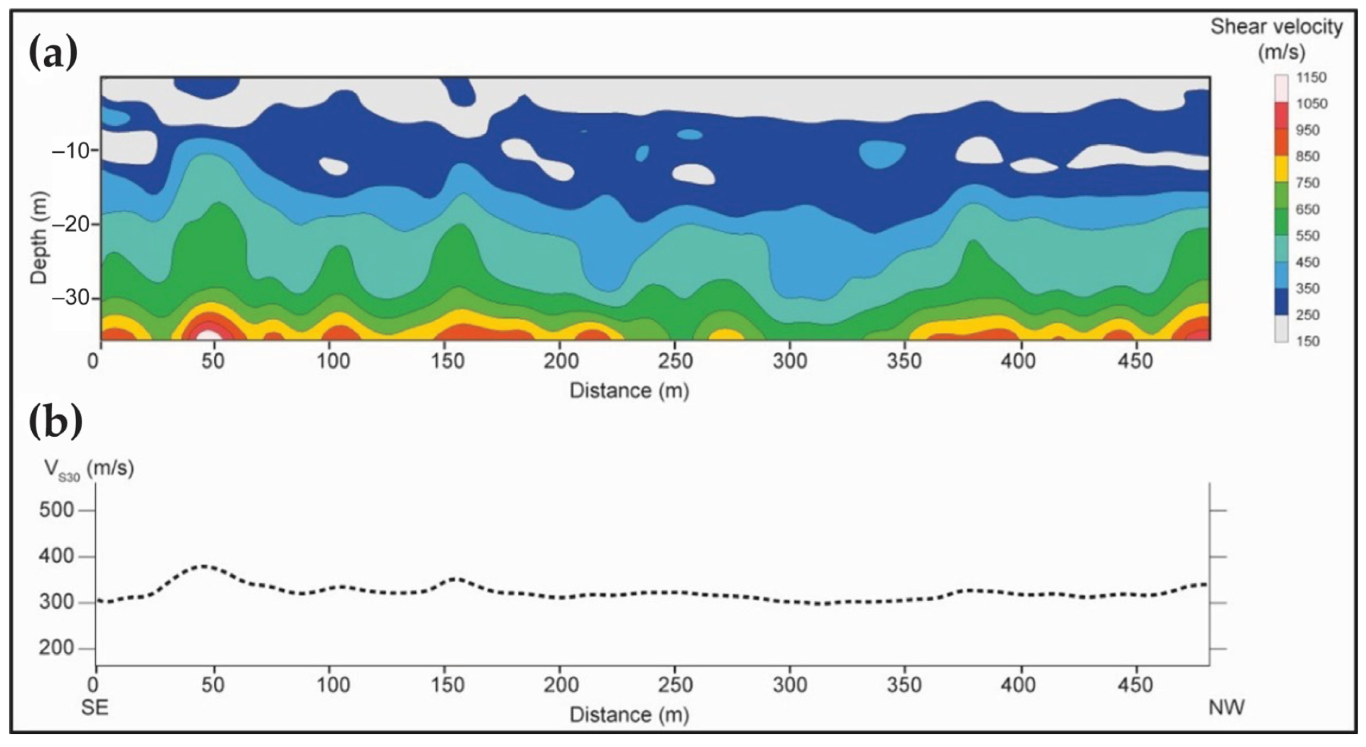
4.2. MASW-Based Vs30 Values
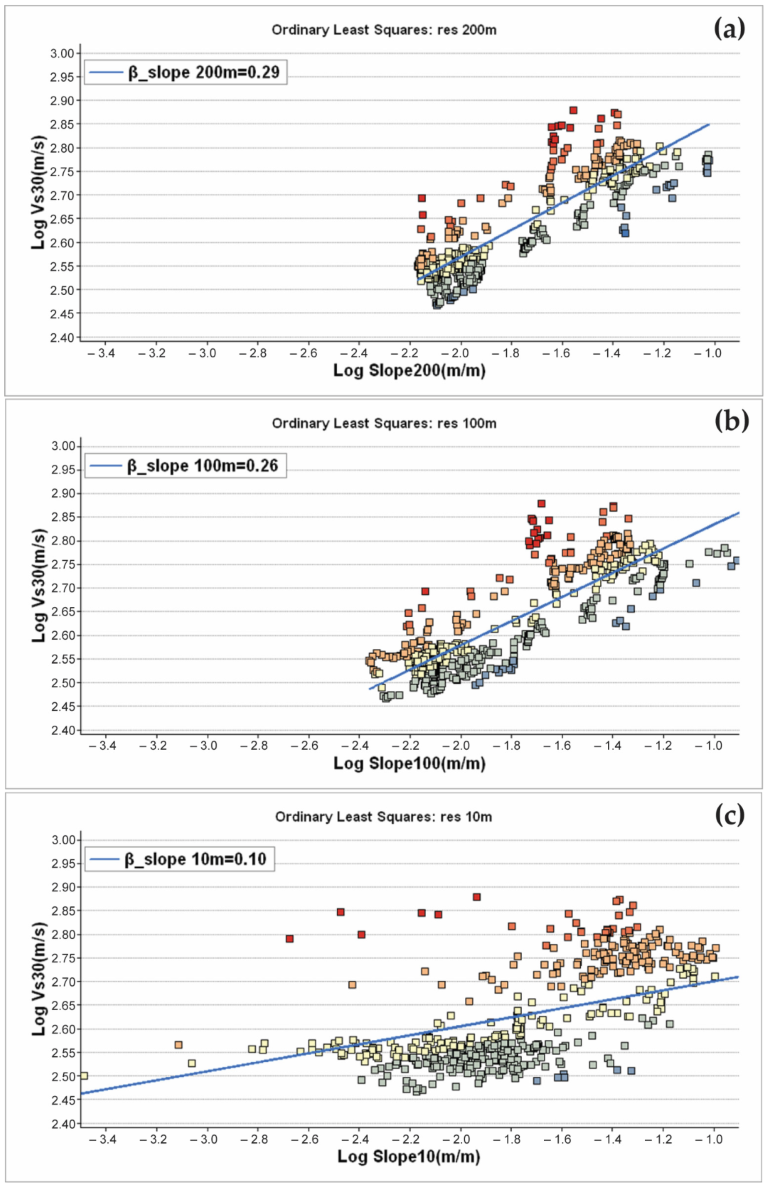
4.3. Topographic Slope-Based Vs30 Values
5. Discussion
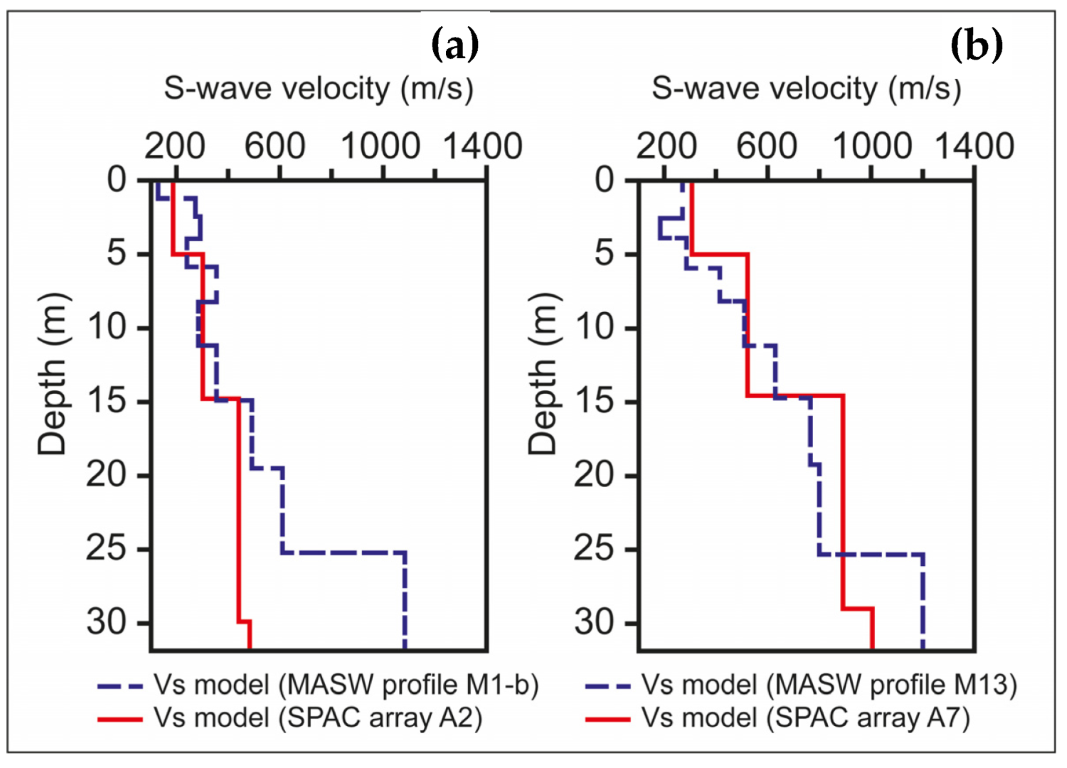
5.1. SPAC Array vs. MASW
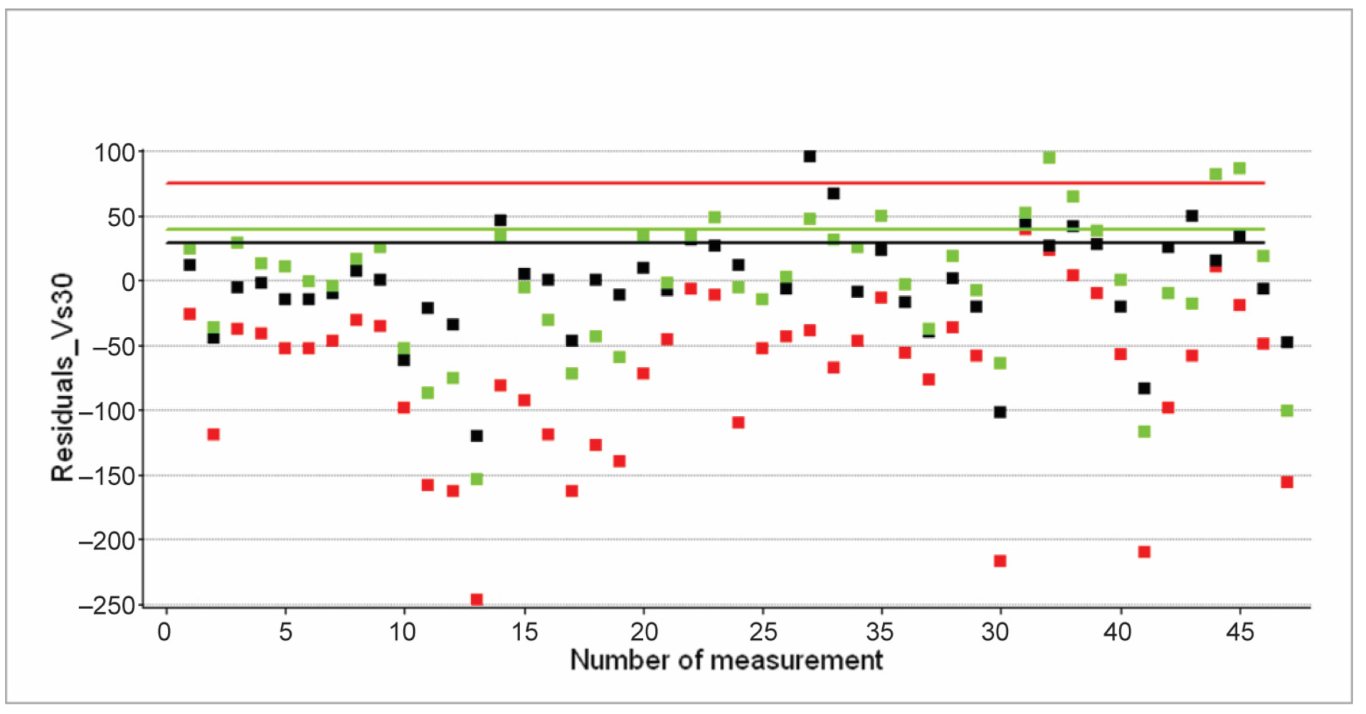
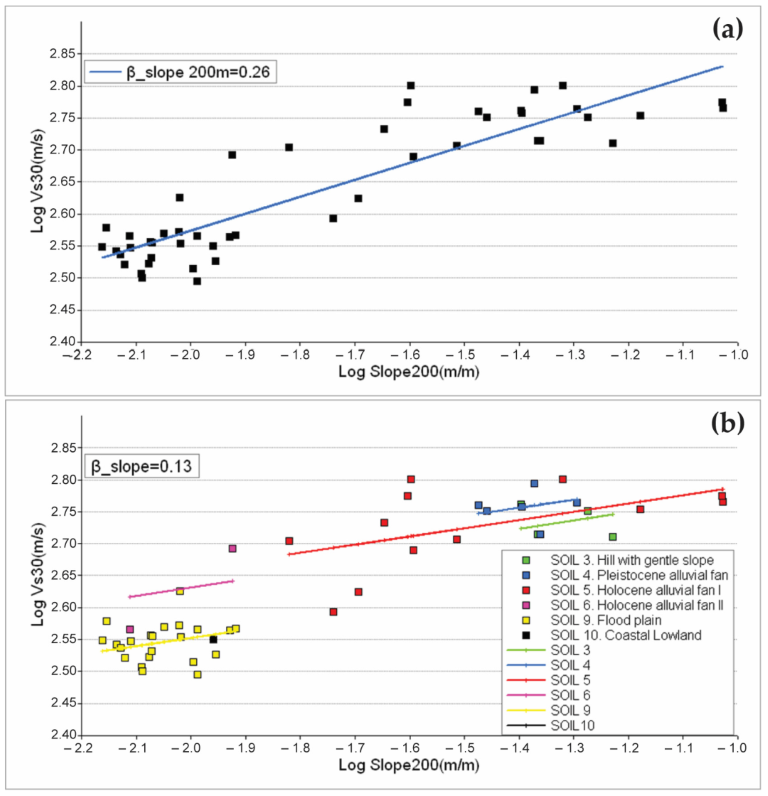
5.2. Topographic Slope-Based Vs30 Values vs. SPAC and MASW
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Navarro, M.; García-Jerez, A.; Alcalá, F.J.; Vidal, F.; Enomoto, T. Local site effect microzonation of Lorca town (SE Spain). Bull. Earthq. Eng. 2014, 12, 1933–1959. [Google Scholar] [CrossRef]
- García-Jerez, A.; Seivane, H.; Navarro, M.; Martínez-Segura, M.; Piña-Flores, J. Joint analysis of Rayleigh-wave dispersion curves and diffuse-field HVSR for site characterization: The case of El Ejido town (SE Spain). Soil Dyn. Earthq. Eng. 2019, 121, 102–120. [Google Scholar] [CrossRef]
- Benito, M.B.; Navarro, M.; Vidal, F.; Gaspar-Escribano, J.; García-Rodríguez, M.J.; Martínez-Solares, J.M. A new seismic hazard assessment in the region of Andalusia (Southern Spain). Bull. Earthq. Eng. 2010, 8, 739–766. [Google Scholar] [CrossRef]
- Torres, Y.; Molina, S.; Martínez-Cuevas, S.; Navarro, M.; Martínez-Díaz, J.J.; Benito, B.; Galiana-Merino, J.J.; Belizaire, D. A first approach to earthquake damage estimation in Haiti: Advices to minimize the seismic risk. Bull. Earthq. Eng. 2016, 14, 39–58. [Google Scholar] [CrossRef]
- Molina, S.; Navarro, M.; Martínez-Pagan, P.; Pérez-Cuevas, J.; Vidal, F.; Navarro, D.; Agea-Medina, N. Potential damage and losses in a repeat of the 1910 Adra (Southern Spain) earthquake. Nat. Hazards 2018, 92, 1547–1571. [Google Scholar] [CrossRef]
- Borcherdt, R.D. On the observation, characterisation, and predictive GIS mapping of strong ground shaking for seismic zonation. Bull. New Zealand Soc. Earthq. Eng. 1991, 24, 287–305. [Google Scholar] [CrossRef]
- Borcherdt, R. Simplified Site Classes and Empirical Amplification Factors for Site-Dependent Code Provisions and Initial “Proposed Vs30 Definition of Site Classes and Site Class Amplification Factors” for Revision of NEHRP Recommended Code Provisions; University of Southern California: Los Angeles, CA, USA, 1992. [Google Scholar]
- Borcherdt, R.D. Estimates of Site-Dependent Response Spectra for Design (Methodology and Justification). Earthq. Spectra 1994, 10, 617–653. [Google Scholar] [CrossRef]
- FEMA 222A. 1994 Edition: NEHRP Recommended Provisions for Seismic Regulations for New Buildings; Federal Emergency Management Agency: Washington, DC, USA, 1994; pp. 4–7. [Google Scholar]
- Sairam, B.; Singh, A.P.; Patel, V.; Chopra, S.; Kumar, M.R. VS30 mapping and site characterization in the seismically active intraplate region of Western India: Implications for risk mitigation. Near Surf. Geophys. 2019, 17, 533–546. [Google Scholar] [CrossRef]
- Borcherdt, R.D. VS30—A site-characterization parameter for use in building Codes, simplified earthquake resistant design, GMPEs, and ShakeMaps. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Ramírez Gaytan, A.; Flores Estrella, H.; Preciado, A.; Bandy, W.L.; Lazcano, S.; Alcántara Nolasco, L.; Aguirre González, J.; Korn, M. Subsoil classification and geotechnical zonation for Guadalajara City, México: Vs30, soil fundamental periods, 3D structure and profiles. Near Surf. Geophys. 2020, 18, 175–188. [Google Scholar] [CrossRef]
- Sil, A.; Sitharam, T.G. Dynamic Site Characterization and Correlation of Shear Wave Velocity with Standard Penetration Test ‘N’ Values for the City of Agartala, Tripura State, India. Pure Appl. Geophys. 2014, 171, 1859–1876. [Google Scholar] [CrossRef]
- Sairam, B.; Rastogi, B.K.; Aggarwal, S.; Chauhan, M.; Bhonde, U. Seismic site characterization using Vs30 and site amplification in Gandhinagar region, Gujarat, India. Curr. Sci. 2011, 100, 754–761. [Google Scholar]
- Socco, L.V.; Strobbia, C. Surface-wave method for near-surface characterization: A tutorial. Near Surf. Geophys. 2004, 2, 165–185. [Google Scholar] [CrossRef]
- Carnevale, M.; Park, C.B. Wave-Energy Source for MASW? In Symposium on the Application of Geophysics to Engineering and Environmental Problems 2010; Symposium on the Application of Geophysics to Engineering and Environmental Problems Proceedings; Environment and Engineering Geophysical Society: Denver, CO, USA, 2010; pp. 517–527. [Google Scholar]
- Martínez-Pagán, P.; Navarro, M.; Pérez-Cuevas, J.; Alcalá, F.J.; García-Jerez, A.; Vidal, F.R. Shear-wave velocity structure from MASW and SPAC methods: The case of Adra town, SE Spain. Near Surf. Geophys. 2018, 16, 356–371. [Google Scholar] [CrossRef]
- Aki, K. Space and Time Spectra of Stationary Stochastic Waves, with Special Reference to Microtremors. Bull. Earthq. Res. Inst. 1957, 35, 415–456. [Google Scholar]
- Park, C.B.; Miller, R.D.; Xia, J. Multichannel analysis of surface waves. Geophysics 1999, 64, 800–808. [Google Scholar] [CrossRef]
- Crespo, M.J.; Benjumea, B.; Moratalla, J.M.; Lacoma, L.; Macau, A.; González, Á.; Gutiérrez, F.; Stafford, P.J. A proxy-based model for estimating VS30 in the Iberian Peninsula. Soil Dyn. Earthq. Eng. 2022, 155, 107165. [Google Scholar] [CrossRef]
- Magistrale, H.; Rong, Y.; Silva, W.; Thompson, E. A Site Response Map of the Continental US. In Proceedings of the Fifteenth World Conference on Earthquake Engineering 2012, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Allen, T.I.; Wald, D.J. Topographic Slope as a Proxy for Seismic Site-Conditions (VS30) and Amplification around the Globe; US Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Thompson, E.M.; Wald, D.J.; Worden, C. A VS30 map for California with geologic and topographic constraints. Bull. Seismol. Soc. Am. 2014, 104, 2313–2321. [Google Scholar] [CrossRef]
- Vilanova, S.; Narciso, J.; Carvalho, J.; Lopes, I.; Ferreira, M.; Pinto, C.; Moura, R.; Borges, J.; Nemser, E. Developing a Geologically-Based Vs30 Site-Conditions Model for Portugal: Methodology and Assessment of the Performance of Proxies. Bull. Seismol. Soc. Am. 2018, 108, 322–337. [Google Scholar] [CrossRef]
- Wills, C.J.; Petersen, M.; Bryant, W.; Reichle, M.; Saucedo, G.; Tan, S.; Taylor, G.; Treiman, J. A site-conditions map for California based on geology and shear-wave velocity. Bull. Seismol. Soc. Am. 2000, 90, S187–S208. [Google Scholar] [CrossRef]
- Wald, D.J.; Allen, T.I. Topographic Slope as a Proxy for Seismic Site Conditions and Amplification. Bull. Seismol. Soc. Am. 2007, 97, 1379–1395. [Google Scholar] [CrossRef]
- Wald, D.; McWhirter, L.; Thompson, E.; Hering, A. A New Strategy for Developing Vs30 Maps. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 5–9 December 2011; p. 2300. [Google Scholar]
- Sanz de Galdeano, C.; López Casado, C.; Delgado, J.; Peinado, M.A. Shallow seismicity and active faults in the Betic Cordillera. A preliminary approach to seismic sources associated with specific faults. Tectonophysics 1995, 248, 293–302. [Google Scholar] [CrossRef]
- Buforn, E.; Sanz de Galdeano, C.; Udías, A. Seismotectonics of the Ibero-Maghrebian region. Tectonophysics 1995, 248, 247–261. [Google Scholar] [CrossRef]
- IGN-UPM Working Group. Actualización de Mapas de Peligrosidad Sísmica de España 2012; Editorial Centro Nacional de Información Geográfica: Madrid, Spain, 2013; Available online: https://www.ign.es/web/ign/portal/libros-digitales/peligrosidad-sismica2012 (accessed on 12 June 2022). (In Spanish)
- Martínez-Díaz, J.J.; Hernández-Enrile, J.L. Neotectonics and morphotectonics of the southern Almería region (Betic Cordillera-Spain) kinematic implications. Int. J. Earth Sci. 2004, 93, 189–206. [Google Scholar] [CrossRef]
- García-Mayordomo, J.; Insua-Arévalo, J.M.; Martínez-Díaz, J.J.; Jiménez-Díaz, A.; Martín-Banda, R.; Martín-Alfageme, S.; Álvarez-Gómez, J.A.; Rodríguez-Peces, M.; Pérez-López, R.; Rodríguez-Pascua, M.A.; et al. The Quaternary Faults DB of Iberia (QAFI v.2.0). J. Iber. Geol. 2012, 38, 285–302. [Google Scholar] [CrossRef]
- Navarro, M.; Enomoto, T.; Sánchez, F.J.; Matsuda, I.; Iwatate, T.; Posadas, A.M.; LuzóN, F.; Vidal, F.; Seo, K. Surface Soil Effects Study Using Short-period Microtremor Observations in Almería City, Southern Spain. In Earthquake Microzoning; Roca, A., Oliveira, C., Eds.; Birkhäuser: Basel, Switzerland, 2001; pp. 2481–2497. [Google Scholar]
- Aldaya, F.; Baena, J.; Ewert, K.; Granados, L.F.; Pan-Arana, T.; Fernández-Luanco, M.C.; Ruiz, P.; Instituto Geológico y Minero de España (IGME). Geologic Maps of Spain (MAGNA Series), Scale 1:50000. 1983. Available online: https://info.igme.es/cartografiadigital/geologica/Magna50Hoja.aspx?Id=967&language=es (accessed on 13 September 2022).
- Foti, S.; Hollender, F.; Garofalo, F.; Albarello, D.; Asten, M.; Bard, P.-Y.; Comina, C.; Cornou, C.; Cox, B.; Di Giulio, G.; et al. Guidelines for the good practice of surface wave analysis: A product of the InterPACIFIC project. Bull. Earthq. Eng. 2018, 16, 2367–2420. [Google Scholar] [CrossRef]
- Martínez-Pagán, P.; Navarro, M.; Pérez-Cuevas, J.; Alcalá, F.J.; García-Jerez, A.; Sandoval-Castaño, S. Shear-wave velocity based seismic microzonation of Lorca city (SE Spain) from MASW analysis. Near Surf. Geophys. 2014, 12, 739–750. [Google Scholar] [CrossRef]
- Park, C. MASW for geotechnical site investigation. Lead. Edge 2013, 32, 656–662. [Google Scholar] [CrossRef]
- Boiero, D.; Socco, L.V.; Stocco, S.; Wisén, R. Bedrock mapping in shallow environments using surface-wave analysis. Lead. Edge 2013, 32, 664–672. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Imaging dispersion curves of surface waves on multi-channel record. In SEG Technical Program Expanded Abstracts 1998; SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 1998; pp. 1377–1380. [Google Scholar]

| SPAC | Δf (Hz) | ΔcR (m/s) | ΔVs (m/s) | Vs30 (m/s) | EC8 1 |
|---|---|---|---|---|---|
| A1 | 4.8–17.0 | 215–412 | 176–625 | 293 | C |
| A2 | 3.0–21.8 | 191–419 | 185–474 | 317 | C |
| A3 | 3.0–13.9 | 312–554 | 283–665 | 359 | C |
| A4 | 6.4–29.8 | 471–674 | 378–748 | 595 | B1 |
| A5 | 7.0–20.0 | 288–701 | 214–824 | 490 | B2 |
| A6 | 2.0–18.0 | 257–904 | 293–1136 | 368 | B2 |
| A7 | 10.5–30.0 | 397–775 | 345–997 | 596 | B1 |
| A8 | 10.0–25.0 | 362–882 | 290–1711 | 513 | B1 |
| A9 | 10.0–19.9 | 495–707 | 415–1374 | 564 | B1 |
| A10 | 10.0–21.8 | 362–554 | 288–589 | 365 | B2 |
| Profile | Street | Length (m) | ΔVs30 (m/s) | Vs30 Average (m/s) | EC8 1 |
|---|---|---|---|---|---|
| M1 | Mediterráneo | 700 | 293–383 | 352 | C |
| M2 | Mediterráneo | 200 | 336–412 | 367 | B2 |
| M3 | Mediterráneo | 110 | 335–483 | 419 | B2 |
| M4 | Mediterráneo | 40 | 479–535 | 505 | B1 |
| M5 | Mediterráneo | 170 | 463–699 | 538 | B1 |
| M6 | Mediterráneo | 160 | 540–770 | 640 | B1 |
| M7 | Mediterráneo | 220 | 471–624 | 547 | B1 |
| M8 | Mediterráneo | 180 | 522–611 | 574 | B1 |
| M9 | Mediterráneo | 160 | 542–704 | 605 | B1 |
| M10 | Mediterráneo | 180 | 523–649 | 566 | B1 |
| M11 | Mediterráneo | 60 | 525–643 | 569 | B1 |
| M12 | Mediterráneo | 120 | 416–637 | 522 | B1 |
| M13 | Pedro Jover | 250 | 494–763 | 603 | B1 |
| M14 | San Juan | 70 | 555–609 | 585 | B1 |
| M15 | San Juan | 50 | 537–604 | 567 | B1 |
| M16 | Braulio Moreno | 200 | 406–727 | 502 | B1 |
| M17 | Bilbao | 480 | 299–355 | 333 | C |
| M18 | Lérida | 310 | 326–446 | 356 | C |
| M19 | José Morales Abad | 240 | 314–434 | 354 | C |
| M20 | La Marina | 270 | 317–497 | 372 | B2 |
| M21 | Chile | 160 | 330–378 | 354 | C |
| M22 | Chile | 80 | 333–388 | 349 | C |
| M23 | Gerona | 250 | 375–507 | 409 | B2 |
| M24 | Adolfo Suárez | 360 | 307–376 | 345 | C |
| Landform | Mean Vs30 (m/s) | |
|---|---|---|
| SPAC | MASW | |
| 1. Mountain (MT) | ||
| 2. Hill with steep slope (HSS) | ||
| 3. Hill with gentle slope (HGS) | 539 ± 26 | 548 ± 30 |
| 4. Pleistocene alluvial fan (PAF) | 573 ± 30 | |
| 5. Holocene alluvial fan I (HAF-I) | 560 ± 50 | 531 ± 80 |
| 6. Holocene alluvial fan II (HAF-II) | 431 ± 63 | |
| 7. Valley flat I (VF-I) | ||
| 8. Valley flat II (VF-II) | ||
| 9. Flood plain (FP) | 330 ± 21 | 356 ± 23 |
| 10. Coastal Lowland (CL) | 355 ± 0 | |
| 11. Reclaimed land (RL) | ||
| Landform | Mean Slope (%) | Mean Vs30 (m/s) | |||
|---|---|---|---|---|---|
| Estimated Values | Measured Values | ||||
| MD1 | MD2 | MD3 | |||
| 1. Mountain (MT) | 12.7 ± 5.7 | 784 ± 252 | 720 ± 84 | 720 ± 84 | |
| 2. Hill with steep slope (HSS) | 5.5 ± 1.7 | 497 ± 54 | 584 ± 50 | 584 ± 50 | |
| 3. Hill with gentle slope (HGS) | 3.8 ± 1.4 | 437 ± 51 | 525 ± 52 | 521 ± 26 | 543 ± 28 |
| 4. Pleistocene alluvial fan (PAF) | 3.5 ± 2.0 | 425 ± 82 | 507 ± 75 | 551 ± 41 | 573 ± 30 |
| 5. Holocene alluvial fan I (HAF-I) | 3.1 ± 1.7 | 411 ± 58 | 500 ± 58 | 524 ± 29 | 539 ± 74 |
| 6. Holocene alluvial fan II (HAF-II) | 1.4 ± 0.9 | 334 ± 40 | 396 ± 54 | 439 ± 29 | 431 ± 63 |
| 7. Valley flat I (VF-I) | 5.6 ± 2.4 | 496 ± 78 | 580 ± 67 | 580 ± 67 | |
| 8. Valley flat II (VF-II) | 3.8 ± 0.8 | 441 ± 31 | 533 ± 29 | 533 ± 29 | |
| 9. Flood plain (FP) | 1.1 ± 0.3 | 322 ± 14 | 379 ± 26 | 358 ± 12 | 352 ± 24 |
| 10. Coastal Lowland (CL) | 2.9 ± 5.1 | 392 ± 179 | 445 ± 118 | 379 ± 46 | 355 ± 0 |
| 11. Reclaimed land (RL) | 3.2 ± 5.4 | 378 ± 198 | 415 ± 173 | 415 ± 173 | |
| Landform | Vs30 (m/s) | ||
|---|---|---|---|
| Residuals at Sample Points | |||
| MD1 | MD2 | MD3 | |
| 1. Mountain (MT) | |||
| 2. Hill with steep slope (HSS) | |||
| 3. Hill with gentle slope (HGS) | 65 | 44 | 24 |
| 4. Pleistocene alluvial fan (PAF) | 120 | 41 | 18 |
| 5. Holocene alluvial fan I (HAF-I) | 115 | 68 | 54 |
| 6. Holocene alluvial fan II (HAF-II) | 107 | 59 | 49 |
| 7. Valley flat I (VF-I) | |||
| 8. Valley flat II (VF-II) | |||
| 9. Flood plain (FP) | 41 | 22 | 19 |
| 10. Coastal Lowland (CL) | 37 | 29 | 5 |
| 11. Reclaimed land (RL) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, F.; Navarro, M.; Martínez-Pagán, P.; García-Jerez, A.; Pérez-Cuevas, J.; Enomoto, T. Vs30 Structure of Almeria City (SE Spain) Using SPAC and MASW Methods and Proxy Correlations. Geosciences 2022, 12, 403. https://doi.org/10.3390/geosciences12110403
López F, Navarro M, Martínez-Pagán P, García-Jerez A, Pérez-Cuevas J, Enomoto T. Vs30 Structure of Almeria City (SE Spain) Using SPAC and MASW Methods and Proxy Correlations. Geosciences. 2022; 12(11):403. https://doi.org/10.3390/geosciences12110403
Chicago/Turabian StyleLópez, Fernando, Manuel Navarro, Pedro Martínez-Pagán, Antonio García-Jerez, Jaruselsky Pérez-Cuevas, and Takahisa Enomoto. 2022. "Vs30 Structure of Almeria City (SE Spain) Using SPAC and MASW Methods and Proxy Correlations" Geosciences 12, no. 11: 403. https://doi.org/10.3390/geosciences12110403
APA StyleLópez, F., Navarro, M., Martínez-Pagán, P., García-Jerez, A., Pérez-Cuevas, J., & Enomoto, T. (2022). Vs30 Structure of Almeria City (SE Spain) Using SPAC and MASW Methods and Proxy Correlations. Geosciences, 12(11), 403. https://doi.org/10.3390/geosciences12110403










