Back-Analysis of the Abbadia San Salvatore (Mt. Amiata, Italy) Debris Flow of 27–28 July 2019: An Integrated Multidisciplinary Approach to a Challenging Case Study
Abstract
1. Introduction
2. Overview of the Study Area
2.1. The 27–28 July 2019 Event
3. Methodologies
3.1. Hydrological Modelling: The FLO-2D Model
Data Input of the Hydrological Modelling
- : to obtain the domain for the case study, two Digital Elevation Models (DEMs) were merged, one based on LiDAR acquisition with a cell size of 1 m, and one with a cell size of 10 m, since the first one did not cover the Mt. Amiata summit area [55].
- : this parameter expresses the minimum flow depth [m] before runoff volume is exchanged with adjacent grid elements and represents the volume of water stored in small depressions (puddles) that do not become part of the overland runoff or infiltration.
- Impervious areas (%): the portion of a grid element that is impervious to infiltration (e.g., rock outcrops or urban areas).
- Initial abstraction (mm): the initial loss of rainfall that precedes infiltration and excess rainfall-runoff (e.g., vegetation interception).
3.2. The Debris-Flow Mixture Hydrograph
3.3. Debris Flow Modelling: The TRENT2D Model
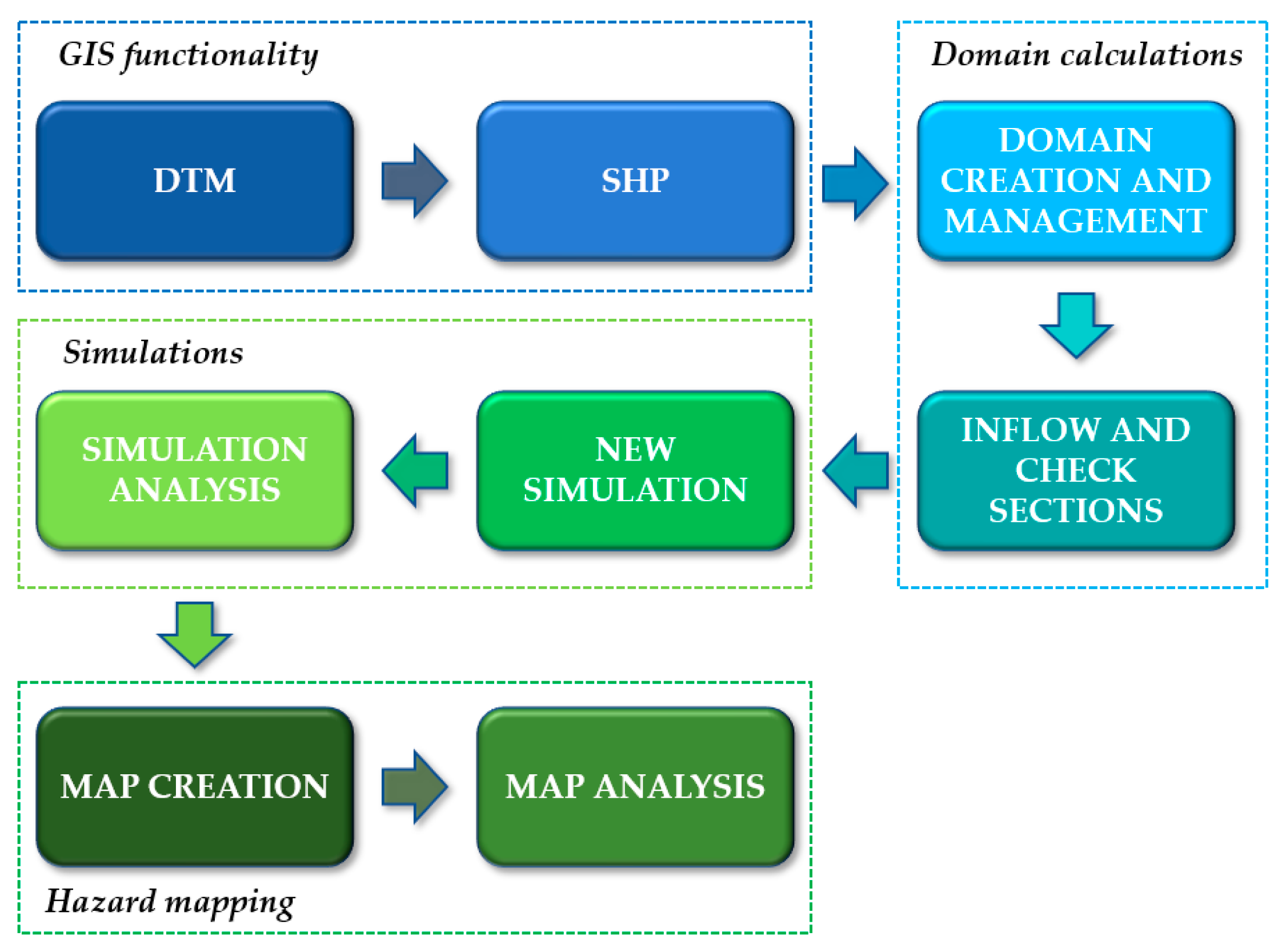
3.3.1. The WEEZARD System
3.4. A Novel Approach for the Simulation of Culvert Clogging
3.4.1. Strategy and Data Input of the Pre-Clogging Phase
- Computational domain: the first element to be defined is the computational domain constituted by a square Cartesian grid defining the altimetric base of the study area. Moreover, non-erodible areas and erodible areas with the associated depth of the erodible material can be specified.
- Inflow conditions: the inflow condition must be imposed in the section where the debris flow is expected to enter the computational domain. By using the WEEZARD system, the mixture hydrograph is evaluated automatically, given and the inflow section as described in Section 3.2.
- Debris parameters: include the values of the sediment bed concentration , the dynamic friction angle , and the reduced relative sediment density .
- can be evaluated by using an average value of the transported grain size and a reference depth along the flow.
- is determined by assuming a local uniform flow condition in the input section with the resistance law according to [61]:
3.4.2. Strategy and Data Input of the Post-Clogging Phase
- Instead of the artificial channel bed, the original ground level must be restored along the culvert path.
- In the channel upstream of the culvert, from the inlet section to the culvert initial section, the original DEM must be changed according to the bed modifications obtained in the pre-clogging phase. The resulting DEM can be used as the initial condition for this phase.
4. Results
4.1. Hydrological Modelling: Parameter Values and Results
- : the two DEMs with different spatial resolutions were mosaicked and resampled to a common cell size of 5 m, obtaining a good compromise between the representation of the hydrographic network and the computational time necessary to run the simulation.
- : The minimum value of 0.0012 m was used, as recommended in the FLO-2D manual [13]. Using higher values would result in larger quantities of water that do not become part of the overland runoff or infiltration. A situation that, due to the characteristics of the study area, would not be justified from a hydrological point of view.
- Rain: to apply the IDW method for the entire study area considering the data from the AS, LV, and VA rain gauges (Figure 1) only, an auxiliary gauge was placed south of the southern border of the Risola catchment, allowing us to extend the rainfall maps to the Risola catchment area. This was achieved by placing a barrier feature between the auxiliary gauge and the existing rain gauges without altering their rainfall data. A barrier is a polyline dataset used as a breakline that limits the searching region for input sample points: only those points located on the same side of the barrier are considered. Thus, a representation of the rainstorm distributed in time and space was obtained.
- : a specific survey was conducted through constant-head measurements with an Aardvark-type permeameter [64] to determine the value of field saturated hydraulic conductivity. Thirteen borehole tests were performed within the sandy soil above the BEL2 and QRT volcanic formations, investigating depths between 0.30–1.50 m. Given the homogenous nature of the unconsolidated material in the study area, the average value (140 mm/h) was uniformly assigned throughout the catchment.
- : in the five days preceding the event, the three rain gauges close to the study area (Figure 1) recorded no rainfall accumulation, and considering a longer period (i.e., 60 days), only 28 mm were recorded. This extended drought period and the permeable nature of the unconsolidated material indicate that the antecedent moisture conditions before the event were dry. Thus, the assumed value for modelling is 0.35, as also specified in the FLO-2D manual [13]. Only in the last stretch of the Risola up to the culvert (~1 km) can the soil be considered saturated. In fact, some ephemeral springs with a flow rate of only a few l/s (negligible if compared to the discharge developed during the event) bring water into the stream bed.
- : the obtained value of this parameter is equal to 30 mm. This is in agreement with the values proposed by [65].
- Given the geological characteristics of the study area (Section 2), no impermeable boundary was imposed at the bottom of the unconsolidated material of the catchment.
- Impervious areas (%): as described in Section 2, the bedrock of the study area is affected by widespread weathering. For this reason, infiltration is set to zero for the fractured bedrock portion (type (i) in Section 2; ~15% of the total catchment area) even though no data are available on the rock mass fracturing degree and the related infiltration patterns. It may be noted that this assumption is probably reasonable for the study area only in the case of short and intense rainstorms, such as the one analyzed here.
- Initial abstraction (mm): it represents the initial loss of rainfall that precedes infiltration and excess rainfall-runoff (e.g., vegetation interception). This parameter was assigned using the values proposed in the FLO-2D manual [13].
4.2. The Debris Flow Hydrograph
- Debris parameters: the values of , , and parameters used in this study are those generally accepted in debris flow dynamics [61] and are reported in Table 3. This assumption stems from the fact that the material involved does not have any peculiar geotechnical characteristics that would necessitate changing the values of these three parameters.
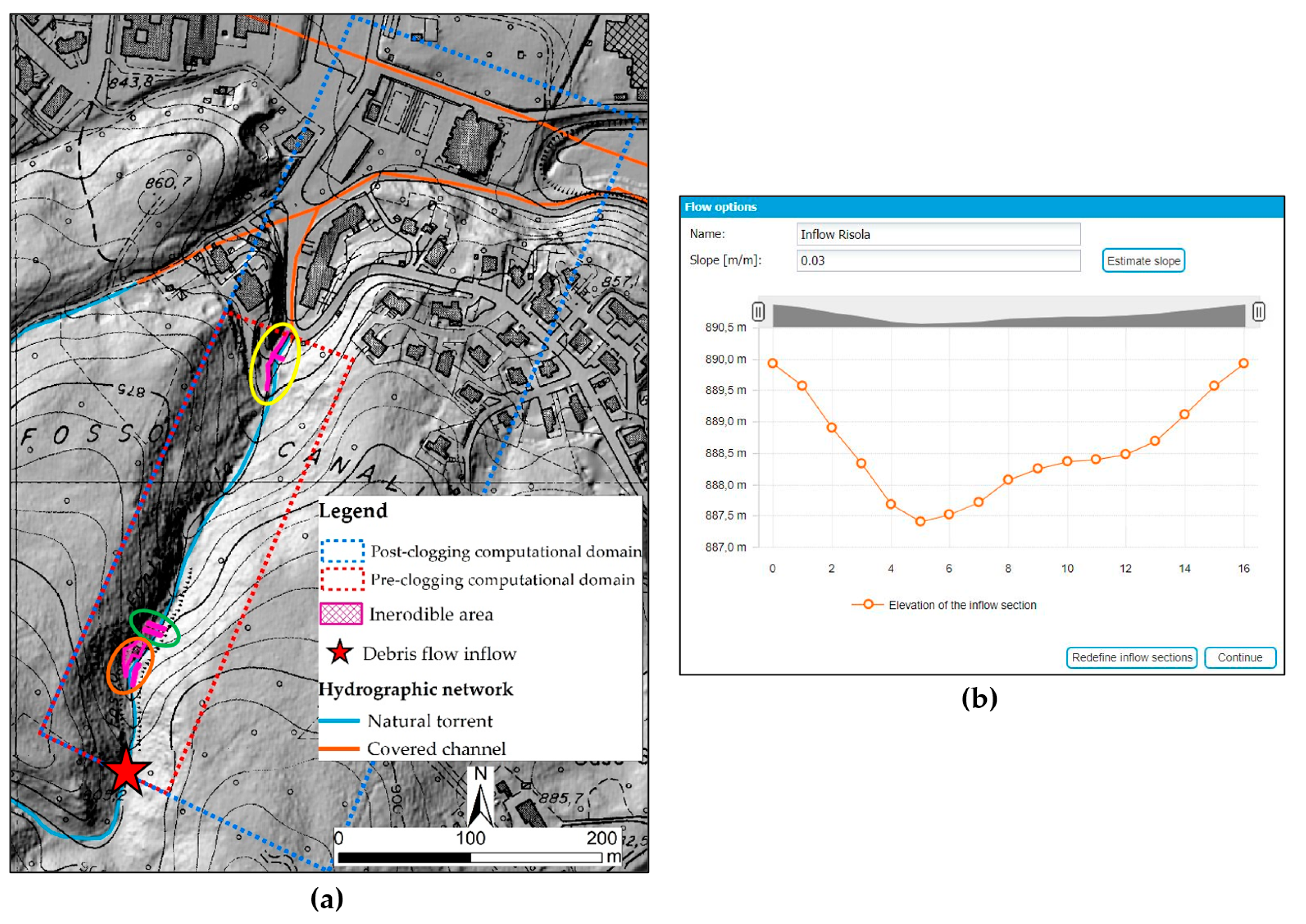
- : the slope of the inflow section was set according to the morphological characteristics of the stream, equal to 0.03 m/m, i.e., the average value between the upstream and downstream reaches of the input section, with slopes of about 0.01 m/m and 0.05 m/m, respectively. This choice derives from the geomorphological characteristics of the Risola just upstream of the red star in Figure 1, where an abrupt change in direction and slope of the creek occurs (see Section 2).
4.3. Pre-Clogging Debris Flow Modelling: Parameter Values and Results
- Computational domain: an available DEM [55] with a cell size of 1 m × 1 m, based on LiDAR acquisition, was used to produce the domain, which is delimited with a red dashed rectangle in Figure 10a. The resulting morphology of the inflow section (Figure 10b) is referred to as the red star in Figure 10a. To represent the culvert width with a reasonable approximation and considering that its width is 1.4 m, the original DEM was resampled to a cell size of 0.5 m × 0.5 m. In this way, the channel is represented by using three cells, namely with a width of 1.5 m, and the deviation of 0.1 m was assumed to be negligible for the modelling results. In addition, as the base of the culvert is located 1.5 m below the road level, the resampled DEM was lowered by 1.5 m along the path of the culvert. In the analyzed stretch, some anthropogenic structures are present, thus erodible, and non-erodible zones have been defined accordingly. One of these structures is a small building preceded by a short (~25 m) non-erodible artificial portion of the bottom of the creek, and a wall on the right bank of the stream (orange circle in Figure 10a). In addition, three check dams are located along the Risola: two of them are placed immediately downstream of the building described previously (see the green circle in Figure 10a), and the last check dam is located just upstream of the culvert inlet section. In this last area, two walls bound the creek before the entrance to the covered portion (yellow circle in Figure 10a). These structures, which are correctly represented by the DEM used for the modelling, are treated as non-erodible areas with null erodible thickness. On the other hand, the rest of the torrent is treated as an erodible area.
- : to choose the optimal value for this parameter, we performed tests with values of 15, 10 and five. Results show that for values of 15 and 10 the flow depths are too shallow compared to those observed. At the same time, the erosions were excessive, generating a higher concentrated flow and, consequently, culvert clogging time earlier than observed. On the other hand, for , both the flow depths along the stream and the culvert clogging time were found to be consistent with the observations.
- the value of the transport parameter used for the numerical modelling was obtained considering the submergence as and considering the values of other parameters appearing in Equation (7) as reported in Table 3.
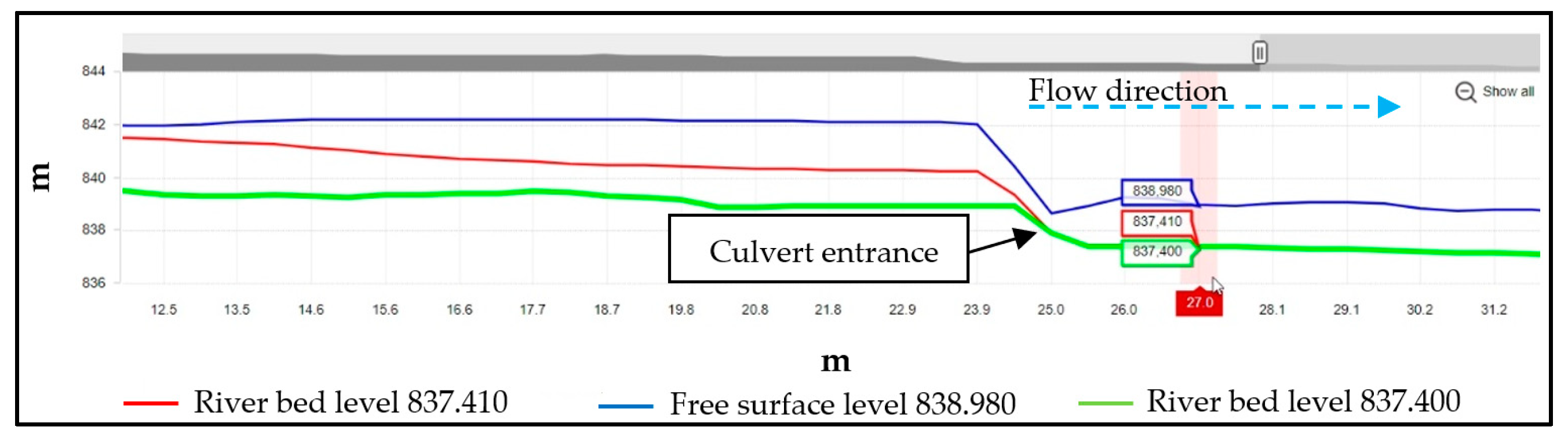
4.4. Debris Flow Back-Analysis: Post-Clogging Phase Results
5. Discussion
5.1. Geological and Geomorphological Analysis
5.2. The Choice of the Models
5.3. The Culvert Clogging and Its Numerical Simulation
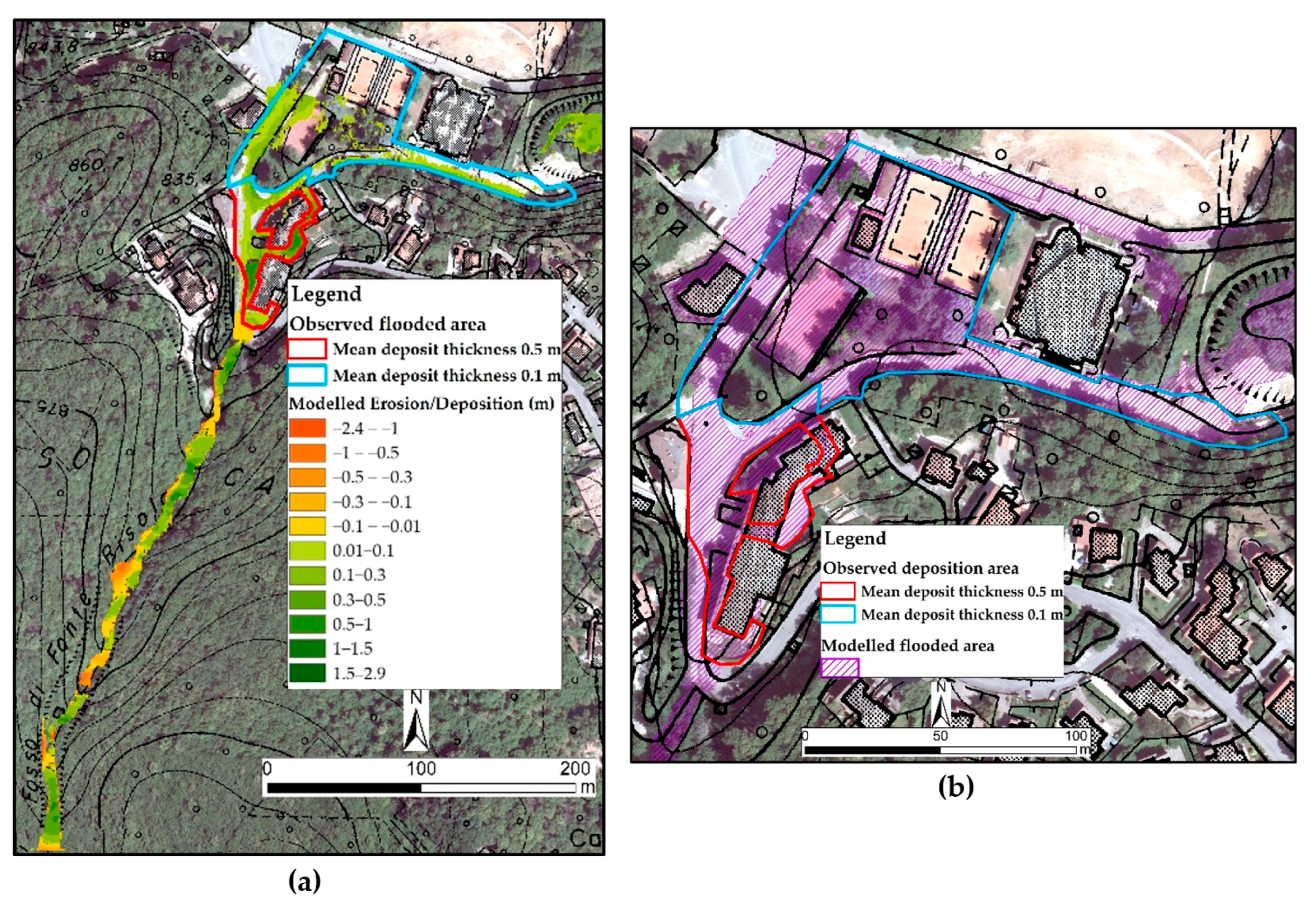
5.4. Comparison of Simulated and Observed Data
6. Conclusions
- A geological-geomorphological model based on the integration of detailed mapping and specific engineering geological field investigations is a fundamental prerequisite for further accurate numerical debris flow modelling.
- The overall methodological approach used in this study, namely a cascade of models composed of a hydrological model for the estimation of the hydraulic forcing, estimation of the mixture flow rate with the amplification factor, and two-phase modelling of the debris flow in the final reach, provides reasonable outputs for the simulation of debris flows with hydrological forcing.
- The modelling assumptions introduced to overcome some of the limitations of the model used, namely the definition of the conventional occlusion time and the subdivision of the simulation into pre- and post-clogging, proved to be effective.
- The two-phase approach for debris flow present in the TRENT2D model allows an effective and straightforward description of all the phenomena involving granular debris flows in challenging situations.
- The WEEZARD system allowed us to handle complex and sophisticated simulations simply, achieving a methodology in line with the European Floods Directive.
- An additional important result should be emphasized. As the back-analysis was implemented mostly using a priori fixed parameters (as they are physically based) and the parameters determined by calibration (Y and consequently β) are very close to values that can be reasonably a priori estimated, the modelling approach implemented also has a good predictive capability. Indeed, as the observed local mixture depth values range along the stream between 0.30 m and 1.50 m, and assuming an average diameter of the transported material of 0.20 m, the Y parameter can reasonably be in the range 1.5–7.5. This results in an average value of 4.5, which very close to the value of five used in the modelling.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
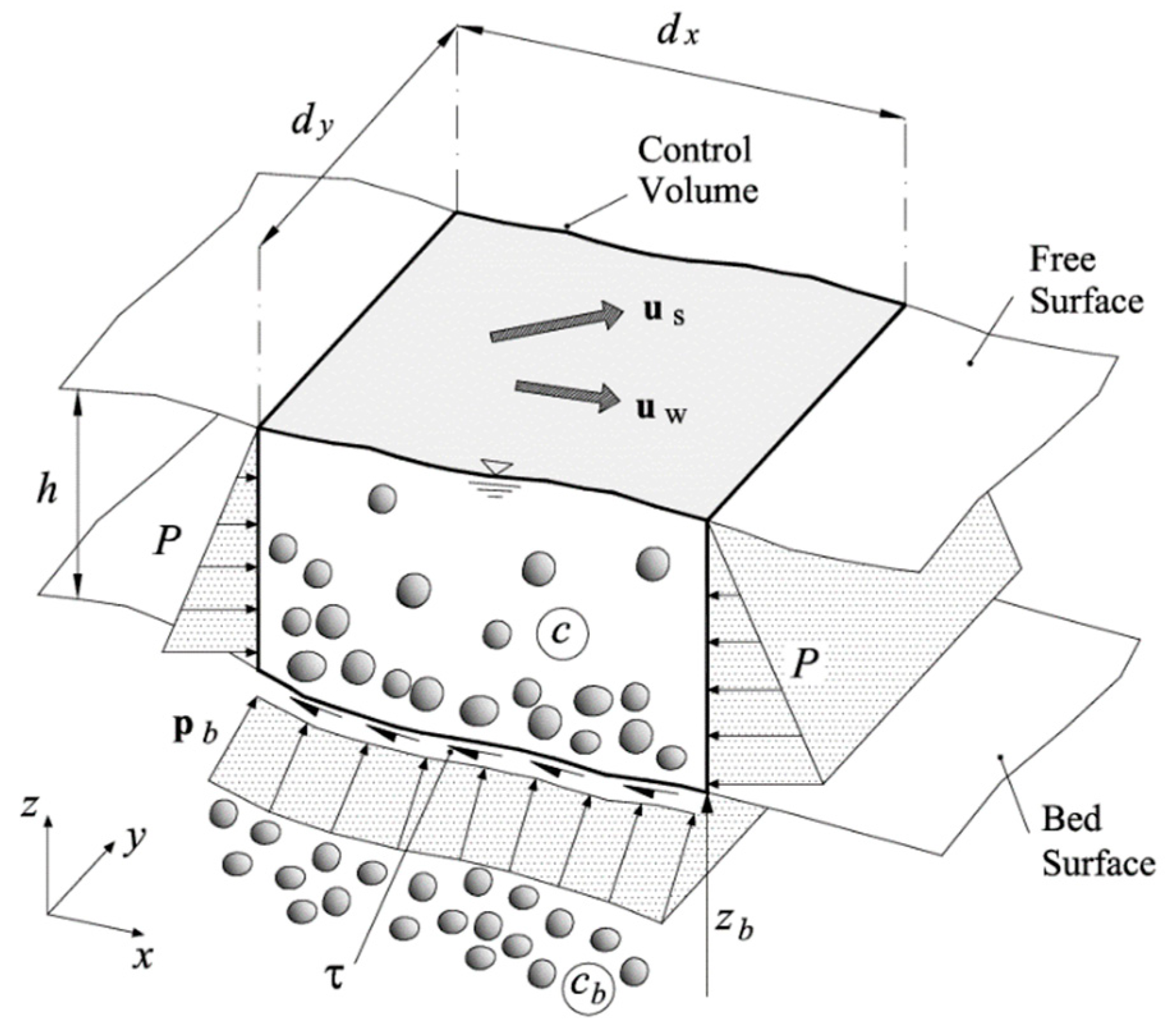
Appendix A. Differential Equations of the Two-Dimensional TRENT2D Model
- the motion of the debris flow occurs predominantly along a flat or weakly curved surface, so the motion is negligible in the direction orthogonal to that surface (a direction assimilated to the vertical), it is well represented through average quantities over the depth, and the pressure distribution is linear.
- the solid phase is characterized by a representative sediment diameter and constant density.
- the concentration in the bed is constant.
- the velocity of the two phases is the same (isokinetic assumption).
References
- Varnes, D.J. Slope Movement Types and Processes. Transportation Research Board Special Report. In Landslides: Analysis and Control; Transportation Research Board: Washington, DC, USA, 1978; Volume 176, pp. 11–33. [Google Scholar]
- Takahashi, T. Debris Flow: Mechanics, Prediction and Countermeasures; Taylor & Francis: Oxfordshire, UK, 2007. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Milne, F.D.; Brown, M.J.; Knappett, J.A.; Davies, M.C.R. Centrifuge modelling of hillslope debris flow initiation. Catena 2012, 92, 162–171. [Google Scholar] [CrossRef]
- Ancey, C. Geomorphological Fluid Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 582. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article “Assessment of economic flood damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Petrucci, O.; Aceto, L.; Bianchi, C.; Bigot, V.; Brázdil, R.; Pereira, S.; Kahraman, A.; Kılıç, Ö.; Kotroni, V.; Llasat, M.C.; et al. Flood Fatalities in Europe, 1980–2018: Variability, Features, and Lessons to Learn. Water 2019, 11, 1682. [Google Scholar] [CrossRef]
- IPCC. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Stoffel, M.; Mendlik, T.; Schneuwly-Bollschweiler, M.; Gobiet, A. Possible impacts of climate change on debris-flow activity in the Swiss Alps. Clim. Chang. 2014, 122, 141–155. [Google Scholar] [CrossRef]
- EU. Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks; European Environment Agency: Copenhagen, Denmark, 2007; pp. 27–34.
- Armanini, A.; Fraccarollo, L.; Rosatti, G. Two-dimensional simulation of debris flows in erodible channels. Comput. Geosci. 2009, 35, 993–1006. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Julien, P.Y.; Fullerton, W.T. Two-dimensional water flood and mudflow simulation. Hydrol. Eng. 1993, 119, 244–261. [Google Scholar] [CrossRef]
- FLO-2D. FLO-2D Reference Manual. Nutrioso AZ.: FLO-2D; FLO-2D Software Inc.: Nutrioso, AZ, USA, 2018. [Google Scholar]
- Christen, M.; Buhler, Y.; Bartelt, P.; Leine, R.; Glover, J.; Schweizer, A. Numerical simulation tool “RAMMS” for gravitational natural hazards. In Proceedings of the 12th congress INTERPRA EVENT, Grenoble, France, 23–26 April 2012. [Google Scholar]
- RAMMS. RAMMS: DEBRISFLOW User Manual. Davos, Switzerland: ETH. 2017. Available online: https://ramms.slf.ch/ramms/downloads/RAMMS_DBF_Manual.pdf (accessed on 1 January 2020).
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B.W. Comparison of flow resistance relations for debris flows using a one-dimensional finite element simulation model. Nat. Hazards Earth Syst. Sci. 2006, 6, 155–165. [Google Scholar] [CrossRef]
- Rickenmann, D.; Laigle, D.; McArdell, B.W.; Hübl, J. Comparison of 2D debris–flow simulation models with field events. Comput. Geosci. 2006, 10, 241–264. [Google Scholar] [CrossRef]
- Cesca, M.; D’Agostino, V. Comparison between FLO-2D and RAMMS in debris-flow modelling: A case study in the Dolomites. WIT Trans. Eng. Sci. 2008, 60, 197–206. [Google Scholar] [CrossRef]
- Simoni, A.; Mammoliti, M.; Graf, C. Performance of 2D debris flow simulation model RAMMS. Back-analysis of field events in Italian Alps. In Proceedings of the annual international conference on geological and earth sciences GEOS, Singapore, 3–4 December 2012. [Google Scholar]
- Mikoš, M.; Bezak, N. Debris Flow Modelling Using RAMMS Model in the Alpine Environment With Focus on the Model Parameters and Main Characteristics. Front. Earth Sci. 2021, 8, 605061. [Google Scholar] [CrossRef]
- Gregoretti, C.; Degetto, M.; Bernard, M.; Boreggio, M. The debris flow occurred at Ru Secco Creek, Venetian Dolomites, on 4 August 2015: Analysis of the phenomenon, its characteristics and reproduction by models. Front. Earth Sci. 2018, 6, 80. [Google Scholar] [CrossRef]
- Chen, M.L.; Liu, X.N.; Wang, X.K.; Zhao, T.; Zhou, J.W. Contribution of Excessive Supply of Solid Material to a Runoff-Generated Debris Flow during Its Routing Along a Gully and Its Impact on the Downstream Village with Blockage Effects. Water 2019, 11, 169. [Google Scholar] [CrossRef]
- Iqbal, U.; Barthelemy, J.; Li, W.; Perez, P. Automating Visual Blockage Classification of Culverts with Deep Learning. Appl. Sci. 2021, 11, 7561. [Google Scholar] [CrossRef]
- Hürlimann, M.; Copons, R.; Altimir, J. Detailed Debris Flow hazard Assessment in Andorra: A Multidisciplinary Approach. Geomorphology 2006, 78, 359–372. [Google Scholar] [CrossRef]
- Tang, Y.; Guo, Z.; Wu, L.; Hong, B.; Feng, W.; Su, X.; Li, Z.; Zhu, Y. Assessing Debris Flow Risk at a Catchment Scale for an Economic Decision Based on the LiDAR DEM and Numerical Simulation. Front. Earth Sci. 2002, 10, 821735. [Google Scholar] [CrossRef]
- Vagnon, F.; Kurilla, L.J.; Clusaz, A.; Pirulli, M.; Fubelli, G. Investigation and numerical simulation of debris flow events in Rochefort basin (Aosta Valley—NW Italian Alps) combining detailed geomorphological analyses and modern technologies. Bull. Eng. Geol. Environ. 2022, 81, 378. [Google Scholar] [CrossRef]
- Brogi, A. The structure of the Mt. Amiata volcano-geothermal area (Northern Apennines, Italy): Neogene-Quaternary compression versus extension. Int. J. Earth Sci. 2008, 97, 677–703. [Google Scholar] [CrossRef]
- Regione Toscana—Settore Idrologico e Geologico Regionale–DATI/Archivio Storico. Available online: https://www.sir.toscana.it/pluviometria-pub (accessed on 17 May 2022).
- Regione Toscana–SITA: Fototeca e Punti Geodetici e di Appoggio Fotografico. Available online: https://www502.regione.toscana.it/geoscopio/fototeca.html (accessed on 5 June 2020).
- Marroni, M.; Moratti, G.; Costantini, A.; Conticelli, S.; Benvenuti, M.G.; Pandolfi, L.; Bonini, M.; Cornamusini, G.; Laurenzi, M.A. Geology of the Monte Amiata region, Southern Tuscany, Central Italy. Ital. J. Geosci. 2015, 134, 171–199. [Google Scholar] [CrossRef]
- Regione Toscana–DB Geologico. Available online: http://www502.regione.toscana.it/geoscopio/geologia.html (accessed on 17 February 2022).
- Conticelli, S.; Boari, E.; Burlamacchi, L.; Cifelli, F.; Moscardi, F.; Laurenzi, M.A.; Ferrari Pedraglio, L.; Francalanci, L.; Benvenuti, M.G.; Braschi, E.; et al. Geochemistry and Sr-Nd-Pb isotopes of Monte Amiata Volcano, Central Italy: Evidence for magma mixing between high-K calc-alkaline and leucititic mantle-derived magmas. Ital. J. Geosci. 2015, 134, 268–292. [Google Scholar] [CrossRef]
- Certini, G.; Wilson, M.J.; Hillier, S.J.; Fraser, A.R.; Delbos, E. Mineral weathering in trachydacitic derived soils and saprolites involving formation of embryonic halloysite and gibbsite at Mt. Amiata, Central Italy. Geoderma 2006, 133, 173–190. [Google Scholar] [CrossRef]
- Principe, C.; Vezzoli, L.; La Felice, S. Stratigrafia ed evoluzione geologica del vulcano di Monte Amiata. In Il vulcano di Monte Amiata; Principe, C., Lavorini, G., Vezzoli, L., Eds.; Edizioni Scientifiche e Artistiche: New Orleans, LA, USA, 2017; pp. 81–101. [Google Scholar]
- Principe, C.; Vezzoli, L. Characteristics and significance of intravolcanic saprolite paleoweathering and associate paleosurface in a silicic effusive volcano: The case study of Monte Amiata (middle Pleistocene, Tuscany, Italy). Geomorphology 2021, 392, 107922. [Google Scholar] [CrossRef]
- Irfan, T.Y. Structurally controlled landslides in saprolitic soils in Hong Kong. Geotech. Geol. Eng. 1998, 16, 215–238. [Google Scholar] [CrossRef]
- Aydin, A. Stability of saprolitic slopes: Nature and role of field scale heterogeneities. Nat. Hazards Earth Syst. Sci. 2006, 6, 89–96. [Google Scholar] [CrossRef]
- Bovis, M.J.; Jakob, M. The role of debris supply conditions in predicting debris flow activity. Earth Surf. Process. Landf. 1999, 24, 1039–1054. [Google Scholar] [CrossRef]
- D’Agostino, V. Analisi quantitativa e qualitativa del trasporto solido torrentizio nei bacini montani del Trentino orientale–Scritti dedicati a Giovanni Tournon. In Sistemazione dei Bacini Montani e Difesa del Suolo; Associazione Italiana di Ingegneria Agraria; Ferro, V., Ed.; Nuova BIOS: Castrovillari, Italy, 1996; pp. 111–123. ISBN 9788860930422. [Google Scholar]
- Regione Toscana–Direzione Difesa del Suolo e Protezione Civile Centro Funzionale della Regione Toscana–Consorzio LaMMA–Settore Idrologico “REPORT DI EVENTO 27–28 LUGLIO 2019” Ultimo Aggiornamento: 30/07/2019. Available online: http://www301.regione.toscana.it/bancadati/atti/DettaglioAttiD.xml?codprat=2019AD00000023965 (accessed on 1 January 2020).
- Facebook.com. Available online: https://www.facebook.com/munteanu.camy/videos/2578268685525337 (accessed on 23 May 2022).
- Amiatanews © 2014. Available online: http://www.amiatanews.it/abbadia-s-salvatore-alluvione-riconosciuto-lo-stato-di-emergenza (accessed on 26 September 2019).
- Rosatti, G.; Zugliani, D.; Pirulli, M.; Martinengo, M. A new method for evaluating stony debris flow rainfall thresholds: The Backward Dynamical Approach. Heliyon 2019, 5, e01994. [Google Scholar] [CrossRef]
- Rosatti, G.; Zorzi, N.; Zugliani, D.; Piffer, S.; Rizzi, A. A web service ecosystem for high-quality, cost-effective debris-flow hazard assessment. Environ. Model. Softw. 2018, 100, 33–47. [Google Scholar] [CrossRef]
- Quan Luna, B.; Blahut, J.; van Westen, C.J.; Sterlacchini, S.; van Asch, T.W.J.; Akbas, S.O. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef]
- Petroselli, A.; Arcangeletti, E.; Allegrini, E.; Romano, N.; Grimaldi, S. The influence of the net rainfall mixed Curve Number–Green Ampt procedure in flood hazard mapping: A case study in Central Italy. J. Agric. Eng. 2013, 44. [Google Scholar] [CrossRef][Green Version]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Schladow, G. Flood inundation assessment for the Hanoi central area, Vietnam under historical and extreme rain-fall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef]
- Hwang, J.; Lee, H.; Lee, K. Effects of Nonhomogeneous Soil Characteristics on the Hydrologic Response: A Case Study. Water 2020, 12, 2416. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G. Studies of soil physics, part I–the flow of air and water through soils. J. Ag. Sci. 1919, 4, 1–24. [Google Scholar]
- Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. New analytic solution related to the Richards, Philip, and Green-Ampt equations for infiltration. Vadose Zone J. 2009, 8, 127–135. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Kavvas, M.L.; Jones, S.E.; Rolston, D.E. Use of Green-Ampt model for analyzing one-dimensional convective transport in unsaturated soils. J. Hydrol. 1996, 178, 337–350. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, S.Y.; Su, D.Y.; Gao, G.Y.; Huo, Z.L. Modeling water infiltration in a large layered soil column with a modified Green-Ampt model and HYDRUS-1D. Comput. Electron. Agric. 2010, 71, S40–S47. [Google Scholar] [CrossRef]
- Silburn, D.M.; Connolly, R.D. Distributed parameter hydrology model (ANSWERS) applied to a range of catchment scales using rainfall simulator data I: Infiltration modelling and parameter measurement. J. Hydrol. 1995, 172, 87e104. [Google Scholar] [CrossRef]
- Wang, L.L.; Li, Z.J.; Bao, H.J. Development and comparison of Gridbased distributed hydrological models for excess-infiltration runoffs. J. Hohai Univ. Nat. Sci. 2010, 38, 123–128. (in Chinese). [Google Scholar] [CrossRef]
- Regione Toscana–SITA: Cartoteca. Available online: http://www502.regione.toscana.it/geoscopio/cartoteca.html? (accessed on 12 November 2019).
- Regione Toscana–SITA: Uso e Copertura del Suolo. Available online: https://www502.regione.toscana.it/geoscopio/usocoperturasuolo.html (accessed on 12 November 2019).
- Arcement, G.J.; Schneider, V.R. Guide for selecting Manning’s roughness coefficients for natural channels and flood plains. USGS Water Supply Pap. 2000, 2339. [Google Scholar]
- Homer, C.; Dewitz, J.; Fry, J.; Coan, M.; Hossain, N.; Larson, C.; Herold, N.; McKerrow, A.; Van Driel, J.N.; Wickham, J. Completion of the 2001 National Land Cover Database for the conterminous United States. Photogramm. Eng. Remote Sens. 2007, 73, 337–341. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Rosatti, G.; Zugliani, D. Modelling the transition between fixed and mobile bed conditions in two-phase free-surface flows: The composite Riemann problem and its numerical solution. J. Comput. Phys. 2015, 285, 226–250. [Google Scholar] [CrossRef]
- Takahashi, T. Mechanical characteristics of debris flow. J. Hydraul. Div. 1978, 8, 1153–1169. [Google Scholar] [CrossRef]
- WEEZARD. Available online: https://tool.weezard.eu (accessed on 20 May 2022).
- WEEZARD–Tutorial. Available online: http://www.weezard.eu/index.php/tutorial (accessed on 23 May 2022).
- Theron, E.; Le Roux, P.; Hensley, M.; Van Rensburg, L. Evaluation of the Aardvark constant head soil permeameter to predict saturated hydraulic conductivity. WIT Trans. Ecol. Environ. 2010, 134, 153–162. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-Ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Lewin, J.; Warburton, J. Debris Flows in an Alpine Environment. Geography 1994, 79, 98–107. Available online: http://www.jstor.org/stable/40572407 (accessed on 1 January 2020).
- Palamakumbura, R.; Finlayson, A.; Ciurean, R.; Nedumpallile-Vasu, N.; Freeborough, K.; Dashwood, C. Geological and geomorphological influences on a recent debris flow event in the Ice-scoured Mountain Quaternary domain, western Scotland. Proc. Geol. Assoc. 2021, 132, 456–468. Available online: https://www.sciencedirect.com/science/article/pii/S0016787821000390 (accessed on 1 January 2020). [CrossRef]
- Bezak, N.; Jež, J.; Sodnik, J.; Jemec Auflič, M.; Mikoš, M. An extreme May 2018 debris flood case study in northern Slovenia: Analysis, modelling, and mitigation. Landslides 2020, 17, 2373–2383. [Google Scholar] [CrossRef]
- Kiesel, J.; Schmalz, B.; Brown, G.; Fohrer, N. Application of a hydrological-hydraulic modelling cascade in lowlands for investigating water and sediment fluxes in catchment, channel and reach. J. Hydrol. Hydromech. 2013, 61, 334–346. [Google Scholar] [CrossRef][Green Version]
- Wei, Z.L.; Xu, Y.P.; Sun, H.Y.; Xie, W.; Wu, G. Predicting the occurrence of channelized debris flow by an integrated cascading model: A case study of a small debris flow-prone catchment in Zhejiang Province, China. Geomorphology 2018, 308, 78–90. [Google Scholar] [CrossRef]
- Tillery, A.C.; Rengers, F.K. Controls on debris-flow initiation on burned and unburned hillslopes during an exceptional rainstorm in southern New Mexico, USA. Earth Surf. Process. Landf. 2020, 45, 1051–1066. [Google Scholar] [CrossRef]
- RAMMS. Available online: https://ramms.slf.ch/en/modules/debrisflow/theory/erosion.html (accessed on 25 September 2022).
- Takahashi, T. Debris Flow. Annu. Rev. Fluid Mech. 1981, 13, 57–77. Available online: http://dx.doi.org/10.1146/annurev.fl.13.010181.000421 (accessed on 1 January 2020).
- HEC. HEC-RAS 2D User’s Manual v6.1. 2021. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/r2dum/latest (accessed on 25 September 2022).
- Gibson, S.; Moura, L.Z.; Ackerman, C.; Ortman, N.; Amorim, R.; Floyd, I.; Eom, M.; Creech, C.; Sánchez, A. Prototype Scale Evaluation of Non-Newtonian Algorithms in HEC-RAS: Mud and Debris Flow Case Studies of Santa Barbara and Brumadinho. Geosciences 2022, 12, 134. [Google Scholar] [CrossRef]
- Open TELEMAC-MASCARET. Available online: http://www.opentelemac.org/index.php/modules-list/17-telemac-2d-presentation (accessed on 25 September 2022).
- Smolders, S.; Leroy, A.; Teles, M.J.; Maximova, T.; Vanlede, J. Culverts modelling in TELEMAC-2D and TELEMAC-3D. In Proceedings of the XXIIIrd TELEMAC-MASCARET User Conference 2016, Paris, France, 11–13 October 2016; pp. 21–33. [Google Scholar]
- Rosatti, G.; Begnudelli, L. Two-dimensional simulation of debris flows over mobile bed: Enhancing the TRENT2D model by using a well-balanced Generalized Roe-type solver. Comput. Fluids 2013, 71, 179–195. [Google Scholar] [CrossRef]






| Area (km²) | H Min (m a.s.l.) | H Max (m a.s.l.) | H Mean (m a.s.l.) | Mean Slope (°) | Risola Channel Length (km) | Risola Channel Mean Slope (°) | N° Melton (-) |
|---|---|---|---|---|---|---|---|
| 2.80 | 833 | 1584 | 1185 | 16 | 4.46 | 7 | 0.48 |
| FLO-2D Parameter | Rainfall | G-A Input Data | |||||
|---|---|---|---|---|---|---|---|
| Soil Properties | Additional Parameter (Land Use) | ||||||
| 5 | Rain (mm) | Dist. | (mm/h) | 140 | Impervious areas (%) | Dist. | |
| (s/m1/3) | Dist. | (mm) | 30 | Initial abstraction (mm) | Dist. | ||
| (m) | 0.0012 | (-) | 0.35 | ||||
| 0.5 | |
| (°) | 38 |
| (-) | 0.65 |
| (-) | 1.65 |
| (-) | 5 |
| (m/m) | 0.03 |
| (-) | 9.78 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaddii, M.; Rosatti, G.; Zugliani, D.; Marzini, L.; Disperati, L. Back-Analysis of the Abbadia San Salvatore (Mt. Amiata, Italy) Debris Flow of 27–28 July 2019: An Integrated Multidisciplinary Approach to a Challenging Case Study. Geosciences 2022, 12, 385. https://doi.org/10.3390/geosciences12100385
Amaddii M, Rosatti G, Zugliani D, Marzini L, Disperati L. Back-Analysis of the Abbadia San Salvatore (Mt. Amiata, Italy) Debris Flow of 27–28 July 2019: An Integrated Multidisciplinary Approach to a Challenging Case Study. Geosciences. 2022; 12(10):385. https://doi.org/10.3390/geosciences12100385
Chicago/Turabian StyleAmaddii, Michele, Giorgio Rosatti, Daniel Zugliani, Lorenzo Marzini, and Leonardo Disperati. 2022. "Back-Analysis of the Abbadia San Salvatore (Mt. Amiata, Italy) Debris Flow of 27–28 July 2019: An Integrated Multidisciplinary Approach to a Challenging Case Study" Geosciences 12, no. 10: 385. https://doi.org/10.3390/geosciences12100385
APA StyleAmaddii, M., Rosatti, G., Zugliani, D., Marzini, L., & Disperati, L. (2022). Back-Analysis of the Abbadia San Salvatore (Mt. Amiata, Italy) Debris Flow of 27–28 July 2019: An Integrated Multidisciplinary Approach to a Challenging Case Study. Geosciences, 12(10), 385. https://doi.org/10.3390/geosciences12100385










