Abstract
We forecast the impact that the lahars triggered on the summit of the Cotopaxi volcano in Ecuador would have upon the Hidroagoyán Dam should an 1877-type catastrophic eruption occur nowadays, with disastrous implications for the energy production of Ecuador. The Cotopaxi’ lahars have been simulated with the use of different computational models, yet none of them were so extended as to map their entire path to the dam. To fill this gap, we applied a version of the semi-empirical Cellular Automata LLUNPIY model to simulate primary and secondary lahars flowing from the summit of the Cotopaxi volcano until they reach the Hidroagoyán Dam in Baños. This version of LLUNPIY accounts for the triggering event by pyroclastic bombs and has already been validated by its successful simulation of the northbound 1877 cataclysmic lahars of the Cotopaxi volcano. The likely consequences of a similar disaster are discussed considering present territorial conditions. Computer simulations of natural hazards of this type represent a powerful tool that can be used when planning for the mitigation of environmental and social risks.
1. Introduction
Many natural events and phenomena, whose dynamics are highly complex as a result of the local interactions of their constituents, can be described and simulated according to the computing paradigm known as Cellular Automata (CA) [1,2]. For example, complex surface flows have been studied by adopting a modelling and simulation (MS) semi-empirical methodology [3]. The applications of MS are of different types, among them being lava flows [4], debris/mud/granular flow [5], soil erosion due to rainfall [6], pyroclastic flows [7], lahars [8], snow avalanches [9], variably saturated flow in porous media [10], and even forest fires [11]. The particular focus on natural hazards is mainly due to the need for the application of reliable models in the mitigation of the territorial and environmental disasters that they can cause. A considerable effort by researchers in this field has been devoted to the forecast and study of lahars near volcanic areas, as this is one of the most devastating natural phenomena when material losses and fatalities are taken into account.
Lahars, also called volcanic debris flows, result from the mixing of processes of water from several sources and pyroclastic sediments. They are characterized by their high density and viscosity, and speeds of up to 60–70 km/h when they run down steep volcanic slopes. Whenever the local orography assists them, they may travel huge distances before stopping as they are channeled along the bottom of riverine valleys [12]. The ultimate scale of these events is determined by the total amount of available water and volcanic sediments [13]. The initial triggering flow may be relatively scanty [12], yet the subsequent lahar can expand in volume and mass very quickly while running down the volcanic slopes, entraining enormous quantities of loose sediments, rocks, and water. All this produces an increase in the lahar’s original size by several orders of magnitude. Along the steeper upper tracts of volcanoes, the triggered flow adds water from any source—rainfalls, creeks, and torrents that come directly or indirectly from the melting of glaciers and snow fields. The rapidly forming lahars unstoppably erode and entrain all volcanic tephra debris deposited by previous eruptive episodes, even loading boulders of huge dimensions and masses. When entering regions of decreasing slopes, the lahars sprawl out and start to release and deposit the coarsest sediment components. The motion of a lahar is that of a dense mud or concrete flow carrying constituents of very different sizes, from thin clay particles to huge rocks and boulders up to a dozen meters in diameter [14].
Few flows on earth have the capability of the lahars in terms of destructive power. They can annihilate downstream villages and towns in a few seconds, killing hundreds or even thousands of unaware inhabitants. Lahars can irreversibly alter entire landscapes, wreaking havoc on infrastructures of strategic importance or burying crucial agricultural lands underneath several layers of detritus and rubble [15]. Lahars are identified as primary when the water required for its formation and development is supplied directly by the volcanic activity or eruption. In this case, lava and pyroclastic flows are the agents of melting snow fields and glaciers, or are responsible for breaking barriers and dikes that impound natural water catchments.
In order to model the behavior of lahars and the risks posed to downstream communities [16], many approaches that are different from the paradigms based on CA [8] have been adopted. These include approximating numerical methods of complex physical behavior of lahar based on Partial Differential Equations [17,18], empirical models based on smart correlations of phenomenon observables [19,20], and simple rheological and hydrological models that assume acceptable simplifications as composition-independent flow behavior or Newtonian flow behavior [21,22].
LLUNPIY (an acronym for Lahar modelling by Local rules based on an UNderlying PIck of Yoked processes, and comes from the Quechua word “llunp’iy”, which means flood) is a three-dimensional model that delivers, in correspondence with each computational step and each CA cell, values of average altitude, lahar thickness, depth of erodible stratum, lahar outflows size, and kinetic head [8,14,15,23,24,25,26]. To reliably simulate primary lahars, it is necessary to introduce well-defined mechanisms of the triggering process in the model. In a former model version of primary lahars [18], the worst-case scenario of the instantaneous melting of white snow and blue ice by a volcanic eruption was considered as the sudden trigger of primary lahars. In this way, the sadly famous 1877 cataclysmic lahars of the Cotopaxi volcano in Ecuador were simulated, and the obtained results were compared with the available historical records of the actual event [27,28].
The occurrence of a new 1877-like Cotopaxi catastrophic eruption cannot be excluded as it is a threat to more than 300,000 persons living within reach of its potential lahars. Cotopaxi is now going through a mild yet worrisome eruptive episode that started in August 2015. For this reason, the volcano is continuously monitored; indeed, it is one of the most surveyed volcanos in the world. Even if the results of the simulation were the best ones in the literature to our knowledge, the model has been extended to the present LLUNPIY-PB version (PB being an acronym for Primary lahars with Bombing triggering). The action of pyroclastic bombs was used in the modeling process in order to obtain a reliable rendition of the actual triggering, i.e., the gradual melting of ice and snow. This model has been successfully validated by the simulation of the 1877 cataclysmic lahars of the Cotopaxi volcano. The potential consequences of the occurrence of a similar disaster have been forecasted, considering the environmental and territorial conditions of present-day Ecuador.
Cotopaxi’s lahars usually take three main geographical directions: southward, northward, and eastward. The southward-bound lahars were simulated by exploiting the predictive capability of LLUNPIY-PB. Such simulations stop just beyond Latacunga, while the lahar, as reported in the contemporaneous chronicles of the 1877 eruption [27,28], actually kept going down its southward-bound path. The flow then turned eastward along the upper Pastaza river’s gorge, bypassing the area of the present Hidroagoyán Dam in Baños and eventually sprawling out into the Amazon lowlands. Additionally, the simulations based on the standard PDEs [18] were not able to bypass Salcedo, which is just beyond Latacunga, in the central Andean altiplano.
The present research represents the first attempt to explore two possible overall scenarios, in which a lahar front from Cotopaxi eventually impacts the Hidroagoyán Dam (whose location is shown in Figure 1) as a consequence of a future, hypothetical, 1877-type eruption of the Cotopaxi volcano. These scenarios were developed after extending previous simulations [29,30], whose outputs are mainly dependent on the chosen values of input parameters such as the thickness of the Cotopaxi glacier.
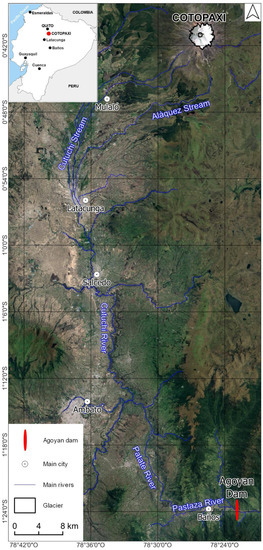
Figure 1.
Google Earth image of the study area.
The miscellanea of aspects implied in a research work such as this demands an effort to orderly present manifoldly interconnected information, ranging from how catastrophic the 1877 Cotopaxi eruption might have actually been, to the technical features of the Hidroagoyán energy production, and to the methodology that needs to be implemented when running CA simulations. In order to smooth the gaps clearly present in the midst of such diverse matters, we have organized the layout of this paper as follows. In the next section, we shortly describe the 1877 eruption of the Cotopaxi volcano. In Section 3, a brief overview of the main technical characteristics of the dam is given. Section 4 summarizes the essential features of the LLUNPIY-PB model. The fifth section is devoted to the simulations and the obtained results. Finally, Section 6 contains a discussion of the results and conclusions.
2. The 1877 Eruption of the Cotopaxi Volcano
On 26 June 1877, Cotopaxi entered an explosive, eruptive episode that would generate immediately after one of the most catastrophic mudflows in the entire history of the volcano. During the eruption tephra, bombs and scoria-rich pyroclastic flows [31] were violently emitted from the vent, causing the melting of enormous chunks of the summit glacier and thus triggering ruinous lahars. Sodiro [27] and Wolf [28], in their poignant first-hand chronicles, reported passage times and extensions of the lahars flowing in different directions, consequently flooding and devastating inhabited nearby areas and agricultural lands. Some later observations estimated that at least 1/10–1/5 of the total volume of the glacier disappeared in a matter of minutes [28].
The water mass, originated by the melting of the glacier, quickly mixed with the erupted pyroclastic material and the pre-existing volcanoclastic materials deposited along the Cotopaxi slopes. The resulting debris flows sprawled across all directions. They poured into the Valle de los Chillos in the north, destroying the villages of Sangolquí and San Rafael and eventually reaching the Pacific Ocean via the course of the Esmeraldas river. The flows along the eastern flanks and the Tambo river valley reached the Amazon basin near the town of Tena. The three main debris flows that eventually headed toward the southern direction are of particular interest for the present research. The provenance of two of them was in the upper catchments of the Río Cutuchi and the Río Saquímala, reaching their converging spot at about 3000 m a.s.l. The third one proceeded along the Río Barrancas-Aláquez upper valley, intercepting the main lahar further south. All the southward and part of the westward-bound upper branches of the lahar flowed into the lower Cutuchi valley, wreaking havoc in the towns of Latacunga and Salcedo. They subsequently moved further, running down the bottom of the deep Pastaza river gorge until they poured into and sprawled across the Amazon basin and the lowlands of the present-day town of Puyo. These lahars possessed speeds between 10 and 30 m/s, depending on the slope gradients, and reached the town of Latacunga city in about 30 min, as local witnesses report [27,28]. If an 1877-type lahar from Cotopaxi bypassed the location of the present-day San Martín bridge, just upstream of the town of Baños, it would immediately after flow into the reservoir of almost two million cubic meters of water impounded by the Hidroagoyán Dam.
3. The Hidroagoyán Dam
Since 1877, the use of territory in Ecuador has utterly changed. Everywhere, the country’s once tiny and scattered villages have grown into fully interconnected towns, thus expanding the agricultural frontier, devoting wide areas to public installations, and building strategic infrastructures such as dams wherever and whenever an opportunity for the massive production of the much-needed hydro energy is given. Unlike in 1877, a new lahar from Cotopaxi, which would have enough energy to reach the upper Pastaza river, could impact the water reservoir impounded by the Hidroagoyán Dam; this dam built in the decade of the 1980s just downstream of the city of Baños. On average, this reservoir receives 120 m3/s of water from the Chambo river and the Cutuchi-Patate river (together draining a total catchment area of 8237 km2), which merge just at the entrance of Baños, thus forming the Pastaza river, a left tributary of the Amazon river. The power production of Hidroagoyán is calibrated to that water flow, which can hugely increase during the rainy season. However, it is often under the threshold, and water is so scarce due to many climatic and anthropogenic causes that the hydroelectric plant does not always receive the required input.
The Hidroagoyán Dam (Figure 2), located at 1°23′55″ S 78°22′39″ O, began its operations in 1988, five years after its construction (the main dam wall, 45 m high and 300 m long, was built using 1.78 × 105 m3 of concrete); it was foreseen to produce hydroelectricity for at least 50 years, until 2038. It is presently run by CELEC E.P. (Corporación Eléctrica del Ecuador), a strategic state company created in 2010. The total water volume of the reservoir is kept at 1.85 × 106 m3, with the reservoir itself being about 2 km long and 100 m wide on average (except for the front area near the dam, where it is about 300 m wide), parallel to the local axis of the upper Pastaza valley. The level of the reservoir is maintained between the minimum operational level at 1645 m a.s.l. and the maximum operational level at 1651 m a.s.l. The rim of the dam is at 1653 m a.s.l., and the reservoir dead volume is below 1645 m, which amounts to 1.09 × 106 m3. In order to produce the required annual average energy of 2520 GWh, the turbined water during 2022 should be 2.72 × 109 m3 on average, i.e., 2.93 m3/kWh; thus, the dam has to process about 7.6 × 105 m3 of water daily between the two operational levels.

Figure 2.
The reservoir of the Hidroagoyán Dam. The dam is visible on the bottom part of the image (courtesy CELEC E.P.).
Whenever the flow of the Pastaza river bypasses worrisome levels, three vertical gates that are 12 m wide and 15 m high can be opened, each of which discharges up to 1260 m3/s of water, thus forcing the maximum surface level of the reservoir to be kept below the dam rim. In addition, two further scour outlet gates in the center of the dam wall, which are routinely operated during cleaning operations in the reservoir, have been specifically designed to protect the hydroelectric plant; their entrance slab is at 1626 m a.s.l., and each one of them allows a discharge of up to 1000 m3/s of water and sediments when completely raised. Hence, once the two scour outlet gates are fully opened, it would take about 15 min to empty the entire reservoir to its bottom. Due to the high concentration of sediments carried by the upper Pastaza river, the cleaning operation is carried out every 20–22 days.
The total energy production of Hidroagoyán is 2520 GWh, which roughly corresponds to 10% of the national demand. This total energy is finally transported and injected into the national network via the Totoras substation, 43 km away.
We are aware, of course, of how difficult it is to employ scientific tools and techniques that could rigorously predict the damages and losses should an 1877-type Cotopaxi lahar impact strategic installations such as the ones just described. Based on previous investigations of the like and on the results obtained when simulating and reproducing the northward-bound lahars triggered by the 1877 Cotopaxi eruption [30], we are confident that the approach that the CA provides would facilitate an informed perception of the main consequences of a similarly disastrous event. As a matter of fact, we are also aware of the implications that the results of this research can originate when they are devoted to plan any emergency and mitigation program. Therefore, it is important to present, even in a succinct manner, the scientific foundations of our CA approach. The hope is to reassure local, regional, and national politicians, leaders, and stakeholders that their strategic agenda of foreseeing and facing emergencies, such as the ones contemplated here, can be developed based on a previous scientific effort that is as prudent as it is sound.
4. The LLUNPIY Model for Primary Lahars Simulation
In this section, we briefly summarize the CA model on which the simulations of the Cotopaxi lahars, which flow along the upper Pastaza river, are based. Readers who are eager to obtain technical and mathematical knowledge about the model are invited to view the extensive bibliography on the subject [8,14,15,23,24,25,26,29,30,32]. CA can be described as a space that is regularly partitioned into cells, each one embedding an identical input/output computing unit. Each cell is characterized by its state; hence, let S be the finite set of the states. The input to each cell is local and determined by the states of its m neighboring cells, where the neighborhood conditions are assigned by a pattern invariant in time and space. At time (step) 0, the cells are in arbitrary states (initial conditions), and the CA evolve, simultaneously modifying the state of all the cells at discrete time intervals. The modification takes place according to local evolution rules, as established in relation to the transition function and depending on the states of the cell itself and its neighbors, namely [16,25].
By their very nature, CA are appropriate for modeling spatially extended and complex natural phenomena such as lahars, whose dynamics is mainly described in terms of local interactions among the parts into which the system can be subdivided.
Lahars are an example of complex systems; they are catastrophic surface flows resulting from a mixture of volcanic debris and water that are triggered on and near volcanoes, therefore making them good candidates for modelling by MCA. The hot material ejected by a volcano eruption can directly generate lahars (primary lahars), e.g., by melting ice fields, when these exist, or sometimes through the collapse of lake or pond rims, which often exist within dormant craters near the summit. Lahars can vertiginously expand their original volumes during their downward courses along ravines, gorges, and valley bottoms by entraining loose rocks and erodible sediments, while water from converging streams and rivers is incorporated. Unconsolidated pyroclastic material can be easily eroded by superficial water forming dilute sediment-laden flows, which can bulk-up to debris flows, whose magnitude will depend upon the volume of both the water and the demobilized material.
The LLUNPIY model we apply here (see [14] for a comprehensive presentation) is a particular two-dimensional MCA with a hexagonal tessellation, and it is defined by the septuple , where:
- is the set of points with integer co-ordinates that identify the regular hexagonal cells, and R is the region where the phenomenon develops;
- is the set of cells that correspond to the glacier, where the primary lahar is triggered after the hot pyroclastic material melts the ice;
- , the neighbourhood index, identifies the geometrical pattern of cells, which determines the evolution of the state of the cell (Figure 3a); the cell is called the central cell with index 0, its adjacent cells are labelled with indexes 1–6 (Figure 3b);
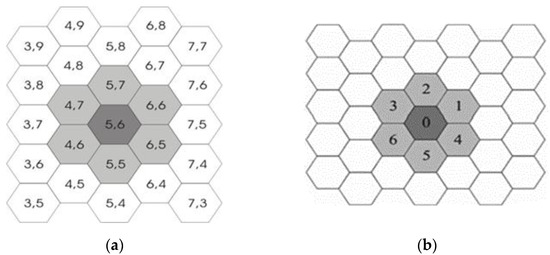 Figure 3. (a) A fraction of the cellular space with neighboring cells surrounding the central cell (5,6) in dark grey; (b) neighboring indexes.
Figure 3. (a) A fraction of the cellular space with neighboring cells surrounding the central cell (5,6) in dark grey; (b) neighboring indexes. - is the finite set of states of the finite automaton embedded in the cell; it is equal to the Cartesian product of the sets of sub-states (Table 1). The third dimension in LLUNPIY is managed by sub-states (Figure 4a); this allows the model to be three-dimensional despite the fact that this CA is two-dimensional;
 Table 1. Sub-states.
Table 1. Sub-states.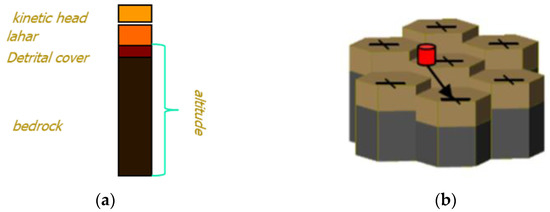 Figure 4. (a) Third dimension sub-states; (b) the outflow from the central cell to an adjacent cell.
Figure 4. (a) Third dimension sub-states; (b) the outflow from the central cell to an adjacent cell. - is the set of global physical and empirical parameters, which account for the general frame of the model and the physical characteristics of the phenomenon (Table 2);
 Table 2. Physical and empirical parameters.
Table 2. Physical and empirical parameters. - is the cell deterministic state transition in , consisting of the following “elementary processes”:
- ○
- , Lahar Outflows Determination and Shift;
- ○
- , Turbulence and Viscosity Correction;
- ○
- , Flow Composition;
- ○
- , Pyroclastic Stratum Mobilization;
- is a stochastic function describing the external influence as “Pyroclastic Bombing” due to the impact of the pyroclastic material upon the glacier (G cells). It describes the change of the state of the ice into a lahar, when the entraining of the pyroclastic mass is included in the initial CA steps. ℕ here refers to the step number.
In summary, the LLUNPIY model simulates lahars in a discretized space-time, where the values of the altitude, erodible soil depth, lahar thickness, kinetic head, and lahar outflows are updated for each cell after each step according to the functions , , , , . A graphical representation of the local elementary processes upon which the mechanisms of the transition function rely can be easily given (Figure 4b).
The execution of an elementary process updates the sub-states: means sub-state of the neighborhood cell with index ; or refers to the central cell; means variation of the sub-state . We now describe in some detail the underlying physical processes that characterize the debris flow.
4.1. Lahar Outflows
The outflow computation is performed in two steps: Firstly, we determine the outflows by applying the Algorithm for the Minimization of Differences (AMD) to the “heights” of the cell neighborhood. Secondly, we calculate the shift of the outflows. AMD theorems allow for a computation of the outflows of a distributable physical observable from the central cell towards the outer cells of the neighborhood in order to minimize their differences [3,33]. In the case of lahars, and for any surface flow as well, all AMD may be normalized to the third dimension since the lahar volume in the cell is simply expressed by its thickness; this is because the cell surface is constant. In addition, AMD application to surface flows involves a type of data alteration regarding the height values in order to account for the run-up effects of kinetic energy. The terms of AMD are the height () of the neighbourhood cells (), whose difference has to be minimized by outflows from the central cell (), and whose sum is equal to the observable quantity distributed amongst the neighboring cells. Here, flows are not yet differentiated into external and internal outflows, and the flow towards the central cell is the remaining quantity in that cell. Formal specifications are as follows:
The application of AMD minimizes the quantity, expressed as follows:
The adherence parameter accounts for the amount of lahar that cannot leave the cell and describes a minimum quantity threshold, below which there can be no flow. It represents the weakest form of deposition. It is not constant for other surface flows, e.g., for lava flows, because in this case, it depends on its fluidity and therefore on its temperature. The barycenter coordinates and of moving quantities are common to the entire lahar inside the cell, whose form is ideally that of a “cylinder” that is tangent to the next edge of the hexagonal cell (Figure 4b). An ideal distance , is considered between the laharitic central cell barycenter and the center of the adjacent cell at its height (altitude plus lahar thickness). The slope with respect to the horizontal level is specified by the angles ; finally, the spatial shift of is computed for the lahar flow according to the following simple formula:
The motion of , equates the barycenter motion of a cylindrical body along a constant slope with a constant friction coefficient , where is the gravity acceleration and the initial velocity . The motion involves three possibilities: (1) only internal flow—the shifted cylinder is completely inside the central cell; (2) only external flow—all the shifted cylinder is inside the adjacent cell; (3) the shifted cylinder is partially internal to the central cell—the flow is divided between the central and the adjacent cell, forming two cylinders with barycenters corresponding to those of the internal and the external debris flow. The kinetic head variation is computed according to the new position of internal and external flows, while the energy dissipation is treated as a turbulence effect in the former elementary process.
4.2. Turbulence and Viscosity Corrections
The previous equation referring to the case of an “inclined plane with friction” represents a kind of approximation that needs to be integrated by a further elementary process. In fact, according to the inclined plane equation, the velocity of the lahar’s front would keep increasing as time passes. It is known that any viscous fluid such as a lahar cannot indefinitely increase its velocity because of the effects of turbulence and internal friction, which dissipate energy on their own. Accordingly, some corrections must be introduced to get a reliable description. The effect of the turbulence and viscosity is heuristically modelled by a proportional kinetic head loss at each LLUNPIY step:
This means that the viscosity imposes a top limit to the kinetic energy, as in the case of ideal flows with constant viscosity and slope [34]. In the present context, the viscosity continuously changes along the path of the lahar as a consequence of both water addition and solid entrainment within the watercourses. To describe such a regime, a limit to the kinetic head was imposed while considering an “average viscosity”. Such a parameter is empirically determined by hypothesizing different values and considering their effects during their variation.
4.3. Flows Composition
When debris outflows are computed, the newly updated situation implies that external flows left the cell, internal flows remain in the cell with different co-ordinates, and inflows (trivially derived by the values of external flows of the neighbouring cells) may occur. The new value of is assigned, considering the balance of the inflows and outflows with the remaining debris within the cell. A kinetic energy reduction is accounted for by the loss of flows, while an increment is given by the inflows. The new value of the kinetic head is deduced from the computed kinetic energy. The determination of co-ordinates is calculated as the average weight of and considering the remaining debris within the central cell, the internal flows, and the inflows.
4.4. Mobilization Effects (Bulking)
When the kinetic head value overcomes an opportune threshold () depending on the soil features and its saturation state, then a mobilization of the detrital cover occurs in proportion to the quantity overcoming the threshold. This takes place in such a way that the detrital cover depth diminishes as the debris thickness increases, which is expressed by the following empirical formula:
The corresponding kinetic head loss is specified according to the following expression:
Simulation input data are: actual DTM/DEM, erodible pyroclastic cover, extension of the Cotopaxi ice cap, duration and frequency of pyroclastic bombs. By modifying the parameters or the input data, LLUNPIY is able to predict several different hazard scenarios, which as a whole represent a reliable forecast of what might happen to the Hidroagoyán Dam and the energy production of Ecuador in the case of a novel eruption of the Cotopaxi volcano.
5. LLUNPIY-PB Simulations
A potential future eruption of the Cotopaxi volcano would impact regions whose condition and use have changed during the last century and a half. On top of the volcano, the extension of the glacier has also considerably been reduced in size with respect to its size in 1877, a factor that must be considered as one of the inputs of the present simulations. Our attempt to foresee and study potential impact scenarios for the Hidroagoyán Dam is based on the parameter calibration and simulations first carried out in [29], which are now extended just beyond the dam. In order to obtain different dynamical evolutions of the lahar flows, we developed two possible scenarios by assuming different values of the glacier thickness as input and by varying the LLUNPIY “kinetic head limit-” parameter. In summary, the two scenarios are as follows: (1) The “S25_125” scenario, where the glacier thickness is a uniform stratum of 25 m, and 125 m; (2) The “S50_500” scenario, where the glacier thickness is a uniform stratum of 50 m, and 500 m. Of course, the idea underlying the shaping of these two scenarios is that of studying the consequences caused by a “minor” S25_125 eruptive episode vs. the ones following a “major” S50_500 eruption, and this is so just because it is difficult to foresee a priori the actual magnitude and intensity of Cotopaxi’s potential reactivation process.
The glacier planimetric extension is approximately equal to 13.5 km2, as obtained from the 2020 Google Earth satellite image [35]. Furthermore, the following values of input data have been adopted: (i) A 5 m thick uniform erodible pyroclastic stratum. (ii) SRTM elevation data (Shuttle Radar Topography Mission, in orbit in February 2000) with a spatial resolution of 1 arc-second, approximately 30 m at ground level, downloaded from NASA (National Aeronautics and Space Administration) servers [36]. The linear vertical absolute height error is less than 16 m, while the linear vertical relative height error is less than 10 m [37]. This data set, which reproduces the actual morphology of the study area, enables the prediction of hazardous scenarios for those regions potentially vulnerable to a future event such as the one that occurred in June 1877. (iii) The fall of 50 pyroclastic bombs per step during the first 10,000 steps. (iv) Each pyroclastic bomb melts 15 m of ice underneath the impact cell; the fall of the pyroclastic bombs is random and a glacier 25 m thick is considered. A bomb that hits a hexagonal cell produces a water volume of about 11,700 m3; if a second bomb were to hit the same cell, the volume would be around 7800 m3 (considering a remaining 10 m ice thickness). We stress the fact that the glacier melting is neither a complete nor a homogeneous process. It is rather a local and cumulative process in which each bomb, melting the ice beneath the point of impact, generates an amount of water that initially hollows out deep holes and gorges. Subsequently, on its way down the steepest slopes, it converges into flows capable of entraining sediments and boulders which may cut their path towards the valley bottoms. The LLUNPIY simulation parameters are listed in Table 3.

Table 3.
Parameters of LLUNPIY-PB simulations.
Both of the 1877-like eruptive simulated scenarios assume that the melting of the Cotopaxi icecap is triggered by the impacts of the free-falling pyroclastic bombs after they have been progressively ejected upwards by an explosive eruption. This modeling arrangement is adopted to produce the gradual melting of the glacier; hence, the lahar flows in proportion to the amount of available water and to the eroded and entrained pyroclastic sediments. These outlines are consistent with the historical chronicles and field data, since the 1877 deposits are essentially pyroclastic. In general, Cotopaxi’s eruptions may eject not only bombs, but also lava flows, pyroclastic flows, and fragments of lava (tephra, lapilli, etc.), all of which carry significant thermal energy. It is likely that the 1877 Cotopaxi eruption consisted of an entire variety of pyroclastic bombs and flows, all of them systematically melting the glacial cap. We recall, however, that the melting process itself was not instantaneous but rather gradual, although relatively quick, as the first-hand historical reports fairly narrate (see [27,28]). Unsurprisingly, we can consistently find in the literature that several approaches have been adopted when a particular lahar’s triggering process was adopted on top of the eruptive Cotopaxi. For instance, the LAHARZ simulations carried out in [38] assumed a “Many Sources” hypothesis, namely that the southward lahars that eventually formed at the bottom of the Cotopaxi cone were the result of the confluence of those triggered in the upper parts of the three main southern drainage systems (streams: Cutuchi, Sasquímala, and Aláquez). Improved simulations [18] were carried out, taking into account the erosion and considering the lahar that was thus formed at the base of the volcano as the initial lahar. An “Instantaneous Melting” hypothesis, when the ice cap suddenly melting to a fixed depth occurs simultaneously with the eruption, underlies the simulations presented in [24,26]. As for the present study, the assumption that solely pyroclastic bombs are the melting triggers of the Cotopaxi ice cap is clearly a simplification of the actual process. Indeed, it is not within our purposes— at least not now—to provide a detailed description of exactly how the thermal energy transfer to the icecap might occur (which was presumably due to pyroclastic bombs of different sizes and temperatures and lava flows as well). What we need is a triggering process that mimics a gradual yet quick melting of the upper glacier, something that we can achieve by assuming the action of pyroclastic bombs of identical constant size that randomly hit the surface of the glacier.
As expected, the two scenarios lead to different results, both qualitatively and quantitatively. More specifically, the S25_125 simulation (Figure 5a) predicts that after 10,000 steps, i.e., after 10 min and 50 s, the water melted by the pyroclastic bombardment and mixed up with the sediments is already organized into significant debris flows that have reached the base of the volcano, essentially at about 3500 m a.s.l., following the courses of the local impluvia. The maximum value of lahar thickness, which is almost 108 m, can be found in the upper valley of the Aláquez stream, where the flow is naturally confined by the steep walls of the very deep gorge. It does not exceed 40 m elsewhere. The erosion of the pyroclastic sediments reaches its maximum intensity in the deepest ravines, indicating that there is a very high flow of energy.

Figure 5.
LLUNPIY-PB simulations corresponding to a gradual melting scenario of the 2020 icecap due to pyroclastic bombs. The maximum thickness reached by the lahar in each cell is reported from the minimum (higher than zero, nearly zero) to the maximum value according to the color bar. (a) The S25_125 scenario; (b) the S50_500 scenario. The Hidroagoyán area, seen within the red dashed outline, is magnified in Figure 6.
On the other hand, the S50_500 simulations (Figure 5b) might correspond to a more plausible eruptive aftermath, although that of a more catastrophic scale. In fact, if they substantially indicate a trend that is qualitatively similar to that of the S25_125 simulations, the invaded areas will now be clearly wider, and the maximum height of the surface flows will have reached the higher 131 m value within the same deep gorge in the upper valley of the Aláquez stream.
About 10 km downstream of the town of Mulaló, the catchments from the upper western parts of the Cotopaxi volcano converge to form the Cutuchi stream valley. Such an orography gives rise to a single-body lahar of large proportions, consistently visible in both scenarios. The S25_125 scenario predicts that the front of the lahar would reach the current suburbs of the city of Latacunga (step 75,000) in 1 h and 20 min after the pyroclastic bombing starts, travelling with an average speed of about 11 m/s and overflowing densely urbanized areas between the Pumacunchi and the Cunuyacu streams. According to the S50_500 scenario, the first flows would reach Latacunga in 59 min, travelling with an average speed of about 15 m/s, and invading, on the hydrographic left of the Cutuchi river, a wide portion of the city that was spared in the previous scenario.
The S25_125 scenario foresees that about 7 h after the triggering of the lahar (step 400,000), the laharitic front would reach the confluence of the Patate and the Chambo rivers, which form the upper Pastaza river, and about 43 min later, having skirted the city of Baños on the lower slopes of the Tungurahua volcano, the lahar would impact and override the Hidroagoyán Dam (Figure 6a,b).

Figure 6.
Magnification of the Hidroagoyán Dam area. The lahar observables, as predicted by the simulations, are graphically reported, namely Thickness, Maximum Thickness, and Erosion. Panels (a–c) correspond to the S25_125 observables; panels (d–f) correspond to the S50_500 observables, respectively.
The average velocity reached by the flows between the base of the glacier and the dam is predicted to be 5 m/s. When the lahar hits the dam, the flow’s height will not exceed 15 m, and its speed will be about 20 m/s.
On the other hand, according to the S50_500 scenario (Figure 6d,e), the flows would impact the dam 5 h and 40 min (step 320,000) after their triggering, endowed with an average velocity of about 7 m/s. When it hits the dam, the flow’s maximum thickness will be 22 m, and the flow speed is predicted to be approximately 24 m/s.
We emphasize that near Baños, and common to both scenarios (Figure 6c,f), the lahar does not display a notable bottom erosive capacity. The erosion, occurring only along the almost vertical embankments of the Pastaza River canyon, is more intense in the S50_500 simulation. The river bed erosion resumes in correspondence with the Hidroagoyán Dam and beyond, which is most likely a consequence of the increasing gradient downstream of the dam. It appears that the S50_500 scenario is best suited to describe, in terms of arrival times and heights of the flows, the actual historical events reported by the chronicles of the 1877 Cotopaxi eruption [27,28]. Nevertheless, the two scenarios similarly map the lahar’s route every time the debris flows are confined within narrow gorges, following the path of the local waterways. On the other hand, the heights reached by the flows are consistently distinct, because the total volumes of the moving surface flows are systemically different in the two scenarios. Correspondingly, noticeable differences are evident in terms of the vastness of the flooded areas when the lahars predicted by the two scenarios invade almost-flat regions, especially those in proximity to Latacunga, where we can appreciate a significant range in terms of the front width of the invading lahar in the two scenarios.
We stress that no consideration was made with regard to the structural resistance of the dam, an issue that would deserve its own study. Our main focus was the study of the principal dynamical features of the lahar motion along the Cutuchi and upper Pastaza rivers. Thus, the dam is treated as “non-erodible soil”, and the debris flows would bypass it if endowed with sufficient kinetic energy. Nevertheless, it is not difficult to foresee that such an impact would damage, in whole or in part, the Hidroagoyán Dam, which, as seen, is a strategic power infrastructure; this would thus deprive Ecuador of 10% of its national energy production. A brief estimate of the energy transfer during the lahar’s moment of impact against the dam is worthwhile. If the lahar front arrives at the dam with a speed amounting to 20 m/s, and the mass contained in the specific volume moving in one second, i.e., 150 × 103 m3, is assumed to be 225 × 103 tons (after assuming a much diluted lahar of up to 1.5 tons/m3), then the energy transfer in one second, or the released power, would amount to 45 × 106 J. This amount of energy is purely contained within the body of the lahar in motion, which means that the energy due to the bulk of the displaced water originally contained in the reservoir, whose nominal mass is 1.85 × 106 tons, is not considered. This mass would anyway hit the dam wall just a few seconds before the lahar impact, in a sequence of tsunami-like shock waves of considerable proportion. Though we are aware that the dam gates can be raised with sufficient anticipation, we are not sure that such an operation could dilute the energy of the impact in time to guarantee enough protection to the main wall. On the contrary, we cannot exclude a high degree of damage or even the irreversible destruction of the dam infrastructure in any case, with or without the gates opening. However, not only the dam will be in peril, as an assessment of the inhabited areas on the right bank, clearly visible in the photo of Figure 2, demonstrates. Considering that the reservoir will be filled to the maximum operational level at 1651 m a.s.l., the rim of the dam will still be 2 m above the surface of the impounded artificial lake. The water waves generated by the impacting laharitic front would spread not only frontally toward the dam rim, they would also catastrophically inundate the low right bank, wrecking the shores and every accessible landscape. The road visible in Figure 2 could not serve as an evacuation route since it would be cut or closed both upstream and downstream, if not made entirely unpassable by the lahar itself.
6. Comments and Conclusions
In the aftermath of the catastrophic 1877 eruption of the Cotopaxi volcano in Ecuador, the lahars triggered in the summit cone after wreaking havoc in the city of Latacunga flowed into the Pastaza River gorge, eventually reaching the Amazon lowlands. At present, just downstream of the town of Baños, the Hidroagoyán Dam impounds the water of the upper Pastaza River, creating a reservoir of about two million m3, and annually producing 2520 GWh of energy or about the 10% of the national demand of Ecuador. The rationale of the present study is that, should an 1877-scale Cotopaxi eruption occur nowadays, which is not unlikely after the 2015 reactivation of the volcano, lahars that are comparably originated might impact the dam, overwhelming the protective bypass system designed to contain anomalous flood waves from the Pastaza river.
The present preliminary simulation succeeds in describing, for the first time, the flow of the lahars along the Pastaza gorge, reaching the dam in Baños and beyond. The present LLUNPIY-PB version was applied to the description of the dynamics of primary lahars triggered on the summit of the Cotopaxi volcano by pyroclastic bombs (i.e., the gradual melting of the ice/snow cover of the summit of the volcano), which is an improvement of a former version whose main modification consists in triggering the lahars by the instantaneous melting —partial or total—of ice/snow [29]. LLUNPIY-PB demonstrated a high predictive capacity and could be used for hazard assessments, for timely and during quiescent phases, in order to determine the potential path, the areas exposed to the flow inundation, and the impact that lahars may have on strategic public infrastructures such as dams and bridges. Furthermore, LLUNPIY-PB may provide a scientific tool on which the design and installation of an early warning system could be based, e.g., in the form of a wireless sensor network on an active volcano such as Cotopaxi. Such a system would not just monitor any lahar triggering event, but it would also provide information on the lahar’s local arrival times, speeds, and heights—all that should reach the inhabited rural and urban areas that are vulnerable to volcanic hazards in time.
The results of the present research do not claim to be exhaustive, since a truly reliable risk/hazard assessment must assume a range of cases as wide as possible. Nonetheless, we succeeded in showing, for the first time, that the Hidroagoyán Dam lies on the path of potentially catastrophic lahars triggered on the top of the Cotopaxi volcano, should an 1877-type eruption occur nowadays. Before preparing any mitigation plan to reduce or avoid this kind of natural disaster, and by taking into account the complexity of their potential consequences as previously outlined, it is necessary to wisely consider all diverse scenarios. Only then will it be truly possible to devise appropriate, sound measures to reduce, whenever and wherever viable, the impact of the lahar on the Hidroagoyán Dam. At the same time, safety plans for the population can be adopted by, for instance, organizing and testing timely evacuation plans for the areas most exposed to volcanic risks. It is certainly one of our humble ambitions to provide a scientific base for an adequate and reliable tool that could generate hazard maps in case of future Cotopaxi volcano eruptions, and which should eventually be made available to local decision-makers and social stakeholders.
Author Contributions
All the authors contributed, in equal measure, to the implementation of the research, to the analysis of the results, and to the drafting of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the FUCSIE Project (University Forum for Scientific Cooperation between Italy and Ecuador)—Action and Cohesion Plan (PAC) 2014/2020, Specific Objective 10.5—Regional Strategic Project “Calabria Alta Formazione”.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://repositorio.casadelacultura.gob.ec/handle/34000/307; https://www.google.it/intl/it/earth/; https://dwtkns.com/srtm30m/, accessed on 16 September 2022.
Acknowledgments
The preliminary research presented here is part of the activities of FUCSIE (from the Italian “Forum Universitario per la Cooperazione Scientifica tra Italia ed Ecuador”), a wider international program of scientific cooperation amongst Italy’s and Ecuador’s academies and research institutes, of which the University of Calabria, UNACH, and CNR-IRPI are active members. PC thanks ESPOCH for the extraordinary hospitality during the period when the ideas fully developed in this paper were still in their infancy—it was actually when trying to pull over his car in the crowded ESPOCH parking lot that he was stricken by the idea of simulating the impact of a potential southward bound Cotopaxi’s lahar upon the Hidroagoyán Dam. This work is dedicated to the memory of Father Luigi Sodiro S. J. (Vicenza, Italy, 29 May 1836–Quito, Ecuador, 15 May 1909), who witnessed the 1877 Cotopaxi eruption, and whose first-hand report inspired the work presented here.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schiff, J.L. Cellular Automata: A Discrete View of the World; Wiley: Hoboken, NJ, USA, 2008; 280p, ISBN 978-0-470-16879-0. [Google Scholar]
- Chopard, B. Cellular Automata Modeling of Physical Systems. In Encyclopedia of Complexity and Systems Science; Meyers, R., Ed.; Springer: New York, NY, USA, 2009; pp. 865–892. [Google Scholar] [CrossRef]
- Di Gregorio, S.; Serra, R. An empirical method for modelling and simulating some complex macroscopic phenomena by cellular automata. Future Gener. Comput. Syst. 1999, 16, 259–271. [Google Scholar] [CrossRef]
- Crisci, G.M.; Iovine, G.; Di Gregorio, S.; Lupiano, V. Lava-flow hazard on the SE flank of Mt. Etna (Southern Italy). J. Volcanol. Geotherm. Res. 2008, 177, 778–796. [Google Scholar] [CrossRef]
- Lupiano, V.; Machado, G.; Molina, L.P.; Crisci, G.M.; Di Gregorio, S. Simulations of Flow-Like Landslides Invading Urban Areas: A Cellular Automata Approach with SCIDDICA. Nat. Comput. 2018, 17, 553–568. [Google Scholar] [CrossRef]
- D’Ambrosio, D.; Di Gregorio, S.; Gabriele, S.; Gaudio, R. A Cellular Automata Model for Soil Erosion by Water. Phys. Chem. Earth Part B 2001, 26, 33–39. [Google Scholar] [CrossRef]
- Crisci, G.M.; Di Gregorio, S.; Rongo, R.; Spataro, W. PYR: A Cellular Automata Model for Pyroclastic Flows and Application to the 1991 Mt. Pinatubo Eruption. Future Gener. Comput. Syst. 2005, 21, 1019–1032. [Google Scholar] [CrossRef]
- Machado, G.; Lupiano, V.; Avolio, M.V.; Gullace, F.; Di Gregorio, S. A cellular model for secondary lahars and simulation of cases in the Vascún Valley, Ecuador. J. Comput. Sci.-Neth. 2015, 11, 289–299. [Google Scholar] [CrossRef]
- Avolio, M.V.; Errera, A.; Lupiano, V.; Mazzanti, P.; Di Gregorio, S. VALANCA: A Cellular Automata Model for Snow Avalanches. J. Cell. Autom. 2017, 12, 309–332. [Google Scholar]
- Furnari, L.; Senatore, A.; De Rango, A.; De Biase, M.; Straface, S.; Mendicino, G. Asynchronous cellular automata subsurface flow simulations in two- and three-dimensional heterogeneous soils. Adv. Water Resour. 2021, 153, 103952. [Google Scholar] [CrossRef]
- Trunfio, G.A.; Avolio, M.V.; D’Ambrosio, D.; Rongo, R.; Di Gregorio, S. A new Algorithm for Simulating Wildfire Spread Through Cellular Automata. ACM Trans. Model. Comput. Simul. 2012, 22, 6. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Waitt, R.B.; Mastin, L.G.; Begét, J.E. Volcanic-Hazard Zonation for Glacier Peak Volcano; U.S. Geological Survey Open-File Reports Section: Washington, DC, USA, 1995; pp. 1–9. Available online: https://pubs.usgs.gov/of/1995/0499/ (accessed on 7 June 2022).
- Lupiano, V.; Machado, G.; Crisci, G.M.; Di Gregorio, S. A modelling approach with Macroscopic Cellular Automata for hazard zonation of debris flows and lahars by computer simulations. Int. J. Geol. 2015, 9, 35–46. [Google Scholar]
- Lupiano, V.; Chidichimo, F.; Catelan, P.; Machado, G.E.; Molina, L.P.; Straface, S.; Calidonna, C.R.; Crisci, G.M.; Di Gregorio, S. From Examination of Natural Events a Proposal for Risk Mitigation of Lahars by a Cellular Automata Methodology: A Case Study for Vascun Valley, Ecuador. Nat. Hazards Earth Syst. Sci. 2020, 20, 1–20. [Google Scholar] [CrossRef]
- Manville, V.; Major, J.J.; Fagents, S.A. Modeling lahar behavior and hazards. In Modeling Volcanic Processes; Cambridge University Press: Cambridge, UK, 2013; pp. 300–330. [Google Scholar] [CrossRef]
- Pitman, E.; Nichita, C.; Patra, A.; Bauer, A.; Sheridan, M.; Bursik, M. Computing granular avalanches and landslides. Phys. Fluids 2003, 15, 3638–3646. [Google Scholar] [CrossRef]
- Frimberger, T.; Andrade, S.D.; Weber, S.; Krautblatter, M. Modelling future lahars controlled by different volcanic eruption scenarios at Cotopaxi (Ecuador) calibrated with the massively destructive 1877 lahar. Earth Surf. Proc. Land. 2021, 46, 680–700. [Google Scholar] [CrossRef]
- Muñoz-Salinas, E.; Castillo-Rodríguez, M.; Manea, V.; Manea, M.; Palacios, D. Lahar flow simulations using LAHARZ program: Application for the Popocatépetl Volcano, Mexico. J. Volcanol. Geotherm. Res. 2009, 182, 13–22. [Google Scholar] [CrossRef]
- Schilling, S.P. LAHARZ: GIS Programs for Automated Mapping of Lahar Inundation Hazard Zones; U.S. Geological Survey Open-File Reports Section: Washington, DC, USA, 1998; 80p. [CrossRef]
- Costa, J.E. Hydraulic modeling for lahar hazards at cascades volcanoes. Environ. Eng. Geosci. 1997, 3, 21–30. [Google Scholar] [CrossRef]
- O’Brien, J.; Julien, P.; Fullerton, W. Two-dimensional water flood and mudflow simulation. J. Hydraul. Eng. ASCE 1993, 119, 244–261. [Google Scholar] [CrossRef]
- Chidichimo, F.; Di Gregorio, S.; Lupiano, V.; Machado, G.; Molina, L.; Straface, S. Learning from nature: Favoring small lahars formation for hazard mitigation. In Proceedings of the International Meeting Relationality: Between Environmental Awareness and Societal Challenges, Budapest, Hungary, 27–29 May 2016; ISBN 978-88-8286-345-6. [Google Scholar]
- Lupiano, V.; Machado, G.; Crisci, G.M.; Di Gregorio, S. Modelling Fast-Moving Flow-Like Landslides by Cellular Automata: Simulations of Debris Flows and Lahars. In Proceedings of the 8th International Conference on Advances in Environmental and Geological Science and Engineering, Special Session: Analysis and Modelling of Fast-Moving Flow-Like Phenomena (EG’15), Salerno, Italy, 27–29 June 2015. [Google Scholar]
- Machado, G.; Lupiano, V.; Avolio, M.V.; Di Gregorio, S. A Preliminary Cellular Model for Secondary Lahars and Simulation of 2005 Case of Vascún Valley, Ecuador. In Cellular Automata ACRI 2014 Lecture Notes in Computer Science; Wąs, J., Sirakoulis, G.C., Bandini, S., Eds.; Springer: Cham, Switzerland, 2014; Volume 8751, pp. 208–217. [Google Scholar] [CrossRef]
- Machado, G.; Lupiano, V.; Crisci, G.M.; Di Gregorio, S. LLUNPIY, a preliminary extension for simulating primary lahars: Application to the 1877 Cataclysmic Event of Cotopaxi Volcano. In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH’15), Colmar, France, 21–23 July 2015. [Google Scholar] [CrossRef]
- Sodiro, L. Relacion Sobre la Erupcion del Cotopaxi Acaecida el dia 26 de Junio de 1877; Imprenta Nacional: Quito, Ecuador, 1877; pp. 1–40. Available online: http://repositorio.casadelacultura.gob.ec/handle/34000/307 (accessed on 13 June 2022).
- Wolf, T.S. Memoria Sobre el Cotopaxi y su Ultima Erupcion, Acaecida el 26 de Junio de 1877; Imprenta del Comercio: Guayaquil, Ecuador, 1877; pp. 1–48. [Google Scholar]
- Lupiano, V.; Machado, G.; Di Gregorio, S. Revisiting the 1877 Cataclysmic Lahars of Cotopaxi Volcano by a Cellular Automata Model and Implications for Future Events. In Proceedings of the 2nd International Conference on Computer Science and Application Engineering, Hohhot, China, 22–24 October 2018. [Google Scholar] [CrossRef]
- Lupiano, V.; Catelan, P.; Calidonna, C.R.; Chidichimo, F.; Crisci, G.M.; Rago, V.; Straface, S.; Di Gregorio, S. LLUNPIY Simulations of the 1877 Northward Catastrophic Lahars of Cotopaxi Volcano (Ecuador) for a Contribution to Forecasting the Hazards. Geosciences 2021, 11, 81. [Google Scholar] [CrossRef]
- Mothes, P.; Vallance, J. Lahars at Cotopaxi and Tungurahua Volcanoes, Ecuador: Highlights from stratigraphy and observational records and related downstream hazards. In Volcanic Hazards, Risks, and Disasters; Shroder, J.F., Papale, P., Eds.; Elsevier: Amsterdam, The Netherland, 2015; pp. 141–168. [Google Scholar] [CrossRef]
- Machado, G. Cellular Automata for Modeling and Simulating Complex Phenomena: Lahars, Case Studies of Primary and Secondary Lahars in Ecuador. Ph.D. Thesis, Mathematics and Computer Science, Department of Mathematics and Computer Science, University of Calabria, Rende, Italy, 2015. [Google Scholar]
- Avolio, M.V.; Di Gregorio, S.; Spataro, W.; Trunfio, G.A. A Theorem about the Algorithm of Minimization of Differences for Multicomponent Cellular Automata. In Cellular Automata ACRI 2012 Lecture Notes in Computer Science; Sirakoulis, G.C., Bandini, S., Eds.; Springer: Berlin, Germany, 2012; Volume 7495, pp. 289–298. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1987; 558p. [Google Scholar] [CrossRef]
- Google Earth Image, © 2021 Maxar Technologies. Available online: https://www.google.it/intl/it/earth/ (accessed on 1 December 2020).
- 30-Meter SRTM. Available online: https://dwtkns.com/srtm30m/ (accessed on 1 December 2020).
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Pistolesi, M.; Cioni, R.; Rosi, M.; Aguilera, E. Lahar hazard assessment in the southern drainage system of Cotopaxi volcano, Ecuador: Results from multiscale lahar simulations. Geomorphology 2014, 207, 51–63. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).