Analysis of Deformation and Erosion during CME Evolution
Abstract
1. Introduction
2. Modelling Set-Up
3. Detailed Analysis of ICME Evolution
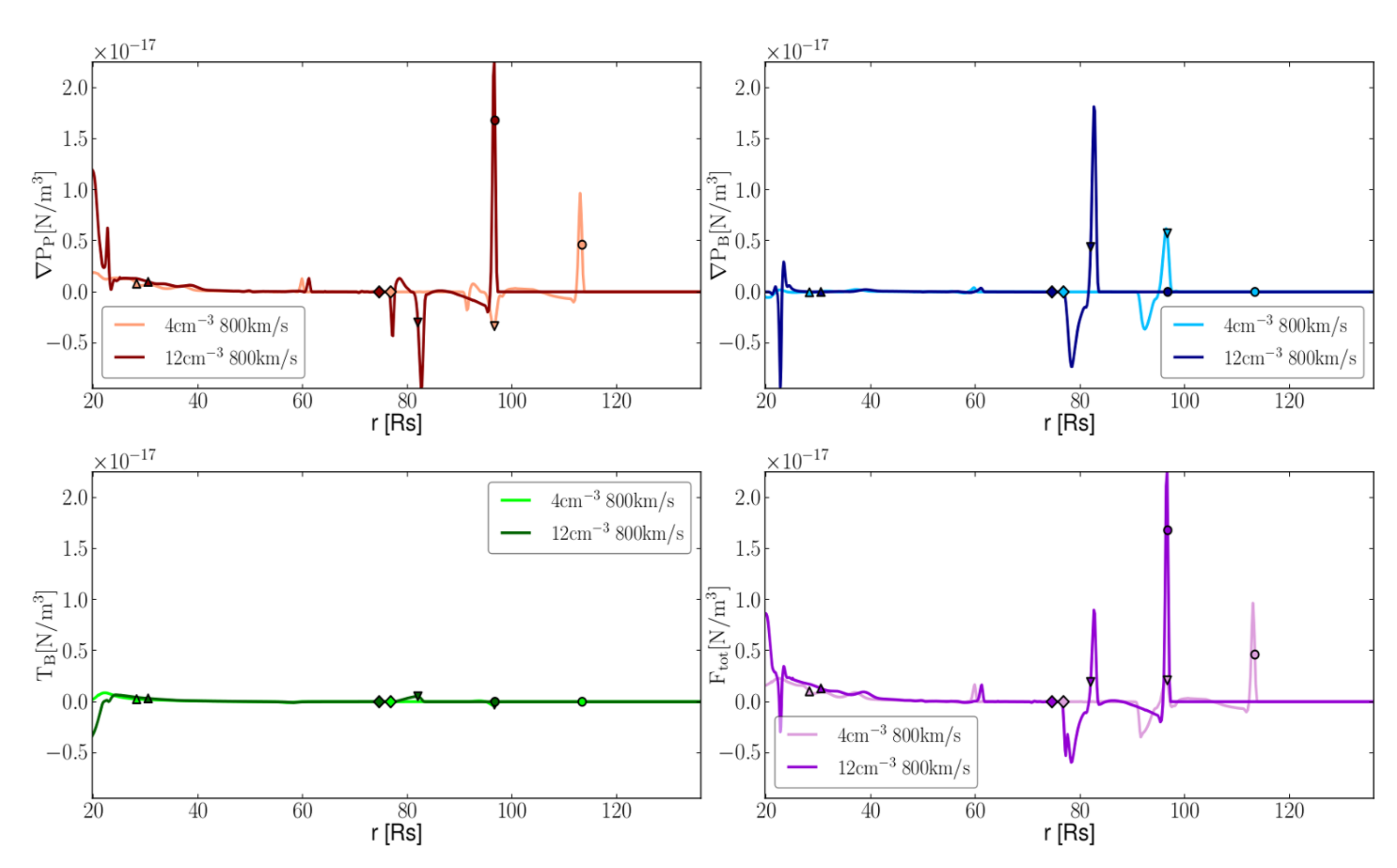
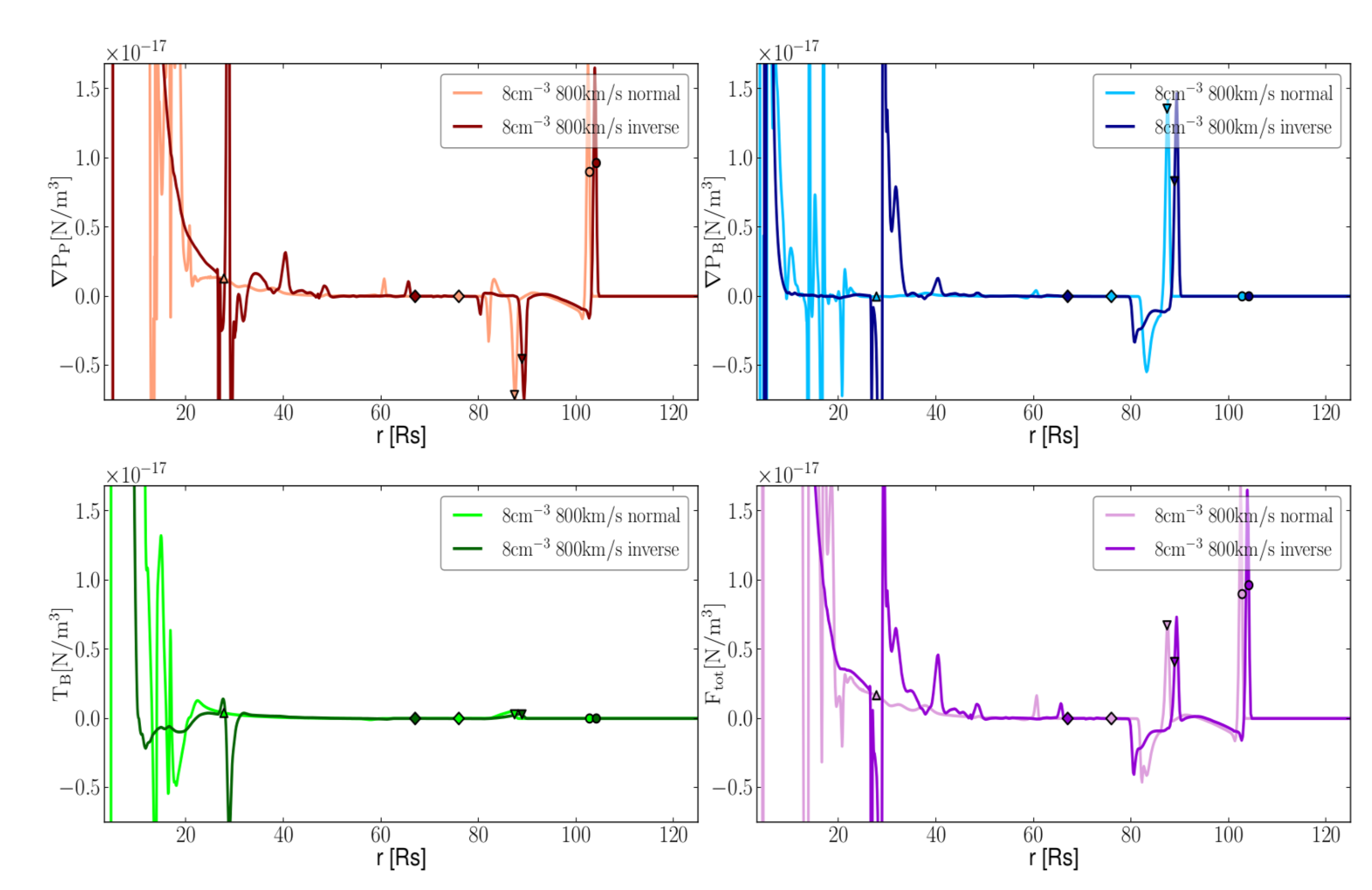
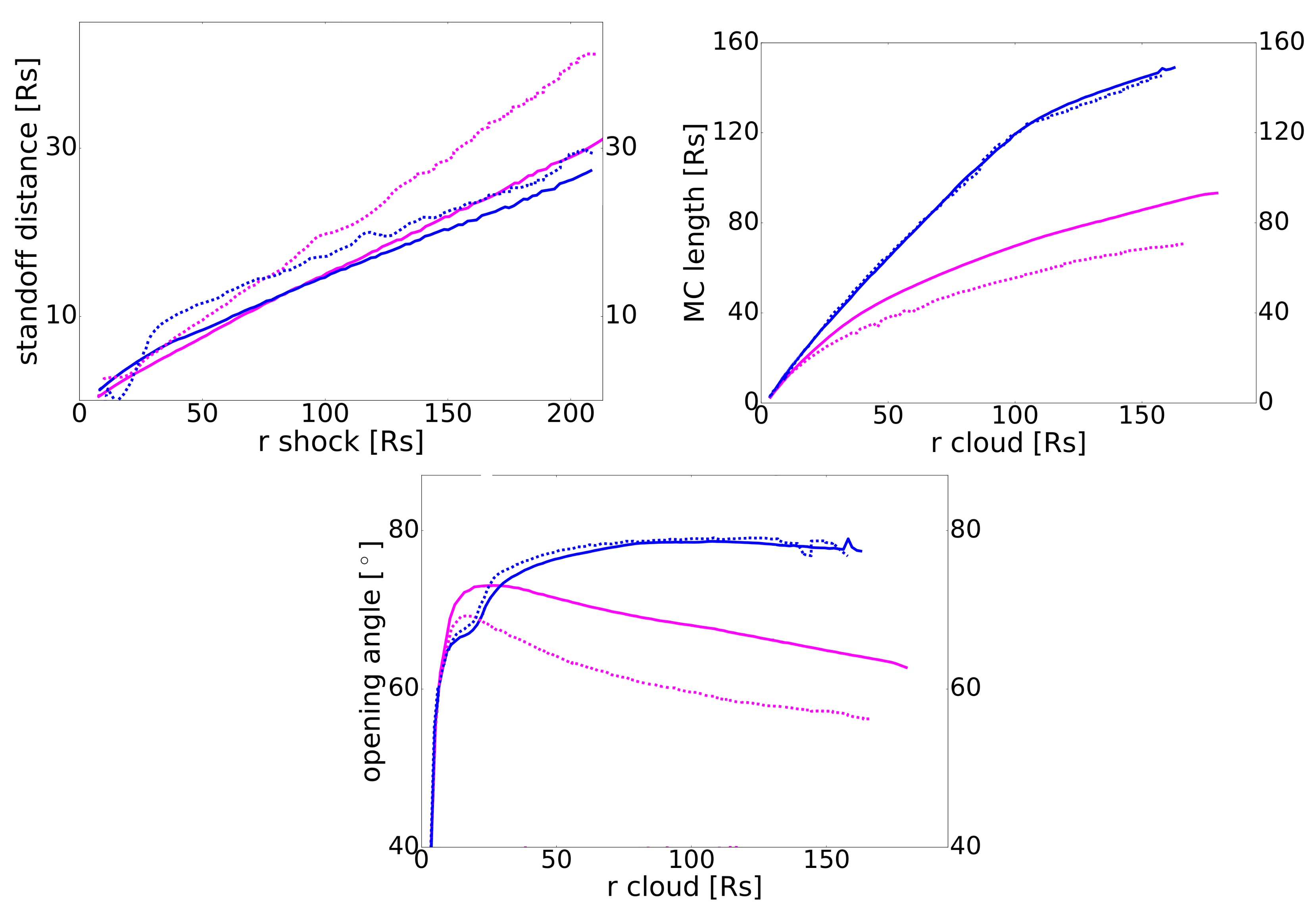
3.1. Thorough Force Analysis
3.1.1. Initial Forces
3.1.2. Force Dynamics
3.1.3. Influence of the Initial Wind Density
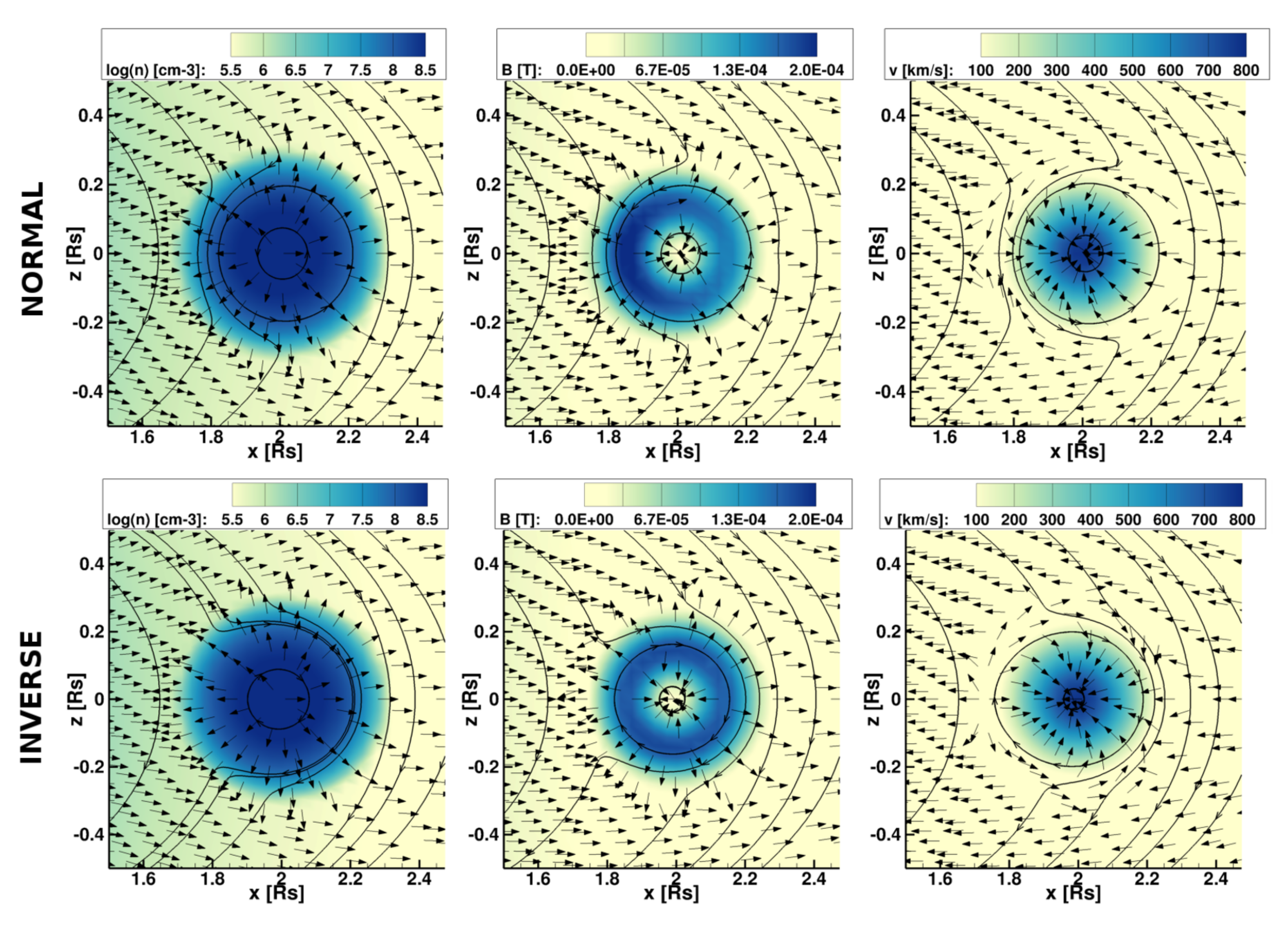
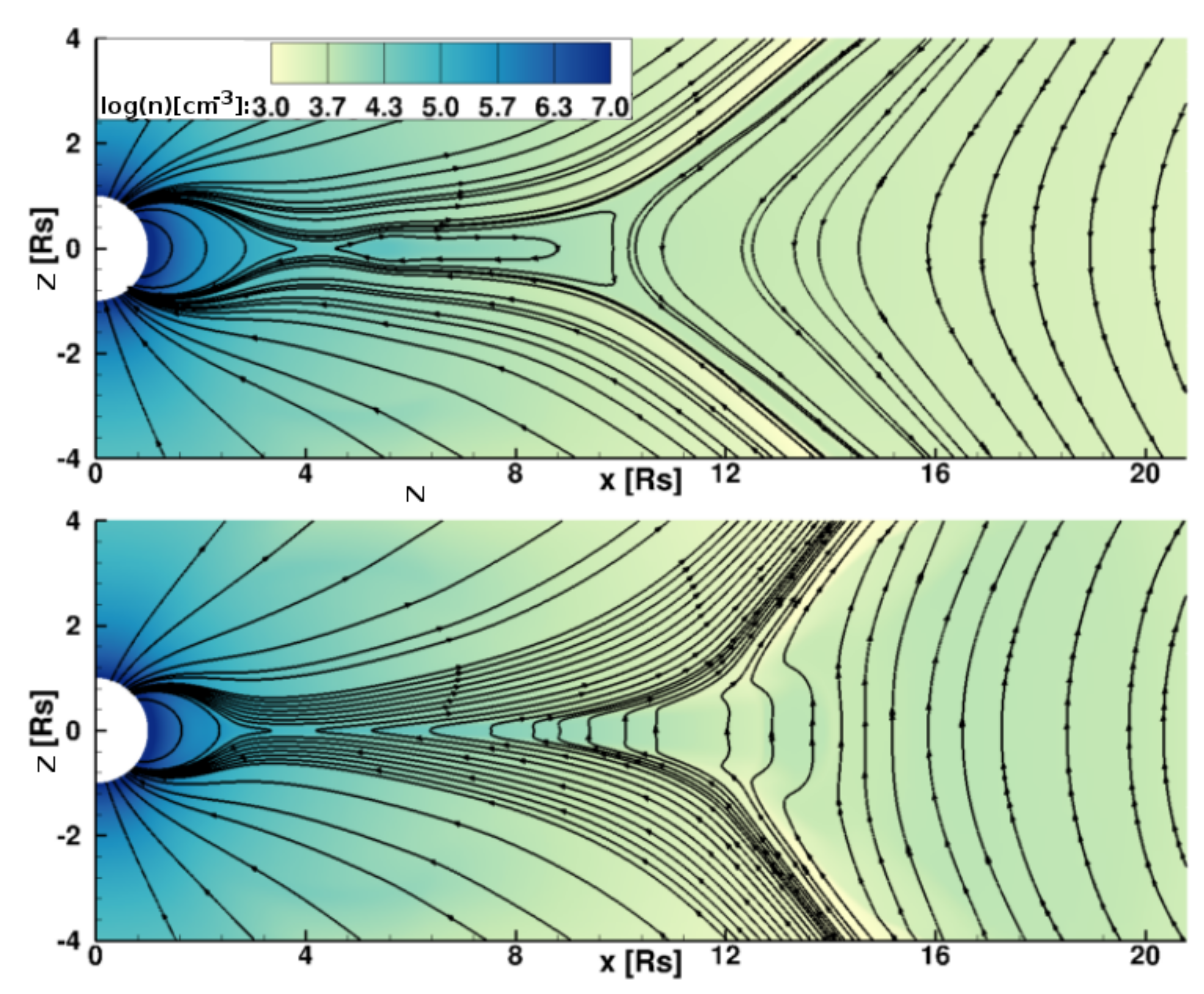
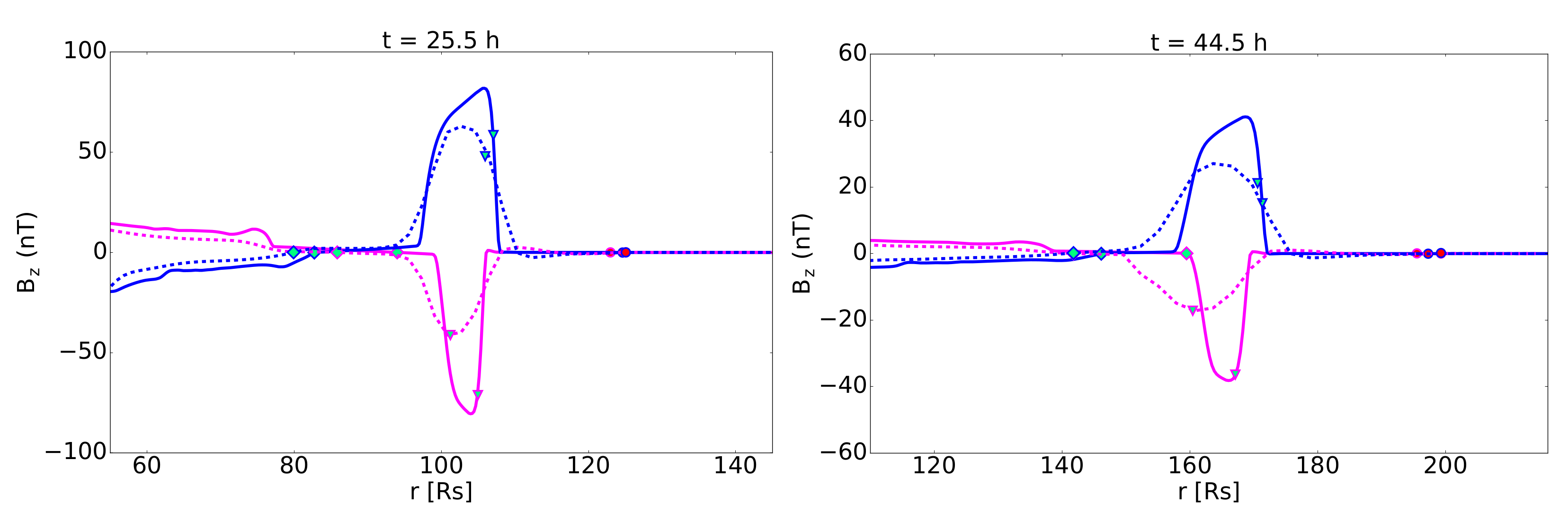
3.2. Erosion
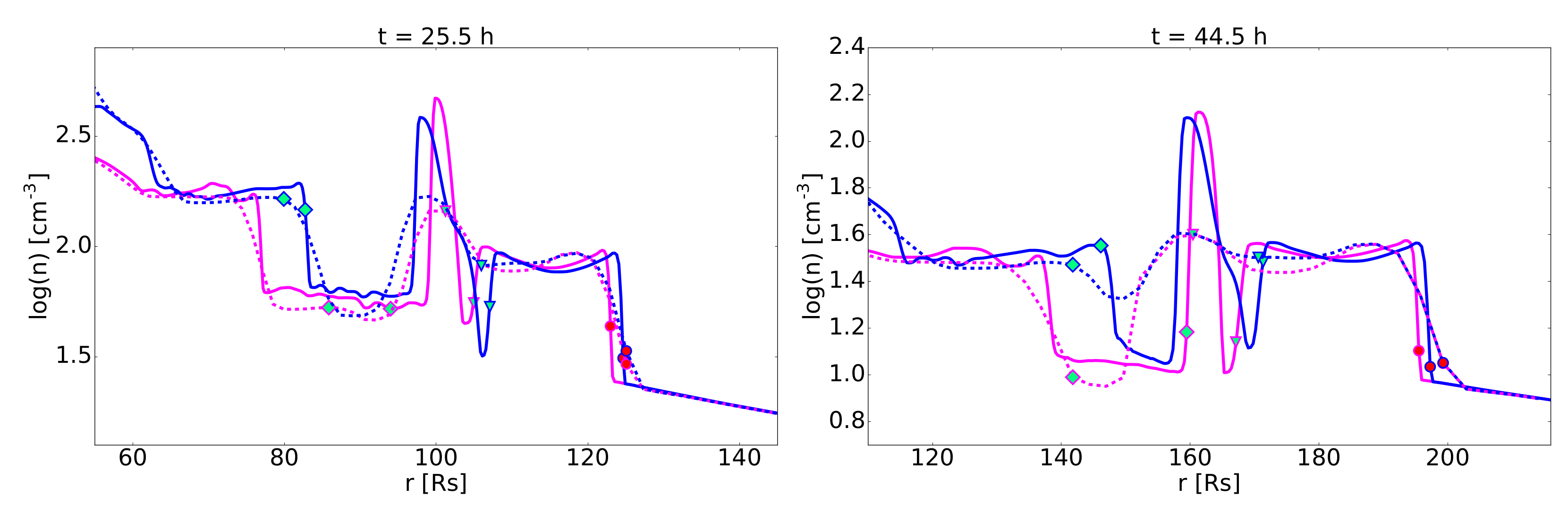
3.2.1. Mass Erosion
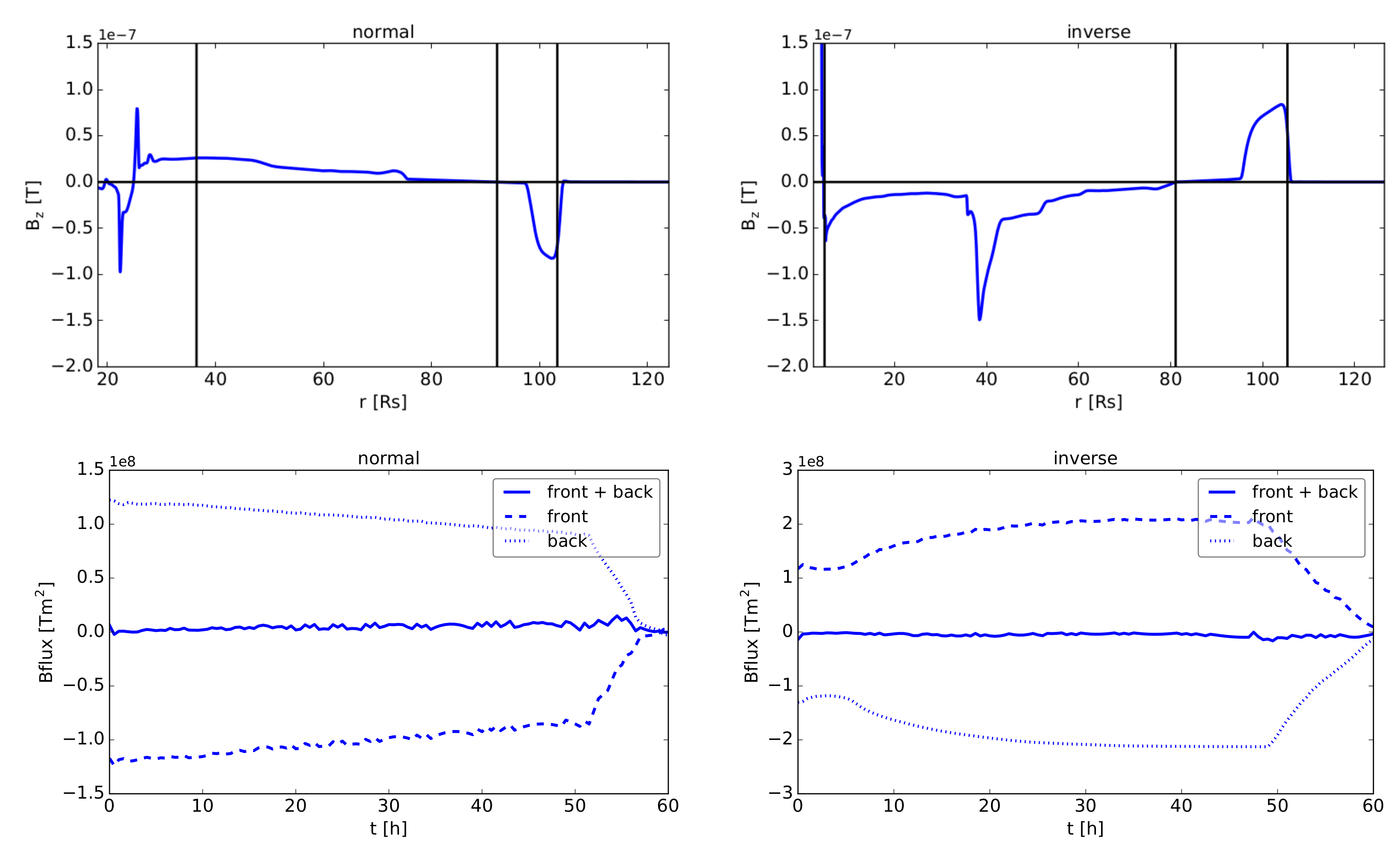
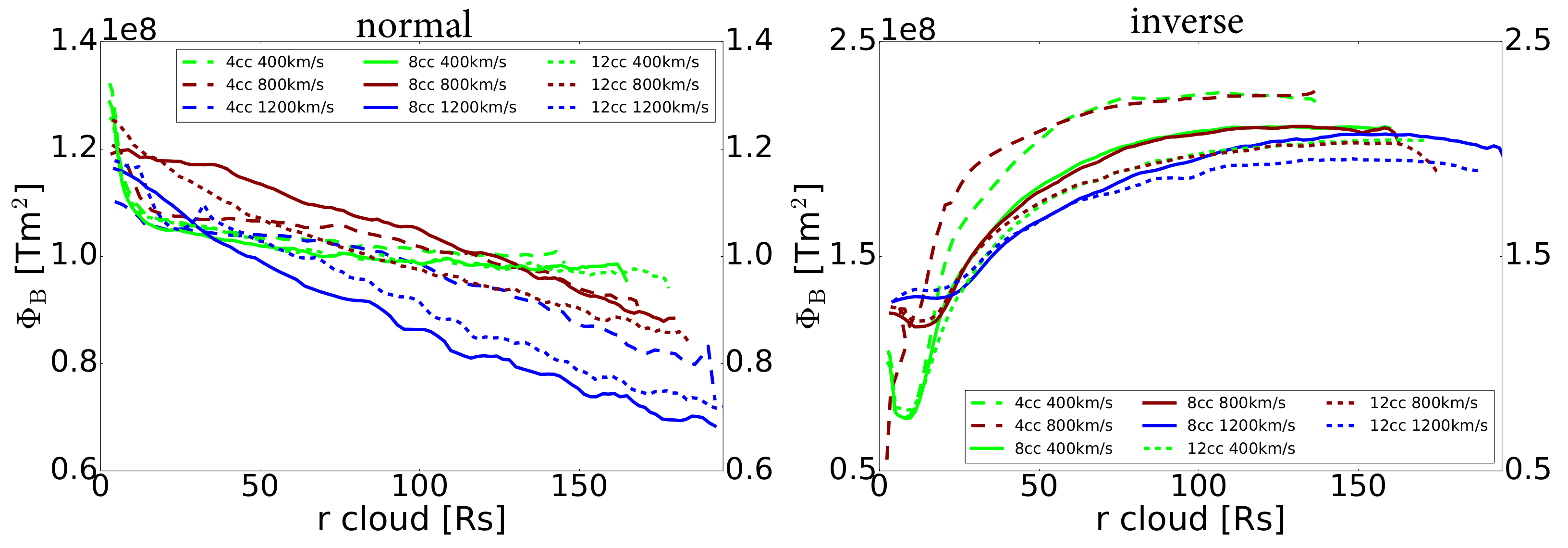
3.2.2. Magnetic Flux Erosion
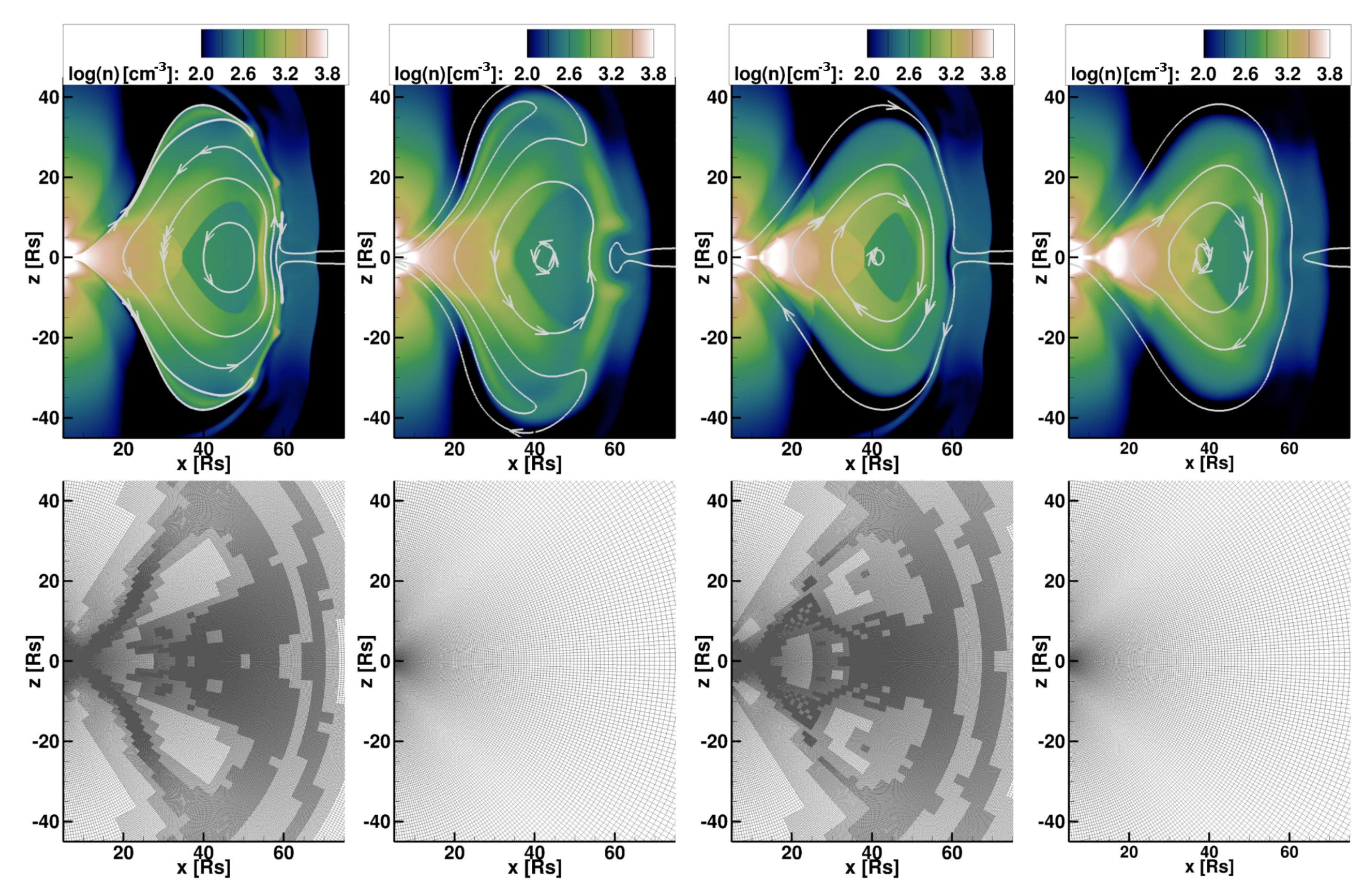
3.3. Effect of Adaptive Mesh Refinement (AMR)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Hosteaux, S.; Chané, E.; Poedts, S. Effect of the solar wind density on the evolution of normal and inverse coronal mass ejections. Astron. Astrophys. 2019, 632, A89. [Google Scholar] [CrossRef]
- Chané, E.; Jacobs, C.; van der Holst, B.; Poedts, S.; Kimpe, D. On the effect of the initial magnetic polarity and of the background wind on the evolution of CME shocks. Astron. Astrophys. 2005, 432, 331–339. [Google Scholar] [CrossRef]
- Chané, E.; van der Holst, B.; Jacobs, C.; Poedts, S.; Kimpe, D. Inverse and normal coronal mass ejections: Evolution up to 1 AU. Astron. Astrophys. 2006, 447, 727–733. [Google Scholar] [CrossRef]
- Chané, E.; Poedts, S.; van der Holst, B. On the combination of ACE data with numerical simulations to determine the initial characteristics of a CME. Astron. Astrophys. 2008, 492, L29–L32. [Google Scholar] [CrossRef][Green Version]
- Jacobs, C.; Poedts, S.; Van der Holst, B.; Chané, E. On the effect of the background wind on the evolution of interplanetary shock waves. Astron. Astrophys. 2005, 430, 1099–1107. [Google Scholar] [CrossRef]
- Savani, N.P.; Shiota, D.; Kusano, K.; Vourlidas, A.; Lugaz, N. A Study of the Heliocentric Dependence of Shock Standoff Distance and Geometry using 2.5D Magnetohydrodynamic Simulations of Coronal Mass Ejection Driven Shocks. Astrophys. J. 2012, 759, 103. [Google Scholar] [CrossRef]
- van der Holst, B.; Poedts, S.; Chané, E.; Jacobs, C.; Dubey, G.; Kimpe, D. Modelling of Solar Wind, CME Initiation and CME Propagation. Space Sci. Rev. 2005, 121, 91–104. [Google Scholar] [CrossRef]
- Mikic, Z.; Linker, J.A. Disruption of coronal magnetic field arcades. Astrophys. J. 1994, 430, 898–912. [Google Scholar] [CrossRef]
- Hosteaux, S.; Chané, E.; Decraemer, B.; Talpeanu, D.C.; Poedts, S. Ultrahigh-resolution model of a breakout CME embedded in the solar wind. Astron. Astrophys. 2018, 620, A57. [Google Scholar] [CrossRef]
- Chané, E.; Poedts, S.; van der Holst, B. CME modeling: The a posteriori approach. In The Dynamic Sun: Challenges for Theory and Observations, Proceedings of the ESPM-11, Leuven, Belgium, 11–16 September 2005; ESA SP-60; Danesy, D., Poedts, S., De Groof, A., Andries, J., Eds.; ESA: Leuven, Belgium, 2005; ISBN 92-9092-911-1. [Google Scholar]
- Török, T.; Downs, C.; Linker, J.A.; Lionello, R.; Titov, V.S.; Mikić, Z.; Riley, P.; Caplan, R.M.; Wijaya, J. Sun-to-Earth MHD Simulation of the 2000 July 14 “Bastille Day” Eruption. Astrophys. J. 2018, 856, 75. [Google Scholar] [CrossRef] [PubMed]
- Manchester, W.B.; Gombosi, T.I.; Roussev, I.; Ridley, A.; de Zeeuw, D.L.; Sokolov, I.V.; Powell, K.G.; Tóth, G. Modeling a space weather event from the Sun to the Earth: CME generation and interplanetary propagation. J. Geophys. Res. Space Phys. 2004, 109, A02107. [Google Scholar] [CrossRef]
- Lugaz, N.; Manchester, W.B.I.; Gombosi, T.I. Numerical Simulation of the Interaction of Two Coronal Mass Ejections from Sun to Earth. Astrophys. J. 2005, 634, 651–662. [Google Scholar] [CrossRef]
- Jin, M.; Manchester, W.B.; van der Holst, B.; Sokolov, I.; Tóth, G.; Mullinix, R.E.; Taktakishvili, A.; Chulaki, A.; Gombosi, T.I. Data-constrained Coronal Mass Ejections in a Global Magnetohydrodynamics Model. Astrophys. J. 2017, 834, 173. [Google Scholar] [CrossRef]
- Gibson, S.E.; Low, B.C. A Time-Dependent Three-Dimensional Magnetohydrodynamic Model of the Coronal Mass Ejection. Astrophys. J. 1998, 493, 460–473. [Google Scholar] [CrossRef]
- Jacobs, C. Magnetohydrodynamic Modelling of the Solar Wind and Coronal Mass Ejections. Ph.D. Thesis, KULeuven, Leuven, Belgium, 2007. [Google Scholar]
- Miller, G.; Turner, L. Force free equilibria in toroidal geometry. Phys. Fluids 1981, 24, 363–365. [Google Scholar] [CrossRef]
- Xia, C.; Teunissen, J.; El Mellah, I.; Chané, E.; Keppens, R. MPI-AMRVAC 2.0 for Solar and Astrophysical Applications. Astrophys. J. 2018, 234, 30. [Google Scholar] [CrossRef]
- Jacobs, C.; van der Holst, B.; Poedts, S. Comparison between 2.5D and 3D simulations of coronal mass ejections. Astron. Astrophys. 2007, 470, 359–365. [Google Scholar] [CrossRef]
- Low, B.C.; Zhang, M. The Hydromagnetic Origin of the Two Dynamical Types of Solar Coronal Mass Ejections. Astrophys. J. 2002, 564, L53–L56. [Google Scholar] [CrossRef]
- Feng, L.; Wang, Y.; Shen, F.; Shen, C.; Inhester, B.; Lu, L.; Gan, W. Why Does the Apparent Mass of a Coronal Mass Ejection Increase? Astrophys. J. 2015, 812, 70. [Google Scholar] [CrossRef]
- Colaninno, R.C.; Vourlidas, A. First Determination of the True Mass of Coronal Mass Ejections: A Novel Approach to Using the Twostereoviewpoints. Astrophys. J. 2009, 698, 852–858. [Google Scholar] [CrossRef]
- Ruffenach, A.; Lavraud, B.; Owens, M.J.; Sauvaud, J.A.; Savani, N.P.; Rouillard, A.P.; Démoulin, P.; Foullon, C.; Opitz, A.; Fedorov, A.; et al. Multispacecraft observation of magnetic cloud erosion by magnetic reconnection during propagation. J. Geophys. Res. Space Phys. 2012, 117, A09101. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosteaux, S.; Chané, E.; Poedts, S. Analysis of Deformation and Erosion during CME Evolution. Geosciences 2021, 11, 314. https://doi.org/10.3390/geosciences11080314
Hosteaux S, Chané E, Poedts S. Analysis of Deformation and Erosion during CME Evolution. Geosciences. 2021; 11(8):314. https://doi.org/10.3390/geosciences11080314
Chicago/Turabian StyleHosteaux, Skralan, Emmanuel Chané, and Stefaan Poedts. 2021. "Analysis of Deformation and Erosion during CME Evolution" Geosciences 11, no. 8: 314. https://doi.org/10.3390/geosciences11080314
APA StyleHosteaux, S., Chané, E., & Poedts, S. (2021). Analysis of Deformation and Erosion during CME Evolution. Geosciences, 11(8), 314. https://doi.org/10.3390/geosciences11080314






