Dispersion Curves of Transverse Waves Propagating in Multi-Layered Soils from Experimental Tests in a 100 m Deep Borehole
Abstract
1. Introduction
2. Mathematical Background
2.1. Waves in Infinite Isotropic Elastic Media
2.2. Waves in an Isotropic Elastic Plane
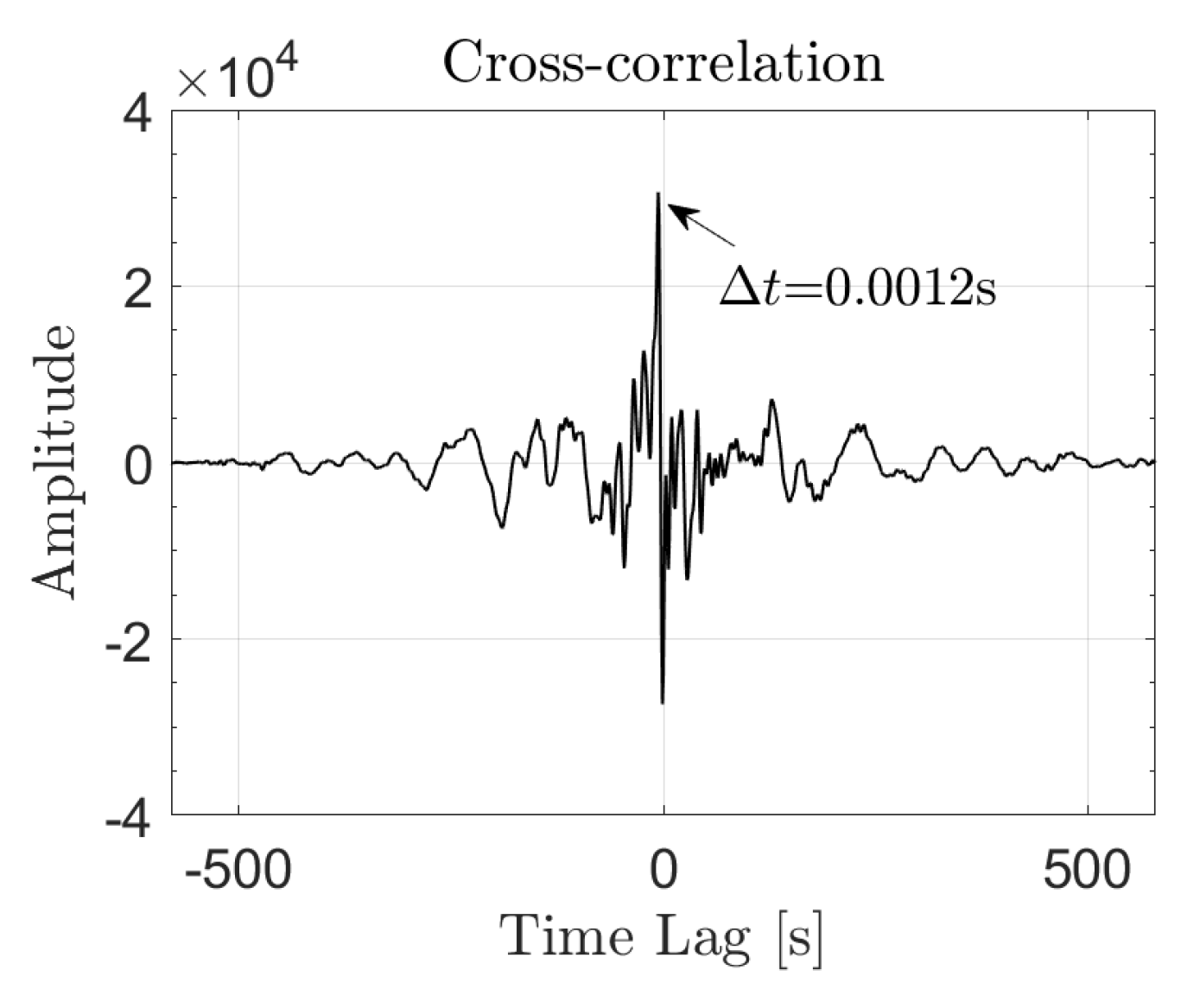
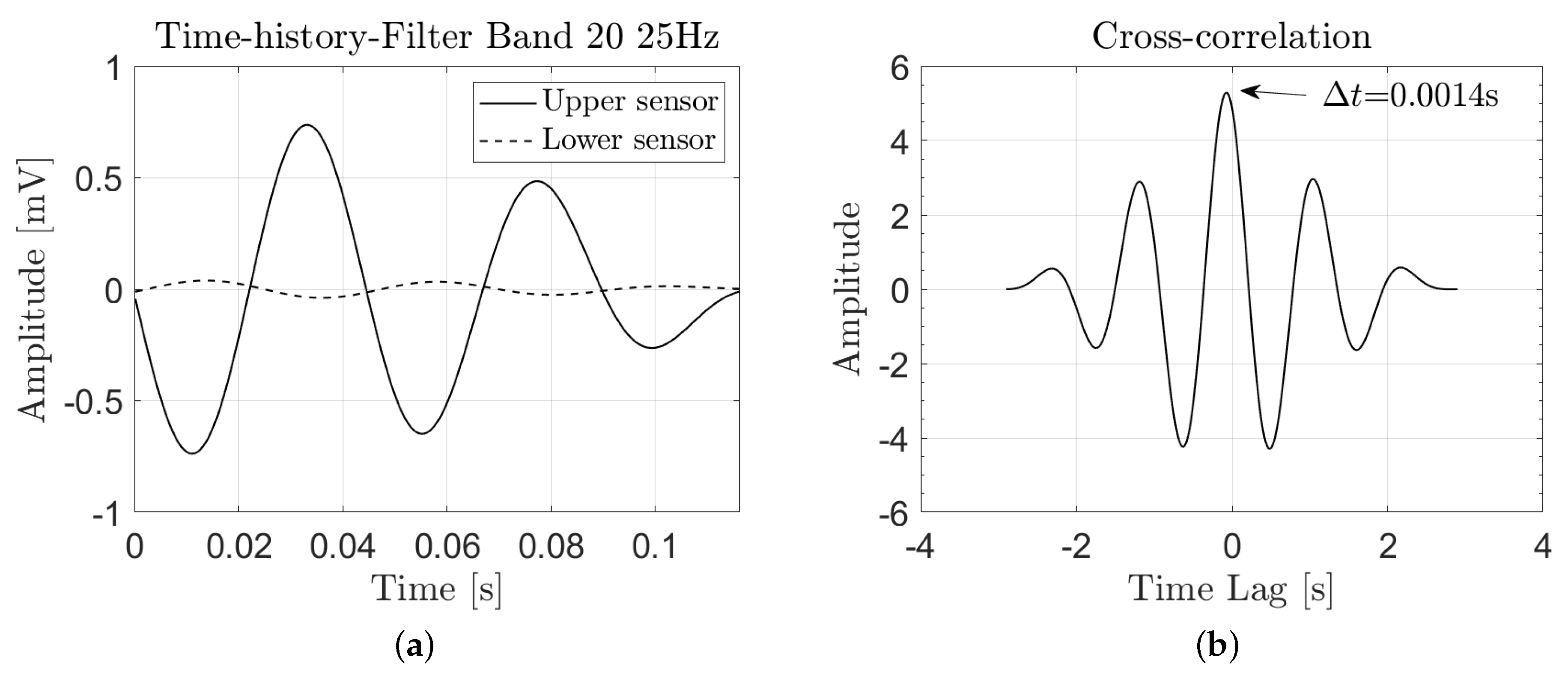
2.3. Empirical Estimate of the Dispersion Law from Acquired Signals
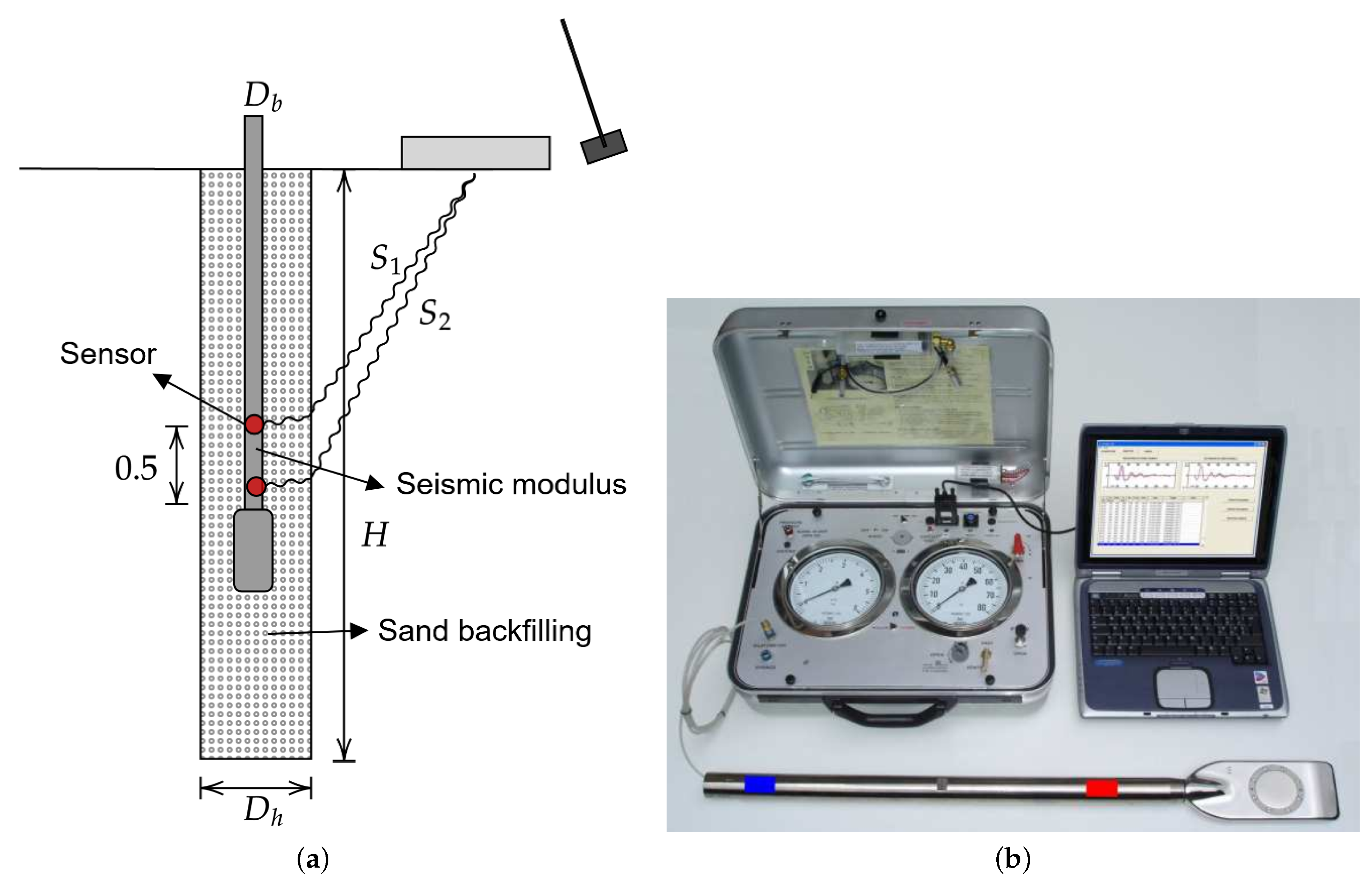
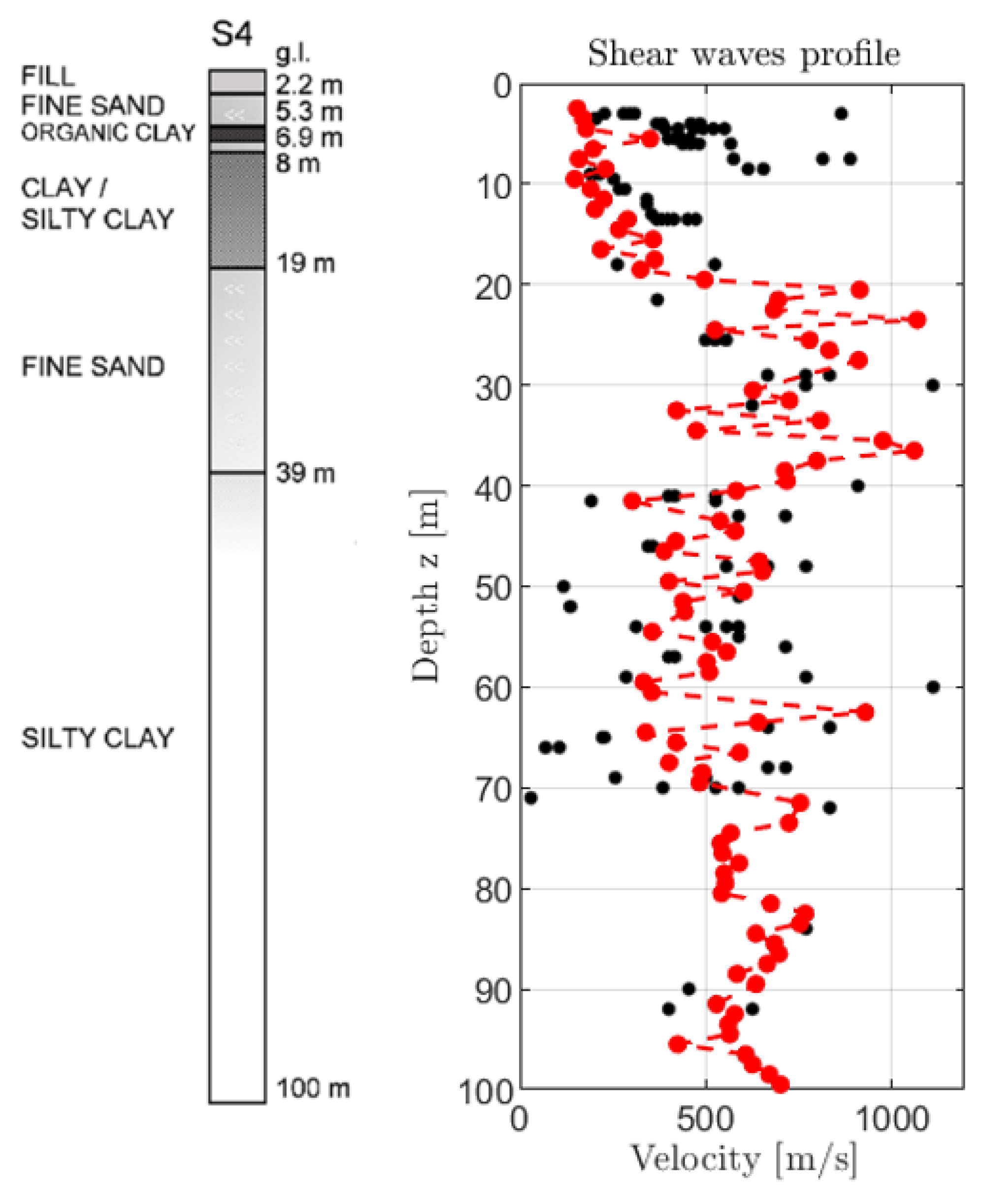
3. Experimental Tests
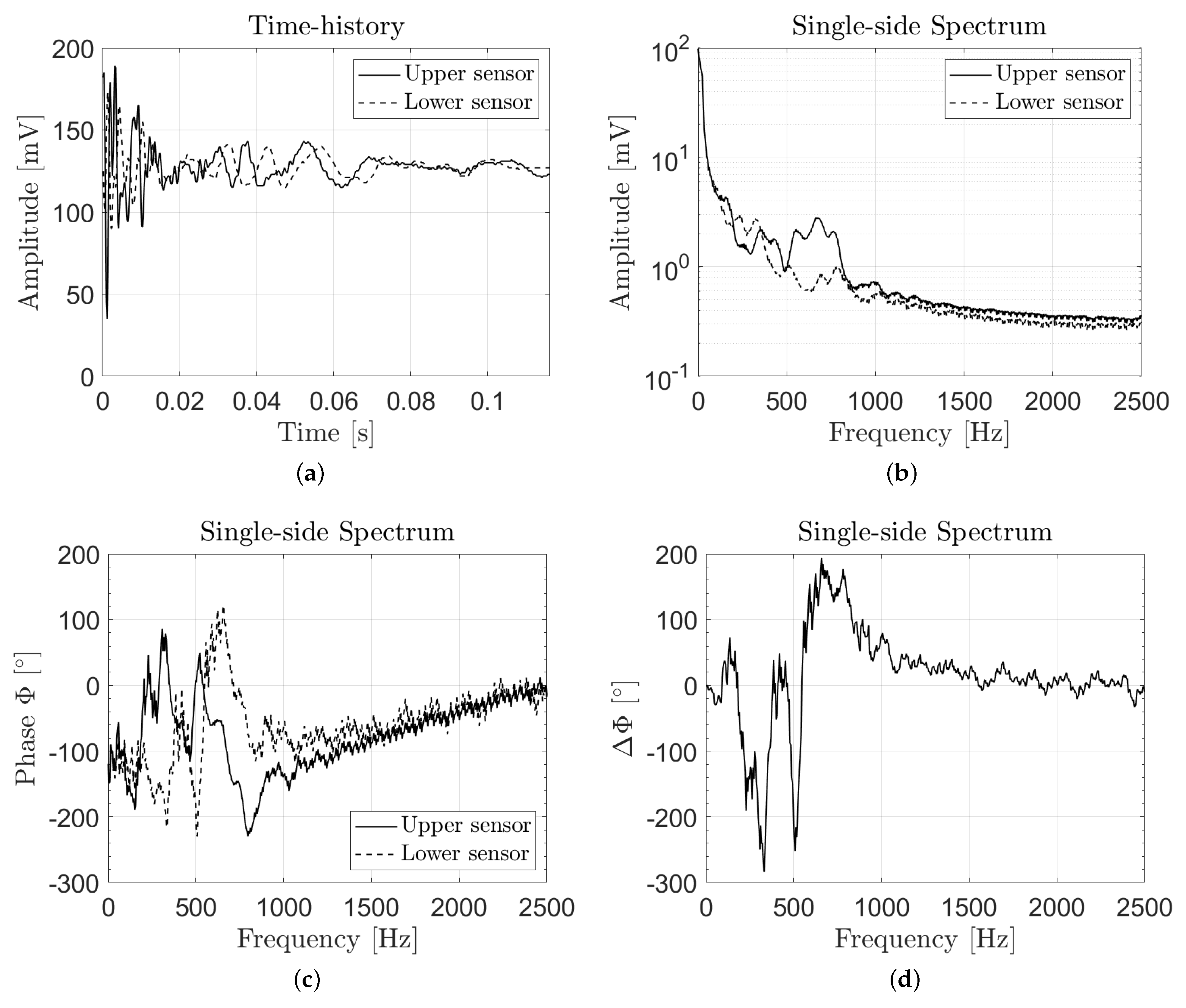
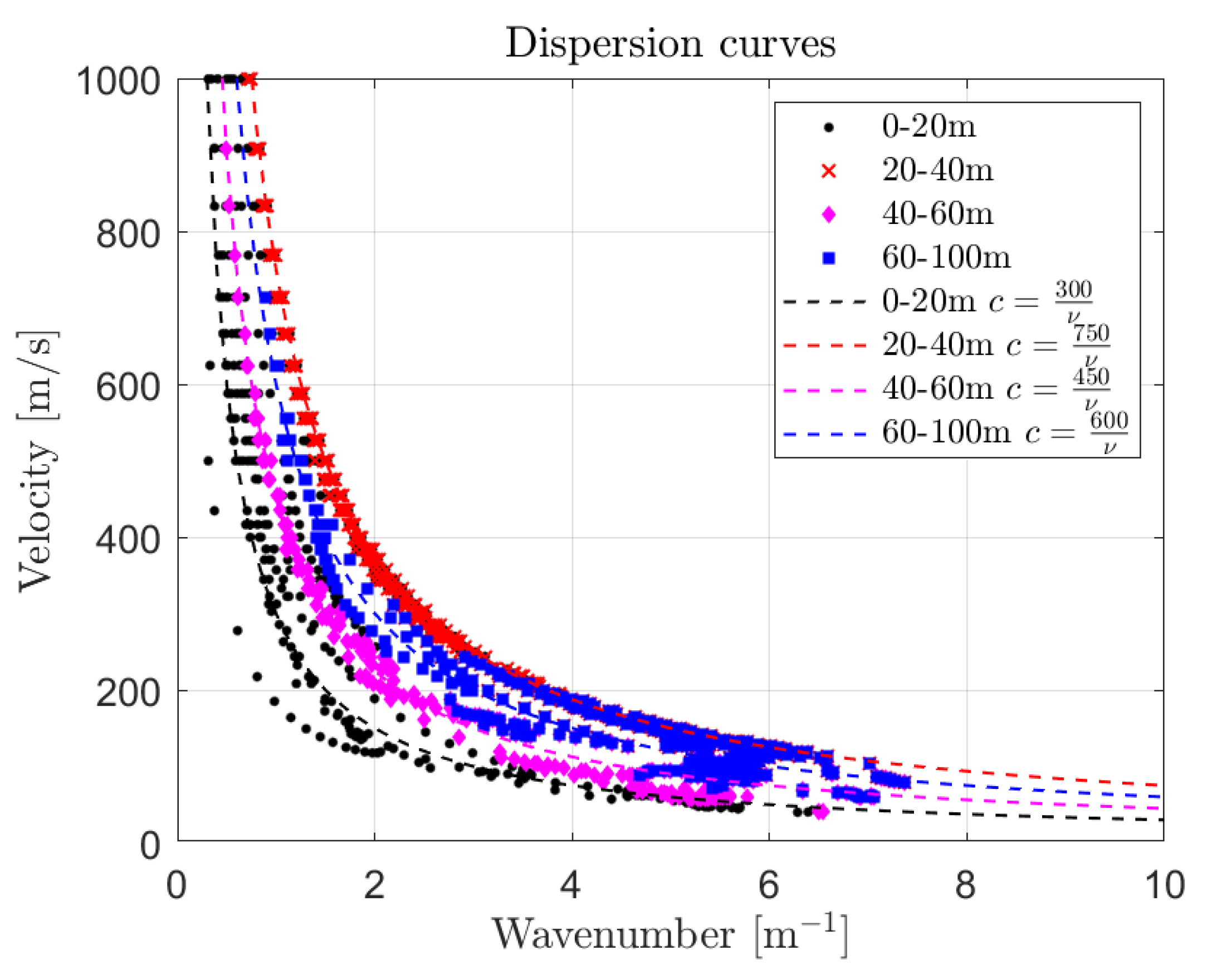
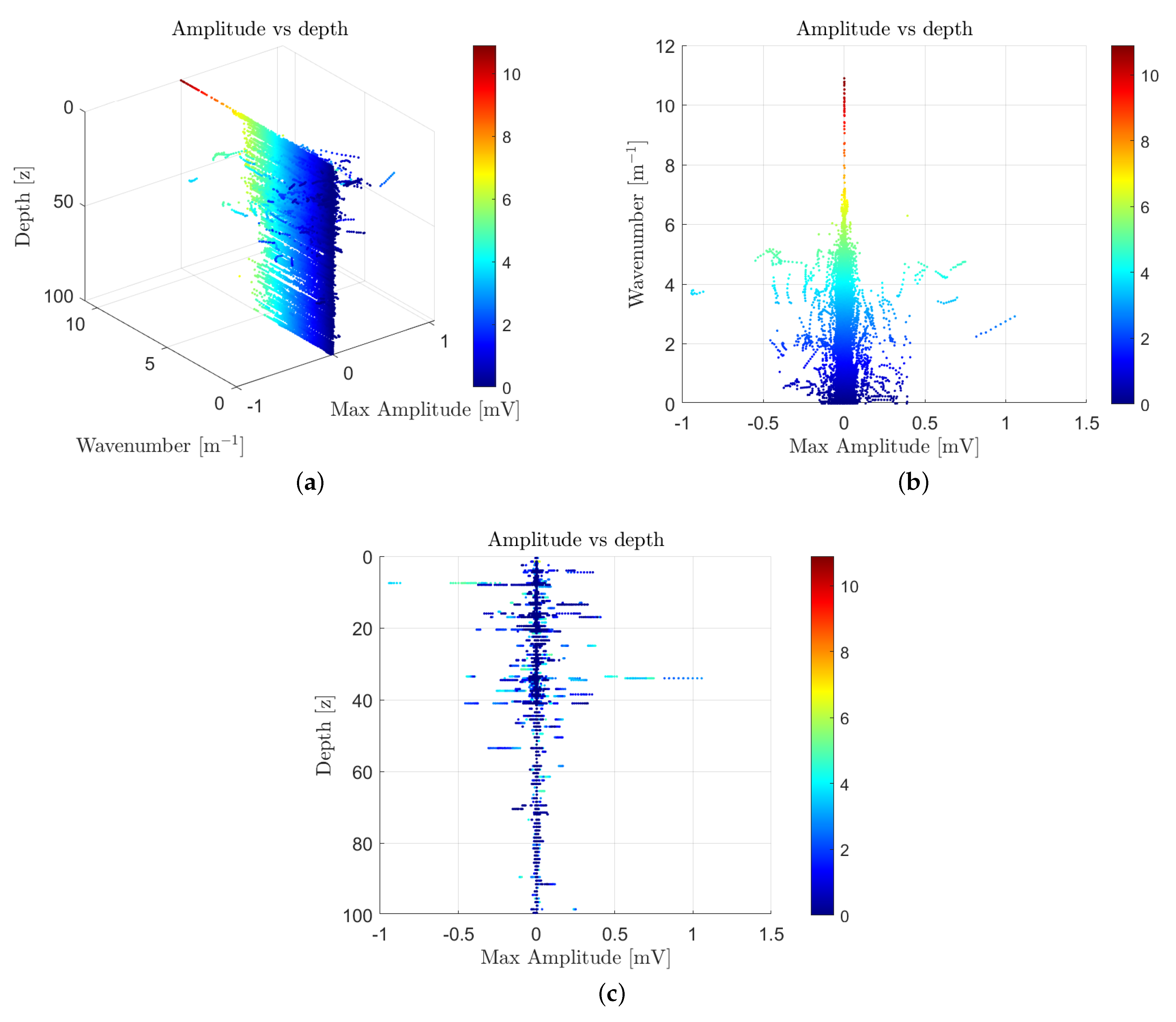
4. Results
The Effect of Dispersion: Results and Discussion
- A first possibility is that the acquired pulses do not correspond to pure shear waves, but they exhibit coupling between the longitudinal and transverse motion mostly explicated in the x-z plane. The directional nature of the input may force the soil grans to move in the x-z plane, while they do not manifest a significant displacement in the y direction. These waves belong to the class of Lamb waves, characterized by a dispersion curve derived in the second section in Equation (21). Therefore, the leading cause of dispersion may stand in the excitation, which forces the particles to move in a plane, as occurs in Lamb waves which can propagate in plates and spheres.
- It is also plausible that the experimenters measure almost pure shear waves and that the primary source of dispersion stands in the granular nature of the medium. Granular media may exhibit hyperbolic-like dispersive curves [60,61]. Therefore, the constitutive nature of the soil, rather than the boundary conditions may determine the observed behavior. There are copious theoretical and numerical researches on the dispersion of continuum models representative of random granular assemblies [3,4,5,6,7,8,9]. These studies mostly deal with high-order deformation gradients, the constitutive relations descend from the Cosserat theory and the grains interact through Hertz-Mindlin contacts [60,61].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Graff, K.F. Wave Motion in Elastic Solids; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Worden, K. Rayleigh and Lamb Waves-Basic Principles. Strain 2001, 37, 167–172. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methoden der Mathematischen Physik; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Digby, P. The effective elastic moduli of porous granular rocks. J. Appl. Mech. 1981, 48, 803–808. [Google Scholar] [CrossRef]
- Muhlhaus, H.B.; De Borst, R.; Aifantis, E. Constitutive models and numerical analyses for ineslastic materials with microstructure. In Proceedings of the 7th International Conference on Computer Methods and Advances in Geomechanics, Cairns, Australia, 6–10 May 1991; pp. 377–385. [Google Scholar]
- Vardoulakis, I.; Aifantis, E. Gradient dependent dilatancy and its implications in shear banding and liquefaction. Ing. Arch. 1989, 59, 197–208. [Google Scholar] [CrossRef]
- Walton, K. The effective elastic moduli of a random packing of spheres. J. Mech. Phys. Solids 1987, 35, 213–226. [Google Scholar] [CrossRef]
- Jenkins, J.T. Volume change in small strain axisymmetric deformations of a granular material. In Studies in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1988; Volume 20, pp. 245–252. [Google Scholar]
- Jenkins, J.T. Anisotropic elasticity for random arrays of identical spheres. In Modern Theory of Anisotropic Elasticity and Applications; SIAM: Philadelphia, PA, USA, 1991; pp. 368–377. [Google Scholar]
- Lambe, T.W.; Whitman, R.V. Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1991; Volume 10. [Google Scholar]
- Borcherdt, R.D. Estimates of site-dependent response spectra for design (methodology and justification). Earthq. Spectra 1994, 10, 617–653. [Google Scholar] [CrossRef]
- Castellaro, S.; Mulargia, F.; Rossi, P.L. VS30: Proxy for seismic amplification? Seismol. Res. Lett. 2008, 79, 540–543. [Google Scholar] [CrossRef]
- Campbell, K.W. Empirical near-source attenuation relationships for horizontal and vertical components of peak ground acceleration, peak ground velocity, and pseudo-absolute acceleration response spectra. Seismol. Res. Lett. 1997, 68, 154–179. [Google Scholar] [CrossRef]
- Wills, C.; Petersen, M.; Bryant, W.; Reichle, M.; Saucedo, G.; Tan, S.; Taylor, G.; Treiman, J. A site-conditions map for California based on geology and shear-wave velocity. Bull. Seismol. Soc. Am. 2000, 90, S187–S208. [Google Scholar] [CrossRef]
- Allen, T.I.; Wald, D.J. On the use of high-resolution topographic data as a proxy for seismic site conditions (VS 30). Bull. Seismol. Soc. Am. 2009, 99, 935–943. [Google Scholar] [CrossRef]
- Tokeshi, K.; Harutoonian, P.; Leo, C.J.; Liyanapathirana, S. Use of surface waves for geotechnical engineering applications in Western Sydney. Adv. Geosci. 2013, 35, 37. [Google Scholar] [CrossRef]
- Karl, L.; Fechner, T.; Schevenels, M.; François, S.; Degrande, G. Geotechnical characterization of a river dyke by surface waves. Near Surf. Geophys. 2011, 9, 515–527. [Google Scholar] [CrossRef]
- Long, M.; Trafford, A.; McGrath, T.; O’Connor, P. Multichannel analysis of surface waves (MASW) for offshore geotechnical investigations. Eng. Geol. 2020, 272, 105649. [Google Scholar] [CrossRef]
- Totani, G.; Monaco, P.; Marchetti, S.; Marchetti, D. VS measurements by seismic dilatometer (SDMT) in non-penetrable soils. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering; IOS Press: Amsterdam, The Netherlands, 2009; Volume 2, pp. 977–980. [Google Scholar]
- Auersch, L. Wave propagation in layered soils: Theoretical solution in wavenumber domain and experimental results of hammer and railway traffic excitation. J. Sound Vib. 1994, 173, 233–264. [Google Scholar] [CrossRef]
- Lai, C.G.; Wilmanski, K. Surface Waves in Geomechanics: Direct and Inverse Modelling for Soils and Rocks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 481. [Google Scholar]
- Rix, G.J. Near-surface site characterization using surface waves. In Surface Waves in Geomechanics: Direct and Inverse Modelling for Soils and Rocks; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–46. [Google Scholar]
- Song, X.; Tang, L.; Lv, X.; Fang, H.; Gu, H. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves. J. Appl. Geophys. 2012, 84, 1–13. [Google Scholar] [CrossRef]
- Pan, Y.; Schaneng, S.; Steinweg, T.; Bohlen, T. Estimating S-wave velocities from 3D 9-component shallow seismic data using local Rayleigh-wave dispersion curves—A field study. J. Appl. Geophys. 2018, 159, 532–539. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Tamura, S.; Kojima, H. Effects of multiple modes on Rayleigh wave dispersion characteristics. J. Geotech. Eng. 1992, 118, 1529–1543. [Google Scholar] [CrossRef]
- Athanasopoulos, G.; Pelekis, P.; Anagnostopoulos, G. Effect of soil stiffness in the attenuation of Rayleigh-wave motions from field measurements. Soil Dyn. Earthq. Eng. 2000, 19, 277–288. [Google Scholar] [CrossRef]
- Addo, K.; Robertson, P. Shear-wave velocity measurement of soils using Rayleigh waves. Can. Geotech. J. 1992, 29, 558–568. [Google Scholar] [CrossRef]
- Viktorov, I.A. Rayleigh and Lamb Waves, Physical Theory and Applications; Acoustics Institute, Academy of Science of the USSR: Moscow, Russia, 1967. [Google Scholar]
- Lamb, H. On the vibrations of an elastic sphere. Proc. Lond. Math. Soc. 1881, 1, 189–212. [Google Scholar] [CrossRef]
- Lamb, H. On waves in an elastic plate. Proc. R. Soc. Lond. 1917, 93, 114–128. [Google Scholar]
- Pilarski, A.; Ditri, J.J.; Rose, J.L. Remarks on symmetric Lamb waves with dominant longitudinal displacements. J. Acoust. Soc. Am. 1993, 93, 2228–2230. [Google Scholar] [CrossRef]
- Lee, B.; Staszewski, W. Modelling of Lamb waves for damage detection in metallic structures: Part I. Wave propagation. Smart Mater. Struct. 2003, 12, 804. [Google Scholar] [CrossRef]
- Mallet, L.; Lee, B.; Staszewski, W.; Scarpa, F. Structural health monitoring using scanning laser vibrometry: II. Lamb waves for damage detection. Smart Mater. Struct. 2004, 13, 261. [Google Scholar] [CrossRef]
- Ng, C.T.; Veidt, M. A Lamb-wave-based technique for damage detection in composite laminates. Smart Mater. Struct. 2009, 18, 074006. [Google Scholar] [CrossRef]
- Hayashi, T.; Inoue, D. Calculation of leaky Lamb waves with a semi-analytical finite element method. Ultrasonics 2014, 54, 1460–1469. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: A review. J. Sound Vib. 2006, 295, 753–780. [Google Scholar] [CrossRef]
- Foti, S. Multistation Methods for Geotechnical Characterization Using Surface Waves; Politecnico di Torino: Turin, Italy, 2000. [Google Scholar]
- Block, L.; Cheng, C.; Fehler, M.; Phillips, W. Structural and geotechnical mapping. Geology 1992, 3, 97–101. [Google Scholar]
- Aloisio, A.; Totani, F.; Totani, G. Experimental dispersion curves of non-penetrable soils from direct dynamic measurements using the seismic dilatometer (SDMT). Soil Dyn. Earthq. Eng. 2021, 143, 106616. [Google Scholar] [CrossRef]
- Rydén, N.; Park, C. Surface waves in inversely dispersive media. Near Surf. Geophys. 2004, 2, 187–197. [Google Scholar] [CrossRef]
- Quqa, S.; Landi, L.; Diotallevi, P.P. Modal assurance distribution of multivariate signals for modal identification of time-varying dynamic systems. Mech. Syst. Signal Process. 2021, 148, 107136. [Google Scholar] [CrossRef]
- Quqa, S.; Landi, L.; Diotallevi, P.P. Seismic structural health monitoring using the modal assurance distribution. Earthq. Eng. Struct. Dyn. 2021. [Google Scholar] [CrossRef]
- Ditommaso, R.; Mucciarelli, M.; Ponzo, F.C. Analysis of non-stationary structural systems by using a band-variable filter. Bull. Earthq. Eng. 2012, 10, 895–911. [Google Scholar] [CrossRef]
- Marchetti, S. In situ tests by flat dilatometer. J. Geotech. Geoenviron. Eng. 1980, 106, 299–321. [Google Scholar]
- Lechowicz, Z.; Fukue, M.; Rabarijoely, S.; Sulewska, M.J. Evaluation of the undrained shear strength of organic soils from a dilatometer test using artificial neural networks. Appl. Sci. 2018, 8, 1395. [Google Scholar] [CrossRef]
- Ferreira, C.; da Fonseca, A.V.; Ramos, C.; Saldanha, A.S.; Amoroso, S.; Rodrigues, C. Comparative analysis of liquefaction susceptibility assessment methods based on the investigation on a pilot site in the greater Lisbon area. Bull. Earthq. Eng. 2020, 18, 109–138. [Google Scholar] [CrossRef]
- Rodrigues, C.; Cruz, N.; Amoroso, S.; Cruz, M. Stiffness Decay in Structured Soils by Seismic Dilatometer. Geotech. Test. J. 2020, 43, 1003–1021. [Google Scholar] [CrossRef]
- Pavithra, E. Dilatometric Methods: Insights of other researchers. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 923, p. 012041. [Google Scholar]
- Hepton, P. Shear wave velocity measurements during penetration testing. In Penetration Testing in the UK, Proceedings of the Geotechnology Conference Organized by the Institution of Civil Engineers, Birmingham, UK, 6–8 July 1988; Thomas Telford Publishing: London, UK, 1989; pp. 275–278. [Google Scholar]
- ASTM. Standard Test Method for Performing the Flat Plate Dilatometer; ASTM: West Conshohocken, PA, USA, 2015. [Google Scholar]
- European Committee for Standardization. Eurocode 7. EN 1997-2:2007 2007: Geotechnical Design—Part 2: Ground Investigation and Testing; European Committee: Brussels, Belgium, 2007. [Google Scholar]
- Marchetti, S.; Monaco, P.; Totani, G.; Marchetti, D. In situ tests by seismic dilatometer (SDMT). In From Research to Practice in Geotechnical Engineering, Proceedings of the Symposium Honoring Dr. John H. Schmertmann for His Contributions to Civil Engineering at Research to Practice in Geotechnical Engineering Congress 2008, New Orleans, LA, USA, 9–12 March 2008; ASCE: Reston, VA, USA, 2008; pp. 292–311. [Google Scholar]
- Foti, S.; Lancellotta, R.; Marchetti, D.; Monaco, P.; Totani, G. Interpretation of SDMT tests in a transversely isotropic medium. In Proceedings of the 2nd International Conference on the Flat Dilatometer, Washington, DC, USA, 2–5 April 2006; pp. 2–5. [Google Scholar]
- Cavallaro, A.; Grasso, S.; Maugeri, M. Clay soil characterization by the new seismic dilatometer Marchetti test (SDMT). In Proceedings of the 2nd International Conference on the Flat Dilatometer, Washington, DC, USA, 2–5 April 2006; pp. 261–268. [Google Scholar]
- Bihs, A.; Long, M.; Marchetti, D.; Ward, D. Interpretation of CPTU and SDMT in organic, Irish soils. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010; Volume 2, pp. 257–264. [Google Scholar]
- Grasso, S.; Maugeri, M. The Seismic Dilatometer Marchetti Test (SDMT) for evaluating liquefaction potential under cyclic loading. In Proceedings of the Geotechnical Earthquake Engineering and Soil Dynamics Congress IV, Sacramento, CA, USA, 18–22 May 2008; pp. 1–15. [Google Scholar]
- Marchetti, S.; Monaco, P. Recent Improvements in the Use, Interpretation, and Applications of DMT and SDMT in Practice. Geotech. Test. J. 2018, 41, 837–850. [Google Scholar] [CrossRef]
- Amoroso, S.; Monaco, P.; Marchetti, D. Use of the Seismic Dilatometer (SDMT) to estimate in situ G-γ decay curves in various soil types. In Geotechnical and Geophysical Site Characterization, Proceedings of the 4th International Conference on Site Characterization ISC-4, Pernambuco, Brazil, 18–21 September 2012; Taylor & Francis Books Ltd.: Abingdon, UK, 2013; Volume 1, pp. 489–497. [Google Scholar]
- Cavallaro, A.; Capilleri, P.P.; Grasso, S. Site characterization by dynamic in situ and laboratory tests for liquefaction potential evaluation during Emilia Romagna earthquake. Geosciences 2018, 8, 242. [Google Scholar] [CrossRef]
- Bachrach, R.; Avseth, P. Rock physics modeling of unconsolidated sands: Accounting for nonuniform contacts and heterogeneous stress fields in the effective media approximation with applications to hydrocarbon exploration. Geophysics 2008, 73, E197–E209. [Google Scholar] [CrossRef]
- Pasternak, E.; Mühlhaus, H.B. Generalised homogenisation procedures for granular materials. In Mathematics and Mechanics of Granular Materials; Springer: Berlin/Heidelberg, Germany, 2005; pp. 199–229. [Google Scholar]
- Koedel, U.; Karl, L. Determination of the damping ratio by multi-channel spectral analysis of seismic downhole data. Soil Dyn. Earthq. Eng. 2020, 136, 106235. [Google Scholar] [CrossRef]
- Amoroso, S.; Comina, C.; Marchetti, D. Combined P-and S-Wave Measurements by Seismic Dilatometer Test (SPDMT): A Case History in Bondeno (Emilia Romagna, Italy). Geotech. Test. J. 2020, 43, 383–393. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aloisio, A.; Totani, F.; Alaggio, R.; Totani, G. Dispersion Curves of Transverse Waves Propagating in Multi-Layered Soils from Experimental Tests in a 100 m Deep Borehole. Geosciences 2021, 11, 207. https://doi.org/10.3390/geosciences11050207
Aloisio A, Totani F, Alaggio R, Totani G. Dispersion Curves of Transverse Waves Propagating in Multi-Layered Soils from Experimental Tests in a 100 m Deep Borehole. Geosciences. 2021; 11(5):207. https://doi.org/10.3390/geosciences11050207
Chicago/Turabian StyleAloisio, Angelo, Ferdinando Totani, Rocco Alaggio, and Gianfranco Totani. 2021. "Dispersion Curves of Transverse Waves Propagating in Multi-Layered Soils from Experimental Tests in a 100 m Deep Borehole" Geosciences 11, no. 5: 207. https://doi.org/10.3390/geosciences11050207
APA StyleAloisio, A., Totani, F., Alaggio, R., & Totani, G. (2021). Dispersion Curves of Transverse Waves Propagating in Multi-Layered Soils from Experimental Tests in a 100 m Deep Borehole. Geosciences, 11(5), 207. https://doi.org/10.3390/geosciences11050207






