Proposed Model for Shale Compaction Kinetics

Abstract

Shales are the most abundant class of sedimentary rocks, distinguished by being very fine-grained, clayey, and compressible. Their physical and chemical properties are important in widely different enterprises such as civil engineering, ceramics, and petroleum exploration. One characteristic, which is studied here, is a systematic reduction of porosity with depth of burial. This is due increases in grain-to-grain stress and temperature. Vertical stress in sediments is given by the overburden less the pore fluid pressure, $\sigma$, divided by the fraction of the horizontal area which is the supporting matrix, $(1-\phi )$, where $\phi$ is the porosity. It is proposed that the fractional reduction of this ratio, $\Lambda$, with time is given by the product of ${\phi }^{4m/3}$, ${(1-\phi )}^{4n/3}$, and one or more Arrhenius functions $Aexp(-E/RT)$ with m and n close to 1. This proposal is tested for shale sections in six wells from around the world for which porosity-depth data are available. Good agreement is obtained above 30–40 °C and fractional porosities less than 0.5. Single activation energies for each well are obtained in the range 15–33 kJ/mole, close to the approximate pressure solution of quartz, 24 kJ/mol. Values of m and n are in the range 1 to 0.8, indicating nearly fractal water-wet pore-to-matrix interfaces at pressure solution locations. Results are independent of over- or under-pressure of pore water. This model attempts to explain shale compaction quantitatively. For the petoleum industry, given porosity-depth data for uneroded sections and accurate activation energy, E, paleo-geothermal-gradient can be inferred and from that organic maturity, indicating better drilling prospects.

1. Introduction

For overburden S and pore pressure p, the vertical stress difference

$$\sigma \equiv (S-p),$$

(1)

can be changed by sedimentation, erosion or fluid flow through rock in this one-dimensional model. Similarly $\sigma$ divided by the fractional area of solid matrix $(1-\phi )$ supporting this stress can be relieved by pressure solution, breakage, relative movement of grains or fluid flow.

$$\Lambda \equiv (S-p)/(1-\phi )=\sigma /(1-\phi ).$$

(2)

Differentiating with respect to time gives

$$\frac{dln\Lambda }{dt}=-\frac{dln(1-\phi )}{dt}+\frac{dln\sigma }{dt}.$$

(3)

The first term deals with local porosity changes, while the second term deals with deposition, erosion, and fluid flow. The second term was treated previously [1,2,3].

Focus here is on the first term, proposing and supporting with previously published porosity data for shale sections a chemical-type expression describing the time evolution of the vertical grain-to-grain pressure, or frame pressure.

2. Proposed Kinetic Equation

It is proposed that the reactions to reduce the frame pressure are proportional to the frame pressure $\Lambda$, to the pore surface area, ${\phi }^{1.33}$, to the frame surface area, ${(1-\phi )}^{1.33}$, and to one (or a sum of) Arrhenius factors, $Aexp-E/RT$. The exponent 1.33 = 4/3 is the fractal dimension of a percolation front and twice the surface dimension 2/3 of smooth solids. R is the ideal gas constant (8.314 J/(mol·deg K), T is temperature in Kelvin. The fractional change in $\Lambda$ thus proposed and supported is

$${\left.\frac{\partial (ln\Lambda )}{\partial t}\right|}_{\sigma }=-{\left(\phi S_w\right)}^{1.33m}{(1-\phi )}^{1.33n}A{e}^{-E/\left(RT\right)}$$

(4)

or equivalently

$${\left.\frac{\partial \left(ln\right(1-\phi \left)\right)}{\partial t}\right|}_{\sigma }=+{\left(\phi S_w\right)}^{1.33m}{(1-\phi )}^{1.33n}A{e}^{-E/\left(RT\right)}.$$

(5)

The Arrhenius frequency factor, A, is not expected to depend strongly on T for the surface reaction. Here m and n are expected to be close to 1.0 and greater than 0.5, contact areas being less than fractal because of the finite size of atoms. m and n may be different because water-to-grain and grain-to-grain interfaces differ. Notably this mechanism is primarily a dimensional argument and lacks terms relating to the sizes, shapes, and composition of pores and grains. (For more inclusive approaches see [4]). Fractional water saturation, $S_w$, might reduce compaction but is set to 1 and omitted hereafter.

3. Data

Porosity versus depth profiles from the literature [5,6,7,8,9] for six shale sections are used here. The shales are unrelated and not chosen because of similarities. Sample-based profiles were included in a recent comprehensive survey of 21 geologic sections and laboratory studies of clays [10]. All profiles are included in an engineering correlation [11] which included two seismicly-inferred porosity profiles [6]. They were chosen because geologic age ranges, basin types, and basin names were available [11]. All porosity—depth profiles will be referred to as ‘wells’ for brevity. Map coordinates were known only for the two Makran seismically-inferred porosity-depth profiles. For actual wells, no formal well names were given, and data from several local wells were combined. Temperatures are not available for any wells. Paleo surface temperature estimates are made on the basis of paleoenvironments, paleolatitude, and geologic age,

Table 1. Description and initial provisional parameters for wells.

Basin Location	Basin Type	Age Range Ma	Paleo- Surface °C	Paleo $\mathbf{\nabla }\mathit{T}$ °C/m	References
Akita,	back-arc	1.5–146	(3 + 13 + 13)/2	0.05	[5]
Hokkaido
Makran1	abyssal	2.6–105	3	0.03	[6]
Makran2	abyssal	2.6–105	3	0.03	[6]
Sulu Sea	deep-water	0–23	13	0.03	[7]
Oklahoma	convergent	252–323	(7 + 14 + 13)/2	0.06	[8]
Maracaibo	back-arc	2.6–105	(3 + 14 + 13)/2	0.05	[9]

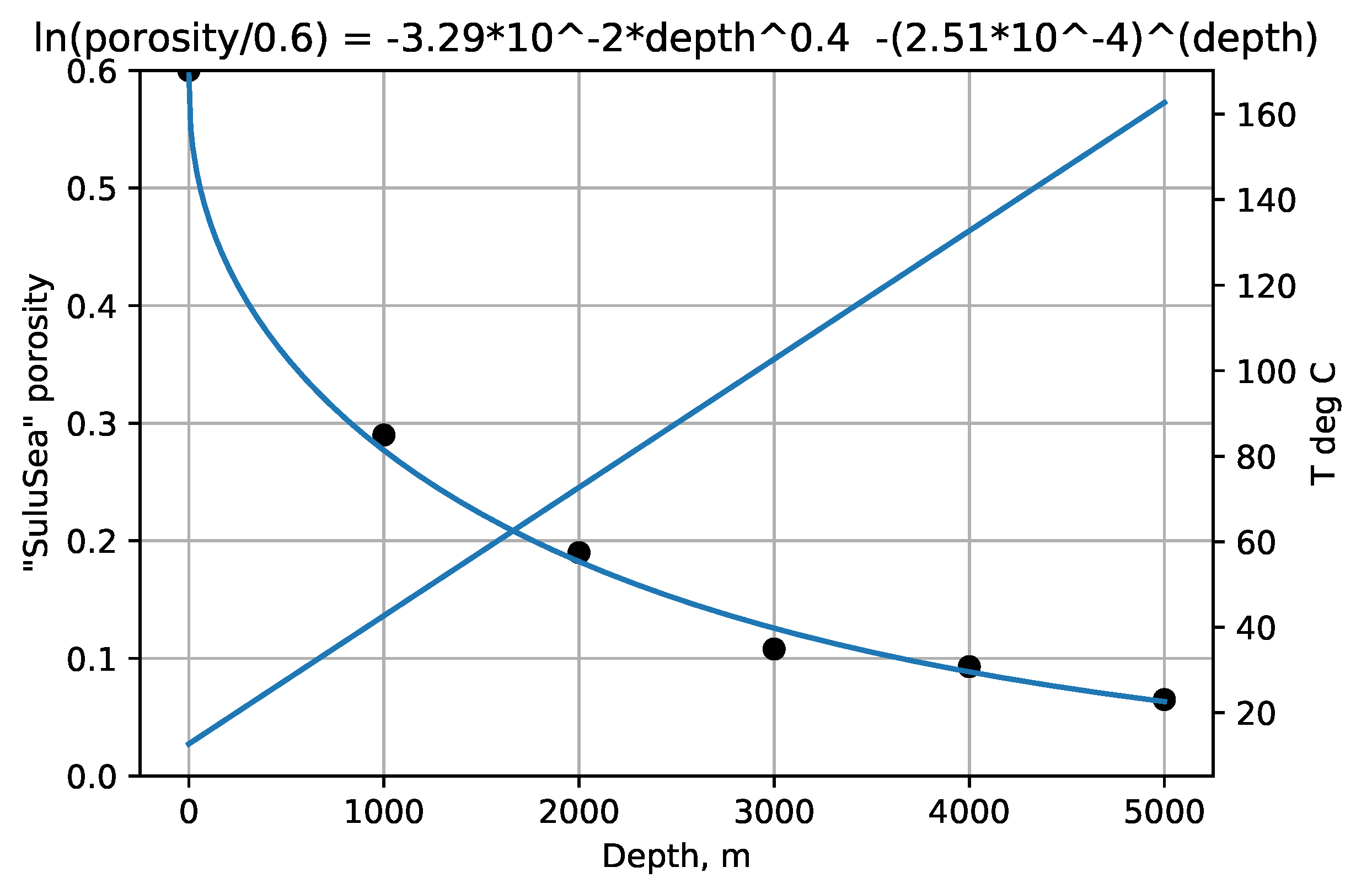
. Sediment surface temperatures of 3 °C are assigned to wells from abyssal plains. Shallow sea [8] or lake environments [9] are assigned expected land paleotemperatures, corrected for paleolatitudes, and for any intervening high temperature events such as the Eocene high [12]. If two estimates are made they are averaged. The sediment surface temperature used for the Sulu Sea, 13 °C, was known for the deepest point [13]. The paleo-surface-temperature estimates are less important to this study than are paleo-geothermal-gradients, as the compaction mechanism discussed hereafter becomes noticable deeper at the higher well temperatures and at porosities less than 0.5. Because the Earth is cooling as radioactivity and initial energy of assembly decline, and because these wells were drilled/investigated in areas where temperatures were supposed to be high enough to generate petroleum, minimum paleo-geothermal-gradients of 0.03 °C/m were initially assigned. The well surface and temperature gradient estimates used here are well within present day experience [14]. 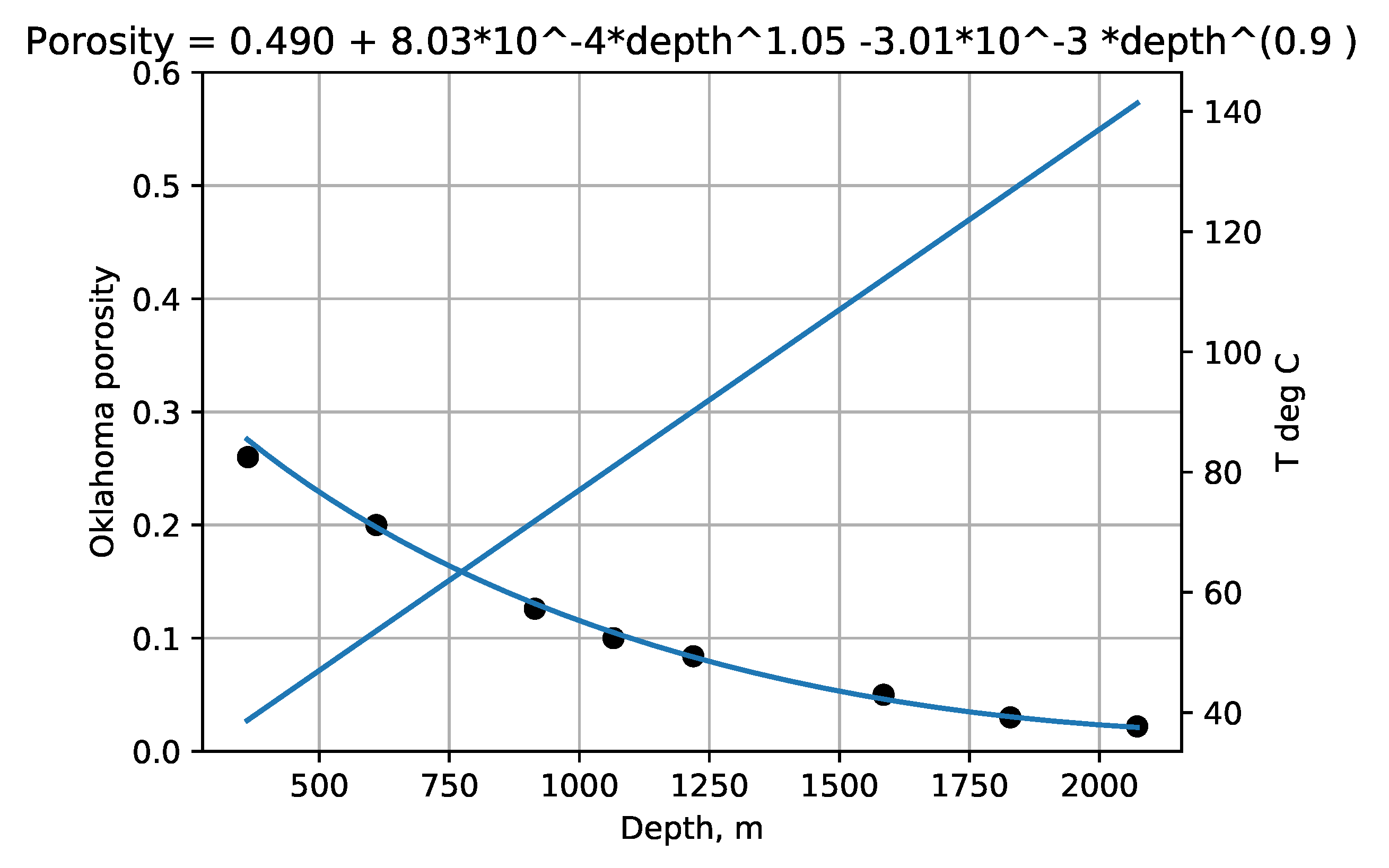A paleo-geothermal-gradient of 0.05 °C/m was assigned to the Akita well, and to the Maracaibo back-arc well, on the basis of necessary organic maturity [5]. In Northeast Oklahoma nearby sedimentary rock mineralization and granite outcrop [15] suggest a higher paleo-geothermal-gradient, perhaps 0.06 °C/m as assigned.

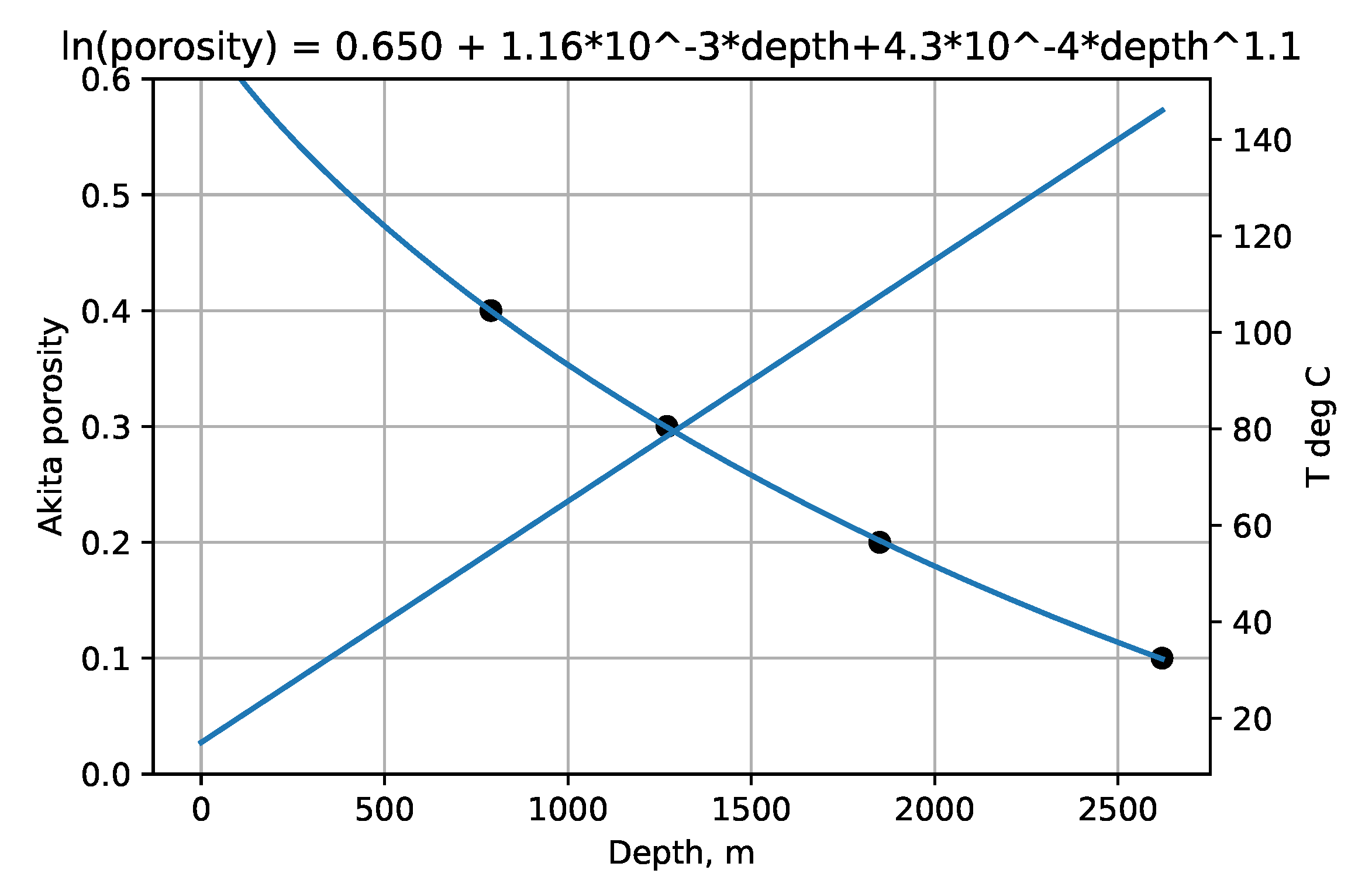
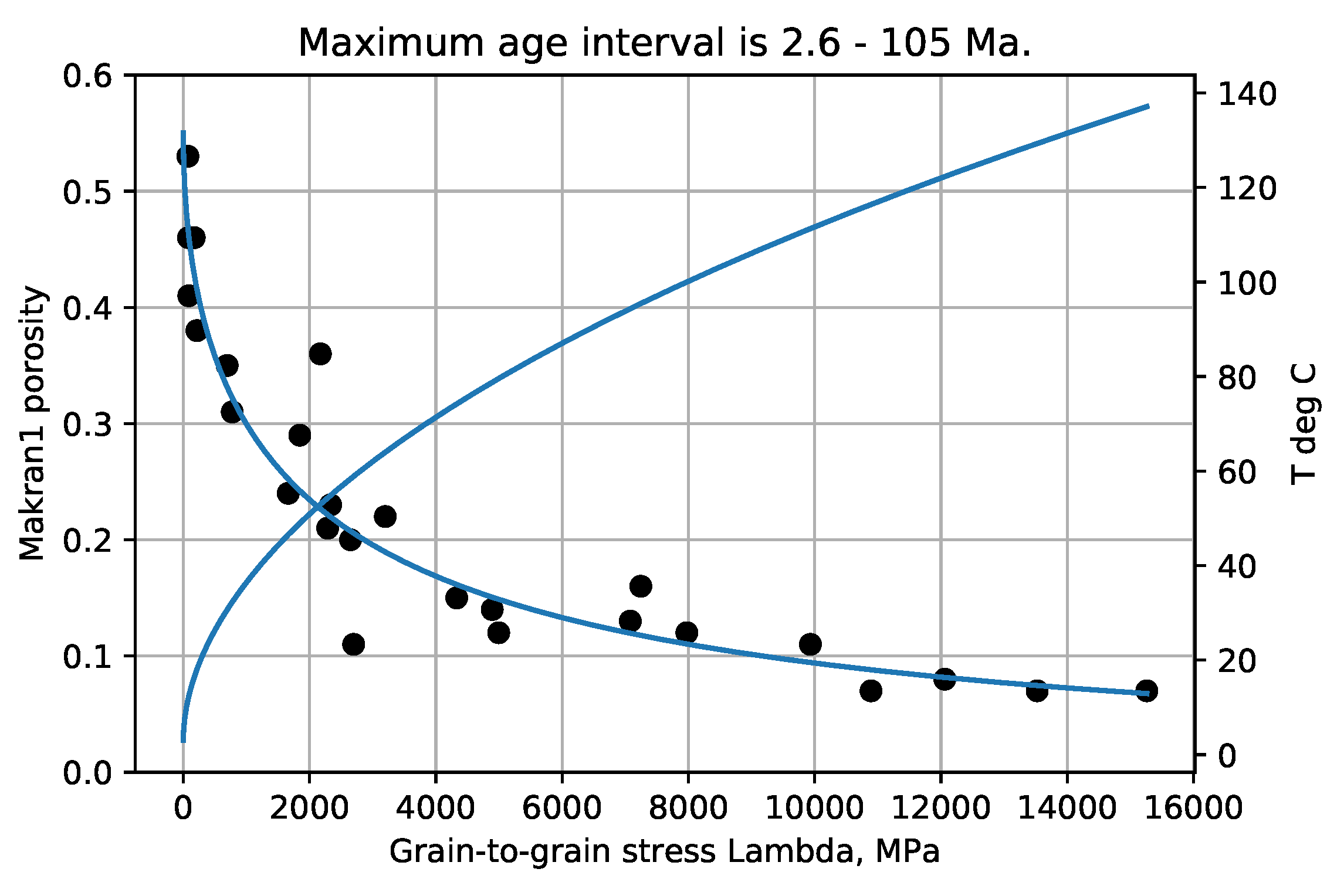
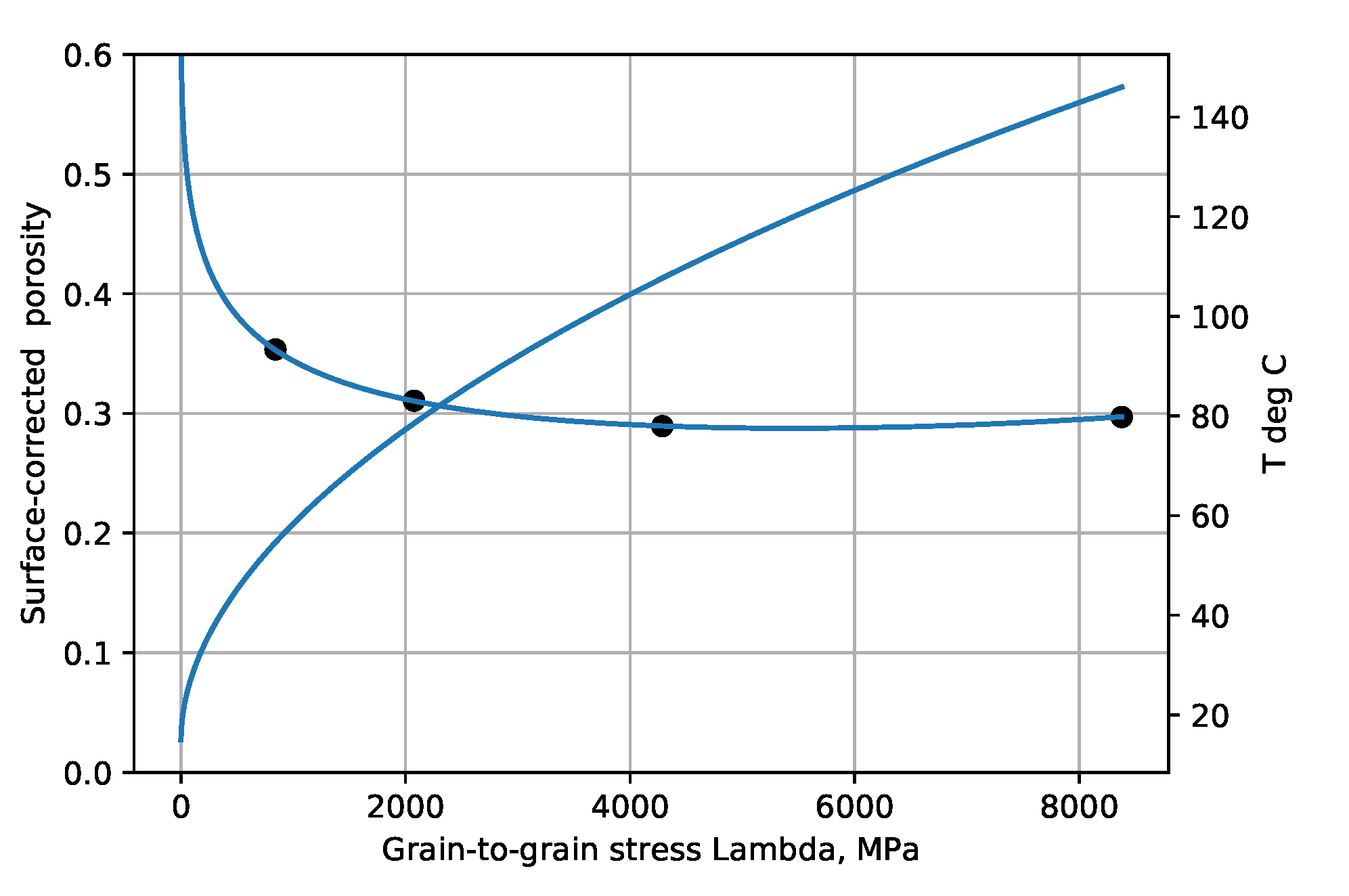
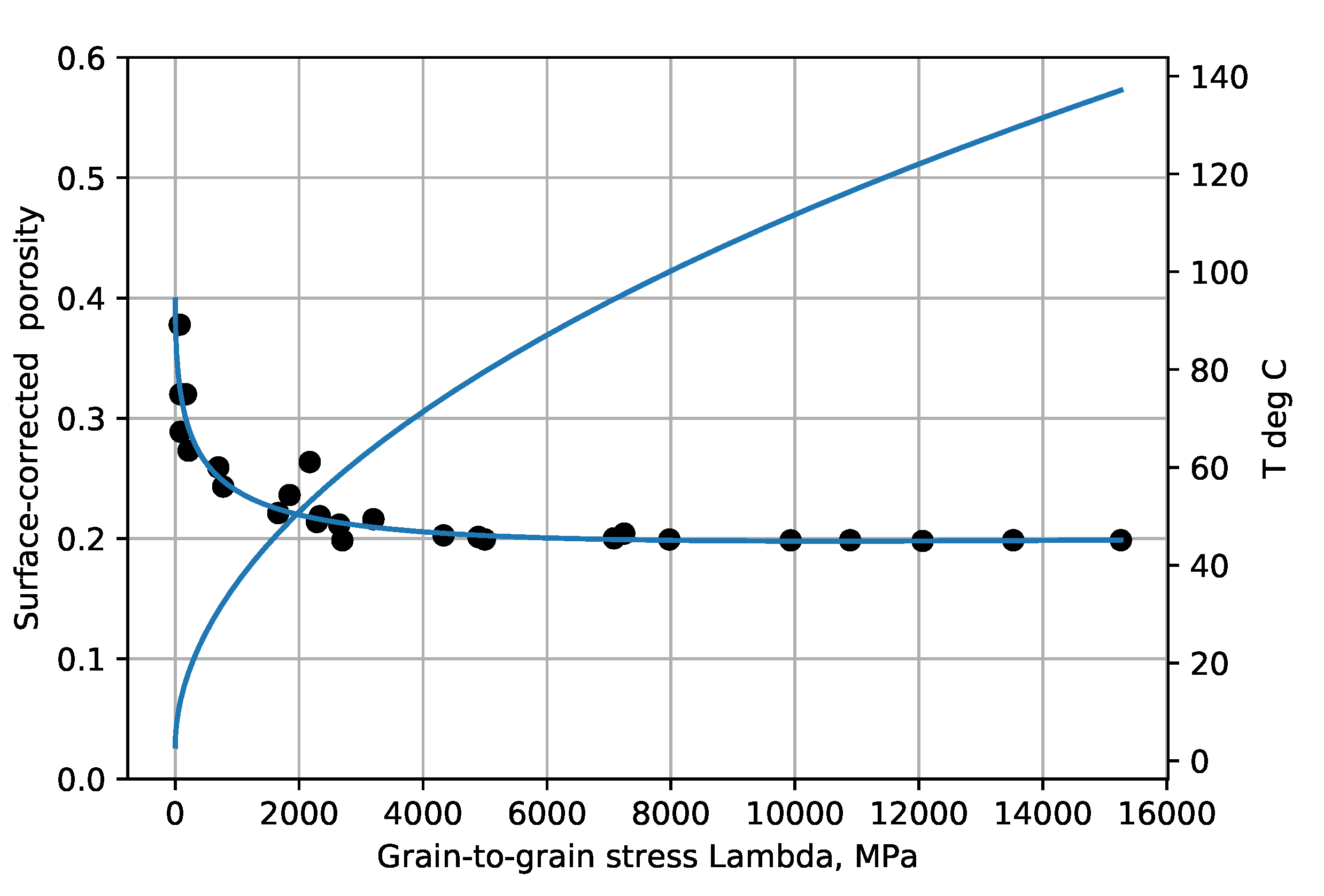
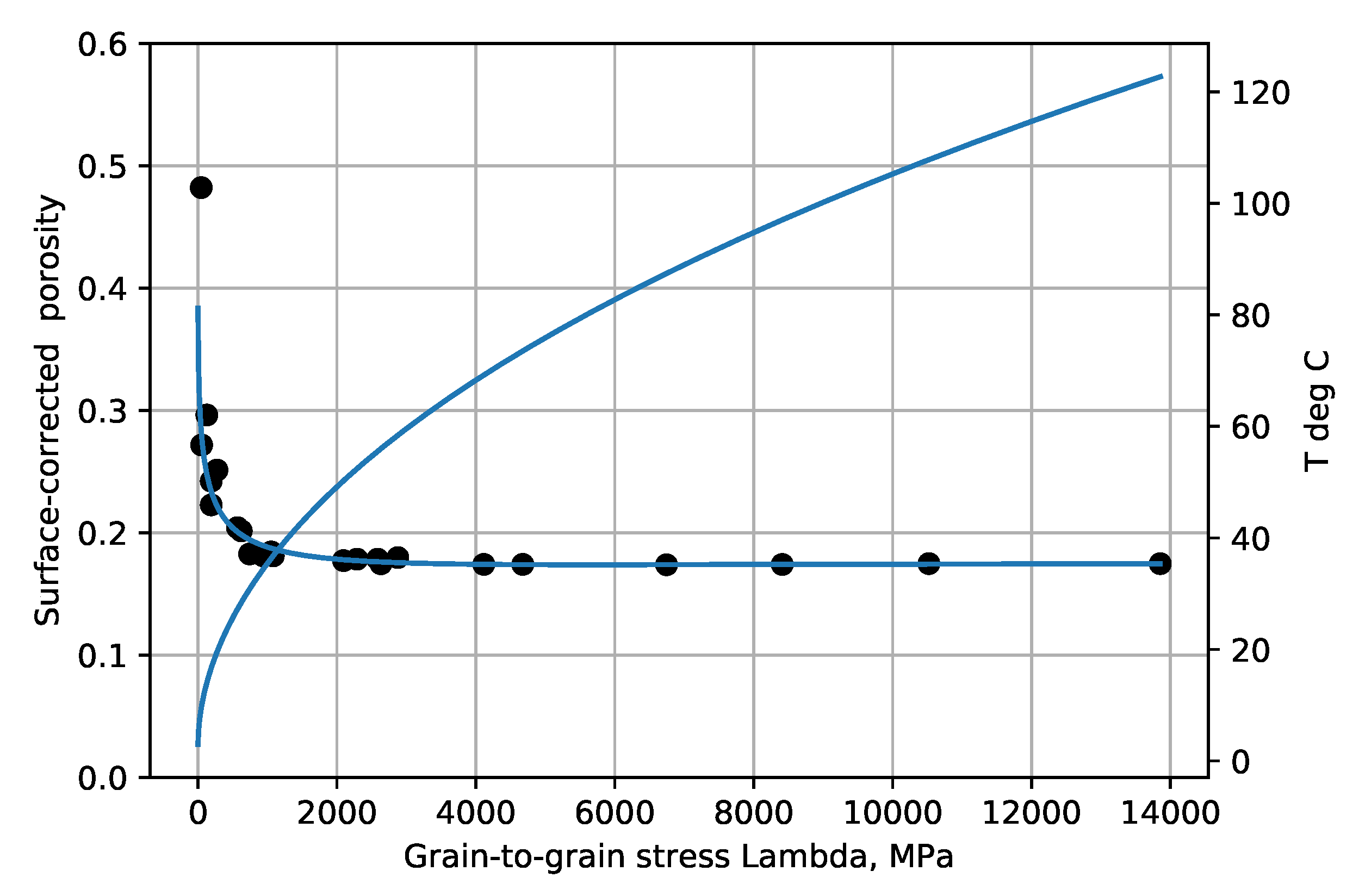
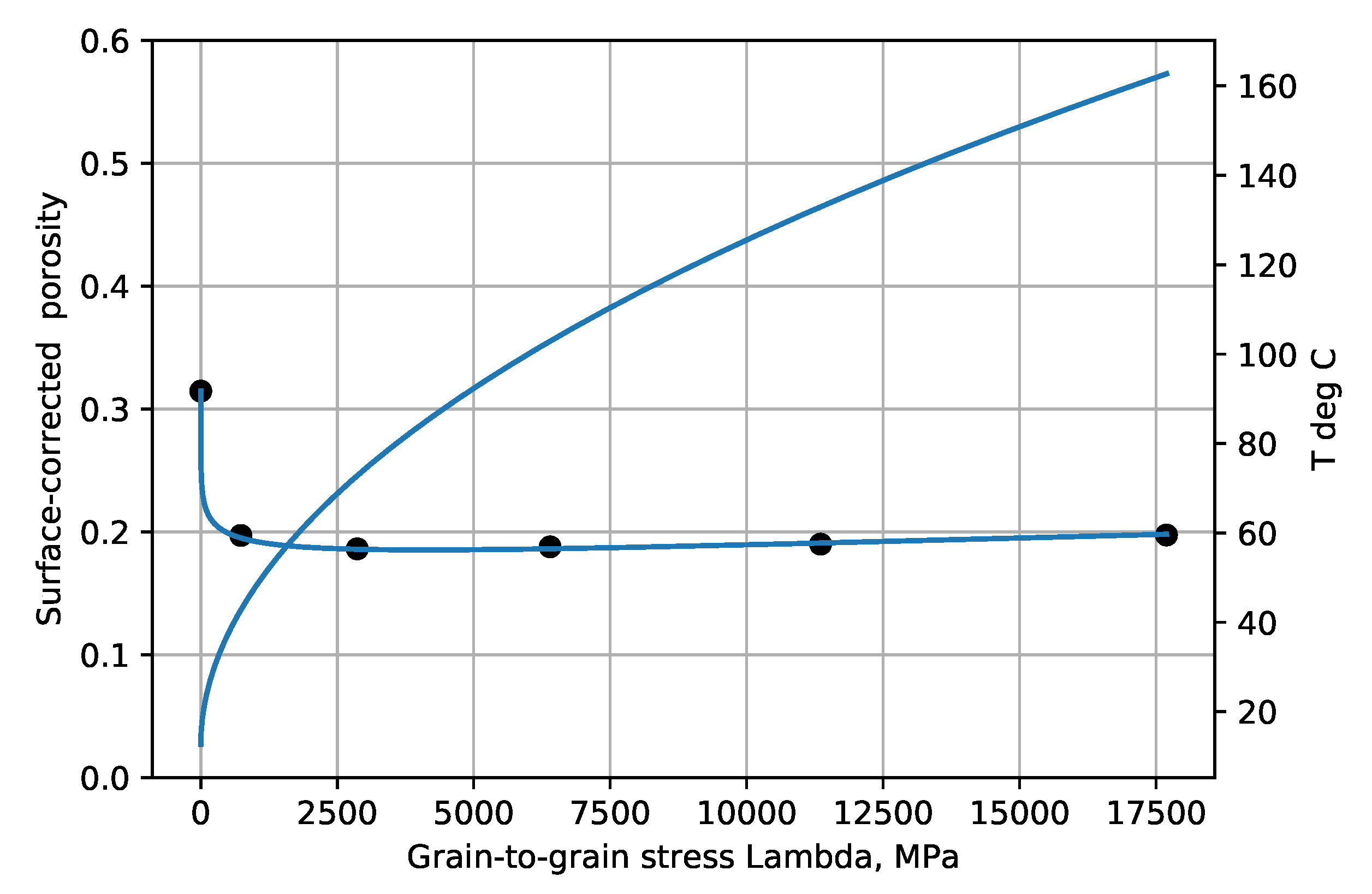
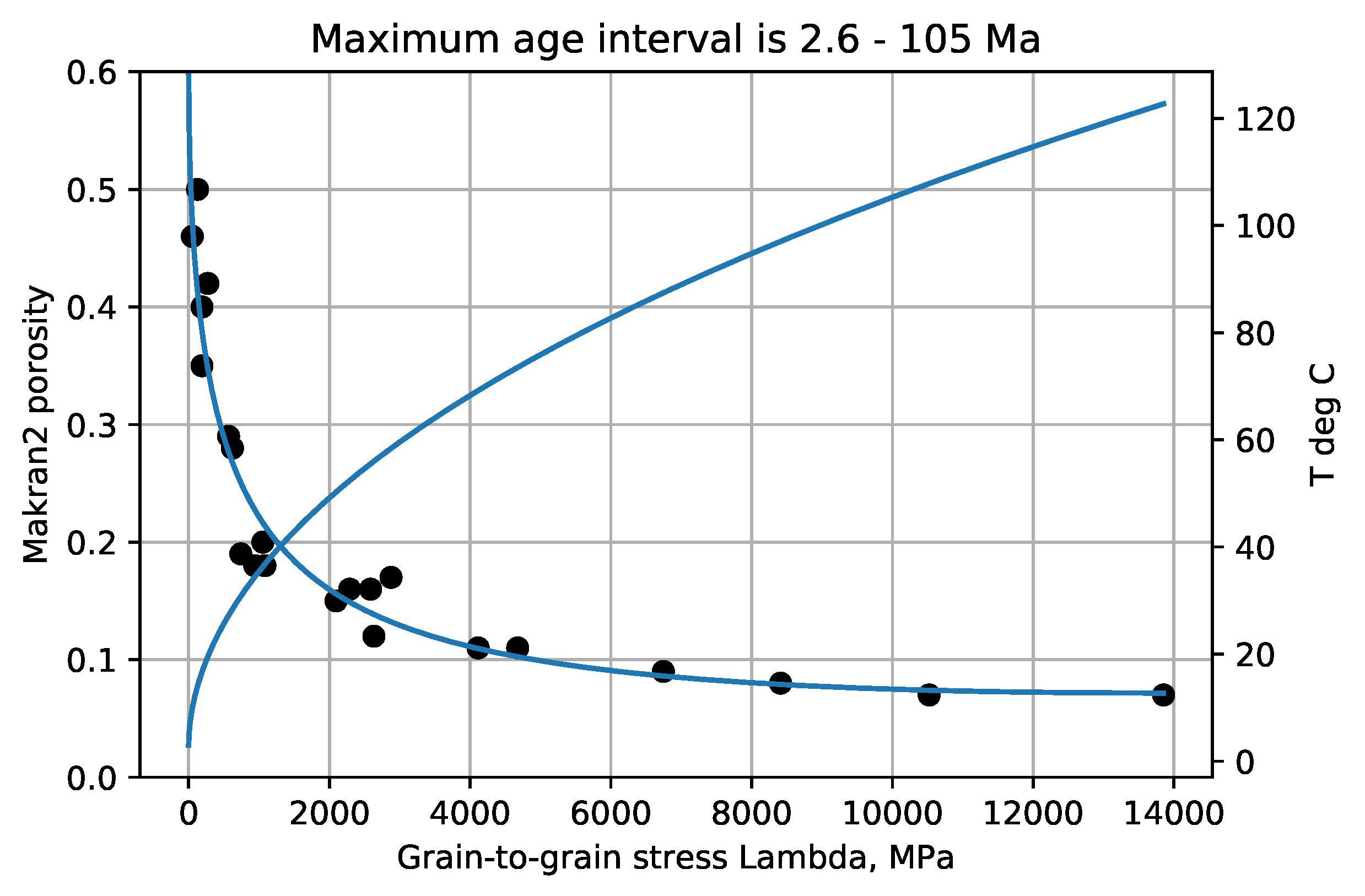
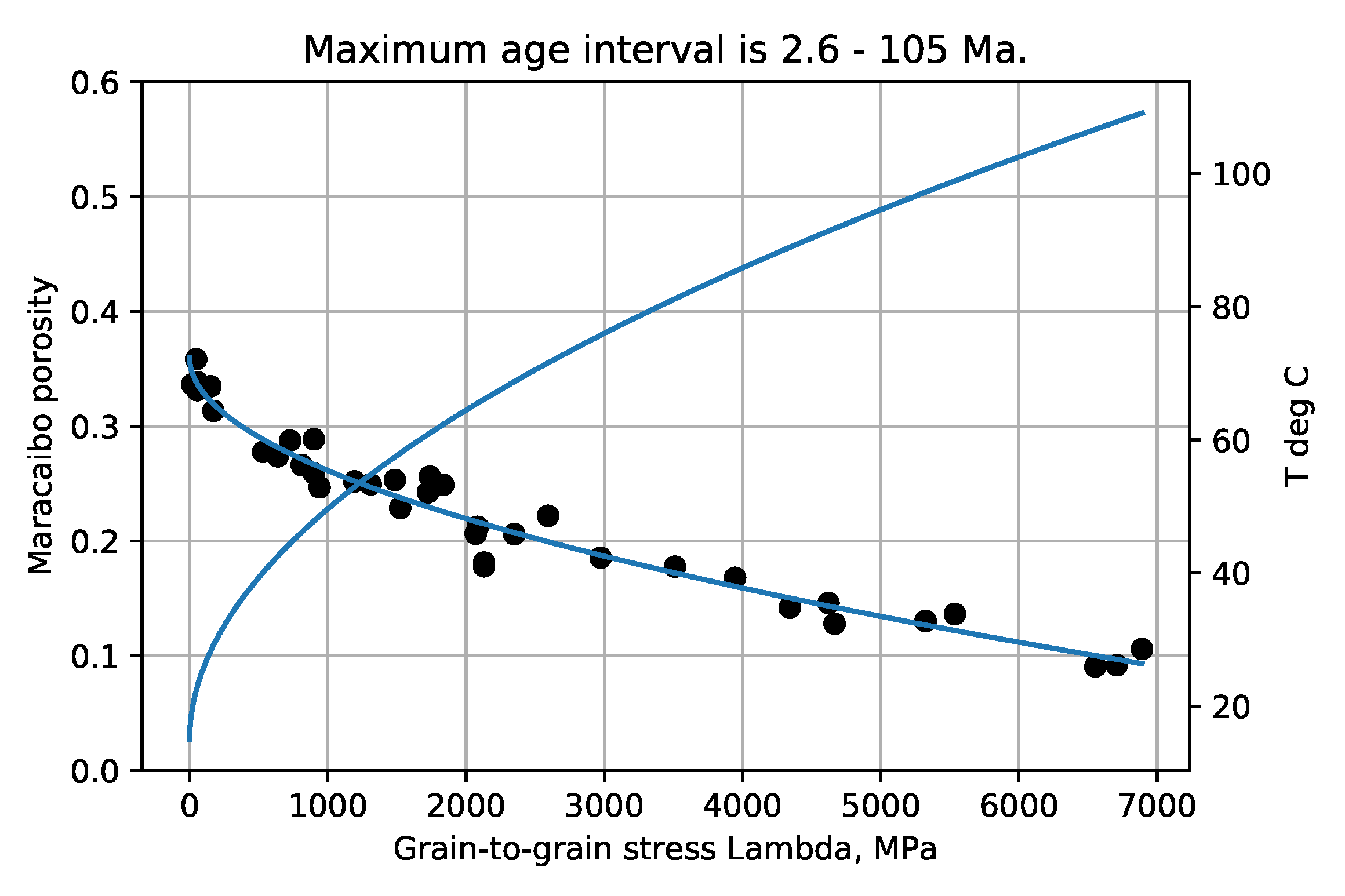
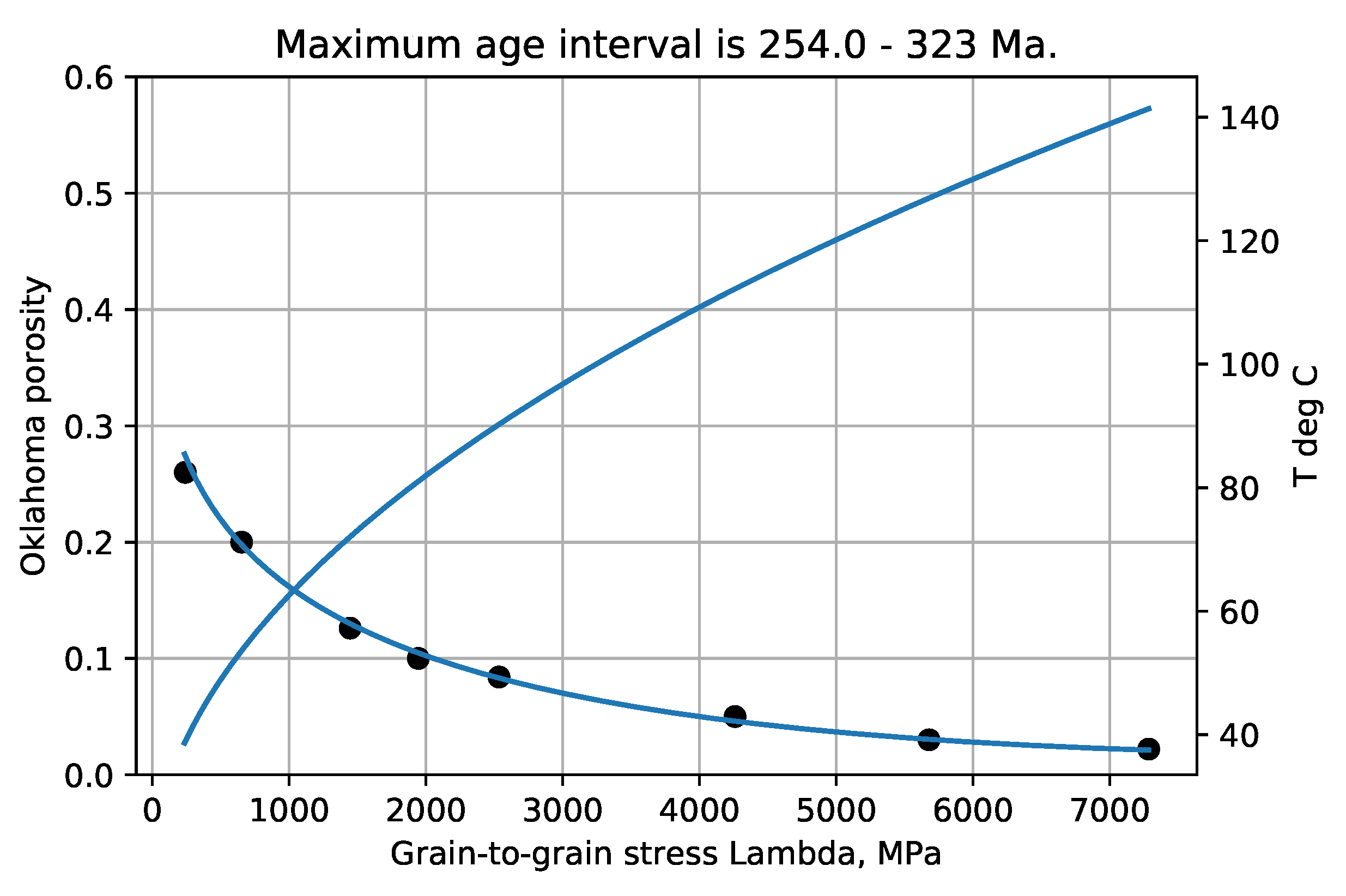
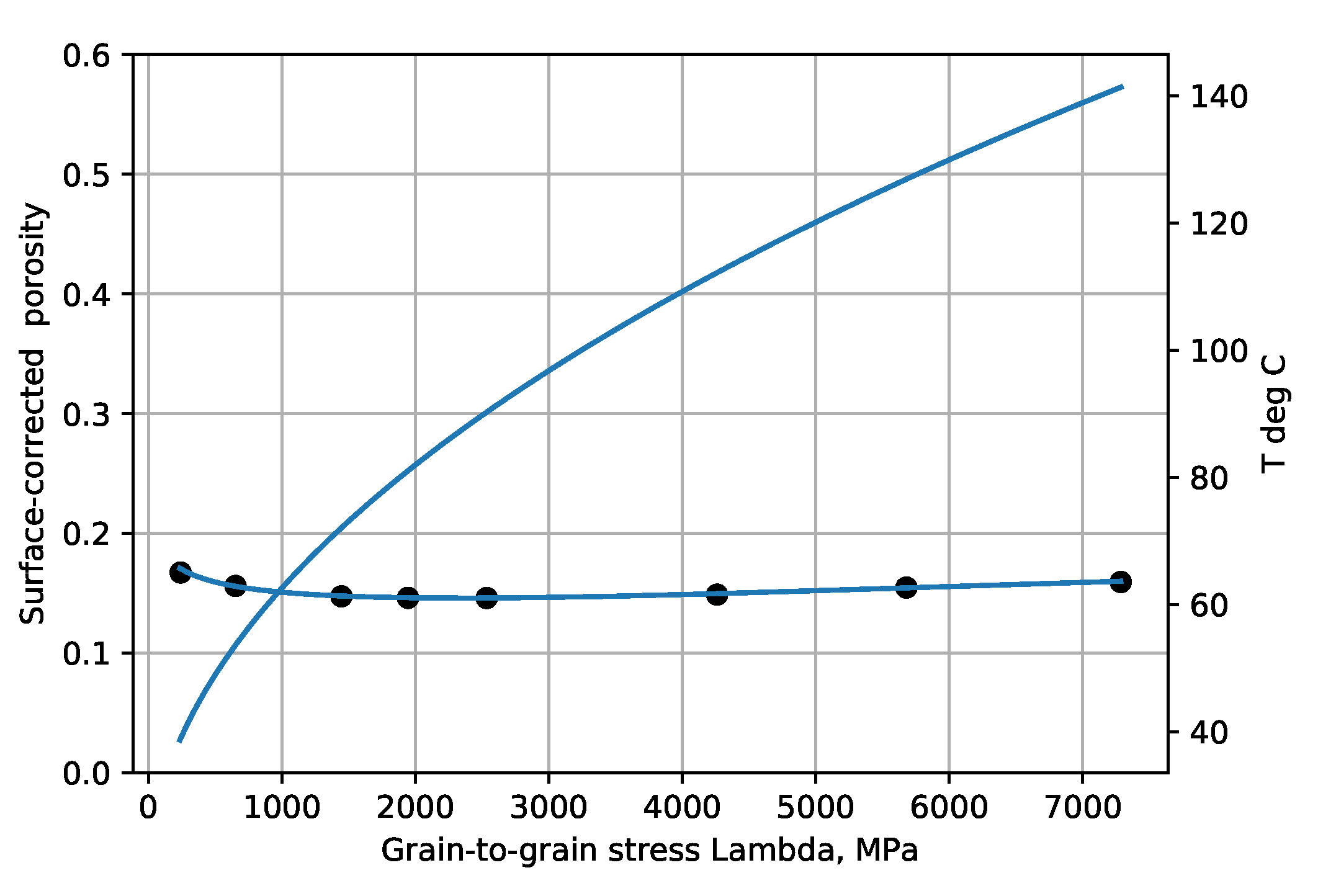
Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show the experimental example porosity-depth relations. Curve fit equations are shown at the top of each plot. ‘Dots’ on the graphs are data points for the Makran and Maracaibo wells, published trend points for Akita wells, and trend points read from graphs for the Oklahoma and Sulu Sea wells. As seen in the figures the provisional maximum paleotemperature is plotted as a linear function of depth, separately for each ‘well’.

It is perspicuous to view porosities versus $\Lambda$, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, which is the force pressing the grains together, and is a more fundamental variable than depth, common to all wells.

The $\Lambda$ axis is approximate. (The approximation $p_w=g{\rho }_{w}z$ for normal water pressure is used to approximate the $\Lambda$ axis as

$$\Lambda \approx g\frac{({\rho }_g-{\rho }_w)}{(1-\phi )}{\int }_0^z(1-\phi )dz.$$

(6)

Here z is sample depth and depth 0 is the sediment upper surface. The grain density and water density are ${\rho }_g$ and ${\rho }_w$ with $({\rho }_g-{\rho }_w)=1.67g/cc$. The water pressures in these wells were not given.) Any mismatch of experimental porosity with approximate $\Lambda$ is not important for illustrative purposes as porosity data points in non-normally-pressured zones are only shifted horizontally, e.g., overpresssured zones appear shifted to the right, and transformed porosity points are shown here next to be nearly constant.

Parameters m and n are fixed so that the well porosity profile in the deeper portion of a well matches the surface reactant terms on the right of Equation (5),

$$\phi {\left(\phi \right)}^{-1.33m}{(1-\phi )}^{-1.33n}\approx c,$$

(7)

where c is a constant. In chemical terms, this means that the ratio of the reacting surfaces terms to pore volume is constant, and indicates that water is a necessary reactant. Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show porosity ’corrected’ in this way and additionally multiplied by a constant factor ${\phi }_{av}^{1.33m}{(1-{\phi }_{av})}^{1.33n}$ which minimizes vertical movement of porosity points for ready comparison to the previous Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. Here ${\phi }_{av}$ means the average porosity over the entire profile.

The corrected deeper porosities have largely moved toward a common value.

These figures indicate that the proposed reaction, Equation (4), is not rate-limiting at temperatures below 30–40 °C, and that longer geologic times (Table 1) or lateral compression can produce greater compaction effects.

Table 2. Derived variables for initial assumptions.

Basin Location	Basin Type	Age Range Ma	E kJ/mol	A ${10}^{15}$/s	Entropy, Relative	m	n
Akita,	back-arc	1.5–146	30	68	0.7	0.95	1.0
Hokkaido
Makran1	abyssal	2.6–105	20	8	0.5	0.85	1.0
Makran2	abyssal	2.6–105	16	3	0.3	0.85	0.95
Sulu Sea	deep-water	0–23	19	18	0.2	0.90	0.80
Oklahoma	convergent	252–323	33	100	0.1	0.85	1.0
Maracaibo	back-arc	2.6–105	22	9	0.2	0.90	0.90

gives m and n, and shows that the scatter of the porosities is reduced using the ratio of the entropy of the porosities after the ‘porosity correction’ to the entropy before the ‘correction’. The convergence of the transformed porosities is good above 30–40 °C and at porosities below 0.5. At porosities greater than 0.5 Equation (4) can have multiple porosity values give the same number, as it has the logistic form. This agrees with deep sea studies which show porosities are chaotic [6] at porosities greater then 0.5. Porosities greater than 0.5 are excluded here in estimating activation energies.

The example wells are scattered around the World. The main task remaining is to find whether Equation (5) predicts the existance of rate-limiting reaction(s) charactorized by one or more activation energies, E, for these wells. Moving the porosity terms to the left hand side (LHS) of Equation (5) gives

$${\left(\phi \right)}^{-1.33m}{(1-\phi )}^{-1.33n}{\left.\frac{\partial \left(ln\right(1-\phi )}{\partial t}\right|}_{\sigma }=A{e}^{-E/\left(RT\right)}.$$

(8)

The left side needs to be evaluated for the well porosity profile in order to obtain E and A. The time derivative- or of equal practical use the derivative of porosity with respect to time—can potentially be obtained from laboratory experiments. Alternatively the time derivative can be obtained if the sediment geologic ages are known at close depth intervals along with the known porosity profile. However only very broad bounding geologic ages are known for these six wells, e.g., the Oklahoma sediments were deposited from early Pennsylvanian to late Permian times which start 323 Myr ago and end 252 Myr ago, Table 1. As these approaches are not currently available, an approximation to the time derivative is used.

Breaking geologic time $\tau$ into many, N, small time increments $\delta t$ it is seen that each term in the sum below is the instantaneous time derivative $ln((1-{\phi }_i)/(1-{\phi }_{i-1}))/\delta t$ for that time. The sum is the average over time of these instantaneous time derivatives and, like the pages of a book, add up to give the (large) finite-difference approximation on the right below, equivalent to only the starting and ending pages of the book as it were.

$${\Sigma }_1^{N}ln\frac{(1-{\phi }_i)}{(1-{\phi }_{i-1})}/N\delta t=ln\frac{(1-\phi )}{(1-{\phi }_0)}/\Delta t.$$

(9)

Here we have put ${\phi }_N=\phi$, the current porosity. ${\phi }_0$ would be the seabed porosity to prevent negative values of the logarithm, but is 0.5 to analyze deeper shales and avoid chaotic behavior close to the seabed.

Porosity changes due to lateral forces and vertical forces are obviously included in the summation of the average, Equation (12), which is used in place of the partial derivative,

$${\left.\frac{\partial \left(ln\right(1-\phi )}{\partial t}\right|}_{\sigma }\to ln\frac{(1-\phi )}{(1-{\phi }_0)}/\Delta t.$$

(10)

This partial derivative on the left of Equation (11) would have come up in the same way if $\sigma$, Equation (3), represented horizontal forces rather than vertical forces. This approximation, or replacement, thus represents overall porosity reduction due to the combined forces and temperatures acting, in natural order, and including changes in overburden and pore fluid pressure, to reduce the potential energy $\Lambda$. This replacement is more appropriate than the partial derivative for computing activation energy, and further cannot be avoided since the actual porosity data result from all these factors. Putting this approximation into Equation (9) gives

$${\phi }^{-1.33m}{(1-\phi )}^{-1.33n}ln\frac{(1-\phi )}{(1-{\phi }_0)}/\Delta t=A{e}^{-E/RT}.$$

(11)

The subscript ‘0’ indicates near the top of the well but at temperatures above ≈40 °C and porosities less than 0.5. (A 60 °C cut-off produces similar results.) Because only a maximum range is known for $\Delta t$, the average $\Delta t$ for the entire section is used in the initial estimates of E in Table 1. 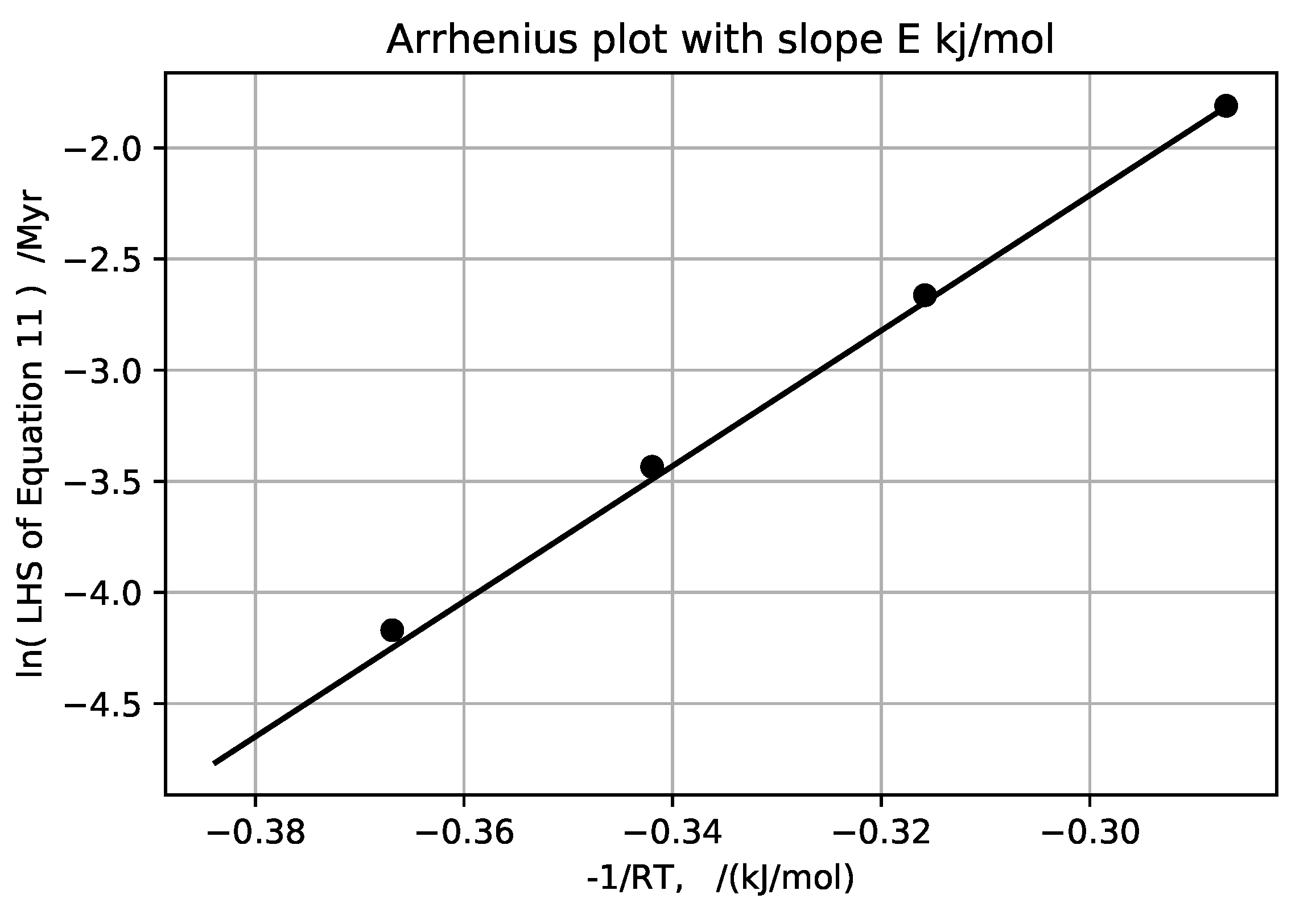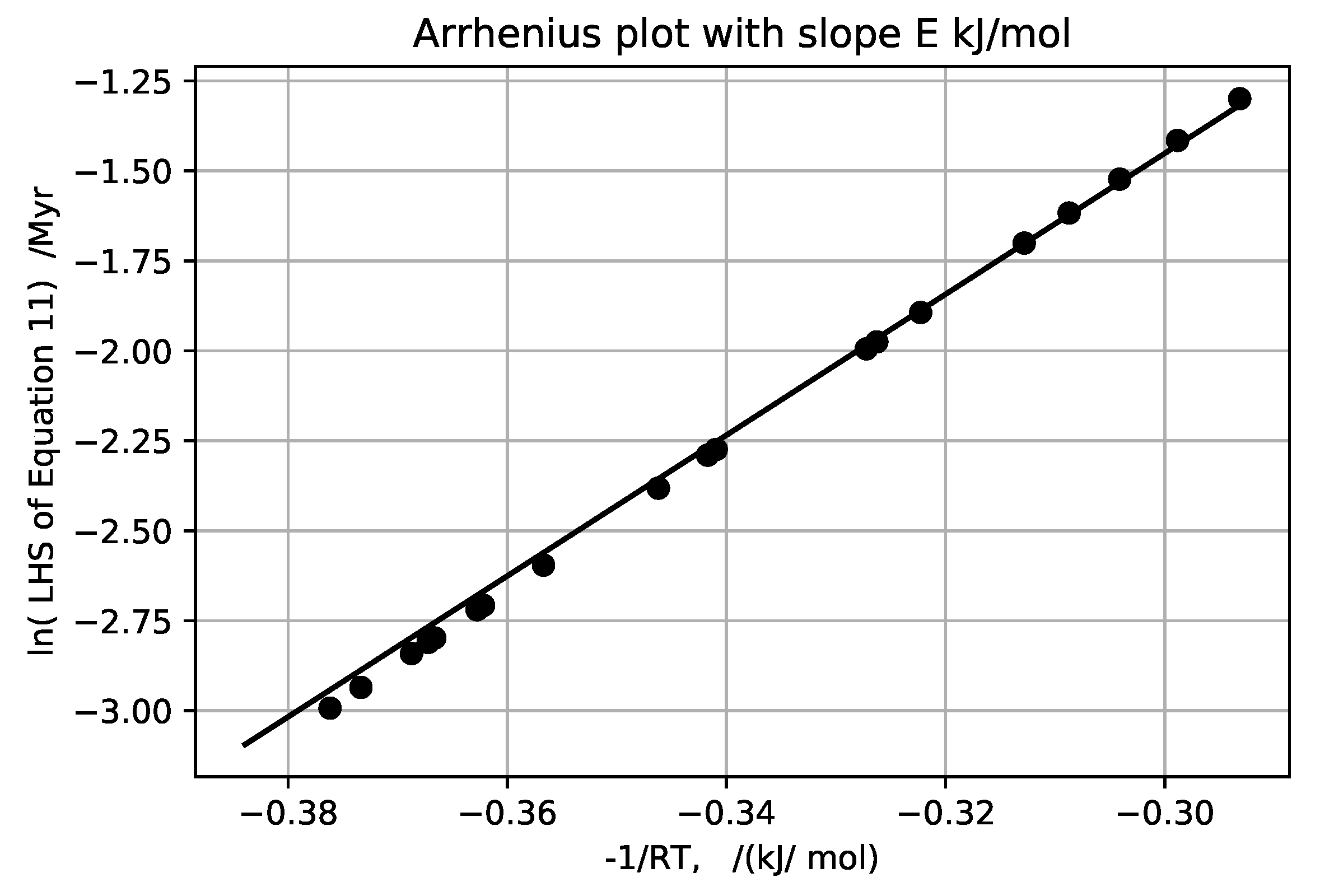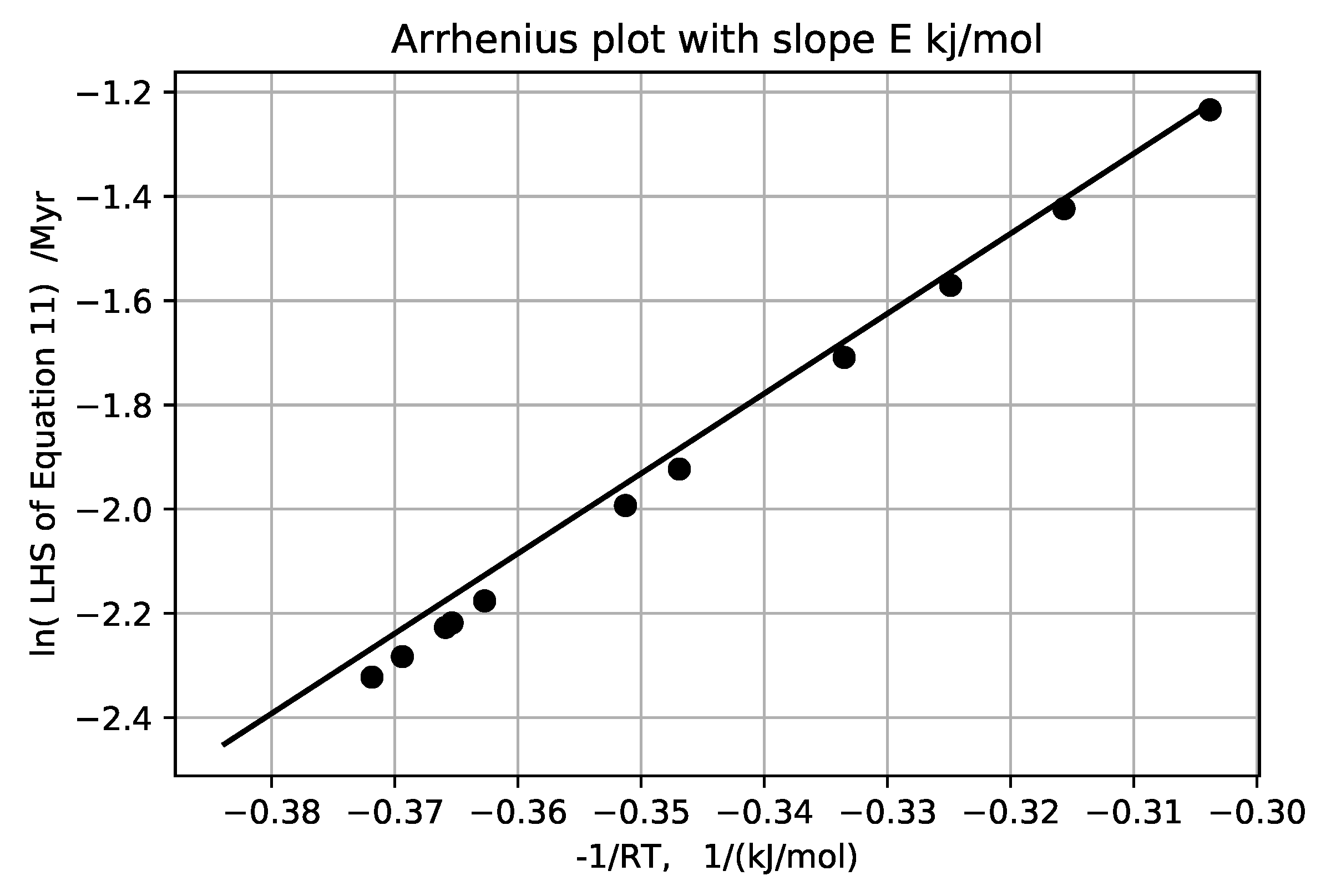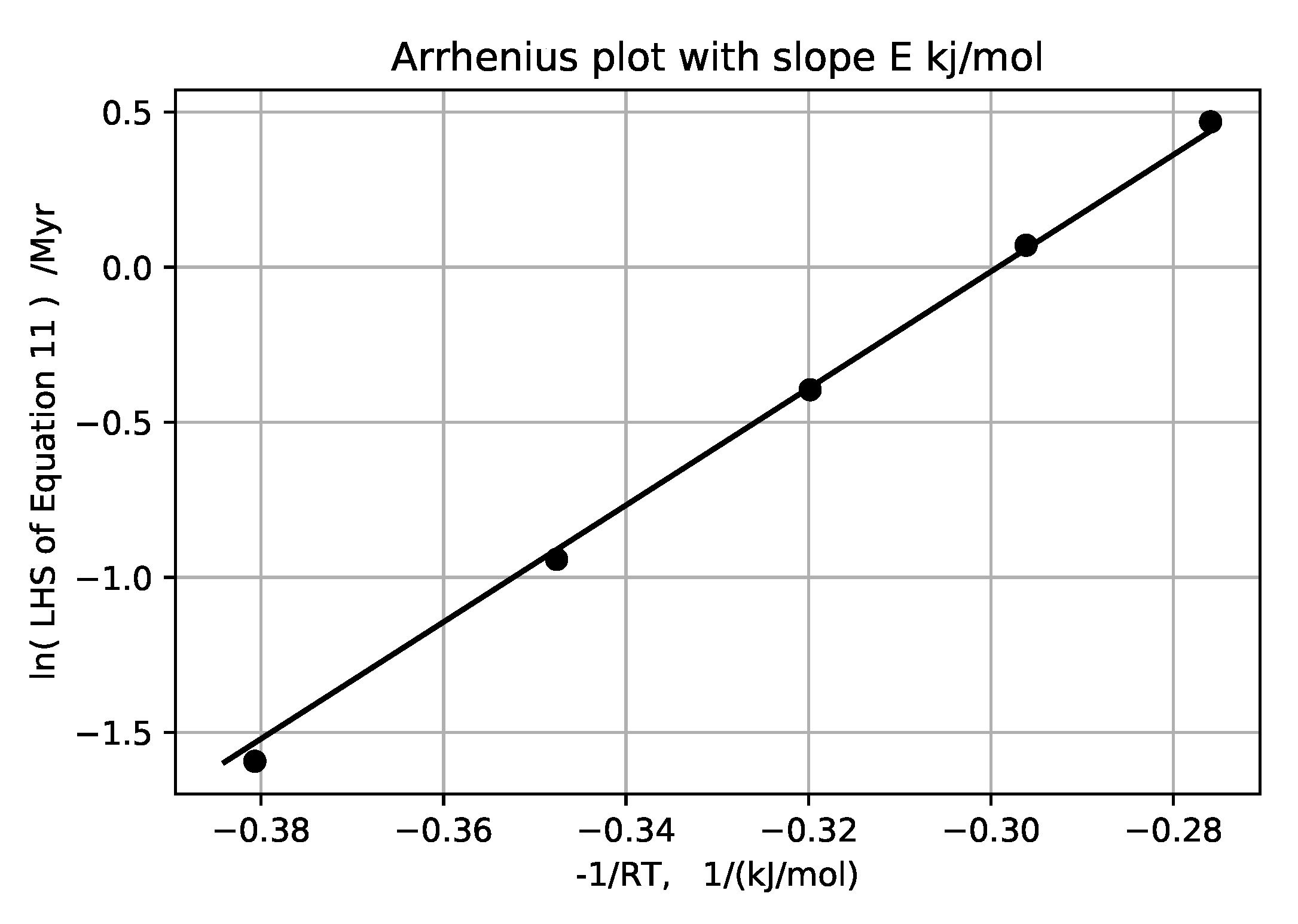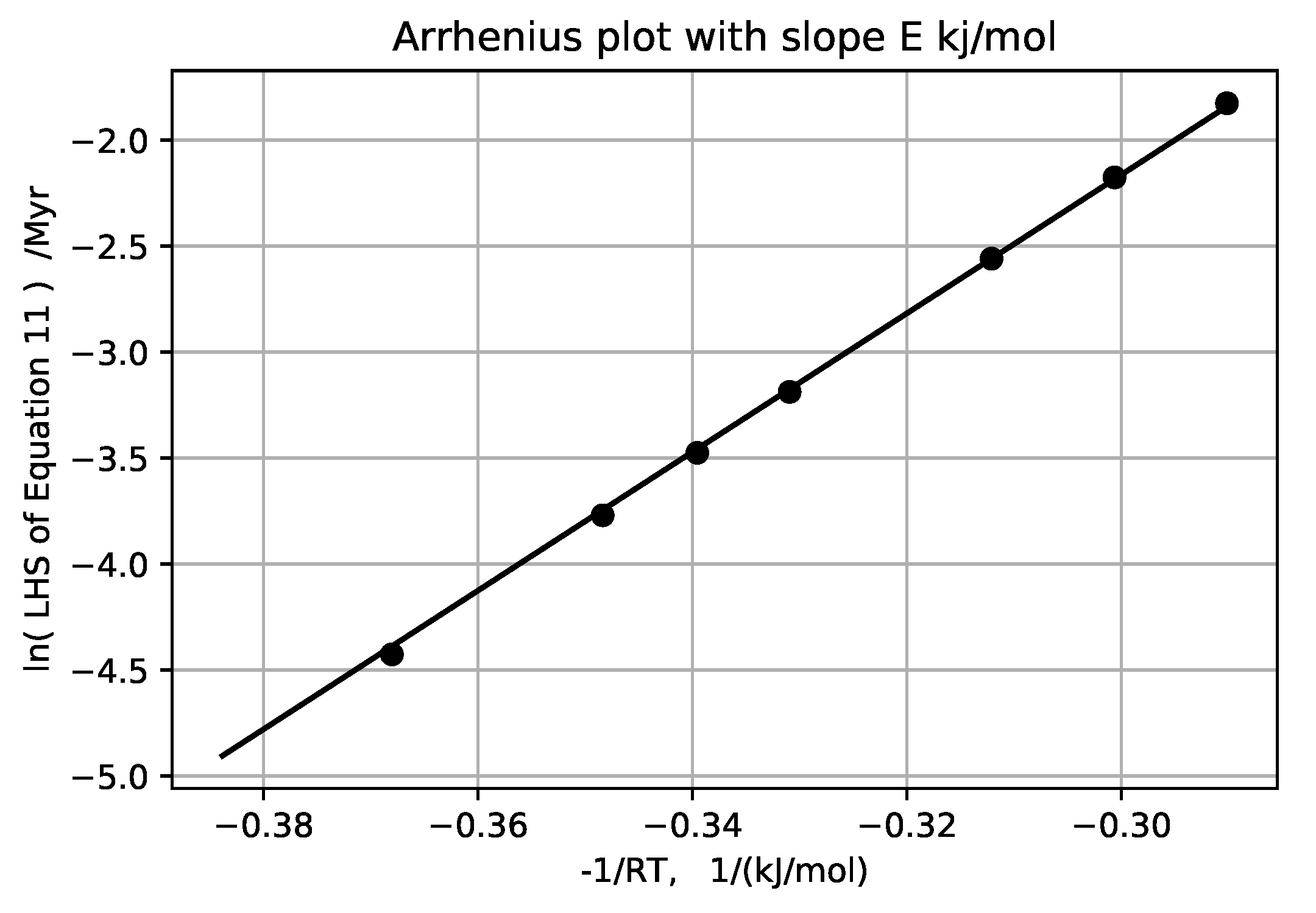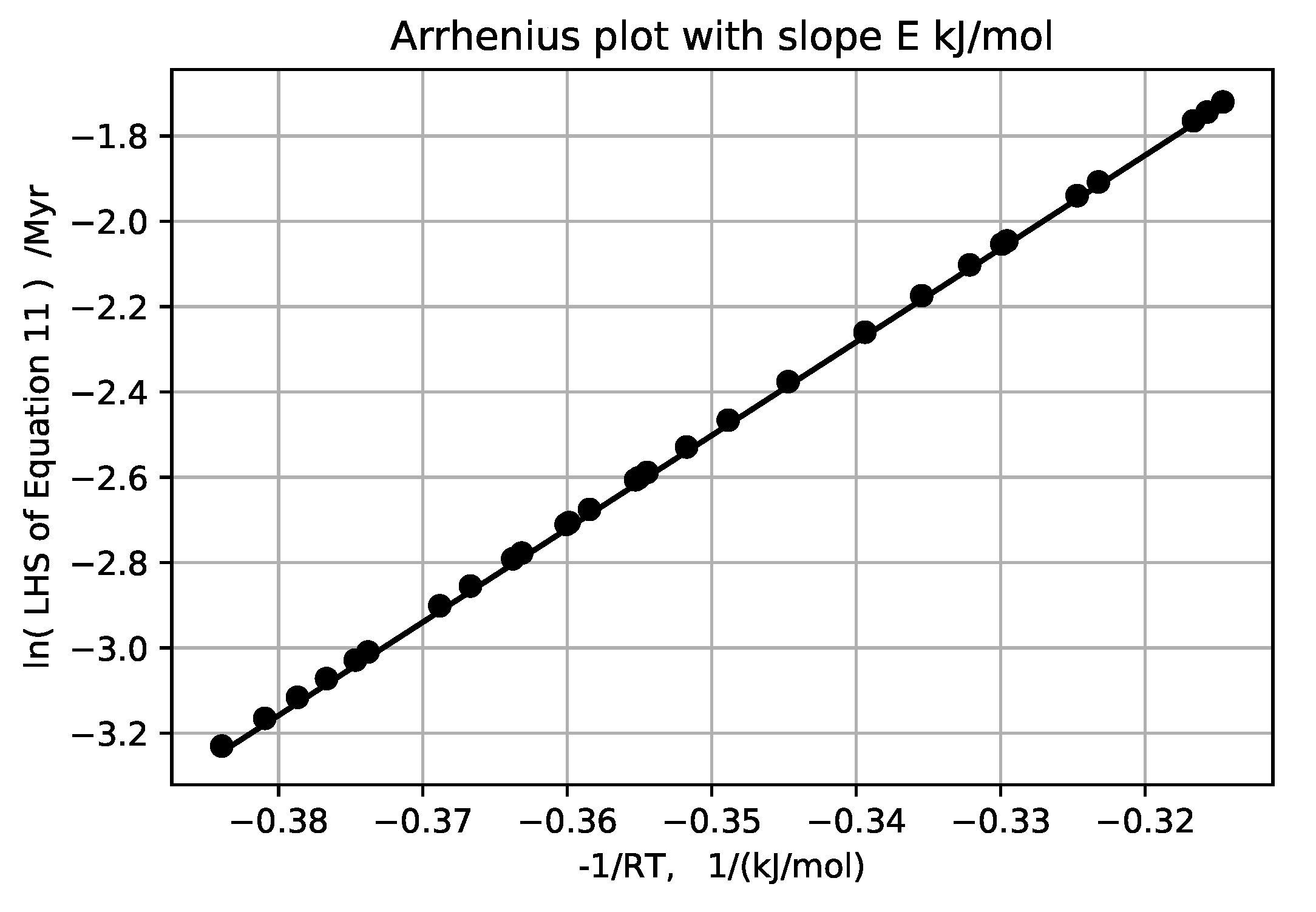Thus the section is supposed to be deposited in a time interval short compared to $\Delta t$ with $ln(\Delta t/\Delta t_{0)}$ zero in this approximation although it is positive for sediments as normally deposited. Plotting the log of the left hand side versus $-1/RT$, gives E and the log of A for the six ‘wells’, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24 and Table 2.

4. Results

As shown in Table 1 the E’s vary from 15 to 33 kJ/mol, averaging 23 ± 6 kJ/mol. Laboratory measurements of the pressure solution of quartz aggregates [16] give 24 ± 15 kJ/mol, suggesting that this is the rate-limiting reaction occurring in shales.

5. Discussion

Averaging the E’s computed from all these provisional temperature gradient assignments, along with the one laboratory measurement, gives an average activation energy of 23 ± 6 kJ/mol. The higher activation energies obtained for Akita and Oklahoma wells are well within the 44 ± 4 kJ/mol activation energy upper bound for solubility of quartz with no load [6], and the Oklahoma well is known to have lost at least 360 m of overburden [8].

With this $E_{av}$ an Oklahoma paleo-geothermal-gradient of 0.12 °C/m was inferred although this is too high if unloading by erosion has been the reason for the higher E. More example wells are needed to sort out this problem. Using an average E assumes the same mechanism occurs in all wells.

With this $E_{av}$, paleo-geothermal-gradients for the other wells were also obtained. These ‘improved’ estimates with other recalculated parameters are shown in

Table 3. Inferred parameters for $E_{av}$ = 23 ± 6 kJ/mol.

Basin Location	Age Range Ma	Paleo $\mathbf{\nabla }\mathit{T}$ C/m	E kJ/mol	A ${10}^{16}$/s	Entropy, Relative	m	n
Akita,	1.5–146	0.06	28	1	0.3	0.95	1.0
Hokkaido
Makran1	2.6–105	0.023	23	6	0.6	0.85	1.0
Makran2	2.6–105	0.017	19	9	0.6	0.85	0.95
Sulu Sea	0–23	0.022	23	16	0.4	0.90	0.80
Oklahoma	254–323	0.12	23	0.1	0.5	0.85	1.0
Maracaibo	2.6–105	0.046	23	2	0.5	0.90	0.90

as far as data convergence allowed. Differences in porosity determination method might have impacted activation energy determinations, e.g., Oklahoma and Maracaibo porosities were measured on hand samples, while as mentioned the Macran porosities are inferred from seismic data.

Current temperature profiles are known privately for thousands of wells. This information would help gain an accurate $E_{av}$, especially for deep-water wells where the paleo-mudline temperature is probably ∼3 °C.

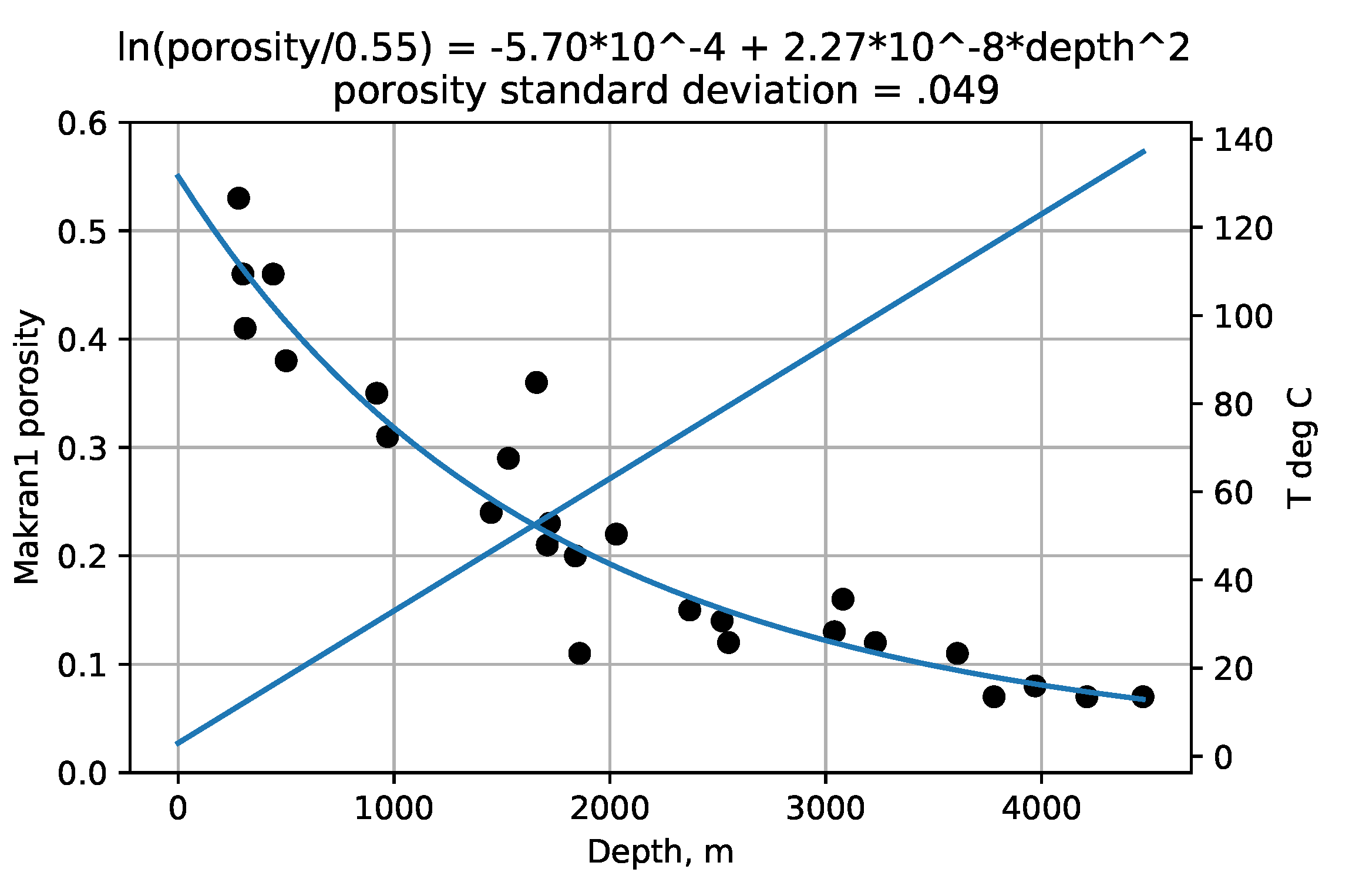
The Makran data, Figure 2 and Figure 3, show that lateral forces in the accretionary wedge (Makran2) produced porosities reduced from nearby abyssal plain (Makran1) porosities. There the major lithology need not be clay throughout, as good reflectors were needed to produce data. The low Oklahoma porosities were also thought to have been reduced by lateral forces [8,9]. Directionally variant lateral forces are often observed in horizontal drilling [16]. The compaction response mechanism to both vertical and horizontal forces is probably the also given by Equation (4).

6. Conclusions

Equation (4) explains shale compaction at temperatures above ≈35 °C with activation energies E ≈ 23 ± 6 kJ/mol, close to 24 ± 15 kJ/mol for the pressure solution of quartz. Problems of mineralogy, grain shapes and sizes, permeability, overpressures and pore connectivity are by-passed. The results support nearly fractal pore interfaces with m and n between 0.8 and 1.0 The reduction in $\Lambda$ is also modeled as proportional to geologic age to the first power. By Equation (12) the one-dimensional problem is recognized as three spatial dimensions. For obtaining activation energy it is assumed that deposition occurs over a comparatively short time period compared to the geologic age. Porosities greater than 0.5 are not used in computing activation energy as near-surface sediments have chaotic porosities. Provisional paleotemperature gradients are used to obtain activation energies which are averaged to bootstrap to hopefully better paleotemperature gradients. Given porosity data for an uneroded section and an average activation energy, $E_{av}$, one can infer or rank maximum paleo-geothermal-gradients and from that organic maturity, thus avoiding unnecessary drilling.