Abstract
As a result of mountain permafrost creep, rock glaciers are common features in high-altitude periglacial areas. From a practical point of view, beyond their localization and inventorying, both the monitoring and prediction of their evolution due to climate changes are crucial. One of the effects of climate change is the thickening of the basal shear zone (the portion of the rock glacier where most deformations are localized), eventually leading to the development of unexpected and unprecedented (in terms of location, magnitude, frequency, and timing) instability phenomena. These phenomena bear consequences for the understanding of landscape evolution, natural hazards, and the safe and sustainable operation of high-mountain infrastructures. Most of the studies about active rock glaciers are focused on the analysis of monitoring data, while just a few studies are focused on modeling their behavior to understand their possible further evolution. The active rock glacier response is characterized by a viscous (rate-dependent) behavior, influenced by seasonal temperature oscillations, and characterized by a seasonal transition from slow to fast. In this work, a new thermo-mechanical model based on the delayed plasticity theory and calibrated on experimental results is proposed. The model is employed to evaluate the influence of geometry and forcing (air temperature) on a real rock glacier (Murtèl-Corvatsch rock glacier) creep behavior.
1. Introduction
The main processes related to climate change in high-mountain environments involve the role of permafrost degradation in promoting slope instability (amongst others, [1,2]). Rock glaciers are globally recognized as an expression of creeping permafrost in the periglacial zones of high-latitude and high-altitude environments (e.g., [3,4]). According to [5], rock glaciers are quaternary forms of perennially frozen debris supersaturated with interstitial ice and ice lenses or even with bodies of massive ice moving downslope.
The long-term monitoring of rock glacier movement in the European Alps indicates that, in recent decades, the increase in ground temperatures [6,7,8] induced rock glacier velocity increases, on both seasonal [9,10,11] and decadal [12,13,14,15,16,17] timescales.
For instance, as shown in [18], in the European Alps, annual terrestrial geodetic surveys suggest that the average rock glacier surface velocity has increments of about +52% each year during the monitoring period (2010–2014), with most of the rock glaciers reaching surface velocity maxima in 2014 [6].
Temperatures inside a rock glacier are governed by heat conduction/convection processes (e.g., [19]), whose boundary conditions are the mean annual air temperature (MAAT) and the permafrost base temperature. Temperature increments may induce local ice melting (e.g., [20]), associated with both variations in water pressure and flow rate in the rock glacier body and a reduction in ice intergranular bonds strength, potentially inducing local instability phenomena [21]. Hence, to correctly analyze the mechanical response of rock glaciers, hydro/thermo/mechanical coupled problems have to be solved. To further increase the complexity of the problem, a severe spatial heterogeneity in ice content and debris grain size, ranging from silty sand to large boulders [22], is usually observed in rock glacier bodies. Smaller volumetric ice content and debris grain size are usually observed in the shear horizons [23,24,25], the parts of the rock glaciers, usually characterized by a thickness of a few meters (e.g., [25]), where most shear strains (up to 90%) and strain rates are concentrated [26]. In addition, local ice melting within different parts of the rock glacier body may induce differential rates of downslope creep and consequently geomorphology variations. However, only a few studies have measured internal movements in rock glaciers [26,27,28], which are essential for investigating rock glacier instability.
The first step for the solution of hydro/thermo/mechanical coupled problems is the definition of constitutive relationships capable of reproducing the material behavior. To this aim, experimental laboratory tests on samples directly collected from rock glaciers (e.g., [21,28,29,30]) were performed. The test results highlighted that the strength of frozen materials essentially depends on their composition, in terms of mixtures of ice and rock elements, and on temperature. The experimental results are, however, quite rare due to difficulties in accessing these areas, and in collecting samples, especially at depth. It is worth mentioning that, with regard to the dimension of the rock elements of a rock glacier body, the response of small-scale laboratory samples is not necessarily representative of large-scale behavior. In the future, to overcome laboratory test limitations, “numerical experimental tests” (for instance, by using the discrete element method, as is shown in [31,32]) can be employed, in the framework of multiscale approaches, for better understanding the global system response.
The constitutive models currently adopted to reproduce the mechanical behavior of this material are an adaptation of Glen’s [33] or Nye’s [34] laws, originally introduced for describing glacier movements. These laws are empirical power law functions, depending on the state of stress, temperature, and ice content. One limitation of these empirical laws is that they cannot satisfactorily reproduce the response of the shear horizons and the rest of the rock glacier body with a single set of constitutive parameters [20]. In other words, they cannot exhaustively describe the heterogeneity of rock glaciers characterized by debris and debris ice-riched layers (e.g., [25,28]). Moreover, as will be shown in Section 2.1, these laws do not always satisfactorily reproduce the previously cited laboratory test results. Several authors (e.g., [12,28,35,36]) demonstrated a strict link between the rising MAAT and accelerating creep velocity of alpine rock glaciers. This acceleration is usually attributed to a variation in the thermal regime of the ground, induced by climate change [14,22,37,38,39].
The final goals of the research carried out are: (i) a better understanding of the currently observed dominant controls on geomorphological changes and (ii) the introduction of reliable and simple tools to model the response of rock glaciers, capable of reproducing both short- and long-term adaptation of these systems to changing environmental factors.
As a first step toward this direction, in this paper, the authors intend to introduce a simplified approach for modeling the thermo-mechanical coupled response of rock glaciers (Section 2). This is based on: (i) the introduction of a new constitutive law, conceived according to the delayed plasticity theory proposed in [40], for describing the mechanical behavior of ice-rock mass mixtures (Section 2.1), (ii) the solution of the heat diffusion equation (Section 2.2) and (iii) the schematization of the rock glacier into a one-dimensional problem (Section 2.3).
To exemplify the practical application of this simplified approach, the case of Corvatsch rock glacier, located in the Swiss Alps is presented and the in-situ measurements compared with the numerical simulation results in Section 3. Finally, in Section 4 the results of a sensitivity analysis allowed us to put in evidence the main geometrical factors influencing rock glacier response.
2. A Simplified Approach to Model Rock Glacier Response
The numerical modeling of the mechanical response of rock glaciers is usually based on the employment of a continuum approach. According to this approach, to solve the problem, a system of partial differential equations describing (i) the balance of momentum, (ii) the compatibility condition and (iii) the material constitutive law (Section 2.1) has to be solved. In addition, since temperature plays an important role, the heat diffusion equation (Section 2.2) also has to be solved and the coupling between mechanical and thermal processes has to be taken into account.
In general, numerical (e.g., finite element or finite difference) models can account for the correct geometry of the system and the heterogeneity/spatial variability of the rock glacier internal structure (e.g., [21,39,41,42]). However, in most of the cases, a reliable description of geometry and heterogeneity/variability is missing. Hereafter, a simplified one-dimensional geometry (Section 2.3) is considered, and the material is assumed to be homogeneous (the material mechanical properties/density/thermal diffusivity are assumed constant along depth).
2.1. Constitutive Relationship
The constitutive relationship proposed by the authors is conceived according to the delayed plasticity theory proposed in [40].
According to this theory, strain rate tensor is decomposed into an instantaneous/reversible and a delayed/irreversible part (). With respect to standard plasticity theory, the consistency condition is abolished (implying that the effective stress state can be either inside or outside the yield locus f) and the flow rule is expressed as it follows:
where g is the plastic potential, is the stress tensor and Φ is the viscous nucleus. Φ can be defined as the distance (measured through a suitably defined mapping rule) between the state of stress and the yield locus position. In most of the cases, Φ is a non-negative and increasing function of f. Under this assumption, f may be interpreted as a scalar measure of the probability of occurrence with time of irreversible strain accumulation.
The elastic law is assumed to be linear and isotropic. The yield function (f), plastic potential (g) and the viscous nucleus (Φ) are defined by starting from the experimental results reported in [29]. According to these results:
- The material mechanical response is practically unaffected by the confining pressure;
- The material shear strength (both peak and residual) depends on temperature;
- During creep tests, the logarithm of the deviatoric strain rate linearly increases with the applied stress deviator.
For the sake of simplicity, the yield function is defined according to the Tresca criterion, where the cohesion (c′) is assumed to depend on temperature (T). Since rock glaciers accumulate large irreversible strains with time, only the residual conditions are accounted for. The yield function is defined in a non-dimensional form:
being
where and are the maximum and the minimum principal stress, respectively. In practice, Equation (3) represents the radius of the Mohr circle associated with the state of stress. The evolution law of c’ with T, defined and calibrated based on the experimental results of [29] (points of Figure 1) and performed on ice–silty sand mixtures, is expressed as:
where c1 and c2 are, in general, expected to be dependent on the ice content. The line reported in Figure 1 is obtained by imposing c1 = 500 kPa and c2 = 1.2 °C, and it is valid for ice content values ranging between 75 and 90%. For T = 0°, when the ice intergranular bonds are completely thawed, cohesion is expected to be nil, since, owing to the large strains developing in the shear zone, the unbonded granular material is expected to be at a critical state (implying the cohesion to be nil). The unbonded material shear strength is expected to be associated with a residual friction angle (an additional parameter that is difficult estimate) and effective stresses (depending on pore water pressure, this can also be difficult estimate). The introduction of this additional contribution surely enriches the model, but it makes the calibration significantly more complex. To provide safe side estimations, the contribution of friction to the material shear strength is disregarded.
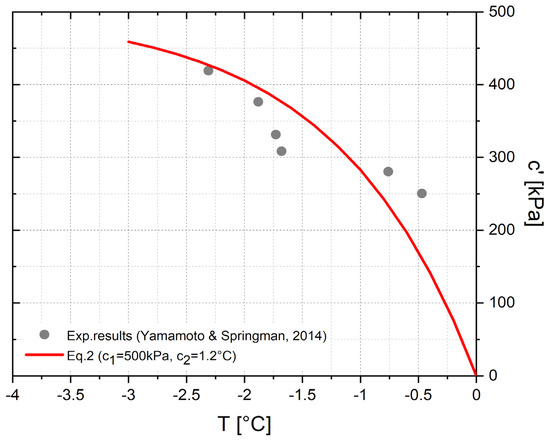
Figure 1.
Variation of cohesion with temperature. Gray points represent experimental results from [29], while the red line represents the fitting of the proposed approach.
The plastic potential is defined as:
where c* is a dummy variable.
The employment of a non-dimensional yield function and of a dimensional plastic potential is particularly convenient, since, under this assumption, the viscous nucleus parameter values are expected not to depend on the applied stresses.
To obtain a linear relationship between deviatoric stress and the logarithm of deviatoric strain rate, an exponential viscous nucleus is employed:
where η and α are constitutive parameters.
To calibrate η and α, the experimental results reported in [29] (triangles of Figure 2) obtained for T values ranging between −1.92 and −1.98 °C were considered. The dashed red line is obtained by integrating the constitutive relationship under triaxial creep stress paths and by imposing T = −1.95 °C and η = 3.5 × 10−7 1/s and α = 5.2 (Table 1).
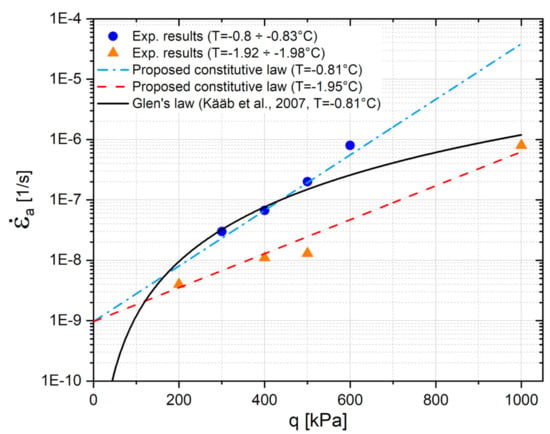
Figure 2.
Variation of axial strain rate with the stress deviator. Orange and blue points represent experimental results from [29] at different temperatures, red dotted and light blue point dotted lines represent the fitting of the proposed approach: finally, the black line represents the commonly used approach.

Table 1.
Summary of imposed and calculated parameters.
To validate the model, the experimental results reported in [29] (circles of Figure 2) for T ranging between −0.8 and −0.83 °C (not employed in the model calibration) are compared with the constitutive model prediction (dashed-dotted line of Figure 2). Even in this case, the agreement is very satisfactory.
For the sake of completeness, in Figure 2, the line obtained by employing the Glen’s law with the parameter values suggested by [12] for T = −0.81 °C is also reported (solid line). This relationship cannot satisfactorily reproduce the experimental results.
2.2. Heat Transmission
By following what has been suggested by other authors [12,20], the heat transmission is assumed to be only governed by conduction. The differential equation describing the variation of temperature in time (t) and space is the well-known heat equation:
It is worth mentioning that the problem hereafter studied is only “partially coupled”: temperature influences the material response (Equation (2)), but the mechanical problem does not influence the thermal one. This implies that the thermal problem can be solved independently, and its results can be employed as input data for the mechanical one.
2.3. One-Dimensional Problem Schematization
Analogously to what was proposed in [12,20], the rock glacier is assimilated to an infinite slope h-thick, θ-inclined (Figure 3) and resting on a rigid bedrock. The rock glacier body is subdivided into three subdomains (Figure 3): (i) an upper part where ice is present only in cold seasons (subdomain 1 of Figure 3), (ii) the shear horizon (subdomain 3 of Figure 3), where most of the strains develop and the particle size distribution is analogous to the one employed by [29] for the experimental tests, and (iii) the portion between the two (subdomain 2 of Figure 3), where strains are negligible owing to the interaction between large rock boulders.
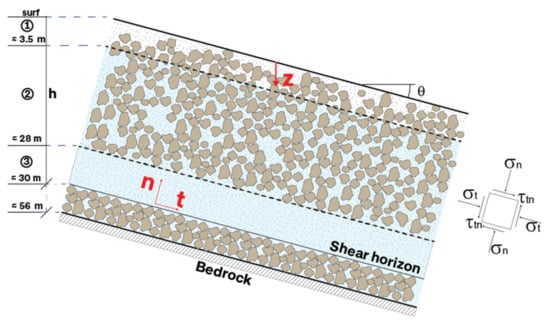
Figure 3.
Schematic profile of the Murtél-Corvatsch rock glacier (after [21]).
For the sake of simplicity, for the material in subdomains 1 and 2, a rigid behavior is assumed, whereas the constitutive law introduced in Section 2.1 is employed to reproduce the mechanical behavior of material belonging to subdomain 3.
The whole domain is under simple shear conditions. Therefore, normal (σn) and tangential stresses (τ) can be assessed by simply imposing the balance of momentum (di Prisco and Pisanò, 2011). Since rock glacier accumulates large strains in the shear horizon, the authors assume the evolution of stress σt (Figure 3), associated with the static redundancy of the problem [43,44], to be ended and, according to the employed (nil) dilatancy angle value (Equation (5)), to be equal to σn [44]. It is worth mentioning that, owing to the employed yield function and plastic potential, the response is not influenced by the value of the intermediate (out-of-plane) stress.
As far as the thermal problem is concerned, only subdomains 2 and 3 are considered. To solve the thermal problem, (i) the initial temperature along the whole stratum and (ii) the variation in time of temperature at the top of subdomain 2 and at the base of the shear horizon have to be known.
In the following section (Section 3), this simplified geometrical scheme will be employed to reproduce the response of Murtèl-Corvatsch rock glacier. This case was chosen since (i) after the first investigations of this area started in of the 1970s [5], it is now one of the best investigated permafrost areas in the Alps and part of the PERMOS network [6,23,45,46] and (ii) the stratigraphies of two boreholes located within a distance of 30 m shows significant small-scale heterogeneities in the rock glacier [28,41].
3. Case Study: Murtél-Corvatsch Rock Glacier
The Murtèl-Corvatsch rock glacier (amongst others: [22,23,28,46]) is situated in the upper Engadine (Figure 4), facing Piz Corvatsch (3300 m a.s.l.), in the southeastern part of Switzerland (UTM, 563 131, 5 142 001; zone 32T). It extends from sea level from 2620 to 2850 m a.s.l. It is 400 m long and 200 m wide (total area of about 0.08 km2), characterized by a mean slope of about 10° and marked furrows and ridges on its surface. Within the area, the Murtél-Corvatsch rock glacier is one of the dominant periglacial features, but further rock glaciers and talus slopes are present to the west (Figure 4). In 1987, a 60 m deep borehole was drilled and equipped with thermistors that have been manually logged in 1 month intervals until 1992, and since then data have been stored automatically by a logger collecting temperature data in 6 h intervals [46]. The site is characterized by a coarse blocky (the diameters of the boulders are in the range of decimeters up to several meters) surface layer of approximately 3–3.5 m in thickness above a massive ice core down to 28–30 m and a frozen blocky layer underneath, reaching from 28 to 50 m, probably adjacent to the bedrock [21] (Figure 5). The ice core has an average temperature of −2 °C at 10 m depth and −1.4 °C at 25 m depth (Figure 6). The active layer has an average thickness of about 2 m. The involved lithologies mainly consist of granodiorite and granite (Schneider et al. 2012), and studies on back-weathering at this site have shown back-weathering rates of 2 mma−1 (Müller et al. 2014). For Corvatsch rock glacier, likely one of the most investigated quaternary forms (e.g., [23,46]), there exists a long-term and continuous data acquisition process (i.e., ground and depth temperatures, superficial displacements). Attempts to determine the age of this rock glacier [47,48] obtained an age of 5000 to 6000 as a minimum value [49]). The rock glacier is characterized by a rather slow creep velocity (10–17 cm/year) and is considered a thick and ice-rich landform with an average volumetric ice content of 60% [20,21,47].
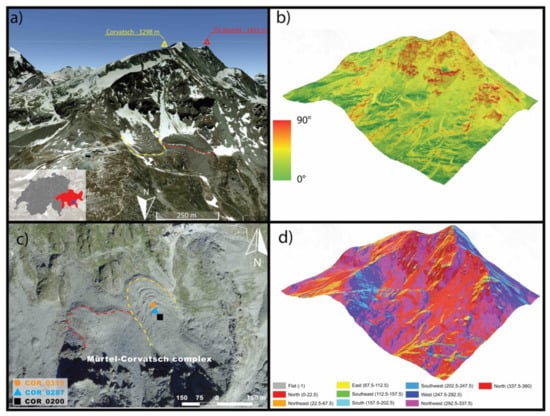
Figure 4.
(a) Murtèl-Corvatsch rock glacier panorama; (b) slope chart of the area; (c) orthophoto of the rock glacier complex (from Google Earth, 2016) with indicated Corvatsch rock glacier (yellow dashed line) and Mùrtel rock glacier (red dashed line); (d) aspect chart of the area.
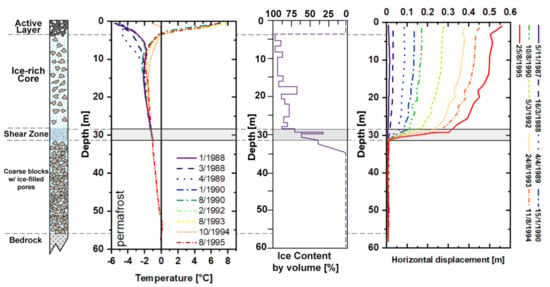
Figure 5.
Stratigraphic column, temperature profile along the rock glacier body, ice content by volume and displacement at depth for the Murtél-Corvatsch rock glacier (modify after [21]).
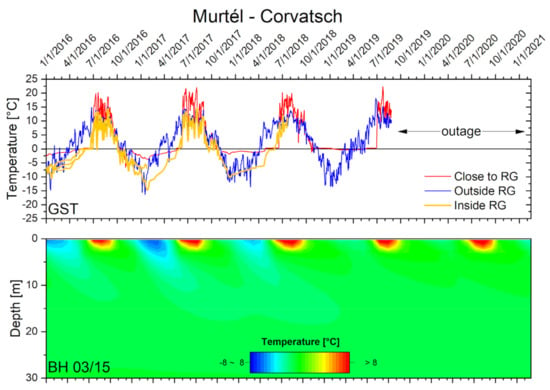
Figure 6.
Ground Surface Temperature (GST) and temperature profile for the Murtèl-Corvatsch rock glacier. Data source: Swiss Permafrost Monitoring Network [6].
Annual precipitation at the site is about 900 mm (982 mm St Moritz 1951–1980; Segl-Maria 978 mm 1979–2021; 900.1 mm Piz Corvatsch 1979–2021) [6]. Typical maximum snow cover thickness is between 1 and 3 m. The mean ground annual surface air temperature is 1.8 °C for the observation period of 2011 to 2019, while the mean annual air temperature since 1979 at Piz Corvatsch weather station (46.41° N 9.82° E, 3305 m a.s.l.) is −5.4 °C.
4. Model Application and Results
The Corvatsch rock glacier case study is discussed by employing the simplified approach presented in Section 2.
The slope inclination is assumed to be equal to 10° and the shear horizon is assumed to be characterized by a thickness equal to 2 m, ranging from a depth from 28 to 30 m (Figure 3).
For the solution of the thermal problem, the in-situ measurements [6] of variation in time of temperature from 2016 to 2020 are employed. In particular, the distribution of temperature on 1 January 2016 is employed as initial conditions (Figure 7a), whereas variation in time of temperature at the base of the shear horizon and variation at the top of subdomain 2 of Figure 3 are employed as boundary conditions (Figure 7b). The numerical results in terms of variation in time of the temperature along depth will be compared with the in-situ measurements in Figure 8.
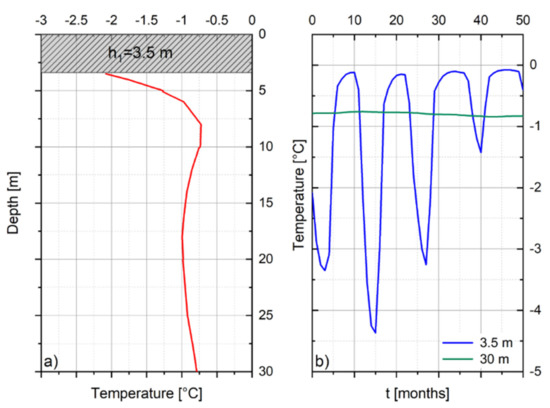
Figure 7.
(a) Initial and (b) boundary conditions for the thermal problem.
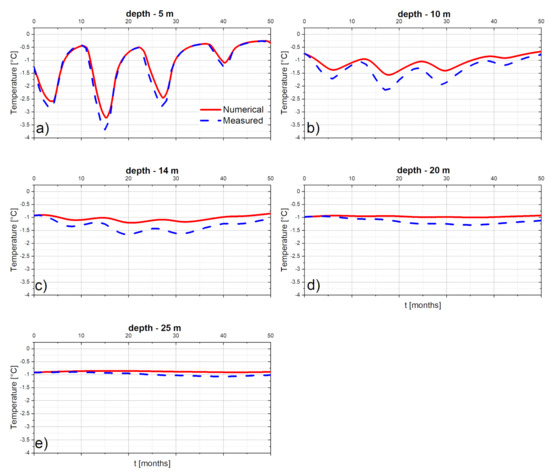
Figure 8.
Comparison of temperature variations with time for different depths: (a) z = 5 m, (b) z = 10 m, (c) z = 14 m, (d) z = 20 m and (e) z = 25 m.
The numerical results in terms of temperature time history are in satisfactory agreement with the experimental measures (Figure 8), confirming the suitability of the simplifying assumptions (Section 2.2). This also suggests that during the considered time-period (50 months) significant variations in the thermal properties of the system (e.g., variations in the ice content or development of melted water flow paths in the rock glacier body) did not take place. Moreover, the results also highlight that those seasonal variations in temperature are observed only in the superficial layers: for the considered period, for depths larger than 14 m, the variation is lower than 1 °C.
By following what was suggested by [12], for calculating stresses acting in the rock glacier body, the ice unit weight is employed. The numerical results are reported as variation in the time of displacement profile along depth in the shear horizon (Figure 9a) and variation in the time of surface velocity (Figure 9b, obtained by GPS measurements). The displacement distributions (Figure 9a) along depth in the shear zone is practically linear, implying that strains are almost constant. The ground surface velocity is almost constant in the considered time period. Its average value (28 cm/year) is in reasonably good agreement with the in-situ measurements (10–17 cm/year).
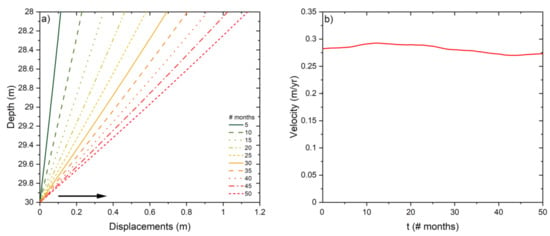
Figure 9.
(a) Variation in time of profiles of displacements in the shear horizon and (b) variation of velocity with time.
A multiscale approach is essential to benefit from physical data in laboratory tests and physical models, as validation and parameter calibration opportunities.
4.1. Sensitivity Analysis
In the previous section, it was shown that the model proposed can reproduce the mechanical response of rock glaciers. In this section, a sensitivity analysis was carried out to explore the influence on the surface velocity of different input geometries and parameters. The difference in shear zone thickness, slope inclination and the depth of shear zone values were considered. For all the cases considered, the thermal boundary and initial conditions are the ones of Figure 7.
The results are summarized in Figure 10. Surface velocity linearly increases with the shear zone thickness, testifying that for all the cases considered almost constant strain distributions in the shear zone were obtained.
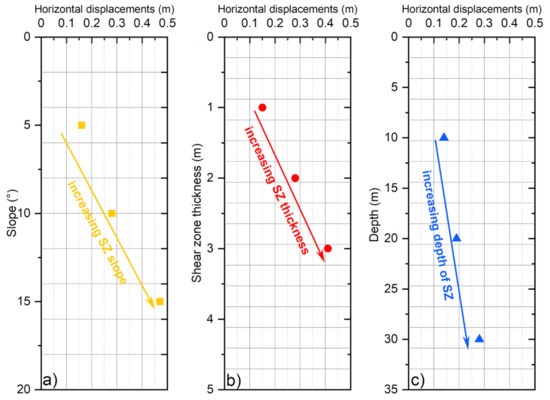
Figure 10.
The sensitivity analysis results varying (a) shear zone slope, (b) shear zone thickness and (c) shear zone depth.
As expected, surface velocity also significantly increases with the inclination.
Considering an increment on shear zone inclination up to three times (5°, 10° and 15°), the results show an increment up to 300% (Figure 10). Absolute mean velocities are strongly affected by variations in geometry, due to changing stress conditions (Equation (3)). However, over the timescales considered in this study (seasonal to multi-annual), the geometry of a rock glacier is not expected to change substantially.
Larger velocity values are also observed for larger shear zone depths. This implies that, for the time-period considered and for the imposed thermal boundary conditions, the influence of the state of stress (stresses increase linearly with depth) is significantly larger with respect to the one of temperature (larger for more superficial layers).
However, this conclusion is not general, since a considerable increase in temperature due to global warming would lead to faster flow, as also reflected in the observational data sets presented in [12,20].
4.2. Model Assumptions and Limitations
For the sake of clarity, in this paragraph the limitations of the proposed model, clarifying the assumptions made, are discussed.
First, we considered the rock glacier dimensions, i.e., a thickness of 30 m circa for the body and 2 m for the shear zone, which are significantly smaller with respect to the planar dimension (400 m). As is also done for landslides in these cases, the assumption of schematizing the geometry as one-dimensional is very common. In principle, the approach proposed here by the authors can also be extended to two- or three-dimensional problems. Nevertheless, in these cases an accurate definition of both ground surface and shear zone geometry is crucial. In all the cases in which an accurate description of geometry is missing, implying that two- and three-dimensional solutions are not necessarily reliable, one-dimensional solutions have to be preferred, at least for these preliminary evaluations.
Furthermore, despite the heterogeneity shown by quaternary forms such as rock glaciers, a simplification on the homogeneity of the shear band is necessary in all the cases in which the information regarding the geometry and the composition/mechanical behavior of the material in the shear zone is very limited. Even if the rock glacier considered here is one of the most studied, an accurate description of the shear horizon, allowing one to properly characterize the heterogeneity, is missing. For this reason, the authors assumed the shear horizon to be homogeneous.
Concerning the thermo-mechanical model, the main assumptions are as follows:
- The thermal problem is characterized by a complex time-varying boundary condition (on the top). In very simple, but unrealistic, cases (e.g., linearly increasing temperature or harmonically varying temperature), a closed form solution can be derived. Unfortunately, for the imposed boundary conditions (Figure 7b), an analytical solution for the thermal problem cannot be derived. Moreover, due to both the thermo-mechanical coupling and to the non-linearity of the constitutive relationship, which are also for the mechanical problem, a closed-form solution cannot be derived.
- The authors assumed that the presence of ice bonds provides a cohesion to the material. When the ice is completely melted, cohesion is expected to be nil. The melted material (a rock fragments–water mixture) is expected to behave as a standard soil at a critical state (i.e., without cohesion). However, since the lack of measurements of pore water pressure, a reliable evaluation of the effective stresses and, therefore, of material (frictional) shear resistance is not possible. For the sake of simplicity, the authors disregarded this contribution.
- From the experimental data of [29] (Figure 2), we derive that during creep tests, the logarithm of the deviatoric strain rate seems to linearly increase with the applied stress deviator. To reproduce this experimental trend, the authors introduced an exponential viscous nucleus.
- When irreversible processes take place (in this case, the accumulation of irreversible strains) energy is dissipated (the dissipation can be measured as the product of stresses and irreversible strain rates). In principle, this dissipated energy is expected to induce a temperature increase (heat generation). For the sake of simplicity, in the proposed model, the authors disregarded this aspect. This assumption, however, does not compromise the model capability of reproducing the experimental results (Figure 8).
5. Conclusions
In this paper, a thermo-elastic–viscoplastic 1D model is proposed. The numerical model couples heat conduction to a temperature-dependent elastic–viscoplastic constitutive relationship, phenomenologically calibrated on a series of experimental laboratory test results. The proposed constitutive law is suitable for reproducing the response of the material belonging to the shear horizon. In principle, the same model can also be employed to reproduce the response of the other parts of the rock glacier body, but, up to now, laboratory test results are not available. In the future, to overcome the limitation of laboratory apparatus, “numerical experimental tests” (for instance, by using the discrete element method) may be employed for understanding the local (at the intergranular ice bonds scale) thermo-mechanical processes and introducing more complex constitutive laws, conceived by following suitable upscaling (micro-macro) approaches.
By comparing the model prediction with in-situ measurements of the tested rock glacier (Murtèl-Corvatsch rock glacier complex), the main findings of this study can be summarized as follows:
- Numerical results in terms of temperature time history are in satisfactory agreement with the experimental measures, confirming the suitability of the proposed model;
- In the considered time period (about 4 years), significant variations in the thermal properties of the system do not take place;
- The proposed model reproduces the correct order of magnitude of mean surface velocities.
Additional sensitivity analysis shows a major correlation between the geometry of the rock glacier body (i.e., characteristics of shear zone) and velocity.
In spite of these limitations, this work represents the first attempt to model in detail, through an elastic–viscoplastic constitutive relationship, the rock glacier response, by considering the intrinsic spatial variability of a rock glacier body and to use laboratory experimental test results as constraints. The approach is very promising but has to be adjusted in some details. The ice bonds provide cohesion to the material, i.e., when the material is melted the cohesion is nil and the material behaves as a soil at a critical state. Therefore, to properly reproduce the behavior, a reliable evaluation of effective stresses is necessary, implying that in situ local measurements of pore water pressure are needed. In the future, the model may be improved by introducing a more sophisticated constitutive relationship considering both intergranular friction and local thermo-mechanical processes taking place on the ice bond scale.
To validate respective models, however, more knowledge on the thermo-mechanical processes in the material has to be gained by performing suitable laboratory tests.
Author Contributions
Conceptualization, S.A. and L.F.; methodology, S.A. and L.F.; software, S.A. and L.F.; validation, S.A. and L.F.; formal analysis, S.A. and L.F.; investigation, S.A. and L.F.; resources, S.A. and L.F.; data curation, S.A. and L.F.; writing—original draft preparation, S.A. and L.F.; writing—review and editing, S.A. and L.F.; visualization, S.A. and L.F.; supervision, S.A. and L.F.; project administration, S.A. and L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We are grateful to Alberto Villa, Riccardo Scotti, Ben Leshchinsky, Giovanni Crosta and Margherita Cecilia Spreafico for stimulating discussions. We thank the editor and two anonymous reviewers for the comments which have ultimately contributed to the robustness of this paper. We would like to thank the Swiss Permafrost Monitoring Network (PERMOS) for providing the measurement as open-source data. The authors are also thankful for the unknown mentor who showed us the wrong way to conduct modeling.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dramis, F.; Govi, M.; Guglielmin, M.; Mortara, G. Mountain permafrost and slope instability in the Italian Alps: The Val Pola Landslide. Permafr. Periglac. Process. 1995, 6, 73–81. [Google Scholar] [CrossRef]
- Mergili, M.; Jaboyedoff, M.; Pullarello, J.; Pudasaini, S.P. Back calculation of the 2017 Piz Cengalo–Bondo landslide cascade with r.avaflow: What we can do and what we can learn. Nat. Hazards Earth Syst. Sci. 2020, 20, 505–520. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.J.A. High-latitude rock glaciers: A case study of forms and processes in the Canadian arctic. Permafr. Periglac. Process. 1993, 4, 17–35. [Google Scholar] [CrossRef]
- Scotti, R.; Brardinoni, F.; Alberti, S.; Frattini, P.; Crosta, G.B. A regional inventory of rock glaciers and protalus ramparts in the central Italian Alps. Geomorphology 2013, 186, 136–149. [Google Scholar] [CrossRef]
- Barsch, D. Permafrost creep and rockglaciers. Permafr. Periglac. Process. 1992, 3, 175–188. [Google Scholar] [CrossRef]
- PERMOS. Swiss Permafrost Bulletin 2018/2019; Pellet, C., Noetzli, J., Eds.; Swiss Permafrost Monitoring Network PERMOS: Fribourg, Switzerland, 2020; p. 20. [Google Scholar] [CrossRef]
- Bodin, X.; Rojas, F.; Brenning, A. Status and evolution of the cryosphere in the Andes of Santiago (Chile, 33.5° S.). Geomorphology 2010, 118, 453–464. [Google Scholar] [CrossRef]
- Müller, J.; Gärtner-Roer, I.; Kenner, R.; Thee, P.; Morche, D. Sediment storage and transfer on a periglacial mountain slope (Corvatsch, Switzerland). Geomorphology 2014, 218, 35–44. [Google Scholar] [CrossRef]
- Kääb, A. Remote sensing of permafrost-related problems and hazards. Permafr. Periglac. Process. 2008, 19, 107–136. [Google Scholar] [CrossRef]
- Perruchoud, E.; Delaloye, R. Short-Term Changes in Surface Velocities on the Becs-de-Bosson Rock Glacier (Western Swiss Alps); Elsevier: Amsterdam, The Netherlands, 2007; pp. 131–136. [Google Scholar]
- Wirz, V.; Gruber, S.; Purves, R.S.; Beutel, J.; Gärtner-Roer, I.; Gubler, S.; Vieli, A. Short-term velocity variations at three rock glaciers and their relationship with meteorological conditions. Earth Surf. Dyn. 2016, 4, 103–123. [Google Scholar] [CrossRef] [Green Version]
- Kääb, A.; Frauenfelder, R.; Roer, I. On the response of rock glacier creep to surface temperature increase. Glob. Planet Chang. 2007, 56, 172–187. [Google Scholar] [CrossRef]
- Kaufmann, V.; Ladstädter, R. Documentation and visualization of the morphodynamics of Hinteres Lang-talkar rock glacier (Hohe Tauern Range, Austrian Alps) based on aerial photographs (1954–2006) and geodetic measurements (1999–2007). In Proceedings of the 10th International Symposium on High Mountain Remote Sensing Cartography, Kathmandu, Nepal, 8–11 September 2008; Volume 30. [Google Scholar]
- Delaloye, R.; Perruchoud, E.; Avian, M.; Kaufmann, V.; Bodin, X.; Hausmann, H.; Ikeda, A.; Kääb, A.; Kellerer-Pirklbauer, A.; Krainer, K.; et al. Recent interannual variations of rock glacier creep in the European Alps. In Proceedings of the 9th International Conference on Permafrost; Springer: Berlin/Heidelberg, Germany, 2008; pp. 343–348. [Google Scholar]
- Scapozza, C.; Lambiel, C.; Bozzini, C.; Mari, S.; Conedera, M. Assessing the rock glacier kinematics on three different timescales: A case study from the southern Swiss Alps. Earth Surf. Process. Landf. 2014, 39, 2056–2069. [Google Scholar] [CrossRef] [Green Version]
- Nickus, U.; Abermann, J.; Fischer, A.; Krainer, K.; Schneider, H.; Span, N.; Thies, H. Rock Glacier Äußeres Hochebenkar (Austria)—Recent results of a monitoring network. Z. Gletsch. Glazialgeol. 2015, 47, 43–62. [Google Scholar]
- Sorg, A.; Kääb, A.; Roesch, A.; Bigler, C.; Stoffel, M. Contrasting responses of Central Asian rock glaciers to global warming. Sci. Rep. 2015, 5, 8228. [Google Scholar] [CrossRef] [Green Version]
- Jones, D.B.; Harrison, S.; Anderson, K.; Whalley, W.B. Rock glaciers and mountain hydrology: A review. Earth-Sci. Rev. 2019, 193, 66–90. [Google Scholar] [CrossRef]
- Mühll, D.V.; Arenson, L.U.; Springman, S.M. Temperature conditions in two Alpine rock glaciers. In Proceedings of the International Conference on Permafrost, Zürich, Switzerland, 21–25 July 2003; pp. 1195–1200. [Google Scholar]
- Cicoira, A.; Beutel, J.; Faillettaz, J.; Gärtner-Roer, I.; Vieli, A. Resolving the influence of temperature forcing through heat conduction on rock glacier dynamics: A numerical modelling approach. Cryosphere 2019, 13, 927–942. [Google Scholar] [CrossRef] [Green Version]
- Arenson, L.; Hoelzle, M.; Springman, S. Borehole deformation measurements and internal structure of some rock glaciers in Switzerland. Permafr. Periglac. Process. 2002, 13, 117–135. [Google Scholar] [CrossRef]
- Haeberli, W.; Hallet, B.; Arenson, L.; Elconin, R.; Humlum, O.; Kääb, A.; Kaufmann, V.; Ladanyi, B.; Matsuoka, N.; Springman, S.; et al. Permafrost creep and rock glacier dynamics. Permafr. Periglac. Process. 2006, 17, 189–214. [Google Scholar] [CrossRef]
- Haeberli, W.; Hunder, J.; Keusen, H.-R.; Pika, J.; Rothlisberger, H. Core drilling through rock-glacier permafrost. In Proceedings of the 5th International Conference on Permafrost; Elsevier: Trondheim, Norway, 1988; Volume 2, pp. 937–942. [Google Scholar]
- Arenson, L.U.; Springman, S.M. Mathematical descriptions for the behaviour of ice-rich frozen soils at temperatures close to 0 °C. Can. Geotech. J. 2005, 42, 431–442. [Google Scholar] [CrossRef]
- Cicoira, A.; Marcer, M.; Gärtner-Roer, I.; Bodin, X.; Arenson, L.U.; Vieli, A. A general theory of rock glacier creep based on in-situ and remote sensing observations. Permafr. Periglac. Process. 2021, 32, 139–153. [Google Scholar] [CrossRef]
- Arenson, L. Unstable Alpine Permafrost: A Potentially Important Natural Hazard. Variations of Geotechnical Behaviour with Time and Temperature; ETH: Zürich, Switzerland, 2002. [Google Scholar]
- Wagner, S. Creep of Alpine permafrost, investigated on the Murtèl rock glacier. Permafr. Periglac. Process. 1992, 3, 157–162. [Google Scholar] [CrossRef]
- Springman, S.M.; Arenson, L.U.; Yamamoto, Y.; Maurer, H.; Kos, A.; Buchli, T.; Derungs, G. Multidisciplinary investigations on three rock glaciers in the Swiss Alps: Legacies and future perspectives. Geogr. Ann. Ser. A Phys. Geogr. 2012, 94, 215–243. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Springman, S.M. Axial compression stress path tests on artificial frozen soil samples in a triaxial device at temperatures just below 0 °C. Can. Geotech. J. 2014, 51, 1178–1195. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Springman, S.M. Three- and four-point bending tests on artificial frozen soil samples at temperatures close to 0 °C. Cold Reg. Sci. Technol. 2017, 134, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Calvetti, F. DEM Simulation of frozen granular soils with high ice content. In Proceedings of the EECE 2020; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 472–480. [Google Scholar]
- Wang, G.; Calvetti, F. DEM modelling of ice filled rock joints. In Proceedings of the Lecture Notes in Civil Engineering; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2021; pp. 941–948. [Google Scholar]
- Glen, J.W. The flow law of ice: A discussion of the assumptions made in glacier theory, their experimental foundations and consequences. IASH Publ. 1958, 47, e183. [Google Scholar]
- Nye, J.F. The mechanics of glacier flow. J. Glaciol. 1952, 2, 82–93. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, A.; Matsuoka, N. Degradation of talus-derived rock glaciers in the Upper Engadin, Swiss Alps. Permafr. Periglac. Process. 2002, 13, 145–161. [Google Scholar] [CrossRef]
- Kellerer-Pirklbauer, A.; Kaufmann, V. About the relationship between rock glacier velocity and climate parameters in central Austria. Austrian J. Earth Sci. 2012, 105, 94–112. [Google Scholar]
- Zimmermann, M.; Haeberli, W. Climatic change and debris flow activity in high-mountain areas—A case study in the Swiss Alps. Greenhouse impact on cold-climate ecosystems and landscapes. Catena 1992, 22, 59–72. [Google Scholar]
- Böckli, L. Characterizing Permafrost in the Entire European Alps: Spatial Distribution and Ice Content. Ph.D. Thesis, Mathematisch-Naturwissenschaftlichen Fakultät der Universität Zürich, Zürich, Switzerland, 2013. Available online: http://www.zora.uzh.ch/89504/ (accessed on 23 June 2016).
- Buchli, T.; Kos, A.; Limpach, P.; Merz, K.; Zhou, X.; Springman, S.M. Kinematic investigations on the Furggwanghorn Rock Glacier, Switzerland. Permafr. Periglac. Process. 2018, 29, 3–20. [Google Scholar] [CrossRef]
- Perzyna, P. The constitutive equations for rate sensitive plastic materials. Q. Appl. Math. 1963, 20, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Arenson, L.U.; Hauck, C.; Hilbich, C.; Seward, L.; Yamamoto, Y.; Springman, S.M. Sub-surface Heterogeneities in the Murtèl: Corvatsch Rock Glacier, Switzerland. In Proceedings of the Joint 63rd Canadian Geotechnical Conference and the 6th Canadian Permafrost Conference; Canadian Geotechnical Society: Vancouver, BC, Canada, 2010; pp. 1494–1500. [Google Scholar]
- Maurer, H.; Hauck, C. Geophysical imaging of alpine rock glaciers. J. Glaciol. 2007, 53, 110–120. [Google Scholar] [CrossRef] [Green Version]
- Di Prisco, C.; Flessati, L. Progressive failure in elastic-viscoplastic media: From theory to practice. Géotechnique 2021, 71, 153–169. [Google Scholar] [CrossRef]
- Di Prisco, C.; Pisano, F. An exercise on slope stability and perfect elastoplasticity. Géotechnique 2011, 61, 923–934. [Google Scholar] [CrossRef]
- Hanson, S.; Hoelzle, M. The thermal regime of the active layer at the Murtèl rock glacier based on data from 2002. Permafr. Periglac. Process. 2004, 15, 273–282. [Google Scholar] [CrossRef]
- Hoelzle, M.; Haeberli, W.; Stocker-Mittaz, C. Miniature ground temperature data logger measurements 2000–2002 in the Murtèl-Corvatsch area, Eastern Swiss Alps. In Proceedings of the 8th International Conference on Permafrost; Balkema: Lisse, The Netherlands, 2003; Volume 21, p. 25. [Google Scholar]
- Haeberli, W. Consequences of global change effects on cryospheric processes and hydrology in alpine environments. In Europe’s Cold Regions: Scenarios for Landscape Responses to Global Change; Grabherr, G., Heal, O.W., Gottfried, M., Pauli, H., Reiter, K., Eds.; Department of Vegetation Ecology and Conservation Biology, Institute of Plant Physiology, University of Vienna: Vienna, Austria, 1999; p. 13. [Google Scholar]
- Laustela, M.; Egli, M.; Frauenfelder, R.; Kääb, A.; Maisch MHaeberli, W. Weathering rind measurements and relative age dating of rockglacier surfaces in crystalline regions of the Eastern Swiss Alps. In Proceedings of the 8th International Conference on Permafrost, Zürich, Switzerland, 21–25 July 2003; Volume 1, pp. 627–632. [Google Scholar]
- Haeberli, W.; Brandova, D.; Burga, C.; Egli, M.; Frauenfelder, R.; Kääb, A.; Maisch, M.; Mauz, B.; Dikau, R. Methods for absolute and relative age dating of rock-glacier surfaces in alpine permafrost. In Proceedings of the 8th International Conference on Permafrost; Balkema: Zürich, Switzerland, 2003; pp. 343–348. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).