Basement Mapping of the Fucino Basin in Central Italy by ITRESC Modeling of Gravity Data
Abstract
:1. Introduction
2. Geological Setting
3. Geophysical Knowledge of the Fucino Plain
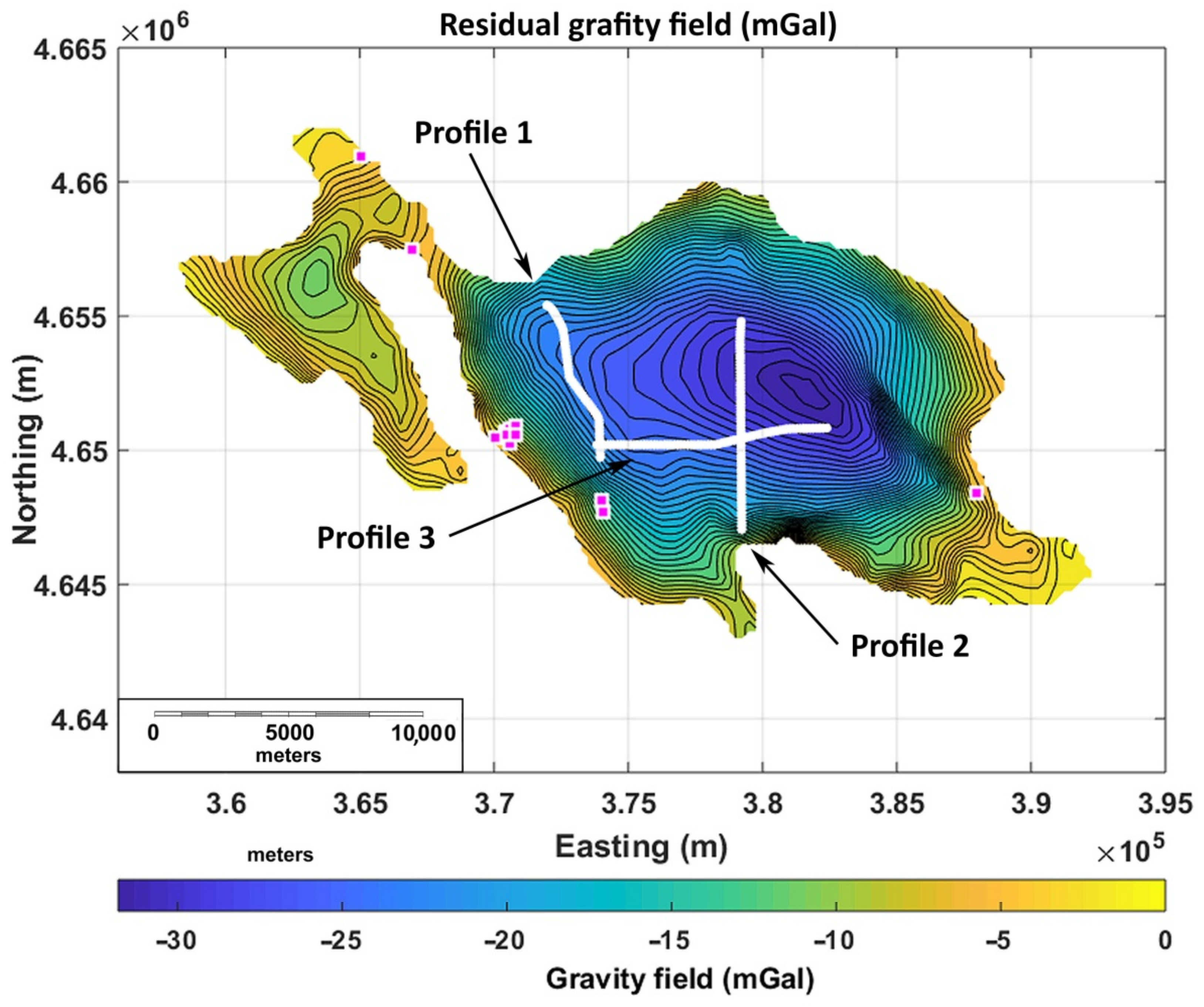
4. Gravity Data
5. Gravity Modelling
5.1. Data Processing
5.2. Preliminary Analysis of Structural Features by Enhanced Horizontal Derivative of Gravity Data
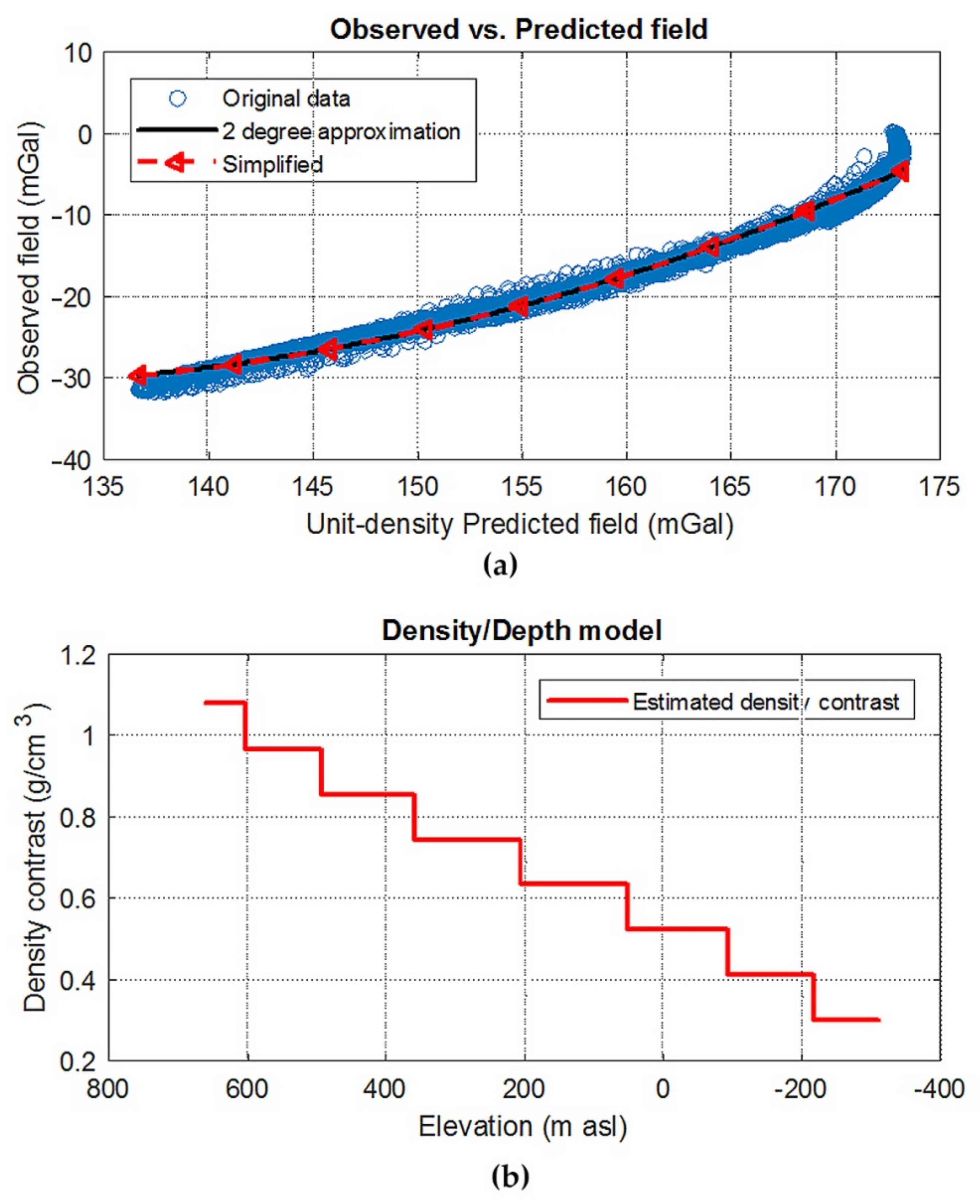
5.2.1. 3D Modelling: The ITRESC Method
- (a)
- (b)
- the ITRESC method incorporates the information on the basement depth given by the available constraints in the definition of a general rescaling law to convert the gravity data into depths, which is valid in all of the basin area;
- (c)
- the density contrast, or its variation with the depth in the entire area, is estimated by a data-driven procedure, combining gravity data and available constraints on the depth to basement;
- (d)
- as with almost all algorithms for the estimation of the basement depth from gravity data, the ITRESC method assumes the absence of any lateral variation in the density contrast.
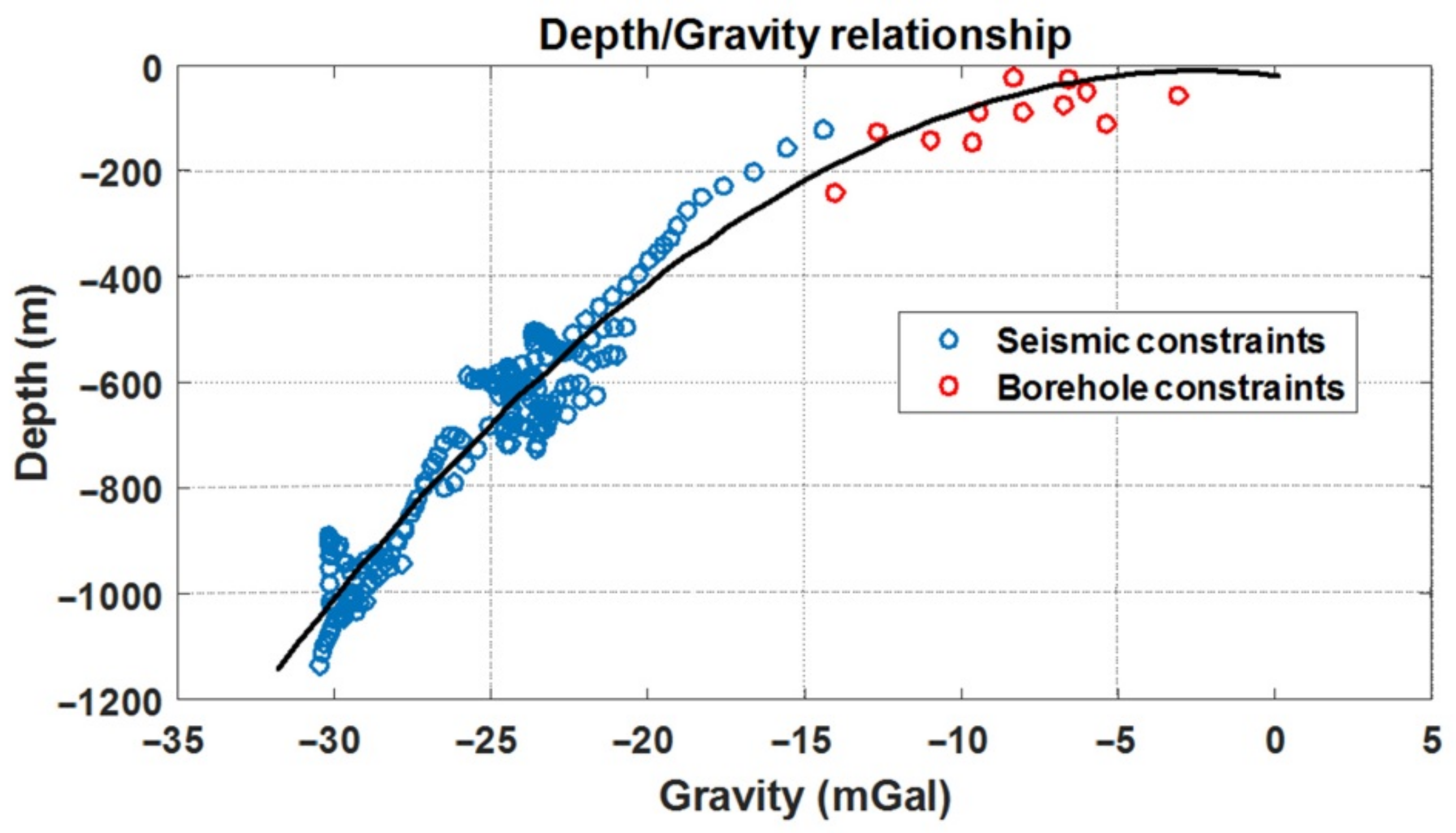
5.2.2. 3D Modelling: Constraints to Gravity Modelling
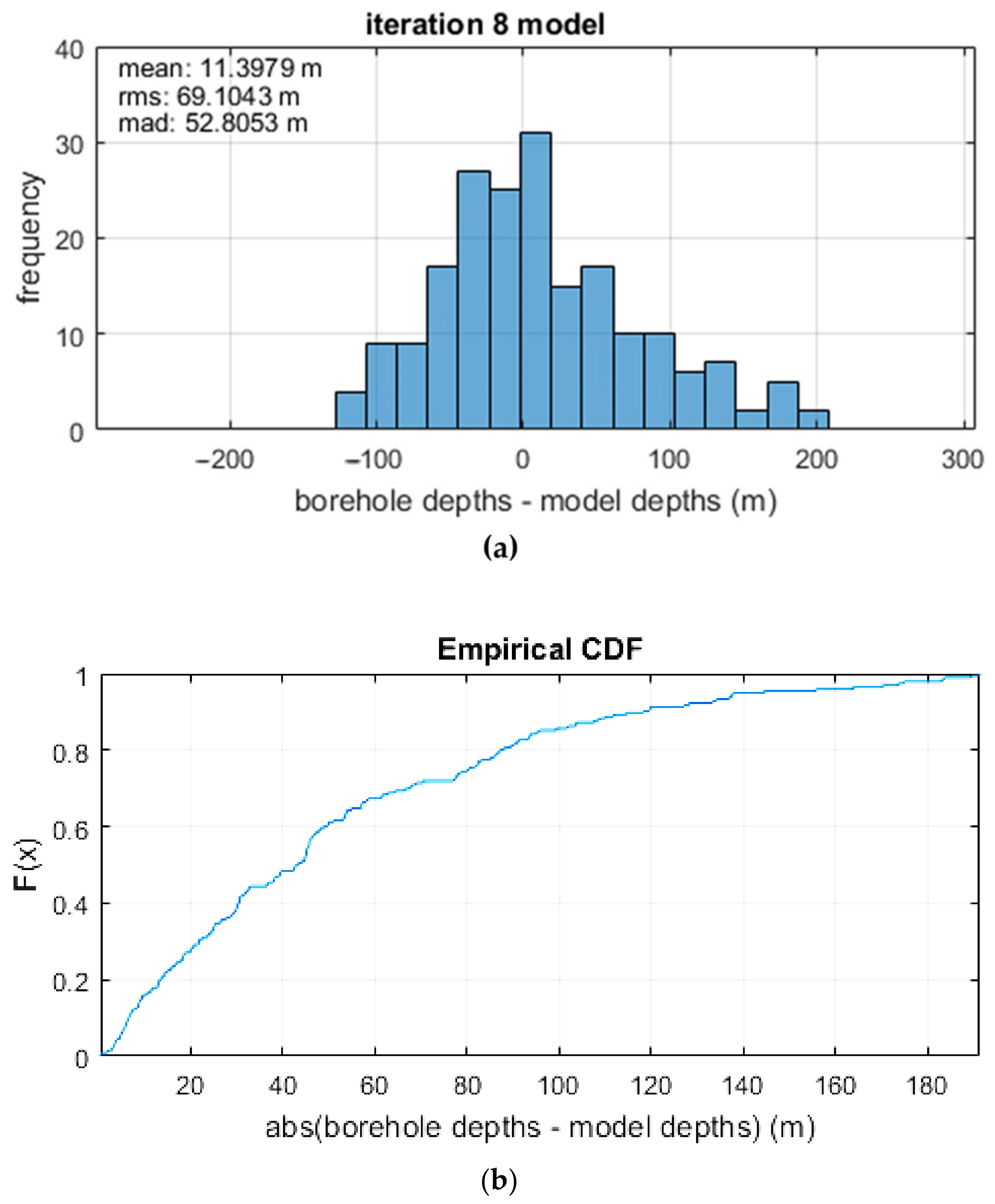
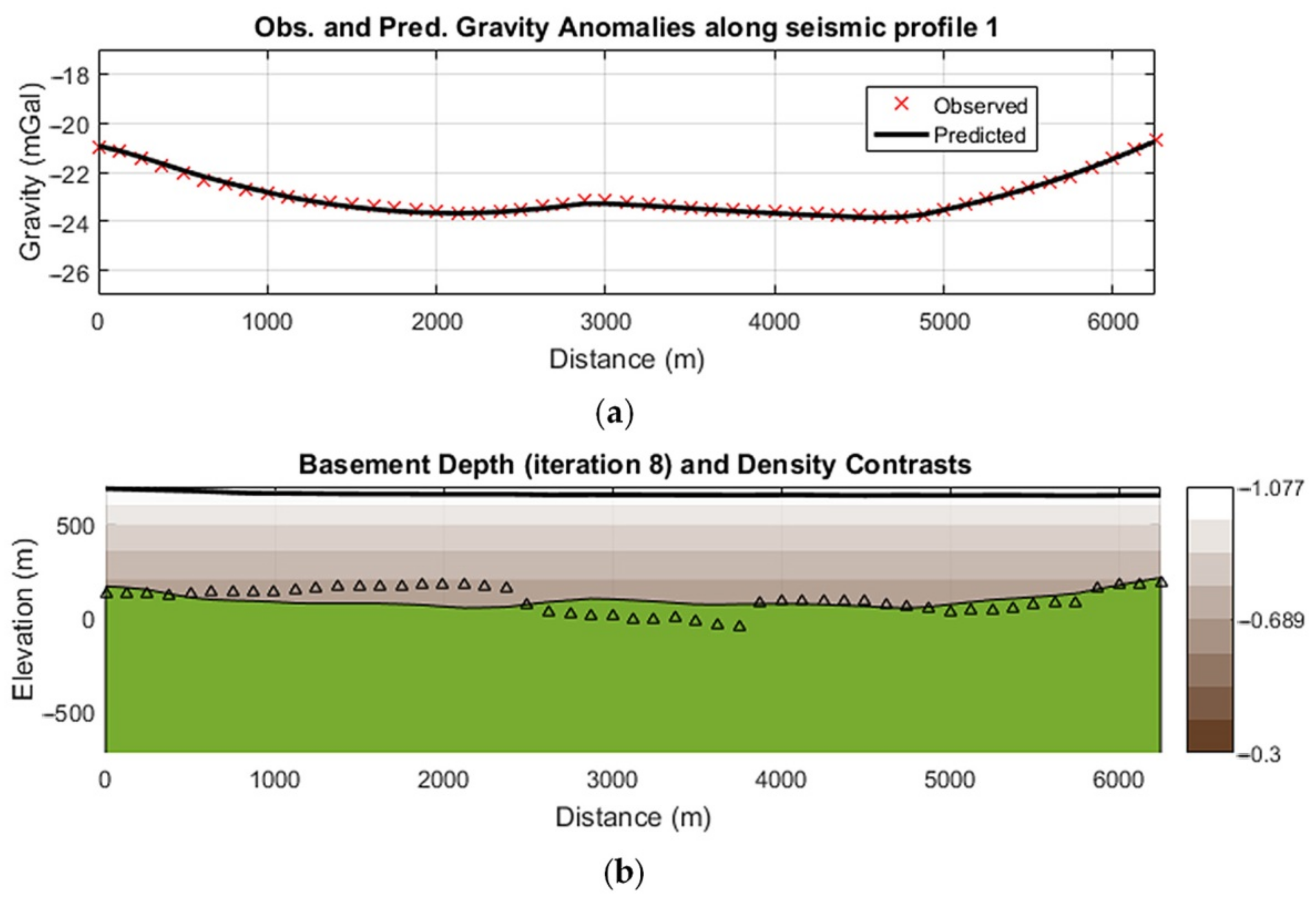
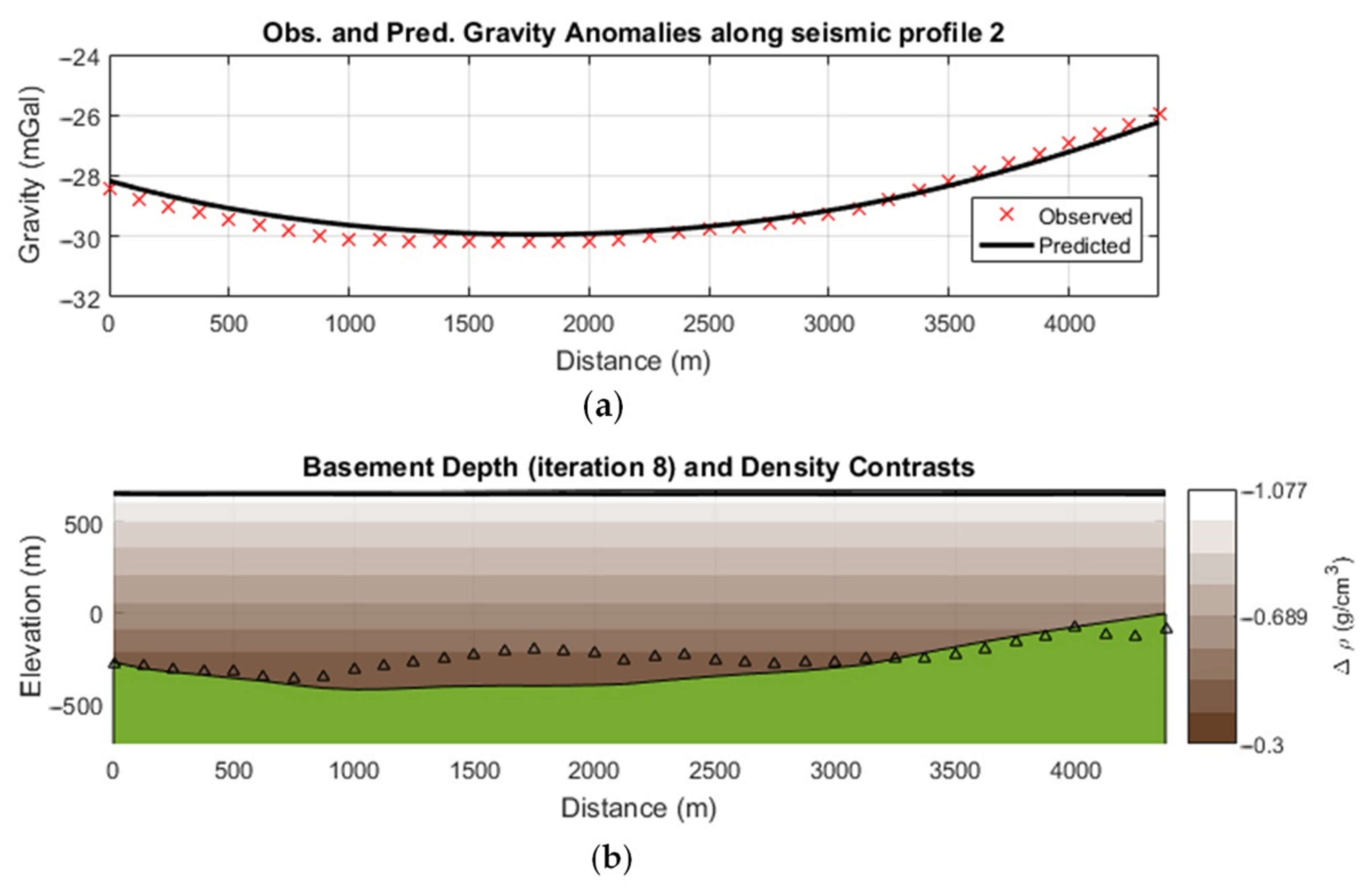
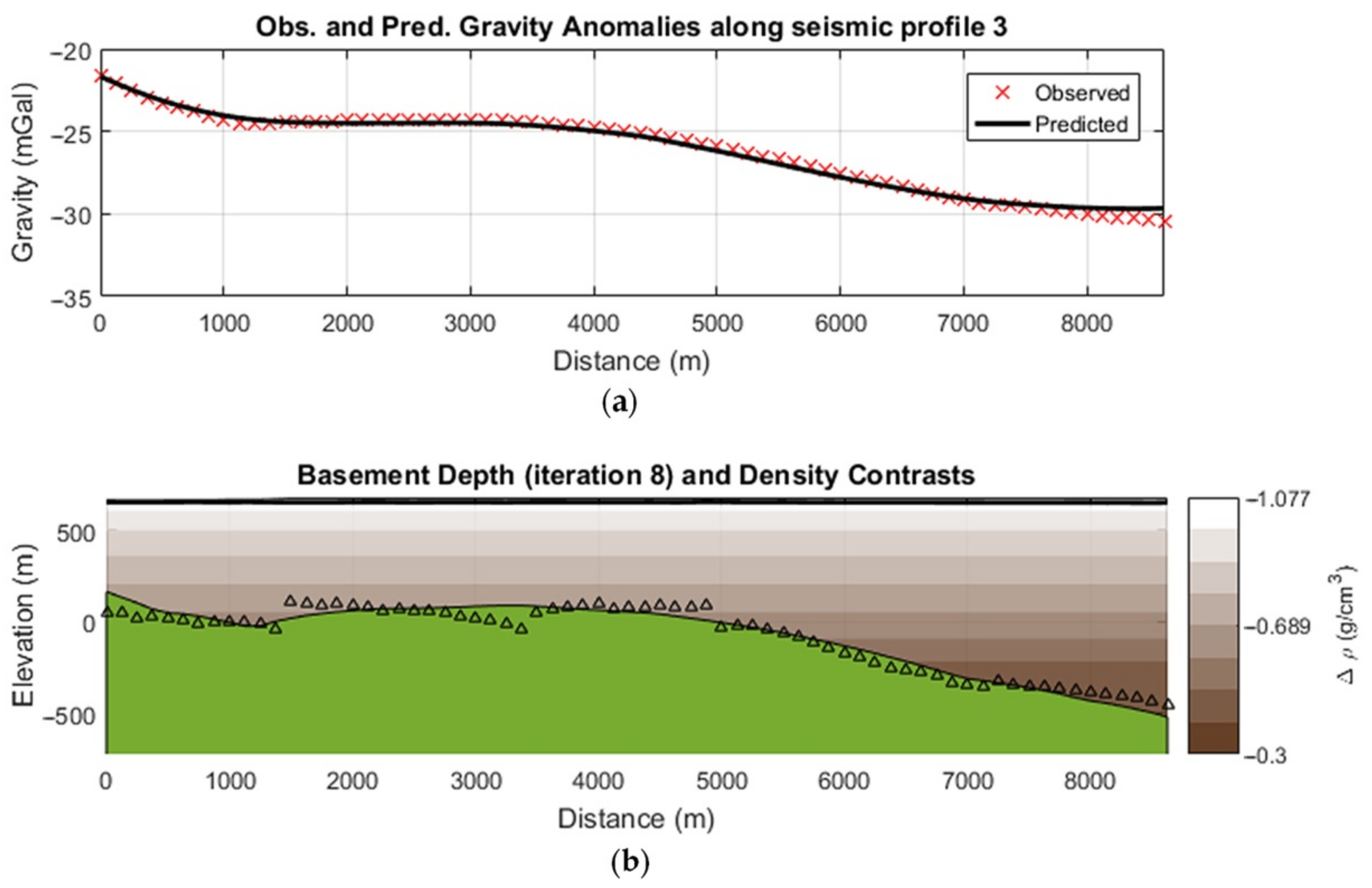
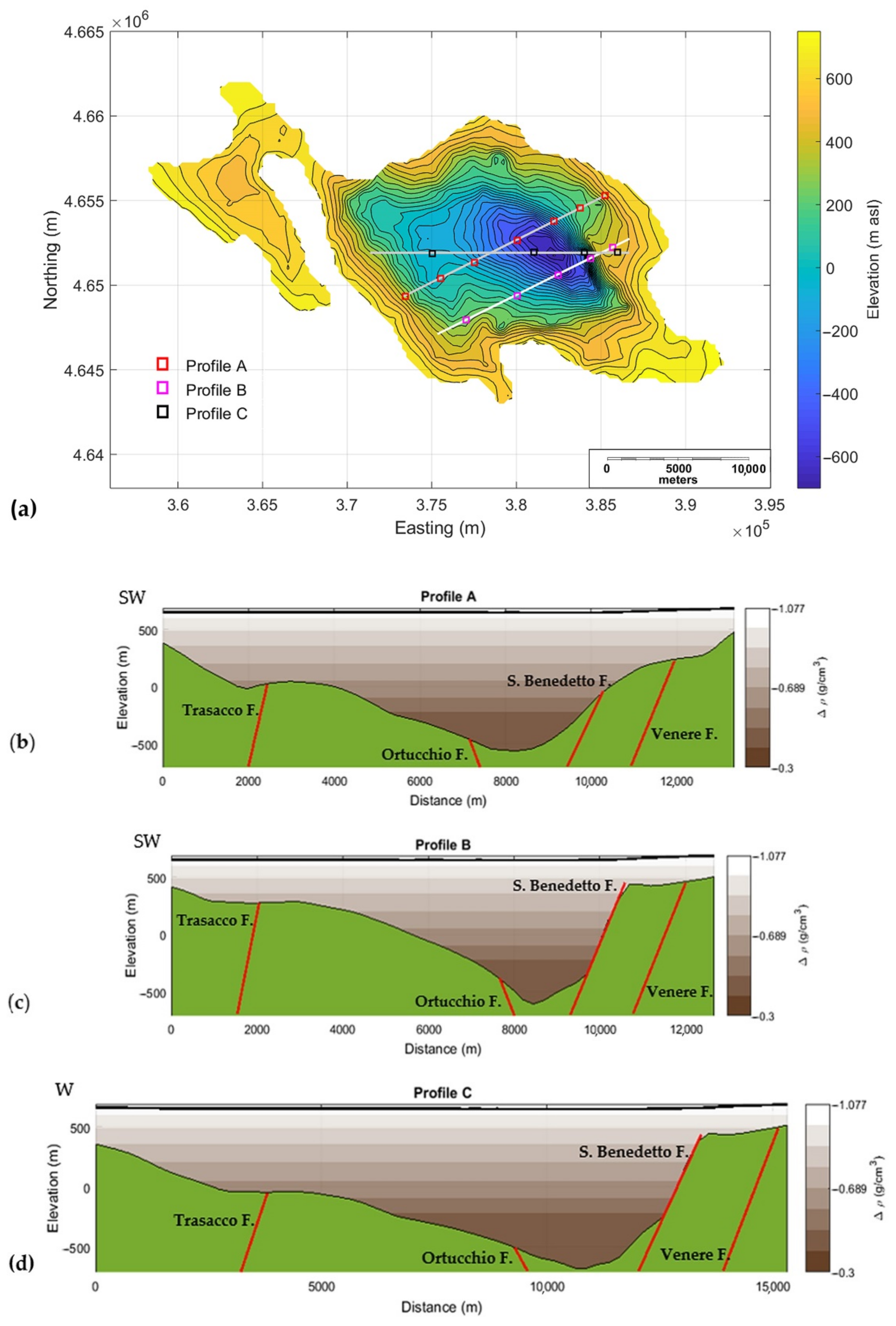
5.2.3. 3D Modelling: ITRESC Application to the Fucino Gravity Anomaly Field
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Aknowledgments
Conflicts of Interest
Appendix A
References
- Patacca, E.; Scandone, P. Geology of the Southern Apennines. Boll. Soc. Geol. Ital. 2007, 7, 75–112. [Google Scholar]
- Cavinato, G.P.; Carusi, C.; Dall’Asta, M.; Miccadei, E.; Piacentini, T. Sedimentary and tectonic evolution of Plio–Pleistocene alluvial and lacustrine deposits of Fucino Basin (central Italy). Sediment. Geol. 2002, 148, 29–59. [Google Scholar] [CrossRef]
- Finetti, I.R. CROP Project. In Deep Seismic Exploration of the Central Mediterranean and Italy, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 1, p. 794. [Google Scholar]
- Patacca, E.; Scandone, P.; Di Luzio, E.; Cavinato, G.P.; Parotto, M. Structural architecture of the central Apennines: Interpretation of the CROP 11 seismic profile from the Adriatic coast to the orographic divide. Tectonics 2008, 27, TC3006. [Google Scholar] [CrossRef]
- Compagnia Mediterranea Idrocarburi, Permesso di Ricerca per Idrocarburi “Cerchio”. In Rapporto Interpretazione Sismica 1982 Riprocessata; 1999; p. 24. (In Italian)
- Cara, F.; Di Giulio, G.; Cavinato, G.P.; Famiani, D.; Milana, G. Seismic characterization and monitoring of Fucino Basin (Central Italy). Bull. Earthq. Eng. 2011, 9, 1961–1985. [Google Scholar] [CrossRef]
- Barchi, M.R.; Ciaccio, M.G. Seismic images of an extensional basin, generated at the hangingwall of a low-angle normal fault: The case of the Sansepolcro basin (Central Italy). Tectonophysics 2009, 479, 285–293. [Google Scholar] [CrossRef]
- Di Naccio, D.; Famiani, D.; Liberi, F.; Boncio, P.; Cara, F.; De Santis, A.; Di Giulio, G.; Galadini, F.; Milana, G.; Rosatelli, G.; et al. Site effects and widespread susceptibility to permanent coseismic deformation in the Avezzano town (Fucino basin, Central Italy): Constraints from detailed geological study. Eng. Geol. 2020, 270, 105583. [Google Scholar] [CrossRef]
- Lanari, R.; Faccenna, C.; Benedetti, L.; Sembroni, A.; Bellier, O.; Menichelli, I.; Primerano, P.; Molin, P. Formation and Persistence of Extensional Internally Drained Basins: The Case of the Fucino Basin (Central Apennines, Italy). Tectonics 2021, 40, e2020TC006442. [Google Scholar] [CrossRef]
- Patruno, S.; Scisciani, V. Testing normal fault growth models by seismic stratigraphic architecture: The case of the Pliocene-Quaternary Fucino Basin (Central Apennines, Italy). Basin Res. 2021, 33, 2118–2156. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. (Eds.) CPTI15, The 2015 Version of the Parametric Catalogue of Italian Earthquakes; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2016; Available online: http://emidius.mi.ingv.it/CPTI15-DBMI15/index_en.htm (accessed on 15 March 2021). [CrossRef]
- Florio, G. Mapping the Depth to Basement by Iterative Rescaling of Gravity or Magnetic Data. J. Geophys. Res. Solid Earth 2018, 123, 9101–9120. [Google Scholar] [CrossRef]
- Florio, G. The Estimation of Depth to Basement under Sedimentary Basins from Gravity Data: Review of Approaches and the ITRESC Method, with an Application to the Yucca Flat Basin (Nevada). Surv. Geophys. 2020, 41, 935–961. [Google Scholar] [CrossRef]
- Compagnoni, B.; Galluzzo, F.; Bonomo, R.; Capotorti, F.; D’Ambrogi, C.; Di Stefano, R.; Graziano, R.; Martarelli, L.; Pampaloni, M.L.; Pantaloni, M.; et al. Carta Geologica d’Italia, 1:1.000.000 Servizio Geologico d’Italia; ISPRA, SELCA: Firenze, Italy, 2011. (In Italian) [Google Scholar]
- Centamore, E.; Crescenti, U.; Dramis, F. Note Illustrative della Carta Geologica d’Italia alla Scala 1:50.000, Foglio 368 “Avezzano”; APAT—Servizio Geologico d’Italia e Regione Abruzzo—Servizio Difesa del Suolo, S.EL.CA.: Firenze, Italy, 2006. (In Italian) [Google Scholar]
- Galadini, F.; Messina, P. Plio–Quaternary tectonics of the Fucino basin and surroundings areas (central Italy). G. Geol. 1994, 56, 73–99. [Google Scholar]
- Ghisetti, F.; Vezzani, L. Interfering paths of deformation and development of arcs in the fold-and-thrust belt of central Apennines (Italy). Tectonics 1997, 16, 523–536. [Google Scholar] [CrossRef]
- Giraudi, C. Evoluzione geologica della piana del Fucino (Abruzzo) negli ultimi 30.000 anni. Il. Quaternario 1988, 1, 131–159. (In Italian) [Google Scholar]
- Boncio, P.; Milana, G.; Cara, F.; Di Giulio, G.; Di Naccio, D.; Famiani, D.; Liberi, F.; Galadini, F.; Rosatelli, G.; Vassallo, M. Shallow subsurface geology and seismic microzonation in a deep continental basin. The Avezzano Town, Fucino basin (central Italy). Nat. Hazards Earth Syst. Sci. Discuss. 2016, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Oddone, E. Gli elementi fisici del grande terremoto Marsicano-Fucense del 13 gennaio 1915. Boll. Soc. Sismol. Ital. 1915, 19, 71–291. (In Italian) [Google Scholar]
- Serva, L.; Blumetti, A.M.; Michetti, A.M. Gli Effetti Sul Terreno Del Terremoto Del Fucino (13 Gennaio 1915); Tentativo di Interpretazione dell’evoluzione Tettonica Recente di Alcune Strutture. Mem. Soc. Geol. It. 1988, 35, 893–907. (In Italian) [Google Scholar]
- Galadini, F.; Galli, P.; Giraudi, C.; Molin, D. Il terremoto del 1915 e la sismicità della Piana del Fucino (Italia centrale). Ital. J. Geosci. 1995, 114, 635–663. (In Italian) [Google Scholar]
- Michetti, A.M.; Brunamonte, F.; Serva, L.; Vittori, E. Trench investigations of the 1915 Fucino earthquake fault scarps (Abruzzo, Central Italy): Geological evidence of large historical events. J. Geophys. Res. 1996, 101, 5921–5936. [Google Scholar] [CrossRef]
- Galadini, F.; Galli, P.; Giraudi, C. Geological investigations of Italian earthquakes: New paleoseismological data from the fucino plain (Central Italy). J. Geodyn. 1997, 24, 87–103. [Google Scholar] [CrossRef]
- Galadini, F.; Galli, P. The Holocene paleoearthquakes on the 1915 Avezzano earthquake faults (central Italy): Implications for active tectonics in the central Apennines. Tectonophysics 1999, 308, 143–170. [Google Scholar] [CrossRef]
- Galli, P.; Messina, P.; Giaccio, B.; Peronace, E.; Quadrio, B. Early Pleistocene to late Holocene activity of the Magnola fault (Fucino fault system, central Italy). Boll. Geofis. Teor. Ed. Appl. 2012, 53. [Google Scholar] [CrossRef]
- ISIDeWorking Group INGV. Italian Seismological Instrumental and Parametric Database. 2021. Available online: http://terremoti.ingv.it/ (accessed on 9 September 2021).
- Geological Map of Italy, Avezzano, Sheet 368. Available online: https://www.isprambiente.gov.it/Media/carg/368_AVEZZANO/Foglio.html (accessed on 9 September 2021).
- Tiberti, M.M.; Orlando, L. 2D gravity modeling along the CROP11 seismic profile, Boll. Geofis. Teor. Appl. 2006, 47, 447–454. [Google Scholar]
- Di Luzio, E.; Mele, G.; Tiberti, M.M.; Cavinato, G.P.; Parotto, M. Moho deepening and shallow upper crustal delamination beneath the central Apennines. Earth Planet. Sci. Lett. 2009, 280, 1–12. [Google Scholar] [CrossRef]
- Carrozzo, M.T.; Chirenti, A.; Luzio, D.; Margiotta, C.; Quarta, T. Carta gravimetrica d’Italia. In Acts of 5 Congress GNGTS; CNR: Rome, Italy, 1986; Volume 2, pp. 913–918. [Google Scholar]
- Vanicek, P.; Krakiwsky, E. Geodesy: The Concepts; North-Holland Publishing: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Agocs, W.B. Least Squares Residual Anomaly Determination. Geophysics 1951, 16, 686–696. [Google Scholar] [CrossRef]
- Dobrin, M.B.; Savit, C.H. Introduction to Geophysical Prospecting; McGraw-Hill: New York, NY, USA, 1960; Volume 4. [Google Scholar]
- Mickus, K.L.; Aiken, C.L.V.; Kennedy, W.D. Regional-Residual Gravity Anomaly Separation Using the Minimum-Curvature Technique. Geophysics 1991, 56, 279–283. [Google Scholar] [CrossRef]
- Fedi, M.; Cella, F.; Florio, G.; Rapolla, A. Multiscale Derivative Analysis of the Gravity and Magnetic Fields of the Southern Apennines (Italy). In CROP PROJECT: Deep Seismic Exploration of the Central Mediterranean and Italy; Finetti, R.I., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 281–318. [Google Scholar]
- Fedi, M.; Florio, G. Detection of Potential fields source boundaries by Enhanced Horizontal Derivative method. Geophys. Prospect. 2001, 49, 40–58. [Google Scholar] [CrossRef]
- Cella, F.; Fedi, M.; Florio, G. Toward a full multiscale approach to interpret potential fields. Geophys. Prospect. 2009, 57, 543–557. [Google Scholar] [CrossRef]
- Luiso, P.; Paoletti, V.; Nappi, R.; Manna, M.; Cella, F.; Gaudiosi, G.; Fedi, M.; Iorio, M. A multidisciplinary approach to characterize the geometry of active faults: The example of Mt. Massico, Southern Italy. Geophys. J. Int. 2018, 213, 1673–1681. [Google Scholar] [CrossRef]
- Luiso, P.; Paoletti, V.; Gaudiosi, G.; Nappi, R.; Cella, F.; Fedi, M. Testing the value of a multi-scale gravimetric analysis in characterizing active fault geometry at hypocentral depths: The 2016-2017 Central Italy seismic sequence. Ann. Geophys. 2018, 61, DA558. [Google Scholar] [CrossRef]
- Fedi, M. Estimation of Density, Magnetization, and Depth to Source: A Nonlinear and Noniterative 3-D Potential-Field Method. Geophysics 1997, 62, 814–830. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature. Can. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Bott, M.H.P. The Use of Rapid Digital Computing Methods for Direct Gravity Interpretation of Sedimentary Basins. Geophys. J. Int. 1960, 3, 63–67. [Google Scholar] [CrossRef] [Green Version]
- Oldenburg, D.W. The inversion and interpretation of gravity anomalies. Geophysics 1974, 39, 526–536. [Google Scholar] [CrossRef]
- Roy, L.; Sen, M.K.; Blankenship, D.D.; Stoffa, P.L.; Richter, T.G. Inversion and Uncertainty Estimation of Gravity Data Using Simulated Annealing: An Application over Lake Vostok, East Antarctica. Geophysics 2005, 70, J1–J12. [Google Scholar] [CrossRef]
- Dipartamento Per Il Servizio Geologico D’Italia—ISPRA. Archivio Nazionale delle Indagini nel Sottosuolo (Legge 464/1984). Available online: http://sgi2.isprambiente.it/indagini/ (accessed on 9 September 2021). (In Italian)
- De Caterini, G.; Blumetti, A.M.; Coen, G.; Della Ventura, G.; Eulilli, V.; Ferri, F.; Guerrieri, L.; Leoni, G.; Lucci, F.; Mariani, M.; et al. New preliminary data on the Late Quaternary evolution of Magliano dei Marsi area (Abruzzo, Central Italy). In Proceedings of the 6th International INQUA Meeting on Paleoseismology, Active Tectonics and Archaeoseismology, Pescina, Italy, 19–24 April 2015; INQUA: Pescina, Italy, 2015; pp. 108–111. [Google Scholar]
- Gori, S.; Falcucci, E.; Ladina, C.; Marzorati, S.; Galadini, F. Active faulting, 3-D geological architecture and Plio-Quaternary structural evolution of extensional basins in the central Apennine chain, Italy. Solid Earth 2017, 8, 319–337. [Google Scholar] [CrossRef] [Green Version]
- Giaccio, B.; Leicher, N.; Mannella, G.; Monaco, L.; Regattieri, E.; Wagner, B.; Zanchetta, G.; Gaeta, M.; Marra, F.; Nomade, S.; et al. Extending the tephra and palaeoenvironmental record of the central Mediterranean back to 430 ka: A new core from Fucino Basin, central Italy. Quat. Sci. Rev. 2019, 225, 106003. [Google Scholar] [CrossRef]
- Progetto Videpi. Available online: https://www.videpi.com (accessed on 6 September 2021).
- Parotto, M.; Cavinato, G.P.; Miccadei, E.; Tozzi, M. Line CROP 11: Central Apennines. La linea CROP 11: Appennino Centrale. Mem. Descr. Carta Geol. d’It. 2003, 62, 145–154. [Google Scholar]
- Grauch, V.J.S.; Cordell, L. Short Note—Limitations of determining density or magnetic boundaries from the horizontal gradient of gravity or pseudogravity data. Geophysics 1987, 52, 118–121. [Google Scholar] [CrossRef]
- Silva, J.B.C.; Santos, D.F.; Gomes, K.P. Fast Gravity Inversion of Basement Relief. Geophysics 2014, 79, G79–G91. [Google Scholar] [CrossRef]
- Bishop Model. Available online: https://wiki.seg.org/wiki/Bishop_Model (accessed on 6 September 2021).
- European Committee for Standardization (CEN). Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings; The European Union: Bruxelles, Belgium, 2003. [Google Scholar]
- Sheriff, R.E.; Geldart, L.P. Exploration Seismology; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ciotoli, G.; Guerra, M.; Lombardi, S.; Vittori, E. Soil gass urvey for tracing seismogenic faults: A case study in the Fucino basin, Central Italy. J. Geophys. Res. 1998, 103, 23781–23794. [Google Scholar] [CrossRef]
- Destro, N. Release fault: A variety of cross fault in linked extensional fault systems, in the Sergipe-Alagoas Basin, NE Brazil. J. Struct. Geol. 1995, 17, 615–629. [Google Scholar] [CrossRef]
- Chiarabba, C.; Bagh, S.; Bianchi, I.; De Gori, P.; Barchi, M. Deep structural heterogeneities and the tectonic evolution of the Abruzzi region (Central Apennines, Italy) revealed by microseismicity, seismic tomography, and teleseismic receiver functions. Earth Planet. Sci. Lett. 2010, 295, 462–476. [Google Scholar] [CrossRef]
- Villani, F.; Improta, L.; Pucci, S.; Civico, R.; Bruno, P.; Pantosti, D. Investigating the architecture of the Paganica Fault (2009 Mw 6.1 earthquake, central Italy) by integrating high-resolution multi-scale refraction tomography and detailed geological mapping. Geophys. J. Int. 2017, 208, 403–423. [Google Scholar] [CrossRef]
- Tallini, M.; Spadi, M.; Cosentino, D.; Nocentini, M.; Cavuoto, G.; Di Fiore, V. High-resolution seismic reflection exploration for evaluating the seismic hazard in a Plio-Quaternary intermontane basin (L’Aquila downtown, central Italy). Quat. Int. 2019, 532, 34–47. [Google Scholar] [CrossRef]
- Luongo, G.; Ferri, M.; Cubellis, E.; Grimaldi, M.; Obrizzo, F. Struttura superficiale della Piana Campana: Interpretazione del profilo Garigliano Campi Flegrei. In Proceedings of the Atti 7 Convegno Annuale GNGTS, Roma, Italy, November 1988; pp. 1121–1128. [Google Scholar]
- Mostardini, F.; Merlini, S. Appennino centro-meridionale. Sezioni Geologiche e Proposta di Modello Strutturale. Mem. Soc. Geol. It. 1986, 35, 177–202. (In Italian) [Google Scholar]
- Carrozzo, M.T.; Nicolich, R. Quantitative interpretation of gravity and magnetic data. Boll. Geof. Teor. Appl. 1977, 19, 236–248. [Google Scholar]
- Gualteri, L.; Valenti, L.; Cassinis, R. Modelling gravimetrico e magnetico nella regione di transizione tra la Liguria orientale e la Toscana. In Studi Geol. Camerti Spec.Vol. 1992/2: “Studi Preliminari All’acquisizione Dati del Profilo CROP 1-1A La Spezia-Alpi Orientali”; Springer: Berlin/Heidelberg, Germany, 1992; Volume 2, pp. 107–114. (In Italian) [Google Scholar]
- D’Aringoli, D.; Cavitolo, P.; Farabollini, P.; Galindo-Zaldivar, J.; Gentili, B.; Giano, S.I.; Lòpez-Garrido, A.C.; Materazzi, M.; Nibbi, L.; Pedrera, A.; et al. Morphotectonic characterization of the quaternary intermontane basins of the Umbria-Marche Apennine (Italy). Rend. Lincei. Sci. Fis. Nat. 2014, 25, 111–128. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1990; p. 770. [Google Scholar]
- D’orefice, M.; Graciotti, R.; Chiessi, V.; Censi Neri, P.; Morri, A.; Roma, M.; Falcetti, S. The Oricola-Carsoli (AQ) intermontane basin: Geological, geomorphological and applicative aspects. Mem. Descr. Carta Geol. d’It. 2014, 111, 7–114. [Google Scholar]
- Coli, M.; Guerri, L.; Rubellini, P. Geotechnical characterization of the Florence (Italy) soils. Jpn. Geotech. Soc. Spec. Publ. 2015, 2, 2648–2653. [Google Scholar] [CrossRef]

| Borehole | Depth to the Meso-Cenozoic Carbonate Basement (m. Below Ground Level) | Data Source |
|---|---|---|
| Avezzano (code 164216) | −80 | [46] |
| Avezzano (code 164110) | −80 | [46] |
| Avezzano (code 164243) | −40 | [46] |
| Pescina (code 165016) | −50 | [46] |
| Celano (code 164250) | −6 | [46] |
| ISMES19 | −22.5 | [19] |
| ISMES18 | −88 | [19] |
| ISMES17 | −140.4 | [19] |
| S1 | −25 | [2] |
| S2 | −88 | [2] |
| S3 | −145 | [2] |
| Magliano dei Marsi | −56 m | [47] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cella, F.; Nappi, R.; Paoletti, V.; Florio, G. Basement Mapping of the Fucino Basin in Central Italy by ITRESC Modeling of Gravity Data. Geosciences 2021, 11, 398. https://doi.org/10.3390/geosciences11100398
Cella F, Nappi R, Paoletti V, Florio G. Basement Mapping of the Fucino Basin in Central Italy by ITRESC Modeling of Gravity Data. Geosciences. 2021; 11(10):398. https://doi.org/10.3390/geosciences11100398
Chicago/Turabian StyleCella, Federico, Rosa Nappi, Valeria Paoletti, and Giovanni Florio. 2021. "Basement Mapping of the Fucino Basin in Central Italy by ITRESC Modeling of Gravity Data" Geosciences 11, no. 10: 398. https://doi.org/10.3390/geosciences11100398
APA StyleCella, F., Nappi, R., Paoletti, V., & Florio, G. (2021). Basement Mapping of the Fucino Basin in Central Italy by ITRESC Modeling of Gravity Data. Geosciences, 11(10), 398. https://doi.org/10.3390/geosciences11100398