Application of ‘Estimation Procedures’ in Unsaturated Soil Mechanics

Abstract

The application of unsaturated soil mechanics in routine geotechnical engineering applications requires the determination of unsaturated soil properties. Unfortunately, the cost of direct measurement of unsaturated soil properties goes beyond the financial budget of most clients. A solution has arisen, however, that involves the measurement of two less costly soil properties functions that can be used in conjunction with a series of assumptions and estimation methodologies. The two laboratory tests involve measurement of the: (i) gravimetric water content versus soil suction, referred to as the soil-water characteristic curve (w-SWCC) and (ii) water content versus void ratio, referred to as the shrinkage curve (SC). These two unsaturated soil property relationships can be used along with saturated soil properties to extend unsaturated soil properties over the full range of soil suctions. “Estimation procedures” have been developed and verified for all physical properties of interest in unsaturated soil mechanics. The use of estimation procedures has meant that the geotechnical engineer must operate within a new paradigm. The new paradigm provides sufficient accuracy for most geotechnical engineering applications. The net result is an increased decision-making capability for geotechnical engineers.

1. Introduction

Geotechnical engineers are often called upon to model both the saturated and unsaturated soil portions of the soil continua. The greatest challenge to do so surrounds the determination of the physical properties for the unsaturated soil zone. All physical properties for the unsaturated soil zone have been shown to take on the form of nonlinear functions of soil suction (i.e., negative pore-water pressure). Unsaturated soils have suctions that can vary widely (i.e., from zero to one million kPa), as a result of responses to imposed weather conditions.

Research studies related to unsaturated soil mechanics have resulted in refined laboratory testing procedures for the measurement of unsaturated soil properties [1,2]. However, to perform these tests requires the availability of specialized laboratory testing equipment and well-trained technicians. The greatest deterrent to measuring unsaturated soil properties in the laboratory has involved the excessive costs of performing the tests. Simply put, clients are not prepared to pay the exorbitant prices associated with measuring the unsaturated soil property functions. The cost of measuring unsaturated soil property functions has typically been found to be 10 to 100 times the costs related to determining saturated soil properties [3]. More recent research has focused on using a new paradigm to bring the complexities of measuring unsaturated soil property functions within a reasonable cost for geotechnical engineering practices.

Addressing the unsaturated soil portion of a soil profile is now possible through measurements of two less costly soil property relations that are then used within the context of a series of estimation methodologies. The two relatively easy-to-measure unsaturated soil relationships are: (i) the gravimetric water content versus soil suction test (w-SWCC) and the (ii) shrinkage curve (SC) test [4]. The measurement of the desorption (or drying) curve and the shrinkage curve is proposed to obtain the basic unsaturated soil property relationships for subsequent analyses. The volume-mass properties of the w-SWCC and SC test specimens need to be independently measured at the start of each of the tests [5]. The results of the two tests are then “blended together” for the calculation of other volume-mass soil-water characteristic curves, such as the: (i) volumetric water content soil-water characteristic curve, θ-SWCC, (ii) void ratio characteristic curve, e-CC, (iii) the dry density (and total density) soil-water characteristic curves (ρ_d-SWCC and ρ-SWCC), and the (iv) degree of saturation soil-water characteristic curve, S-SWCC. Each of the volume-mass SWCC relationships plays an independent role in the estimation of unsaturated soil property functions, USPFs.

Numerous assumptions and estimations are associated with the analysis of unsaturated soil test results. It is important that the most reliable analytical procedures be combined with “smart” assumptions to yield protocols acceptable for engineering practices [6]. Soil suction is assumed to be the single dominant state variable controlling changes in the behavior of unsaturated soils [6]. Soil suction is assumed to be the single dominant state variable controlling changes in the behavior of an unsaturated soils [7]. Therefore, soil suction with an emphasis on the drying SWCC forms the basis for defining unsaturated soil property functions through the use of estimation procedures. The end result is the development of a practical and cost-effective applied science basis for unsaturated soil mechanics.

2. Objective and Scope

The primary objective of this paper is to present a consistent and reliable methodology for the determination of unsaturated soil property functions, USPFs, via laboratory measurements and estimation procedures. Several mathematical analyses are used to generate nonlinear functions that extend the saturated soil properties through the entire range of possible unsaturated soil conditions. The proposed protocols utilize data from two basic laboratory test datasets (i.e., w-SWCC and SC). These two tests, along with saturated soil properties, provide the minimum data required for estimating USPFs associated with physical processes involving unsaturated soils. Data reduction procedures associated with the two mentioned unsaturated soil laboratory tests are used to give continuous mathematical functions that are identified by two or more best-fit parameters. The mathematical relationships embrace the entire range of possible soil suctions that might be encountered in field conditions. The concept of “estimation procedures” is used to reduce excessive costs associated with the application of unsaturated soil mechanics within the historical soil mechanics’ paradigm.

3. Background of an “Estimation Procedure” Approach

It became apparent in early research studies in unsaturated soil mechanics that a new paradigm was likely necessary if there was going to be a breakthrough in using unsaturated soil mechanics in routine geotechnical engineering practice. M. Fredlund [8,9] suggested that a knowledge-based database could be “mined” to obtain information on typical, past-measured soil-water characteristic curve data. This research formed the basis for starting a numerical modeling company called SoilVision Systems Ltd., which focused on modeling soil profiles that consisted of both saturated and unsaturated soil zones.

In 2003, a user’s manual was published that described several procedures that could be used for the estimation of unsaturated soil property functions, USPFs [9]. These procedures involved: (i) database mining procedures, (ii) estimations of the SWCC from grain-size curves, and (iii) estimations based on the laboratory measurement of the SWCC. While extensive research has followed on all the above-mentioned methodologies, it is the laboratory measurement of the SWCC that has prevailed and now forms the basis for “estimation procedures” in unsaturated soil mechanics. Over time, the importance of also measuring the shrinkage curve, SC, has become an important part of laboratory measurements [3,5,10,11]. Research into the application of the combined laboratory measured SWCCs and SCs has now become the focus of research studies in numerous countries.

4. Assumptions Associated with the New Estimation Paradigm

Attempts to implement unsaturated soil mechanics into engineering practices has shown that the estimations of USPFs corresponding to desorption of the soil are adequate for most geotechnical engineering applications [12]. Use of the desorption boundary behavior (i.e., drying w-SWCC and drying SC) appears to provide the minimum information required when modeling the stress state versus volume-mass soil properties for USPFs. The authors are well aware of the hysteretic nature associated with SWCCs and the limitations of focusing primarily on drying behaviors; however, considerable understanding of unsaturated soil behaviors can be accrued by first focusing on the drying behavior and, subsequently, giving consideration to wetting behavior. The effect of hysteresis is dealt with in a limited manner near the later part of this paper.

It is noteworthy that no attempt is made to follow the stress-state pathway that might be followed in the specific field problem being studied. In other words, the in-situ stress path followed in the field is separated from the stress path followed in the laboratory. The intent is to simulate the field stress path as part of the numerical modeling exercise. The laboratory test path is designed to provide upper and lower bounds related to drying and wetting stress paths. The authors are well aware that there are approximations and some limitations associated with this approach. The suggested approach involves the use of wise assumptions that result in a compromise between a rigorous science approach and a reasonable cost approach.

The scope of this paper is limited to the application of the Fredlund and Xing [13] equation for all SWCCs and the M. Fredlund [14] equation for the shrinkage curve. This approach is deliberate in order to remain focused on the goal of illustrating the “estimation methodology” for modeling unsaturated soil mechanic problems. The use of the above-mentioned empirical equations for the SWCC and SC cover the entire range of possible soil suctions. Similar methodologies could be developed using other mathematical equations to represent unsaturated soil properties [15,16].

5. Steps Involved in the Analysis of Laboratory Data

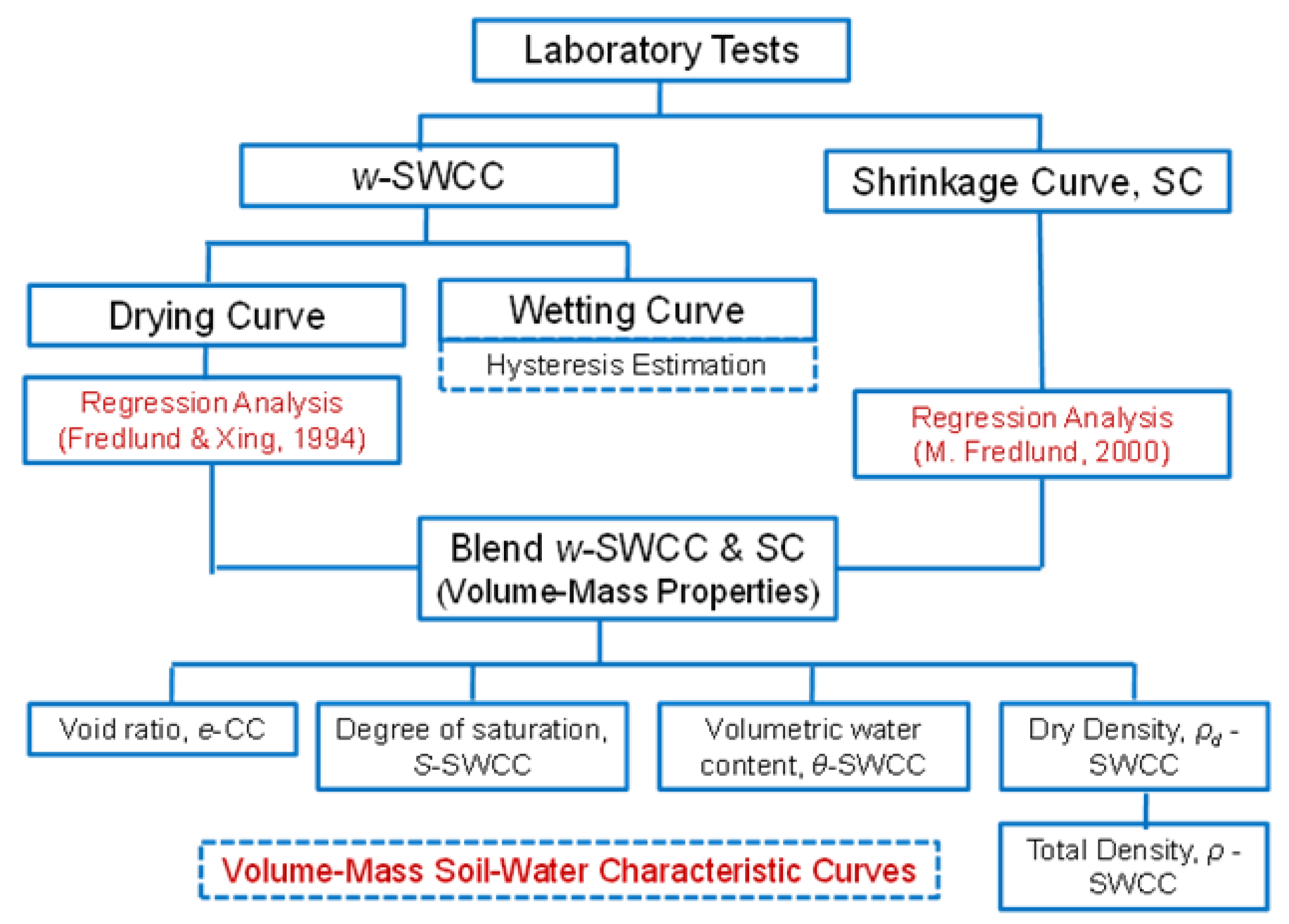
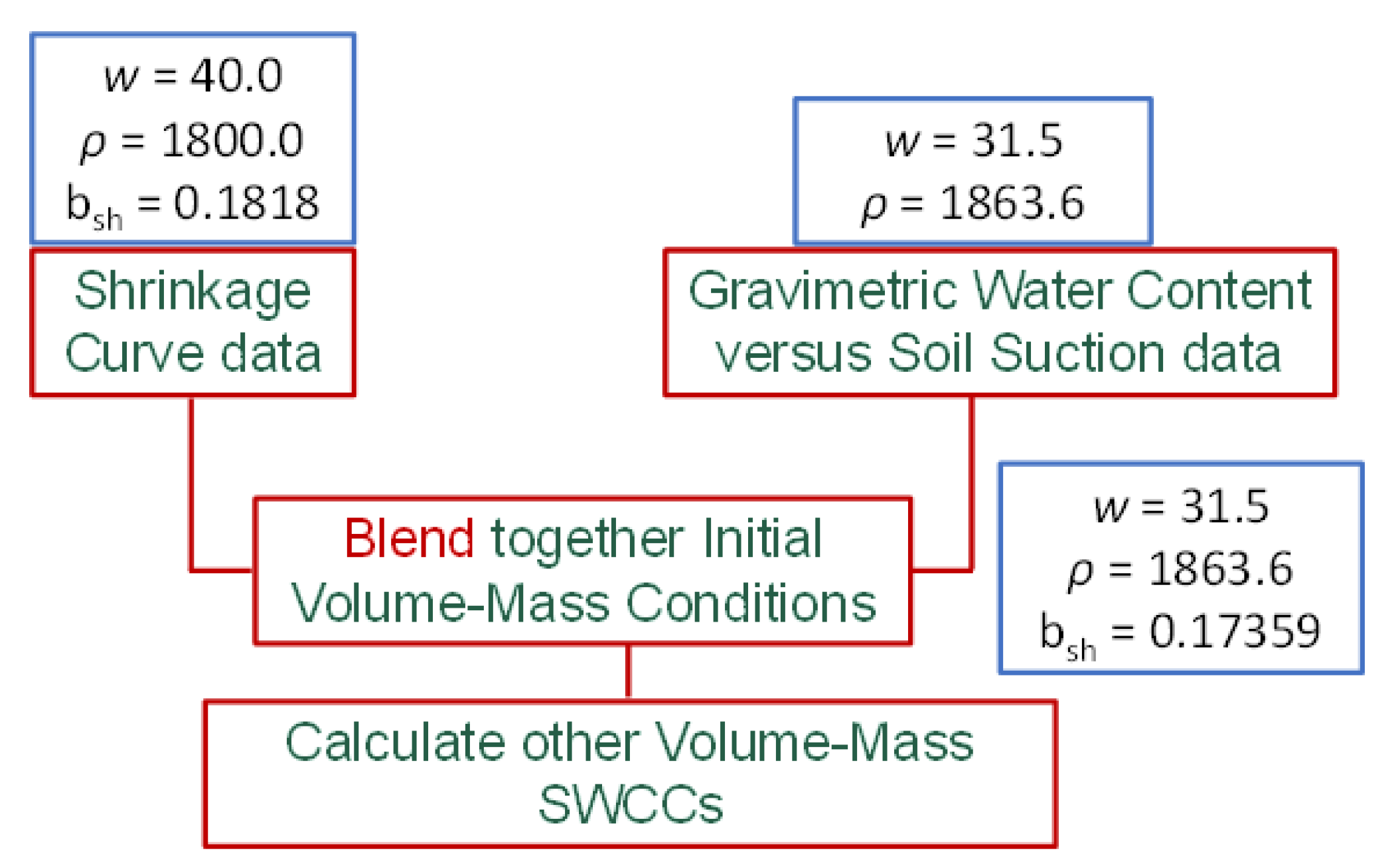
The calculation of unsaturated soil property functions commences with the laboratory measurement of the: (i) desorption (or drying) gravimetric water content versus soil suction data (w-SWCC) and (ii) shrinkage curve data (SC). Figure 1 emphasizes the steps involved in “blending” the w-SWCC and SC laboratory data. The “blending” steps ensures that the analysis of the data starts from a common set of volume-mass soil properties. The w-SWCC and the SC laboratory can then be used to calculate other volume-mass soil property relations, such as (i) void ratio versus soil suction, (ii) degree of saturation versus soil suction, (iii) volumetric water content versus soil suction, and (iv) density versus soil suction.

Once the basic volume-mass properties versus soil suction are calculated, it is possible to proceed with the determination of physical process functions such as: (i) the permeability function, (ii) water storage function, (iii) volume change and density functions, and (iv) shear strength function. EXCEL spreadsheets are used to illustrate the calculations of some of the unsaturated soil property functions (USPFs).

6. Calculation of Volume-Mass Variables

It is assumed that the specific gravity, G_s, has been either independently measured or accurately estimated based on previous experience. When a soil sample is brought into the laboratory, there is a general hierarchy with respect to the measurement of other volume-mass properties. For example, the gravimetric water content, w, and the total density of the soil, ρ, are the first basic measurements to be made. Once these three variables are measured, all other volume-mass variables can be calculated. 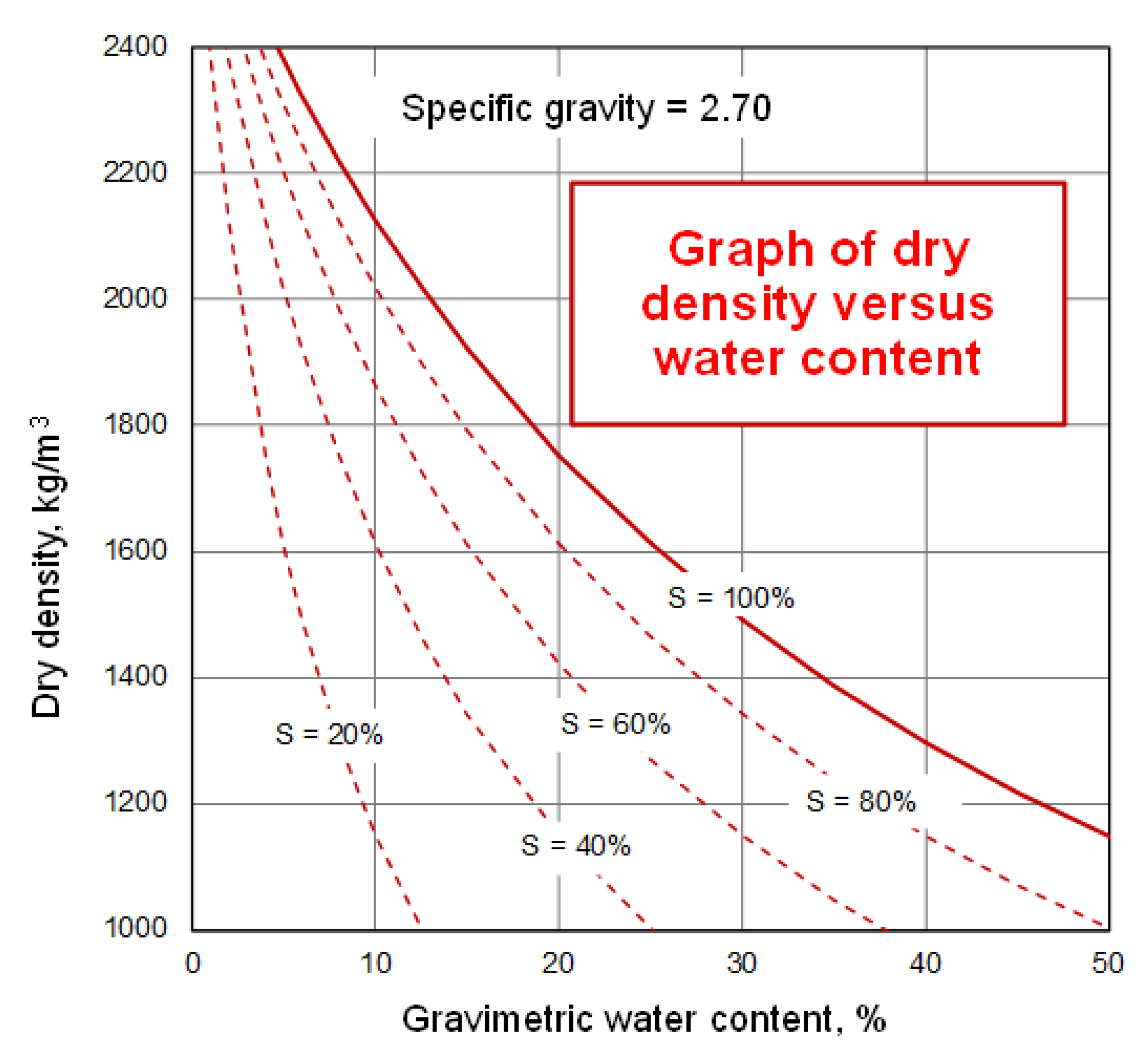Figure 2 emphasizes the difference between the measured and calculated volume-mass variables.

The relationship between volume and mass variables of interest in geotechnical engineering is shown in Figure 3. Saturated soil behaviors follow the solid (red) line, while unsaturated soil behaviors can involve a wide range of possible changes in volume-mass variables.

7. The Shrinkage Curve

A shrinkage curve test commences with a soil specimen that has been allowed to fully imbibe free water (i.e., to near-saturation conditions). The shrinkage curve test provides data on the relationship between volume change (in terms of changes in the void ratio) and gravimetric water content as the soil suction is increased under evaporative conditions, from near-zero conditions to completely dry conditions [16]. Test specimens for the SC test and the w-SWCC test should be prepared from the “same” soil sample. The SC specimen is commonly about 30 mm in diameter and 10 mm thick, while the w-SWCC specimen is commonly about 70 mm in diameter and 30 mm thick [5,17,18,19] (Figure 4).

Figure 5 shows the measurements of the shrinkage of a soil specimen as drying occurs from a wet soil specimen. The initial volume-mass properties should be measured on both the SC specimen and the w-SWCC specimen; however, it is later necessary to “blend” the two sets of laboratory results for the calculations of other volume-mass SWCCs.

M. Fredlund [14] proposed a hyperbolic equation for the best-fitting of measured shrinkage curve data. The shrinkage curve can thus be reduced to two fitting soil parameters, as shown in Equation (1):

$$e\left(w\right)=a_{sh}{\left({\left(\frac{w}{b_{sh}}\right)}^{c_{sh}}+1\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$c_{sh}$}\right.}$$

(1)

where a_sh = the minimum void ratio upon complete drying, c_sh = the variable related to the sharpness of the curvature as the soil desaturates, b_sh = the variable related to the slope of the drying curve calculated as b_sh = (a_sh S_o)/G_s, and S_o = the initial conditioned degree of saturation. The collected data can be entered into a spreadsheet for analysis purposes. The first function involves the calculation of the various volume-mass properties, followed by a regression analysis that converts the measured data into best-fit parameters (Figure 6).

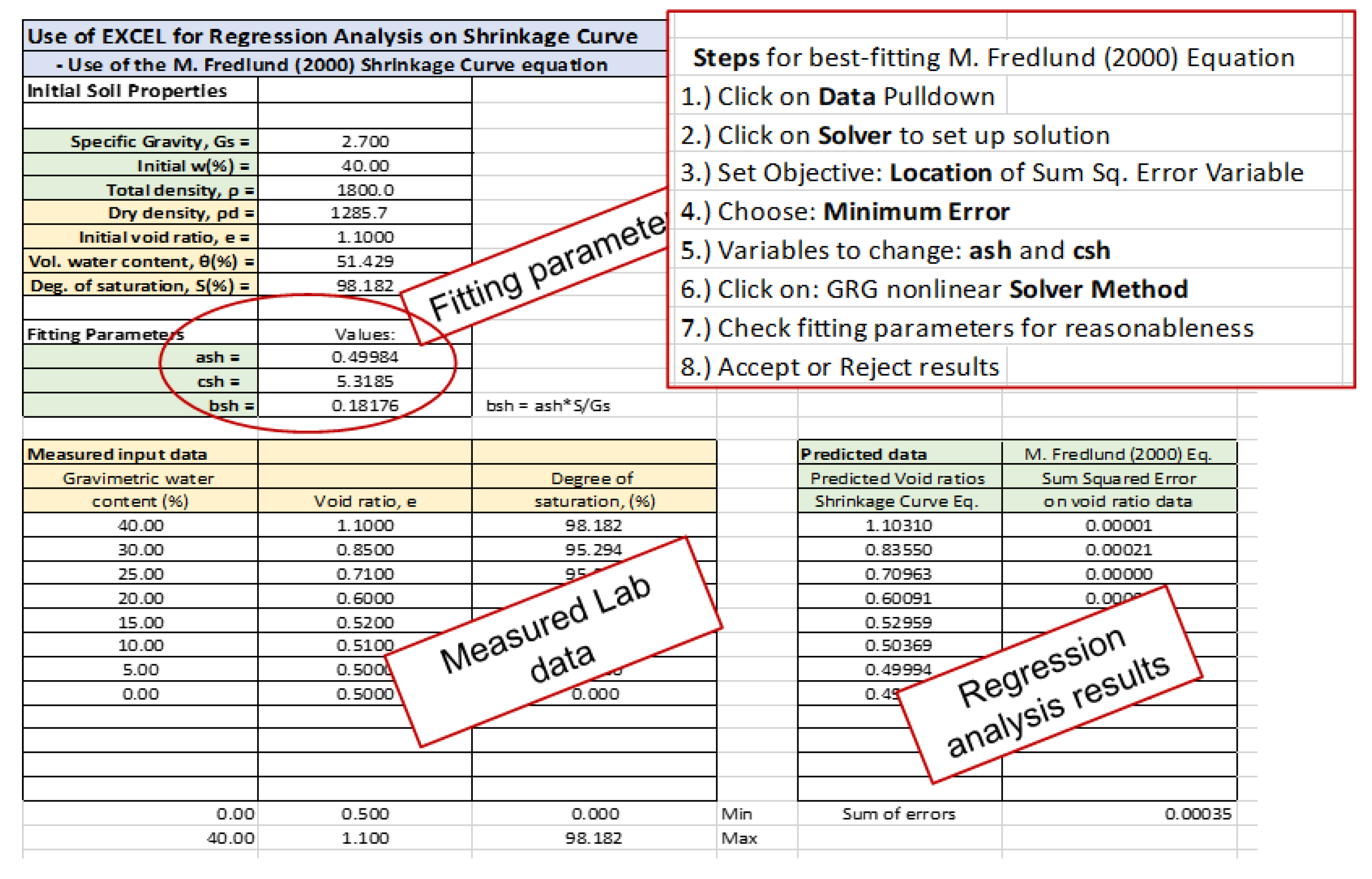
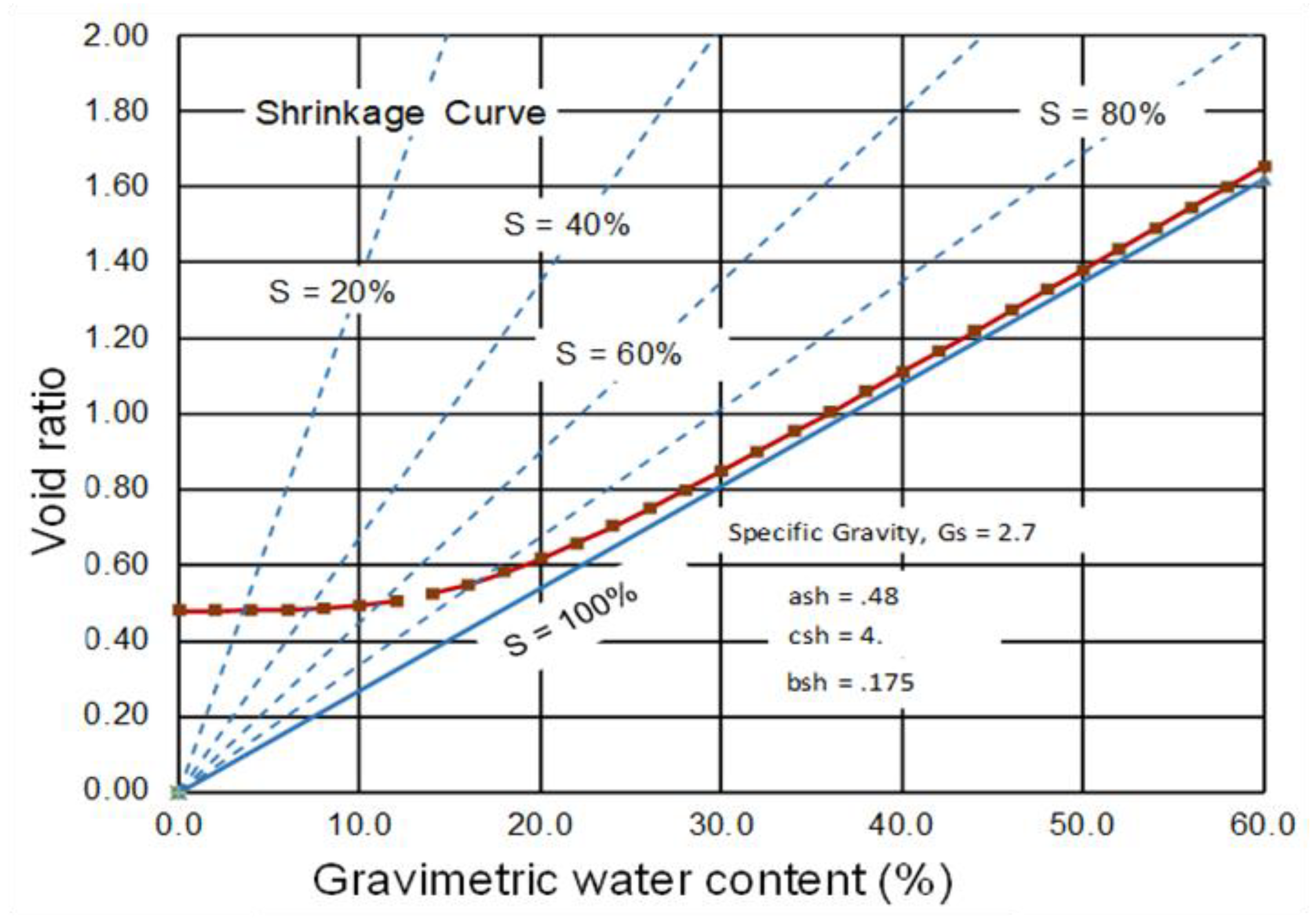
Figure 6 shows the main components of a spreadsheet used to record and reduce the shrinkage curve results. The upper-left portion of the spreadsheet lists the measured and calculated volume-mass soil properties. The volume-mass variables are calculated based on the specific gravity (G_s = 2.70), gravimetric water content (w = 40.0%), and total density (ρ = 1800.0). A series of gravimetric water content, w, and void ratio, e, measurements are made as the soil slowly dries during the SC test. These w and e measurements can be entered in the middle-left portion of the spreadsheet. Usually, five to eight sets of measurements are required as the soil dries.

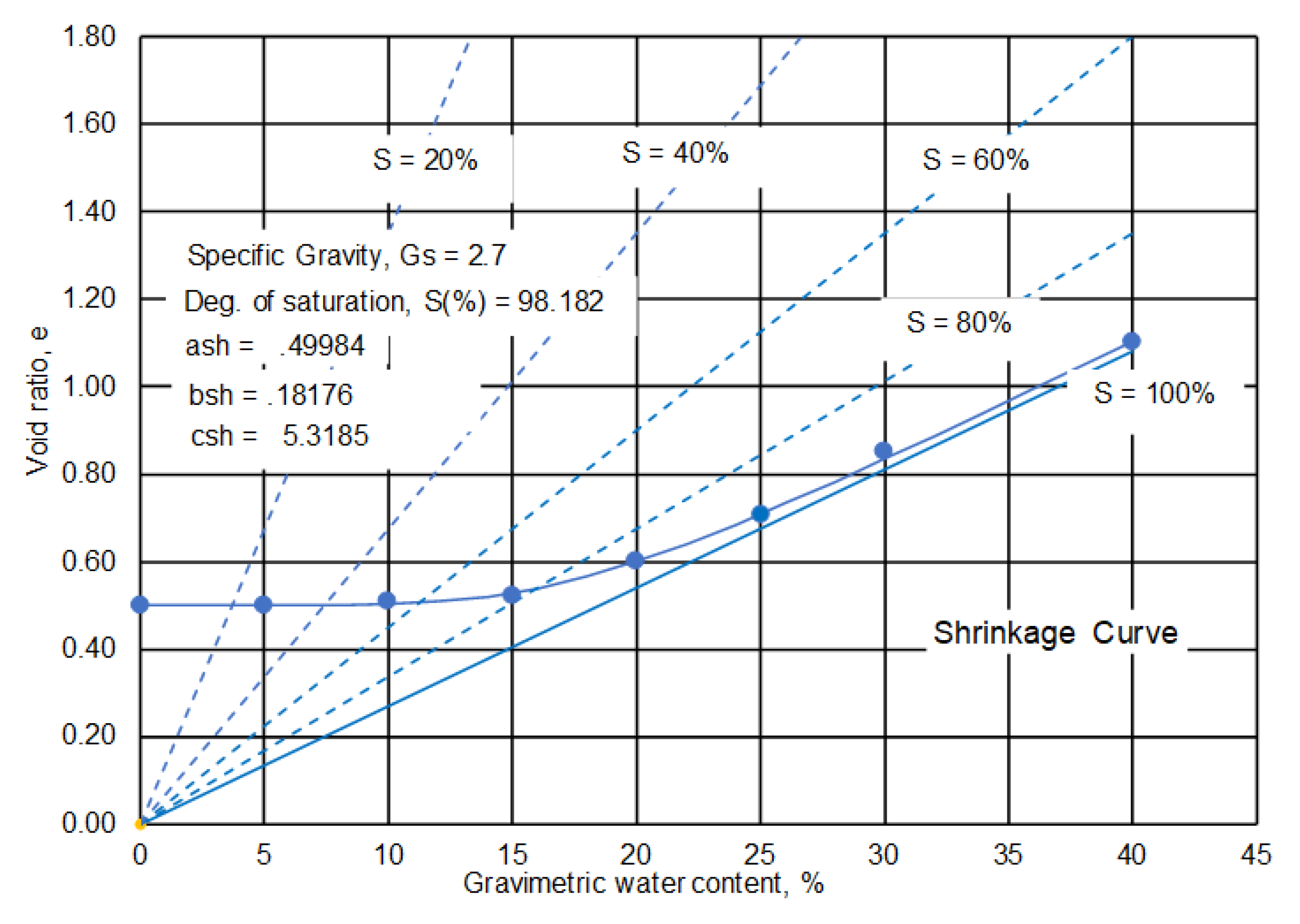
Once the SC data has been entered into the spreadsheet, the series of “steps” listed in the upper-right portion of the spreadsheet can be followed to obtain the fitting parameters using the EXCEL Solver function. The best-fit parameters are a_sh = 0.49984 and c_sh = 5.3185 for the shrinkage curve. The b_sh was calculated to be 0.1818. The drying shrinkage curve behavior can hereafter be referred to in terms of the fitting parameters, and a best-fit continuous line can be plotted as shown in Figure 7.

8. The Drying Gravimetric Water Content versus Soil Suction Curve (w-SWCC)

The second laboratory test involves the measurement of the gravimetric water content versus soil suction, referred to as the soil-water characteristic curve (w-SWCC). The results of the w-SWCC test provides the primary information required for extending the saturated soil behavior into the unsaturated soil range.

The w-SWCC function should be established over the entire soil suction range [20,21] (ASTM D6836-16, 2016). Figure 8 shows a series of pressure plate apparatuses with applied matric suctions up to 500 kPa. Commonly, about eight suctions are applied to the soil specimen, with values ranging from around 2 kPa up to the air-entry value, AEV, of the ceramic disk placed at the bottom of the soil specimen (i.e., AEV ~ 500 kPa). Quite often, the soil specimen is also placed into a pressure plate device that has an air-entry value of 1500 kPa. This provides one additional data point for the w-SWCC.

Measurements are also commonly made in the high suction range using a vapor equilibrium technique. Small soil specimens are prepared and allowed to dry for selected time periods. The water content and total suction are then measured on each specimen. It should be noted the total suctions are measured in the high suction range, whereas the matric suction is measured in the low suction range. In lieu of this seeming inconsistency, the data generally shows a smooth curve throughout the entire suction range. The total suctions can readily be measured using a chilled-mirror PotentiaMeter (Decagon Devices, Pullman, WA, USA) (Figure 9).

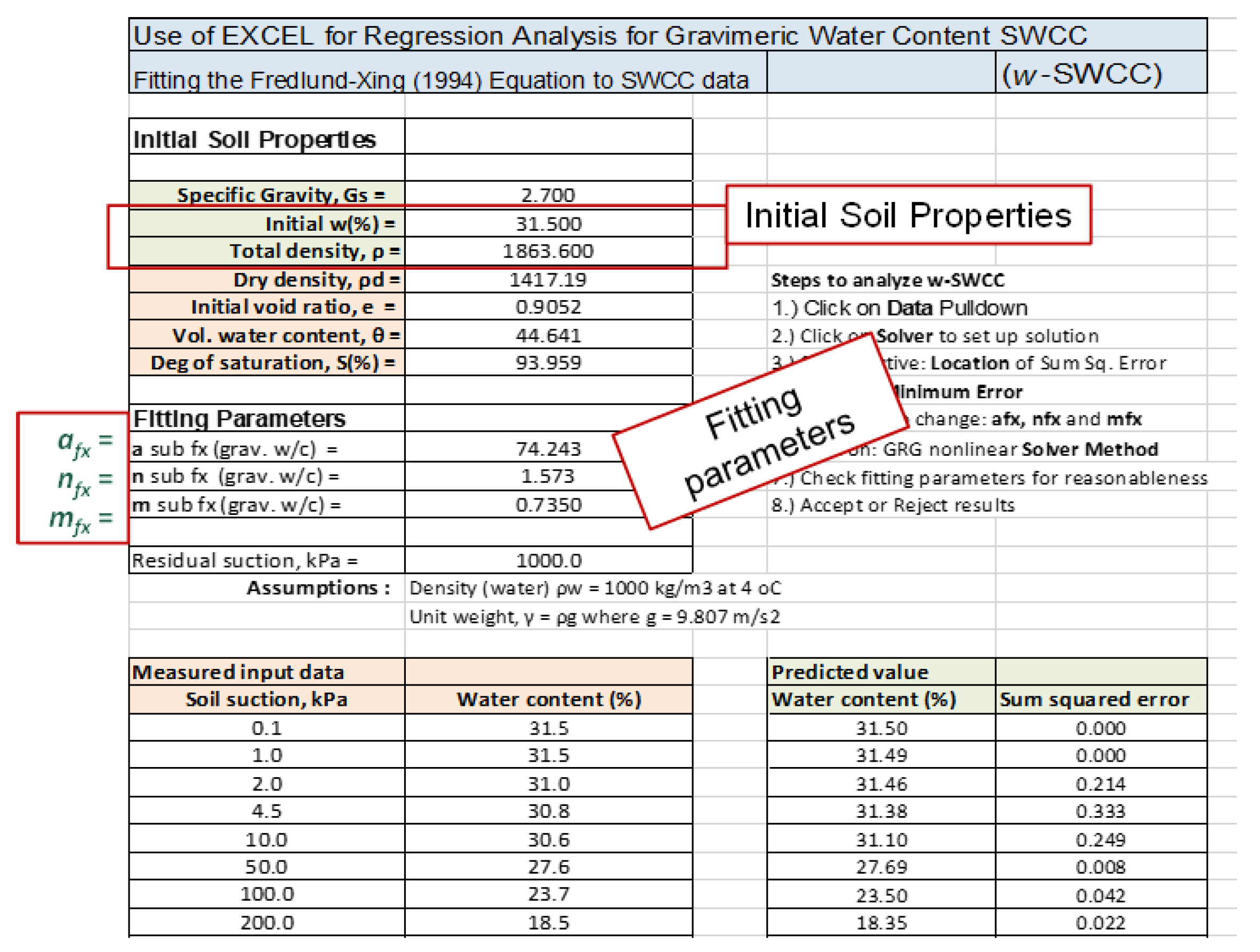
The measured data for the w-SWCC can be entered into a spreadsheet. Figure 10 shows the main components of a spreadsheet used to record and calculate the shrinkage curve results. The upper-left portion of the spreadsheet lists the measured and calculated volume-mass soil properties. The volume-mass variables are calculated based on a measured specific gravity (G_s, = 2.700), the independently measured gravimetric water content (w = 31.50%), and the total density (ρ = 1863.60).

There are numerous equations that have been proposed to best-fit the w-SWCC. This paper is limited to the use of the Fredlund and Xing [13] SWCC equation:

$$w\left(\psi \right)=\frac{w_{s}C\left(\psi \right)}{{\left(\ln \left(\exp \left(1\right)+{\left(\psi /a_f\right)}^{n_f}\right)\right)}^{m_f}}$$

(2)

where w(ψ) = the water content at any soil suction, ψ, a_f = the fitting parameter related to the suction near the inflection point on the w-SWCC, n_f = the fitting parameter related to the maximum rate of the gravimetric water content change, m_f = the fitting parameter related to the curvature near the residual gravimetric water content conditions, ψ_r = the suction near the residual conditions of the soil, and C(ψ) = the correction factor equation directing the w-SWCC function towards a suction of 10⁶ kPa at the zero-water contents (Equation (3)). Residual suction conditions can be approximated using an empirical construction procedure [22].

$$C\left(\psi \right)=1-\frac{\ln \left(1+\raisebox{1ex}{$\psi $}\!\left/ \!\raisebox{-1ex}{${\psi }_r$}\right.\right)}{\ln \left(1+\raisebox{1ex}{${10}^6$}\!\left/ \!\raisebox{-1ex}{${\psi }_r$}\right.\right)}$$

(3)

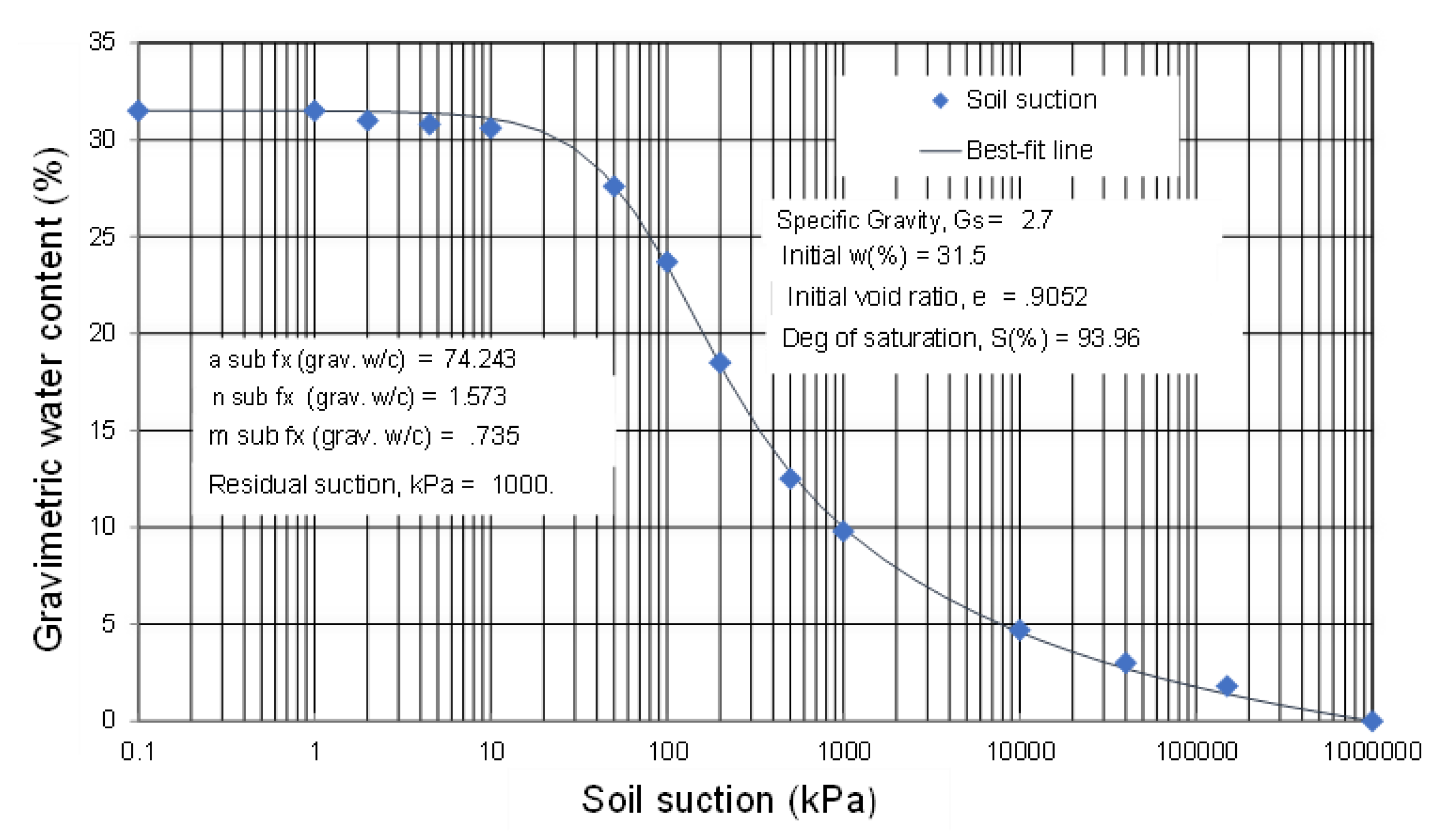
Figure 11 presents the gravimetric water content data based on tests on initially slurry Regina clay [21]. The general layout of the solution is similar to that previously shown for the analysis of the shrinkage curve data. It should be noted that initial volume-mass variables differ somewhat from those calculated for the shrinkage curve. This difference is intentional in order to later illustrate the “blending” of the volume-mass measurements for the SC and w-SWCC. It is suggested that an approximation of the residual suction be estimated prior to solving for the three fitting parameters associated with the Fredlund and Xing [13] equation (i.e., a_f, n_f, and m_f). It is noted that the fitting parameters are only slightly influenced by the estimation of the residual suction. It is adequate to estimate the residual suction within one order of magnitude [22].

The water content at any point along the w-SWCC function can be calculated from the fitting parameters. The inflection point for the w-SWCC function (i.e., a_f) is 74.243 kPa, the rate of the water extraction variable (i.e., n_f) is 1.573, and the m_f variable is 0.7350. These fitting parameters can be used to represent the entire drying w-SWCC function.

Further analyses of the SC and the w-SWCC functions can be undertaken to provide a more complete understanding of the role of each of the volume-mass variables. For example, the coefficient of permeability of an unsaturated soil may undergo a modest change in its magnitude due to void ratio changes while it undergoes a substantial change when the degree of saturation is changed. The volume-mass soil properties versus soil suction can be viewed as independent physical relations. Other volume-mass soil properties versus soil suction can now be calculated based on the limited data collected from the SC and the w-SWCC.

Blending the Results of the SC and w-SWCC Tests

The measured initial volume-mass soil properties may differ somewhat between the SC test and the w-SWCC test. For the example data shown, the initial gravimetric water content for the SC test was 40.0%, while the initial water content was 31.5% for the w-SWCC test. It is recommended that the w-SWCC be used as a reference. In other words, the initial gravimetric water content is assumed to be 31.5%, the total density is 1863.6 kg/m³, the void ratio is 0.9052, and the degree of saturation is 93.96%. The fitting parameters for the w-SWCC remain as previously shown. The initial soil properties for the SC test can be changed to conform to the w-SWCC test values. 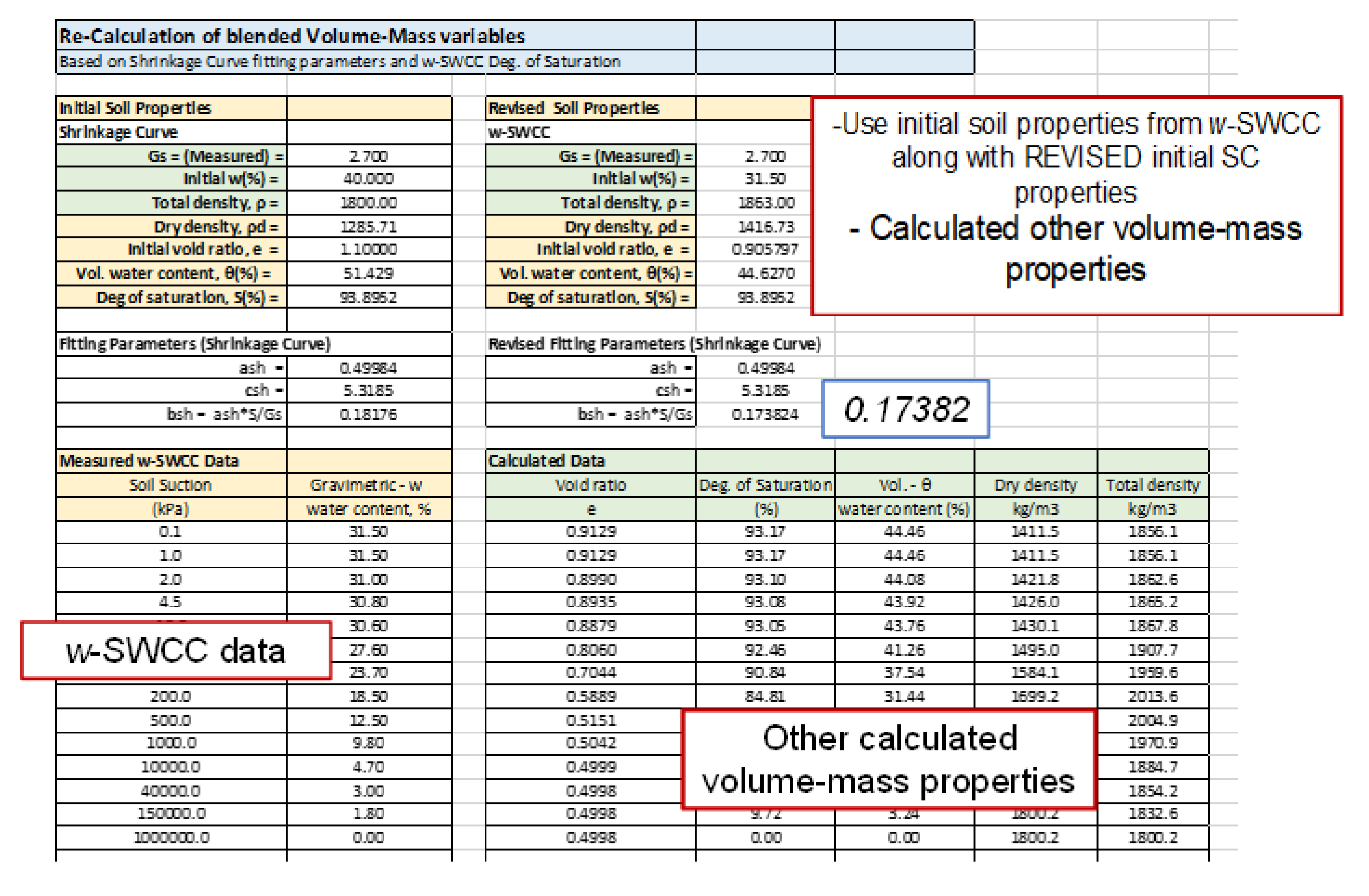Of the three fitting parameters for the SC test, only the b_sh parameter needs to be recalculated using Equation (4).

$$b_{sh} = \left(a_{sh} S_o\right)/G_s$$

(4)

The a_sh and c_sh variables remain the same; however, the b_sh variable must be changed from 0.1801 to 0.17359 due the change in the starting degree of saturation. The adjustment of the b_sh variable means that other volume-mass variables can be calculated corresponding to suction measurements made during the w-SWCC test. Sample calculations for the remaining volume-mass variables are shown in Figure 12.

Once the initial volume-mass properties of the SC and w-SWCC tests are “blended”, then it is possible to extend the measured laboratory data to include the calculations of all other volume-mass variables, as shown in Figure 13, using the equations shown in Figure 2.

9. Void Ratio versus Soil Suction over the Desorption Range (e-CC)

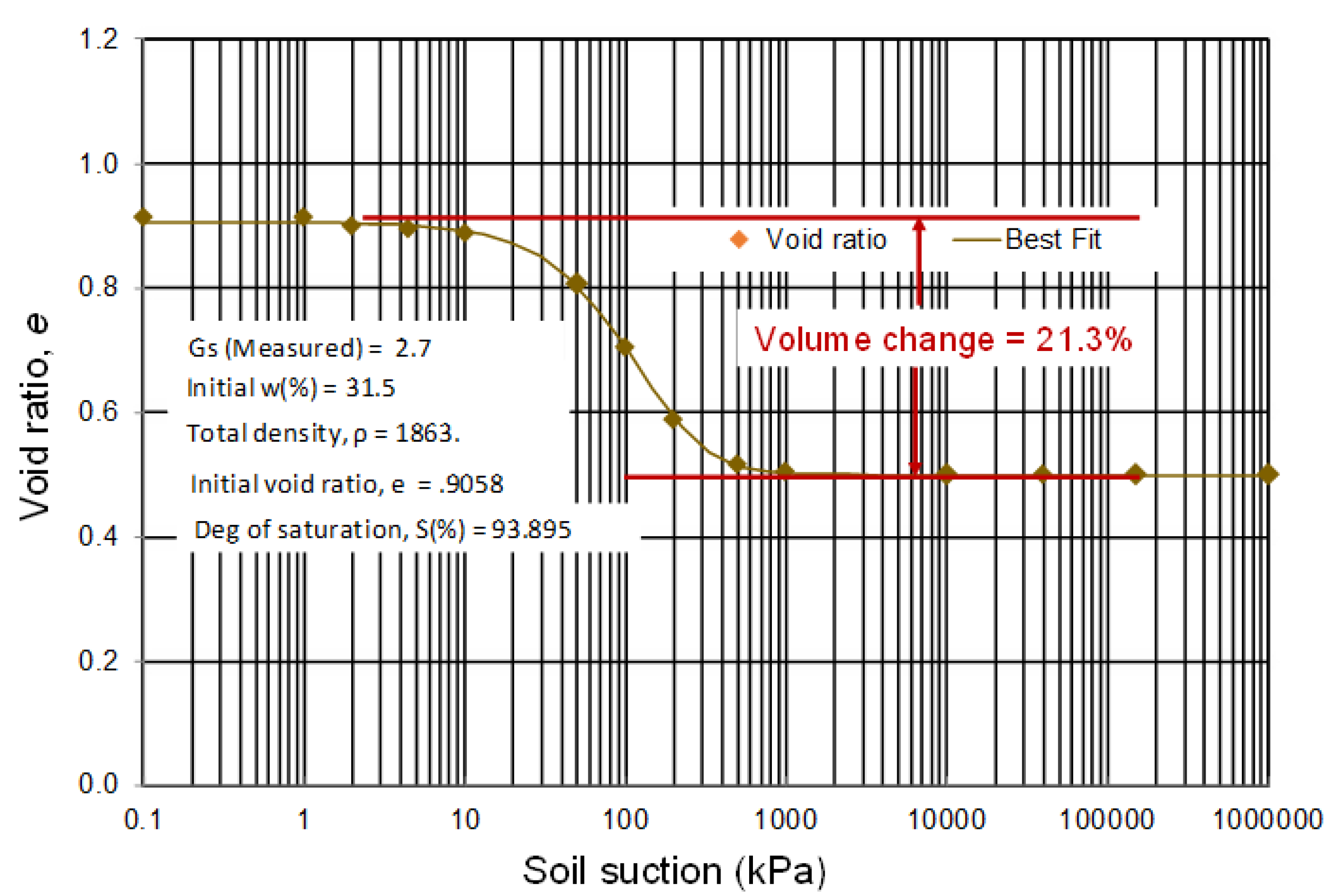
The void ratio versus soil suction characteristic curve (e-CC) can be calculated by substituting the SC equation into the w-SWCC equation, yielding the void ratio as a function of the soil suction. Figure 14 shows the calculation of the void ratio characteristic curve (e-CC), determined from the presented SC and w-SWCC data. The data points corresponding to the laboratory measured results are plotted, along with the best-fit regression analysis results. It can be seen that a different estimation value for residual suction can correspond to each of the volume-mass relations versus soil suction.

The void ratio versus suction relationship can once again be represented by a mathematical equation over the entire range of possible suction values. The Fredlund and Xing [13] equation for the SWCC (i.e., Equation (2)) can be used, along with the assumption that the correction factor (C(ψ)) be omitted (or set to 1.0), since the void ratio becomes asymptotic to a zero slope at suctions beyond the residual suction. The plot shows that the volume change commences at a suction of about 10 kPa and that no further volume change occurs once the suction exceeds about 400 kPa. The maximum overall volume change was about 21.3%.

It is recognized that each of the suction versus volume-mass changes are hysteretic; however, at this time, the shrinkage curve relationship is limited to the drying mode from a near-saturated condition for geotechnical engineering applications.

10. Degree of Saturation versus Soil Suction during Drying (S-SWCC)

The second volume-mass relationship that can be computed is the degree of saturation versus soil suction. The degree of saturation is shown as series of data points calculated at selected suction intervals while adhering to the equation shown in Figure 13 (i.e., the basic volume-mass equation). Three fitting parameters are obtained from the regression analysis when applying the Fredlund and Xing [13] equation (i.e., Equation (2)). The S-SWCC function generated from the fitting parameters for the SC and w-SWCC tests is shown in Figure 15.

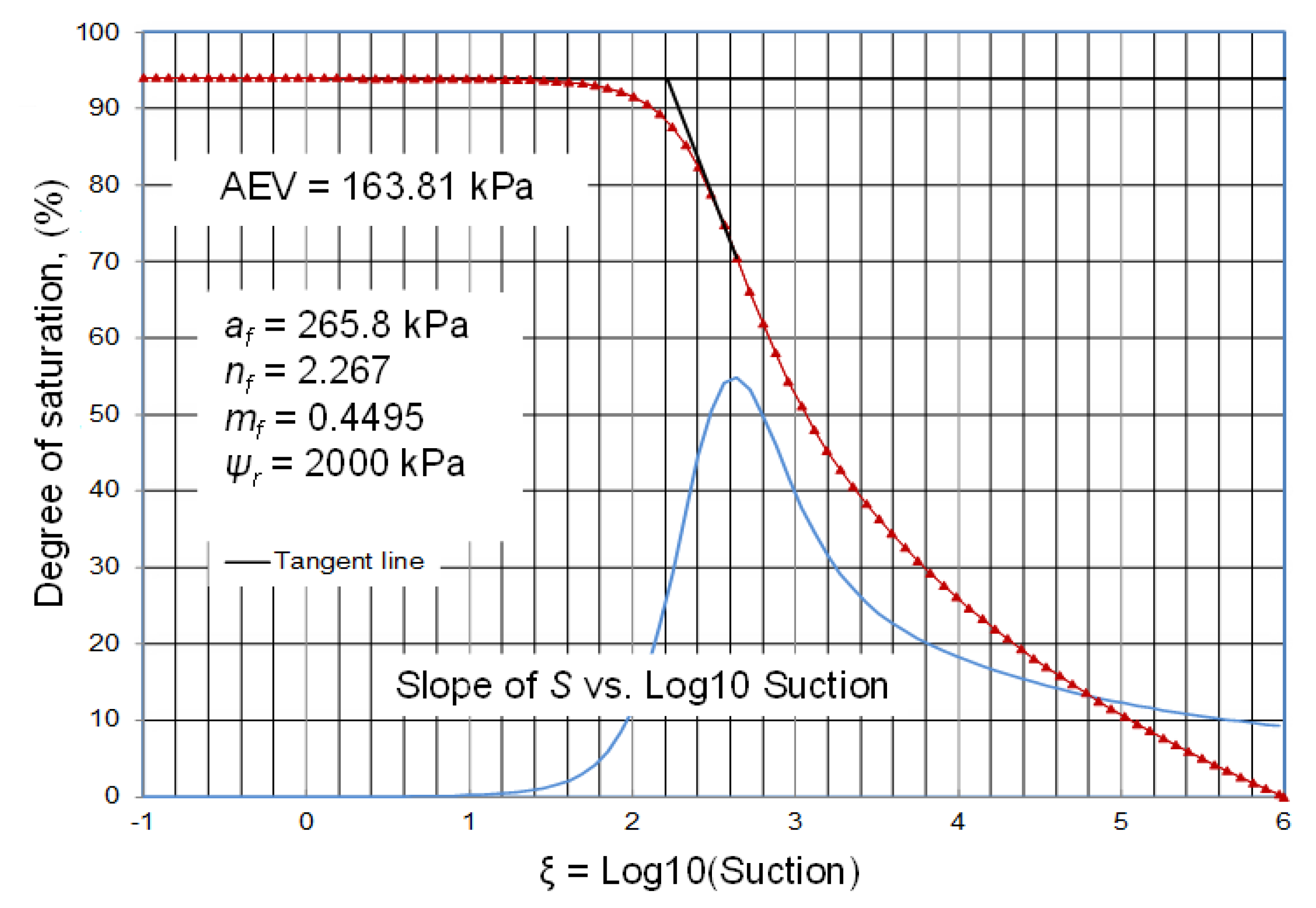
The inflection on the S-SWCC function, a_f, is 265.8 kPa, which is considerably higher than observed when analyzing the w-SWCC (i.e., 74.24). It is the S-SWCC function that indicates the “true” air-entry value for the soil. In other words, the soil remains essentially saturated to considerably higher suction values than would be indicated based on the w-SWCC function. The n_f obtained from the S-SWCC function is also considerably steeper at 2.27, as compared to 1.57 from the w-SWCC function. The m_f fitting parameter is 0.450 from the S-SWCC, as compared to 0.735 from the w-SWCC. The comparison of the analysis of the S-SWCC to the w-SWCC function illustrates the independent functionality of each of the SWCC volume-mass equations.

The logarithm of the soil suction scale can be converted to an equivalent arithmetic scale for the purposes of calculating the “true” air-entry value for the soil. The logarithmic suction scale is converted to an arithmetic scale, ξ, using the following suction scale transform:

$$\xi ={\log }_{10}\left(\psi \right)$$

(5)

where ψ = any soil suction. The degree of saturation SWCC with the transformed suction scale retains the same Fredlund and Xing [13] mathematical form depicted by Equation (2). The degree of saturation as a function on the transformed suction scale is graphically shown in Figure 16. The remaining fitting parameters for the transformed degree of saturation equation, (i.e., a_f, n_f, and m_f) remain the same as calculated for the S-SWCC.

The “true” air-entry value, AEV, corresponds to the intersection point between a horizontal line through the initial degree of saturation and the line of tangency through the inflection point [23]. The inflection point corresponds to the point where the slope of the function is the largest. A line of tangency is drawn through the inflection point in order to calculate the “true” air-entry value. The above numerical solution provides an empirical procedure for the calculation of a unique value for the “true” air-entry value of a soil. 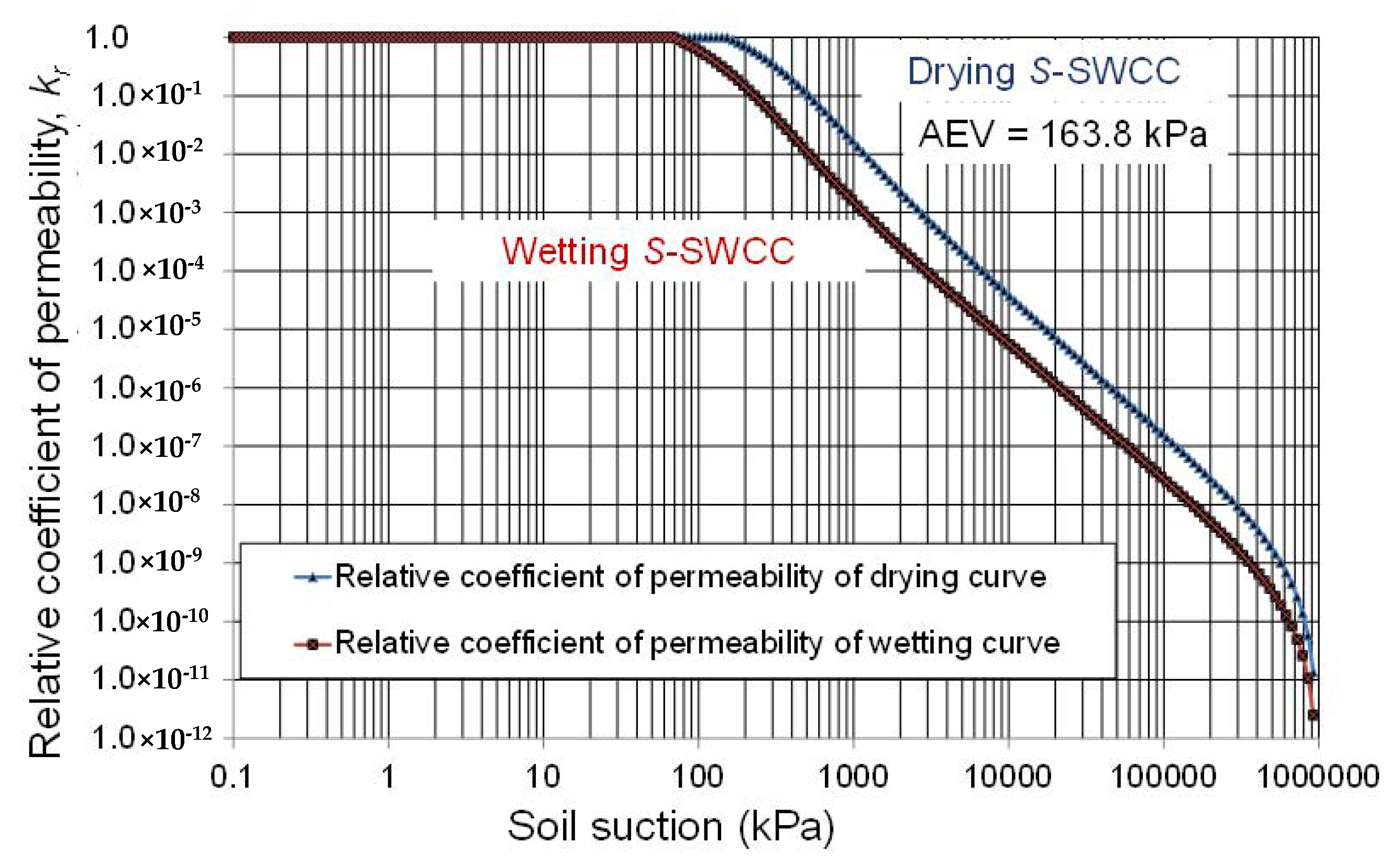Figure 16 shows the determination of a “true” air-entry value, AEV, of 163.81 kPa for the soil. The analysis of the S-SWCC sets the stage for the next steps, which are the estimation of the USPFs (e.g., the coefficient of permeability function) [23].

It should also be noted that a number of assumptions have been made throughout the above-proposed analysis. For example, information on the effect of hysteresis associated with drying and wetting and the effect of total stress confinement during the drying process have not been taken into consideration. It is anticipated that, while hysteresis and the effect of total confinement are important, these factors are not the primary influence on unsaturated soil behaviors.

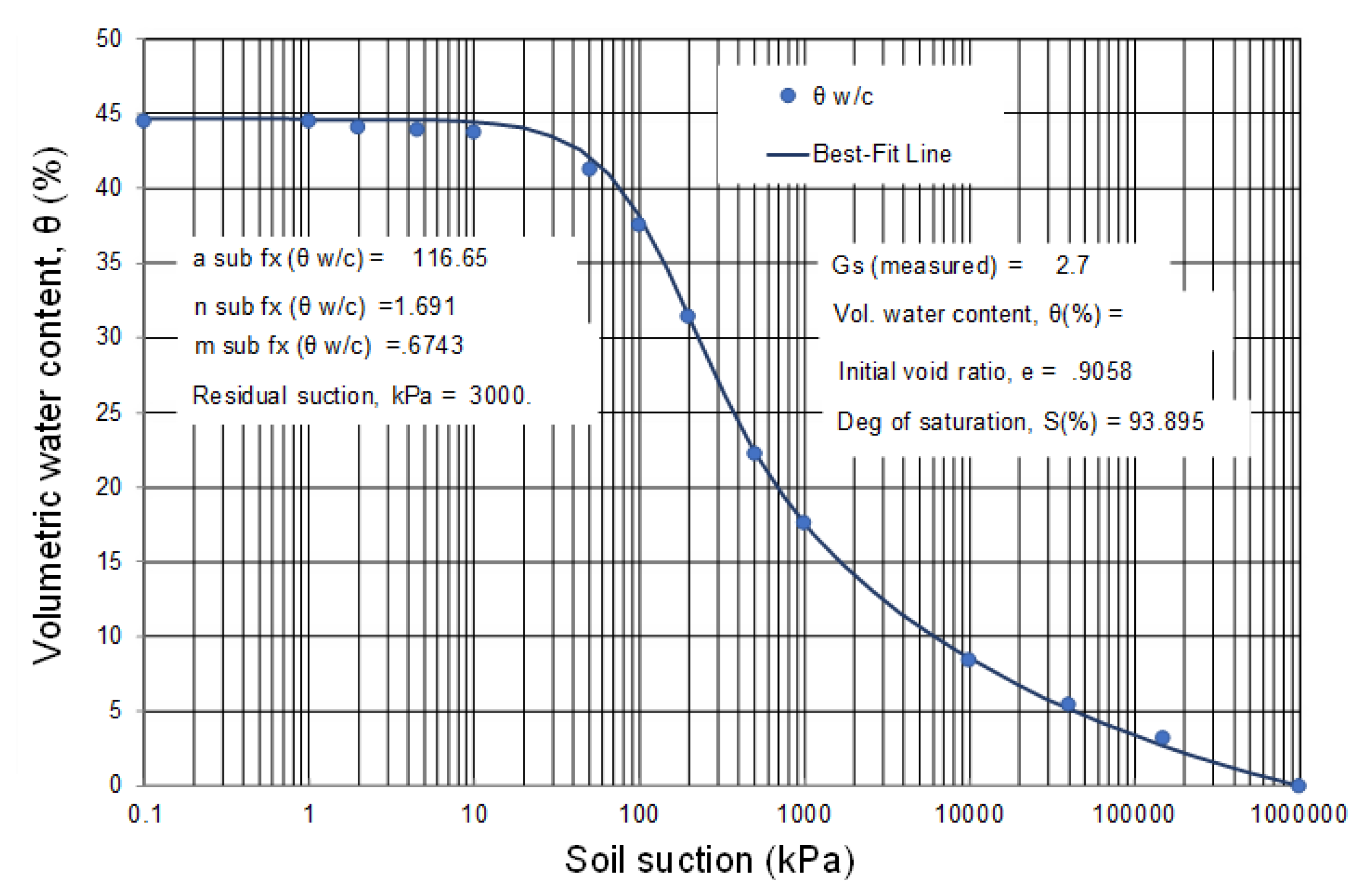
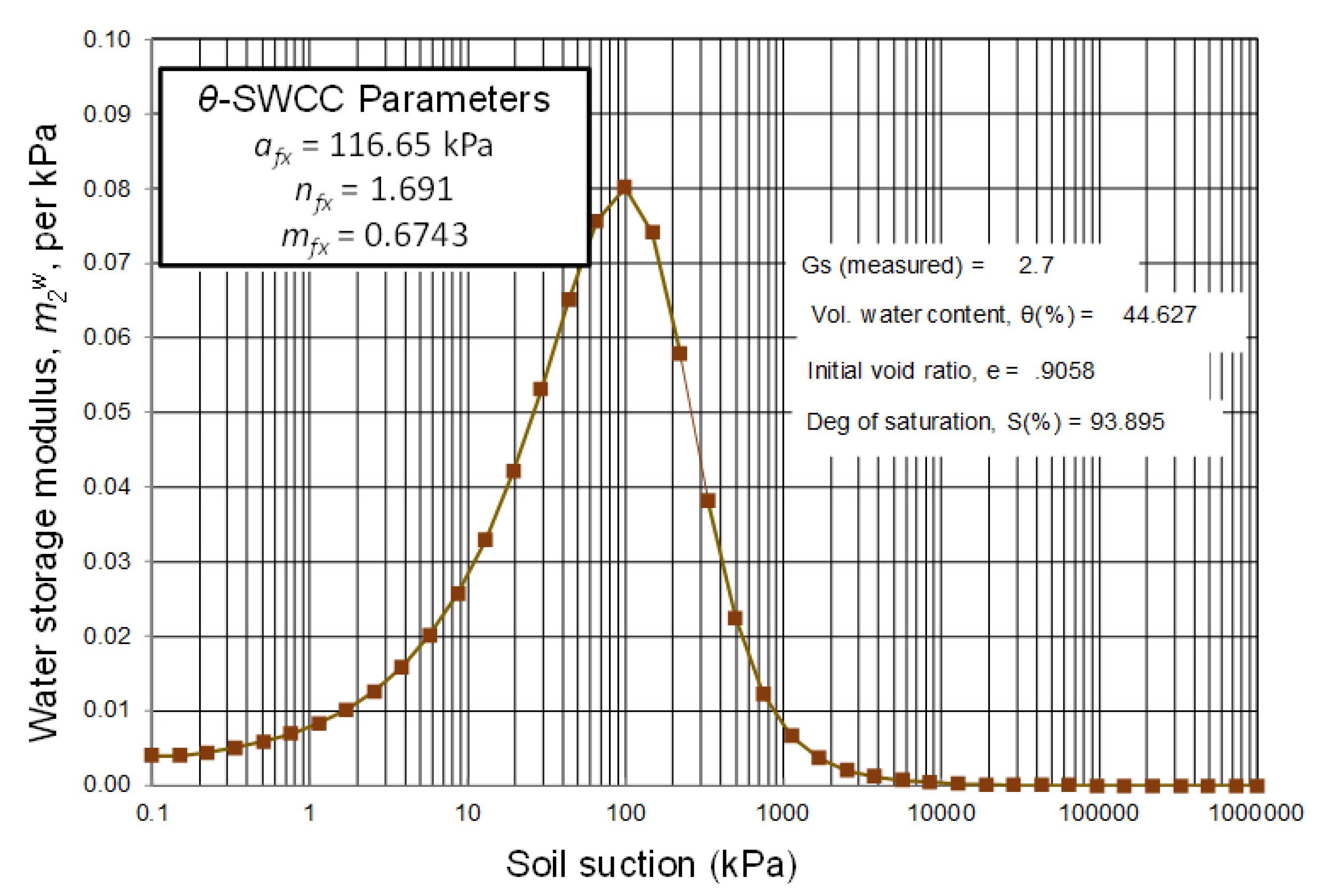
11. Volumetric Water Content versus Soil Suction during Drying (θ-SWCC)

The volumetric water content versus soil suction relationship serves as an independent and important relationship related to water storage in an unsaturated soil. Data points are shown corresponding to the laboratory measured results, as well as the continuous function generated by the fitting parameters (Figure 17). The volumetric water content data points are calculated using the equation shown in Figure 2. Details of the spreadsheet calculations are not included in this manuscript. Differentiation of the volumetric water content SWCC provides the variations in water stored in the soil during the drying process.

The various water content SWCCs (i.e., gravimetric water content, volumetric water content, and degree of saturation) can all be normalized to give the same graph for situations where there is no overall volume change as the suction is changed. However, even a relatively small amount of volume change can have a substantial effect on the various SWCCs.

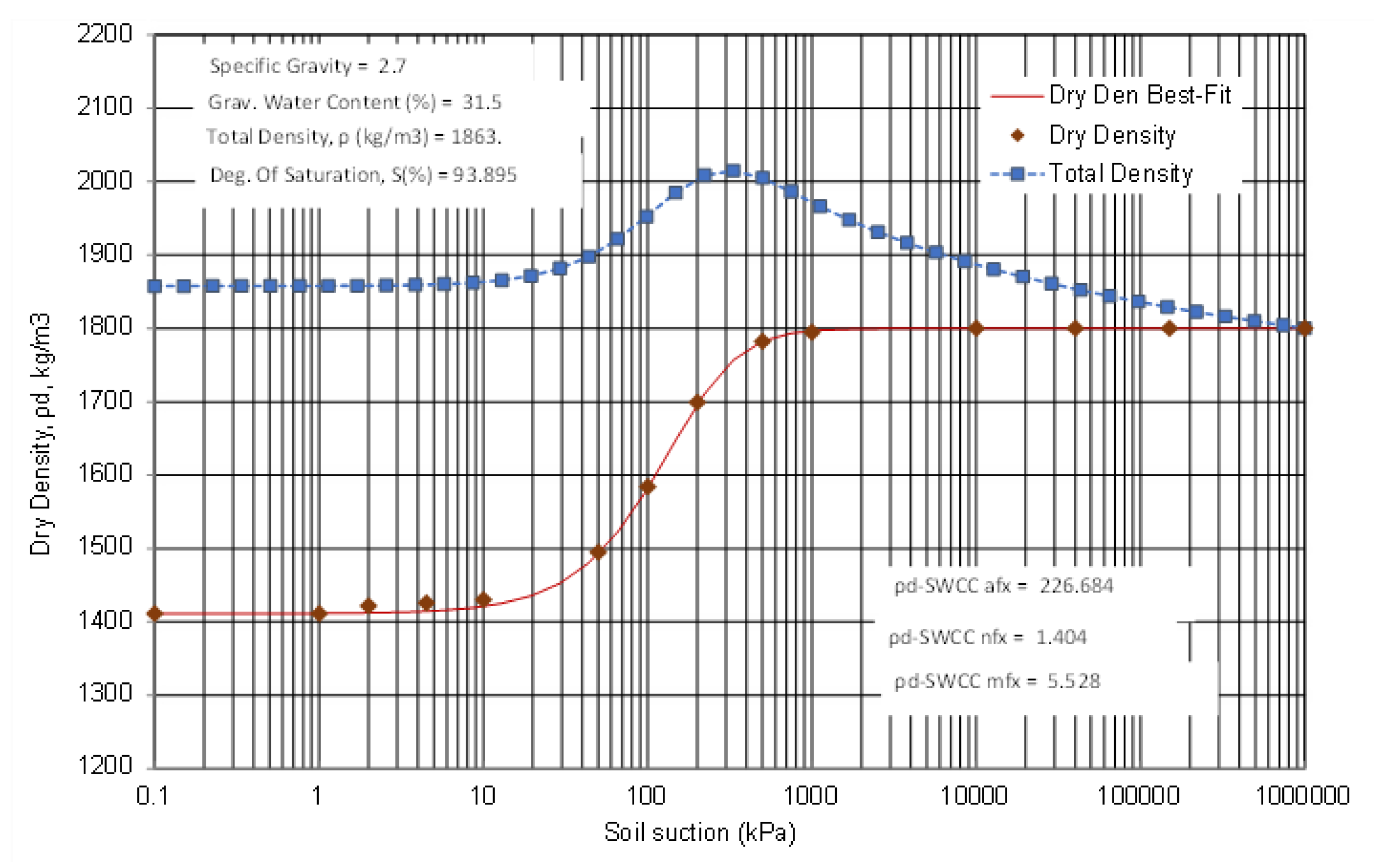
12. Dry Density, ρ_d, (and Total Density, ρ) versus Soil Suction for Desorption Range (ρ_d-SWCC)

Both the dry density and total density versus soil suction relationships can be calculated from the SC and w-SWCC data. A continuous function can be calculated from the fitting parameters, as shown in Figure 18. The dry density function has the reverse appearance to the previously presented void ratio function (e-CC). As the soil dries, the dry density increases, until a plateau is reached where no further volume change occurs with respect to increases in the soil suction.

The total density versus soil suction first increases as the suction increases to a peak value—after which, the total density of the unsaturated soil decreases. The total density function is of interest when analyzing gravity-related problems such as the slope stability. The shape of the total density function is the consequence of two competing mechanisms. During drying, the void ratio decreases to a point, and at the same time, water is being lost from the soil.

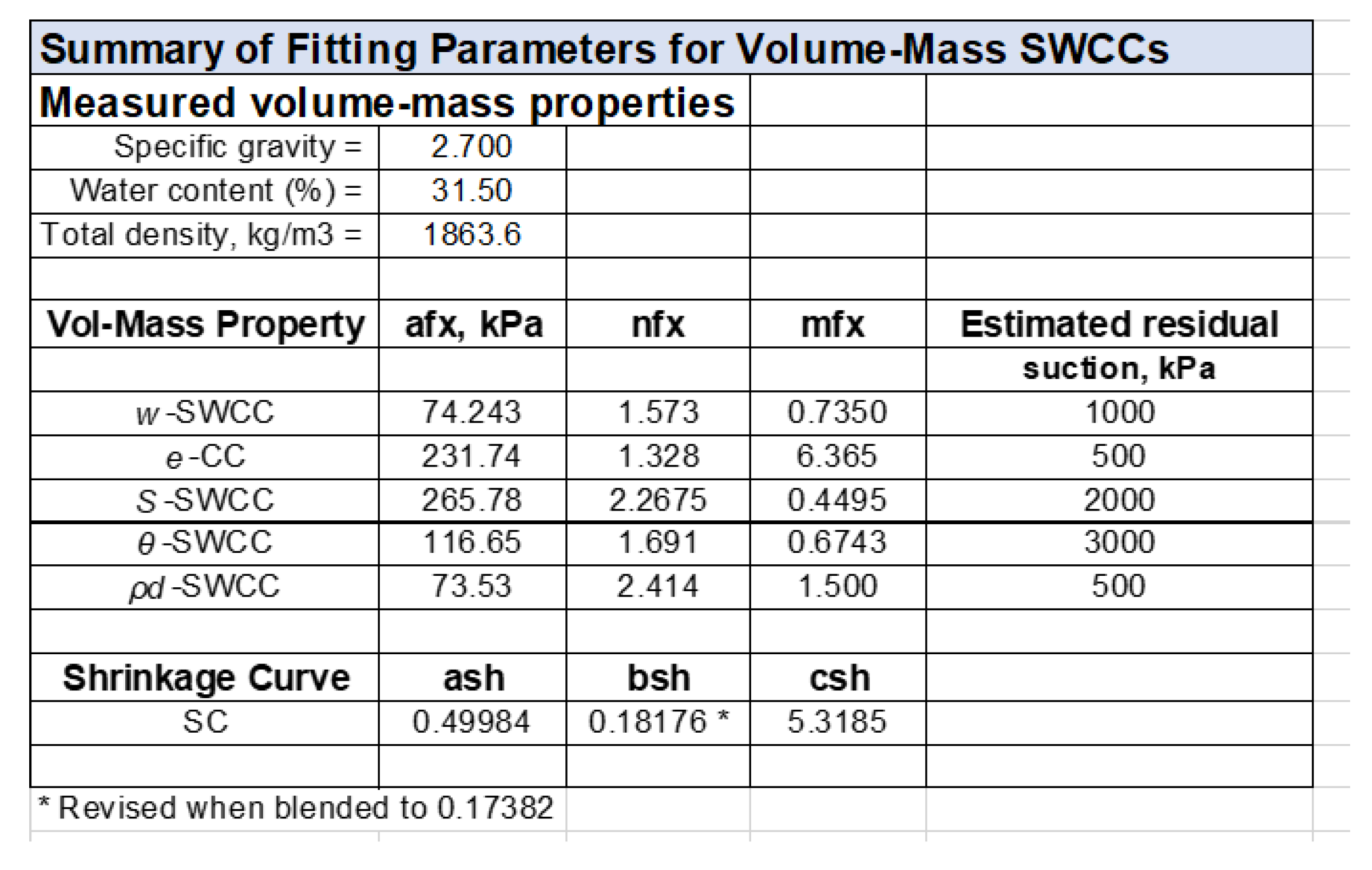
13. Summary of Fitting Parameters for Volume-Mass SWCCs

Figure 19 contains a table summarizing the fitting parameters from each of the volume-mass variables as the soil undergoes drying throughout the entire range of suctions. The initial gravimetric water content and total density were the same for all analyses presented. The results of the shrinkage curve, SC, laboratory data were first analyzed and converted to three fitting parameters. Then, the results of the gravimetric water content versus soil suction, w-SWCC, were converted to three other fitting parameters. The two laboratory test results were then combined to yield all other volume-mass functions versus the soil suction corresponding to the drying mode. In each case, the same Fredlund and Xing [13] sigmoidal equation was used to fit the calculated volume-mass data.

It should be noted that there is no functional relationship between the various fitting parameters calculated for each of the volume-masses versus the suction datasets. In each case, the residual suction value is estimated. It is suggested that the most meaningful value for the residual suction is the value observed on the degree of saturation plot.

The fitting parameters for each volume-mass versus soil suction relationship have a general meaning. For example, the a_fx variable refers to the inflection point along the specific relationship. The n_fx variable refers to the steepness of the function (or rate of change) as the suction increases. The m_fx variable raises and lowers the function in the high suction range of the function. It should also be noted that the fitting parameters are not unique since a change in one of the fitting parameters will influence the other fitting parameters within a single functional relationship.

It is also suggested that the degree of saturation versus suction function provides the most important information on the behavior of an unsaturated soil. In particular, the most meaningful indication of the “true” air-entry (i.e., AEV) is determined from the S-SWCC relationship. Unfortunately, it is difficult to directly measure the degree of saturation SWCC for a soil, and as a result, the degree of saturation function becomes a “calculated” relationship as opposed to a “directly measured” relationship.

14. Estimation of Unsaturated Soil Property Functions

A differentiation is made between the previous “calculation” of volume-mass versus soil suction functions, and the following “estimation” of the unsaturated soil property versus soil suction functions. The term “calculation” is used when reference is made to the “basic volume-mass” relationship [1], and the term “estimation” is used when further assumptions and physical relationships are used in determining the unsaturated soil property functions.

The unsaturated soil property functions associated with the hydraulic properties of an unsaturated soil are first presented. These are (i) the coefficient of permeability (or hydraulic conductivity) as a function of the soil suction and 669 (ii) water storage functions versus the soil suction. This is followed by the estimation of the shear strength and an unsaturated volume change function for an unsaturated soil. Finally, some suggestions are given with respect to accommodating the effects of drying and wetting hysteresis related to the SWCC and the SC.

15. Estimation of the Unsaturated Permeability Function

A variety of methodologies have been proposed for estimating the permeability function for an unsaturated soil [1]. In each case, the proposed method has involved some form of integration along the soil-water characteristic curve to yield an estimation for the unsaturated soil permeability function. The integration process is generally quite cumbersome in comparison to the calculation for the volume-mass functions.

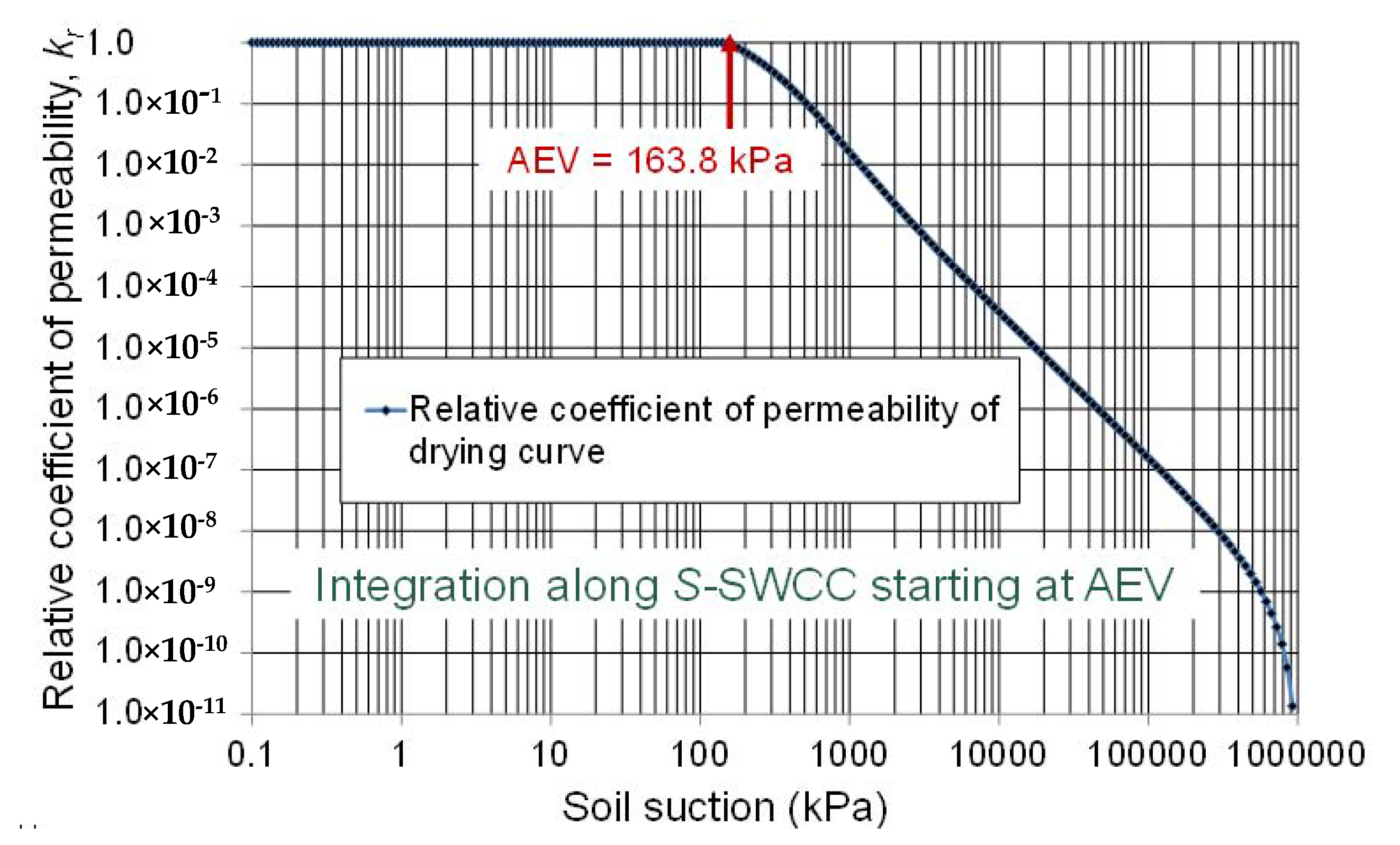
An integration procedure for the permeability function was verified and published by Zhai and Rahardjo [24]. The Fredlund and Xing [13] equation was applied to the S-SWCC and used in the integration process using spreadsheet calculations. Figure 20 graphically presents the calculated permeability function as a series of discrete data points. The integration procedure can also be applied to S-SWCCs with bimodal behaviors.

The permeability function remains at the saturated coefficient of permeability until the “true” air-entry value of the soil is reached. Integration along the S-SWCC commences at this point. The coefficient of permeability rapidly decreases as the soil desaturates. This is essentially the form that Brooks and Corey [26] proposed for the permeability function in 1964 and is similar to the Gardner function [27] proposed in 1958.

16. Calculation of the Water Storage Function

The water storage function is required whenever a transient or unsteady state analysis is being performed [13]. The water storage function is obtained using a differentiation process along the volumetric water content versus soil suction relationship to give the arithmetic slope of the volumetric water content SWCC (Figure 21). The water storage function can never be zero, but it can be a small value for either low or extremely high suction values. The function is also highly nonlinear, showing a maximum value at the inflection point of the volumetric water content SWCC.

17. Shear Strength Function for an Unsaturated Soil

There have been several empirical equations that have been proposed for estimating the shear strength for an unsaturated soil as a function of the soil suction: [28,29,30], to reference a few. Each of the proposed empirical equations appear to have had specific shortcomings. It is beyond the scope of this paper to present a complete analysis of all the proposed shear strength equations for an unsaturated soil.

Ongoing research on the shear strength of unsaturated soils has brought to the fore two common observations. First, a soil behaves as a saturated soil in terms of the shear strength parameters, even when the pore-water pressures are negative, as long as the suction is lower than the air-entry value of the soil. Second, once the soil suction reaches a value near to the residual suction value, there is little further change in shear strength as the suction increases. These two anchor points can be defined in terms of the degree of saturation of the soil [31]. 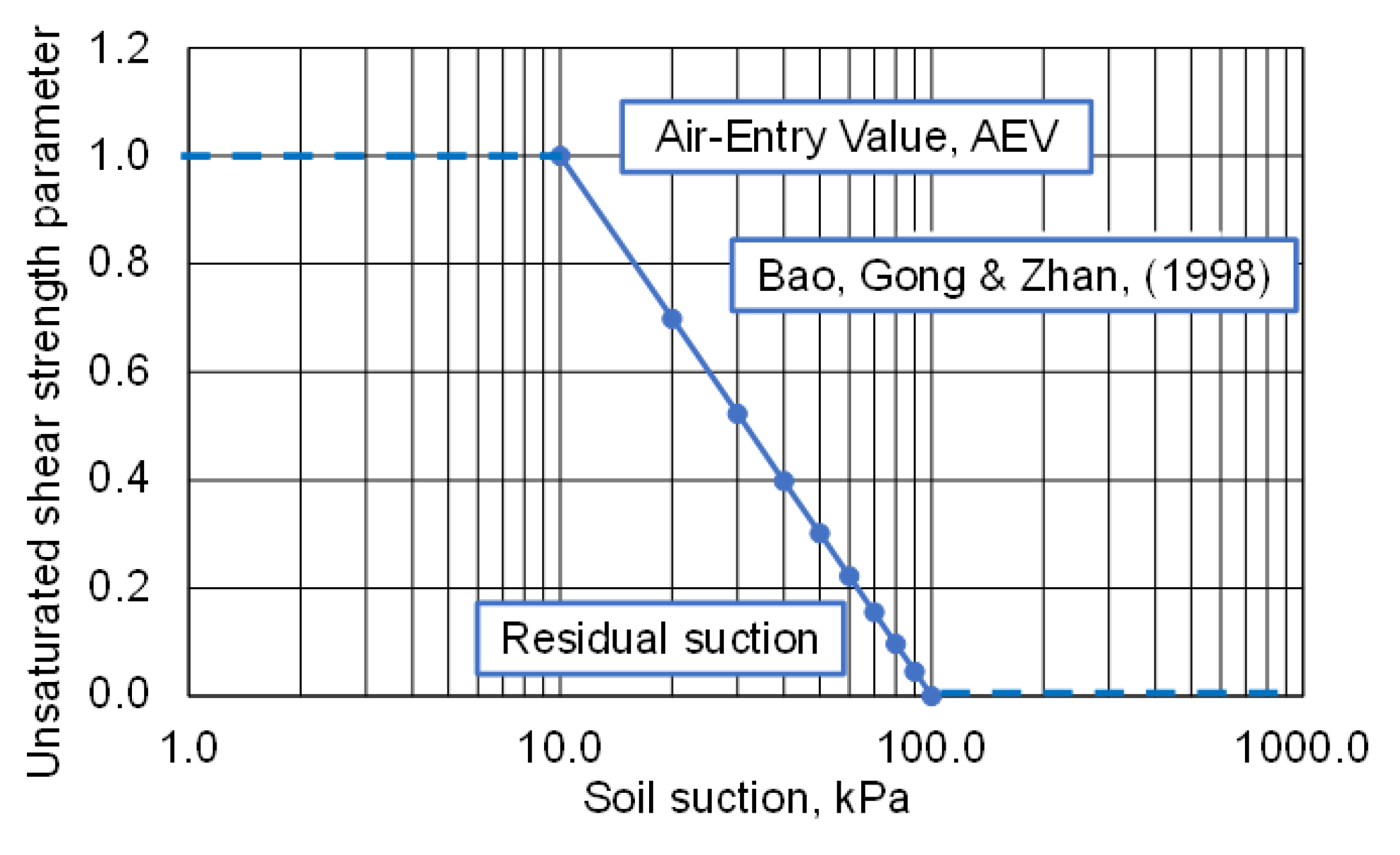The type of function generated for the shear strength envelope is shown in Figure 22.

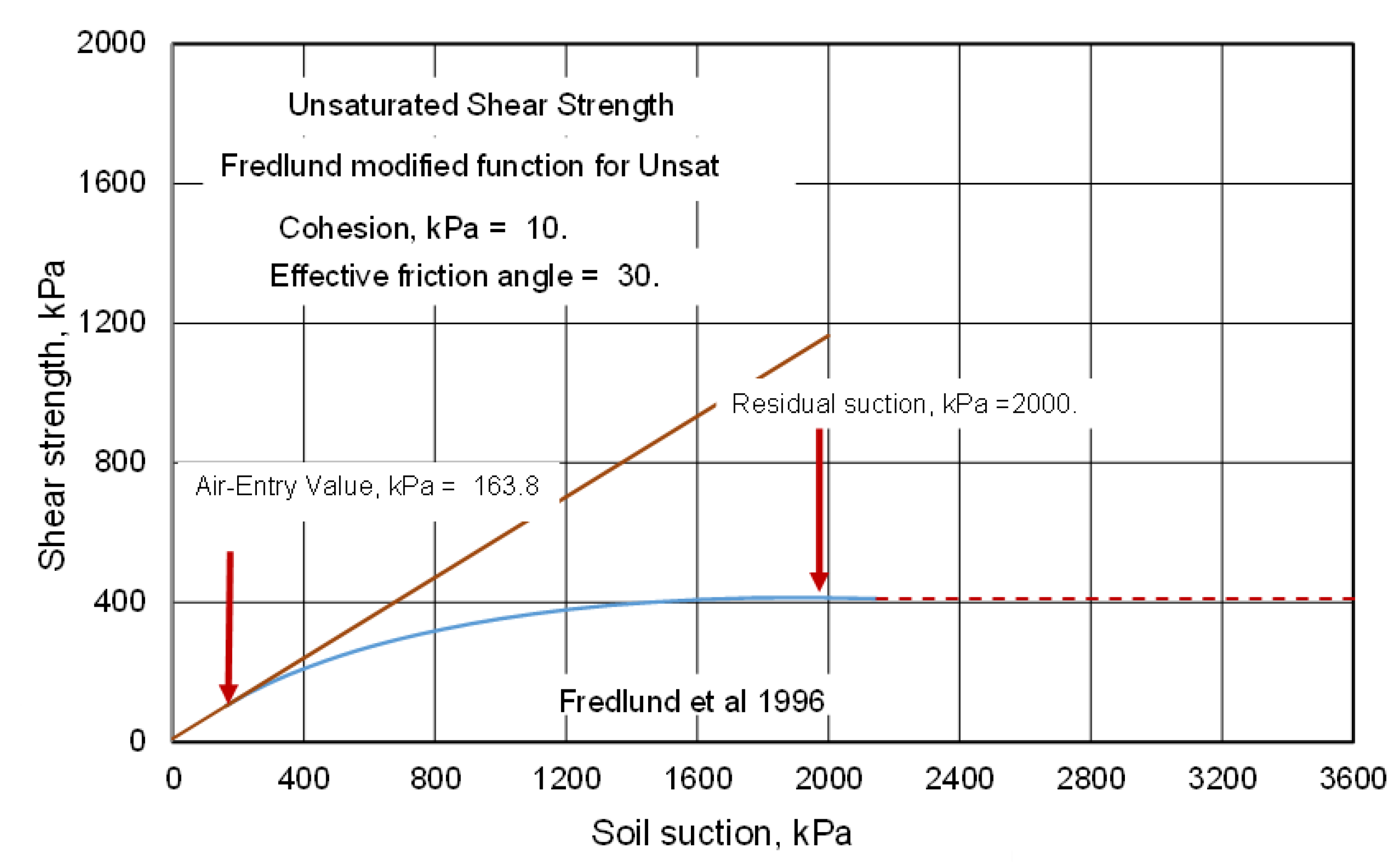
Fredlund [31] suggested that the Bao et al. [30] function be applied to the slope for the unsaturated soil shear strength envelope. In other words, the slope of the shear strength envelope would remain as being equal to the tangent of the internal friction of the soil up to the air-entry value. The slope of the shear strength would decrease as a function of the logarithm of suction and reach a value of zero as the residual suction is reached. Figure 23 shows a typical unsaturated shear strength envelope corresponding to the case where the air-entry value was 163.8 kPa and residual conditions were reached at 2000 kPa. Further studies comparing the estimated shear strength function to experimental laboratory measurements are needed for verification purposes.

18. Volume Change Function for an Unsaturated Soil

One-dimensional oedometer testing has historically been used as input soil parameters for the calculation of the volume change in swelling soils, as well as for collapsible soils. When this procedure is used, it is necessary to make an assumption regarding the final suction in the soil (usually assumed to go to zero).

It should be noted that the shrinkage curve has been used to a lesser extent for the calculations of the volume change during the swelling process [32]. When this approach is used, it is necessary to assume there is no hysteresis between the drying and wetting processes (Figure 24). It should also be noted that, under these conditions, it is necessary to estimate the final gravimetric water content that might be attained upon swelling.

19. Hysteresis between Drying and Wetting SWCCs

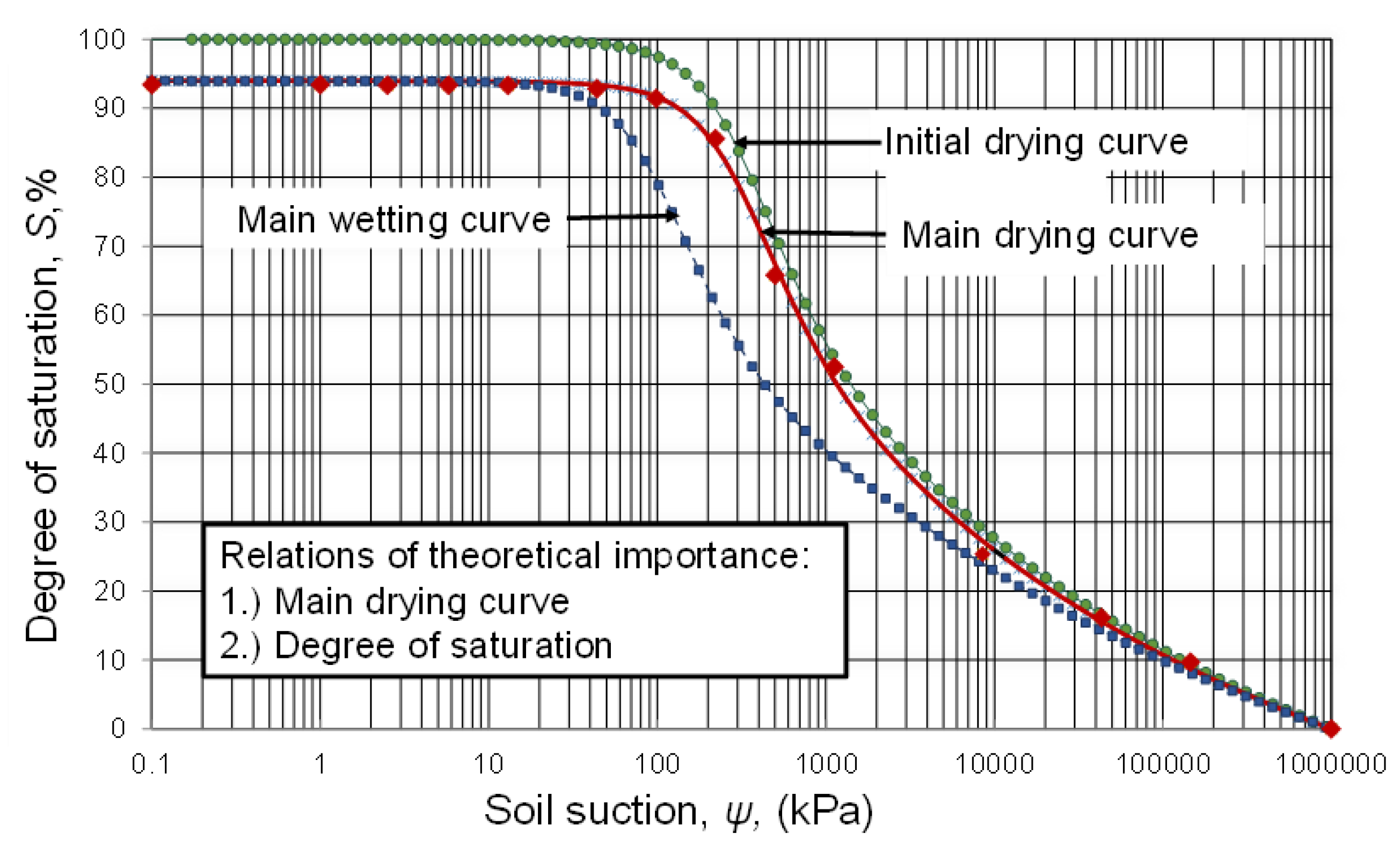
The analysis presented in this paper for the drying volume-mass SWCCs and the corresponding drying unsaturated soil property functions. All calculations have been based on the assumption that the SWCCs are unique. However, this is known to not be the case, since the response of a soil to the drying phenomena is different from the response of the soil to wetting [33,34]. Figure 25 identifies three main suction state paths associated with the S-SWCC family of curves—namely, (i) the initial drying curve, (ii) the main drying curve, and the (iii) main wetting curve. In addition, there are an indefinite number of possible scanning curves that could be followed between the main drying and wetting boundary curves. The drying and wetting processes affect all of the volume-mass SWCCs, as well as the shrinkage curve relationship. It becomes, in part, the geotechnical engineer’s responsibility to find an acceptable pathway forward in light of the complexities of the family of SWCCs.

Following are some suggested assumptions for the path forward. First, consideration of hysteresis will focus on the main drying S-SWCC. It is assumed that the starting degree of saturation is the value attained when the soil specimen is allowed to freely imbibe water (i.e., defined by the main drying curve). Second, it is assumed that the drying and wetting boundary branches of the S-SWCC are congruent (i.e., parallel on a semi-log plot), as shown in Figure 25 [35,36,37]. This means that the Fredlund and Xing [13] equation can be used to best-fit both the drying and wetting curves by changing one variable, the inflection point (i.e., the a_fx variable).

The difference between the drying and wetting branches can be expressed in terms of a percentage of a logarithm cycle. In other words, a hysteresis loop of one log cycle might be a change from an inflection value of 266 kPa on the drying curve to a value of 26.6 kPa on the wetting curve. A relative permeability curve can then be estimated for the wetting curve, as shown in Figure 26.

The results illustrated in Figure 26 show that the drying and wetting permeability functions are congruent on a log-log plot. In other words, the drying and wetting permeability functions scale laterally and are anchored to the saturated coefficient of permeability for the soil.

There could also be another permeability function used to take the changes in volume (i.e., void ratio) into consideration. However, it is beyond the scope of this paper to consider other possible unsaturated soil property functions, USPFs. The possibility of considering the use of scanning curves is not given consideration in this paper.

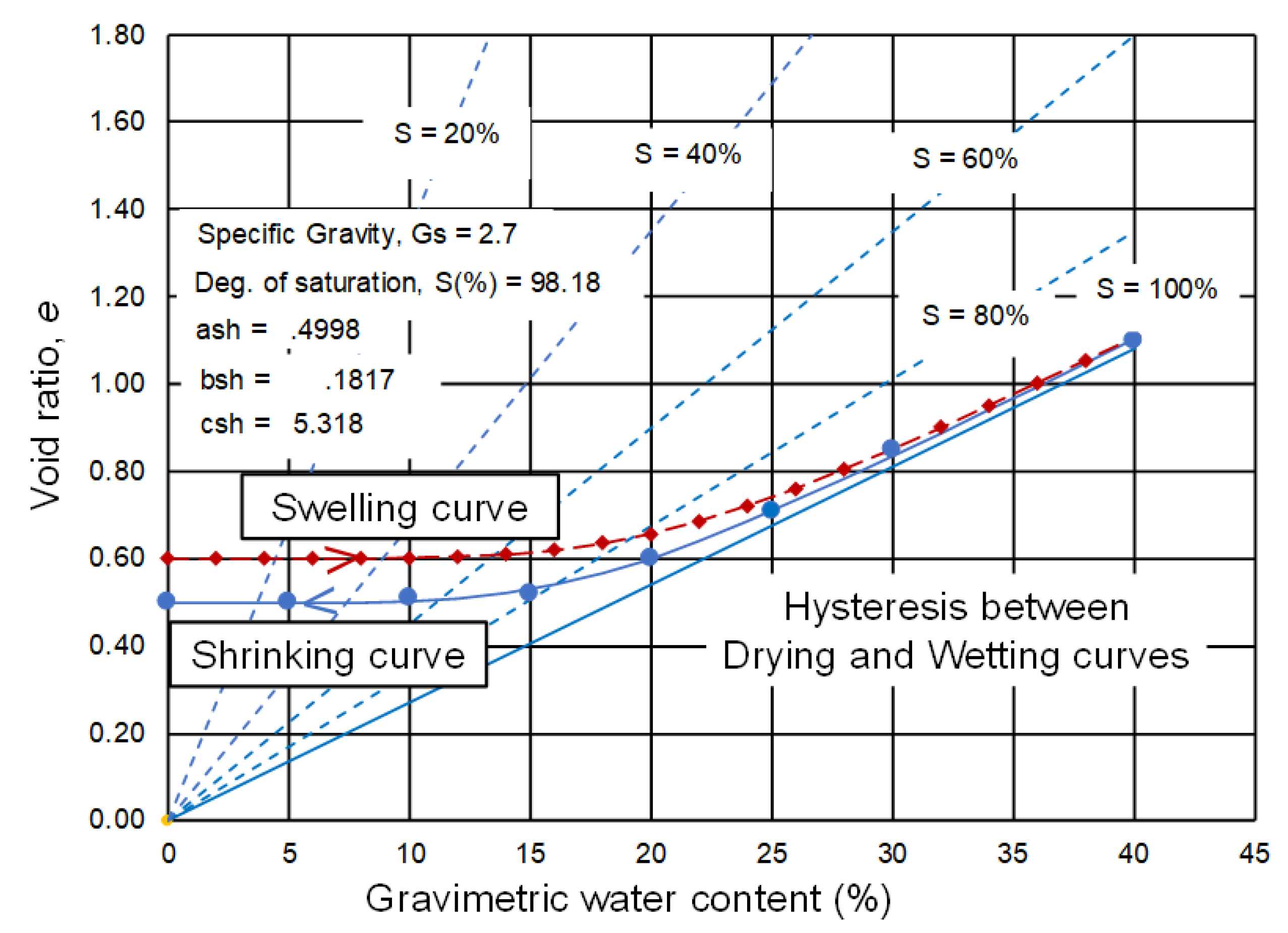
Figure 27 illustrates how hysteresis can be approximated between the drying and wetting shrinkage curve branches. The circular symbols represent the drying SC, and the diamond symbols represent the wetting SC. Once again, only one variable needs to be changed between the drying and wetting SCs—namely, the a_sh fitting parameter (or the intercept on the void ratio axis). The justification for using this difference between the drying and wetting SCs is based on laboratory test programs where drying and wetting SCs have been measured [38].

Further research studies related to hysteresis are welcomed in the future as research studies are conducted on the hysteresis effects of both the SWCCs and the SC.

20. Concluding Remarks

An independent stress-state variable approach based on a soil-water characteristic curve analysis has been proposed for the estimation of volume-mass versus suction relations and related USPFs. The proposed methodology is based off assumptions that appear to be emerging as a result of research studies in unsaturated soil mechanics. The key components are:

• Recognition of the primary and secondary factors influencing the behavior of unsaturated soils as a result of research studies in both soil physics and geotechnical engineering.
• Recognition of the important role of approximations and assumptions in the application of unsaturated soil mechanics.
• Attempts to measure both the drying and wetting bounding curves in the laboratory are not always acceptable from a budget and cost-effective approach; however, in many cases there are approximations that can be made to accommodate hysteresis effects related to a wide range of drying and wetting suction change paths.
• It is suggested that only the drying SWCC be used for estimations of unsaturated soil property functions. This approach builds in a natural bias in analytical solutions towards either an upper-bound or lower-bound soil property function.

The present state of geotechnical engineering practices allows the unsaturated portion of the soil profile to be characterized in a manner of context to that used in saturated soil mechanics. The proposed methodology can be incorporated into numerical modeling software packages [8]. It is recognized that the proposed methodology makes generous usage of approximations and assumptions; however, these may be acceptable for most geotechnical engineering applications.