Abstract
For many geotechnical purposes, the proper estimation of shapes and dimensions of landslide rupture zones is of significant importance. Very often, this exact delineation is difficult due to the lack of information on rupture zone extents in 3D. Based on a global landslide inventory, this work presents statistical analyses correlating dimension-related and shape-related parameters characterizing a rupture zone in 3D to its volume. Dimension-related parameters are approximated by linear regressions increasing with greater volumes, whereas shape-related parameters appear stable throughout the entire range of volumes. Revealing themselves as very stable, these correlations can be used, hence, to extrapolate from a distinct parameter to the volume of a landslide rupture zone. In a second stage, ratios of dimension-related parameters are correlated with rupture zone volumes. Furthermore, this type of correlation delivers very stable results showing that ratios are constant throughout the entire range of volumes. Making use of this ratio consistency, it is possible to deduce one of the two parameters when the other one is given. This latter aspect seems to be promising for remote sensing surveys when initial rupture areas or rupture volumes should be delineated or for numerical modeling of landslides in 3D.
1. Introduction
Across the globe, landslides are triggered by a variety of causes. They regularly lead to loss of life and damage, ranging from smaller to greater extent [1,2]. Common triggers are of tectonic, volcanic, meteorological, and anthropogenic nature or a combination of them [3,4]. As an example illustrating the trail of destruction serves the landslide series triggered during Hurricane Mitch in October 1998, which caused tremendous damage and 2000 fatalities in Nicaragua alone [5]. Another more recent example of devastation is the landslide series after the Sichuan Earthquake in May 2008, with a ten times higher number of victims (20,000) [6].
Over the last decades, major contributions to a better understanding of the phenomenon of landslides in terms of, e.g., geographical localization, area and volume distributions, frequency, and probability analyses, as well as rupture mechanisms, were made by the establishment and consecutive exploration of landslide databases, which could be chronologic (i.e., listing landslides with different triggers over time) or event-based (i.e., listing landslides caused by a particular triggering event). The latter might be tectonic events (e.g., earthquakes, fault ruptures, or volcanic activity), meteorological events (e.g., heavy rain or storms), and climatic changes on a seasonal or long-term scale (e.g., snowmelt or permafrost degradation). Scientific work based on landslide databases with respect to the type of triggering events is exhaustive, and a full overview would be beyond the scope of this publication. Some examples are: studies using global, regional, and event-based databases of earthquake-triggered landslides by Harp and Jibson [7,8], Keefer et al. [9], Prestininzi and Romeo [10], Rodríguez et al. [11], and Tanyaş et al. [12]; studies based on landslide databases related to climatic changes such as snowmelt (e.g., [13]) and general climate change (e.g., [14]); and studies using event-based meteorological databases (e.g., [15]). An even more abundant number of studies on landslide databases became available due to the increasing reliability of remote sensing techniques, which allow for rapid mapping and analyses of single landslides or landslide clusters at different scales all over the globe.
In view of constant population growth and expansion to new and occasionally endangered living environments, proper management of landslide risk is essential for social resilience. In addition, climate change is not to be disdained in this context, as frequency and intensity of extreme meteorological events are expected to increase, which, in turn, can trigger numerous landslides.
Relating to event magnitude and successive consequences, the volume of landslides is considered as one of the most significant parameters [16], which becomes apparent, e.g., when comparing unequal damage potentials of small and frequent events with large and rare events. Exact estimates for landslide volumes are, however, among the most difficult parameters to assess.
Following this essential need for detailed volume assessment of landslides, this publication presents statistical analyses focusing on expected dimensions and shapes of landslide rupture zones in 3D. The term “rupture zone” refers here to the landslide volume that is confined by the rupture surface at the moment of the main rupture event (Figure 1a–d). In contrast to other authors (e.g., [16,17,18,19,20,21,22,23]), who consider landslide zones as the entire zone affected by sliding processes for different purposes (e.g., mapping and inventory work for statistical applications, area-to-volume and area-to-depth correlations, or probability and frequency analyses), this work clearly distinguishes the entire landslide zone from the zone confining the rupture volume of landslides. As the Frank Landslide, Canada (No. 019.00 in Table A1 in the Appendix A), in Figure 2 illustrates, the distinction of both zones implies significant differences in terms of area and volume. Another difference to common landslide inventories is that, here, many more depth-related parameters are available delimiting the rupture zone at different locations, whereas other authors use a single multiplier to account for depth extents (e.g., [24,25,26,27,28]). Both aspects might be of particular interest for application in remote sensing or numerical landslide modeling.
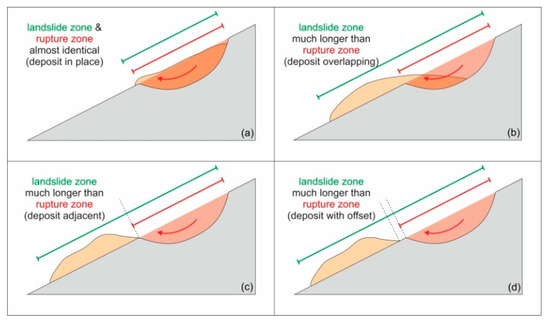
Figure 1.
Comparison (identical (a), overlap (b), adjacent (c), and offset (d)) of rupture zones and landslide zones (i.e., entire zones affected by sliding processes, which are mainly dependent on the location of the landslide deposits).
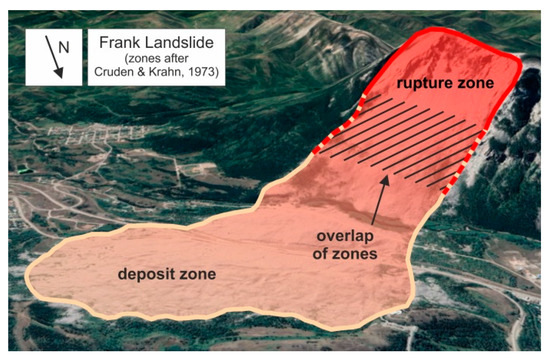
Figure 2.
Difference between the entire landslide zone and the rupture zone exemplified by the Frank Landslide, Canada (No. 019.00 in Table A1 in the Appendix A). Zones are drawn after Cruden and Krahn [29] (satellite imagery from Google Earth Pro [30]).
Statistical analyses are based on a newly created chronologic database presented by Domej et al. [31] comprising 277 landslides in 40 countries across the globe (Figure 3), which will be revisited in the first part of this publication. The second part is dedicated to statistical analyses consisting of correlations between landslide volumes and single parameters characterizing landslide rupture zones and of correlations between landslide volumes and ratios of single parameters. The last section discusses results as well as their potential fields of application. All landslides included in the database are listed with their date, location, and trigger in Table A1 in the Appendix A. Initially designed for seismically induced landslides, the database consists majorly, but by far not exclusively, of earthquake-triggered landslides; triggers also range from precipitation, storms, and anthropogenic influence to unknown causes.
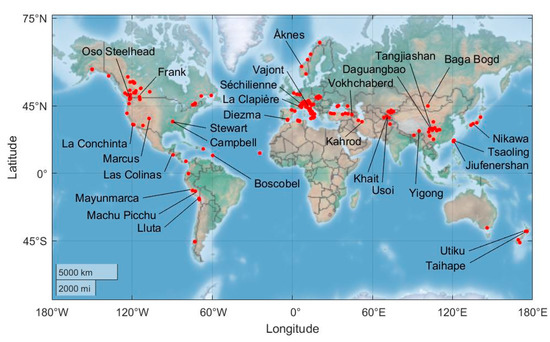
Figure 3.
Locations of the 277 landslides included in the database (map from MATLAB [32]).
2. Statistical Analyses
The analyses aim for a general understanding of the statistical behavior of geometrical parameters characterizing landslide rupture zones (Figure 4) with increasing landslide sizes.
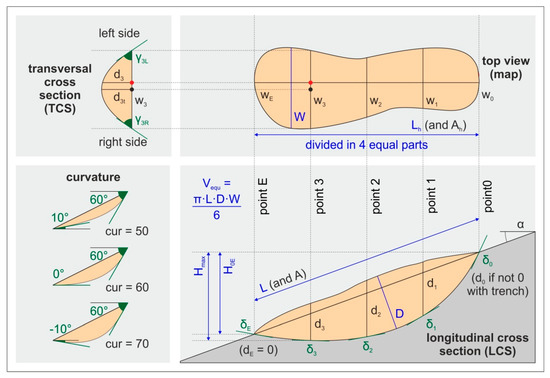
Figure 4.
Description of parameters defining a landslide rupture zone (adapted and further developed from the IAEG Commission on Landslides [33]).
In theory, i.e., if the data coverage is fully exhaustive, a total number of 66 parameters and descriptive notes with respect to longitudinal cross sections (LCS), transversal cross sections (TCS) and top views (maps) are available for each landslide included in the database; they are adapted and further developed from the parameters proposed by the IAEG Commission on Landslides [33]. Individual parameters that are used for the here presented analyses are listed in Table 1 and can be either directly or indirectly derived from available publications. Direct parameters are those that are measured from LCS, TCS, and/or maps published per respective landslide. Indirect parameters are those that are calculated via equations using direct parameters (Table 1). The calculated volume (Vequ) is derived from the equation of Cruden and Varnes [34] as half an ellipsoid (Figure 4) approximating landslides. The curvature—taken as the difference between the angles at points 0 and E (δ0 and δE)—is not an international standard, but was adopted by the authors; the higher the difference is, the higher is the curvature (Figure 4). Being defined via a simple height-over-length-tangent, the calculated slope angle (αequ) also represents the mean slope angle of the rupture zone (Figure 4). The perspective of the TCS represents a view from the landslide toe towards the landslide crest. An example of the measurements of the parameters characterizing the rupture zone is shown in Figure 5 using the Diezma Landslide, Spain (No. 001.00 in Table A1 in the Appendix A).

Table 1.
Description of parameters defining a landslide rupture zone (adapted and further developed from the IAEG Commission on Landslides [33]). The last column indicates the type of statistical distribution of values per individual parameter throughout the database.
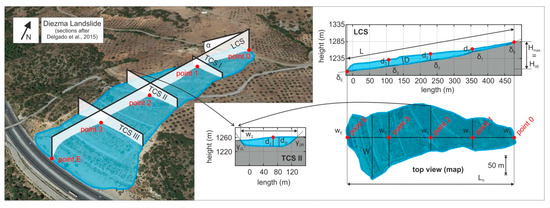
Figure 5.
Schematic example of measurement of the parameters defining the rupture zone of the Diezma Landslide, Spain (No. 001.00 in Table A1 in the Appendix A). Cross sections are drawn after Delgado et al. [35] (satellite imagery from Google Earth Pro [36]).
Usually, the number of evaluable parameters decreases due to the availability of data throughout the database. For 80% of all landslides in the database, a map is available, for 71% there is an LCS, and for 61% there are both a map and an LCS. Only two of the 277 landslides have an exhaustive TCS record. Therefore, parameters that are derived from the respective imagery show different recurrences. All parameters, except the areas (A and Ah) and the reported slope angle (αlit), have a recurrence of 70% or higher throughout the database. This ensures sufficient data availability for exactly those parameters that are most interesting to analyze regarding shapes and dimensions of landslide rupture zones, not only superficially, but also with respect to the extent of the depth.
The analyses follow the approach of simple volume-to-parameter correlation and volume-to-ratio correlation (Figure 6). Although being the most complexly interlinked indirect parameter, the calculated volume (Vequ) was chosen as the first variable of correlation, which is justified by its strikingly high recurrence or 74%. The reported volume (Vlit; not used in this work and not mentioned in Table 1), in contrast, has a recurrence of only 60%, and covers in many cases also parts of the deposit volumes which conflicts with the exclusive assessment of the rupture zone. The argument that the equation of Cruden and Varnes [34] is suitable for rotational slides while misestimating volumes of translational and roto translational geometries, could at least in this work be rebutted. Where the reported volume (Vlit) and the calculated volume (Vequ) clearly refer to the rupture zone, comparisons of the two volume types do not indicate a notable difference [31].
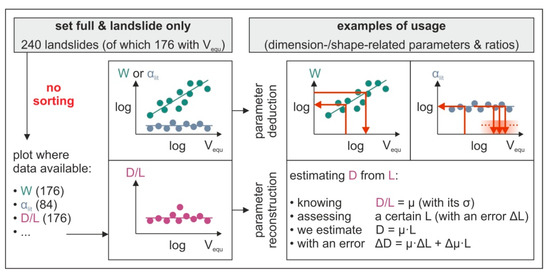
Figure 6.
Schematic representation of the statistical approach. Landslides of a particular set are screened for showing a calculated volume (Vequ). Those that also show a variable of correlation (e.g., maximum depth (D), reported slope angle (αlit), or the ratio of the maximum width and the length along the slope (W/L)) are then used for plots that illustrate the respective correlation. The right part of the figure shows examples of usage of the established correlations.
2.1. Volume-to-Parameter Correlations
One of the two approaches that allow for statistical analyses of the behavior of dimension- and shape-related parameters consists of volume-to-parameter correlations. One variable of correlation is necessarily the calculated volume (Vequ), whereas the place of the second variable of correlation is taken by any of the parameters characterizing the rupture zone in 3D (Figure 4, Table 1).
Here, the choice of suitable variables of correlation is limited by reflections on sample sizes and meaningfulness. Considering the set “full/landslide only”, sample sizes for different parameters vary as a function of the applied filter cascade (Table 2). The term “landslide” refers here to classic landslides sliding on actual sliding surfaces, not displaying local features of other mass movement types such as rock falls, topples, or earth flows [37]. Thereupon apply the filters for the two variables of correlation as uniquely those landslide records showing the calculated volume (Vequ), as well as the respective parameter of interest, can be used for evaluation (Figure 6). For the shape-related parameters, the calculated slope angle (αequ), the angles at points 0 to E (δ0 to δE), and the curvature (cur), the thereby obtained sample sizes are very satisfying and vary between 153 and 176 cases (second columns of Table 3 and Table 4). The reported slope angle (αlit) is to be evaluated for 84 cases, both area types (the reported area (A) and its projection to the horizontal (Ah)) are represented only by 72 cases. All TCS related parameters are quasi-nonrepresented by solely three cases at the maximum and, hence, not considered for the analyses (Table 1). The choice to filter according to rotational (i.e., rather half-elliptical shapes; e.g., Figure 4), translational (i.e., rather flat shapes; e.g., Figure 5) and roto-translational rupture zones is explained by the fact that this information is available for every landslide included in the database. The filter, hence, does not reduce the sample sizes.

Table 2.
Subsets of the database used for analyses with their respective first and second filters.

Table 3.
Results for the volume-to-parameter correlations for the set “full”. For all dimension and shape-related parameters, the regression parameters (R2, RMSE, constant (a) and factor (b) with their 95% confidence intervals; Equation (2)) are given.

Table 4.
Results for the volume-to-parameter correlations for the set “full”. For all shape-related parameters, the mean value (µ) with the respective standard deviation (σ) and the sample size per sigma interval is given.
As for the reported area (A) and its projection to the horizontal (Ah), one might criticize that despite their good representation, they are not included in the volume-to-parameter correlations. Here the argument is that area reports on landslides are to be seen with caution, especially when it comes explicitly to the delineation of rupture zones. Rupture and runout zones can be overlapping, adjacent, or even separated (Figure 1a–d); very often, reported areas refer to the entire area across a slope, which is affected by the sliding process. For several landslides in the database, the distinction between these different area types is not clear, and thus correlations were dismissed. Another argument is that this very uncertainty might become a field of application of the presented statistical correlations.
In contrast to the sifting of unsuitable variables of correlation, also a few new appropriate parameters were also created. They might become of particular interest when delineating average dimensions of rupture zones rather than maximal possible extents in particular locations of rupture zones.
- dav5: average depth of the rupture zone below points 0, 1, 2, 3, E
- dav4: average depth of the rupture zone below points 0, 1, 2, 3
- dav3: average depth of the rupture zone below points 1, 2, 3
- wav5: average width of the rupture zone at points 0, 1, 2, 3, E
- wav3: average width of the rupture zone at points 1, 2, 3
Expecting variable statistical behaviors throughout dimension and shape-related parameters after initial data cloud inspection, fitting tests of different distribution types were applied to each parameter distribution with MATLAB’s Curve Fitting Tool [32]. It appeared that for the climbing trend-prone dimension-related parameters, the best results were obtained by fittings of linear regressions, i.e., of polynomials of the first degree in double-logarithmic diagrams. For the shape-related parameters visibly lacking a climbing trend, such linear regressions were nevertheless “forced” on data clouds in x-semi-logarithmic diagrams with very unsatisfactory results regarding the fitting (i.e., R2 almost 0 and significantly high RMSE). Furthermore, the polynomial factors within these “forced” regressions tended to be low, which emphasized the representation of the respective data clouds by their mean values (µ). Taking into account that both dimension- and shape-related parameters exist within the volume-to-parameter correlations (Table 3 and Table 4), a homogeneous way of analyses had to be adopted. For internal consistency, hence, all distributions of dimension-related parameters underwent the fitting of linear regressions in double-logarithmic diagrams, whereas, for all distributions of shape-related parameters, the mean value (µ) was calculated. Furthermore, the homogeneity of analyses between the concerned volume-to-parameter correlations and the likewise shape-based volume-to-ratio correlations (Table 5; next subsection) was preserved.

Table 5.
Results for volume-to-ratio correlations for the set “full”. For all shape-related parameters (i.e., here the ratios), the mean values (µ) with the respective standard deviations (σ) and the sample sizes per sigma interval are given.
In the following, the analytical procedure for the most comprehensive set “full” is described. It should be mentioned beforehand that the identical procedure was carried out also for all other sets (Table 2) in order to observe potential changes in statistical behaviors. A comparison of the results of all six tested sets is given in the discussion.
Regressions are here of the general type
and appear in a double-logarithmic diagram as
with y defining the respective parameter, a representing the intercept on the y-axis (herein after called “constant”) and b defining the gradient (herein after called “factor”).
y = 10a Vequb,
log10(y) = a + b·log10(Vequ),
Examples of regression fittings are shown in Figure 7a–c for the set “full” for the maximum depth (D), the height between the point 0 and the point E (H0E), and the length along the slope (L). Despite different scatter patterns, all data clouds reveal a clear increasing tendency. Regressions fit with a few exceptions with coefficients of determination (R2) above or equal to the typical threshold of acceptance of 0.7 (Table 3). Furthermore, within the other five tested sets (Table 2), all regressions fit with similar coefficients of determination (R2). Thus, regression fitting seems to be an adequate tool for correlating calculated volumes (Vequ) and dimension-related parameters. Results for the set “full” are listed in Table 3. The last two columns give the constant (a) as well as the factor (b) that must be inserted into Equation (2) in order to reproduce the straight line per parameter in the respective double-logarithmic diagram.
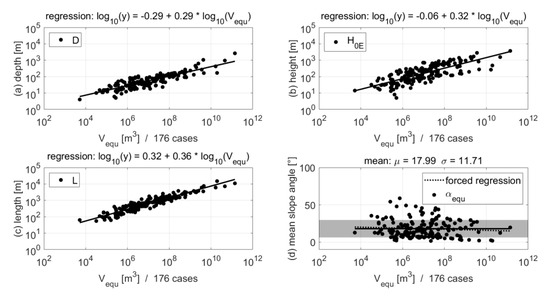
Figure 7.
Examples of volume to parameter correlations for the set “full”. Dimension-related parameters (D (a), H0E (b), and L (c)) are approximated by a regression; for the shape-related parameter (αequ (d)), the mean value (μ) is calculated. The shading indicates the symmetric belts of two standard deviations (±1σ) around the mean value (μ); the latter is very similar to the “forced” regression (regression parameters in Table 3).
Conclusions on dispersion are to be regarded with caution in the case of dimension-related parameters. The main reason is that each point in the data clouds depends only on one value of the calculated volume (Vequ); i.e., there is no option to measure dispersions per distinct volume.
The analytical procedure for shape-related parameters (Table 4) consisted of averaging the values represented by the respective data clouds, since “forced” regression fitting in x-semi-logarithmic diagrams resulted in low factors (b), R2 close to 0, and significantly high RMSE (Figure 7d, Table 3). Besides the assumption of consistency throughout different calculated volumes (Vequ), there is also a second strong argument favoring simple value averaging instead of regression fitting. Considering perfectly normally distributed data, specific fractions of it should lie within symmetric belts of two (±1σ), four (±2σ) and six (±3σ) standard deviations around the mean value (µ). In the case of the set “full”, data of the individual shape-related parameters follow these suggested intervals with minor deviations (Table 4). One can assume, hence, that data of shape-related parameters are normally distributed what emphasizes the representativeness of the respective mean value (µ). Also, the other five tested sets (Table 2) reveal very similar tendencies with respect to the required fraction of data within the three symmetric belts; only in six cases, sigma interval thresholds were missed by more than 5%.
An example of averaging values is shown in Figure 7d for the set “full” for the calculated slope angle (αequ), which shows a slight decreasing tendency for very great calculated volumes (Vequ). This phenomenon is probably due to the fact that slopes cannot become infinitely high. Overall, the mean value (µ) seems, however, representative.
All mean values (µ) are listed in Table 4, together with their standard deviations (σ) and the relations between both types of values (µ/σ) as a measure for dispersion. Here, the information about dispersion is of much bigger interest than the dimension-related parameters.
2.2. Volume-to-Ratio Correlations
The second of the two approaches designed for statistical analyses of the behavior of shape-related parameters consists of volume-to-ratio correlations. From plotting the respective distributions, ratios of dimension-related parameters are assumed to behave like shape-related parameters and can, therefore, be analyzed in a similar way—however, with more sophisticated filtering.
Here, the correlation variable on the y-axis is a ratio of two individual (dimension-related) parameters characterizing the rupture zone in 3D (Figure 4, Table 1); after adding a fifth filter (Table 2), sample sizes for the set “full” are still very high ranging from 146 to 176 (second column of Table 5).
In analogy to the argumentation in the previous subsection, reported areas (A) and their projections to the horizontal (Ah) are less profitable candidates for ratios. This is also the case for separate widths (w0 to wE) and depths (d0 to dE), as they would result in specific ratios that might not be of great use for application; here, it appeared to be more promising to use the newly defined averaged parameters mentioned in the previous subsection (dav5, dav4, dav3, wav5, and wav3) to create meaningful ratios.
With respect to these viewpoints and the aim of not creating ratios within the same types of dimension-related parameters (i.e., between lengths, heights, widths, and depths respectively), and accounting for the difference between maximum (e.g., W) and average parameters (e.g., wav5), 24 significant ratios were identified (Table 5).
Assuming that ratios behave statistically in the same way as other shape-related parameters, they underwent the same procedure of averaging values in order to keep the overall analyses homogeneous and comparable. Again, ratios reveal themselves as constant, emphasizing the assumption of self-similar shapes of rupture zones throughout different ranges of the calculated volume (Vequ). Similar concepts of self-similarity were proposed, e.g., by Guzzetti et al. [18], Malamud et al. [16], and Stark and Guzzetti [38] with respect to the entire landslide zone (Figure 1a–d).
The same strong argument for the representativeness of the mean value (µ) applies to the volume-to-ratio correlations presented here. Table 5 shows for the set “full” that the fractions of data lie with minor deviations within symmetric belts of two (±1σ), four (±2σ) and six (±3σ) standard deviations around the mean value (µ) indicating normal distributions. Also, the other five tested sets (Table 2) reveal very similar tendencies with respect to the required fraction of data within the three symmetric belts; only in five cases, sigma interval thresholds were missed by more than 5%.
Examples for averaging values are shown in Figure 8a–d for the set “full” for the ratio of the height between the point 0 and the point E to the projected length (H0E/Lh), the ratio of the average depth to the length along the slope (dav5/L), the ratio of the average width to the length along the slope (wav5/L), and the ratio of the average depth to the average width (dav5/wav5).
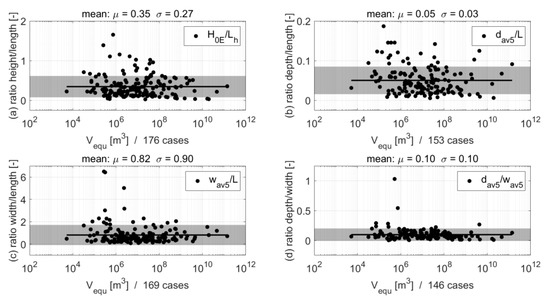
Figure 8.
Examples of volume-to-ratio correlations for the set “full”. For shape-related parameters (i.e., here the ratios; H0E/Lh (a), dav5/L (b), wav5/L (c), and dav5/wav5 (d)), the mean values (µ) are calculated. The shadings indicate the symmetric belts of two standard deviations (±1σ) around the mean values (µ).
Comparing the four examples, the ratio of the average depth to the length along the slope (dav5/L) appears as the most dispersed (Figure 8b), although 75.8% of the data points lie still in symmetric belts of two (±1σ) standard deviations around the mean value (µ). The dispersion reflects the fact that rupture zones of landslides appear to be unequal concerning depth, which is a strong argument of not using a simple multiplier when estimating depths of rupture zones and landslides in general.
The other three examples in Figure 8a–d also show good ratio stability throughout the calculated volumes (Vequ). This is particularly interesting for the ratio of the height between the point 0 and the point E to the projected length (H0E/Lh), as Heim [39] reports a decreasing tendency for greater volumes—considering entire landslide zones, however. The argumentation is similar to the one for the suspicion of the slightly decreasing trend for the calculated slope angle (αequ; Figure 7d) since it corresponds to the inverse tangent of the ratio of the height between the point 0 and the point E to the projected length (H0E/Lh). This minimally (or not distinctly pronounced) decreasing tendency could be due to the focus on the rupture zone only.
All mean values (µ) are listed in Table 5 together with their standard deviations (σ) and the relations between both types of values (µ/σ) as a measure for dispersion.
In contrast to Figure 7a–d, the semi-logarithmic diagrams in Figure 8a–d attest differently dispersed data. Here, the following questions arise: (i) Should extreme outliers, such as in the diagram of the ratio of the average width to the length along the slope (wav5/L; Figure 8c), be discarded from the analyses? (ii) Is the median more representative compared to the mean value (µ)? To answer the first question, it can be argued that the highest points in the data cloud are generated by extremely wide but short rupture zones. To exclude them would require them to be discarded from the entirety of the statistical analyses to ensure consistent datasets. This, however, is wrong, since those landslides are not necessarily responsible for outliers in other diagrams; i.e., the same landslides might present a normal ratio of the height between point 0 and point E to the maximum depth (H0E/D). Hence, datasets cannot be individually curtailed.
Concerning the median, it can be shown via several tests that mean values (µ) and medians are usually very similar; therefore, both appear to be justifiable representatives. Due to the close link between the standard deviation (σ) and the mean value (µ), the latter seems more practical, however.
3. Discussion of Results of All Six Sets
In contrast to the previous two subsections in which the analytical procedures and results were discussed with particular focus on the set “full”, the discussion is dedicated to the comparison of results of all six tested sets (Table 2).
In the first stage, it might be of interest how similar regressions for individual parameters per set are to each other. This question, indeed, concerns only dimension-related parameters whose values increase with greater calculated volumes (Vequ; Table 3). To allow for easy comparison, regressions (Equation (2)) for each dimension-related parameter per set are represented in a separate double-logarithmic diagram (colored lines in Figure 9a–d). Based on the averages of the six constants (a) and the six factors (b) of the individual sets, average constants (a) and factors (b) that define these regressions are to be found in Table 6a (dashed black line in Figure 9a–d).
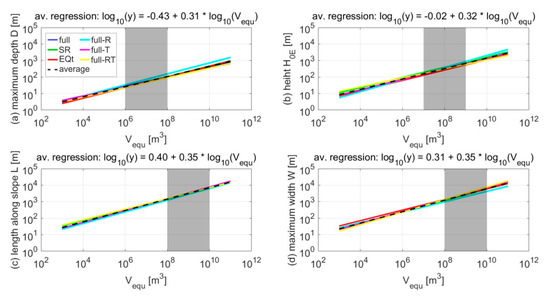
Figure 9.
Comparison of regressions (D (a), H0E (b), L (c), and W (d)) of the six tested sets and the respective average regression, as shown in Table 6a. The shadings indicate the visually derived zones of maximum overlap.

Table 6.
Average results for the volume-to-parameter correlations (a, b) and for the volume-to-ratio correlations (c). For all dimension-related parameters (a), the average regression parameters (constant (a) and factor (b); Equation (2)) are given; for all shape-related parameters (b, c), the table shows the average mean values (µ) with the respective average standard deviations (σ). As d0 contains 0 and dE is always 0, they are not fitted in a double-logarithmic diagram.
Exemplarily, Figure 9a–d shows such regression comparisons for the maximum depth (D), the height between the point 0 and the point E (H0E), the length along the slope (L), and the maximum width (W) in order to display one representative of each type of dimension-related parameters (i.e., depths, heights, lengths, and widths). The diagrams reveal that the regressions are consistent comparing different sets due to very similar constants (a) and factors (b); the average regressions, thus, appear to be reliable representatives.
Comparing these regressions per type of dimension-related parameters (i.e., depths, heights, lengths, and widths), it can be shown that—independently of the initial calculated volume (Vequ)—volume and parameters increase by different factors. Over a volume range that increases with factors following a power series based on 10 (i.e., 10k-1), the other parameter types experience increases by factors that follow more or less a power series based on 2 (i.e., 2.05k-1 to 2.23k-1), which becomes visible as straight regression lines with slightly different gradients in double-logarithmic diagrams (Figure 9a–d) as power-law distributions are scale-invariant.
Moreover, juxtapositions of the diagrams (Figure 9a–d) reveal that the regression parameters (i.e., constants (a) and factors (b); Equation (2)) of depths are generally smaller than those of the heights and that the regression parameters of heights are smaller than those of the lengths and widths. Usually, landslide rupture zones are much higher than deep (Figure 4). Also, the fact that lengths exceed heights seems logical, as in the opposite case, the described setting would be rather atypical for landslides and resemble, e.g., toppling or even rock fall. The interesting detail within these magnitude comparisons is that, on closer inspection, regressions of lengths and widths are particularly similar, suggesting that landslide rupture zones are on average as wide as long in terms of orders of magnitude. Furthermore, ratios relating widths and lengths (W/L, wav5/L, and wav3/L; Table 5 and Table 6c) show values varying around 1. This latter fact might have been overlooked as publications strive rather for the accurate assessment of LCS than for TCS [40]. One of the reasons for this preferential focus could be the so-far predominant limitation of numerical landslide models to 2D. With the recent approaches of landslide modeling in 3D, their lateral extent becomes indispensable, and thus, the roundness or ellipticity defined by lengths and widths of a rupture zone might add relevant information.
Another feature (although visually subjective) is the zone of maximum overlap of the regressions of the six sets and the average regression (Figure 9a–d). For depth parameters (D, d1, d2, d3, dav5, dav4, and dav3) the regression overlap occurs between 106 m3 and 108 m3 of the calculated volume (Vequ), for height parameters (H0E and Hmax) between 107 m3 and 109 m3, and for length and width parameters (L, Lh, W, w0, w1, w2, w3, wE, wav5, and wav3) between 108 m3 and 1010 m3. Thus, it seems, that regressions of parameters with generally higher values tend to overlap better at higher ranges of the calculated volume (Vequ) and vice versa.
In a second stage, it is of particular interest how similar mean values (µ) of individual shape-related parameters are throughout the six sets. Here, this question targets the analyses of the angles at the points 0 to E (δ0 to δE), the curvature (cur) and the slope angles (αequ and αlit) as well as the analyses of all ratios (Table 4 and Table 5). As they are constant over the entire range of the calculated volume (Vequ) showing similar values throughout the six tested sets (Table 2), the choice of the averages of the six mean values (µ) is a very legitimate representative value for each of the shape-related parameters (Table 6b,c). Expected shapes of landslide rupture zones based on these average ratios of dimension-related parameters are shown in Figure 10.
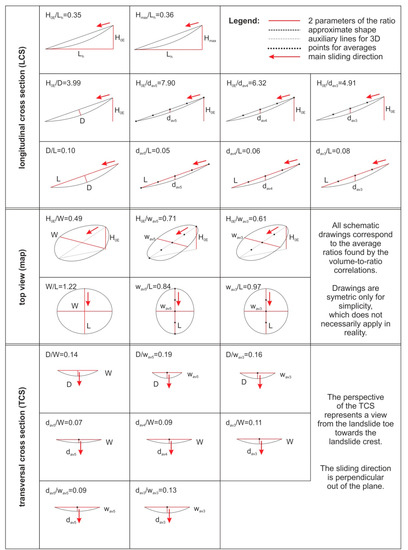
Figure 10.
Schematic representation of ratios of dimension-related parameters. All schematic drawings correspond to the average ratios found by the volume-to-ratio-correlation shown in Table 6c.
In Domej et al. [31], the ratio of the height between the point 0 and the point E to the projected length (H0E/Lh), the ratio of the average depth to the length along the slope (dav5/L), the ratio of the average width to the projected length along the slope (wav5/Lh), and the ratio of the average depth to the average width (dav5/wav5) were evaluated for three sets (“full”, “SR”, and “EQt”) via a grouping approach according to three volume classes (103–106 m3, 106–109 m3 and 109–1012 m3). The hereby obtained ratios (Figure 11a–d, Table 7) match well with those of the analyses presented here.
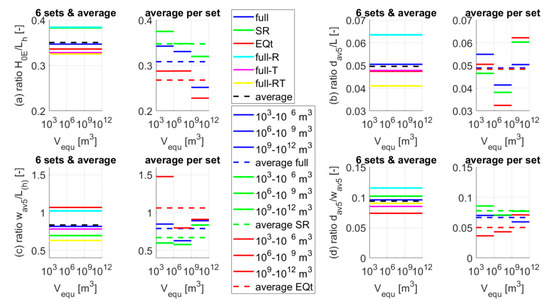
Figure 11.
Comparison (H0E/Lh (a), dav5/L (b), wav5/L(h) (c), and dav5/wav5 (d)) of mean values of ratios (µ) for the six tested sets and the respective average mean value (µ) of this publication (Table 5 and Table 6c; left subplots) and of the average of the mean values (µ) per set as presented in Domej et al. [31] (Table 7; right subplots).

Table 7.
Ratios per volume group as reported in Domej et al. [31]. The value triplets correspond to the ratios per tested set (“full” (a), “SR” (b), and “EQt” (c)).
4. Conclusions and Perspectives
In this work, the newly built, chronologic and global landslide database presented by Domej et al. [31] was revisited with the aim of a detailed exploration of the statistical behavior of dimension- and shape-related parameters characterizing a landslide rupture zone in 3D (Figure 4, Table 1), while the majority of available studies focusses on the entire landslide zone (e.g., [16,17,18,19,20,21,22,23]). For six different sets (Table 2) that were filtered from the landslide database, the analyses are based on volume-to-parameter correlations of all exploitable dimension-related parameters (i.e., depths, heights, lengths, and widths; Table 3) and the eight shape-related parameters (i.e., angles at the points 0 to E (δ0 to δE), curvature (cur), and reported and calculated slope angle (αequ and αlit); Table 4) as well as on volume-to-ratio correlations of all ratios of dimension-related parameters (Table 5).
Independently on the six tested sets (Table 2) characterized by different global distributions, materials, and triggering mechanisms, both types of analyses revealed a significant difference in the statistical behaviors of these two types of parameters. All dimension-related parameters showed a clear scale-invariant increase with greater calculated volumes (Vequ; Figure 7a–c), whereas all shape-related parameters and the ratios of dimension-related parameters remained constant throughout the full range of calculated volumes (Vequ; Figure 7d, Figure 8a–d).
Results are consistent with preliminary analyses of the authors [31] but show a higher degree of detail, allowing for a broader spectrum of use.
Since regressions for dimension-related parameters are very similar (Figure 9a–d, Table 3 and Table 6a), one could use the average regression of a distinct parameter to extrapolate from a given value to the calculated volume (Vequ) of a rupture zone (Figure 6). This potential field of application might be of interest for preliminary assessments of rupture zone dimensions, e.g., during fieldwork or rapid first stage inventories anticipating exact geological, geotechnical, and geophysical surveys. Depending on the desired accuracy, one might consider the average regressions per respective dimension-related parameter, or one of the set specific regressions can be used if the considered landslide is known to match one of the filters (Table 2).
As for the shape-related parameters, the analyses also deliver very satisfactory results compared to those of Domej et al. [31], with those ratios existing in both publications being almost identical (Figure 11a–d, Table 5, Table 6c and Table 7). This work offers, however, a much wider range of possible applications since all eight shape-related parameters and many more ratio combinations were considered. On the one hand, one might benefit here from the finding that the eight shape-related parameters (i.e., angles at the points 0 to E (δ0 to δE), curvature (cur), and reported and calculated slope angle (αequ and αlit); Table 4, Table 6b) are stable throughout all volume ranges a fact that speaks for self-similar shapes of rupture zones (Figure 10), and also finds its application during preliminary assessments of rupture zone dimensions. On the other hand, one might make use of the constancy of ratios of dimension-related parameters (Table 5 and Table 6c) by deducing one of the two parameters when the other one is given (Figure 6). This latter aspect seems to be particularly promising for remote sensing surveys when initial rupture areas or rupture volumes should be delineated. Very often, remote sensing allows for mapping of entire landslide areas that are affected by sliding processes (Figure 1a–d). Here, it could remain unclear where the rupture zone ends due to overlaps or even offsets of landslide deposits. If dimension-related parameters relating to horizontal and/or vertical expansion are known in such cases, and if one relies on constant ratios between them, it could be possible to trace back the rupture areas and/or the rupture volumes of landslides.
Moreover, for numerical modeling of landslides, the volume-to-ratio correlations could be of particular interest. Correlations of depth and length of rupture zones shown in Figure 8b reveal a more significant dispersion compared to other correlations—i.e., depths appear to be highly variable. It might be, therefore, interesting to make use of the here presented depth correlations at different points (Figure 4) when creating 2D or 3D models, instead of using multipliers to estimate depths.
As a final remark on perspectives, it should be mentioned that, although the entire statistical analyses were carried out based on the calculated volume (Vequ) as first variable of correlation for the volume-to-parameter correlations as well as for the volume-to-ratio correlations, it is possible to filter data with respect to different variables of correlation at any moment. Therefore, an almost countless number of options to retrieve and analyze data from the landslide database exists. According to different needs and demands, filters can be customized, and it is likewise possible to create new parameters or ratios from the existing dimension- and/or shape-related parameters.
Author Contributions
The research work (conceptualization, methodology, formal analysis, data curation, writing—original draft preparation, writing—review and editing, visualization) was completed by the main author, G.D. The three co-authors C.B., L.L., and S.M. supervised the interpretation of the results. The manuscript was prepared in close collaboration between G.D. and C.B. and was corrected by the two other co-authors. K.P. provided technical assistance during the import of the assessed landslide data into the database. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Data Sources
Data included in the database does not belong to the authors of this publication. The following references do not include publications associated with the individual landslides in the database. However, it is possible to provide (on demand) a full list of evaluated literature for every case, since the database is—for the time being—not publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Landslides included in the database. Columns from left to right give respectively the identification number in the database, the date of the major failure or the time since when sliding is reported (for active landsides), the name and country codes after ISO 3166-1 alpha-2 [41], the location as latitude and longitude, and the trigger if known (EQ referring to “earthquake”, GW referring to “groundwater”).
Table A1.
Landslides included in the database. Columns from left to right give respectively the identification number in the database, the date of the major failure or the time since when sliding is reported (for active landsides), the name and country codes after ISO 3166-1 alpha-2 [41], the location as latitude and longitude, and the trigger if known (EQ referring to “earthquake”, GW referring to “groundwater”).
| No. | Date | Landslide | C. | Latitude | Longitude | Trigger |
|---|---|---|---|---|---|---|
| 001.00 | 2001-03-18 | Diezma | ES | 37°18′34.00″ N | 003°22′08.70″ W | rain |
| 002.00 | 1949-07-10 | Khait | TJ | 39°11′27.40″ N | 070°55′41.20″ E | Khait EQ |
| 003.01 | paleo | Leupegem Hill 1 | BE | 50°49′25.07″ N | 003°37′18.62″ E | - |
| 003.02 | paleo | Leupegem Hill 2 | BE | 50°49′33.10″ N | 003°37′15.99″ E | - |
| 003.03 | paleo | Leupegem Hill 3 | BE | 50°49′36.13″ N | 003°37′10.17″ E | - |
| 003.04 | paleo | Rotelenberg Hill 4 | BE | 50°48′32.35″ N | 003°34′50.33″ E | - |
| 003.05 | paleo | Rotelenberg Hill 5 | BE | 50°48′37.41″ N | 003°34′36.52″ E | - |
| 003.06 | paleo | Rotelenberg Hill 6 | BE | 50°48′43.61″ N | 003°34′36.17″ E | - |
| 003.07 | paleo | Rotelenberg Hill 7 | BE | 50°48′45.25″ N | 003°34′44.67″ E | - |
| 003.08 | paleo | Rotelenberg Hill 8 | BE | 50°48′48.53″ N | 003°34′52.19″ E | - |
| 003.09 | paleo | Rotelenberg Hill 9 | BE | 50°48′47.08″ N | 003°35′00.05″ E | - |
| 003.10 | paleo | Rotelenberg Hill 10 | BE | 50°48′45.23″ N | 003°35′09.95″ E | - |
| 003.11 | paleo | Rotelenberg Hill 11 | BE | 50°48′43.86″ N | 003°35′17.67″ E | - |
| 003.12 | paleo | Rotelenberg Hill 12 | BE | 50°48′48.64″ N | 003°35′25.54″ E | - |
| 003.13 | paleo | Rotelenberg Hill 13 | BE | 50°48′53.55″ N | 003°35′27.93″ E | - |
| 004.00 | ? | Büyükçekmece | TR | 41°00′34.67″ N | 028°37′02.45″ E | overload |
| 005.01 | 2008-05-12 | Chengxi | CN | 31°49′33.01″ N | 104°26′57.36″ E | Sichuan EQ |
| 005.02 | 2008-05-12 | Xinbei Middle-School | CN | 31°49′46.43″ N | 104°27′36.25″ E | Sichuan EQ |
| 005.03 | 2008-05-12 | Tangjiashan | CN | 31°50′25.30″ N | 104°25′59.14″ E | Sichuan EQ |
| 005.04 | 2008-05-12 | Daguangbao | CN | 31°38′30.91″ N | 104°06′50.34″ E | Sichuan EQ |
| 006.00 | ? | Lushan Hot Spring | TW | 24°01′32.23″ N | 121°11′02.25″ E | storm |
| 007.01 | 1969 | Ain El Hammam | DZ | 36°34′15.18″ N | 004°18′12.23″ E | - |
| 007.02 | 1970 | Tigzirt City | DZ | 36°53′10.39″ N | 004°08′09.57″ E | - |
| 007.03 | 2009 | Tigzirt Port | DZ | 36°53′21.72″ N | 004°07′21.78″ E | - |
| 007.04 | 1952 | Azazga | DZ | 36°45′21.10″ N | 004°23′19.55″ E | - |
| 008.00 | 2014-03-22 | Oso-Steelhead | US | 48°17′06.57″ N | 121°51′03.33″ W | rain |
| 009.01 | 1811-12-16 | Stewart | US | 36°08′32.29″ N | 089°31′43.01″ W | New Madrid EQ (#1) |
| 009.02 | 1811-12-16 | Campbell | US | 36°04′10.18″ N | 089°29′48.84″ W | New Madrid EQ (#1) |
| 010.00 | 1981-03 | Avignonet | FR | 44°56′45.29″ N | 005°40′47.37″ E | - |
| 011.00 | paleo | Braemore | NZ | 39°41′29.60″ S | 174°39′18.97″ E | - |
| 012.00 | 2001-01-13 | Las Colinas | SV | 13°39′46.27″ N | 089°17′11.17″ W | El Salvador EQ |
| 013.00 | 1994-01-08 | La Salle en Beaumont | FR | 44°52′01.15″ N | 005°51′55.74″ E | - |
| 014.00 | 1978 | Harmalière | FR | 44°56′07.42″ N | 005°40′13.33″ E | - |
| 015.00 | 1980-11-23 | Calitri | IT | 40°53′54.88″ N | 015°26′09.31″ E | Irpinia EQ |
| 016.01 | 1999-09-20 | Tsaoling | TW | 23°35′06.14″ N | 120°40′40.83″ E | Chi Chi EQ |
| 016.02 | 1999-09-20 | Jiufenershan | TW | 23°57′27.80″ N | 120°50′33.79″ E | Chi Chi EQ |
| 016.03 | 1999-09-20 | Hungcaiping | TW | 23°57′23.82″ N | 120°48′56.63″ E | Chi Chi EQ |
| 017.00 | 2009-08-09 | Shiaolin | TW | 23°09′54.85″ N | 120°40′00.84″ E | typhoon |
| 018.01 | ? | Lesachriegel | AT | 46°59′17.01″ N | 012°40′58.39″ E | - |
| 018.02 | ? | Gradenbach | AT | 46°59′54.02″ N | 012°51′00.36″ E | - |
| 019.00 | 1903-04-29 | Frank | CA | 49°34′56.75″ N | 114°24′31.93″ W | - |
| 020.01 | 1964-03-28 | Potter Hill | US | 61°05′23.00″ N | 149°50′44.50″ W | Alaska EQ |
| 020.02 | 1964-03-28 | Bluff Road | US | 61°14′01.77″ N | 149°49′30.78″ W | Alaska EQ |
| 020.03 | 1964-03-28 | Turnagain Heights | US | 61°11′56.42″ N | 149°57′43.95″ W | Alaska EQ |
| 020.04 | 1964-03-28 | Point Campbell | US | 61°08′28.76″ N | 150°00′51.40″ W | Alaska EQ |
| 020.05 | 1964-03-28 | Point Woronzof | US | 61°12′09.34″ N | 150°00′33.05″ W | Alaska EQ |
| 020.06 | 1964-03-28 | L Street | US | 61°12′57.46″ N | 149°54′31.52″ W | Alaska EQ |
| 020.07 | 1964-03-28 | 4th Avenue | US | 61°13′11.81″ N | 149°53′05.80″ W | Alaska EQ |
| 020.08 | 1964-03-28 | Government Hill | US | 61°13′39.83″ N | 149°52′23.76″ W | Alaska EQ |
| 020.09 | 1964-03-28 | Native Hospital | US | 61°13′16.85″ N | 149°52′08.26″ W | Alaska EQ |
| 021.00 | 1994-01-17 | Calabasas | US | 34°07′34.43″ N | 118°38′58.68″ W | Northridge EQ |
| 022.00 | 1999-08-17 | Degirmendere | TR | 40°43′19.56″ N | 029°46′56.39″ E | Izmit EQ |
| 023.01 | ? | Vaculov-Sedlo | CZ | 49°23′03.61″ N | 018°04′47.13″ E | - |
| 023.02 | ? | Kobylska | CZ | 49°23′08.18″ N | 018°12′35.24″ E | - |
| 023.03 | ? | Kopce | CZ | 49°13′20.54″ N | 018°02′25.59″ E | - |
| 024.00 | 1980-05-18 | Mt. Saint Helens | US | 46°11′57.51″ N | 122°11′21.29″ W | volcanism |
| 025.00 | paleo | Lluta | CL | 18°24′01.65″ S | 069°46′27.54″ W | - |
| 026.00 | postglacial | Columbia Mountain | US | 48°20′18.79″ N | 114°07′12.57″ W | deglaciation |
| 027.00 | 1990-06 | Eureka River | CA | 56°25′44.79″ N | 119°24′05.27″ W | undercutting |
| 028.00 | 1939-04 | Montagneuse River | CA | 56°17′24.60″ N | 118°52′22.64″ W | - |
| 029.00 | 1959-05-19 | Dunvegan | CA | 55°54′28.33″ N | 118°37′36.10″ W | - |
| 030.01 | 2007-05-05 | Fox Creek East | CA | 55°51′23.82″ N | 118°03′25.25″ W | rain |
| 030.02 | 2007-05-05 | Fox Creek West | CA | 55°51′32.65″ N | 118°04′08.23″ W | rain |
| 031.01 | 1897 | CN50.9 | CA | 50°42′16.63″ N | 121°17′40.51″ W | undercutting |
| 031.02 | 1886 | Goddart | CA | 50°41′14.78″ N | 121°17′43.30″ W | undercutting |
| 032.00 | 1883-10-12 | Beaver Creek | CA | 51°58′56.23″ N | 106°43′16.36″ W | - |
| 033.01 | ? | Mt. Cefalone | IT | 42°14′31.49″ N | 013°25′13.51″ E | - |
| 033.02 | ? | Cima della Fossa | IT | 41°54′06.97″ N | 014°01′32.86″ E | - |
| 033.03 | ? | Villavallelonga | IT | 41°52′03.37″ N | 013°39′09.01″ E | - |
| 033.04 | 1915-01-13 | Casali d’Aschi | IT | 41°58′01.77″ N | 013°40′56.76″ E | Avezzano EQ |
| 033.05 | 1915-01-13 | Gioia dei Marsi | IT | 41°57′11.31″ N | 013°42′27.76″ E | Avezzano EQ |
| 033.06 | 1703-01-14 | Mt. Alvagnano | IT | 42°40′19.15″ N | 013°08′40.50″ E | Norcia EQ |
| 033.07 | ? | Fiamignano | IT | 42°16′28.61″ N | 013°07′19.02″ E | - |
| 033.08 | ? | Pescasseroli | IT | 41°48′52.62″ N | 013°46′21.58″ E | - |
| 034.00 | 1780 | Campo Vallemaggia | CH | 46°17′29.96″ N | 008°29′36.88″ E | - |
| 035.01 | ? | Longobardi | IT | 39°12′41.17″ N | 016°04′19.73″ E | - |
| 035.02 | 1982-12-13 | Ancona | IT | 43°36′05.58″ N | 013°28′41.16″ E | - |
| 036.00 | 1984-04 | La Clapière | FR | 44°15′08.16″ N | 006°56′29.22″ E | - |
| 037.00 | 2006-03-21 | Laalam | DZ | 36°34′50.09″ N | 005°27′24.74″ E | Kherrata EQ |
| 038.00 | 1806-09-02 | Goldau | CH | 47°04′36.94″ N | 008°33′40.84″ E | rain |
| 039.01 | 1980 | Cerentino | CH | 46°18′23.34″ N | 008°32′20.52″ E | - |
| 039.02 | 1834 | Peccia | CH | 46°24′56.52″ N | 008°40′29.50″ E | - |
| 039.03 | 1846 | Val Canaria | CH | 46°33′25.52″ N | 008°38′49.57″ E | - |
| 039.04 | 1896-10 | Val Colla | CH | 46°05′15.13″ N | 009°01′08.71″ E | - |
| 040.01 | 1755-11-01 | Güevéjar I | ES | 37°15′37.99″ N | 003°35′15.10″ W | Lisbon EQ |
| 040.02 | 1884-12-25 | Güevéjar II | ES | 37°15′37.99″ N | 003°35′15.10″ W | Arenas del Rey EQ |
| 041.00 | 1683 | Montelparo | IT | 43°01′11.75″ N | 013°32′31.04″ E | - |
| 042.00 | 1933-10 | Sesa | IT | 45°54′01.40″ N | 010°20′14.35″ E | rain |
| 043.01 | ? | Ráztoka | SK | 48°50′01.71″ N | 019°24′20.03″ E | - |
| 043.02 | ? | Polská Tomanová | SK | 49°12′21.83″ N | 019°54′57.46″ E | - |
| 044.00 | 2002-10-31 | Salcito | SK | 41°44′17.16″ N | 014°31′55.14″ E | Molise EQ |
| 045.01 | paleo | Belbek | UA | 44°40′15.92″ N | 033°42′51.45″ E | EQ (?) |
| 045.02 | paleo | Frontovoye | UA | 44°42′04.50″ N | 033°44′45.30″ E | EQ (?) |
| 045.03 | paleo | Kacha 1 | UA | 44°44′47.93″ N | 033°43′47.38″ E | EQ (?) |
| 045.04 | paleo | Kacha 2 | UA | 44°45′44.59″ N | 033°43′31.12″ E | EQ (?) |
| 045.05 | paleo | Alma | UA | 44°51′16.53″ N | 033°52′43.01″ E | EQ (?) |
| 045.06 | paleo | Vishennoye | UA | 45°07′57.59″ N | 034°36′59.23″ E | EQ (?) |
| 046.01 | 1692-09-18 | Battice 1 | BE | 50°39′13.63″ N | 005°50′24.10″ E | Verviers EQ |
| 046.02 | 1692-09-18 | Battice 2 | BE | 50°39′00.46″ N | 005°50′32.57″ E | Verviers EQ |
| 046.03 | 1692-09-18 | Battice 3 | BE | 50°38′52.31″ N | 005°50′51.36″ E | Verviers EQ |
| 046.04 | 1692-09-18 | Battice 4 | BE | 50°38′58.66″ N | 005°51′29.41″ E | Verviers EQ |
| 046.05 | 1692-09-18 | Battice 5 | BE | 50°39′00.28″ N | 005°51′59.18″ E | Verviers EQ |
| 046.06 | 1692-09-18 | Battice 6 | BE | 50°39′06.65″ N | 005°52′35.11″ E | Verviers EQ |
| 046.07 | 1692-09-18 | Battice 7 | BE | 50°39′41.62″ N | 005°52′38.99″ E | Verviers EQ |
| 046.08 | 1692-09-18 | Battice 8 | BE | 50°38′27.28″ N | 005°51′09.95″ E | Verviers EQ |
| 046.09 | 1692-09-18 | Battice 9 | BE | 50°38′37.36″ N | 005°51′52.67″ E | Verviers EQ |
| 046.10 | 1692-09-18 | Battice 10 | BE | 50°38′35.84″ N | 005°50′45.61″ E | Verviers EQ |
| 046.11 | 1692-09-18 | Battice 11 | BE | 50°37′53.96″ N | 005°49′40.06″ E | Verviers EQ |
| 046.12 | 1692-09-18 | Battice 12 | BE | 50°37′45.13″ N | 005°49′40.99″ E | Verviers EQ |
| 046.13 | 1692-09-18 | Battice 13 (Manaihan) | BE | 50°37′34.66″ N | 005°49′40.57″ E | Verviers EQ |
| 047.01 | 2007-04-21 | Acantilada Bay | CL | 45°23′49.80″ S | 072°53′09.00″ W | Aysén EQ |
| 047.02 | 2007-04-21 | Punta Cola | CL | 45°22′46.80″ S | 072°59′54.00″ W | Aysén EQ |
| 047.03 | 2007-04-21 | Mentirosa Island | CL | 45°24′03.00″ S | 072°58′05.40″ W | Aysén EQ |
| 047.04 | 2007-04-21 | Frío Creek | CL | 45°23′55.20″ S | 072°56′40.20″ W | Aysén EQ |
| 047.05 | 2007-04-21 | Marta River 1 | CL | 45°20′19.80″ S | 073°00′15.60″ W | Aysén EQ |
| 047.06 | 2007-04-21 | Fernández Creek | CL | 45°23′25.20″ S | 072°54′17.40″ W | Aysén EQ |
| 047.07 | 2007-04-21 | Marta River 2 | CL | 45°20′56.40″ S | 072°58′52.20″ W | Aysén EQ |
| 047.08 | 2007-04-21 | Pescado River | CL | 45°25′26.40″ S | 073°06′05.40″ W | Aysén EQ |
| 048.00 | 1987-03-05 | Salado | EC | 00°11′27.68″ S | 077°41′39.36″ W | Ecuador EQ |
| 049.00 | 1679-06-04 | Vokhchaberd | AM | 40°09′59.75″ N | 044°38′17.21″ E | Armenia EQ |
| 050.00 | 1881-09-10 | Castel Frentano | IT | 42°11′55.53″ N | 014°21′35.41″ E | Lanciano EQ |
| 051.00 | 1997-10-11 | Mt. Nuria | IT | 42°21′44.73″ N | 013°00′21.11″ E | - |
| 052.01 | 1990-06-20 | Galdian | IR | 36°48′01.95″ N | 049°25′37.05″ E | Manjil-Rudbar EQ |
| 052.02 | 1990-06-20 | Fatalak | IR | 36°50′20.41″ N | 049°29′13.48″ E | Manjil-Rudbar EQ |
| 053.00 | 1963-10-09 | Vajont | IT | 46°15′27.65″ N | 012°20′25.93″ E | rain, GW, bedding |
| 054.00 | 2003-09-10 | Tsaitichhu | BT | 27°25′52.19″ N | 091°06′40.49″ E | - |
| 055.00 | 2007-03-01 | S. Giovanni | IT | 38°16′11.31″ N | 015°47′54.28″ E | tunneling |
| 056.00 | 1950 | Rasdeglia | IT | 46°27′29.72″ N | 009°19′07.28″ E | - |
| 057.00 | 1992-08-19 | Suusamyr | KG | 42°12′29.82″ N | 073°36′33.08″ E | Suusamyr EQ |
| 058.01 | paleo | Kokomeren | KG | 41°55′35.84″ N | 074°13′35.99″ E | EQ (?) |
| 058.02 | 1885 | Aksu | KG | 42°32′33.01″ N | 073°59′21.27″ E | Belovodsk EQ (?) |
| 058.03 | paleo | Beshkiol | KG | 41°25′00.00″ N | 074°30′00.00″ E | EQ (?) |
| 058.04 | paleo | Karakudjur | KG | 41°57′43.72″ N | 075°53′09.05″ E | EQ (?) |
| 058.05 | 1946 | Sarychelek | KG | 41°52′00.00″ N | 072°00′00.00″ E | Chatkal EQ (?) |
| 058.06 | paleo | Kugart | KG | 41°10′00.00″ N | 073°20′60.00″ E | EQ (?) |
| 059.00 | ? | Rosone | IT | 45°26′17.72″ N | 007°23′58.78″ E | rain |
| 060.00 | 2000-04-09 | Yigong | CN | 30°13′46.30″ N | 094°59′28.88″ E | - |
| 061.00 | 1911-02-18 | Usoi | TJ | 38°18′21.64″ N | 072°36′46.40″ E | Sarez EQ |
| 062.01 | 1989-01-22 | Okuli | TJ | 38°29′10.43″ N | 068°37′41.70″ E | Gissar EQ |
| 062.02 | 1989-01-22 | May 1 | TJ | 38°29′15.91″ N | 068°37′21.13″ E | Gissar EQ |
| 062.03 | 1989-01-22 | Firma | TJ | 38°29′23.60″ N | 068°38′19.45″ E | Gissar EQ |
| 062.04 | 1989-01-22 | Sharara | TJ | 38°29′17.39″ N | 068°38′51.46″ E | Gissar EQ |
| 063.00 | 1984 | Klasgarten | AT | 46°57′08.59″ N | 010°45′02.24″ E | - |
| 064.00 | 1975 | Niedergallmigg | AT | 47°06′04.31″ N | 010°36′30.03″ E | - |
| 065.01 | 1992 | Huayuanyangjichang | CN | 30°44′57.32″ N | 108°25′43.70″ E | GW |
| 065.02 | 1996 | Jinjinzi | CN | 30°33′39.48″ N | 108°18′17.38″ E | GW |
| 065.03 | 1999 | Yangjiaba | CN | 30°26′05.48″ N | 108°14′10.50″ E | GW |
| 066.00 | postglacial | Atemkopf | AT | 46°56′34.29″ N | 010°43′19.17″ E | - |
| 067.00 | 2002-10 | La Mania | IT | 46°27′24.06″ N | 012°43′41.15″ E | - |
| 068.00 | 1960 | Beauregard | IT | 45°37′09.03″ N | 007°02′36.21″ E | - |
| 069.00 | 1965-01-09 | Hope | CA | 49°18′21.72″ N | 121°14′22.42″ W | EQ (?) |
| 070.00 | ? | Anlesi | CN | 30°49′45.44″ N | 108°20′38.63″ E | rain |
| 071.01 | 1914-05-30 | Cà di Malta | IT | 44°17′26.61″ N | 011°07′14.63″ E | - |
| 071.02 | 1934-03-06 | Rocca Pitigliana | IT | 44°13′56.49″ N | 011°00′11.74″ E | - |
| 072.00 | 1957-07-02 | Kahrod | IR | 36°03′59.80″ N | 052°14′36.17″ E | Mazandaran EQ |
| 073.00 | 2008-09 | Cerca del Cielo | US | 18°02′22.22″ N | 066°40′28.98″ W | rain |
| 074.00 | ? | Kutlugün | TR | 40°56′31.61″ N | 039°43′58.04″ E | - |
| 075.00 | 1987-07-28 | Val Pola | IT | 46°22′42.87″ N | 010°20′11.95″ E | rain |
| 076.01 | ? | Varco d’Izzo | IT | 40°38′45.97″ N | 015°51′40.67″ E | - |
| 076.02 | ? | Costa della Gaveta | IT | 40°38′40.44″ N | 015°51′07.42″ E | - |
| 077.00 | 1979-08-08 | Abbotsford | NZ | 45°53′37.02″ S | 170°26′16.35″ E | mining |
| 078.00 | 17th cent. | Tortum | TT | 40°39′56.10″ N | 041°38′31.18″ E | EQ (?) |
| 079.00 | 18th cent. | Slumgullion | US | 37°59′36.97″ N | 107°15′11.29″ W | rain |
| 080.00 | 1999-05-13 | Rufi | CH | 47°11′15.97″ N | 009°04′46.13″ E | rain |
| 081.00 | 2007 | Zhujiadian | CN | 31°02′48.86″ N | 110°23′57.86″ E | GW |
| 082.00 | 1982 | Minor Creek | US | 40°57′57.27″ N | 123°49′59.74″ W | rain |
| 083.00 | 2005-03-17 | Kuzulu | TR | 40°20′50.13″ N | 037°39′16.20″ E | snowmelt |
| 084.00 | 1995 | Huangtupo | CN | 31°02′34.17″ N | 110°23′07.89″ E | GW |
| 085.00 | 1998 | Fosso Spineto | IT | 40°37′38.66″ N | 016°17′28.67″ E | undercutting |
| 086.00 | 500000 BP | Marcus | US | 33°40′47.72″ N | 111°47′50.06″ W | - |
| 087.00 | 2003-11-09 | Afternoon Creek | US | 48°41′33.94″ N | 121°14′23.26″ W | rain |
| 088.00 | 2009-04-26 | Valgrisenche | IT | 45°41′05.20″ N | 007°07′12.24″ E | rain |
| 089.00 | ? | Aka-Kuzure | JP | 35°21′28.03″ N | 138°12′26.26″ E | - |
| 090.00 | ? | Ivancich | IT | 43°04′00.00″ N | 012°37′30.00″ E | - |
| 091.00 | 1999-11-12 | Bakacak | TR | 40°45′19.23″ N | 031°22′18.69″ E | Düzce EQ |
| 092.00 | postglacial | Triesenberg | LI | 47°07′06.22″ N | 009°32′54.51″ E | deglaciation |
| 093.00 | 1783-02-06 | Scilla | IT | 38°14′53.00″ N | 015°42′05.84″ E | Calabria EQ (#2) |
| 094.00 | 1972 | San Donato | IT | 40°23′31.15″ N | 016°33′54.20″ E | - |
| 095.00 | ? | La Salsa | IT | 40°31′09.71″ N | 016°32′50.78″ E | - |
| 096.00 | 1996 | Grohovo | HR | 45°21′58.08″ N | 014°26′53.11″ E | - |
| 097.00 | 35000 BP | Uspenskoye | RU | 44°53′14.01″ N | 041°25′29.77″ E | EQ (?) |
| 098.00 | 1995-01-16 | Nikawa | JP | 34°46′23.83″ N | 135°20′29.40″ E | Kobe EQ |
| 099.00 | paleo | Dúdar | ES | 37°11′39.28″ N | 003°29′19.66″ W | EQ (?) |
| 100.01 | ? | Machu Picchu A | PE | 13°09′58.60″ S | 072°32′26.91″ W | GW, faults |
| 100.02 | ? | Machu Picchu B | PE | 13°09′48.07″ S | 072°32′41.83″ W | GW, faults |
| 101.01 | 2002 | Keillor Road | CA | 53°30′41.08″ N | 113°32′28.92″ W | GW |
| 101.02 | 1999-10-23 | Whitemud Road | CA | 53°28′56.19″ N | 113°35′17.61″ W | GW |
| 102.00 | 1627-07-30 | Vasto | IT | 42°06′16.33″ N | 014°42′50.53″ E | Gargano EQ (?) |
| 103.00 | 1963 | Kostanjek | HR | 45°49′15.46″ N | 015°51′22.44″ E | GW, mining |
| 104.00 | 1997-07 | Mt. Munday | HR | 51°20′46.26″ N | 125°14′29.02″ W | - |
| 105.00 | 2010-08-06 | Mt. Meager | HR | 50°37′27.17″ N | 123°30′05.53″ W | volcanism |
| 106.00 | 10000 BP | Downie | HR | 51°30′17.38″ N | 118°32′06.37″ W | deglaciation |
| 107.00 | 2005-01-10 | La Conchita | US | 34°21′54.51″ N | 119°26′40.69″ W | rain |
| 108.00 | postglacial | Séchilienne | FR | 45°03′49.44″ N | 005°48′16.13″ E | - |
| 109.00 | 2004 | Ogoto | JP | ? | ? | GW |
| 110.00 | 2003 | Kuchi-Otani | JP | ? | ? | typhoon |
| 111.00 | 1854-12-23 | Zentoku | JP | 33°53′07.14″ N | 133°50′19.94″ E | Tokai EQ (?) |
| 112.00 | 2003-05-26 | Tsukidate | JP | 38°43′41.19″ N | 141°00′35.41″ E | Sanriku-Minami EQ |
| 113.01 | 1997-01 | Slesse Park | CA | 49°05′05.87″ N | 121°48′27.42″ W | rain, logging |
| 113.02 | 1973-05-26 | Attachie | CA | 56°12′13.84″ N | 121°27′19.17″ W | rain |
| 114.00 | 1963-09-03 | Lesueur | CA | 53°36′05.81″ N | 113°18′41.57″ W | mining |
| 115.00 | 1933-07 | Brazeau | CA | 52°23′21.12″ N | 117°04′19.41″ W | - |
| 116.00 | 1990-06-17 | Saddle River | CA | 55°47′12.20″ N | 118°26′20.37″ W | rain |
| 117.00 | 2010-01 | Cenes de la Vega | ES | 37°10′24.38″ N | 003°32′01.50″ W | rain, pipe leak |
| 118.00 | 1993-12-29 | Acquara-Vadoncello | IT | 40°44′03.30″ N | 015°12′42.45″ E | - |
| 119.00 | 1901-10-01 | Boscobel | BB | 13°16′27.13″ N | 059°34′19.83″ W | - |
| 120.00 | paleo | Mt. Nuovo | IT | 40°44′08.83″ N | 013°53′17.08″ E | volcanism |
| 121.00 | 140000 BP | Baga Bogd | MN | 44°57′37.88″ N | 101°32′23.34″ E | deglaciation |
| 122.00 | 1974-04-25 | Mayunmarca | PE | 12°39′12.37″ S | 074°41′43.58″ W | - |
| 123.00 | 1612 | Corniglio | IT | 44°28′00.76″ N | 010°04′40.82″ E | - |
| 124.00 | ? | Vallcebre | ES | 42°12′21.23″ N | 001°49′59.40″ E | - |
| 125.00 | 10000 BP | Corvara | IT | 46°32′19.74″ N | 011°54′13.37″ E | - |
| 126.00 | 1786-06-01 | Dadu River | CN | 29°37′52.69″ N | 102°09′28.84″ E | Kangding EQ |
| 127.00 | 10000 BP | Fogo | CV | 14°57′06.61″ N | 024°21′32.88″ W | volcanism |
| 128.00 | 1906 | Petacciato | IT | 42°01′07.49″ N | 014°52′39.16″ E | - |
| 129.01 | 20000 BP | El Petruso | ES | 42°48′03.45″ N | 000°24′33.85″ W | rain |
| 129.02 | 20000 BP | Sextas | ES | 42°46′12.79″ N | 000°22′31.28″ W | rain |
| 129.03 | 20000 BP | La Selva | ES | 42°45′43.54″ N | 000°21′10.30″ W | rain |
| 130.00 | 1996 | Halden Creek | CA | 58°20′02.94″ N | 123°07′45.52″ W | clay |
| 131.00 | 10000 BP | Åknes | NO | 62°10′37.29″ N | 006°59′47.45″ E | - |
| 132.00 | 10000 BP | Kykula | SK | 49°26′32.86″ N | 018°57′52.44″ E | - |
| 133.00 | paleo | Latagualla | CL | 19°15′25.20″ S | 069°35′42.00″ W | EQ (?) |
| 134.00 | 1920-12-16 | Huihuichuan | CN | 35°57′07.79″ N | 105°40′07.55″ E | Gansu EQ |
| 135.00 | 1980 | Amloke Nakka | PK | 34°34′25.76″ N | 073°08′40.24″ E | clay |
| 136.00 | 1960-10 | Tessina | IT | 46°11′21.78″ N | 012°24′08.15″ E | - |
| 137.00 | paleo | Krynica | PL | 49°25′01.78″ N | 020°57′38.80″ E | deglaciation |
| 138.00 | paleo | Collinabos | BE | 50°46′11.40″ N | 003°34′34.26″ E | loess |
| 139.00 | 2002-09-06 | Cerda | IT | 37°56′03.10″ N | 013°50′09.54″ E | Cerda EQ |
| 140.00 | 2011-09-16 | Shibangou | CN | 32°14′27.00″ N | 106°44′45.00″ E | rain |
| 141.00 | 1996-04-28 | Quesnel Forks | CA | 52°39′36.09″ N | 121°40′12.02″ W | rain |
| 142.00 | ? | Riou-Bourdoux Valley | FR | 44°25′06.29″ N | 006°37′20.21″ E | rain |
| 143.00 | 2000-11-18 | Slano Blato | SI | 45°54′55.45″ N | 013°51′49.12″ E | rain |
| 144.00 | 1958-07-10 | Lituya Bay | US | 58°40′53.44″ N | 137°29′11.39″ W | Alaska EQ |
| 145.00 | 1976-05-06 | Mt. Boscatz | IT | 46°17′19.52″ N | 013°04′37.20″ E | Friuli EQ |
| 146.00 | 1949 | Kualiangzi | CN | 30°39′01.00″ N | 104°53′40.00″ E | rain |
| 147.00 | 6th cent. | Ropice | CZ | 49°36′18.57″ N | 018°35′08.10″ E | - |
| 148.00 | 1982 | La Valette | FR | 44°24′40.11″ N | 006°38′52.84″ E | rain, flysch |
| 149.00 | postglacial | Heather Hill | CA | 51°26′52.08″ N | 117°28′24.24″ W | deglaciation |
| 150.00 | 2008-11-23 | Gongjiafang | CH | 31°03′57.62″ N | 109°55′11.88″ E | GW |
| 151.00 | paleo | Utiku | NZ | 39°44′51.09″ S | 175°50′16.88″ E | - |
| 152.00 | paleo | Taihape | NZ | 39°40′56.56″ S | 175°47′30.16″ E | - |
| 153.01 | paleo | Stromboli | IT | 38°47′46.85″ N | 015°12′27.06″ E | volcanism |
| 153.02 | paleo | La Fossa | IT | 38°24′39.37″ N | 014°58′02.48″ E | volcanism |
| 154.00 | 1909-11 | East Lirio | PA | 09°02′21.69″ N | 079°39′02.93″ W | excavation work |
| 155.01 | 2010-11 | Cischele | IT | 45°42′42.50″ N | 011°13′24.67″ E | - |
| 155.02 | ? | Ochojno | PL | 49°57′39.36″ N | 019°57′15.56″ E | - |
| 156.00 | postglacial | Gammajunni 3 | NO | 69°28′48.90″ N | 020°33′39.86″ E | - |
| 157.00 | postglacial | La Frasse | CH | 46°21′31.21″ N | 007°02′10.04″ E | - |
| 158.00 | 1953-01-31 | Miramar | UK | 51°22′22.79″ N | 001°09′17.08″ E | clay |
| 159.00 | ? | Mahouane Dam | DZ | 36°17′24.02″ N | 005°21′24.67″ E | clay |
| 160.00 | paleo | Pianello | IT | 41°14′48.93″ N | 015°20′25.04″ E | clay |
| 161.00 | 2011 | St. Maria Maddalena | IT | 44°13′05.72″ N | 011°11′37.98″ E | tunneling |
| 162.00 | ? | Zhaoshuling | CN | 31°02′38.04″ N | 110°20′46.82″ E | GW |
| 163.00 | ? | Dúrcal | ES | 36°55′57.60″ N | 003°31′42.36″ W | - |
| 164.00 | 1935 | Aggenalm | DE | 47°40′00.28″ N | 012°03′28.04″ E | - |
| 165.00 | ? | Huangshipan | CN | 31°54′16.57″ N | 106°36′53.68″ E | - |
| 166.00 | postglacial | Lake Wanaka | NZ | 44°22′13.00″ S | 169°11′43.61″ E | EQ (?) |
| 167.00 | 2015-02-02 | Mofjellbekken | NO | 59°28′10.11″ N | 010°18′02.55″ E | clay |
| 168.00 | ? | Badu | CN | 24°42′36.27″ N | 105°47′56.88″ E | excavation work |
| 169.01 | paleo | Number 1 | CN | 26°57′25.06″ N | 102°57′54.94″ E | - |
| 169.02 | paleo | Number 2 | CN | 27°00′10.31″ N | 102°52′53.13″ E | - |
| 170.01 | 2005-12-10 | Saint Barnabé | CA | 46°22′48.83″ N | 072°49′24.93″ W | clay |
| 170.02 | 2010-05-10 | Saint Jude | CA | 45°48′16.72″ N | 072°57′49.13″ W | clay |
| 170.03 | 1994-04-21 | Sainte Monique | CA | 46°10′41.46″ N | 072°33′05.56″ W | clay |
| 171.00 | 1970 | Bird | NZ | 39°37′54.07″ S | 175°49′38.10″ E | - |
| 172.00 | 2013-12-03 | Montescaglioso | IT | 40°32′31.06″ N | 016°39′10.96″ E | - |
| 173.00 | 19th cent. | Spriana | IT | 46°12′41.31″ N | 009°52′30.02″ E | - |
| 174.00 | ? | Piscopio I Tunnel | IT | 38°47′05.67″ N | 016°33′03.52″ E | tunneling |
| 175.00 | ? | La Saxe | IT | 45°49′02.33″ N | 006°58′13.17″ E | - |
| 176.00 | ? | Erguxi | CN | 31°35′59.57″ N | 102°49′06.14″ E | - |
| 177.01 | 1955-12-07 | Hawkesbury | CA | 45°34′49.52″ N | 074°32′47.16″ W | blast (?) |
| 177.02 | 1962-05-23 | Toulnustouc | CA | 49°57′47.64″ N | 068°08′42.84″ W | blast (?) |
| 177.03 | 1996-06-20 | Finneidfjord | NO | 66°10′55.96″ N | 013°47′44.52″ E | blast (?) |
| 177.04 | 2009-03-13 | Kattmarka | NO | 64°28′26.16″ N | 011°26′06.42″ E | blast (?) |
| 177.05 | 2009-08-01 | La Romaine | CA | 50°13′24.23″ N | 060°40′14.07″ W | blast (?) |
| 178.01 | 1960 | Bumper | AU | 37°40′52.09″ S | 145°53′55.81″ E | rain |
| 178.02 | 1960 | Siphon Gully | AU | 37°41′10.59″ S | 145°54′11.54″ E | rain |
References
- Bird, J.F.; Bommer, J.J. Earthquake losses due to ground failure. Eng. Geol. 2004, 75, 147–179. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Ciurleo, M.; Mandaglio, M.C.; Moraci, N. Landslide susceptibility assessment by TRIGRS in a frequently affected shallow instability area. Landslides 2019, 16, 175–188. [Google Scholar] [CrossRef]
- USGS. Landslide Types and Processes. United States Geological Survey Fact Sheet 2004, 3072, 4. Available online: https://pubs.usgs.gov/fs/2004/3072/pdf/fs2004-3072.pdf (accessed on 25 October 2019).
- Lott, N.; McCown, S.; Graumann, A.; Ross, T.; Lackey, M. Hurricane Mitch 1999—The Deadliest Atlantic Hurricane since 1780; National Climatic Data Center of the National Oceanic and Atmospheric Administration: Asheville, NC, USA, 1999. Available online: ftp://ftp.ncdc.noaa.gov/pub/data/extremeevents/specialreports/Hurricane-Mitch-1998.pdf (accessed on 8 October 2019).
- Yin, Y.P.; Wang, F.W.; Sun, P. Landslide hazards triggered by the 2008 Wenchuan earthquake, Sichuan, China. Landslides 2009, 6/2, 139–151. [Google Scholar] [CrossRef]
- Harp, E.L.; Jibson, R.W. Inventory of landslides triggered by the 1994 Northridge, California earthquake. United States Geol. Surv. Open File Rep. 1995, 95, 17. Available online: https://geo-nsdi.er.usgs.gov/metadata/open-file/95-213/ (accessed on 20 May 2020).
- Harp, E.L.; Jibson, R.L. Landslides triggered by the 1994 Northridge, California earthquake. Bull. Seismol. Soc. Am. 1996, 86, S319–S332. [Google Scholar]
- Keefer, D.K. Landslides caused by earthquakes. Bull. Geol. Soc. Am. 1984, 9, 406–421. [Google Scholar] [CrossRef]
- Prestininzi, A.; Romeo, R. Earthquake-induced ground failures in Italy. Eng. Geol. 2000, 58, 387–397. [Google Scholar] [CrossRef]
- Rodríguez, C.E.; Bommer, J.J.; Chandler, R.J. Earthquake-induced landslides: 1980–1997. Soil Dyn. Earthq. Eng. 1999, 18, 325–346. [Google Scholar] [CrossRef]
- Tanyaş, H.; Van Westen, C.J.; Allstadt, K.E.; Nowicki Jessee, M.A.; Görüm, T.; Jibson, R.W.; Godt, J.W.; Sato, H.P.; Schmitt, R.G.; Marc, O.; et al. Presentation and Analysis of a Worldwide Database of Earthquake-Induced Landslide Inventories. J. Geophys. Res. Earth Surf. 2017, 122, 1991–2015. [Google Scholar] [CrossRef]
- Cardinali, M.; Ardizzone, F.; Galli, M.; Guzzetti, F.; Reichenbach, P. Landslides triggered by rapid snow melting: The December 1996—January 1997 event in Central Italy. In Proceedings of the 1st Plinius Conference, Maratea, Italy, 14–16 October 1999; Claps, P., Siccardi, F., Eds.; Bios Publisher: Cosenza, Italy, 2000; pp. 439–448. [Google Scholar]
- Schlögel, R.; Torgoev, I.; De Marneffe, C.; Havenith, H.B. Evidence of a changing size–frequency distribution of landslides in the Kyrgyz Tien Shan, Central Asia. Earth Surf. Proc. Land. 2011, 36/12, 1658–1669. [Google Scholar] [CrossRef]
- Bucknam, R.C.; Coe, J.A.; Chavarria, M.M.; Godt, J.W.; Tarr, A.C.; Bradley, L.A.; Rafferty, S.; Hancock, D.; Dart, R.L.; Johnson, M.L. Landslides Triggered by Hurricane Mitch in Guatemala—Inventory and Discussion. United States Geol. Surv. Open File Rep. 2001, 443, 40. Available online: https://www.sciencebase.gov/catalog/item/4f4e4b1be4b07f02db6a91b2 (accessed on 20 May 2020). [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Proc. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Guzzetti, F.; Rossi, M. Probability distributions of landslide volumes. Nonlinear Process. Geophys. 2009, 16, 179–188. [Google Scholar] [CrossRef]
- Guzzetti, F.; Malamud, B.D.; Turcotte, D.L.; Reichenbach, P. Power-law correlations of landslide areas in central Italy. Earth Planet. Sci. Lett. 2002, 195, 169–183. [Google Scholar] [CrossRef]
- Guzzetti, F.; Ardizzone, F.; Cardinali, M.; Galli, M.; Reichenbach, P.; Rossi, M. Distribution of landslides in the Upper Tiber River basin, central Italy. Geomorphology 2008, 96, 105–122. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Korup, O. Distribution of landslides in southwest New Zealand. Landslides 2005, 2, 43–51. [Google Scholar] [CrossRef]
- Larsen, I.J.; Montgomery, D.R.; Korup, O. Landslide erosion controlled by hillslope material. Nat. Geosci. 2010, 3, 247–251. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Poesen, J.; Govers, G.; Verstraeten, G.; Demoulin, A. Characteristics of the size distribution of recent and historical landslides in a populated hilly region. Earth Planet. Sci. Lett. 2007, 256, 588–603. [Google Scholar] [CrossRef]
- Guzzetti, F.; Ardizzone, F.; Cardinali, M.; Rossi, M.; Valigi, D. Landslide volumes and landslide mobilization rates in Umbria, central Italy. Earth Planet. Sci. Lett. 2009, 279, 222–229. [Google Scholar] [CrossRef]
- Havenith, H.B.; Strom, A.; Torgoev, I.; Torgoev, A.; Lamair, L.; Ischuk, A.; Abdrakhmatov, K. Tien Shan Geohazards Database: Earthquakes and landslides. Geomorphology 2015, 249, 16–31. [Google Scholar] [CrossRef]
- Hovius, N.; Stark, C.P.; Allen, P.A. Sediment flux from a mountain belt derived by landslide mapping. Geology 1997, 25, 231–234. [Google Scholar] [CrossRef]
- Korup, O. Effects of large deep-seated landslides on hillslope morphology, western Southern Alps, New Zealand. J. Geophys. Res. Earth Surf. 2006, 111, 18. [Google Scholar] [CrossRef]
- Ten Brink, U.S.; Geist, E.L.; Andrews, B.D. Size distribution of submarine landslides and its implication to tsunami hazard in Puerto Rico. Geophys. Res. Lett. 2006, 33, 4. [Google Scholar] [CrossRef]
- Cruden, D.M.; Krahn, J. A Reexamination of the Geology of the Frank Slide. Can. Geotech. J. 1973, 10, 581–591. [Google Scholar] [CrossRef]
- Google Earth Pro; Version 7.3.2. Frank Landslide, Canada, 49°35’19.10"N & 114°23’39.35"W, eye altitude 2.53 km, Google 2018, CNES/Airbus 2019, 2019a; Google: Mountain View, CA, USA, 2018.
- Domej, G.; Bourdeau, C.; Lenti, L.; Martino, S.; Pluta, K. Mean landslide geometries inferred from a global database of earthquake- and non-earthquake-triggered landslides. Ital. J. Eng. Geol. Environ. 2017, 17, 87–107. [Google Scholar] [CrossRef]
- MATLAB; Version 9.7.0 (R2019b); The MathWorks Inc.: Natick, MA, USA, 2019.
- IAEG Commission on Landslides. Suggested nomenclature for landslides. Bull. Int. Assoc. Eng. Geol. 1990, 41, 13–16. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides: Investigation and Mitigation, 1st ed.; Special Report 247; Turner, A.K., Schuster, R.L., Eds.; National Research Council, Transportation Research Board: Washington, DC, USA, 1996; pp. 36–75. [Google Scholar]
- Delgado, J.; Garrido, J.; Lenti, L.; Lopez-Casado, C.; Martino, S.; Sierra, F.J. Unconventional pseudostatic stability analysis of the Diezma landslide (Granada, Spain) based on a high-resolution engineering-geological model. Eng. Geol. 2015, 184, 81–95. [Google Scholar] [CrossRef]
- Google Earth Pro; Version 7.3.2. Diezma Landslide, Spain, 37°18’34.00"N & 3°22’8.70"W, eye altitude 2.03 km, Google 2018, Europa Technologies 2018, 2019b; Google: Mountain View, CA, USA, 2018.
- Varnes, D.J. Slope movement types and processes. In Landslides—Analysis and Control, 1st ed.; Special Report 176; Schuster, R.L., Krizek, R.J., Eds.; National Research Council, Transportation Research Board: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Stark, C.P.; Guzzetti, F. Landslide rupture and the probability distribution of mobilized debris volumes. J. Geophys. Res. Earth 2009, 114, 16. [Google Scholar] [CrossRef]
- Heim, A. Bergsturz und Menschenleben, Beiblatt zur Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich no. 20; Fretz & Wasmuth: Tübingen, Germany, 1932; p. 218. [Google Scholar]
- Domej, G. Seismically Induced Effects and Slope Stability In Urbanized Zones by Numerical Modeling. Ph.D. Thesis, Institut Français des Sciences et Technologies des Transports, de l’Aménagement et des Réseaux & Université Paris–Est, Paris, France, 2018; p. 266. [Google Scholar]
- ISO. ISO 3166 Country Codes; International Organization for Standardization: Geneva, Switzerland, 2013; Available online: https://www.iso.org/iso-3166-country-codes.html (accessed on 25 October 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).