Comparison of MODIS and Model-Derived Snow-Covered Areas: Impact of Land Use and Solar Illumination Conditions
Abstract
1. Introduction
2. Materials and Methods
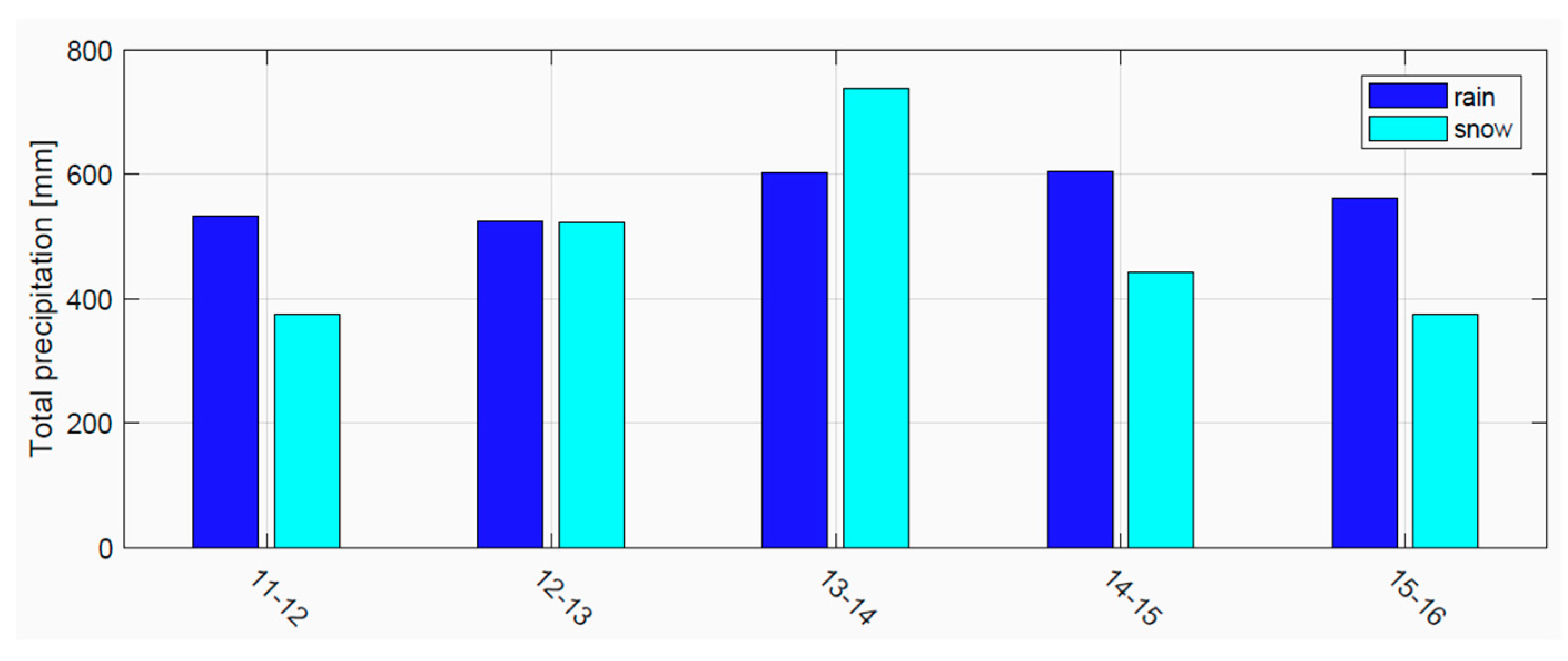
2.1. Study area and dataset
2.2. MODIS Snow Detection Algorithm
2.3. Snowpack Model: TOPMELT
2.4. Snow Compaction Model
2.5. Spatial Representation of the Snowpack
2.6. Model Parameter Conditioning
3. Results and Discussion
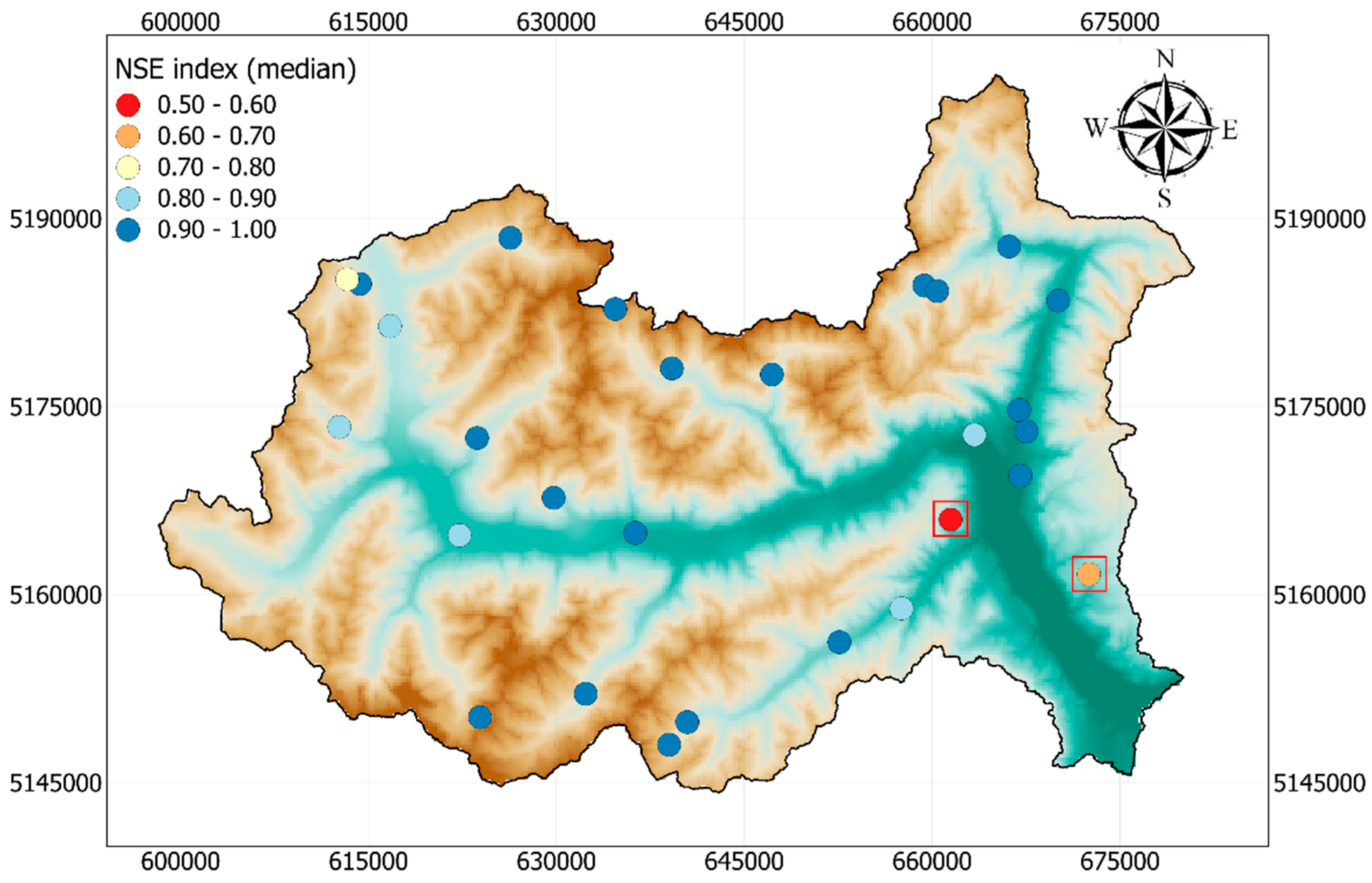
3.1. Snowpack Model Validation
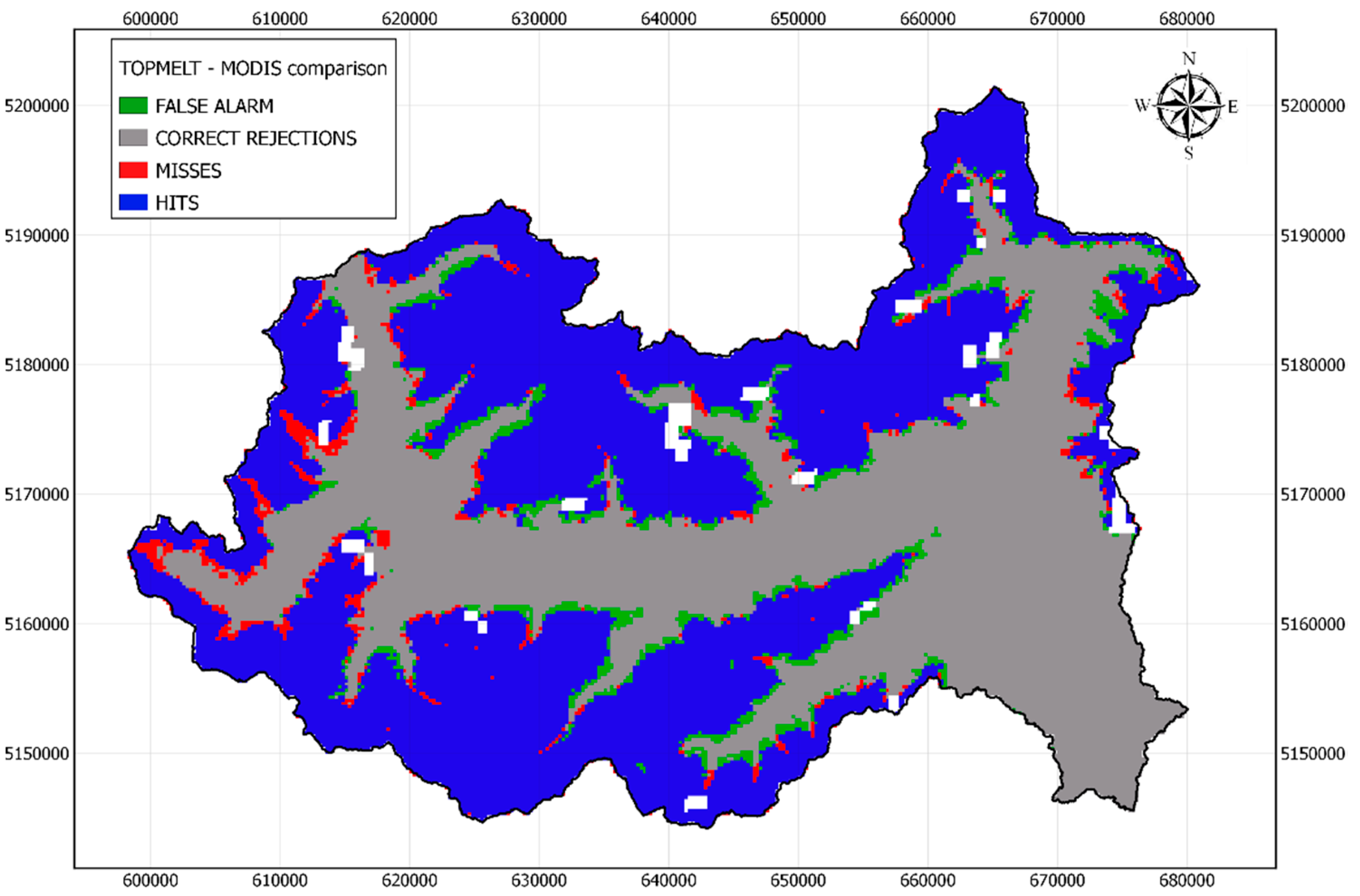
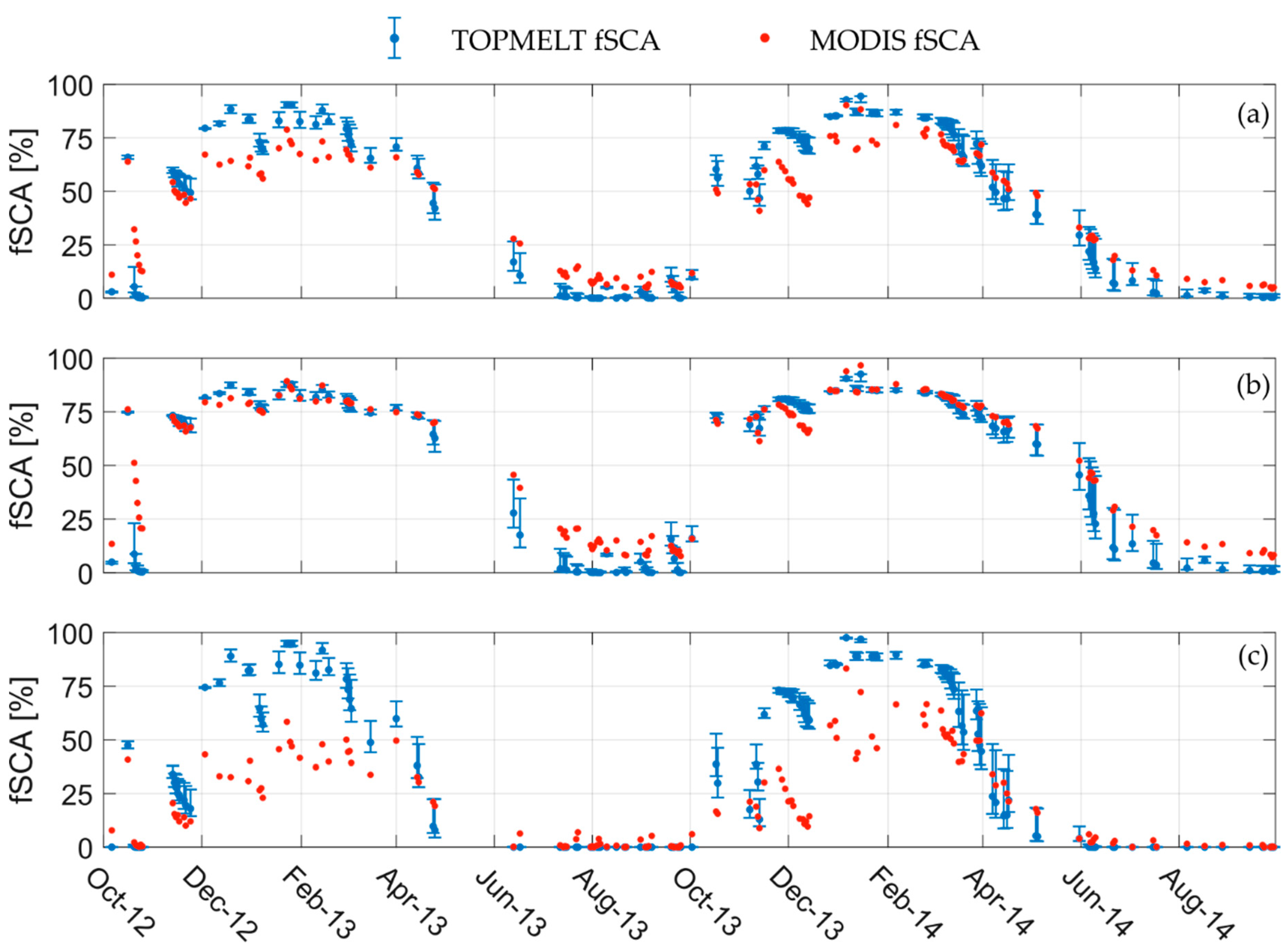
3.2. Satellite-derived and Simulated Snow Cover Area Comparison
3.3. A criterion to Identify Critical Areas for Satellite-Derived Snow Detection
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sturm, M.; Goldstein, M.A.; Parr, C. Water and life from snow: A trillion dollar science question: Snow and life. Water Resour. Res. 2017, 53, 3534–3544. [Google Scholar] [CrossRef]
- Clark, M.P.; Hendrikx, J.; Slater, A.G.; Kavetski, D.; Anderson, B.; Cullen, N.J.; Kerr, T.; Örn Hreinsson, E.; Woods, R.A. Representing spatial variability of snow water equivalent in hydrologic and land-surface models: A review: Representing Spatial Variability of Swe in Models. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Formetta, G.; Kampf, S.K.; David, O.; Rigon, R. Snow water equivalent modeling components in NewAge-JGrass. Geosci. Model Dev. 2014, 7, 725–736. [Google Scholar] [CrossRef]
- Zeinivand, H.; De Smedt, F. Hydrological Modeling of Snow Accumulation and Melting on River Basin Scale. Water Resour. Manag. 2009, 23, 2271–2287. [Google Scholar] [CrossRef]
- Essery, R.; Morin, S.; Lejeune, Y.; B Ménard, C. A comparison of 1701 snow models using observations from an alpine site. Adv. Water Resour. 2013, 55, 131–148. [Google Scholar] [CrossRef]
- Magnusson, J.; Wever, N.; Essery, R.; Helbig, N.; Winstral, A.; Jonas, T. Evaluating snow models with varying process representations for hydrological applications. Water Resour. Res. 2015, 51, 2707–2723. [Google Scholar] [CrossRef]
- Shakoor, A.; Burri, A.; Bavay, M.; Ejaz, N.; Ghumman, A.R.; Comola, F.; Lehning, M. Hydrological response of two high altitude Swiss catchments to energy balance and temperature index melt schemes. Polar Sci. 2018, 17, 1–12. [Google Scholar] [CrossRef]
- Carenzo, M.; Pellicciotti, F.; Rimkus, S.; Burlando, P. Assessing the transferability and robustness of an enhanced temperature-index glacier-melt model. J. Glaciol. 2009, 55, 258–274. [Google Scholar] [CrossRef]
- Heynen, M.; Pellicciotti, F.; Carenzo, M. Parameter sensitivity of a distributed enhanced temperature-index melt model. Ann. Glaciol. 2013, 54, 311–321. [Google Scholar] [CrossRef]
- Thirel, G.; Salamon, P.; Burek, P.; Kalas, M. Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter. Remote Sens. 2013, 5, 5825–5850. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating remotely sensed snow observations into a macroscale hydrology model. Adv. Water Resour. 2006, 29, 872–886. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. The value of MODIS snow cover data in validating and calibrating conceptual hydrologic models. J. Hydrol. 2008, 358, 240–258. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images–potential for snow cover mapping: Spatio-temporal combination of modis images. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Parajka, J.; Holko, L.; Kostka, Z.; Blöschl, G. MODIS snow cover mapping accuracy in a small mountain catchment–comparison between open and forest sites. Hydrol. Earth Syst. Sci. 2012, 16, 2365–2377. [Google Scholar] [CrossRef]
- Gascoin, S.; Hagolle, O.; Huc, M.; Jarlan, L.; Dejoux, J.-F.; Szczypta, C.; Marti, R.; Sánchez, R. A snow cover climatology for the Pyrenees from MODIS snow products. Hydrol. Earth Syst. Sci. 2015, 19, 2337–2351. [Google Scholar] [CrossRef]
- Notarnicola, C.; Duguay, M.; Moelg, N.; Schellenberger, T.; Tetzlaff, A.; Monsorno, R.; Costa, A.; Steurer, C.; Zebisch, M. Snow Cover Maps from MODIS Images at 250 m Resolution, Part 1: Algorithm Description. Remote Sens. 2013, 5, 110–126. [Google Scholar] [CrossRef]
- Engel, M.; Notarnicola, C.; Endrizzi, S.; Bertoldi, G. Snow model sensitivity analysis to understand spatial and temporal snow dynamics in a high-elevation catchment. Hydrol. Process. 2017, 31, 4151–4168. [Google Scholar] [CrossRef]
- Parajka, J.; Bloschl, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci. 2006, 3, 1569–1601. [Google Scholar] [CrossRef]
- Klein, A. Validation of daily MODIS snow cover maps of the Upper Rio Grande River Basin for the 2000–2001 snow year. Remote Sens. Environ. 2003, 86, 162–176. [Google Scholar] [CrossRef]
- Zaramella, M.; Borga, M.; Zoccatelli, D.; Carturan, L. TOPMELT 1.0: A topography-based distribution function approach to snowmelt simulation for hydrological modelling at basin scale. Geosci. Model Dev. Discuss. 2019, 12, 5251–5265. [Google Scholar] [CrossRef]
- Rittger, K.; Painter, T.H.; Dozier, J. Assessment of methods for mapping snow cover from MODIS. Adv. Water Resour. 2013, 51, 367–380. [Google Scholar] [CrossRef]
- Liu, J.; Woodcock, C.E.; Melloh, R.A.; Davis, R.E.; McKenzie, C.; Painter, T.H. Modeling the View Angle Dependence of Gap Fractions in Forest Canopies: Implications for Mapping Fractional Snow Cover Using Optical Remote Sensing. J. Hydrometeorol. 2008, 9, 1005–1019. [Google Scholar] [CrossRef]
- Notarnicola, C.; Duguay, M.; Moelg, N.; Schellenberger, T.; Tetzlaff, A.; Monsorno, R.; Costa, A.; Steurer, C.; Zebisch, M. Snow Cover Maps from MODIS Images at 250 m Resolution, Part 2: Validation. Remote Sens. 2013, 5, 1568–1587. [Google Scholar] [CrossRef]
- Simic, A.; Fernandes, R.; Brown, R.; Romanov, P.; Park, W. Validation of VEGETATION, MODIS, and GOES+ SSM/I snow-cover products over Canada based on surface snow depth observations. Hydrol. Process. 2004, 18, 1089–1104. [Google Scholar] [CrossRef]
- Thirel, G.; Notarnicola, C.; Kalas, M.; Zebisch, M.; Schellenberger, T.; Tetzlaff, A.; Duguay, M.; Mölg, N.; Burek, P.; de Roo, A. Assessing the quality of a real-time Snow Cover Area product for hydrological applications. Remote Sens. Environ. 2012, 127, 271–287. [Google Scholar] [CrossRef]
- Finger, D.; Vis, M.; Huss, M.; Seibert, J. The value of multiple data set calibration versus model complexity for improving the performance of hydrological models in mountain catchments. Water Resour. Res. 2015, 51, 1939–1958. [Google Scholar] [CrossRef]
- Brock, B.W.; Willis, I.C.; Sharp, M.J. Measurement and parameterization of albedo variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2000, 46, 675–688. [Google Scholar] [CrossRef]
- Cazorzi, F.; Dalla Fontana, G. Snowmelt modelling by combining air temperature and a distributed radiation index. J. Hydrol. 1996, 181, 169–187. [Google Scholar] [CrossRef]
- Vionnet, V.; Brun, E.; Morin, S.; Boone, A.; Faroux, S.; Le Moigne, P.; Martin, E.; Willemet, J.-M. The detailed snowpack scheme Crocus and its implementation in SURFEX v7.2. Geosci. Model Dev. 2012, 5, 773–791. [Google Scholar] [CrossRef]
- Saloranta, T.M. Operational snow mapping with simplified data assimilation using the seNorge snow model. J. Hydrol. 2016, 538, 314–325. [Google Scholar] [CrossRef]
- Dawson, N.; Broxton, P.; Zeng, X. Evaluation of Remotely Sensed Snow Water Equivalent and Snow Cover Extent over the Contiguous United States. J. Hydrometeor. 2018, 19, 1777–1791. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Carturan, L.; Dalla Fontana, G.; Borga, M. Estimation of winter precipitation in a high-altitude catchment of the Eastern Italian Alps: Validation by means of glacier mass balance observations. Geogr. Fis. Din. Quat. 2012, 35, 37–48. [Google Scholar]
- Teweldebrhan, A.T.; Burkhart, J.F.; Schuler, T.V. Parameter uncertainty analysis for an operational hydrological model using residual-based and limits of acceptability approaches. Hydrol. Earth Syst. Sci. 2018, 22, 5021–5039. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.; Matott, L.S. Uncertainty-based multi-criteria calibration of rainfall-runoff models: A comparative study. Stoch. Environ. Res. Risk Assess. 2014, 28, 1493–1510. [Google Scholar] [CrossRef]
- Franks, S.W.; Gineste, P.; Beven, K.J.; Merot, P. On constraining the predictions of a distributed model: The incorporation of fuzzy estimates of saturated areas into the calibration process. Water Resour. Res. 1998, 34, 787–797. [Google Scholar] [CrossRef]
- Tuo, Y.; Marcolini, G.; Disse, M.; Chiogna, G. Calibration of snow parameters in SWAT: Comparison of three approaches in the Upper Adige River basin (Italy). Hydrol. Sci. J. 2018, 63, 657–678. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Turcotte, R. Improvement of springtime streamflow simulations in a boreal environment by incorporating snow-covered area derived from remote sensing data. J. Hydrol. 2010, 390, 35–44. [Google Scholar] [CrossRef]
- Lv, Z.; Pomeroy, J.W. Detecting intercepted snow on mountain needleleaf forest canopies using satellite remote sensing. Remote Sens. Environ. 2019, 231, 111222. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, S.; Song, G. Review on the influence of forest canopy on the process of snowfall interception. Shuikexue Jinzhan/Adv. Water Sci. 2017, 28, 462–471. [Google Scholar]
- Gascoin, S.; Grizonnet, M.; Bouchet, M.; Salgues, G.; Hagolle, O. Theia Snow collection: High-resolution operational snow cover maps from Sentinel-2 and Landsat-8 data. Earth Syst. Sci. Data 2019, 11, 493–514. [Google Scholar] [CrossRef]
- Strasser, U.; Warscher, M.; Liston, G.E. Modeling Snow–Canopy Processes on an Idealized Mountain. J. Hydrometeorol. 2011, 12, 663–677. [Google Scholar] [CrossRef]
- Pu, Z.; Xu, L.; Salomonson, V.V. MODIS/Terra observed seasonal variations of snow cover over the Tibetan Plateau. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Hall, D.; Riggs, G. Algorithm Theoretical Basis Document (ATBD) for the MODIS Snow and Sea Ice-Mapping Algorithms. Available online: https://eospso.gsfc.nasa.gov/sites/default/files/atbd/atbd_mod10.pdf (accessed on 4 April 2020).
- Mair, E.; Leitinger, G.; Della Chiesa, S.; Niedrist, G.; Tappeiner, U.; Bertoldi, G. A simple method to combine snow height and meteorological observations to estimate winter precipitation at sub-daily resolution. Hydrol. Sci. J. 2016, 61, 2050–2060. [Google Scholar] [CrossRef][Green Version]
- López-Moreno, J.I.; García-Ruiz, J.M. Influence of snow accumulation and snowmelt on streamflow in the central Spanish Pyrenees/Influence de l’accumulation et de la fonte de la neige sur les écoulements dans les Pyrénées centrales espagnoles. Hydrol. Sci. J. 2004, 49, 802. [Google Scholar] [CrossRef]
- Jenicek, M.; Seibert, J.; Zappa, M.; Staudinger, M.; Jonas, T. Importance of maximum snow accumulation for summer low flows in humid catchments. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 7023–7056. [Google Scholar] [CrossRef]
- Duethmann, D.; Peters, J.; Blume, T.; Vorogushyn, S.; Güntner, A. The value of satellite-derived snow cover images for calibrating a hydrological model in snow-dominated catchments in Central Asia. Water Resour. Res. 2014, 50, 2002–2021. [Google Scholar] [CrossRef]
- Tuo, Y.; Marcolini, G.; Disse, M.; Chiogna, G. A multi-objective approach to improve SWAT model calibration in alpine catchments. J. Hydrol. 2018, 559, 347–360. [Google Scholar] [CrossRef]
- Arslan, N.A.; Tanis, M.C.; Metsämäki, S.; Aurela, M.; Böttcher, K.; Linkosalmi, M.; Peltoniemi, M. Automated Webcam Monitoring of Fractional Snow Cover in Northern Boreal Conditions. Geosciences 2017, 7. [Google Scholar] [CrossRef]
- Salvatori, R.; Plini, P.; Giusto, M.; Valt, M.; Salzano, R.; Montagnoli, M.; Cagnati, A.; Crepaz, G.; Sigismondi, D. Snow cover monitoring with images from digital camera systems. Ital. J. Remote Sens. 2011, 43. [Google Scholar] [CrossRef]

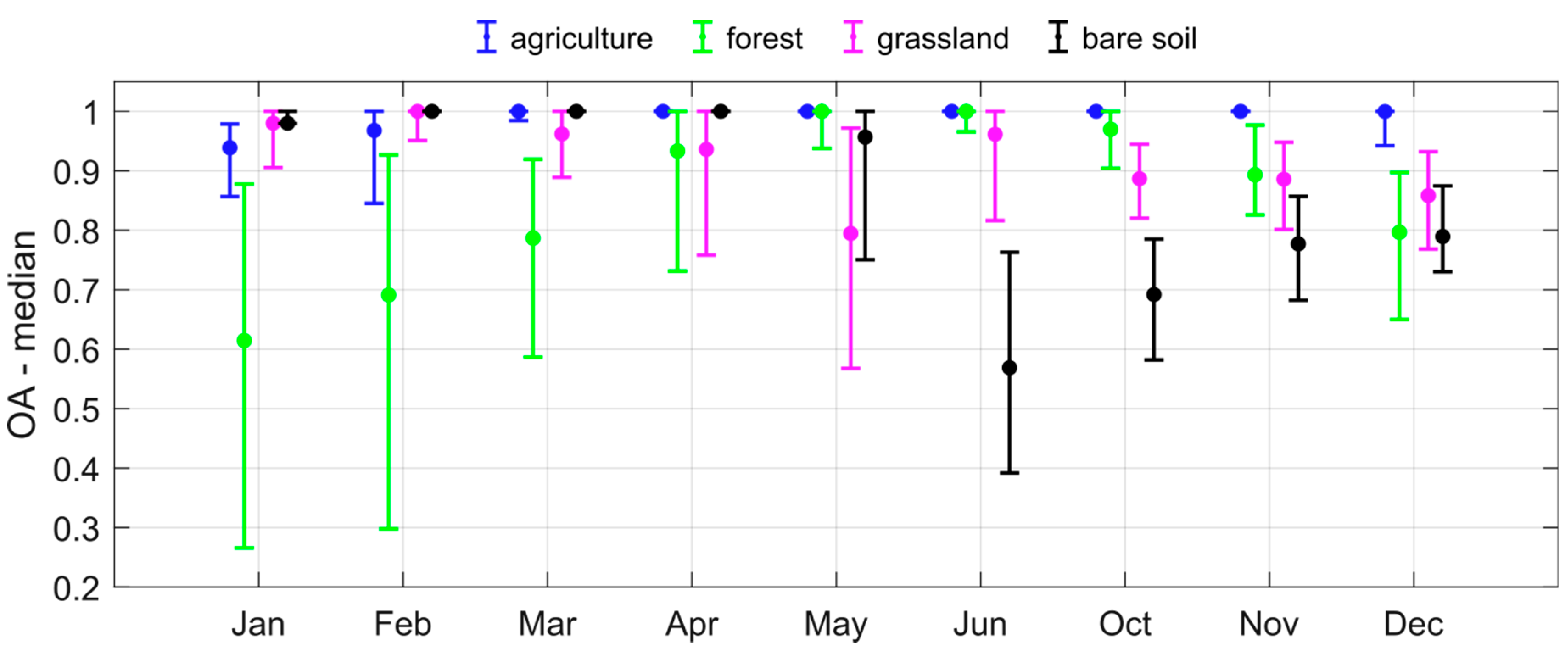
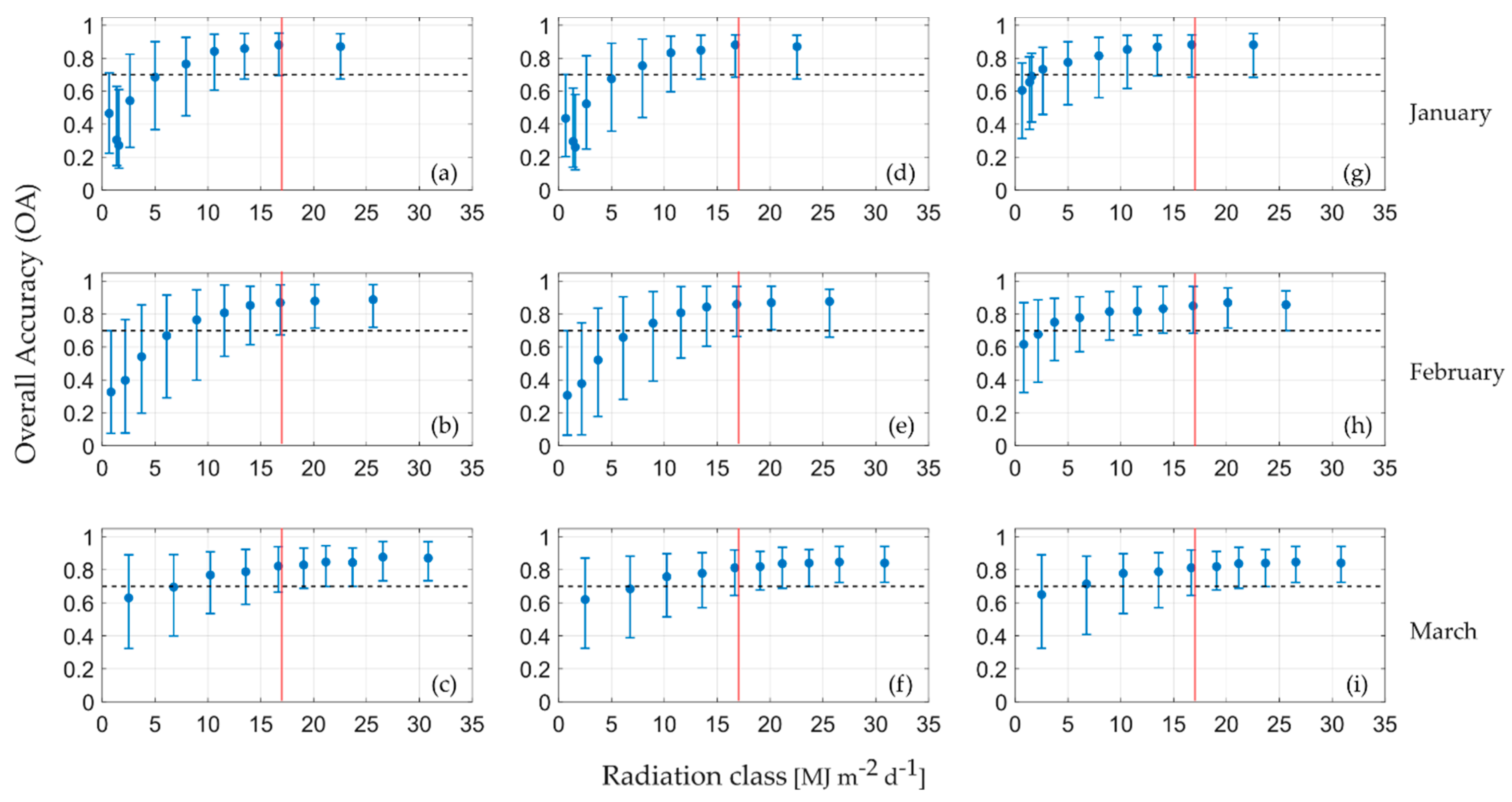
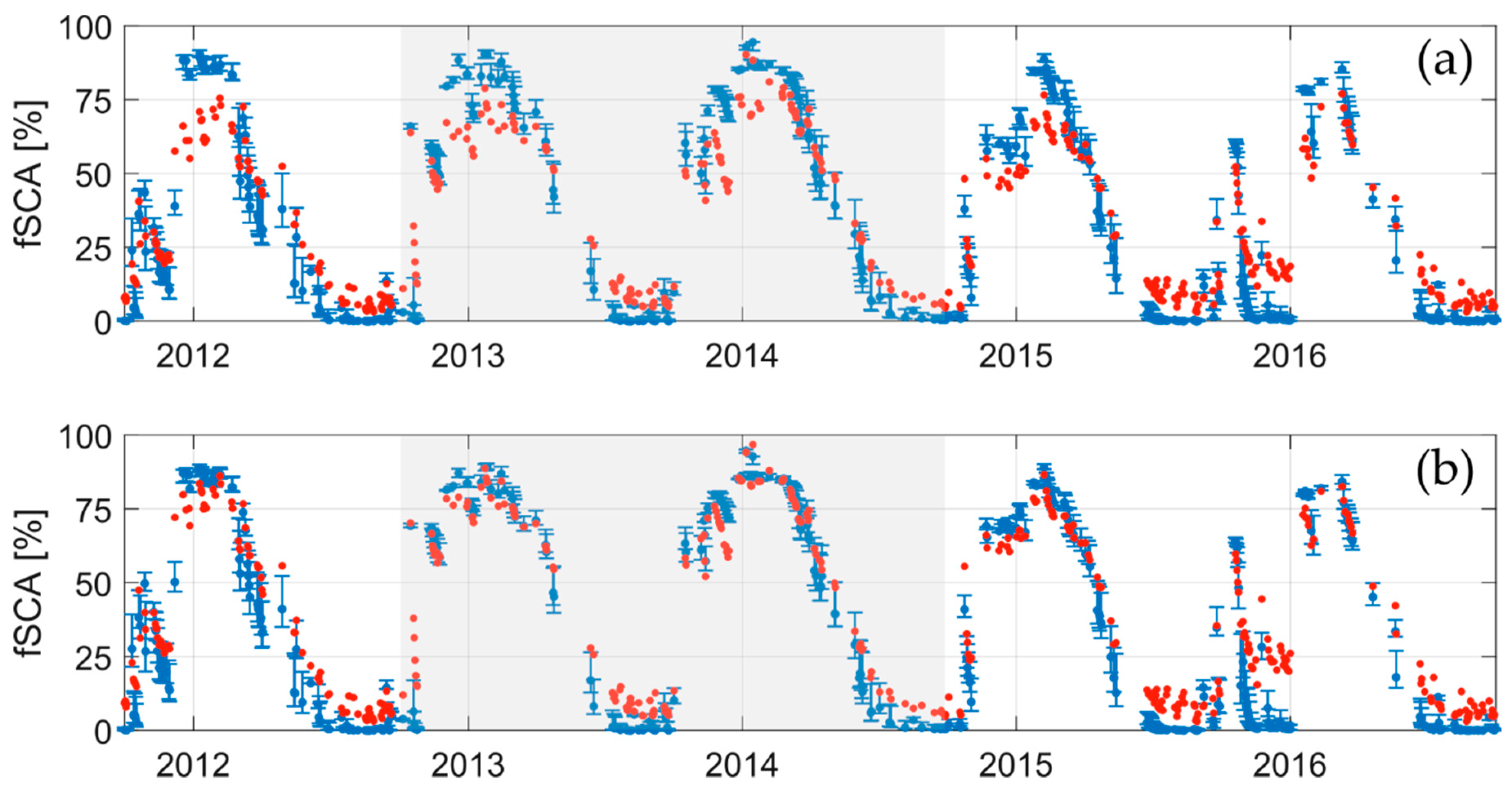
| Urban | Agriculture | Forest | Grassland | Bare Soil and Rock Up-Crops | Water Bodies | |
|---|---|---|---|---|---|---|
| Area [%] | 1.34 | 9.08 | 32.17 | 39.48 | 17.52 | 0.41 |
| Mean elevation [m] | 532 | 684 | 1514 | 2130 | 2822 | 1503 |
| TOPMELT Parameter | Units | Min. Value | Max. Value |
|---|---|---|---|
| Precipitation Correction Factor (PCF) | [-] | 1 | 1.4 |
| Combined Melt Factor (CMF) | [mm m2 °C−1 MJ−1 h−1] | 0.010 | 0.020 |
| Altitudinal gradient (G) | [% mm km−1] | 0.15 | 0.45 |
| Fresh snow albedo (albs) | [-] | 0.7 | 0.9 |
| Period | Regime | Overall Catchment | Forest Free Catchment | Forested Areas |
|---|---|---|---|---|
| April−June | early snowmelt | 7.9 | 9.4 | 6.3 |
| July−September | late snowmelt | 8.2 | 12.2 | 2.0 |
| November−March | snow accumulation | 12.0 | 2.9 | 30.2 |
| Period | Regime | Overall Catchment | Catchment Fraction Matching the Proposed Criterion |
|---|---|---|---|
| April−June | early snowmelt | 9.8 | 10.5 |
| July−September | late snowmelt | 7.3 | 7.6 |
| November−March | snow accumulation | 12.4 | 7.5 |
| Month | Forested Area (%) with Clear-Sky Solar Radiation > 17 MJ m−2 d−1 |
|---|---|
| October | 52 |
| November | 26 |
| December | 13 |
| January | 11 |
| February | 19 |
| March | 41 |
| April | 71 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Marco, N.; Righetti, M.; Avesani, D.; Zaramella, M.; Notarnicola, C.; Borga, M. Comparison of MODIS and Model-Derived Snow-Covered Areas: Impact of Land Use and Solar Illumination Conditions. Geosciences 2020, 10, 134. https://doi.org/10.3390/geosciences10040134
Di Marco N, Righetti M, Avesani D, Zaramella M, Notarnicola C, Borga M. Comparison of MODIS and Model-Derived Snow-Covered Areas: Impact of Land Use and Solar Illumination Conditions. Geosciences. 2020; 10(4):134. https://doi.org/10.3390/geosciences10040134
Chicago/Turabian StyleDi Marco, Nicola, Maurizio Righetti, Diego Avesani, Mattia Zaramella, Claudia Notarnicola, and Marco Borga. 2020. "Comparison of MODIS and Model-Derived Snow-Covered Areas: Impact of Land Use and Solar Illumination Conditions" Geosciences 10, no. 4: 134. https://doi.org/10.3390/geosciences10040134
APA StyleDi Marco, N., Righetti, M., Avesani, D., Zaramella, M., Notarnicola, C., & Borga, M. (2020). Comparison of MODIS and Model-Derived Snow-Covered Areas: Impact of Land Use and Solar Illumination Conditions. Geosciences, 10(4), 134. https://doi.org/10.3390/geosciences10040134





