A Review of Russian Snow Avalanche Models—From Analytical Solutions to Novel 3D Models

Abstract

The article is a review of mathematical models of snow avalanches that have been proposed since the middle of the 20th century and are still in use. The main attention is paid to the work of researchers from the Soviet Union and Russia, since many of their works were published only in Russian and are not widely available. Mathematical models of various levels of complexity for avalanches of various types—from dense to powder-snow avalanches—are discussed. Analytical solutions including formulas for the avalanche front speed are described. The results of simulations of the movement of avalanches are given that were used to create avalanche hazard maps. The last part of the article is devoted to constructing models of a new type, in which avalanches are considered as laminar or turbulent flows of non-Newtonian fluids, using the full (not depth-averaged) equations of continuum mechanics. The results of a numerical study of the effect of non-Newtonian rheology and mass entrainment on the avalanche dynamics are presented.

1. Introduction

Mathematical modeling is an important tool for solving engineering problems related to the protection of people and structures in mountainous areas against snow avalanches. The modeling approach is used more and more widely. This is facilitated by the development of computer technology. The first, very simple mathematical models for avalanches were proposed many years ago. Nevertheless, the creation and development of new models, as well as new computer codes, continues.

In this paper, we provide an overview of the mathematical models of snow avalanches that were developed from the middle of the 20th century to the present time. However, we will not consider all models developed around the world. Many articles have been published that provide a more or less complete overview of such model, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13]. We focus on the work of researchers from the Soviet Union and Russia, since many of their works have been published only in Russian and are not known in the scientific literature. Moreover, we will not describe the models in detail. Our goal is to discuss the features of models, as well as the statements of problems and solutions that are fundamentally new compared to those developed simultaneously or later by other research communities. We believe that some of these ideas and results are still relevant, and they should be considered in the models that are currently in use. Examples are: (i) the importance of the flow stability conditions (Section 3); (ii) the introduction of an upper limit for the value of bottom friction (Section 2.2.5); (iii) using simplified equations to describe motions with different scales (Section 3); (iv) importance of redistribution of mass in the flow during movement (Section 3), etc.

In the former Soviet Union, the area of avalanche hazardous territory was about 3,500,000 ${\mathrm{km}}^2$. In Russia, about 3,000,000 ${\mathrm{km}}^2$ of the country are subject to avalanches [14,15]. Therefore, the problem of protecting roads, settlements, mines and other objects from avalanches was very urgent. In 1935, the Tbilisi Research Institute of Structures in Georgia (TBNIIS) proposed a theory in which an avalanche was considered as a mass point moving along an inclined plane under gravity, Coulomb friction and environmental resistance proportional to the first degree of velocity [16,17]. The TBNIIS formula was used quite widely in the former Soviet Union and, in particular, was included in the “Guide on snow-measuring operations in mountains” (1958). A significant contribution to the development of mass point models was made by S.M. Kozik, whose book [18] was published in 1962. The author reviews, improves and generalizes the mass-point mathematical models for avalanches. It is worth noting that, while explaining and estimating the terms related to friction, environmental resistance and mass entrainment in the equations, S.M. Kozik speaks of the avalanche as of a stream. Dense avalanches on wide slopes and in channels, as well as powder avalanches, are considered. Environmental resistance in [18] is proportional to the square of the velocity. Practical methods for calculating the velocity and run-out distances are described; auxiliary tables and computational charts are given (recall that the book was written before the computer era).

Development, generalization and use of mass-point or block models for avalanches continue to this day (see, e.g., [19]). After calibration, these models can provide approximate estimates for the velocity and run-out distance of avalanches. In this paper we do not discuss mass-point models in order to save space for the models that explicitly take into account the internal structure of avalanche flows. Two groups of such models will be considered in Section 2, Section 3, Section 4, Section 5, Section 6 and Section 7, respectively.

Section 2, Section 3, Section 4 and Section 5 are devoted mainly to the so-called hydraulic models. An avalanche is treated either as a one-layer or a multilayered flow in these models. The main parameters studied are the layer depth and the velocity (and the density, in multilayered flows) averaged over the layer depth or over the flow cross-section. The models proposed by researchers in the former Soviet Union and Russia are described. Examples of analytical solutions and numerical simulations are given in Section 3 and Section 5.

In Section 6 and Section 7, we discuss the problems that arise when constructing new, three-dimensional, models for avalanches. Such models are based on the full (i.e., not averaged over the flow depth) equations of continuum mechanics. They are to describe the structure of the flow not only along its body, as in hydraulic models, but also in the direction perpendicular to the slope. Models for dense laminar and turbulent flows on long homogeneous slopes are suggested. Results of the numerical study of the influence of the flow rheological properties and entrainment of the underlying material in laminar and turbulent flows are presented.

2. Dense Avalanches Hydraulic Models

In this section, we consider models for dynamics of dense avalanches. The term “dense” here means that the density of snow in an avalanche is much higher than the density of the surrounding air, so that the mixing with air does not occur. Moreover, as a rule, we will assume that the density of snow in an avalanche differs little from the density in the layer of the static snow that participated in the avalanche formation.

Commonly, the depth of dense avalanche flows (a few meters) is substantially less than their longitudinal size (hundreds or even thousands of meters). It is reasonable for such flows to use equations averaged over the depth (or over the cross-section) of the flow. This approach is adopted in the shallow water theory and in hydraulics. Here and further, we refer to such models as hydraulic models.

It is widely recognized that A. Voellmy was the first author who suggested the equations to describe an avalanche as a fluid flow using a hydraulic model [20]. However, we should note that A. Voellmy did not present a complete system of differential equations for calculation of the depth and the depth-averaged velocity: he did not consider the differential continuity equation. Therefore, it is impossible to calculate the variable flow depth by his theory. Moreover, A. Voellmy assumed the depth and the depth-averaged velocity to be the same at all points of the avalanche, which means that in fact the avalanche moves as a solid block. The first paper, which contained a complete system of partial differential equations to describe the motion of dense avalanches in the hydraulic approximation, was the paper published in 1967 by S. S. Grigoryan, M. E. Eglit and Yu. L. Yakimov [21].

2.1. The MSU-1D Model

The first hydraulic model for an avalanche was formulated under the assumption that the avalanche is a 1D turbulent flow on a wide slope [21,22,23,24,25]. Here and further we refer to this model as MSU-1D (after Moscow State University) model. Below, we shortly describe this model and we compare it to the Voellmy model [20] as well as to models used in hydraulics of water flows.

The continuity and momentum equations are

$${\displaystyle \frac{\partial h}{\partial t}+\frac{\partial hv}{\partial x}=0,}$$

(1)

$${\displaystyle \frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}=-\frac{1}{2h}\frac{\partial }{\partial x}\left(h^{2}gcos\psi \right)+gsin\psi -\frac{\tau }{\rho h}.}$$

(2)

Here, t and x are the time and the coordinate along the slope; $v(x,t)$ and $h(x,t)$ are the depth-averaged velocity and the depth (thickness) of the flow measured along the normal to the slope; $\psi \left(x\right)$ is the slope angle; g is the gravity acceleration; $\tau$ is the friction at the bottom per unit area, $\rho$ is the density of the avalanche snow (Figure 1). The friction $\tau$ is a function of h and v consisting of two parts: the so-called dry friction ${\tau }_d$ which does not vanish at $v=0$ and the hydraulic friction ${\tau }_h$. The Coulomb law for ${\tau }_d$ and dependence on the velocity squared for ${\tau }_h$ are assumed in [21,22,23,24,25]:

$$\tau ={\tau }_d+{\tau }_h,{\tau }_d=\mu \rho hgcos\psi \frac{\mathbf{v}}{v},{\tau }_h=k\rho v\mathbf{v}.$$

(3)

In these relations, $\mu$ is the coefficient of dry friction and k is the coefficient of hydraulic turbulent friction.

Significant difference between the system (1)–(3) and the equations of standard hydraulics is due to the following facts. First, the meaning of h is different: it is the depth along normal to the slope, while h is usually the vertical depth in hydraulics. This difference is essential since avalanches mainly move along the bottom with a large inclination angle. Second, the friction at the bottom contains the term that does not vanish at zero speed: avalanches, unlike water flows, can stop on an inclined surface. Third, an avalanche has a leading edge, and the medium in front of it (snowpack) differs from the medium in the avalanche; the latter behaves like a fluid, while the snowpack is considered as a solid in this theory.

Equations (1) and (2) do not contain the terms related to the snow entrainment by the avalanche. However, it is known that entrainment significantly affects the flow dynamics. The following mechanism of entrainment (the so-called “frontal entrainment”) is considered in [21,22,23,24,25]. It is assumed that the entrainment occurs at the avalanche leading edge. The avalanche operates like a bulldozer pushing the snow ahead of it, breaking the snow structure and involving it in the motion. Thus, in [21,22,23,24,25] the entrainment is accounted for by conditions at the leading edge ($x=X_f\left(t\right)$). These conditions follow from the the mass and momentum conservation laws

$$\begin{array}{c}\overline{h}(w-\overline{v})=h_{0}w,\\ {\displaystyle h_{0}w\overline{v}=\frac{{\overline{h}}^{2}gcos\psi }{2}-\frac{{\sigma }_{*}}{\rho }{h}_0\equiv P\mathrm{at}P\ge 0.}\end{array}$$

(4)

Here, w is the speed of the avalanche leading edge, $\overline{h}$ and $\overline{v}$ are the depth and the flow velocity on the front; ${\sigma }_{*}$ is the compressional strength of the snowpack layer that can be entrained by the avalanche, $h_0$ is its thickness; $\rho$ is the density of snow in the avalanche (which is assumed equal to the density in the snow cover).

In [26] an avalanche behavior in the run-out zone was considered. The avalanche decelerates in this zone. Decrease in the velocity leads to the decrease in the height of the avalanche front, i.e., P decreases. When $P=0$ the front stops, according to (4). However, it does not mean stopping the entire avalanche since the rear parts continue to move. The snow piles at the front, so that P increases and the motion continues. If for some reason $P<0$, i.e., the force exerted by an avalanche on a layer of snow located in front of it becomes insufficient to disrupt it, then, instead of the relationships (4), one of the following conditions can be used in calculations

$$a)w=\overline{v}=0;b)h_0=\frac{\rho {\overline{h}}^{2}gcos\psi }{2{\sigma }_{*}};c)w=\overline{v},\overline{h}=h_0=0.$$

(5)

They mean, respectively, (a) stopping of the avalanche; (b) stopping and further movement with entrainment of a thinner layer of snow; (c) motion over the snow cover without entrainment. The situation with $P<0$ can arise in a run-out zone. A study of the structure of the avalanche deposits shows that at the end of the path the avalanche ceases to entrain snow, that is, the third condition in (5) is fulfilled. Calculations show that any of the conditions (5) give an almost equal run-out distance [26].

Relationships (4) or (5) are the boundary conditions for Equations (1) and (2) at the avalanche leading edge ($x=X_f$). At the rear edge ($x=0$) the conditions $h=0,v=0$ are assumed. The initial conditions set the velocity and depth in the area of the initially destroyed snow, which turned into an avalanche: $v=v_0\left(x\right),h=h_0\left(x\right)$ at $t=0,0\le x\le l_0$ where $l_0$ is the length of the region. In reality, the functions $v_0\left(x\right)$ and $h_0\left(x\right)$ are not known. Calculations show that when an avalanche moves with mass entrainment down a long slope, the influence of the initial data becomes insignificant some time after the start. When moving without entrainment, the initial mass of snow that is set in motion is important, while the effect of the initial velocity and thickness distributions decreases.

So, if the frontal entrainment takes place, the leading edge of the avalanche is a kind of hydraulic jump: on one side of it $h=h_0,v=0$, and on the other side, $h=\overline{h},v=\overline{v}$. Note that this jump differs from a usual hydraulic jump because the media at different sides of the jump are not the same—ahead of the jump it is a solid and behind it behaves like a fluid. Therefore, the leading edge can be considered as a phase transition boundary.

To conclude the description of the MSU-1D model, let us compare it again to the Voellmy model [20]. The formulas for friction at the bottom are common to both models, though different notations are used for hydraulic friction coefficient: it is denoted by k in the MSU-1D model and by $\mathrm{g}/\xi$ in the Voellmy formula. The crucial difference is the following. The model MSU-1D contains two coupled partial differential equations, which allow one to calculate the velocity and thickness variation in time and their variation and mass distribution along the body of the avalanche as well. In contrast, the Voellmy model contains only one ordinary differential equation to calculate the velocity variation in time under the assumptions that the velocity is the same in all points of the avalanche and the thickness is constant and known. Other important issues are an explicit introduction of flow leading edge and modeling mass entrainment.

The results of analytical and numerical investigation of the MSU-1D model as well as its further development and use for simulation natural avalanches are presented in Section 2.2 and Section 3, Section 4 and Section 5.

2.2. Further Development of the MSU-1D Model

2.2.1. Two-Dimensional Motion

The following equations for two-dimensional motion of an avalanche were formulated in [27,28,29,30]:

$${\displaystyle \frac{\partial h}{\partial t}+\mathrm{d}ivh\mathbf{v}=\mathbf{0},}$$

(6)

$${\displaystyle \frac{d\mathbf{v}}{dt}=-\frac{g}{2h}\mathrm{g}rad(h^{2}cos\psi )+gsin\psi \mathbf{e}-F(v,h,x,y)\mathbf{v}.}$$

(7)

Here, $\mathbf{v}$ is the depth-averaged velocity vector, $\psi$ is the local angle between the horizontal plane and the plane tangent to the slope (the bed surface), $\mathbf{e}$ is the vector directed along the line of maximum slope in the tangent plane, $F(v,h,x,y)\mathbf{v}$ is the friction force per unit mass, t is time, x, y are coordinates at the bed surface; $\mathrm{d}iv$ and $\mathrm{g}rad$ are two-dimensional operators at the bed surface. An example of an expression for the friction force reads (compare to (3))

$${\displaystyle F(v,h,x,y)\mathbf{v}=\mu gcos\psi \frac{\mathbf{v}}{\left|v\right|}+k\frac{\left|v\right|\mathbf{v}}{h}.}$$

(8)

If the frontal entrainment mechanism is assumed, then the conditions at the avalanche front are (compare to (4))

$$\begin{array}{c}h(w_n-v_n)=h_0{w}_n,\\ {\displaystyle \rho h_0{w}_n\mathbf{v}=\frac{1}{2}\rho g{h}^{2}cos\psi \mathbf{n}-h_0{\sigma }^{*}\mathbf{n}.}\end{array}$$

(9)

Here, $\mathbf{n}$ is the unit vector directed along the normal to the avalanche leading edge, $w_n$ is the normal component of the local propagation velocity of the leading edge, $v_n$ is the normal component of the snow velocity at the leading edge, $\rho$ is the avalanche snow density and ${\sigma }^{*}$ is the compression strength for the snow layer to be entrained.

Equations (6)–(9) allow to model the lateral spreading of an avalanche.

The two-dimensional movement of an avalanche down a slope with smoothly varying properties, taking into account the complex shape of the fracture line that could develop in time, was studied analytically in [27]. Several variants of the fracture line and the avalanche behavior were considered. Simulations of real avalanches in Caucasus and Khibiny mountains were performed using the two-dimensional model [28,30,31,32].

2.2.2. Channeled Avalanches

Paths of the real avalanches often include channels. The equations obtained by averaging over the flow cross-section were written. Channels with different variable shapes of cross-sections were considered in [29,30,33,34,35,36]. The influence of the chute width variation on the velocity and depth of the avalanche is shown in Figure 2. The equations contain terms related to friction against the side walls. The wall friction increases with increasing the depth of the flow, in contrast to the situation with friction against the bottom. Friction on the side walls affects the velocity and thickness of the avalanche. It can also lead to qualitatively new shapes of the flow, in particular, to the existence of zones of sharp decrease in the thickness of the flow [29,30,34]. Simulations of real channeled avalanches were performed [31,32,33,37,38,39,40]. Analytical solutions were obtained for motion in chutes with constant inclination angle and constant shape and dimensions of their cross-sections. In simulations of real avalanches [31,32,33,37,38,39,40] the shape of the channel cross-sections was approximated by a trapezoid with a variable width of the base and variable angles of inclination of the sides.

2.2.3. Influence of the Slope Surface Curvature

Equations for motion at a curvilinear slope were derived and used in [26,41]. For 1D motion of a dense avalanche with frontal entrainment, these equations are (compare to Equations (1) and (2))

$$\begin{array}{c}{\displaystyle \frac{\partial h}{\partial t}+\left(1+\frac{h}{R}\right)\frac{\partial hv}{\partial x}=0,}\\ {\displaystyle \frac{\partial v}{\partial t}+\left(1+\frac{h}{R}\right)v\frac{\partial v}{\partial x}=gsin\psi -\left(1+\frac{h}{2R}\right)\left(\frac{1}{2h}\frac{\partial }{\partial x}\left(h^{2}gcos\psi +\frac{h^2{v}^2}{R}\right)-\frac{\tau }{\rho h}\right).}\end{array}$$

(10)

Here, R is the radius of curvature of the slope; $R>0$ in the concave sections of the slope and $R<0$ in the convex sections. The equations have been derived assuming that $\left|R\right|\gg h$; terms of the order $h^2/R^2$ and higher have been neglected. The slope curvature causes a change in bottom friction $\tau$. In particular, if a part of the friction ${\tau }_d$ is proportional to the pressure at the bottom, then this part should be written as (compare to Equation (3))

$${\displaystyle {\tau }_d=\mu \rho \left(ghcos\psi +\frac{v^2}{R}\right).}$$

(11)

If the frontal entrainment takes place, then the conditions at the avalanche leading edge are

$$\begin{array}{c}\rho \overline{h}(w-\overline{v})={\rho }_0{h}_{0}w,\\ {\displaystyle {\rho }_0{h}_{0}w\overline{v}=0,5\rho h^2\left(gcos\psi +\frac{{\overline{v}}^2}{R}\right)-{\sigma }^{*}{h}_0\equiv P(P\ge 0).}\end{array}$$

(12)

The influence of the curvature of the slope on the dynamics of the avalanche is mainly due to the presence of a centrifugal force. It can be seen from Equations (10) to (12) that this force affects the speed and run-out distance of the avalanche in two ways. On a concave slope, it increases friction, which leads to a decrease in the velocity. On the other hand, the centrifugal force increases the pressure gradient, including the pressure of the avalanche on the snow in front of it. This leads to an increase of the avalanche velocity. The result of the combined action of both factors can be either an increase or a decrease in the velocity and therefore in the run-out distance, depending on the values of the friction coefficient and the radius of curvature. Numerical study of the influence of the curvature of the path on the avalanche dynamic parameters and run-out distance was performed in [26,41,42].

2.2.4. Entrainment

The gradual entrainment from the underlying snow layer was considered in addition to, or instead of entrainment at the front in [41,43,44,45,46,47,48,49]. In fact, the entrainment of snow at the front described in the previous subsection does not obligatory mean the plough entrainment by the avalanche front. It can be related to a graduate entrainment from the underlying layer if it occurs in the narrow zone adjacent to the front. Field observations confirm that usually a significant fraction of the entrainment takes place in the relatively narrow front part of the avalanche (within the first few tens of meters) [50]. This front part can be either replaced by a jump in mathematical modeling as is done in MSU-1 model or it can be considered as a narrow zone with gradual entrainment. Moreover, the gradual entrainment from the underlying layer can continue (at diminishing rate) along the body of the avalanche outside of the frontal part, if all available snow is not entrained by the frontal part. This should be accounted for by the model.

If the gradual entrainment is considered, then additional terms enter the equations. For the 1D motion on a wide slope, the continuity equation now reads

$${\displaystyle \frac{\partial h}{\partial t}+\frac{\partial hv}{\partial x}=q,}$$

(13)

where q is the rate of volume entrainment per unit area at the flow bottom. Different formulas to determine q were suggested and used in [41,43,44,45,46,47,48,49,51,52,53]. A review of various ways of incorporating the entrainment effect into models of flows of different physical nature can be found in [44]. In particular, in [43], it is assumed that the boundary between the moving avalanche snow and the underlying static snow layer is a shock wave inclined to the bottom, in which the snowpack is broken up and entrained into the avalanche. At certain additional hypotheses, this approach leads to the formulae

$$q=k\sqrt{h-h^{*}}\mathrm{if}h>h^{*};q=0\mathrm{if}h\le h^{*}.$$

(14)

where k is a model parameter and $h^{*}$ is the value of the flow thickness at which the pressure at the flow bottom reaches the compression strength of the underlying snow. Some critical comments on this approach can be found in [44,52].

Another mechanism for basal entrainment is considered for dry dense, powder, and mixed avalanches in [41,45,46,47,48,49,53], see Section 4. It is supposed to be similar to mixing in turbulent jets. Mixing is largely driven by the instability at the flow boundaries leading to formation and breaking of waves there. The growth rate of the disturbances is known to be proportional to the velocity difference between the flow and the ambient medium with the coefficient depending on the density ratio [54]. It is reasonable to assume that the entrainment rate meets the same rule. Then for dry dense avalanches entrainment rate from the underlying still snow layer is [45,46]

$$q=m_{10}v{\displaystyle \frac{\sqrt{\rho {\rho }_0}}{\rho +{\rho }_0}},$$

where $m_{10}$ is the coefficient and v is the velocity of snow in the avalanche; ${\rho }_0$ and $\rho$ are the densities in the underlying snow layer and in the avalanche, respectively. For more details see Section 4.

2.2.5. Friction

The expressions (3) and (4) for both dry and hydraulic frictions were modified. First, following Grigorian [55] the Coulomb’s law for dry friction ${\tau }_d$ was changed by introduction of an upper limit for its value [55]. The new law states that the bottom shear stress ${\tau }_d$ is equal to $\mu p$, where $\mu$ is the friction coefficient and p is the bottom pressure, unless $\mu p$ is not larger than the minimal shear strength ${\tau }_{*}$ of the moving and underlying materials. Otherwise, ${\tau }_d$ equals ${\tau }_{*}$ (Figure 3):

$${\tau }_d=\mu p\mathrm{if}\mu p<{\tau }_{*};{\tau }_d={\tau }_{*}\mathrm{if}\mu p\ge {\tau }_{*}.$$

(15)

Grigorian proposed formula (15) based on the general concept that for every process, there is a limit stress that it can withstand for each material. In particular, one of the goals was to explain the observed excessively large run-out distances for large avalanches. The phenomenon can be formally described by introducing the dependence of the Coulomb friction coefficient $\mu$ on the avalanche volume [38,56]. However, this assumption does not correlate with the physical meaning of $\mu$ as a local characteristic determined by local properties of the moving snow and the bottom. Let us show that there is no need to introduce the dependency of $\mu$ on the avalanche volume if the formulas (15) are respected. If the bottom pressure is $p=\rho gcos\psi h$, then ${\tau }_d=\mu \rho ghcos\psi$ until $h\le h_{*}$ where $h_{*}={\tau }_{*}/(\mu \rho gcos\psi )$. Thus, the dry friction per unit mass ${\tau }_d/\left(\rho h\right)=\mu gcos\psi$ does not depend on h. However, for $h>h_{*}$ one has ${\tau }_d/\left(\rho h\right)={\tau }_{*}/\left(\rho h\right)$. Therefore, for avalanches with $h\ge h_{*}$ the dry friction force per unit mass will decrease with h. That is why large avalanches move faster and extend farther than small ones with the same value of the friction coefficient $\mu$.

Formula (15) for dry friction and its modifications to account friction against side walls for channeled avalanches were used in [30,34,35,37,38,41,57]. In particular, it was found that replacing the Coulomb law with formula (15) would result not only in a change in the values of v and h but also in a qualitative change in the shape of the flow. Thus, regions with a sharp decrease in v and h can appear at the back of the avalanche [35].

Further development of the formulas for bottom friction concerns the stopped parts of the avalanche [26,41]. The friction force can be less than the dynamic friction there. The static friction is equal to the active forces (gravity) [26]. This could be important in the run-out zone where the front parts of the avalanche can stop while the rear parts continue to move.

The expression for the hydraulic friction ${\tau }_h$ depends on three factors: the flow regime (turbulent or laminar), the rheology of the moving material and the shape of the channel cross-section (for channeled avalanches). For 1D turbulent flow down a wide slope it is reasonable to use formula (3) with ${\tau }_h$ proportional to $v^2$ at $\mathrm{Re}\ge {\mathrm{Re}}_{cr}$, where $\mathrm{Re}$ is the Reynolds number. If the flow is laminar ($\mathrm{Re}<{\mathrm{Re}}_{cr}$), then the formula for ${\tau }_h$ depends on the moving snow rheology (see Section 3). For linear viscous medium ${\tau }_h/\left(\rho h\right)=k_{1}v/h^2$. Besides, the flow regimes can be different in different parts of the avalanche; this should be taken into account when choosing formulas for ${\tau }_h$ [26,41].

2.3. Flow Stability Conditions

It is known that flows in open channels and on slopes can lose stability. Then, the so-called roll waves can appear. The waves have hydraulic jumps at their fronts whose height can be much greater than the depth of the flow. This leads to a restructuring of the entire flow including a change in the velocity (see Section 3). Whether a flow with constant or slowly varying parameters is stable or not depends on the magnitudes of the flow parameters and the properties of the path. It is known [29,58] that a 1D flow with constant h and v is stable with respect to disturbances propagating along the flow direction if and only if the following condition is fulfilled:

$$a_{-}\le a\le a_{+}\mathrm{where}{a}_{\pm }=v\pm c,c=\sqrt{\mathrm{g}cos\psi }.$$

(16)

Here, a and $v\pm c$ are the propagation velocities of small disturbances in large-scale and small-scale approximations, respectively (see Section 3), and $c=\sqrt{\mathrm{g}hcos\psi }$ is the propagation velocity of small-scale disturbances relative to the flow particles.

In [59] the stability criteria for flows at wide homogeneous slopes have been derived for 2D perturbations propagating at arbitrary angles to the flow velocity (see examples in Section 3). A homogeneous flow on a wide slope is stable if the following conditions are fulfilled:

$${\displaystyle \mathrm{Fr}\left|\frac{{\displaystyle \tau -h\frac{\partial \tau }{\partial h}}}{{\displaystyle v\frac{\partial \tau }{\partial v}}}\right|\le 1\mathrm{if}2\tau \ge v\frac{\partial \tau }{\partial v};}$$

(17)

$${\displaystyle \mathrm{Fr}\left|\frac{{\displaystyle \tau -h\frac{\partial \tau }{\partial h}}}{{\displaystyle v\frac{\partial \tau }{\partial v}}}\right|\le {\xi }_{*}\mathrm{if}2\tau <v\frac{\partial \tau }{\partial v},\mathrm{where}{\xi }_{*}=\frac{2\tau }{v}{\left(\frac{\partial \tau }{\partial v}\right)}^{-1}\sqrt{\frac{v}{\tau }\frac{\partial \tau }{\partial v}-1}.}$$

(18)

Here, $\mathrm{Fr}=\left|v\right|/\sqrt{\mathrm{g}hcos\psi }$ is the Froude number.

The information about the flow stability is of particular importance for numerical modeling. If it is expected that stability criteria are not met in some sections of the avalanche path, then a numerical scheme with low numerical viscosity must be used [25].

The stability criteria for laminar and turbulent motions on wide slopes and in channels with different expressions for the friction are given in [25,29,34,35,59,60,61].

2.4. Comments to a History of Dense Avalanche Hydraulic Models

The one-dimensional model MSU-1 was published in 1967. In the model, an avalanche was considered as a flow of a continuous medium, and the depth-averaged partial differential equations of the mass and momentum balance were used. Over the next two decades, in the Soviet Union, the further development of this model was intensively carried out (e.g., the two-dimensional model—1973; Grigorian law of friction—1979). These models were used for estimation of the avalanche parameters and creation of avalanche hazard maps [28,31,40,62,63].

Meanwhile, researchers and engineers developed and used mathematical models considering an avalanche as a moving solid block. The PCM (Perla, Cheng and McClung) [64] and VSG (Voellmy, Salm, Gubler) [65] models are two widely known examples. Only in the late 1980s did the hydraulic approach find its recognition in the western scientific literature. In [66] the so-called NIS (Norem, Irgense, Shieldrop) model was described. Another model published in 1989 [67] became known as the Savage–Hutter model. In 1993, the Savage–Hutter model was extended for two-dimensional flows [68], and in 1999 the channelized flows were studied [69].

The Savage–Hutter model presented in [67] differs from the MSU-1 model in two aspects: (1) it does not include velocity-dependent part of friction; (2) it introduces the so-called earth pressure coefficients $k_{actpass}$. Both of these points are questionable. Due to the absence of the velocity-dependent friction, the Savage–Hutter models cannot describe a steady homogeneous flow at a slope with constant incline. However, it is widely believed that such flow can occur in the transit part of an avalanche path. In fact, the models including the velocity-dependent friction have continued to develop [5,13,56,70]. The introduction of the coefficient $k_{actpass}$ is reasonable in statics of soil. However, in fast turbulent flows, the moving material is destructed and behaves like a fluid rather than a structured solid. Besides, $k_{actpass}$ is a discontinuous function of the flow and the slope parameters. This make the governing equations extremely nonlinear. The models and computational codes that are developed currently do not include both mentioned features of the Savage–Hutter models, and they are closer to the MSU-1 model and its modifications [13,56].

3. Analytical Solutions

In this section we describe asymptotic (as $t\to \infty$) analytical solutions for dense avalanche dynamics [24,25,27,29,34,35,60,61]. Such solutions allow one to estimate the avalanche parameters at long slopes and in long chutes without complicated calculations. Besides, they can serve to verify numerical schemes and computer codes proposed for more detailed modeling.

In the following section, we describe a method for obtaining analytical solutions to the problems of avalanche dynamics based on the use of equations in the large-scale approximation. Examples of analytical solutions are given as well.

3.1. Large-Scale and Small-Scale Motions

The key idea in constructing analytical solutions is to use the simplified equations in large-scale approximation. Consider, for example, the flows described by the MSU-1D model [25]. Denote by L and T the distance and time, at which the magnitudes of v and h change significantly; L and T are termed the length and time scales for the flow. Usually $T=L/V$ for problems in study, where the typical velocity magnitude V is known. Denote by H the typical magnitude of h and by F the typical value of friction per unit mass $\tau /\left(\rho h\right)$. According to definitions of L and T, the following estimates for the magnitudes of the space and time derivatives of v and h hold:

$${\displaystyle \frac{\partial v}{\partial x}\sim \frac{V}{L},\frac{\partial h}{\partial x}\sim \frac{H}{L},\frac{\partial v}{\partial t}\sim \frac{V}{T}=\frac{V^2}{L}.}$$

Let us compare different terms in the momentum Equation (2). The left-hand side of this equation and the first term in its right-hand side are of the orders $V^2/L$ and $gHcos\psi /L$, respectively. The orders of their ratios to the friction term are

$${\displaystyle \frac{V^2}{FL},\frac{gHcos\psi }{FL}.}$$

If L is large, namely, if

$${\displaystyle L\gg max\left(\frac{V^2}{F},\frac{gHcos\psi }{F}\right),}$$

(19)

then we can neglect the differential terms in the momentum Equation (2) to obtain its large-scale approximation

$${\displaystyle gsin\psi -\frac{\tau }{\rho h}=0}$$

(20)

This equation together with the continuity Equation (1) describes the large-scale motions. The theory based on Equations (1) and (20) is referred to as the kinematic waves theory [58,71].

Since $\tau$ is a known function of h and v, Equation (20) determines v as a function of h

$$v=V\left(h\right).$$

Substituting this expression into the continuity equation we come to the equation for h

$$\frac{\partial h}{\partial t}+a\frac{\partial h}{\partial x}=0,a\left(h\right)\equiv \frac{\partial hV}{\partial h}.$$

This equation has a characteristic form, and $a\left(h\right)$ is the characteristic speed. In particular, small disturbances propagate with the velocity $a\left(h\right)$.

When friction is expressed by formula (3) the condition under which we can neglect the differential terms can be written as

$$L\gg max\left(\frac{H}{k},\frac{H}{tan\psi -\mu }\right).$$

(21)

A different approximation can be used for small-scale motions, when

$${\displaystyle L\ll min\left(\frac{V^2}{F},\frac{gHcos\psi }{F}\right).}$$

(22)

At these conditions, the space and time derivatives of v and h are relatively large, and the friction can be neglected in the momentum equation. The resulting system of differential equations has two families of characteristics. The propagation velocities of small perturbations in this approximation are $v\pm c$ where is $c=\sqrt{\mathrm{g}hcos\psi }$.

3.2. Analytical Solution for a 1D Flow at a Long Wide Homogeneous Slope

Let us consider first the one-dimensional problem for a dense avalanche moving down a long wide homogeneous slope [24,25,29]. Assume that the movement is described by the MSU-1D model, including frontal entrainment (see Section 2.1). The slope angle $\psi$, the depth $h_0$ and the strength ${\sigma }_{*}$ of the entrainable snow layer are constant. The avalanche is not very large (${\tau }_d<{\tau }_{*},h<h_{*}$), so the traditional Coulomb law can be used; the motion under Grigorian friction was considered in [35]. The slope is steep enough ($tan\psi >\mu$) so that the avalanche does not stop on this slope.

Suppose that when moving down a long homogeneous slope with entrainment ($h_0\ne 0$), the velocity of the avalanche leading front tends to a constant with increasing time, while the length of the avalanche increases. The latter is due to the fact that the hydraulic friction per unit mass decreases with increasing the thickness of the flow. Therefore, the thicker frontal part of the avalanche moves faster than its less thick rear part. Numerical studies confirm this behavior of the flow [24,25]. Consequently, at a large amount of time, the derivatives of h and v with respect to x and t are small everywhere except, possibly, a zone adjacent to the leading edge of the avalanche. We can conventionally divide the avalanche into two zones: a long zone 2 with a large length scale $L_2$ (of the order of the avalanche length) and a relatively narrow zone 1 adjacent to the avalanche leading edge. Note that such division is reasonable if the stability conditions for the flow with slowly varying parameters are satisfied. Otherwise, the length scale is determined not by the length of the avalanche but by the length of the waves appearing in it due to instability; then $L_2$ cannot be large despite the large length of the whole avalanche. In the problem in study, the stability condition for the flow in zone 2 is [59]:

$$tan\psi -\mu \le 4k.$$

(23)

3.2.1. Solution for the Large-Scale Zone 2

Let the condition (23) be respected. In the large scale zone 2, we can use the simplified momentum Equation (20). With account for the relationships (3), this equation reads

$${\displaystyle f(h,v)\equiv \mathrm{g}sin\psi -\mu \mathrm{g}cos\psi -k\frac{v^2}{h}=0.}$$

(24)

Equation (24) allows one to find v as a function of h

$$v=V\left(h\right)=\sqrt{\frac{h\mathrm{g}cos\psi (tan\psi -\mu )}{k}}.$$

(25)

Substituting this result into the continuity Equation (1) we obtain the equation for h

$$\frac{\partial h}{\partial t}+a\frac{\partial h}{\partial x}=0,$$

(26)

where

$$a\left(h\right)\equiv \frac{\partial hV}{\partial h}=V+h\frac{\partial V\left(h\right)}{\partial h}=\frac{3}{2}V\left(h\right)=\frac{3}{2}\sqrt{\frac{h\mathrm{g}cos\psi (tan\psi -\mu )}{k}}.$$

(27)

Equation (26) has a characteristic form, and $a\left(h\right)$ is the velocity of characteristics. Large-scale disturbances of h (and v since $v=V\left(h\right)$) propagate with the velocity $a\left(h\right)$.

Let us discuss the boundary conditions for zone 2 at its boundary with zone 1. Since zone 1 is narrow in comparison to large-scale zone 2, we can replace the entire zone 1 by a jump (a shock) when constructing the solution to Equation (26). We will refer to this jump as a kinematic jump. Further we will consider the solution in zone 1, which actually describes the structure of this kinematic jump.

The only conservation law on the kinematic jump is the condition of mass conservation

$$h_i(w-V\left(h_i\right))=h_{0}w\mathrm{or}w=\frac{h_{i}V\left(h_i\right)}{h_i-h_0},$$

(28)

where w is the jump speed and $h_i$, $v_i=V\left(h_i\right)$ are the flow depth and velocity behind the kinematic jump. If there are no other conditions at the jump, then it follows from the Lax evolutionarity condition [72] that

$$a\left(h_i\right)\ge w.$$

(29)

On the other hand, it follows from the definition of the leading edge of zone 2 that $w\ge a\left(h_i\right)$. Combining this inequality with the Lax condition (29) gives

$$w=a\left(h_i\right).$$

(30)

Besides, there is formula (28) for w. Therefore,

$$w=\frac{h_{i}V\left(h_i\right)}{h_i-h_0}=a\left(h_i\right)=\frac{3}{2}V\left(h_i\right),\mathrm{i}.\mathrm{e}.,h_i=3h_0,w=\frac{3}{2}V\left(h_i\right).$$

(31)

Let us find the distribution of h and v inside zone 2. Equation (26) can be rewritten as

$${\displaystyle \frac{dh}{dt}=0\mathrm{at}\frac{dx}{dt}=a\left(h\right),\mathrm{i}.\mathrm{e}.,h=\mathrm{const}\mathrm{at}x=a\left(h\right)t+x_0.}$$

The solution is a Riemann wave. The region of initial perturbation, from which the avalanche has developed, is small from the large-scale point of view, and it can be replaced by a point $x=0$. Then the solution in zone 2 is given by the formulas

$$a\left(h\right)=\frac{x}{t},v=V\left(h\right)\mathrm{at}0\le x\le a\left(h_i\right)t;h_i=3h_0.$$

(32)

By use of formulas (25) and (27), we write the solution in explicit form

$${\displaystyle h=\frac{4k}{9gcos\psi (tan\psi -\mu )}\frac{x^2}{t^2},v=\frac{2}{3}\frac{x}{t}\mathrm{at}0\le x\le a\left(h_i\right)t,}$$

(33)

$${\displaystyle w=\frac{3}{2}\sqrt{\frac{3h_0\mathrm{g}cos\psi (\tan \psi -\mu )}{k}}.}$$

(34)

However, this solution is valid only if there exists a solution in zone 1, which determines the structure of the kinematic jump.

3.2.2. About Solution for Zone 1 (Adjacent to the Leading Edge)

The entire zone 1 (it may be called “the head” of the avalanche) was replaced by a jump in constructing the solution for zone 2. However, knowledge of h and v inside zone 1 is also important. So, we need to find a solution to the full (not simplified) Equations (1), (2) and (4) at the following conditions.

• It is stationary in the coordinate system moving at a speed w: the flow cannot change significantly over a period of time that is small from a large-scale point of view.
• The velocity $\overline{v}$ and thickness $\overline{h}$ at the avalanche leading edge $x=X_f$ satisfy the relationships (4).
• At the rear boundary, h and v tend to $h_i$ and $V\left(h_i\right)$ satisfying (25).

Due to condition 1, the solution in zone 1 can be written as $h=h\left(\xi \right)$, $v=v\left(\xi \right)$, where $\xi =x-wt$. Then the continuity equation gives

$$(w-v)h=w{h}_0\equiv Q,\mathrm{i}.\mathrm{e}.,v=w-{\displaystyle \frac{Q}{h}}.$$

Using the latter relationship, the momentum equation is transformed into an ordinary differential equation for h, which can be written as [29]

$$\frac{dh}{dt}={\displaystyle \frac{hf(h,v)}{(a_{+}-w)(w-a_{-})}},$$

(35)

where $v=w-Q/h$, $a_{\pm }=v\pm \sqrt{\mathrm{g}hcos\psi }$; $f(h,v)$ is defined by formula (24) and w is a parameter that, in general, can be arbitrary. The question is whether Equation (35) has a solution that satisfies the boundary conditions 2 and 3 with w determined by the formulas (31) and (34). A rather complicated investigation [25,29] shows that the answer depends on the value of the strength ${\sigma }_{*}$ of the snow that the avalanche entrains. If ${\sigma }_{*}$ is large enough, namely, if

$${\sigma }_{*}\ge \widehat{\sigma },\widehat{\sigma }\equiv \rho \mathrm{g}cos\psi h_0\left(4-\frac{9}{2}\frac{\tan \psi -\mu }{k}\right),$$

(36)

then the required solution for zone 1 exists. This means that the solution (33) and, in particular, formulas (31) and (34) for the avalanche front speed are valid. The solution in zone 1 can be found by solving Equation (35) numerically. The magnitudes of the velocity $\overline{v}$ and thickness $\overline{h}$ at the leading edge are calculated by Equations (4) taking into account the known value (31) of w (Figure 4a).

However, for ${\sigma }_{*}<\widehat{\sigma }$ Equation (35) has a solution that satisfies the boundary conditions 2 and 3 only if

$$\overline{h}=h_i.$$

The latter is a new condition at the kinematic jump in addition to (28). The evolutionarity condition now reads $w>a\left(h_i\right)$. It means that for ${\sigma }_{*}<\widehat{\sigma }$, formula (31) obtained without consideration of the kinematic jump structure is no longer valid. In this case, the magnitudes of w, $\overline{h}=h_i$ and $\overline{v}$ are calculated by Equations (4) and (28). Finally, the solution for both zones 1, 2 for ${\sigma }_{*}<\widehat{\sigma }$ is

$$\begin{array}{c}{\displaystyle h=\frac{4k}{9gcos\psi (\tan \psi -\mu )}\frac{x^2}{t^2},v=\frac{2}{3}\frac{x}{t}\mathrm{at}0\le x\le a\left(h_i\right)t,}\\ h=h_i\mathrm{at}a\left(h_i\right)t\le x\le wt.\end{array}$$

(37)

The shape of the avalanche in this case is shown in Figure 4b.

3.3. 1D Motion without Entrainment

Consider an avalanche moving down a long homogeneous steep slope without entrainment [25]. Denote the initially released mass per unit width by M; $M=\mathrm{const}$ during motion. The statement of the problem is similar to that described in previous subsections except the conditions at the leading edge: to describe motion without entrainment we just set $h_0=0$. In this case, there is no jump at the leading edge, and an asymptotic solution with $w=\mathrm{const}$ does not exist. However, the length of the avalanche increases with time and the derivatives over t and x decrease everywhere except the narrow zone 1 adjacent to the leading edge. Therefore, at large time we can use the large-scale approach and obtain

$${\displaystyle h=\frac{4k}{9g(sin\psi -\mu cos\psi )}\frac{x^2}{t^2},v=\frac{2}{3}\frac{x}{t}.}$$

The speed of the avalanche front can be found by using the condition of mass conservation. Neglecting the length of zone 1, we write

$$\underset{0}{\overset{x_f}{\int }}\rho h(x,t)dx=\frac{4k\rho }{27\mathrm{g}(sin\psi -\mu cos\psi )}\frac{x_f^3}{t^2}=M,$$

where $x_f$ is the front position. Therefore,

$$w\equiv \frac{d{x}_f}{dt}=\sqrt[3]{\frac{2M\mathrm{g}(sin\psi -\mu cos\psi )}{\rho kt}}=\sqrt{\frac{3M\mathrm{g}(sin\psi -\mu cos\psi )}{\rho k{x}_f}},\overline{h}=\frac{3M}{\rho x_f}.$$

These formulas show that in motion down a long homogeneous slope without snow entrainment, the avalanche front speed tends to zero even if $tan\psi >\mu$. This is due to redistribution of mass over the avalanche body.

3.4. Solution under the Instability of Smooth Flows

The analytical solutions described above were obtained under the essential condition that the flow is stable. If the stability condition is not met, then it is impossible to use the equations in large-scale approximation. Waves and hydraulic jumps can appear in zone 2. Moreover, the small disturbances that arise in zone 2 will propagate into zone 1; they can possibly reach the leading edge and change its velocity. To clarify this situation, consider the solution in zone 1. First, it is known that the flow just behind a hydraulic jump (in particular, behind the avalanche leading edge) is subcritical: $w-\overline{v}<c\left(\overline{h}\right)$, $c\left(h\right)\equiv \sqrt{\mathrm{g}hcos\psi }$, i.e., ${\overline{a}}_{+}\equiv \overline{v}+c\left(\overline{h}\right)>w$ (see Section 2.3 and Section 3.1). Second, in the general case, $a_{+}>w$ everywhere in zone 1. The flow cannot become supercritical anywhere because the solution to Equation (35) is not valid near the critical point $h=h_{cr}$ (where $w-v=c$, i.e., $w=a_{+}$): the denominator in Equation (35) is zero at this point. Third, it follows from the assumed instability of the flow in zone 2 that $a>a_{+}$ in this zone (a is the propagation speed of small disturbances in zone 2, see the relations (16)). Thus, we may come to the following conclusion. If a smooth flow is unstable, then $a>a_{+}>w$; the disturbances arising in the rear part of the avalanche reach the leading front and change its speed. The flow with constant w does not exist. However, this is not always true! Note, that the magnitude of w is not prescribed in our reasoning. We can choose w to satisfy the relation $f(h,w-Q/h)=0$ at $h=h_{cr}$. Then both the denominator and the numerator on the right side of the Equation (35) tend to zero at the critical point, i.e., the following two relationships are satisfied

$$f(h,v)=0,and{a}_{+}=w,wherev=Q/h,Q=w{h}_0.$$

(38)

In this case, the transition through the critical point is possible, and it is carried out in the solution to Equation (35). In the rear part of zone 1, the velocities of small perturbations are less than the front speed w. Therefore, the disturbances arising in zone 2 do not reach the avalanche front and cannot affect its speed [25,29]. It is this solution that describes the front zone of the avalanche at large values of time if a smooth flow in the rear part of the avalanche is unstable. If the flow is described by the MSU-1 model, then the instability condition is

$$tan\psi -\mu >4k$$

and the value of the leading edge speed calculated by Equation (38) is [25]

$$w=\sqrt{\mathrm{g}{h}_{0}cos\psi }{\left(1+\sqrt{\frac{tan\psi -\mu }{k}}\right)}^{3/2}.$$

(39)

Calculations performed in [24,25] confirm this result. A possible shape of the avalanche is shown in Figure 5.

3.5. Concluding Remarks to Analytical Solutions for MSU-1 Model

Remark 1.

The obtained solutions are valid for the flow at large time from the start of motion (as $t\to \infty$). However, calculations by the initial (not simplified) system of Equations (1)–(4) show that in fact the flow parameters, including the leading edge velocity, become close to those given by the analytical formulas shortly after the start of movement [24].

Remark 2.

It is worth mentioning that the approximate formula by Voellmy [20] relating the velocity and thickness for a 1D avalanche at a long constant slope

$$v=\sqrt{\xi hcos\psi (tan\psi -\mu )},\xi =\mathrm{g}/k$$

is suitable for large-scale parts of the flow. The formula is not suitable for parts with sharp variation of the flow parameters, e.g., for zone adjacent to the leading edge. The solutions described above emphasize that accounting for the flow depth variation is very important, see Section 3.3.

3.6. Other Analytical Solutions

The method described above has been applied to construct analytical asymptotic (as $t\to \infty$) solutions for various flows. Some time after the start of movement down a long homogeneous slope, a zone with large scales is formed, where the flow parameters satisfy the simplified momentum equation for 1D motion

$${\displaystyle gsin\psi -\frac{\tau }{\rho R_h}=0,}$$

where $R_h$ is the hydraulic radius. For 2D motion, the equation becomes

$${\displaystyle gsin\psi \mathbf{e}-\frac{\tau }{\rho h}=0}$$

(see Section 2.2.1). In the hydraulic approach, the friction $\tau$ is a function of v and h. In general, the formulas for $\tau$ depend on the flow regime (turbulent or laminar), the flow rheology and the bottom properties. The same factors determine stability conditions for homogeneous flows; such conditions must be accounted for while constructing solutions.

3.6.1. 1D Laminar Flow of Generalized Power-Law Fluid

For 1D laminar flows of a power-law fluid, the friction model can be generalized by including the Coulomb friction. The friction at the bed is then the following function of the depth-averaged velocity v and the flow depth h:

$${\displaystyle \tau =\mu \rho \mathrm{g}hcos\psi \frac{\mathbf{v}}{\left|v\right|}+K{\left(\frac{2n+1}{n}\right)}^n\frac{v^{n-1}\mathbf{v}}{h^n}.}$$

Here, $\mu$ is the coefficient of Coulomb friction; $K$ and n are the rheological coefficients of the power-law fluid: in simple shear flow of a standard power-law fluid (without dry friction) the shear stress $\tau$ is related to the shear rate $\dot{\gamma }$ by the formula $\left|\tau \right|=K|\dot{\gamma }{|}^n$. If $n=1$ and $\mu =0$, then the fluid is linear-viscous (Newtonian) and K is the viscosity coefficient. If the avalanche moves down a long homogeneous steep slope ($tan\psi >\mu )$, it is possible to construct an asymptotic (as $t\to \infty )$ analytical solution. Such solution for the laminar 1D flow was obtained for $n=1$ in [60] and for arbitrary n in [61]. Following the approach described in the previous subsections, the flow is divided into two parts: large-scale main body (zone 2) and a head (zone 1). In zone 2, the system of equations is

$$\begin{array}{c}{\displaystyle \frac{\partial h}{\partial t}+\frac{\partial hv}{\partial x}=0,}\\ {\displaystyle f\equiv \mathrm{g}sin\theta -\mu \mathrm{g}cos\theta -\nu {\left(\frac{2n+1}{n}\right)}^n\frac{v^n}{h^{(n+1)}}=0,}\end{array}$$

(40)

where $\nu =K/\rho$. It follows from the second equation above that

$${\displaystyle v=V\left(h\right)=\frac{n}{2n+1}{\left(\frac{\mathrm{g}sin\theta -\mu \mathrm{g}cos\theta }{\nu }\right)}^{1/n}{h}^{(n+1)/n}.}$$

(41)

The solution in the large-scale zone 2 is

$$\begin{array}{c}{\displaystyle v=\frac{n}{2n+1}\frac{x}{t},h={\left(\frac{\nu }{\mathrm{g}sin\psi -\mu \mathrm{g}cos\psi }\right)}^{1/(n+1)}{\left(\frac{x}{t}\right)}^{n/(n+1)}at0\le x\le wt,}\\ {\displaystyle w={\left(\frac{\mathrm{g}sin\psi -\mu \mathrm{g}cos\psi }{\nu }\right)}^{1/n}{\left(\beta h_0\right)}^{(n+1)/n},\beta \equiv \frac{2n+1}{n+1}.}\end{array}$$

(42)

However, this solution is valid only if the following two conditions are satisfied.

First, the flow with slowly varying parameters should be stable. The stability conditions in the case study are [59]

$${\displaystyle \mathrm{F}r\le \frac{n}{n+1}\mathrm{if}n\le \frac{2tan\psi }{tan\psi -\mu };\mathrm{F}r\le \frac{n}{n+1}{\xi }_{*}\mathrm{if}n>\frac{2tan\psi }{tan\psi -\mu }.}$$

(43)

Here, $\mathrm{F}r=v/\sqrt{\mathrm{g}hcos\psi }$ is the Froude number, and ${\xi }_{*}$ is defined by the formulas

$${\xi }_{*}=\frac{2}{\lambda }\sqrt{\lambda -1},\lambda \equiv \frac{n(tan\psi -\mu )}{tan\psi }.$$

The stability conditions can be rewritten by use of formula (41) for v:

$$\begin{array}{c}{\displaystyle {\left(\frac{\mathrm{g}sin\psi -\mu \mathrm{g}cos\psi }{\nu }\right)}^{\frac{1}{n}}{h}^{\frac{n+1}{n}}\le {\xi }_{*}\beta \sqrt{\mathrm{g}hcos\psi },}\\ {\displaystyle {\xi }_{*}=1\mathrm{if}\lambda \le 2;{\xi }_{*}=\frac{2}{\lambda }\sqrt{\lambda -1}\mathrm{if}\lambda >2.}\end{array}$$

The second condition for the solution (42) to be valid is related to zone 1: a suitable solution for zone 1 should exist. It was proved in [60,61] that the required solution in zone 1 exists, if the strength ${\sigma }_{*}$ of the entrainable layer satisfies the condition

$$\begin{array}{c}{\displaystyle {\sigma }_{*}\ge \widehat{\sigma },where}\\ {\displaystyle \widehat{\sigma }=\rho {\beta }^2\left(\frac{\mathrm{g}{h}_{0}cos\psi }{2}-\frac{n{h}_0^2}{2n+1}{\left(\frac{\beta h_0\mathrm{g}(sin\psi -\mu cos\psi )}{\nu }\right)}^{2/n}\right).}\end{array}$$

(44)

If at least one of the conditions (43) and (44) is not satisfied, the solutions will differ from those given by Equations (42). More details are not presented here; they can be found in [61].

3.6.2. 2D Motion on Slopes with Smoothly Varying Properties

Consider a two-dimensional flow down a slope with smoothly varying steepness and snow cover properties [27]. This means that the linear scale $L^{*}$ of change in the slope and snow cover parameters is large enough. Denote the typical scale and the characteristic time of variation of the solution by L and T, respectively. It is obvious that $L\le L*$. For sufficiently large values of L, the differential terms in momentum Equation (7) can be neglected. Then this equation takes the form

$$gsin\psi \mathbf{e}=F\mathbf{v},$$

where $\mathbf{e}$ is a unit vector along the steepest descent line, and $F\mathbf{v}$ is the friction per unit mass (cf. Equation (24)). Therefore, in the large-scale approximation, $\mathbf{v}$ is parallel to $\mathbf{e}$ and the avalanche moves along the steepest descent lines. Such lines are known if the slope topography is given. The following method was proposed for constructing a solution [27]. Divide the entire slope into narrow stripes along the steepest descent lines. Then the avalanche is a collection of one-dimensional flows in the corresponding stripes. These one-dimensional flows interact only through their leading edges. Thus, to solve a two-dimensional problem, a number of one-dimensional problems can be solved together with additional conditions on the flows’ leading edges. This method was applied (without reference to the theory of kinematic waves) by Ostroumov in simulations of the Tubri avalanche in Georgia [40].

3.6.3. About the Other Analytical Solutions

In addition to the solutions described above, the asymptotic analytical solutions have been constructed (i) for avalanches obeying the Grigorian dry friction law (15) [29,35,57]; (ii) for avalanches moving in long narrow chutes with different cross-sections shapes [29,34,36,57].

A common feature of those problems is that in the large-scale zone, the dependence of the speed of the characteristics $a\left(h\right)$ (or $a\left(S\right)$—for chute avalanches, S is the flow cross-sectional area) on the flow depth h (or S) is not monotonous. This is due to the special dependence of the friction on the depth. For example, let us consider a flow in a chute. Until the flow becomes deep enough, the contribution of friction on the sides of the chute is small, and the total friction per unit mass decreases with increasing depth. At large depth of the flow, the contribution of friction against the chute walls becomes significant, which leads to an increase in the total friction with an increase of the flow depth. Figure 6 shows the typical variations of the flow rate Q. For a one-dimensional motion on a wide slope, $Q=hV\left(h\right)$. For motion along a chute, $Q=SV\left(S\right)$ where S is the flow cross-section area. The velocities of characteristics in large-scale equations are: ${\displaystyle a\left(h\right)=\frac{\partial hV}{\partial h}}$ and ${\displaystyle a\left(S\right)=\frac{\partial SV}{\partial S}}$, respectively. For the cases shown in Figure 6b,c, they are not monotonous. In such cases, jumps can occur either with increasing or decreasing the flow depth (Figure 7). This should be taken into account when performing numerical calculations.

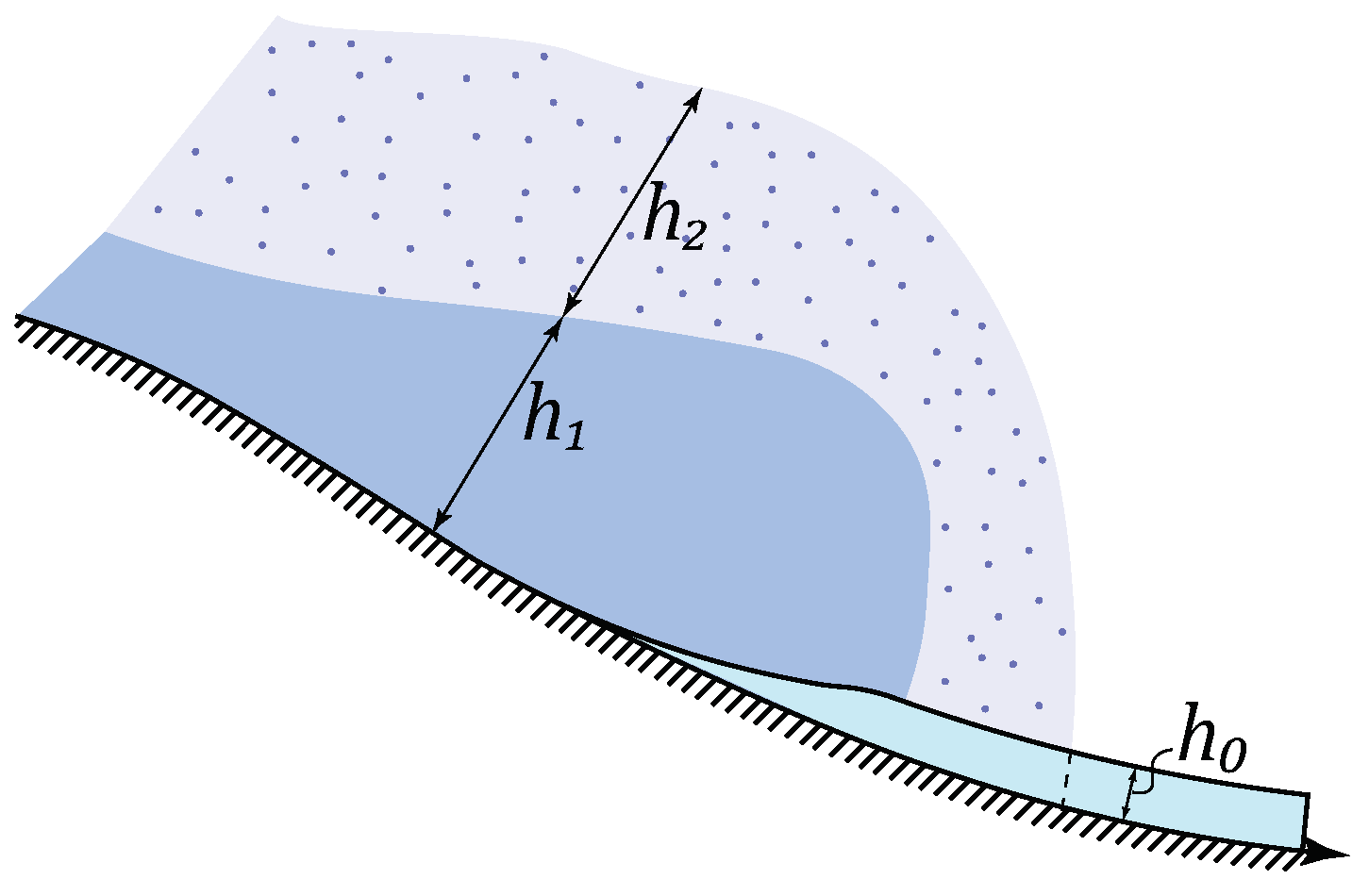
4. Powder Snow Avalanches and Mixed Avalanches

One of the main features of powder avalanches (Figure 8) is an intensive mixing of snow with ambient air, which leads to a decrease in the density and increase in the avalanche height. In this section, we outline very briefly three groups of mathematical models proposed and used for modeling powder snow avalanches, as well as mixed-type avalanches consisting of a dense core and a powder layer above it. More details and a review can be found in [49,73].

4.1. Powder-Snow Cloud

The models of the first group treat the avalanche as a snow-air cloud with a given geometric shape. These models contain equations for calculating the velocity of the center of mass of the cloud, the cloud size, mass and average density. The first model of this type was proposed in [53] and investigated in [10,74,75]. This model is cited in literature as KS model [3,10,75]. The shape of the longitudinal section of the cloud is assumed to be a semi-ellipse. The longitudinal diameter is the length of the avalanche L, and half the second diameter is the height of the avalanche h. The governing system of equations in KS-model consists of four equations.

In addition to the mass and longitudinal momentum conservation equations, it includes the equation for avalanche volume variation due to entrainment of ambient air

$$\frac{dA}{dt}=b{V}_1$$

(45)

and the Lagrange equation which is related to the motion inside the cloud

$$\frac{d}{dt}\left(\frac{\partial T}{\partial \dot{h}}\right)-\frac{\partial T}{\partial h}=Q_1+Q_2.$$

(46)

In Equations (45) and (46), A and b are the cloud volume and its upper surface area per unit width, respectively; $V_1$ is the volume of air entrained by the cloud per unit time and per unit surface area; T is the kinetic energy of the internal motion resulting in deformation of the cloud; $Q_1$ is the gravity force component normal to the slope, and $Q_2$ is the lift force appearing due to the pressure gradient on the top boundary of the cloud (due to overflow of the cloud by air).

The model takes into account the air and underlying snow entrainment, particles sedimentation, ground friction and air drag. The formulas for the air and snow entrainment rates, as well as for the ground friction and air drag are taken to be similar to those used in the theories of turbulent jets and flows in channels. In particular, the air entrainment rate $V_1$ is assumed to be proportional to the avalanche velocity U and the square root of the ratio of the cloud density $\rho$ and the air density ${\rho }_a$

$$V_1=kU\sqrt{\rho /{\rho }_a}.$$

This formula with the value $k=0.055$ was used by Onufriev [76] to simulate the motion of circular vortex representing the front zone of lifting warm air jet. Results of simulations using KS-model are presented in [74,75]. In [75] these results are compared to experiments described in [77,78].

The KS model was published in 1977. A few years later, there appeared the papers [77,78] which proposed a model that looked similar to the KS model. The same semi-elliptic shape of the cloud is considered. However, Equations (45) and (46) are not included. Instead, the following empirical relations for growth the cloud dimensions are proposed

$${\displaystyle \frac{dh}{d{x}_f}={\alpha }_1,\frac{dL}{d{x}_f}={\alpha }_2,}$$

where $x_f$ is coordinate of the front edge, and ${\alpha }_1$, ${\alpha }_2$ depend on the slope angle only. The values of ${\alpha }_1$ and ${\alpha }_2$ have been determined in experiments with a flow of salt fluid along a flat bottom in a water tank [77,78]. The detailed comparison of this model with the KS model can be found in [75,79].

In [80] the KS model was extended to describe a 3D cloud. It is assumed that the cloud has the form of a half-ellipsoid with variable length, height and width. In particular, the lateral spreading of the cloud can be calculated. The entrainment of air and snow by an avalanche as well as snow sedimentation are included. The forces are the gravity force, bottom friction, air drag and the pressure gradient due to the flow of air over the cloud. The inner motion inside the cloud is taken into account, and two Lagrange equations are formulated with the cloud height and width used as the generalized coordinates. A series of test calculations aimed to study the qualitative behavior of a 3D cloud and the influence of the model coefficients and initial conditions have been conducted. Special calculations were made to understand whether the model described the experimental results of Beghin and Olagne, who studied the motion of 3D clouds of salt fluid along constant slopes in a tank filled by clear water [81]. Neither entrainment of the underlying layer nor sedimentation were modeled in these experiments. Accordingly, in the calculations, the corresponding terms of the equations were excluded. It was found that the qualitative behavior is in agreement with the experimental data from [81]. In particular, (a) in a certain range of the slope angles, the cloud dimensions increase linearly along the path except the initial stage of motion; (b) the height growth rate for a 3D cloud is less than that in the 2D case; (c) the height growth rate can be approximated by a linear function of the slope angle; (d) the growth rate of width is much larger than that of height and it can be approximated as being independent of the slope angle. If the cloud does not entrain the underlying snow, then the cloud velocity first increases and then decreases as the cloud moves along. Calculations show that entrainment of snow changes this behavior of the velocity. Thus, the velocity can continue to increase.

4.2. Hydraulic Models for Powder and Mixed Avalanches

The models of the next group are formulated to describe elongated powder avalanches and mixed avalanches (a dense core and a layer of snow powder above it). These models are of hydraulic type: the flow consists of several layers (Figure 9), and the equations in each layer are averaged over the depth [41,45,46,47,48,49].

The equations for a mixed avalanche are written below [41]. These equations describe a one-dimensional motion down a wide slope with the inclination angle $\psi$. Three layers are considered. The lowest layer is the layer of static snow; ${\rho }_0$, $h_0$ are its density and depth. The middle layer models the dense core of the avalanche; its parameters are marked by sub-index 1. The parameters of the upper (powder) layer are marked by sub-index 2; ${\rho }_a$ is the ambient air density.

The volume, mass and momentum conservation equations for the powder layer are

$$\frac{\partial h_2}{\partial t}+\frac{\partial h_2{v}_2}{\partial x}=V_{2a}+V_{21}-V_s,$$

$$\frac{\partial {\rho }_2{h}_2}{\partial t}+\frac{\partial {\rho }_2{h}_2{v}_2}{\partial x}={\rho }_a{V}_{2a}+{\rho }_1{V}_{21}-({\rho }_2-{\rho }_a)V_s,$$

$$\frac{\partial {\rho }_2{h}_2{v}_2}{\partial t}+\frac{\partial {\rho }_2{h}_2{v}_2^2}{\partial x}=({\rho }_2-{\rho }_a)h_{2}sin\psi -\frac{\partial }{\partial x}\frac{({\rho }_2-{\rho }_a)h_2^{2}gcos\psi }{2}-$$

$$-{\tau }_{2a}-{\tau }_{21}-({\rho }_2-{\rho }_a)V_s{v}_2+{\rho }_1{V}_{21}{v}_1-g{h}_2({\rho }_2-{\rho }_a)cos\psi \frac{\partial (h_0+h_1)}{\partial x}.$$

Here, $V_{2a}$, $V_{21}$ and $V_s$ are the rates of change in height due to the entrainment of air, snow and sedimentation, respectively; ${\tau }_{2a}$ and ${\tau }_{21}$ are friction forces at the avalanche air boundary and snow powder layer and dense layer boundary, respectively. The equations for the dense layer are

$$\frac{\partial h_1}{\partial t}+\frac{\partial h_1{v}_1}{\partial x}=-V_{21}+V_{10}+V_s,$$

$$\begin{array}{c}{\displaystyle \frac{\partial {\rho }_1{h}_1}{\partial t}+\frac{\partial {\rho }_1{h}_1{v}_1}{\partial x}={\rho }_1{h}_{1}gsin\psi -\frac{\partial {\rho }_2{h}_{2}gcos\psi }{\partial x}{h}_1-{\tau }_{12}-{\tau }_{10}-}\\ {\displaystyle -\frac{\partial }{\partial x}\frac{{\rho }_1{h}_1^{2}gcos\psi }{2}-{\rho }_1{h}_{1}gcos\psi \frac{\partial h_0}{\partial x}-{\rho }_1{V}_{21}{v}_1+({\rho }_2-{\rho }_a)V_s{v}_2.}\end{array}$$

Here $V_{10}$ and ${\tau }_{10}$ are the rate of height variation and friction force related to an interaction with the snow cover upon which the avalanche moves, respectively.

The equation describing variation of $h_0$ is

$$\frac{\partial h_0}{\partial t}=-V_{10}.$$

The main problem in modeling multilayered flows is to establish reasonable formulas that determine the mass transfer at the boundaries of the layers, as well as mixing with the ambient air and entrainment of snow from the snow cover. In [41,45,46,47,48] the mechanism of mass transfer is associated with the instability of the boundaries of the layers. Such instability leads to the formation of internal waves, their development and destruction. Then the following formulas are reasonable

$${\displaystyle V_{ij}=m_{ij}|v_i-v_j|\frac{\sqrt{{\rho }_i{\rho }_j}}{{\rho }_i+{\rho }_j}.}$$

Here, the indices $i,j$ denote layers with the numbers i and j, respectively, and $m_{ij}$ are empirical coefficients. Their values can be determined by fitting the modeling results for avalanches whose velocity and other parameters have been measured. The complete system of equations and their modifications are presented in [41,45,46,47,48]. The calculations show that the transformation of a dry dense avalanche into a powder one can be described by this model [47,48]. The simulation of real powder and mixed avalanches in Khibiny and Pamir mountains using the multilayered model was performed by Nazarov [46,47,48] and by several students at Moscow University, whose works, unfortunately, have not been published (see the Section 5).

Historical remark. The paper [41] that suggested multilayered hydraulic model for mixed avalanches was published in 1983. During the following decade, the other papers mentioned above appeared [45,46,47,48]. Later, similar models but with different assumptions concerning the formulas for friction and entrainment were published in the western literature [70].

The Analogy of Powder Avalanches and Turbidity Currents

Turbidity currents are flows of a sediment-water mixture moving in ambient water along a sloping bottom under gravity. Physical processes that determine the behavior of such currents are the same as for powder snow avalanches. Both are “flows induced by the action of gravity upon a turbid mixture of fluid and (suspended) sediment, by virtue of the density difference between the mixture and the ambient fluid” [82]. Therefore, mathematical models for powder avalanches and turbidity currents can be similar. There exist different mathematical models for turbidity currents, including hydraulic models [83,84,85,86]. The hydraulic models differ by the formulas that determine the water and sediment entrainment rates. A review of various formulas can be found in [44]. In [85,86] a turbidity current is considered as a turbulent flow. The entrainment rate of ambient fluid is supposed to be proportional to the depth-averaged turbulent mean squared velocity q in the current, i.e., $V_{2a}=\sigma q$, where $\sigma$ is an empirical constant. To have a complete system of equations, the authors use the Reynolds averaged energy equation with the assumption that the turbulent energy dissipation equals $\kappa q^3$ where $\kappa$ is a second empirical constant. In [85] the values $\sigma =0.15$ and $\kappa =0.9$ are suggested.

4.3. Powder Avalanche Models with Resolution in Normal to Bed Direction

The next group presents models based on full (i.e., not averaged over the flow depth, or over the entire body of the avalanche) equations. One of the first models of this type was proposed in [60]. In this paper, a powder avalanche is considered as a turbulent flow of a two-component snow-air mixture. The basic equations are the Reynolds’ equations. The proposed new semi-empirical model for turbulent stresses is in some aspects similar to the well-known Prandtl model. Namely, the stresses can depend on the distance from the bottom. However, the essential difference is that the turbulent stress is assumed to depend also on the integral of the vertical gradient of averaged velocity rather than on the averaged shear rate. Such modification of the Prandtl theory is needed because the vertical profile of the flow velocity is not monotonous in a powder avalanche: the velocity equals zero at the bottom and tends to zero at the upper surface. Some test calculations were made by using this new model, but in those days (1974) no attempts were made to use it to simulate a real avalanche.

Later, 3D models began to develop for powder avalanches and a powder layer in mixed avalanches. They were based on some other semi-empirical turbulence models (mainly the k-epsilon model and its modifications) [87,88,89,90].

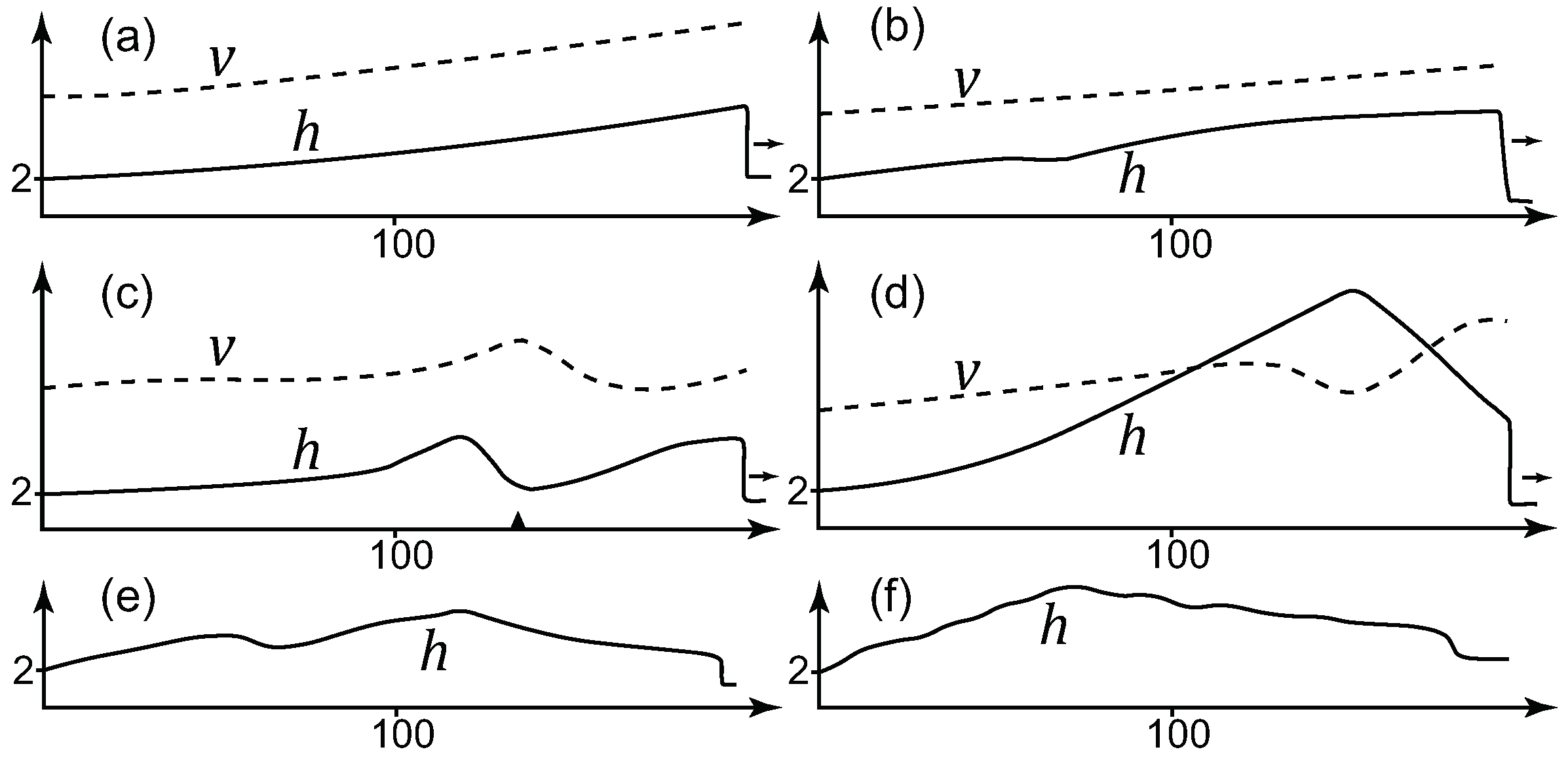
5. Calculations

Calculations by using the models can be divided into two groups. The first group contains numerical investigation of the models and calculations for different hypothetical slopes. The second group deals with avalanches on real mountain slopes.

The aim of the calculations of the first group was to estimate the effect of different terms and coefficients in the equations as well as the initial conditions and the morphometric parameters of the slope. The sensitivity of the model to the errors in the input data was also studied [37,38,45,46,91,92,93]. Numerous calculations using different combinations of values of the parameters and comparison with the data known from observations permitted to obtain possible ranges of the model coefficients.

The results of test calculations are useful for constructing regional empirical formulae to calculate the dynamical parameters and runout distances of avalanches [92].

Below the results of simulations of avalanches occurring in real avalanche catchments are given. Some results concern the catchments, for which the avalanche velocities and depths were not measured. The calculations were based on the data about the boundaries of avalanche deposits and snow distribution before and after the avalanche event. Several avalanches were recorded by stereophotogrammetric methods [94,95]. Two of them were simulated with the use of the models described above.

One of the simulated avalanches is a so-called “Home avalanche” that descends from the slope of the Mount Cheghet (Elbrous region, central Caucasus) several times every winter. The Lomonosov Moscow State University Research Station is situated quite close to this avalanche site. The data about Home avalanche can be found in [96]. Home avalanche was simulated by Ostroumov [33] by using 1D models different for different parts of the avalanche path. The Home avalanche catchment consists of three sections: the starting zone that has a shape of a great funnel, the transit zone—a channel and a runout zone that has a shape of a cone. Ostroumov assumed that the snow in a starting zone moves along the lines of the steepest descent. He replaced the starting zone by a set of channels bounded by these lines and calculated the velocity and the flow thickness at the end of the starting zone using the 1D model for a flow in such a representative channel. The transit zone of the path was approximated by a channel with a rectangular cross-section. The width of the channel was prescribed according to the large-scale map of the slope. In the runout zone, the motion was supposed to occur along the elements of the cone, thus being one-dimensional in polar coordinates. Ostroumov found that the values $\mu =0.45$, $k=0.05$ and ${\sigma }^{*}=2·{10}^4 \mathrm{Pa}$ led to a good agreement of calculated and measured run-out distances for the avalanche.

Ostroumov also simulated avalanches in a catchment Tubri (Low Svanetia, central Caucasus) with the aim to prove the project of constructing a special damb in order to protect a village [40]. The values of the coefficients he used were $\mu =0.22$, $k=0.08$ and ${\tau }_{*}/\rho =16{\mathrm{m}}^2/{\mathrm{s}}^2$.

Simulation of two observed wet avalanches in Apkhiz (west Caucasus) for two similar avalanche catchments II and III above the Moon Glade was made by Mironova [31] using the data obtained by Volodicheva and Oleinikov. Calculations for starting zones and channeled parts were made by using a 1D model, while a 2D model was applied to calculate the motion in the runout zones. The data about the avalanche II were used to find the values of model coefficients: $\mu =0.3$, $k=0.1$, ${\tau }^{*}/\rho =30{\mathrm{m}}^2/{\mathrm{s}}^2$. Using these values, the motion of the avalanche III was simulated and good agreement with the observed data was obtained concerning the runout distance, lateral spreading and the deposits area. Calculations with different possible values of the avalanches volumes were also made. They were used to refine the avalanche hazard maps drawn for that region by using geographical methods.

A similar approach (1D model for a chute and 2D model for runout zone) was applied by Mironova [30] to simulate a dry avalanche in the avalanche catchment 22 in the Khibiny mountains (Figure 10). The motion was recorded by use of sterephotogrammetry [95]. The values of coefficients were found to be $\mu =0.245$, $k=0.05$ and ${\tau }^{*}/\rho =10{\mathrm{m}}^2/{\mathrm{s}}^2$.

On 9 January 1987, a great avalanche that was called Koghutaiskaya descended from the Mount Koghutai (3819 m), Elbrus region. It reached a hotel standing at the foot and destroyed several small buildings. Detailed measurements of the avalanche deposits were made immediately after the event. The data about the snowpack and meteorological conditions were recorded. The map in scale 1:10,000 was also available for the region.

Similar large avalanches were observed at the place in 1932 and 1954. Their traces can be seen even now. Simulations of all these avalanches were made by Mironova [30] by 1D and 2D models. To obtain a good agreement with the measured runout zone boundaries, she modified the equations to include successive layered deposition of the snow in a deposit zone [32]. The values of coefficients for the avalanche 1987 were taken to be $\mu =0.2$, $k=0.02$, ${\tau }^{*}/\rho =10{\mathrm{m}}^2/{\mathrm{s}}^2$.

Simulations of dry avalanches with formation of snow powder clouds were performed in [47] by using 1D two-layer model. A Home avalanche (Elbrus region) and an avalanche in Khibiny mountains were calculated. Both avalanches produced a powder cloud that continued to move after stopping of the dense part. For Home avalanche, the dynamical pressure and its variation in time and space were compared with the measured values [97]. For Khibiny avalanche, the calculated dependencies of the thickness and velocity of the avalanche front on the front coordinate were compared with the measured ones. The agreement was good at $\mu =0.4$, $k=0.02$, ${\tau }^{*}/\rho =6{\mathrm{m}}^2/{\mathrm{s}}^2$ for Home avalanche, $\mu =0.25$, $k=0.02$, ${\tau }^{*}/\rho =10{\mathrm{m}}^2/{\mathrm{s}}^2$ for Khibiny avalanche and $\mu =0.3$, $k=0.02$, ${\tau }^{*}/\rho =5{\mathrm{m}}^2/{\mathrm{s}}^2$ for Pamir avalanches. The data about Pamir powder avalanches can be found in [98] and results of their simulations are presented in [48]. One should have in mind that the two-layer model contains a number of extra coefficients besides $\mu$, k and ${\tau }_{*}$ for a dense layer. These coefficients determine the forces and mass transfer at the dense layer, powder layer and at avalanche ambient air boundaries.

Note that the suggested values for the hydraulic friction coefficients k for all avalanches mentioned above were rather high. Recall that the Voellmy friction coefficient $\xi$ is linked to k by the formula $\xi =g/k$ where g is the gravity force acceleration. Thus, the values of $\xi$ varied from 100 ${\mathrm{m}}^2/\mathrm{s}$ to 500 ${\mathrm{m}}^2/\mathrm{s}$. Similar low values of $\xi$ have been obtained in simulations of avalanches in Ile (Zailiyskiy) Alatau range (Tian-Shan Mountains) [19,38,39].

6. Models Based on Full Equations of Continuum Mechanics Problems

6.1. Weak Points of Hydraulic Models

Hydraulic models for avalanches are fairly easy to use; they can even give analytical formulas for the velocity and other dynamic parameters of avalanches. However, the following two features of hydraulic models call for more advanced three-dimensional models.

First, hydraulic models allow one to calculate only the depth-averaged flow parameters. The velocity and density profiles cannot be calculated. Detailed velocity and densities distributions are very important, for example, for calculating the forces that act on the objects upon impact with an avalanche. Figure 11 shows the result of an avalanche impact against a vertical wall [99,100]. The distribution of the pressure in the flow, and in particular at the wall and on the slope in front of the wall, is very complicated. There are areas of both high and low pressure. This result illustrates that models with the cross-flow resolution are actually needed.

The second weak point of hydraulic models is the presence of empirical coefficients. These coefficients are not related to the physical properties of the moving snow and the underlying material explicitly. To find their magnitudes, a calibration is required for each region, each type of snow and the slope, etc.

3D models that describe the processes inside the avalanche will be free from these shortcomings of hydraulic theories.

For powder snow avalanches, three-dimensional models which account for the vertical structure of the flow were proposed earlier (see, e.g., [12] for a review). Recently, such models for dense avalanches began to develop actively [101,102,103,104,105,106,107]. The next sections are devoted to new models, mainly for dense avalanches.

6.2. Problems Arising at Construction of 3D Models for Dense Avalanches

The first problem, which arises in the formulation of a 3D model, is connected with the so-called rheological relationships for the moving snow, i.e., the dependences of the stresses on strains or strain-rates inside the avalanche. Recall that in hydraulic models, it is sufficient to know the stress on the bottom only. To obtain the rheological relationships, measurements inside the avalanche are needed. The moving snow in dense avalanches can hardly be modeled as an ordinary Newtonian fluid with high viscosity: Newtonian flow cannot stop at an incline, while dense avalanches can.

The second problem is related to the the entrainment of snow by an avalanche. The entrainment law should be based on the physical mechanism of the process, and at the same time it should be expressed in terms of the flow macroscopic parameters. Again, data from experiments and field measurements are needed.

The third problem arises in modeling of turbulence in avalanches. Many semi-empirical models have been proposed for various turbulent flows. Commonly, the existing theories concern flows of Newtonian fluids in pipes. There is no widely accepted turbulence model for 3D open flows of media with complex rheology.

A possible way to create a model that answers all the problems mentioned is as follows.

• Formulation of more or less reasonable hypotheses that are in qualitative agreement with the measurement data.
• Incorporation of the accepted hypotheses into a mathematical and numerical model.
• Investigation of the influence of accepted hypotheses on the flow behavior by solving various simple, specific problems.
• Comparison of the results with the data of measurements to support or reject the accepted hypotheses.

Papers [103,104,105,106] that will be reviewed below follow this method. They contain a study of the influence of hypotheses concerning (a) the rheological relations for moving snow, (b) the entrainment law and (c) the turbulence model. A complete system of equations is formulated only for homogeneous flows on long homogeneous slopes.

6.3. Basic Hypotheses

6.3.1. Rheological Relationships for the Moving Snow

For moving snow, many different rheological models have been proposed, ranging from linearly viscous (Newtonian) fluid to more complex models (see References in [103]). In [103,104,105,106] most of the simulations are based on the use of the so-called Herschel–Bulkley rheological model. This model allows one to describe typical velocity profiles observed in dense avalanches as well as the possibility of stopping an avalanche on an incline. In a simple shear flow, the Herschel–Bulkley model is based on the following relationships:

$$\left\{\begin{array}{cc}\frac{dv}{dz}=0,\hfill & \hfill \mathrm{if}|{\tau }_{xz}|\le {\tau }_y,\\ |{\tau }_{xz}|={\tau }_y+K{\left|\frac{dv}{dz}\right|}^n,\hfill & \hfill \mathrm{if}|{\tau }_{xz}|>{\tau }_y.\end{array}\right.$$

(47)

Here, the x-axis is directed along the flow velocity and the z-axis is directed along the normal to the bottom. K is the consistency index, n is the power-law index and ${\tau }_y$ is a yield stress. The fluid behaves as a solid if the values of the tangential stresses are less than ${\tau }_y$.

For ${\tau }_y=0$ and $n=1$, the model is reduced to a linear viscous fluid. If ${\tau }_y\ne 0$ and $n=1$, Equations (47) correspond to a Bingham fluid. If the power-law index is less than 1, the fluid is pseudoplastic (shear thinning); if n is larger than 1, the fluid is dilatant (shear thickening). Bingham and Herschel–Bulkley fluids with different values of ${\tau }_y$, K and n were suggested for the modeling of snow avalanches, debris flows and other natural slope flows; see

Table 1. Orders of rheological constants in the Hersche–Bulkley model for different natural flows.

$\mathit{\rho }$, kg/m3	${\mathit{\tau }}_{\mathit{y}}$, Pa	K, Pa·s${}^{\mathit{n}}$	n	Comment
200	0	$0.2$	1	dense dry snow avalanche [108]
$400\pm 50$	$740\pm 100$	$0.033$	2	dense snow [109]
2000	400	100	$0.33$	water-debris flow mixture of the concentration $68.4\%$ [110,111]
1300	10	$0.03$	$0.8$	mineral particles suspension of the concentration $3–5\%$ [112]
2600	${10}^5$	${10}^9$	1	silicic lava [113]

for the examples.

In [105] the Cross rheological model is considered, in addition to the Herschel–Bulkey model. For a simple shear flow, the rheological relationship of the Cross model is

$$|{\tau }_{xz}|=\frac{{\displaystyle {\mu }_0+{\mu }_1{k}_c\left|\frac{dv}{dz}\right|}}{{\displaystyle 1+k_c\left|\frac{dv}{dz}\right|}}\left|\frac{dv}{dz}\right|.$$

(48)

Here, ${\mu }_0$, ${\mu }_1$ and $k_c$ are empirical coefficients. An effective viscosity ${\mu }_{eff}\equiv |{\tau }_{xz}/\dot{\gamma }|$ varies between two limits with variation of the shear rate: ${\mu }_{eff}\to {\mu }_0$ at $\dot{\gamma }\to 0$ and ${\mu }_{eff}\to {\mu }_1$ at $\dot{\gamma }\to \infty$ ($\dot{\gamma }\equiv dv/dz$). The Cross model was used in [109] for modeling of a snow flow in a chute.

In papers [103,104,105,106] the rheological relations (47) and (48) for dense avalanches with various values of the coefficients $\mu$, ${\tau }_y$, K, n, ${\mu }_0$, ${\mu }_1$, $k_c$ are used to model the moving snow properties.

6.3.2. The Entrainment Hypothesis

In [103,104,105,106] the entrainment of the underlying material (the basal entrainment) and its influence on the avalanche dynamics are investigated. The approach that was suggested in [51,102] is adopted. Namely, it is assumed that the entrainment of the underlying material occurs if the shear stress at the bottom of the flow (${\tau }_b$) reaches the shear strength ${\tau }_c$ of the underlying layer; ${\tau }_b$ cannot exceed the value ${\tau }_c$. This statement is referred to as the entrainment henceforth (hypothesis I).

6.3.3. Turbulence Models

The snow motion in most large natural avalanches is turbulent. The most common approach for mathematical modeling of turbulent flows is based on the separation of the time-averaged flow characteristics and those for turbulent pulsations. The averaged momentum equations are called the Reynolds equations. They contain turbulent stresses together with the averaged molecular stresses. Then the additional equations for turbulent stresses and, probably, for some other turbulent characteristics should be formulated to obtain the complete system of equations. These equations determine the so-called turbulence model.

In [103,104,106] models based on the Reynolds averaging are used. Then the stresses are the sums of the averaged molecular stresses and turbulent stresses. Two problems arise in this approach. The first one concerns averaging the nonlinear molecular viscosity. In [103,104,106] it is assumed that the rheological relations retain their structure under averaging. The other problem concerns the formulation of the turbulence model. Several turbulence models have been proposed in the literature beginning with the well-known Prandtl model [114]. The main results were obtained in [103,104,106] by the Luschik-Paveliev-Yakubenko (LPY) model described in [103,115].

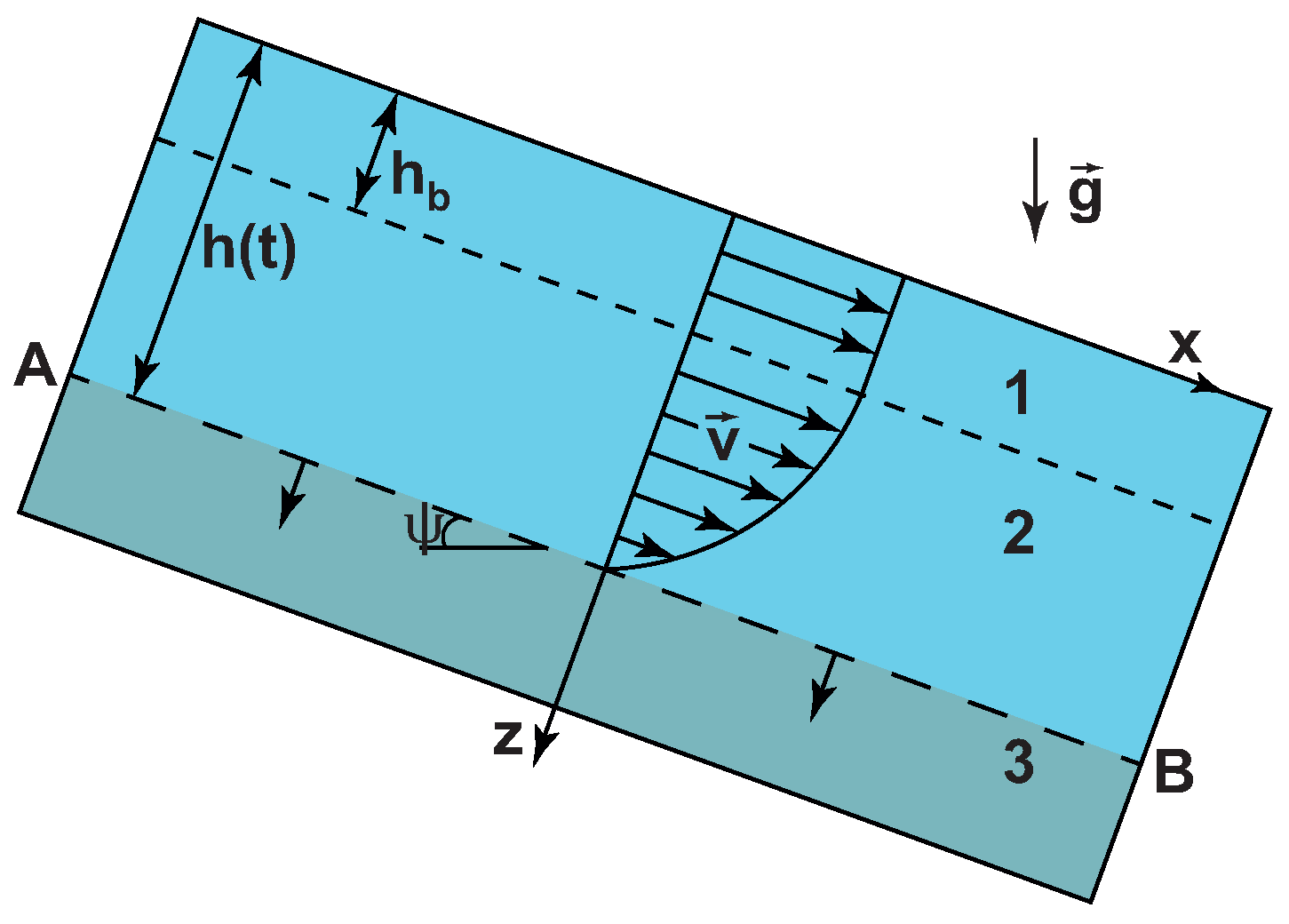
7. Unsteady Uniform Flow down a Slope with Constant Inclination

Construction of a three-dimensional model for dense avalanches on real slopes is a complex problem. Therefore, it is worth starting from a simplified formulation, in which only some properties of the flow are considered. A flow down a slope with constant properties and inclination was investigated in [103,104,105,106]. The main goal was to investigate the basal entrainment and its influence on the dynamics of flows with different rheology.

7.1. Mathematical Statement of the Problem

An unsteady two-dimensional laminar or turbulent flow moving down a slope with constant inclination angle $\psi$ and constant bed material properties (${\tau }_c=\mathrm{const}$) is considered. (Bed material properties are taken into account through the shear strength ${\tau }_c$.) The moving material is incompressible. The flow depth h is constant along the flow, but it can vary in time due to entrainment of the bottom material: $h=h\left(t\right)$.

The coordinate system is shown in the Figure 12. We assume that $v_x=v(z,t)$, $v_z=0$ where $v_x$, $v_z$ are the velocity components for the laminar flow, and they are the Reynolds-averaged (time-averaged) velocity components for the turbulent flow. The longitudinal momentum equation is

$$\frac{\partial v}{\partial t}=gsin\psi +\frac{\partial {\tau }_{xz}}{\partial z},$$

(49)

where g is the gravity force acceleration; ${\tau }_{xz}$ is the shear stress, for the turbulent flow it is a sum of the time-averaged viscous stress and the turbulent Reynolds stress. The momentum equation in the z direction yields the hydrostatic pressure distribution.

The initial conditions for (49) are

$${v(z,t)|}_{t=0}=v_0\left(z\right)(\mathrm{and}h{|}_{t=0}=h_0).$$

(50)

The boundary conditions are following:

• Zero friction at the upper free surface:

  $${{\tau }_{xz}|}_{z=0}=0.$$

  (51)
• No-slip condition at the bottom:

  $${v|}_{z=h}=0.$$

  (52)
  Note that a question whether the no-slip condition is suitable for various natural slope flows has no definite answer yet (see a discussion in [103]).
• An additional condition at the bottom, which is fulfilled for the entraining flow:

  $$|{\tau }_{xz}{|}_{z=h}={\tau }_c.$$

  (53)

The last condition allows to find the position of the entrainment front (see line AB in Figure 12, which is the boundary between the moving medium and the underlying material).

To obtain a closed system of equations, one needs to specify rheological properties of the moving medium, i.e., to add to (49)–(53) certain relations between shear stresses ${\tau }_{xz}$ and strain rates $e_{xz}$. The linear viscous and the Bingham fluids have been considered in [103,106]; the power-law and the Herschel–Bulkley fluids with $n=2$ and the Cross model have been considered in [103,104,105].

7.2. Laminar Flows Entraining the Underlying Snow

The following results have been obtained in [103,105] for laminar flows entraining the bottom material. All of the results listed below are qualitatively the same for flows with all considered rheological properties (see also [102]).

(1) The entrainment starts in two cases: first, if the initial depth $h_0{=h|}_{t=0}$ of the flow is larger than the depth of the stationary flow ($h_{st}$) with the shear stress at the bottom $|{\tau }_b|$ equal to the shear strength of the bed material ${\tau }_c$: $h_0>h_{st}$; second, if the shear strength of the bottom material ${\tau }_c$ is less than the shear stress at the bottom in the flow ${\tau }_b$: ${\tau }_c<\left|{\tau }_b\right|$.

(2) If entrainment occurs, the flow depth, mean and maximum velocities increase. At a large amount of time from the start of entrainment, their dependences on time are approximately linear. This effect does not depend on the rheology of the moving medium (see also [102]). Figure 13 shows the dependences of the flow depth and mean velocity on time for the Herschel–Bulkley fluid with the parameters

$$n=2,\rho =500\frac{\mathrm{kg}}{{\mathrm{m}}^3},K=0.044\frac{\mathrm{kg}}{\mathrm{m}},{\tau }_y={10}^3\mathrm{Pa},$$

(54)

which are close to the parameters found in [116] and for the Cross fluid with the parameters

$$\frac{{\mu }_0}{\rho }=2.52\frac{{\mathrm{m}}^2}{\mathrm{s}},\frac{{\mu }_1}{\rho }=0.29·{10}^{-2}\frac{{\mathrm{m}}^2}{\mathrm{s}},k_c=1.153\mathrm{s}.$$

(55)

The values (55) of the rheological constants have been chosen so that the stationary velocity profile of the flow with the Cross rheology is close to that of the flow of the Herschel–Bulkley fluid with parameters (54).

(3) The velocity profiles have an approximately linear part that is adjacent to the bottom and expanding with time. Examples of the velocity profiles in the flows of the Herschel–Bulkley and the Cross fluids with entrainment are shown in Figure 14. The velocities and the flow depths are close for the flows of the Herschel–Bulkley fluid and the Cross fluid with the parameters (54) and (55).

(4) The entrainment rate $q\equiv dh/dt$ tends to a constant $q^{as}$ with increasing time (Figure 13a,c and Figure 15). The values of $q^{as}$ are different for different rheological models, slope angles and shear strengths of the bottom material.

7.3. Asymptotic Analytical Solution for the Entrainment Rate

An asymptotic analytical formula for the entrainment rate can be derived for large time from the start of the entrainment. Consider the flow layer adjacent to the bottom. In accordance with the calculation results described above, assume the following:

• Due to entrainment, the lower boundary of this layer (the bottom) moves down at a constant speed: $dh/dt=q=\mathrm{const}$.
• The flow is stationary in the coordinate system $(x,\zeta )$, $\zeta =h-z$, which moves with the bottom.

In the moving coordinate system $v_{\zeta }=q$, and the momentum equation in x-direction is

$$q\frac{d{v}_x}{d\zeta }=gsin\psi +\frac{d{\tau }_{x\zeta }}{d\zeta }.$$

(56)

A solution of Equation (56) can be found for the flow of a linear viscous fluid, for which ${\tau }_{x\zeta }=\mu d{v}_x/d\zeta$. Using the condition $v_x{|}_{\zeta =0}$, we have

$$v_x=C_1\left(e^{\frac{q\zeta }{\mu }}-1\right)+\frac{gsin\psi }{q}\zeta ,C_1=\mathrm{const}.$$

(57)

The constant $C_1$ should be equal to zero because $v_x$ cannot grow exponentially with $\zeta$. This yields the result:

$$v_x=\frac{gsin\psi }{q}\zeta =\frac{gsin\psi }{q}(h-z).$$

Therefore, the velocity profile is linear,

$$\frac{d{v}_x}{d\zeta }=A=\mathrm{const},\mathrm{where}A=\frac{gsin\psi }{q}.$$

Using the boundary condition at the bottom

$${\tau }_{x\zeta }{|}_{\zeta =0}={\tau }_c,$$

(58)

and the rheological relation

$${\tau }_{x\zeta }=\mu \frac{d{v}_x}{d\zeta },$$

we obtain

$$\frac{\mu gsin\psi }{q}={\tau }_c.$$

Hence, an asymptotic formulae for the entrainment rate $q^{as}$ and the velocity profile for linear viscous flow are

$$q^{as}=\frac{\mu gsin\psi }{{\tau }_c},v_x^{as}=\frac{{\tau }_c}{\mu }(h-z).$$

For a non-linear dependence of ${\tau }_{x\zeta }$ on $d{v}_x/d\zeta$, Equation (56) cannot be solved analytically. However, we can construct the solution using the additional assumption: at large time values the velocity profile is linear in the considered layer, $v_x=A\zeta$. The validity of such assumption is demonstrated by the computation results shown in Figure 14. Since $A=\mathrm{const}$, i.e., $d{v}_x/d\zeta =A=\mathrm{const}$ and ${\tau }_{x\zeta }=\mathrm{const}$, Equation (56) is reduced to

$$qA=gsin\psi ,\mathrm{where}A=\frac{d{v}_x}{d\zeta }=\mathrm{const}={\left.\frac{d{v}_x}{d\zeta }\right|}_{\zeta =0}.$$

Therefore, the following asymptotic formula for $q^{as}$ is valid for flows with arbitrary dependence of the shear stresses on the shear rates:

$${\displaystyle q^{as}=\frac{gsin\psi }{A}=\frac{gsin\psi }{{\left.\frac{d{v}_x}{d\zeta }\right|}_b}=\frac{gsin\psi }{{\left|\frac{d{v}_x}{dz}\right|}_b},}$$

(59)

where the subindex b marks the value at the bottom. The value of $A={\left.\frac{d{v}_x}{d\zeta }\right|}_b$ can be found from the boundary condition (58). For instance, for the Herschel–Bulkley fluid

$$\begin{array}{c}{\tau }_{x\zeta }{|}_b={\tau }_y+K{\left.{\left(\frac{\partial v_x}{\partial \zeta }\right)}^n\right|}_b={\tau }_y+K{A}^n={\tau }_c,\mathrm{therefore},A={\left(\frac{{\tau }_c-{\tau }_y}{K}\right)}^{\frac{1}{n}}.\end{array}$$

When the constant A is found for corresponding rheological model, the asymptotic formulae for the entrainment rate $q^{as}$ and flow velocity $v_x^{as}\left(\zeta \right)$ can be obtained

• for the Herschel–Bulkley fluid

  $$q^{as}=gsin\psi {\left(\frac{K}{{\tau }_c-{\tau }_y}\right)}^{\frac{1}{n}},v_x^{as}={\left(\frac{{\tau }_c-{\tau }_y}{K}\right)}^{\frac{1}{n}}\zeta ,$$

  (60)
• for the Cross fluid

  $$q^{as}=\frac{2{\mu }_1{k}_{c}gsin\psi }{{\tau }_c{k}_c-{\mu }_0+\sqrt{{({\mu }_0-{\tau }_c{k}_c)}^2+4{\mu }_1{\tau }_c{k}_c}},v_x^{as}=\frac{{\tau }_c{k}_c-{\mu }_0+\sqrt{{({\mu }_0-{\tau }_c{k}_c)}^2+4{\mu }_1{\tau }_c{k}_c}}{2{\mu }_1{k}_c}\zeta .$$

  (61)

Recall that $\zeta =h-z$, z-axis is directed from the upper boundary to the bottom (see Figure 12).

Expressions for the asymptotic entrainment rates and flow velocities for a linear viscous, power-law and Bingham fluids follow from (60) if ${\tau }_y=0$, $n=1$; or ${\tau }_y=0$, $n\ne 1$; or $n=1$, ${\tau }_y\ne 0$, respectively.

Analytical formulae (60) and (61) show that the asymptotic entrainment rate depends on the gravity acceleration, slope angle $\psi$, bed material shear strength ${\tau }_c$ and rheological constants of the moving medium. Note that the dependence of $q^{as}$ on $sin\psi$ is linear. The entrainment rate q is higher for higher yield stress ${\tau }_y$ (see (60) and Figure 16).

The values of the entrainment rate $q^{as}$ obtained analytically are in agreement with the results of calculations. For instance, formula (60) gives $q=0.073$ m/s for parameters (54) (see Figure 15); formula (61) gives $q=0.059$ m/s for the set of parameters (55). In [50] the value of basal entrainment rate $0.05$ m/s is given for the flow with the density $\rho =200$ kg/m³. The order of entrainment rate in [50] is close to entrainment rates obtained in our calculations. Thus, it can be expected that our approach is suitable for modeling the avalanche basal entrainment.

Remark 3.

The solutions described above were constructed for large values of time, strictly speaking, for $t\to \infty$. Therefore, we assumed an infinitely large thickness of the entrainable layer. However, calculations show that the dependences of h on t become linear, and, accordingly, the entrainment rate becomes approximately constant within a few seconds after the start of the enrainment. The thickness of the layer that was entrained during these seconds is not large (see Figure 13a,c and Figure 15). In fact, asymptotic formulas can be used after a fairly short period of time from the start of the entrainment.

Remark 4.

Simulations have been performed for idealized situations: homogeneous flows on homogeneous slopes. Besides, the values of the coefficients defining the rheological properties of the moving medium and of the shear strength of the bottom material do not exactly correspond to any real materials. Therefore, the results cannot be directly applied to describe a real avalanche. However, they show certain qualitative features of the flows entraining the bottom material, which can be confirmed (or refuted) by observations.

7.4. Turbulent Motion of Avalanches. Results of Numerical Investigation

This section is devoted to turbulent unsteady open slope flows. The results of investigation of the effect of rheological properties and of the entrainment of the underlying material are presented. The entrainment hypothesis I described in Section 6.3.2 is used to model the basal entrainment. As in the previous sections, the homogeneous flows on long homogeneous slopes are studied (see Figure 12). In [103,104,106] the models for such flows are proposed based on the Reynolds-averaged equations and the generalized Lushchik-Paveliev-Yakubenko (LPY) three-parameter turbulence model [115].

LPY-model contains three differential equations for turbulence parameters T (the turbulent shear stress per unit mass), E (the turbulence kinetic energy per unit mass) and $\omega =E/L^2$ where L is the turbulence length scale. A detailed description of application of LPY-model for slope flows modeling, as well as the equations for T, E, $\omega$, and the values of the model coefficients are given in [103,104,106]. Numerical methods have been developed and software has been created by the authors to simulate steady and unsteady turbulent flows. Series of simulations of stationary and non-stationary flows of media with different rheological properties have been performed. The velocity, turbulent stress and turbulent energy profiles, as well as the magnitudes of the bed material entrainment rate were calculated and compared. Their variations with time were investigated [103,104,106].

First, the turbulent flows without entrainment were considered. In particular, the effect of the yield stress on the flow velocity was studied. In laminar stationary flows (without entrainment), the increase in the yield stress ${\tau }_y$ leads to the flow velocities decrease (Figure 17b). For turbulent flows, the influence of the yield stress can be the opposite. For the studied range of yield stresses, an increase in the yield stress leads to an increase in the velocity throughout the flow except for a thin layer near the bottom. A possible explanation for this effect is that the presence of a yield strength reduces the turbulence intensity. In Figure 17a, the velocity profiles in stationary turbulent flows of linear viscous (${\tau }_y=0$) and Bingham (${\tau }_y/\rho =0.2{\mathrm{m}}^2/{\mathrm{s}}^2$) fluids are compared. The results shown in Figure 17 have been obtained using the following input data: $\theta ={30}^{\circ }$; $\nu =0.001{\mathrm{m}}^2{\mathrm{s}}^{-1}$, $h=1\mathrm{m}$ for turbulent flows, and $\nu =0.01{\mathrm{m}}^2{\mathrm{s}}^{-1}$, $h=0.5\mathrm{m}$ for laminar flows.

Turbulent stresses and turbulent viscosity coefficient defined as the ratio $\left|\rho T\right|$ to $|\partial v_x/\partial z|$, are smaller in the Bingham flow than that in the linearly viscous one (Figure 18).

The following results concern the turbulent flows with entrainment. One of the results is related to the flow velocity profiles. In entraining turbulent flows of fluids with different rheologies (linear viscous, power-law and Bingham rheological models) the velocity profiles, contrary to laminar flows, have no expanding linear parts adjacent to the bottom. The near-bottom velocity profiles in terms of the so-called “wall” variables ($v^{+}$, $z^{+}$, see [104] for definition of these variables) do not depend on the flow rheology.

The next results concern the influence of entrainment on the flow velocities. In entraining turbulent flows with different rheologies, the flow depth, maximal and mean velocities increase in time. At large time from the start of the entrainment, their dependencies on time are approximately linear, similarly to laminar flows with entrainment. The entrainment rate at large time tends to a constant in turbulent flows, as it does also in laminar flows. However, the magnitude of the entrainment rate is significantly higher in turbulent flows.

Turbulent stress $\left|T\right|$ and turbulent energy density E distributions have two local maxima in entraining flows. One of these maxima is located near the bottom, while the other is in the central part of the flow. If the bottom material entrainment continues, the turbulent parameters at points of their maximum will increase near the bottom and decrease in the main flow.

8. Conclusions

We have presented a review of the studies of dynamics of natural slope flows conducted in USSR and Russia over the last 50 years.

In recent years, some attempts have been made to develop models of dense snow avalanches based on full, non-depth-averaged equations of continuum mechanics. Validation of such models is difficult because it requires accurate experimental data about the distributions of the velocity, shear stresses and turbulent characteristics across the entire flow. The other problem is related to the modeling of turbulence. For most common turbulence models based on the Reynolds averaging, the model coefficients have been fitted for flows of Newtonian fluids only. True avalanche simulations need to take into account non-Newtonian properties of the moving medium. Therefore, a large amount of work is needed in order to determine the constants of the turbulence models for media with different rheology.

The hydraulic-type models discussed in Section 2 are significantly simpler than the models based on the equations of continuum mechanics, and they require less experimental data for confirmation of their validity. Thus, exact distributions of the dynamic characteristics across the flow are not needed, and only depth-averaged values are important. Nevertheless, the models can incorporate rather complex phenomena typical for dense snow avalanches such as the possibility of the flow to stop at the slope and the entrainment of the underlying material and the snow in front of the avalanche. Analytical solutions discussed in Section 3 can be used for validation of increasingly evolving numerical models.

To use the theoretical models described here, one should know the values of model coefficients. Relations between the coefficients’ values and conditions at a slope are not established reliably because of lack of measurements for real moving avalanches. Still, there are some data that can be used to estimate avalanche parameters by mathematical simulations.