Abstract
Flow and transport processes in fractured systems are not yet fully understood, and it is challenging to determine the respective parameters experimentally. Studies on 10 samples of 2 different sandstones were used to evaluate the reproducibility of tracer tests and the calculation of hydraulic transport properties under identical boundary conditions. The transport parameters were determined using the advection–dispersion equation (ADE) and the continuous time random walk (CTRW) method. In addition, the fracture surface morphology and the effective fracture aperture width was quantified. The hydraulic parameters and their variations were studied for samples within one rock type and between both rock types to quantify the natural variability of transport parameters as well as their experimental reproducibility. Transport processes dominated by the influence of fracture surface morphology experienced a larger spread in the determined transport parameters between repeated measurements. Grain size, effective hydraulic aperture and dispersivity were identified as the most important parameters to evaluate this effect, as with increasing fracture aperture the effect of surface roughness vanishes and the experimental reproducibility increases. Increasing roughness is often associated with the larger effective hydraulic aperture canceling out the expected increased influence of the fracture surface morphology.
1. Introduction
Fractures are often the dominant fluid pathways in the subsurface due to the usually low intrinsic permeability of the reservoir rocks. Detailed investigations of flow and transport processes in a single fracture contribute to the understanding of flow and solute transport in complex natural fractured systems [1,2,3,4,5]. Such investigations and the understanding of those processes are very important for practical applications, such as geothermal energy production [6] and the effective remediation of pollutants [7].
The flow in single fractures is laminar or turbulent depending on the Reynolds number (Re). Laminar flow allows the application of Darcy’s Law, whereas turbulent flow requires nonlinear relationships between flow velocity and hydraulic gradient, as given in Forchheimer’s equation. Several studies suggest limits for the transition from laminar to turbulent flow in rough, single fractures ranging from Re = 10 [8] to Re = 500 [9,10], and even up to Re = 2000 [11]. The occurrence of turbulent flow is mainly due to roughness [1,12], because surface roughness affects the permeability of a single fracture due to a heterogeneous aperture distribution. Variable aperture distributions result in higher proportions of preferential flow channels [5,7,13] and low velocity zones that include turbulent flow features like eddies [2,3,14]. The surface morphology of a fracture can be determined in the laboratory using different methodologies, such as profilometry [15], photogrammetry [16], microCT [17] and laser scans [18,19,20]. Since the specific area decreases with growing aperture, the influence of roughness on the permeability decreases with increasing aperture [16,21]. There are various measures to quantitatively describe various features of the surface roughness (e.g., [22,23]). Very common, especially in geotechnical applications, is the joint roughness coefficient (e.g., [24]) based on the Z2-coefficient [25]. Surface roughness evaluation is often based on the analysis of height variations along profiles, but triangulation-based measures become more common (e.g., [26,27]).
A more complex velocity field of a rough fracture compared to a smooth fracture is the cause for additional dispersion, as shown in the numerical study of [19]. Dispersion is the governing process influencing the solute transport in a single fracture. After [28], one can theoretically distinguish between molecular diffusion, Taylor dispersion and macrodispersion. In experimental studies, such a differentiation is not possible, although all three processes have a different impact on dispersion depending on the Peclet number [29]. In a common approach to determine transport parameters, an analytical solution of the advection–dispersion equation (ADE) [7,30,31,32,33] or of the continuous time random walk (CTRW) method is fitted to the measured breakthrough curves (BTCs) resulting from the tracer tests [30,34,35,36,37]. Long tailing and early arrival times of the BTCs often reveal non-Fickian transport behavior, which can usually be well described by the CTRW method but not by the ADE. A higher proportion of turbulent flow also affects solute transport with a higher degree of non-Fickian transport [3,30]. Random walks methods have also been applied successfully in simulations covering tracer transport across scales, from pore to reservoir scales [38]. In a different approach, fractional derivatives have been used to couple a modified flux law for complex flow fields with a classical mass conservation to describe transport in fractured low-permeable material [39].
In recent years, several experimental and numerical investigations of flow and transport behavior in single fractures have been carried out covering both reactive and non-reactive processes. Various types of rocks have been studied using tracer tests, including granite [40], diorite [13], dolomite [7], limestone [41], marble [34] and also sandstone [30,42]. Fracture surfaces were also scanned frequently and reconstructed on the basis of these scans [31,32,35,36]. Often, those studies focused the change in the fracture surface structure due to dissolution or precipitation processes and its influence on flow and transport processes [31,40,41]. The influence of flow velocity on the shape of BTCs [34] as well as on fracture heterogeneity and its effect as a retardation mechanism [13] has also been studied experimentally. It remains a challenge in all these studies to determine the transport parameters for single fractures due to differences in the experimental procedures and the used analysis method to determine these parameters.
However, hydraulic and transport experiments on drill cores, often in combination with geostatistical analysis, are a very common source for hydrogeological numerical simulations on fracture flow. Laboratory tests are usually the preferred method in comparison to values taken from the literature, because they provide more local information. In the context of fractures, it also very rare to recover fractured core samples with sufficient size and quality for laboratory flow tests. Artificial fracturing on intact drill cores in the laboratory is often the only possibility to study fracture flow. However, coping with measurement uncertainty and spatial variability is challenging in those numerical models due to the usually underdetermined subsurface parameters and a very limited number of drill cores. Furthermore, there is a natural variability between fractures due to their unique surface morphology. To quantify this variability, a sufficient number of rock samples and tests is required. To experimentally reveal this natural variability, reproducible laboratory tests are necessary.
In this work, we analyze repeated tracer tests in ten rock samples with a single fracture in each of two different types of sandstones. The flow and transport parameters, such as flow velocity, dispersivity and dispersion coefficient, are determined using ADE and CRTW fits. A comparison of the parameters is made between (i) both calculation methods; (ii) samples drilled from the same material area; (iii) samples from different sections; and between (iv) the two types of sandstone. Through this analysis, we can quantify the reproducibility of tracer tests within a single fracture as well as the natural variability of flow and transport parameters of single fractures. Laboratory tests and the parameters determined by those tests are often the base for the parameterization of numerical models. Including the heterogeneity of fracture parameters in such models is challenging due to the unknown conditions in the subsurface and the described shortcoming of conventional laboratory tests. Our experiments allow an estimation of the value range of hydraulic and transport parameters in single fractures representing their natural variability. Therefore, in the following, we characterize the used samples and describe sample preparation as well as the applied experimental procedure. We explain the applied analysis methods for the tracer tests using the ADE and the CTRW. We further relate the results to the characteristics of the different types of used sandstones such as grain size distribution and homogeneity.
2. Materials and Methods
2.1. Samples and Sample Preparation
Two different sandstones were used for the investigations: Flechtinger and Remlinger sandstones. Flechtinger sandstone is quarried at the Flechtinger mountain ridge (Saxony-Anhalt, Germany). The samples were taken from a quarry in Bebertal. It is a reddish-brown colored, well consolidated, well-sorted, cross-bedded and fine-grained Permian sandstone [43,44] with a matrix permeability in the order of 10−17 to 10−16 m2 [44,45,46]. The mean grain size is between 0.1 and 0.4 mm [44], and the porosity was determined in ranges between 6% and 11% [43,44,45]. The porosity of intact samples was determined with a mean value of 9.6 (±0.1)%. The mean permeability was determined as 4.96 × 10−17 (±1.01 × 10−18) m2. Optically, the Flechtinger sandstone seemed to show a high heterogeneity and anisotropy.
The Remlinger sandstone was selected in a quarry at the Thüngersheimer Anticline in Würzburg (Bavaria, Germany). The Remlinger sandstone can be assigned to the Triassic (Upper Buntsandstein) and, in contrast to the Flechtinger, has a much stronger red color. There are hardly any investigations using the Remlinger sandstone. The porosity of intact samples was determined with a mean value of 12.90 (±0.28)%, and the permeability was determined with a mean value of 5.50 × 10−17 (±8.24 × 10−18)m2 by [30]. Therefore, the Remlinger samples had intrinsically a higher porosity than the Flechtinger samples, but both sandstone types had a similar permeability. Visually, the Remlinger sandstone seemed much finer grained and more homogeneous and isotropic than the Flechtinger sandstone.
Samples were drilled from different blocks from the respective quarries with a length of 150 mm (y-/flow-direction) and a diameter of 100 mm (x-direction). Drilling was performed perpendicular to the stratification. The samples were labeled with three characters to determine their origin (either “Fle” or “Rem”): the number of the block they were drilled from, the diameter and the number of core drilled from the block. As an example: the samples “Rem_4_100_S2” and “Rem_4_100_S3” are both Remlinger sandstones from the same block “4” with 100 mm diameter. The drilled samples were fractured through a Brazilian test over the length of the sample, and the drill core halves were marked with a red and black sign to distinguish them. The reassembled core halves were covered with a shrinking tube (PTFE 400–101, 6/25, 4 mm (4”)–nature, wall thickness before shrinkage approx. 0.1 mm) and saturated using a desiccator connected to a vacuum pump prior to the flow-through experiments. Prior to the Darcy and tracer tests, the samples were fixed in a clamping device with sealing rings at the top and bottom (P 583/NBR 70, 90 mm diameter, 4 mm cord thickness) and manufactured Teflon devices with tube connections. The conical shape at the inside of the Teflon devices avoided dead water volume or turbulences. Through the clamping device, all parts were pressed together to seal the system.
2.2. Experimental Setup and Procedure
All Darcy and tracer experiments were performed under the same boundary conditions to conduct reproducible experiments in a laboratory setup (Figure 1). A pressure difference dh of 0.7 m between inflow at the bottom and outflow at the top of the sample was applied over the sample length dx of 0.15 m. This resulted in a hydraulic gradient i(x) of 4.67. The pressure difference was obtained using an overflow tank and constant recharge. Darcy tests were performed to ensure a constant fluid flux and to determine the flow rate by weighing the volume of water that flowed through the fracture with a laboratory scale (accuracy 0.1 g) in relation to time. The measuring interval was set to 1 min, and the measurement duration was 30 min for the Darcy tests once constant fluid flux was achieved. Tracer experiments were used to determine transport parameters (velocity, dispersivity, dispersion coefficient). The tracer injection was a pulse with a duration of one second with a volume of 1 mL of a 2 molar NaCl solution. The electrical conductivity (EC) was measured at the outflow with a WTW Multi 3510 (Xylem Analytics Germany Sales GmbH & Co. KG, WTW Weilheim, Germany) conductivity logger and an associated Tetracon 925c conductivity sensor (measuring accuracy for electric conductivity 0.5% of the measured value and 0.1 °C for temperature) with an interval of 1 s. To convert the measured electric conductivity of the breakthrough curve into the tracer concentration, a calibration curve was obtained by preparing NaCl solutions of different concentrations (0.001 to 0.02 mol/L). These were then used to measure the resulting electrical conductivity. We achieved a linear regression (c (g/L) = 5.0523 × 10−4 × EC with R2 = 0.9997) for the conversion from conductivity into concentration. The apparatus used for the flow-through experiments is described in more detail in [30].
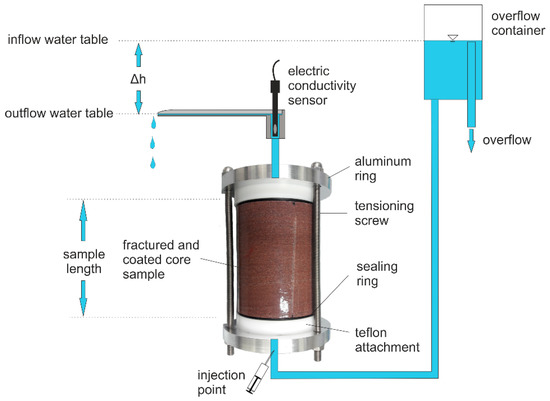
Figure 1.
Experimental setup used for the Darcy and tracer experiments.
2.3. Determination of Hydraulic Parameters
The effective fracture opening width aeff (m) of the samples was determined by a conversion of the cubic law [47,48].
with flow rate Q (m3/s), the dynamic viscosity µ (kg/ms), the density ρ (kg/m3), fracture width LW (m), gravitational acceleration g (m/s2), hydraulic pressure difference dh (m), aperture length in flow direction LL (m) and the dimensionless Reynolds number Re (–). The Reynolds number was determined following [48].
where νkin (m2/s) is the kinematic viscosity. The fracture permeability K (m2) was determined following [49] based on Darcy’s Law [50,51,52].
2.4. Determination of Transport Parameters
The one-dimensional ADE describes the evolution of the tracer concentration c (kg/m3) over time t (s) in flow direction for a steady transport velocity v (m/s) and dispersion coefficient DL(m2/s) without retardation effects.
There is an analytical solution to this equation for a pulse injection of length t0 (s) and pulse concentration c0 and the initial condition c(y,t = 0) = 0.
with
Using a least square fit routine, the analytical solution can be fitted to experimentally-obtained BTCs to determine the parameters v and DL.
The CTRW is a Laplace transformation of Equation (4) using a memory function M [53]. Using the Laplace variable u (1/s) and applying similar boundary and initial conditions as above, Equation (4) can be expressed in the Laplace space as
with velocity v and dispersivity D in the Laplace space. For a comparison of parameters between ADE and CTRW, v and D need to be transformed into the time domain. The memory function is given by
with a characteristic time tchar and function φ, which can have different shapes to represent microscopic heterogeneity. The truncated power law (TPL) is a common choice for fracture flow (e.g., [54,55]) but introduces three additional parameters that need to be defined during the fitting process: transition time t1 marking the beginning of the power law behavior; t2, the cut-off time; and the parameter β. The latter was successfully interpreted in terms of surface roughness and as an indication of non-Fickian transport behavior (e.g., [30,36]). Especially, a complex flow field and a heterogeneous dispersion can be represented with the TPL. The TPL is given as
With the CTRW Toolbox (version 4.0) provided by [55], a solution of Equation (7) can be numerically obtained in the Laplace space and transformed into the time domain for comparison and interpretation of parameters.
For both procedures, ADE and CTRW, starting values of the least-square fitting procedure using the MATLAB (Mathworks Inc.) curve fitting toolbox were obtained through trial and error to obtain a visually good fit. The minimization process was conducted until a step size tolerance of less than 10−9 was achieved. The fitting error was expressed by the squared residual norm.
2.5. Characterization of Fracture Roughness
The surfaces of the cores were scanned prior to their reassembling with the 3D laser scanner (NextEngine ScanStudio PRO). A resolution of 17,000 points per square inch was used. The scanned surfaces were filtered for obvious outliers, rotated and aligned to the horizontal and subsequently interpolated to a regular grid. The relative height was calculated to an interpolated reference plane (Figure 2). A closed surface was obtained from the point cloud using the Delauney triangulation. For quantitative analysis, the surface angularity and the Z2s coefficient of the surface were calculated. The Z2s coefficient for a rectangular surface with Nx points in x-direction and Ny points in y-direction with relative height dz is defined as
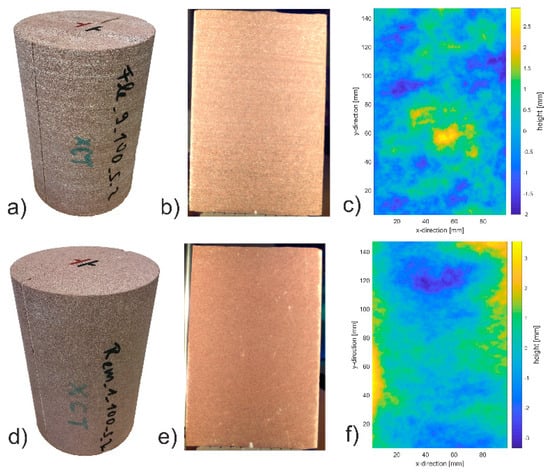
Figure 2.
Exemplary fractured samples of Flechtinger (a) and Remlinger sandstone (d), one fracture surface scan of the same Flechtinger (b) and Remlinger (e) sample, and the calculated relative height values based on the surface scan (c,f).
For the triangulated surface, the surface angularity θs is defined as the mean angle between all normal vectors of the triangles of the closed surface and the normal vector of the horizontal.
3. Results
3.1. Determination of Hydraulic Parameters
Fracture opening width and permeability were determined for each tracer test after reaching a constant flow rate (Table 1). Three tracer experiments were carried out for each core in order to test its reproducibility and to allow statistical evaluation of the results. For both sandstone types, the fracture permeability was several magnitudes larger than the permeability of the intact samples. Therefore, fracture flow was dominant and matrix flow could be neglected for the duration of the experiments. The calculation of the Reynolds numbers (Equation (2)) resulted in values between 12 and 25 for the experiments with the Flechtinger samples and between 2 and 10 for the Remlinger cores. Based on the extensive discussion about the upper limit of the Reynolds number in the literature for the transition from laminar to turbulent flow regimes, we assumed for our experiments laminar flow conditions in the fracture following the limits defined by [56].

Table 1.
Results of the calculations for aperture width and permeability of the core fractures, including standard deviation.
The Flechtinger samples had a substantially larger effective aperture width of around 130 μm, corresponding to a permeability of approximately 1.30 × 10−9 m2. The Remlinger samples had effective aperture widths of around 90 μm, corresponding to a permeability of around 7.00 × 10−10 m2. Both permeability values were absolutely reasonable for fresh rock fractures. The standard deviations of the Remlinger samples were significantly larger than for the Flechtinger samples, and, relatively, the spread of effective aperture widths across the Remlinger samples was larger than for the Flechtinger samples.
3.2. Determination of Transport Parameters Using CTRW
The CTRW fit was calculated for the 30 experiments conducted to determine the transport velocity, dispersion coefficient and dispersivity α (m). Transport velocity and dispersion coefficient are closely related to the effective fracture aperture width. The dispersivity is the ratio of dispersion coefficient and velocity and can therefore be considered independent from the hydraulic behavior. However, fitting parameters of the CTRW are v and DL. The α was calculated afterwards based on those results (Table 2). For each sample three repetitive experiments were conducted and analyzed separately. From the three repetitive experiments, mean and standard deviation were calculated for the obtained parameters from the CTRW fit.

Table 2.
Mean values and standard deviation of transport parameters determined by the continuous time random walk (CTRW) fit.
Reasonable CTRW fits were achieved for all curves. Slightly better fits were achieved for the Remlinger experiments than for the Flechtinger. In correspondence with the hydraulic parameters (Table 1), the transport velocities and dispersion coefficients of the Flechtinger samples were larger than for the Remlinger samples. Tests on both rock types resulted in similar values for the dispersivity. While the standard deviation was roughly around 15% of the mean value, several samples had significantly larger standard deviations of up to 50% or more. An example of the separate tests for both rock types is given in Table 3.

Table 3.
Transport parameters determined by the CTRW fit for two samples.
There was not just a varying degree in the parameters determined by the numerical analysis method, which is subject to modeling error and fitting accuracy, but also a variety in the experimentally obtained BTCs (Figure 3). While the quantitative difference between the rock types seen for the mean values was also visible on the separate tests, the BTCs also showed qualitative differences. In addition to the transport parameters, the TPL parameter β is also shown in Table 3. The obtained values were very similar across tests and rock samples.
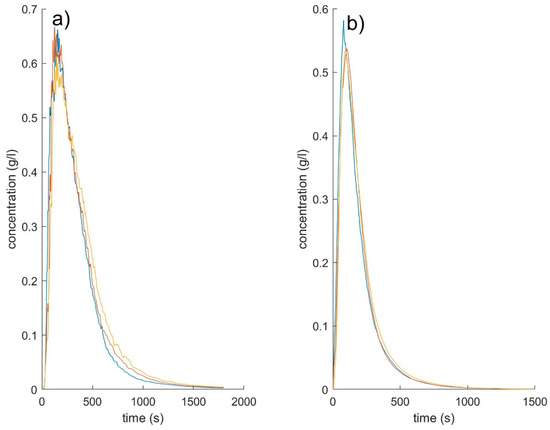
Figure 3.
Experimentally obtained breakthrough curves (BTCs) for (a) Remlinger Rem_1_100_S1 and (b) Flechtinger Fle_9_100_S1. Colors indicate the separate repeated measurements.
The Remlinger sample showed more high frequency oscillations overlaying the general BTC behavior. Due to the lower transport velocity, the tracer curve had a longer duration of approximately 1800 s to decline to the background concentration. In the shown Flechtinger sample, the background concentration could be observed after approximately 1300 s. Visually, the BTCs of the Flechtinger sample were more difficult to distinguish than the Remlinger BTCs, indicating that the variation between the repeated measurements was smaller. The repeated measurements of the Remlinger sample could be more easily distinguished visually due to the high-frequency oscillations and due to differences in peak concentrations. The BTCs of the Flechtinger tests showed almost no variation in peak concentration and very little variations in the tailing (Figure 4). The onset of the BTC was not quantitatively evaluated but was in agreement with the calculated velocities. The beginning of the BTCs was visibly earlier in the Flechtinger samples than in the Remlinger samples.
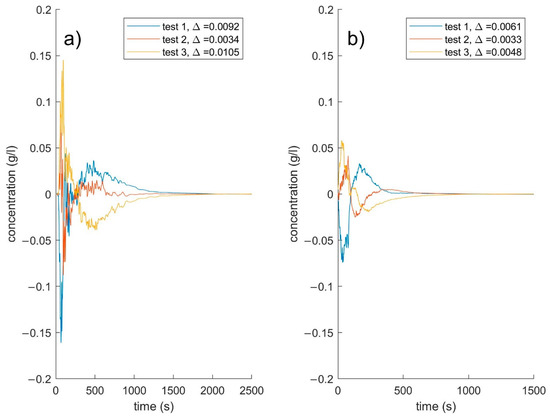
Figure 4.
Difference of the three repeated measurements from a common mean BTC for the (a) Remlinger Rem_1_100_S1 and (b) Flechtinger Fle_9_100_S1 with the absolute mean difference Δ.
It is obvious from the BTCs that the Remlinger samples had significant more divergence between the repeated measurements in comparison to the Flechtinger samples (Figure 3). If a common mean BTC for the three repeated measurements of a sample was calculated and then the difference of each BTC to this common mean was calculated, the difference between Flechtinger and Remlinger became even more obvious (Figure 4). The divergence between Remlinger samples was almost three times larger in amplitude than for the Flechtinger samples and remained for significantly longer times in the Remlinger samples. The strongest variations in concentrations were observed at the peak of the BTCs. Quantitatively, the deviations between repeated tests of the Remlinger samples were up to twice as large as those between repeated tests of the Flechtinger samples. However, due to the smaller hydraulic aperture, these obvious differences between repeated measurements were not as obvious in the standard deviations of the calculated parameters or in the relative error, as was expected from the visual differences of the BTCs.
3.3. Determination of Transport Parameters Using ADE
The same experiments that were studied using the CTRW fit were also used to fit the analytical solution of the ADE. Similar to the CTRW, transport velocity and dispersion coefficient were the fitting parameters, and the dispersivity was calculated subsequently (Table 4). Again, for most experiments, reasonable fits were achieved, as expressed by a squared residual norm smaller than 1. However, there were a few samples, such as Rem_2_100_S1 and Rem_1_100_S2, for which the residual was comparably high. The obtained values for the transport velocities and dispersion coefficients were larger for Flechtinger than for Remlinger samples. In the dispersivity, no clear separation between both sandstones could be observed. In general, transport velocities and dispersion coefficients determined using the ADE are higher than those using the CTRW. In addition, the dispersivity values were higher in the ADE fit, indicating that velocity and dispersion coefficient did not increase equally in the ADE compared to the CTRW.

Table 4.
Mean values and standard deviations of transport parameters determined by the advection–dispersion equation (ADE) fit.
The parameters determined using the ADE fit for same two exemplary samples from Table 3 are shown in Table 5. All three tests resulted in quite similar values for the fitting parameters for each sample, but the difference between the different samples was obvious. Only dispersivity was again quite comparable for both samples with slightly higher values for the Remlinger sample. Quite clearly, the ADE fit was a better match for the Flechtinger than for the Remlinger sample.

Table 5.
Transport parameters determined by the ADE fit for the two samples.
Both fits, CTRW and ADE, were visually in quite good agreement with the experimental data, as also expressed by the squared residual norm (Figure 5). However, in detail it could be seen that the ADE fit was a better match for the Flechtinger than for the Remlinger sample. The ADE fit was unable to match the tailing of the BTC in the Remlinger sample. Peak concentration, onset and shape of the BTC, as well as the duration of the tracer tests, were reproduced by both fitting methods. BTCs with multiple peaks could only be approximated correctly by the CTRW, causing larger residuals in the ADE (e.g., Rem_2_100_S3).
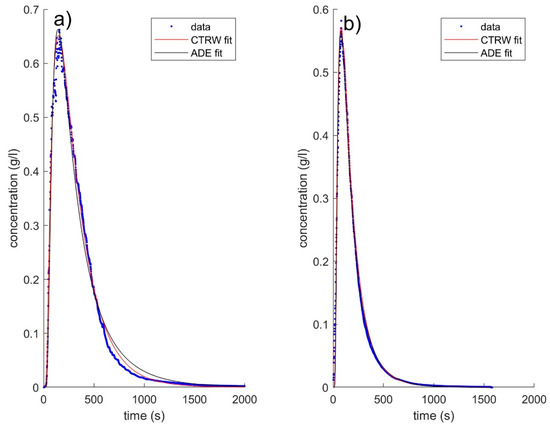
Figure 5.
Experimentally obtained BTCs and forward modeling of parameters obtained from the CTRW and ADE fits for (a) Remlinger Rem_1_100_S1 and (b) Flechtinger Fle_9_100_S1.
Naturally, both fitting methods smoothed the experimental data. The observed and previously described high frequency oscillations interfering with the general trend, especially in the Remlinger sample, could not be reproduced by any of the fitting methods. These oscillations were especially high around the peak concentration, so that the fitting was blurred there and a median fit describing the experimentally data best with all the variations was calculated based on the used non-linear least square fit.
3.4. Comparison of Fracture Surface Morphology
The two calculated surface roughness measures revealed very similar behaviors between the samples (Figure 6). Most significantly, the Flechtinger samples had a higher Z2s value as well as a higher surface angularity. Both quantities followed a similar trend across most samples. For example, the sample Fle_10_100_S1 had the highest Z2s value as well as the highest surface angularity. However, small differences between both quantities were detectable. The sample Fle_9_100_S2 had, relative to the sample Fle_9_100_S1, a higher Z2s value but almost the same surface angularity. Compared to the variation across the Flechtinger samples, this difference was small. The absolute difference between Flechtinger and Remlinger samples was around 5° for the surface angularity and around 0.1 for Z2s value. Considering that typical surface angularities can be up to 40 degrees or more and that Z2s values can be larger than 0.5 for many rock types, both sandstones were intermediately rough. The difference in roughness between both rock types was distinct but not overwhelmingly large, as all samples were sandstone. The quantitative comparison of the surface roughness agreed well with the purely visual and qualitative inspection of the samples identifying the Flechtinger as the more heterogeneous sample with larger grain sizes compared to the Remlinger sandstone.
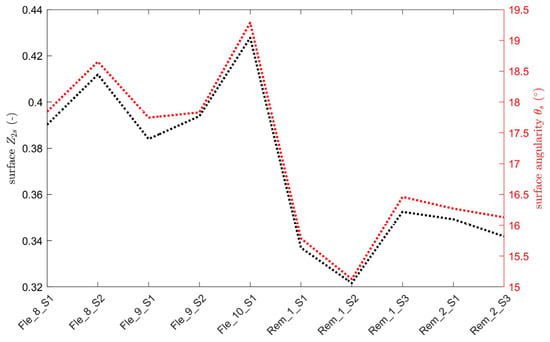
Figure 6.
Surface roughness of the fracture surfaces of the 10 tested samples expressed by Z2s and surface angularity.
4. Discussion
4.1. Dependence of Rock Type and Spatial Heterogeneity
Two samples were drilled from each of two blocks of Flechtinger sandstone and one additional sample from another block. The determined transport properties of the fractures do not show any specific similarity, most probably due to the separate fracture generation in each drill core. The fracture properties are independent from the original location in the quarry, and fracture heterogeneity is significant even within small blocks of around 0.1 m3. For the Remlinger sandstone, two and three drill cores were obtained from each of two different blocks. Similar to the Flechtinger samples, there is no specific similarity in the transport parameters within the samples from one block. However, the influence of effective aperture width is significant and related to the rock type and even the respective block. This is more pronounced in the Remlinger samples, where Rem_2 has significant smaller effective aperture widths than the block Rem_1. With respect to surface roughness, a clear trend between blocks is not observable but is between rock types. The Flechtinger samples have a clearly rougher surface than the Remlinger samples, correlating with higher effective aperture widths. The difference in effective aperture width causes differences in velocity and dispersion coefficient, but the dispersivity does not show any difference between rock types, as the value ranges of both rock types overlap largely. Therefore, no relationship between dispersivity and surface roughness was found.
4.2. Reproducibility of Tracer Tests in a Single Rough Fracture
There are tracer tests that are not well-described by one or both of the applied fitting curves. However, in the 30 experiments presented here, this is only the case for very few tracer tests (e.g., test 2 of Fle_9_100_S2). In general, the curves can be well described by both analytical models, and the residual norm is small. The standard deviation of the transport parameters does not correlate with the fitting quality. The mentioned Fle_9_100_S2 has a high residual norm in the CTRW fit, but the standard deviation of the determined parameters is smaller than for Fle_10_100_S1, which has much smaller residual values. Therefore, the observed variation in transport parameters is not primarily due to numerical inaccuracy but is based on the obtained experimental BTCs. The experimental procedure is straightforward, automated and has very few possible error sources. The required flow volume to transport all the tracer is equal for all tests and is around 1 L, independent of the rock type. While the duration of the BTC strongly depends on aeff, the volume can be used as a measure of quality for the tests. The variation of BTCs for the repeated measurements are much larger than the experimental accuracy of the used equipment. Therefore, we conclude that the observed variation in the repeated measurements and the derived transport parameters is intrinsic for the dispersive transport process along fractures with complex surface morphology. This imposes a limit on the reproducibility of tracer test experiments in single fractures.
The Remlinger samples have a smaller effective aperture width and a slightly smoother surface compared to the Flechtinger samples. Due to the smaller aperture width, the absolute values of velocity and dispersion coefficient are smaller for Remlinger than for Flechtinger samples. Furthermore, the BTCs of the Remlinger exhibit high frequency oscillations on top of the general trend of the BTCs. Those high frequency oscillations have previously been connected with flow and transport channeling along rough fractures [2,30,54]. However, it is also known that the effect of roughness decreases with growing aperture width [54,57]. The Flechtinger samples with a larger aeff do not show these high frequency oscillations. Furthermore, the dispersivity does not show any dependence on the rock types. In addition, molecular diffusion damps the effects of roughness on the tracer transport but for a study of this effect, variations in viscosity and temperature would be required. Consequently, the effective hydraulic aperture of the Flechtinger samples is sufficiently large, so that the effects of the surface roughness can be neglected. Laboratory tracer tests are more reproducible in fractures with smoother surfaces or sufficiently large effective aperture widths, so that the influence of surface roughness on the transport process can be neglected.
4.3. Comparison of Parameters Determined by CTRW and ADE
It is well known that the ADE is unable to match multi-peak BTCs and long tailings [3,32]. On the other hand, the CTRW is well-known to reproduce those non-Fickian transport characteristics. This is observable in the experiments presented in this work (Figure 4). The β value has previously been correlated with surface roughness measures, such as the Hurst exponent [29]. In this work, β values between 2 and 9 were observed. A β value larger than 2 was used as a reference value of dominating non-Fickian transport behavior [17,53]. However, the difference in the parameters determined by ADE and CTRW is distinct but small compared to the overall range. The differences of the mean values for each sample using CTRW and ADE given in Table 2 and Table 4 are larger than the standard deviations of the repeated measurements. As an example, the velocity of Fle_8_100_S1 using the CTRW fit is 9.09 × 10−4 ± 1.70 × 10−5 m/s and 1.16 × 10−3 ± 5.85 × 10−5 m/s using the ADE fit. The difference between CTRW and ADE fit is 2.51 × 10−4 m/s and substantially larger than the standard deviations between the three tests for both fitting methods. Similar results are obtained for the dispersion coefficient and the dispersivity. The ADE systematically results in larger flow velocities and dispersion coefficients compared to the CTRW. The overall range of parameters determined by ADE and CTRW is very similar (Table 6). The mean values of the transport parameters across all tests of each rock type agree within the respective standard deviation for CTRW and ADE fits.

Table 6.
Mean values for each rock type determined by the CTRW and ADE fit.
The ADE has smaller residual values for the Flechtinger samples than for the Remlinger samples. As discussed above, the BTCs of the Flechtinger samples are smoother and less influenced by the surface roughness. It also is the faster process with higher flow velocities due to the larger effective aperture width, resulting in shorter tailings of the BTCs. The ADE is therefore a more suitable fit to the Flechtinger than to the Remlinger samples, However, it is noteworthy that the β value is always larger than 2, and there is no systematic difference in the β value between Remlinger and Flechtinger samples. Recent studies also suggested larger limits than 2 for β for the dominance of non-Fickian transport behavior [30]. Furthermore, the standard deviations of the transport parameters do not follow a systematic trend between the two fitting methods. This again indicates that the observed variability of the transport parameters is due to the experimentally obtained data and not based on the numerical method used. Numerically, the parameters are well reproducible through both fitting methods for all conducted tests with the known limitations of each method.
4.4. Natural Variability and Parameter Uncertainty in Fracture Flow Modeling
Even within a small sample volume, heterogeneity can be observed so that close sampling locations can be sufficient to reveal the full range of natural variability in fracture properties. This might be different in greater reservoirs and more complex geological settings. The observed limits on experimental reproducibility of tracer tests with parameters exhibiting standard deviations of up to 50% of the mean values pose a challenge to numerical simulations of narrow fractures with small effective hydraulic apertures and substantial surface roughness, as such variability is difficult to represent in a deterministic numerical model. Therefore, parameter variations are especially crucial to study the influence of the natural variability of transport properties. In this work, grain size, effective hydraulic aperture and dispersivity were identified as the most important parameters to describe flow transport in single fractures.
Dispersivity is independent of flow velocity and surface roughness. For quantitative analysis, dispersivity can be used to calculate the dispersion for numerically determined flow velocities based on an applied pressure gradient and an effective hydraulic aperture width. The grain size is related to fracture surface roughness, and surface roughness is related to effective hydraulic aperture. Grain size estimations are usually easy to obtain for rock types, and effective hydraulic aperture widths can also be determined through field tests. Based on those two quantities, the influence of fracture surface morphology on the transport processes can be estimated. The stronger the influence of surface roughness, the larger the range of possible dispersivities. For the sandstones tested in this work, both being typical geothermal reservoir rocks in Germany, the fine grained samples with an aperture of approximately 90 μm experienced a significant influence of roughness on the transport behavior, while the rougher samples with apertures of approximately 120 μm did not experience such a strong influence of roughness on the transport behavior. Therefore, our experiments enable a pre-analysis of the importance of surface roughness for transport processes in single fractures and the related uncertainty on dispersivity.
In this work, only single fractures were studied, but for realistic reservoir calculations, fracture networks need to be studied. The results of this work can be transferred to the reservoir scale in principle, but through the interaction of fractures of different types, e.g., different fracture apertures, the found results might be distorted. The observed variability in transport parameters in the tested samples in this work provide a first estimation of the possible bandwidth to be expected in fractured reservoirs. Discrete fracture models can be used to specifically study the effect of fracture network topology on large scale contaminant transport processes using the findings of this work to describe the transport in each individual fracture.
5. Conclusions
Five drill cores were obtained from two different type of sandstones, fractured by the Brazilian test and subsequently investigated by tracer tests. The hydraulic and transport parameters were determined using ADE and CTRW fitting methods. From the results we can conclude the following:
- (1)
- When the influence of surface roughness on the flow and transport behavior is significant, there are variations in the transport behavior between repeated measurements, which are beyond experimental control. This limits the experimental reproducibility of tracer tests.
- (2)
- Roughness dominated tracer transport is signaled by high frequency oscillations overlaying the BTCs. In principle, a rougher surface exhibits more of those oscillations, but usually a rougher surface also causes higher effective hydraulic apertures, canceling the effect of the increased roughness.
- (3)
- The effective aperture width correlates with fracture surface roughness and grain size. A smoother surface is observed at samples with smaller grain size, causing a smaller effective aperture width. The transport behavior is largely dominated by the effective aperture width, but dispersivity has no observable dependence on rock type or fracture surface roughness.
- (4)
- For numerical fracture models, fracture aperture width and dispersivity were identified as the most crucial parameters from which velocity and dispersion can be estimated. The smaller the effective aperture width is, the more dominant is the influence of surface roughness on the transport behavior.
- (5)
- The mean values of the transport parameters for the all Flechtinger and Remlinger sandstones are summarized in Table 6. Relatively, the variance of the transport parameters across the Flechtinger samples is around 30% to 50% of the mean values and is in general higher, up to 100%, for the Remlinger samples. However, the relative error of repeated measurements of the Remlinger samples is only around 10%, while it is around 10–30% for the Flechtinger samples (Table 2). The variability of the repeated measurements is therefore significantly smaller than the overall spread in parameters across the separate samples.
In our experiments, we tested only the transport behavior of single fractures in sandstones, but in principle there is no limit to the transfer of the results to other rock types. Substantial differences between natural fractures and artificially generated fractures have been observed but do not affect the general findings of this work. For the comparison of the different rock fractures, all tests have been conducted with a constant hydraulic gradient. However, this makes it impossible to study the influence of the hydraulic gradient on the transport behavior.
Author Contributions
Conceptualization, S.F., T.H. and S.W.; methodology, S.F. and M.R.; software, T.H.; validation, S.F. and T.H.; formal analysis, S.F. and T.H.; investigation, S.F., T.H., M.R. and S.W.; resources, S.F.; data curation, S.F. and T.H.; writing—original draft preparation, S.F., T.H. and S.W.; writing—review and editing, S.F., T.H. and S.W.; visualization, S.F. and T.H.; supervision, T.H. and S.W.; project administration, S.W.; funding acquisition, T.H. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry for Economic Affairs and Energy (Project Management Jülich), grant number 032444D, and by the German Research Foundation (DFG), grant number HE 8194/2 1.
Acknowledgments
The authors very much appreciate the support and help from the guest editors Corrado Fidelibus and Chaoshui Xu. The authors acknowledge support by the DFG Open Access Publication Funds of the Ruhr-University Bochum.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dou, Z.; Sleep, B.; Zhan, H.; Zhou, Z.; Wang, J. Multiscale roughness influence on conservative solute transport in self-affine fractures. Int. J. Heat Mass Transf. 2019, 133, 606–618. [Google Scholar] [CrossRef]
- Briggs, S.; Karney, B.W.; Sleep, B.E. Numerical modeling of the effects of roughness on flow and eddy formation in fractures. J. Rock Mech. Geotech. Eng. 2017, 9, 105–115. [Google Scholar] [CrossRef]
- Chen, Z.; Zhan, H.; Zhao, G.; Huang, Y.; Tan, Y. Effect of Roughness on Conservative Solute Transport through Synthetic Rough Single Fractures. Water 2017, 9, 656. [Google Scholar] [CrossRef]
- Dou, Z.; Zhou, Z.F. Lattice Boltzmann simulation of solute transport in a single rough fracture. Water Sci. Eng. 2014, 7, 277–287. [Google Scholar]
- Bodin, J.; Delay, F.; de Marsily, G. Solute transport in a single fracture with negligible matrix permeability: 1. fundamental mechanisms. Hydrogeol. J. 2003, 11, 418–433. [Google Scholar] [CrossRef]
- Meller, C.; Bremer, J.; Baur, S.; Bergfeldt, T.; Blum, P.; Canic, T.; Eiche, E.; Gaucher, E.; Hagenmeyer, V.; Heberling, F. Integrated research as key to the development of a sustainable geothermal energy technology. Energy Technol. 2017, 5, 965–1006. [Google Scholar] [CrossRef]
- Keller, A.A.; Roberts, P.V.; Blunt, M.J. Effect of fracture aperture variations on the dispersion of contaminants. Water Resour. Res. 1999, 35, 55–63. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Yeo, I.W. Fluid flow in rock fractures: From the navier-stokes equations to the cubic law. Geophys. Monograph Ameri. Geophys. Union 2000, 122, 213–224. [Google Scholar]
- Kohl, T.; Evans, K.; Hopkirk, R.; Jung, R.; Rybach, L. Observation and simulation of non-darcian flow transients in fractured rock. Water Resour. Res. 1997, 33, 407–418. [Google Scholar] [CrossRef]
- Louis, C. Strömungsvorgänge in klüftigen Medien und ihre Wirkung auf die Standsicherheit von Bauwerken und Böschungen im Fels, 1st ed.; Veröffentlichungen des Institutes für Bodenmechanik und Felsmechanik der Univ. Karlsruhe: Karlsruhe, Germany, 1967; p. 167. (In German) [Google Scholar]
- Unger, A.J.A.; Mase, C.W. Numerical Study of the Hydromechanical Behavior of Two Rough Fracture Surfaces in Contact. Water Resour. Res. 1993, 29, 2101–2114. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Y.F.; Ma, G.W.; Zhou, J.Q.; Zhou, C.B. Influence of surface roughness on nonlinear flow behaviors in 3d self-affine rough fractures: Lattice Boltzmann simulations. Adv. Water Resour. 2016, 96, 373–388. [Google Scholar] [CrossRef]
- Huber, F.; Enzmann, F.; Wenka, A.; Bouby, M.; Dentz, M.; Schäfer, T. Natural micro-scale heterogeneity induced solute and nanoparticle retardation in fractured crystalline rock. J. Contam. Hydrol. 2012, 133, 40–52. [Google Scholar] [CrossRef] [PubMed]
- Boutt, D.F.; Grasselli, G.; Fredrich, J.T.; Cook, B.K.; Williams, J.R. Trapping zones: The effect of fracture roughness on the directional anisotropy of fluid flow and colloid transport in a single fracture. Geophys. Res. Lett. 2006, 33, L21402. [Google Scholar] [CrossRef]
- Plouraboué, F.; Kurowski, P.; Boffa, J.M.; Hulin, J.P.; Roux, S. Experimental study of the transport properties of rough self-affine fractures. J. Contam. Hydrol. 2000, 46, 295–318. [Google Scholar] [CrossRef]
- Zambrano, M.; Pitts, A.D.; Salama, A.; Volatili, T.; Giorgioni, M.; Tondi, E. Analysis of fracture roughness control on permeability using sfm and fluid flow simulations: Implications for carbonate reservoir characterization. Geofluids 2019, 2019, 4132386. [Google Scholar] [CrossRef]
- Wang, L.; Bayani Cardenas, M. Transition from non-Fickian to Fickian longitudinal transport through 3-D rough fractures: Scale-(in)sensitivity and roughness dependence. J. Contam. Hydrol. 2017, 198, 1–10. [Google Scholar] [CrossRef]
- Tian, X.; Deng, Y.; Jing, D.; Peng, X.; Duan, M. Research on the influence of geometry on nonlinear flow in constructed rough fractures by lattice Boltzmann simulation. Arab. J. Geosci. 2020, 13, 1–18. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of solute transport in a 3d rough-walled fracture–matrix system. Transp. Porous Media 2017, 116, 1005–1029. [Google Scholar] [CrossRef]
- Singh, K.K.; Singh, D.N.; Gamage, R.P. Effect of sample size on the fluid flow through a single fractured granitoid. J. Rock Mech. Geotech. Eng. 2016, 8, 329–340. [Google Scholar] [CrossRef]
- Zambrano, M.; Tondi, E.; Mancini, L.; Lanzafame, G.; Trias, F.X.; Arzilli, F.; Materazzi, M.; Torrieri, S. Fluid flow simulation and permeability computation in deformed porous carbonate grainstones. Adv. Water Resour. 2018, 115, 95–111. [Google Scholar] [CrossRef]
- Gadelmawla, E.; Koura, M.; Maksoud, T.; Elewa, I.; Soliman, H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Bhushan, B. Surface roughness analysis and measurement techniques. In Modern Tribology Handbook: Volume One: Principles of Tribology, 1st ed.; Bhushan, B., Ed.; CRC Press: Washington, DC, USA, 2000. [Google Scholar]
- Tse, R.; Cruden, D.M. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 303–307. [Google Scholar] [CrossRef]
- Myers, N. Characterization of surface roughness. Wear 1962, 5, 182–189. [Google Scholar] [CrossRef]
- Belem, T.; Homand-Etienne, F.; Souley, M. Quantitative Parameters for Rock Joint Surface Roughness. Rock Mech. Rock Eng. 2000, 33, 217–242. [Google Scholar] [CrossRef]
- Grasselli, G.; Wirth, J.; Egger, P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing. Int. J. Rock Mech. Min. Sci. 2002, 39, 789–800. [Google Scholar] [CrossRef]
- Roux, S.; Plouraboué, F.; Hulin, J.P. Tracer dispersion in rough open cracks. Transp. Porous Media 1998, 32, 97–116. [Google Scholar] [CrossRef]
- Dou, Z.; Zhou, Z.; Wang, J.; Huang, Y. Roughness scale dependence of the relationship between tracer longitudinal dispersion and Peclet number in variable-aperture fractures. Hydrol. Proces. 2018, 32, 1461–1475. [Google Scholar] [CrossRef]
- Frank, S.; Heinze, T.; Wohnlich, S. Comparison of Surface Roughness and Transport Processes of Sawed, Split and Natural Sandstone Fractures. Water 2020, 12, 2530. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, B.; Wu, T.; Wu, S.; Sha, H.; Zhou, P. Flow and solute transport through a single fracture during the biodegradation of residual toluene. J. Appl. Fluid Mech. 2017, 10, 1669–1677. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, J.Z.; Qin, H. Experimental study of the non-darcy flow and solute transport in a channeled single fracture. J. Hydrodyn. 2011, 23, 745–751. [Google Scholar] [CrossRef]
- Neretnieks, I.; Eriksen, T.; Tahtinen, P. Tracer movement in a single fissure in granitic rock: Some experimental results and their interpretation. Water Resour. Res. 1982, 18, 849–858. [Google Scholar] [CrossRef]
- Yan, X.; Qian, J.; Ma, L.; Wang, M.; Hu, A. Non-Fickian solute transport in a single fracture of marble parallel plate. Geofluids 2018, 2018, 7418140. [Google Scholar] [CrossRef]
- Nowamooz, A.; Radilla, G.; Fourar, M.; Berkowitz, B. Non-fickian transport in transparent replicas of rough-walled rock fractures. Transp. Porous Media 2013, 98, 651–682. [Google Scholar] [CrossRef]
- Bauget, F.; Fourar, M. Non-fickian dispersion in a single fracture. J. Contam. Hydrol. 2008, 100, 137–148. [Google Scholar] [CrossRef]
- Jiménez-Hornero, F.; Giráldez, J.; Laguna, A.; Pachepsky, Y. Continuous time random walks for analyzing the transport of a passive tracer in a single fissure. Water Resour. Res. 2005, 41, W04009. [Google Scholar] [CrossRef]
- Noetinger, B.; Roubinet, D.; Russian, A.; Le Borgne, T.; Delay, F.; Dentz, M.; Gouze, P. Random walk methods for modeling hydrodynamic transport in porous and fractured media from pore to reservoir scale. Trans. Porous Media 2016, 115, 345–385. [Google Scholar] [CrossRef]
- Albinal, A.; Holy, R.; Sarak, H.; Ozkan, E. Modeling of 1D Anomalous Diffusion in Fractured Nanoporous Media. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2016, 71, 56. [Google Scholar] [CrossRef]
- Stoll, M.; Huber, F.; Trumm, M.; Enzmann, F.; Meinel, D.; Wenka, A.; Schill, E.; Schäfer, T. Experimental and numerical investigations on the effect of fracture geometry and fracture aperture distribution on flow and solute transport in natural fractures. J. Contam. Hydrol. 2019, 221, 82–97. [Google Scholar] [CrossRef]
- Tenchine, S.; Gouze, P. Density contrast effects on tracer dispersion in variable aperture fractures. Adv. Water Res. 2005, 28, 273–289. [Google Scholar] [CrossRef]
- Zimmerman, M.D.; Bennett, P.C.; Sharp, J.M., Jr.; Choi, W.J. Experimental determination of sorption in fractured flow systems. J. Contam. Hydrol. 2002, 58, 51–77. [Google Scholar] [CrossRef]
- Hassanzadegan, A.; Blöcher, G.; Zimmermann, G.; Milsch, H. Thermoporoelastic properties of Flechtinger sandstone. Int. J. Rock Mech. Min. 2012, 49, 94–104. [Google Scholar] [CrossRef]
- Heiland, J. Permeability of Triaxially Compressed Sandstone: Influence of Deformation and Strain-rate on permeability. Pure Appl. Geophys. 2003, 160, 889–908. [Google Scholar] [CrossRef]
- Stanchits, S.; Mayr, S.; Shapiro, S.; Dresen, G. Fracturing of porous rock induced by fluid injection. Tectonophysics 2011, 503, 94–104. [Google Scholar] [CrossRef]
- Blöcher, G.; Zimmermann, G.; Milsch, H. Impact of poroelastic response of sandstones on geothermal power production. Pure Appl. Geophys. 2009, 166, 1089–1106. [Google Scholar] [CrossRef]
- Tsang, Y.W. Usage of “Equivalent Apertures” for Rock Fractures as Derived from Hydraulic and Tracer Tests. Water Resour. Res. 1992, 28, 1451–1455. [Google Scholar] [CrossRef]
- Becker, T.A. Zur Strömungssimulation in Einzelklüften: Gegenüberstellung von Numerischen Methoden und Experiment; Dissertation; Rheinisch-Westfälische Technische Hochschule Aachen: Aachen, Germany, 2008. [Google Scholar]
- De Marsily, G. Quantitative Hydrogeology-Groundwater Hydrology for Engineers, 1st ed.; Academic Press: Orlando, FL, USA, 1986. [Google Scholar]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; Balkema: Leiden, The Netherlands, 2005. [Google Scholar]
- Bear, J. Hydraulics of Groundwater, 1st ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Darcy, H. Exposition et Application des Principes a Suivre et des Formulesa Employer dans les Questions de Distribution d’Eau. In Les Fontaines Publiques de la Ville de Dijon, 1st ed.; Dalmont, V., Ed.; Libraire des Corps Imperiaux des Ponts et Chausseés et des Mines: Paris, France, 1856. (In French) [Google Scholar]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling Non-fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, 1–49. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, W.; Zhan, L.; Ye, Z.; Chen, Y. Non-Fickian Solute Transport in Rough-Walled Fractures: The Effect of Contact Area. Water 2020, 12, 2049. [Google Scholar] [CrossRef]
- Cortis, A.; Berkowitz, B. Computing “anomalous” contaminant transport in porous media: The CTRW MATLAB toolbox. Ground Water 2005, 43, 947–950. [Google Scholar] [CrossRef]
- Brown, S.R.; Stockman, H.W.; Reevs, S.J. Applicability of the Reynolds Equation for Modeling Fluid Flow between Rough Surfaces. Geophys. Res. Lett. 1995, 22, 2537–2540. [Google Scholar] [CrossRef]
- Drazer, G.; Koplik, J. Transport in rough self-affine fractures. Phys. Rev. E 2002, 66, 026303. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).