Numerical Modelling to Evaluate Sedimentation Effects on Heat Flow and Subsidence during Continental Rifting
Abstract
1. Introduction
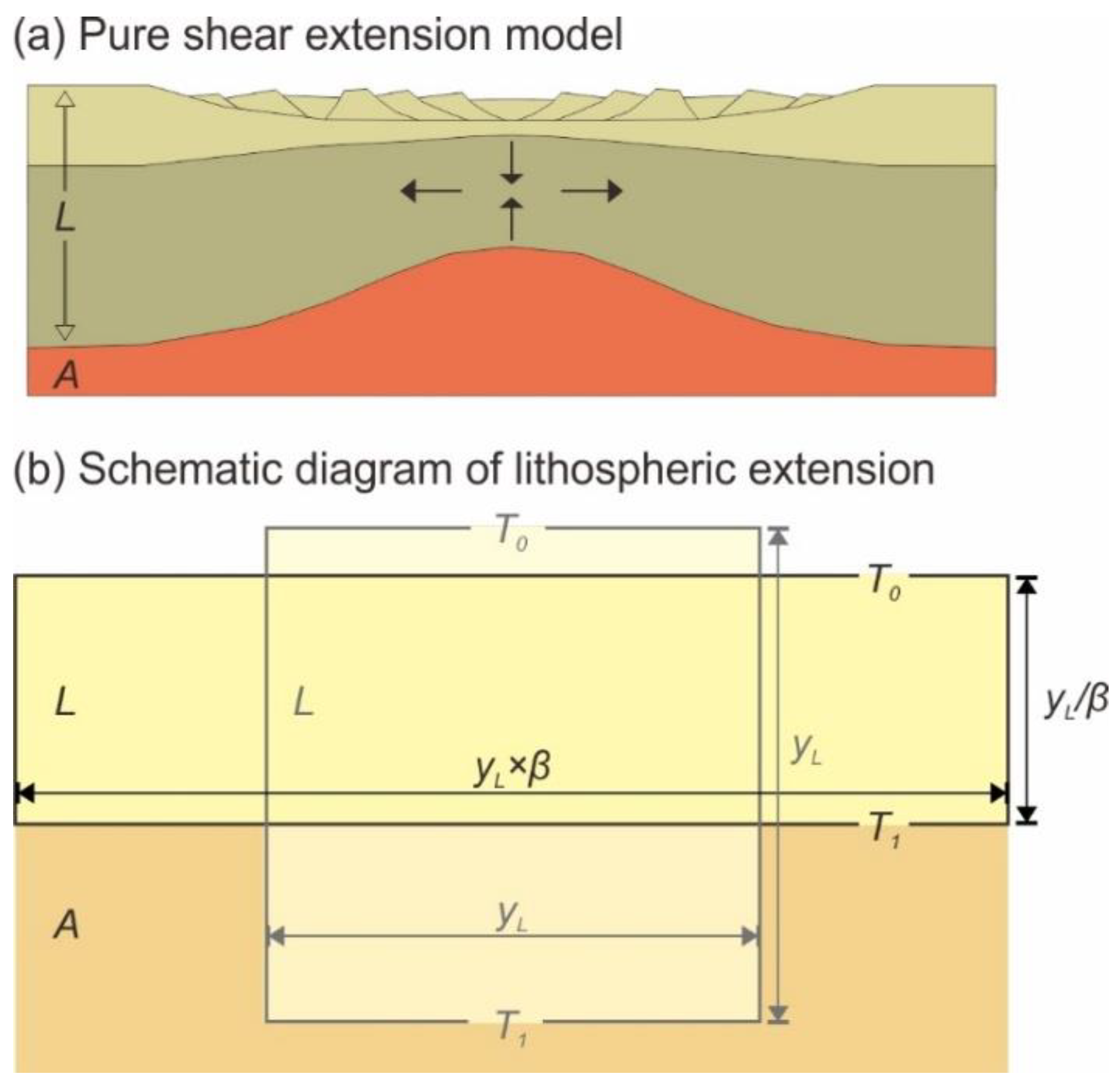
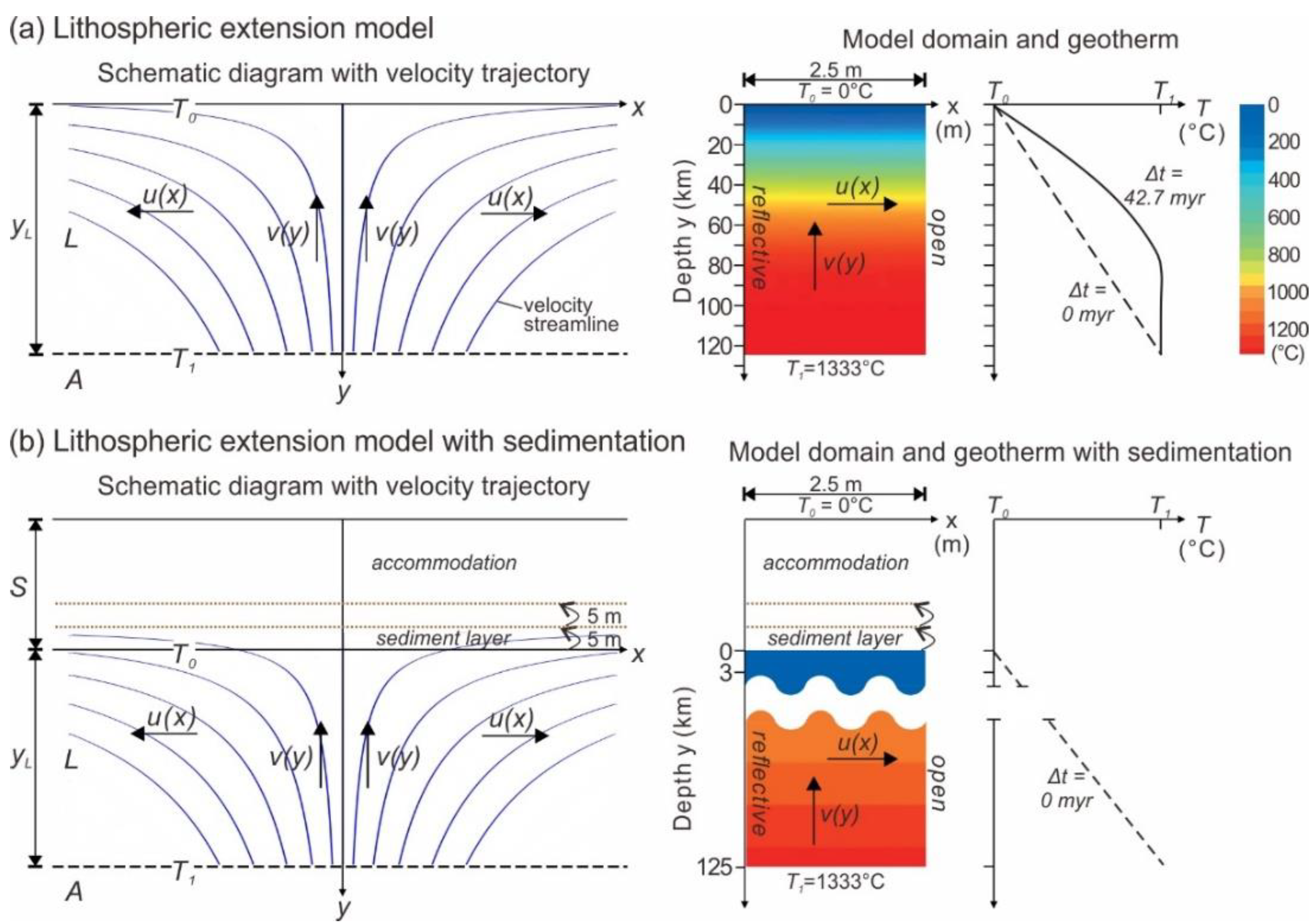
2. Numerical Solutions
2.1. Numerical Domain Setup
2.2. Temperature and Subsidence Calculations
3. Numerical Modelling of Heat Flow and Subsidence
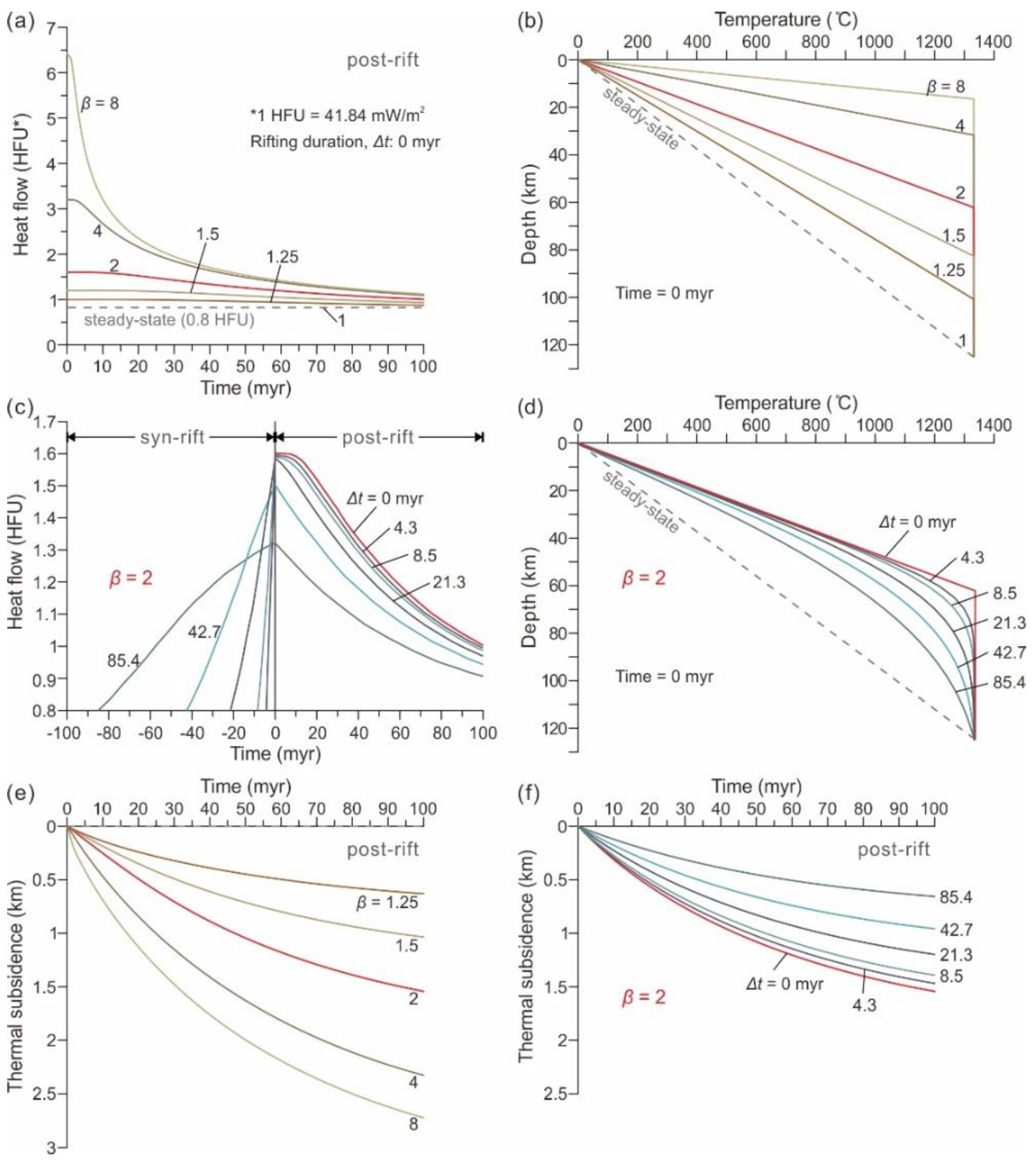
3.1. Benchmarking Models without Sedimentation
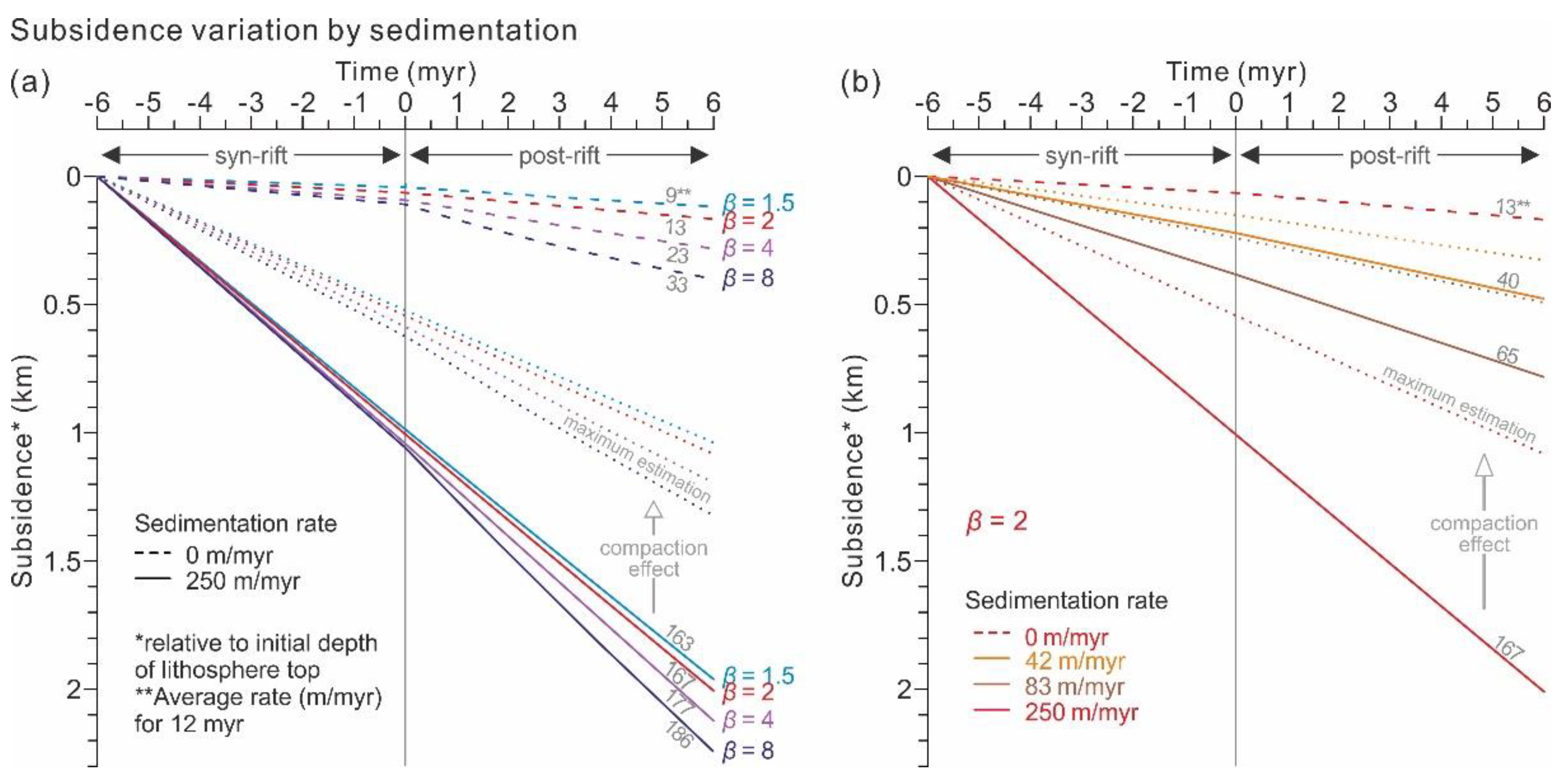
3.2. Heat Flow and Subsidence Models with Sedimentation
4. Geological Application, Limitations, and Requirements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Corti, G. Continental rift evolution: From rift initiation to incipient break-up in the Main Ethiopian Rift, East Africa. Earth Sci. Rev. 2009, 96, 1–53. [Google Scholar] [CrossRef]
- Cowie, P.A.; Underhill, J.R.; Behn, M.D.; Lin, J.; Gill, C.E. Spatio-temporal evolution of strain accumulation derived from multi-scale observations of Late Jurassic rifting in the northern North Sea: A critical test of models for lithospheric extension. Earth Planet. Sci. Lett. 2005, 234, 401–419. [Google Scholar] [CrossRef]
- Gaina, C.; Müller, R.D.; Brown, B.; Ishihara, T.; Ivanov, S. Breakup and early seafloor spreading between India and Antarctica. Geophys. J. Int. 2007, 170, 151–169. [Google Scholar] [CrossRef]
- Gibbons, A.D.; Barckhausen, U.; van den Bogaard, P.; Hoernle, K.; Werner, R.; Whittaker, J.M.; Müller, R.D. Constraining the Jurassic extent of Greater India: Tectonic evolution of the West Australian margin. Geochem. Geophys. Geosyst. 2012, 13, Q05W13. [Google Scholar] [CrossRef]
- Morgan, P.; Seager, W.R.; Golombek, M.P. Cenozoic thermal, mechanical and tectonic evolution of the Rio Grande rift. J. Geophys. Res. Solid Earth 1986, 91, 6263–6276. [Google Scholar] [CrossRef]
- Sclater, J.G.; Christie, P.A. Continental stretching: An explanation of the post-mid-Cretaceous subsidence of the central North Sea basin. J. Geophys. Res. Solid Earth 1980, 85, 3711–3739. [Google Scholar] [CrossRef]
- Steckler, M.S. Uplift and extension at the Gulf of Suez: Indications of induced mantle convection. Nature 1985, 317, 135–139. [Google Scholar] [CrossRef]
- Veevers, J.J. Updated Gondwana (Permian-Cretaceous) earth history of Australia. Gondwana Res. 2006, 9, 231–260. [Google Scholar] [CrossRef]
- Williams, S.E.; Whittaker, J.M.; Granot, R.; Müller, D.R. Early India–Australia spreading history revealed by newly detected Mesozoic magnetic anomalies in the Perth Abyssal Plain. J. Geophys. Res. Solid Earth 2013, 118, 3275–3284. [Google Scholar] [CrossRef]
- Allen, P.A.; Allen, J.R. Basin Analysis: Principles and Application to Petroleum Play Assessment, 3rd ed.; John Wiley and Sons: New York, NY, USA, 2013. [Google Scholar]
- Peron-Pinvidic, G.; Manatschal, G. The “IMAGinING RIFTING” Workshop Participants, Rifted Margins: State of the Art and Future Challenges. Front. Earth Sci. 2019, 7, 218. [Google Scholar] [CrossRef]
- Stein, S.; Stein, C.A.; Elling, R.; Kley, J.; Keller, G.R.; Wysession, M.; Rooney, T.; Frederiksen, A.; Moucha, R. Insights from North America’s failed Midcontinent Rift into the evolution of continental rifts and passive continental margins. Tectonophysics 2018, 744, 403–421. [Google Scholar] [CrossRef]
- Whitmarsh, R.B.; Manatschal, G.; Minshull, T.A. Evolution of magma-poor continental margins from rifting to seafloor spreading. Nature 2001, 413, 150–154. [Google Scholar] [CrossRef] [PubMed]
- Buck, W.R.; Martinez, F.; Steckler, M.S.; Cochran, J.R. Thermal consequences of lithospheric extension: Pure and simple. Tectonics 1988, 7, 213–234. [Google Scholar] [CrossRef]
- Franke, D. Rifting, lithosphere breakup and volcanism: Comparison of magma-poor and volcanic rifted margins. Mar. Pet. Geol. 2013, 43, 63–87. [Google Scholar] [CrossRef]
- Gueydan, F.; Morency, C.; Brun, J.-P. Continental rifting as a function of lithosphere mantle strength. Tectonophysics 2008, 460, 83–93. [Google Scholar] [CrossRef]
- Huismans, R.S.; Beaumont, C. Symmetric and asymmetric lithospheric extension: Relative effects of frictional-plastic and viscous strain softening. J. Geophys. Res. Solid Earth 2003, 108, 2496. [Google Scholar] [CrossRef]
- Koptev, A.; Burov, E.; Gerya, T.; Le Pourhiet, L.; Leroy, S.; Calais, E.; Jolivet, L. Plume-induced continental rifting and break-up in ultra-slow extension context: Insights from 3D numerical modeling. Tectonophysics 2018, 746, 121–137. [Google Scholar] [CrossRef]
- Liao, J.; Gerya, T. From continental rifting to seafloor spreading: Insight from 3D thermo-mechanical modeling. Gondwana Res. 2015, 28, 1329–1343. [Google Scholar] [CrossRef]
- Storey, B.C. The role of mantle plumes in continental breakup: Case histories from Gondwanaland. Nature 1995, 377, 301–308. [Google Scholar] [CrossRef]
- Zeyen, H.; Volker, F.; Wehrle, V.; Fuchs, K.; Sobolev, S.V.; Altherr, R. Styles of continental rifting: Crust-mantle detachment and mantle plumes. Tectonophysics 1997, 278, 329–352. [Google Scholar] [CrossRef]
- Zwaan, F.; Schreurs, G.; Adam, J. Effects of sedimentation on rift segment evolution and rift interaction in orthogonal and oblique extensional settings: Insights from analogue models analysed with 4D X-ray computed tomography and digital volume correlation techniques. Glob. Planet. Chang. 2018, 171, 110–133. [Google Scholar] [CrossRef]
- Gawthorpe, R.L.; Leeder, M.R. Tectono-sedimentary evolution of active extensional basins. Basin Res. 2000, 12, 195–218. [Google Scholar] [CrossRef]
- Busby, C.; Azor, A. Tectonics of Sedimentary Basins: Recent Advances; Blackwell Publishing Ltd.: Chicester, UK, 2012. [Google Scholar]
- Lee, E.Y.; Novotny, J.; Wagreich, M. Subsidence Analysis and Visualization for Sedimentary Basin Analysis and Modelling; SpringerBriefs in Petroleum Geoscience and Engineering; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Gac, S.; Hansford, P.A.; Faleide, J.I. Basin modelling of the SW Barents Sea. Mar. Pet. Geol. 2018, 95, 167–187. [Google Scholar] [CrossRef]
- Lee, E.Y.; Novotny, J.; Wagreich, M. Compaction trend estimation and applications to sedimentary basin reconstruction (BasinVis 2.0). Appl. Comput. Geosci. 2020, 5, 100015. [Google Scholar] [CrossRef]
- Lee, E.Y.; Wolfgring, E.; Tejada, M.L.G.; Harry, D.L.; Wainman, C.C.; Chun, S.S.; Schnetger, B.; Brumsack, H.-J.; Maritati, A.; Martinez, M.; et al. IODP Expedition 369 Science Party, Early Cretaceous subsidence of the Naturaliste Plateau defined by a new record of volcaniclastic-rich sequence at IODP Site U1513. Gondwana Res. 2020, 82, 1–11. [Google Scholar] [CrossRef]
- Roberts, A.M.; Kusznir, N.J.; Corfield, R.I.; Thompson, M.; Woodfine, R. Integrated tectonic basin modelling as an aid to understanding deep-water rifted continental margin structure and location. Pet. Geosci. 2013, 19, 65–88. [Google Scholar] [CrossRef]
- Steckler, M.S.; Watts, A.B. Subsidence of the Atlantic-type continental margin off New York. Earth Planet. Sci. Lett. 1978, 41, 1–13. [Google Scholar] [CrossRef]
- Steinberg, J.; Roberts, A.M.; Kusznir, N.J.; Schafer, K.; Karcz, Z. Crustal structure and post-rift evolution of the Levant Basin. Mar. Pet. Geol. 2018, 96, 522–543. [Google Scholar] [CrossRef]
- Zhao, Z.; Sun, Z.; Wang, Z.; Sun, Z. The mechanics of continental extension in Qiongdongnan Basin, northern South China Sea. Mar. Geophys. Res. 2014, 36, 197–210. [Google Scholar] [CrossRef]
- Hutchison, I. The effects of sedimentation and compaction on oceanic heat flow. Geophys. J. Int. 1985, 82, 439–459. [Google Scholar] [CrossRef]
- Karner, G.D. Sediment blanketing and the flexural strength of extended continental lithosphere. Basin Res. 1991, 3, 177–185. [Google Scholar] [CrossRef]
- Lucazeau, F.; Le Douaran, S. The blanketing effect of sediments in basins formed by extension: A numerical model. Application to the Gulf of Lion and Viking graben. Earth Planet. Sci. Lett. 1985, 74, 92–102. [Google Scholar] [CrossRef]
- Wangen, M. The blanketing effect in sedimentary basins. Basin Res. 1995, 7, 283–298. [Google Scholar] [CrossRef]
- Zhang, Y.K. The thermal blanketing effect of sediments on the rate and amount of subsidence in sedimentary basins formed by extension. Tectonophysics 1993, 218, 297–308. [Google Scholar] [CrossRef]
- Martín-Martín, M.; Robles-Marín, P. Alternative methods for calculating compaction in sedimentary basins. Mar. Pet. Geol. 2020, 113, 104132. [Google Scholar] [CrossRef]
- Gallagher, K.; Lambeck, K. Subsidence, sedimentation and sea-level changes in the Eromanga Basin, Australia. Basin Res. 1989, 2, 115–131. [Google Scholar] [CrossRef]
- McKenzie, D.P. Some remarks on the development of sedimentary basins. Earth Planet. Sci. Lett. 1978, 40, 25–32. [Google Scholar] [CrossRef]
- Jarvis, G.T.; Mckenzie, D.P. Sedimentary basin formation with finite extension rates. Earth Planet. Sci. Lett. 1980, 48, 42–52. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, C. A benchmark for thermal structure evolution of extensional basin. J. Geol. Soc. Korea 2016, 52, 885–900. [Google Scholar] [CrossRef]
- Hulbert, G.M.; Chung, J. Explicit time integration algorithms for structural dynamics with optimal numerical dissipation. Comput. Methods Appl. Mech. Eng. 1996, 137, 175–188. [Google Scholar] [CrossRef]
- Tunwal, M.; Mulchrone, K.F.; Meere, P.A. Constraining basin parameters using a known subsidence history. Geosciences 2020, 10, 263. [Google Scholar] [CrossRef]
- Giles, M.R. Diagenesis: A Quantitative Perspective. Implications for Basin Modelling and Rock Property Prediction; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Kim, Y.; Lee, C.; Lee, E.Y. Numerical analysis of sedimentary compaction: Implications for porosity and layer thickness variation. J. Geol. Soc. Korea 2018, 54, 631–640. [Google Scholar] [CrossRef]
- Botor, D.; Anczkiewicz, A.A.; Mazur, S.; Siwecki, T. Post-Variscan thermal history of the Intra-Sudetic Basin (Sudetes, Bohemian Massif) based on apatite fission track analysis. Int. J. Earth Sci. 2019, 108, 2561–2576. [Google Scholar] [CrossRef]
- Carr, A.D.; Uguna, C.N. Some thoughts on the influence of pressure and thermal history assumptions on petroleum systems modelling. J. Pet. Geol. 2015, 38, 459–465. [Google Scholar] [CrossRef]
- Ceriani, A.; Di Giulio, A.; Fantoni, R.; Scotti, P. Cooling in rifting sequences during increasing burial depth due to heat flow decrease. Terra Nova 2006, 18, 365–371. [Google Scholar] [CrossRef]
- Harry, D.L.; Tejada, M.L.G.; Lee, E.Y.; Wolfgring, E.; Wainman, C.C.; Brumsack, H.-J.; Schnetger, B.; Kimura, J.-I.; Riquier, L.; Borissova, I.; et al. Evolution of the southwest Australian rifted continental margin during breakup of East Gondwana: Results from IODP Expedition 369. Geochem. Geophy. Geosyst. 2020. (accepted). [Google Scholar]
- Misra, A.A.; Maitra, A.; Sinha, N.; Dey, S.; Mahapatra, S. Syn-to post-rift fault evolution in a failed rift: A reflection seismic study in central Cambay Basin (Gujarat), India. Int. J. Earth Sci. 2019, 108, 1293–1316. [Google Scholar] [CrossRef]
- White, L.T.; Gibson, G.M.; Lister, G.S. A reassessment of paleogeographic reconstructions of eastern Gondwana: Bringing geology back into the equation. Gondwana Res. 2013, 24, 984–998. [Google Scholar] [CrossRef]
- Boston, B.; Nakamura, Y.; Gallais, F.; Hackney, R.; Fujie, G.; Kodaira, S.; Miura, S.; Kaiho, Y.; Saito, S.; Shiraishi, K.; et al. Delayed subsidence after rifting and a record of breakup for Northwestern Zealandia. J. Geophys. Res. Solid Earth 2019, 124, 3057–3072. [Google Scholar] [CrossRef]
- Dafoe, L.T.; Keen, C.E.; Dickie, K.; Williams, G.L. Regional stratigraphy and subsidence of Orphan Basin near the time of breakup and implications for rifting processes. Basin Res. 2017, 29, 233–254. [Google Scholar] [CrossRef]
- Ball, P.; Eagles, G.; Ebinger, C.; McClay, K.; Totterdell, J. The spatial and temporal evolution of strain during the separation of Australia and Antarctica. Geochem. Geophys. Geosyst. 2013, 14, 2771–2799. [Google Scholar] [CrossRef]
- Whittaker, J.M.; Williams, S.E.; Müller, R.D. Revised tectonic evolution of the Eastern Indian Ocean. Geochem. Geophys. Geosyst. 2013, 14, 1891–1909. [Google Scholar] [CrossRef]
- Jones, I.; Verdel, C.; Crossingham, T.; Vasconcelos, P. Animated reconstructions of the Late Cretaceous to Cenozoic northward migration of Australia, and implications for the generation of east Australian mafic magmatism. Geosphere 2017, 13, 460–481. [Google Scholar] [CrossRef]
- Direen, N.G.; Stagg, H.M.J.; Symonds, P.A.; Colwell, J.B. Dominant symmetry of a conjugate southern Australian and East Antarctic magma-poor rifted margin segment. Geochem. Geophys. Geosyst. 2011, 12, Q02006. [Google Scholar] [CrossRef]
- MacLeod, K.G.; White, L.T.; Wainman, C.C.; Martinez, M.; Jones, M.M.; Batenburg, S.J.; Riquier, L.; Haynes, S.J.; Watkins, D.K.; Bogus, K.A.; et al. Late Cretaceous stratigraphy and paleoceanographic evolution in the Great Australian Bight Basin based on results from IODP Site U1512. Gondwana Res. 2020, 83, 80–95. [Google Scholar] [CrossRef]
- Sauermilch, I.; Whittaker, J.M.; Bijl, P.K.; Totterdell, J.M.; Jokat, W. Tectonic, Oceanographic, and Climatic Controls on the Cretaceous-Cenozoic Sedimentary Record of the Australian-Antarctic Basin. J. Geophys. Res. Solid Earth 2019, 124, 7699–7724. [Google Scholar] [CrossRef]
- Doglioni, C.; Prosser, G. Fold uplift versus regional subsidence and sedimentation rate. Mar. Pet. Geol. 1997, 14, 179–190. [Google Scholar] [CrossRef]
- Knierzinger, W.; Wagreich, M.; Palzer-Khomenko, M.; Gier, S.; Meszar, M.; Lee, E.Y.; Koukal, V.; Strauss, P. Provenance and palaeogeographic evolution of Lower Miocene sediments in the eastern North Alpine Foreland Basin. Swiss J.Geosci. 2019, 112, 269–286. [Google Scholar] [CrossRef]
- Wan, L.; Bianchi, V.; Hurter, S.; Salles, T. Evolution of a delta-canyon-fan system on a typical passive margin using stratigraphic forward modelling. Mar. Geol. 2020, 429, 106310. [Google Scholar] [CrossRef]
- Wainman, C.C.; Borissova, I.; Harry, D.L.; Hobbs, R.W.; Mantle, D.J.; Maritati, A.; Lee, E.Y. The Expedition 369 Scientists, Evidence for non-marine Jurassic to earliest Cretaceous sediments in the pre-breakup section of the Mentelle Basin, southwestern Australia. Aust. J. Earth Sci. 2020, 67, 89–105. [Google Scholar] [CrossRef]
- Perrin, C.; Marquez, X.; Flores, J.; Berthereau, G. Porosity Depth Saturation (PDS) model: Quantification of porosity preservation with burial in carbonate oil reservoirs, and application to infer oil charging time. Mar. Pet. Geol. 2020, 120, 104515. [Google Scholar] [CrossRef]

| Symbol | Description | Unit | Value |
|---|---|---|---|
| yL | Thickness of lithosphere | km | 125 |
| T0 | Temperature of the surface | °C | 0 |
| T1 | Temperature of the asthenospheric mantle | °C | 1333 |
| Density of the lithosphere at 0 °C | kg/m3 | 2800 | |
| Density of the upper lithosphere (crust) at 0 °C | kg/m3 | 2800 | |
| Density of the lower lithosphere at 0 °C | kg/m3 | 3330 | |
| Density of the asthenospheric mantle at 0 °C | kg/m3 | 3330 | |
| Density of the sediments at 0 °C | kg/m3 | 2000 | |
| Density of the air at 15 °C | kg/m3 | 1.225 | |
| k | Thermal conductivity | W/(m·°C) | 3.139 |
| Cp | Heat capacity | J/kg·°C | 1.402 × 103 [40] 1.172 × 103 [41] |
| Thermal diffusivity () | m2/s | 7.994 × 10−7 [40] 8.045 × 10−7 [41] | |
| g | Gravity | m/s2 | 9.81 |
| Thermal expansion coefficient | °C−1 | 3.28 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Huh, M.; Lee, E.Y. Numerical Modelling to Evaluate Sedimentation Effects on Heat Flow and Subsidence during Continental Rifting. Geosciences 2020, 10, 451. https://doi.org/10.3390/geosciences10110451
Kim Y, Huh M, Lee EY. Numerical Modelling to Evaluate Sedimentation Effects on Heat Flow and Subsidence during Continental Rifting. Geosciences. 2020; 10(11):451. https://doi.org/10.3390/geosciences10110451
Chicago/Turabian StyleKim, Yeseul, Min Huh, and Eun Young Lee. 2020. "Numerical Modelling to Evaluate Sedimentation Effects on Heat Flow and Subsidence during Continental Rifting" Geosciences 10, no. 11: 451. https://doi.org/10.3390/geosciences10110451
APA StyleKim, Y., Huh, M., & Lee, E. Y. (2020). Numerical Modelling to Evaluate Sedimentation Effects on Heat Flow and Subsidence during Continental Rifting. Geosciences, 10(11), 451. https://doi.org/10.3390/geosciences10110451







