1. Introduction
The shear strength of sand is the sum of the critical state component and dilatancy component [
1,
2,
3,
4]. The critical state component is represented by the critical state friction angle (
). It is commonly assumed that the critical state friction angle is independent of the deformation mode and stress level [
3,
4,
5,
6]. For siliceous sands, critical state friction angle values range between 30° and 36° depending on the sand grading and grain roundness [
7]. Loose sand is compacted during shear and reaches maximum resistance at critical state (
). Dense sand exhibits maximum resistance (
) at failure accompanied by maximum dilatancy and minimum resistance at the ultimate state (
).
Triaxial drained compression (TXC) tests are most often performed in soil mechanics laboratories. Triaxial extension tests (TXE) and the plane strain condition (biaxial compression tests; BXC) are more sensitive to small errors than the triaxial compression tests are, e.g., [
2,
8,
9,
10] and are less commonly used.
Triaxial extension tests of cylindrical samples provide similar or 2°–4° higher angles of friction than cylindrical compression tests [
2,
11,
12]. Cuboidal triaxial extension tests provide higher strength than cylindrical extension tests [
11]. Compression tests at the plane strain compression (BXC) always exhibit a higher angle of friction than triaxial compression tests [
4,
5].
Rowe’s stress-dilatancy relationships [
3,
13], positively verified theoretically by Horne [
14] and experimentally with some additional dilatancy conditions assumed in this paper, give the possibility of finding relationships between the angle of friction for TXC, BXC, and TXE. Bolton’s [
4] relationships also give the possibility of finding relationships between angles of friction for TXC and BXC [
14,
15].
The general stress-dilatancy relationship obtained from the frictional state concept [
16,
17,
18], with some assumptions for dilatancy at failure, give the possibility of finding theoretical relationships between friction angles at TXC, BXC, and TXE.
The strength criteria presented in the literature for soils also give the possibility of finding relationships between angles of friction for different deformation modes, especially TXC, BXC, and TXE. In this paper, only the Coulomb–Mohr [
1], Matsuoka-Nakai [
19], and Lade-Duncan [
20] criteria are taken for analysis.
Primarily, for sand the correctness of stress-dilatancy relationships obtained from the frictional state concept [
16,
17,
18] for drained conventional TXC, BXC, and TXE tests are proven by comparison with Bolton’s [
4] and Rowe’s [
3,
13] relationships. Later, the excess of friction angles (
ϕ′ − ϕ°) for BXC and TXE, as a function of excess friction angle for TXC with use of different theories, are shown. Finally, the difference between angles of friction for BXC and TXE and angle of friction for TXC, as a function of excess angle of friction for TXC, is shown. Obtained results are consistent with theoretical and experimental findings of soil mechanics.
2. Stress-Dilatancy Relationship for Sand
Rowe [
3,
13] presented a stress-dilatancy theory based on evaluating energy loses during shearing. He proposed the stress-dilatancy relationships in the form
and
where
and
where
is the semi-empirical friction angle. For TXC, the value of
ranges between
and
and for BXC
. The value of
depends on the relative density and stress level [
5,
6]. The minimum value
when sand is sheared in the densest state and the maximum
when sand is sheared in the loosest state.
is the angle of friction between mineral particles of sand and
is the critical state angle. Rowe also indicated that the dilatancy factor
D* is equal to 1.0 for sand in the loosest state and 2.0 for sand in the densest state. This means for the loosest state at failure it is
and for the densest state
. For the convenience of further consideration, we sign values with subscripts c, b, and e for the TXC, BXC, and TXE deformation modes, respectively. Therefore, the stress ratios for TXC, BXC, and TXE are signed as
,
,
, respectively, and the strain increment ratios for TXC, BXC, and TXE are signed
,
, and
, respectively.
In this paper, it is assumed that at failure
The identical stress ratios at failure for TXC and BXC
are proved by Bolton [
4]. Assuming
give
D* = 2 in shearing of densest sand in TXC and TXE as suggested by Rowe [
3,
13].
In this paper, it is also assumed that
and
We can see that for the shearing of sand in the loosest state at failure,
and
and for the shearing of sand in the densest state
,
the angle
, as suggested by Rowe. The strain increment ratio at failure is a function of not only density but also stress level. Therefore, we assume that Equations (4) and (5) are generally correct for sands.
Bolton [
4] analyzed the stress ratios and friction angles of 17 silica sands for TXC and BXC and proposed relationships
and
where I
R = I
D (10 − ln p′) − 1 is the relative dilatancy index defined by Bolton [
4], I
D is the density index and p’ is in units of kilonewtons per square meter. Equations (6)–(8) are correct for 0 ≤
IR ≤ 4. Therefore,
. These ranges of strain increment ratios are taken later for calculation.
Comparing Equations (6)–(8) we can write
where
and
are the angles of friction for TXC and BXC, respectively. Bolton [
4] did not give a similar relationship for TXE.
Schanz and Vermeer [
14,
15], after analyzing Bolton’s relationship, gave the relation between friction angles for TXC and BXC in the simple form
In engineering practice, the relation between the friction angle for TXC and BXC most frequently presented in literature has the form [
20]
From the frictional state concept [
16] the stress ratio may be expressed by Equation
where
| , | , | , |
| , | , | , |
In the above formulas,
is a critical frictional state angle, and
and
are new parameters of soil. For sands,
and at failure, α = 0, β = 1.0 for TXC and TXE and α = 0 and β = 1.4 for BXC [
16]. The
θ and
θε are the Lode’s angles for stresses and strain increments respectively. The parameters α and β represent the difference between current and frictional states [
16,
17,
18]. At failure, δp′ = 0; therefore, the elastic parts of the strain increments vanish and the global strain increment is equal to the plastic strain increment, and symbol “p” is omitted in the remainder of this paper.
For BXC, [
18]
The value b at failure ranges between 0.2 and 0.3 (13° <
θb < 19°) and depends on the contact conditions on the confining platens, initial porosity, and the height-to-width ratio of the sample [
18,
21,
22]. In later calculations, it is assumed
θb = 15°. The stress ratio at failure is calculated from Equation (13) with use of Equations (16)–(18).
The secant friction angle may be calculated from the following Equations:
or
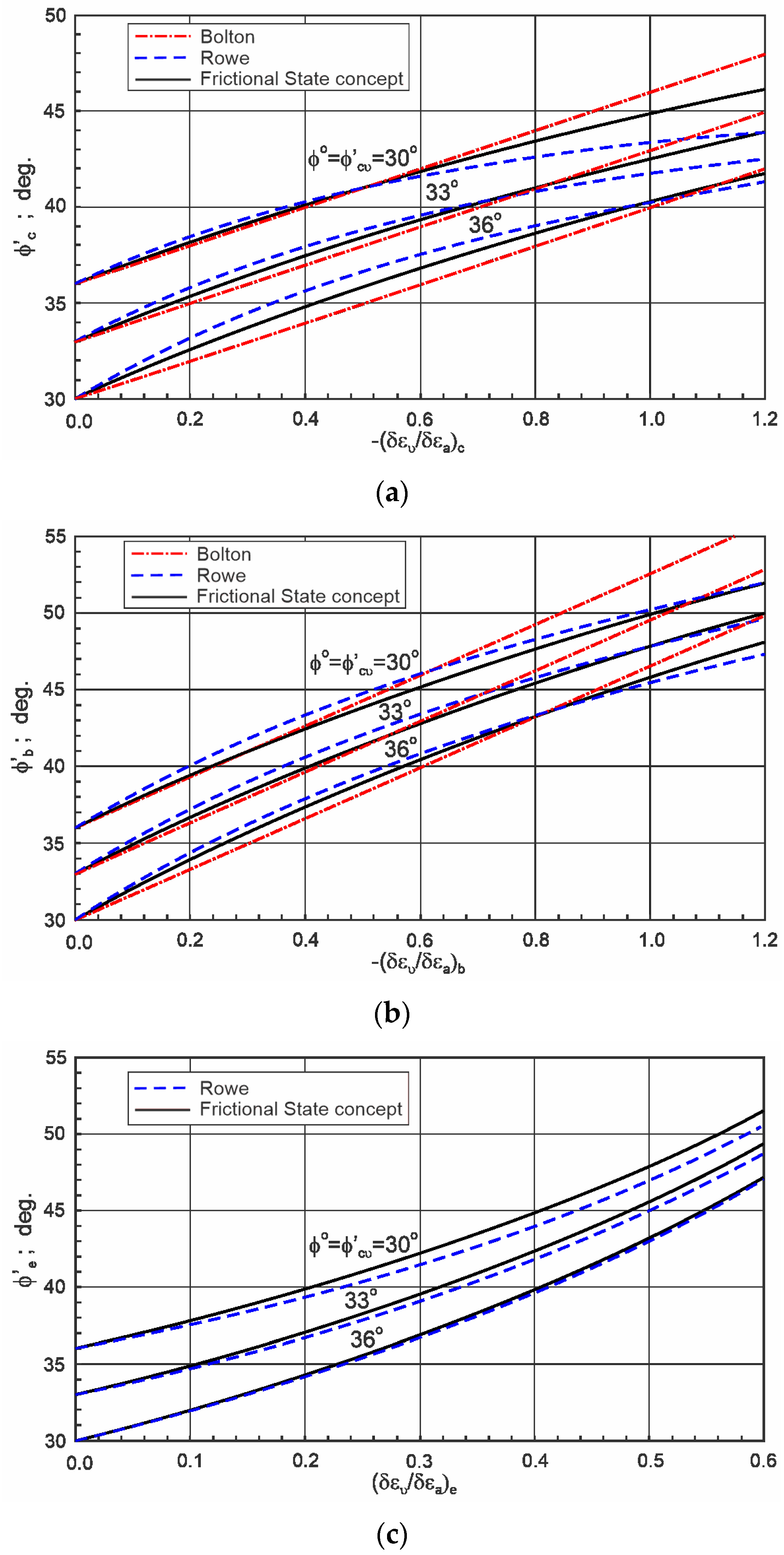
In
Figure 1 the friction angles as functions of strain increment ratios are shown.
The friction angles obtained from the frictional state concept are close and very close, respectively, to those calculated using Bolton’s and Rowe’s relationships. This means that the general stress-dilatancy equations obtained from the frictional state concept are correct. The correctness of this relationship was also presented in [
17,
18].
3. Relation between the Friction Angle of Sand at TXC, BXC, and TXE
Because the general stress-dilatancy relationship obtained from the frictional state concept is correct, it is possible to find the relation between the friction angle at TXC, BXC, and TXE. Assuming the value of the friction angle at TXC, the strain increment ratio can be back calculated. Because for a similar stress level at failure , the friction angle of sand for BXC and TXE can be calculated using the general frictional state and Bolton’s and Rowe’s stress-dilatancy relationships can be used.
The Mohr–Coulomb failure criterion assumes that intermediate stress does not influence friction angle and
. Using this failure criterion in engineering practice gives a conservative solution. In practice, the most frequently used are failure criteria given by Lade and Duncan [
20]
or Matsuoka-Nakai [
19]
where
I1,
I2,
I3 are invariants of the effective stress tensor. For assumed values of friction angle for TXC, the friction angles for BXC and TXE can be simply calculated and the relation between them specified.
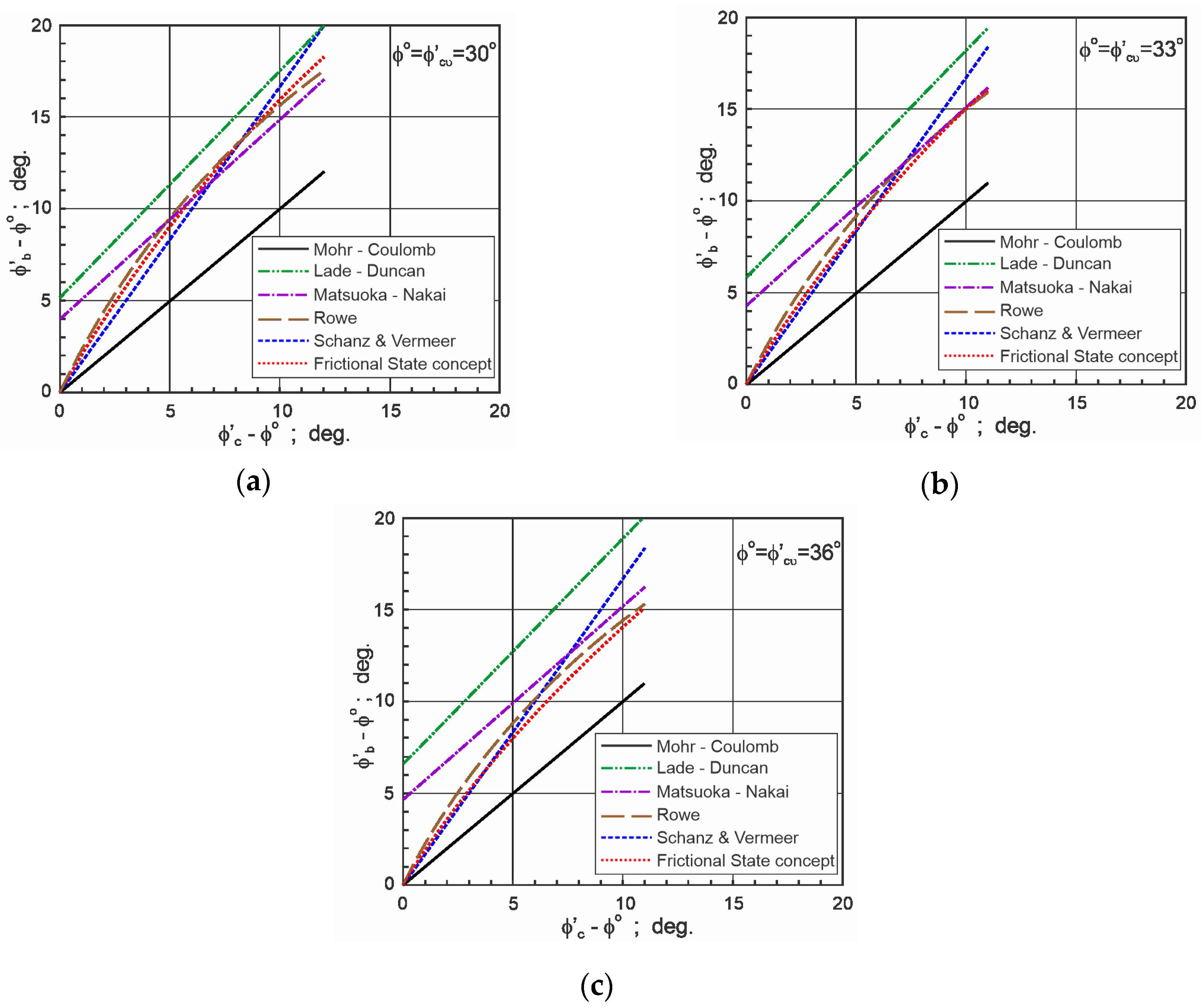
Because stress-dilatancy relationships are functions of the critical frictional state angle, it is more convenient to use the excess of friction angles , , instead of , , .
In
Figure 2, the relationships between the excess angle for BXC, as a function of the excess angle for TXC, are shown for
30°, 33°, and 36°.
The maximum excess angle for = 30° and about 11° for = 33° and 36°. Excesses of friction angles for BXC, obtained using the frictional state concept (Bolton’s and Rowe’s theories), are similar and grow with the growth of the excess friction angle for TXC.
For sand sheared in the loosest state at failure, the critical state is reached; therefore, and as obtained from the frictional state concept (Bolton’s and Rowe’s theories). The excess of friction angles for BXC obtained from the Lade-Duncan and Matsuoka-Nakai failure criteria are about 4°−5° and 5°−6°, respectively. We can see that excesses of friction angles for sand sheared at the dense state are similar. Generally, the friction angle for BXC is higher than for TXC.
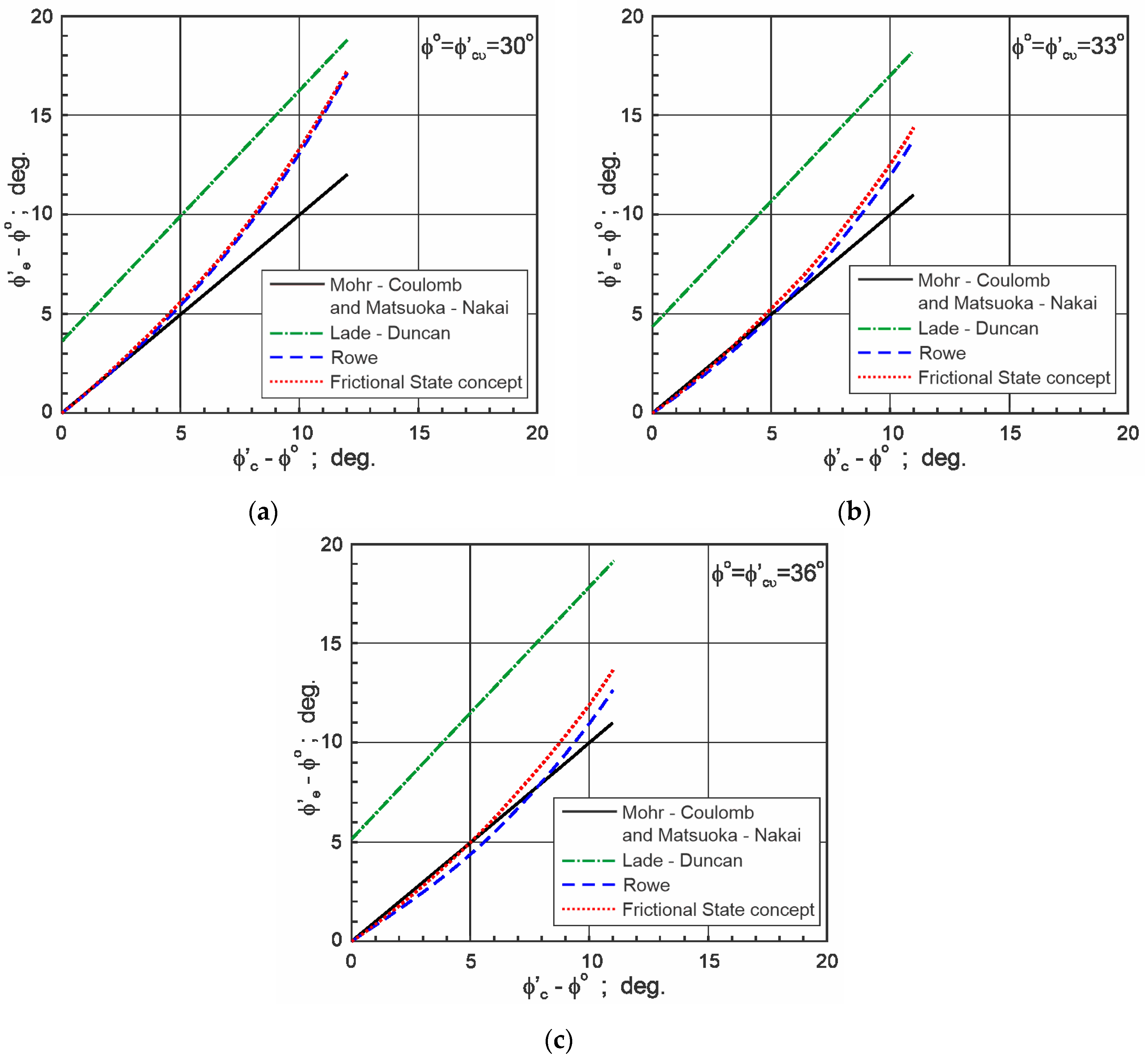
A similar relation between excesses of friction angles for TXE and TXC is shown in
Figure 3.
Mohr-Coulomb and Matsuoka-Nakai failure criteria assume that , and . Frictional state and Rowe’s theories give for and for . The maximum difference is 3°−4°. The Lade-Duncan failure criterion gives about 5° higher friction angle than that obtained using the frictional state and Rowe’s theories.
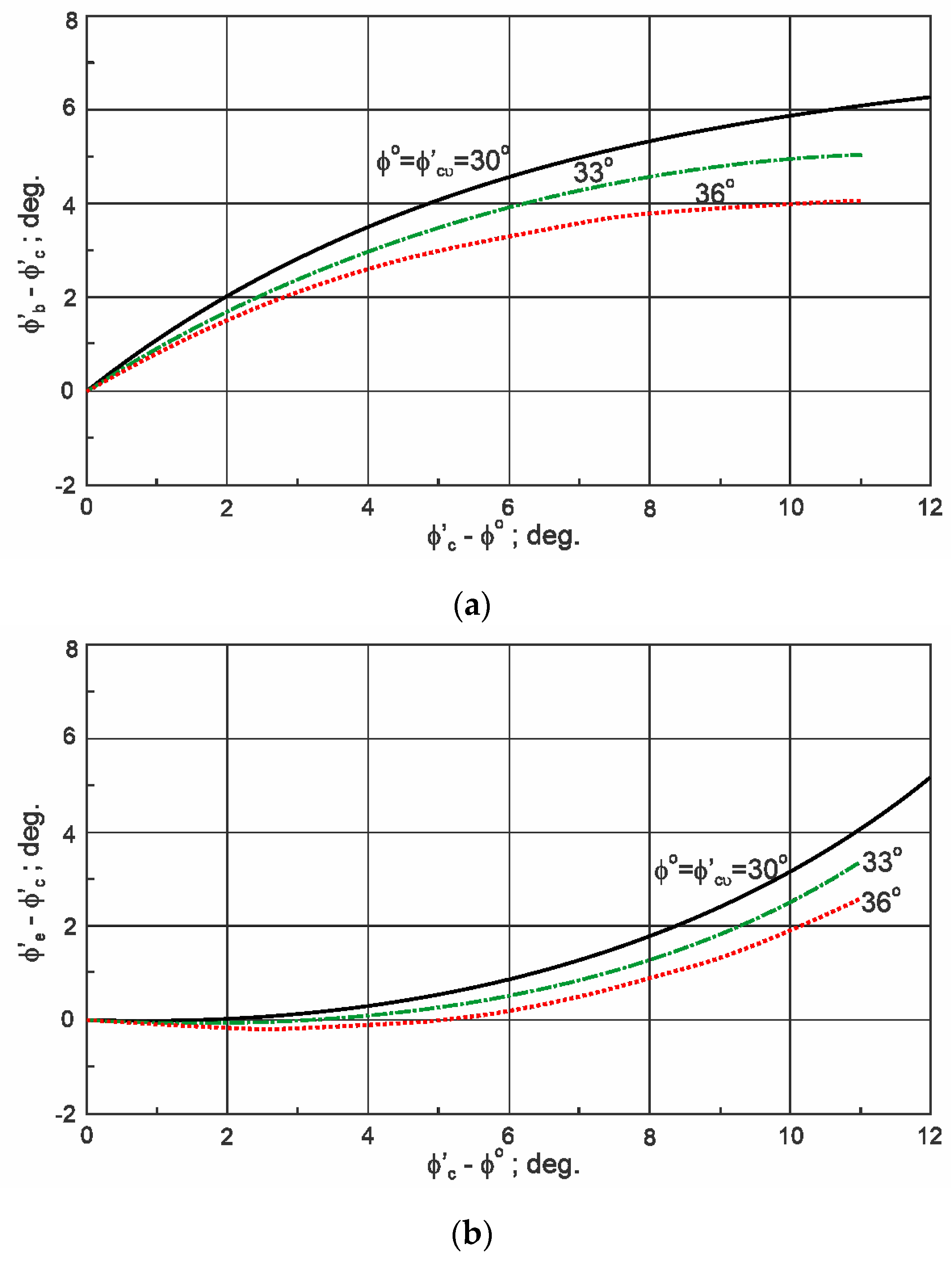
In
Figure 4, the difference between friction angles for BXC and TXC as a function of the excess angle for TXC obtained using the frictional state concept is shown.
We can see that the angle of friction for BXC is always higher than that for TXC. The difference grows with the growth of the excess angle. The maximum difference is about 6°, 5°, and 4° for
30°, 33°, and 36°, respectively. For the shear of sand in the loose and medium dense states,
, the friction angles for TXE and TXC are very similar. For the shear of sand in the dense state, the angle of friction for TXE is a little higher than that for TXC. The maximum difference is about 5°, 3°, and 2° for
30°, 33°, and 36°, respectively. Theoretically obtained differences between friction angles for BXC or TXE and TXC correspond with those obtained in laboratory tests [
1]. In engineering practice, it is most frequently assumed that
and
.
4. Conclusions
The assumptions proposed in this paper, that at failure and angle in Rowe’s equations is a function of the strain increment ratio, are correct.
Friction angles calculated using the frictional state and Bolton’s and Rowe’s stress-dilatancy relationships are similar.
Relations between friction angles for drained TXC, BXC, and TXE obtained using the general stress-dilatancy equation of the frictional state concept are correct for the dilative behavior of sand during shear.