Comparative Study of Single-Trait and Multi-Trait Genomic Prediction Models
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Statement
2.2. Animals
2.3. Genotyping
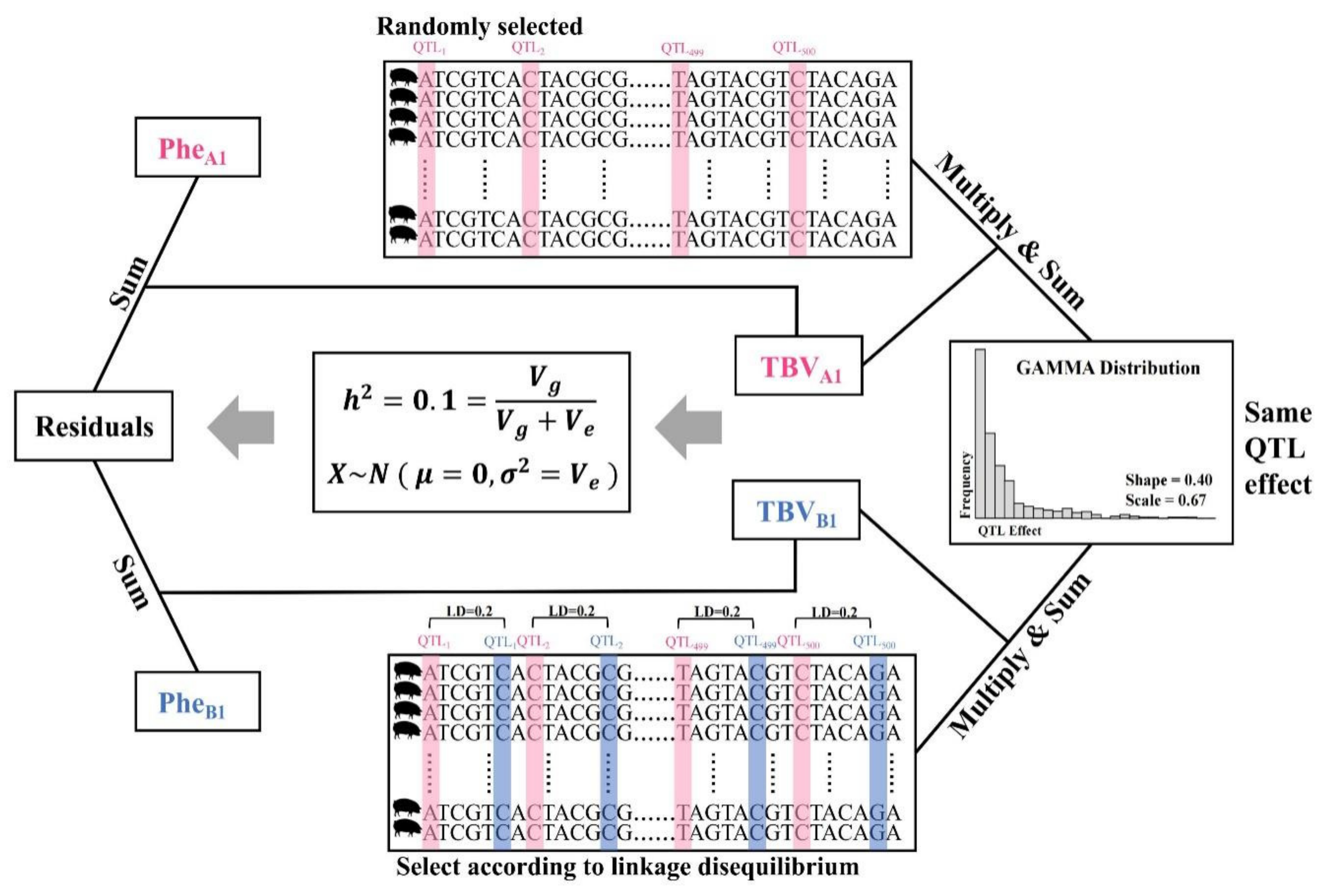
2.4. Simulate F1 Genotypes and Phenotypes
2.5. Construction of Single-Trait Models and Multi-Trait Models
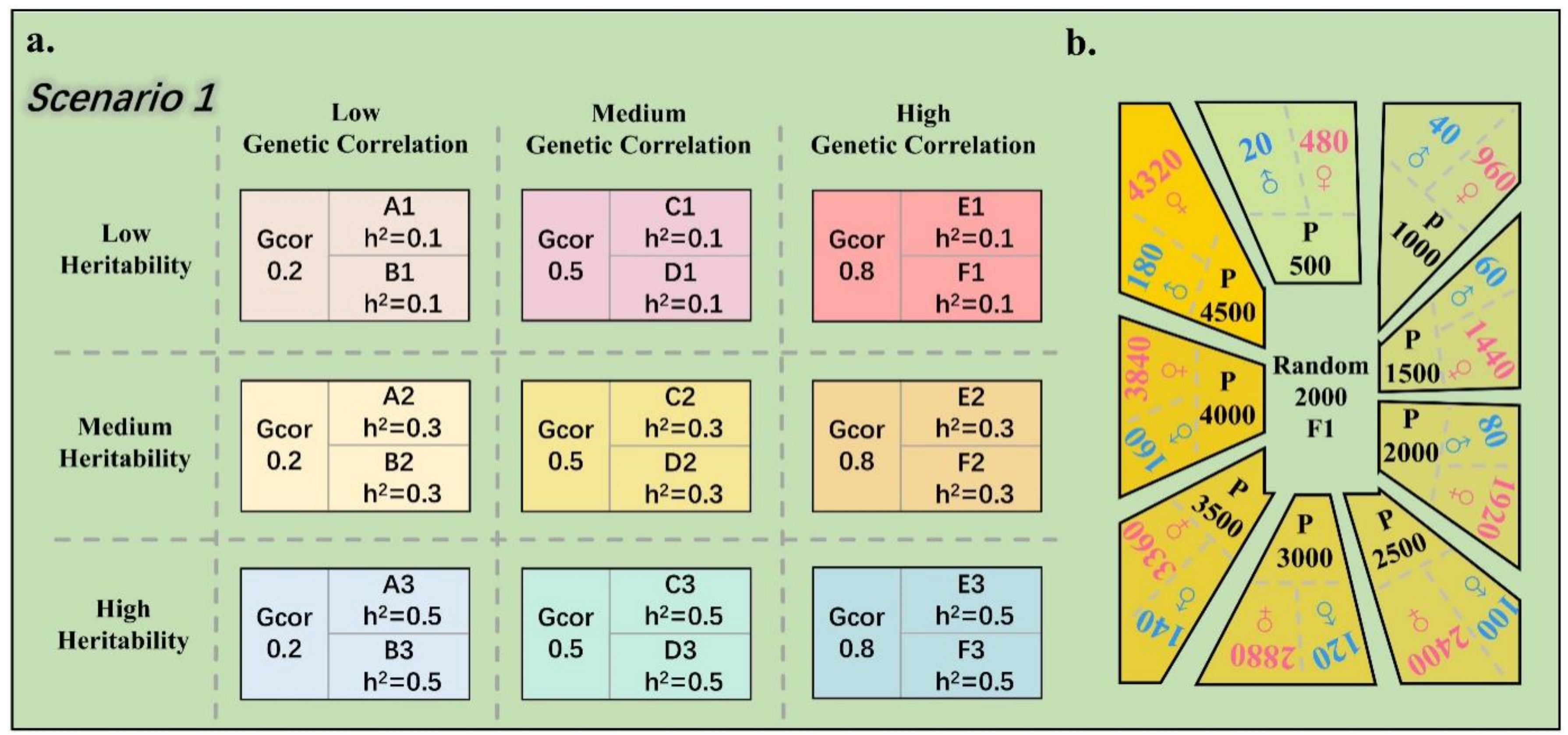
2.6. Two Evaluation Scenarios of the Multi-Trait Model
3. Results
3.1. Descriptive Statistical Analysis of Simulation Results
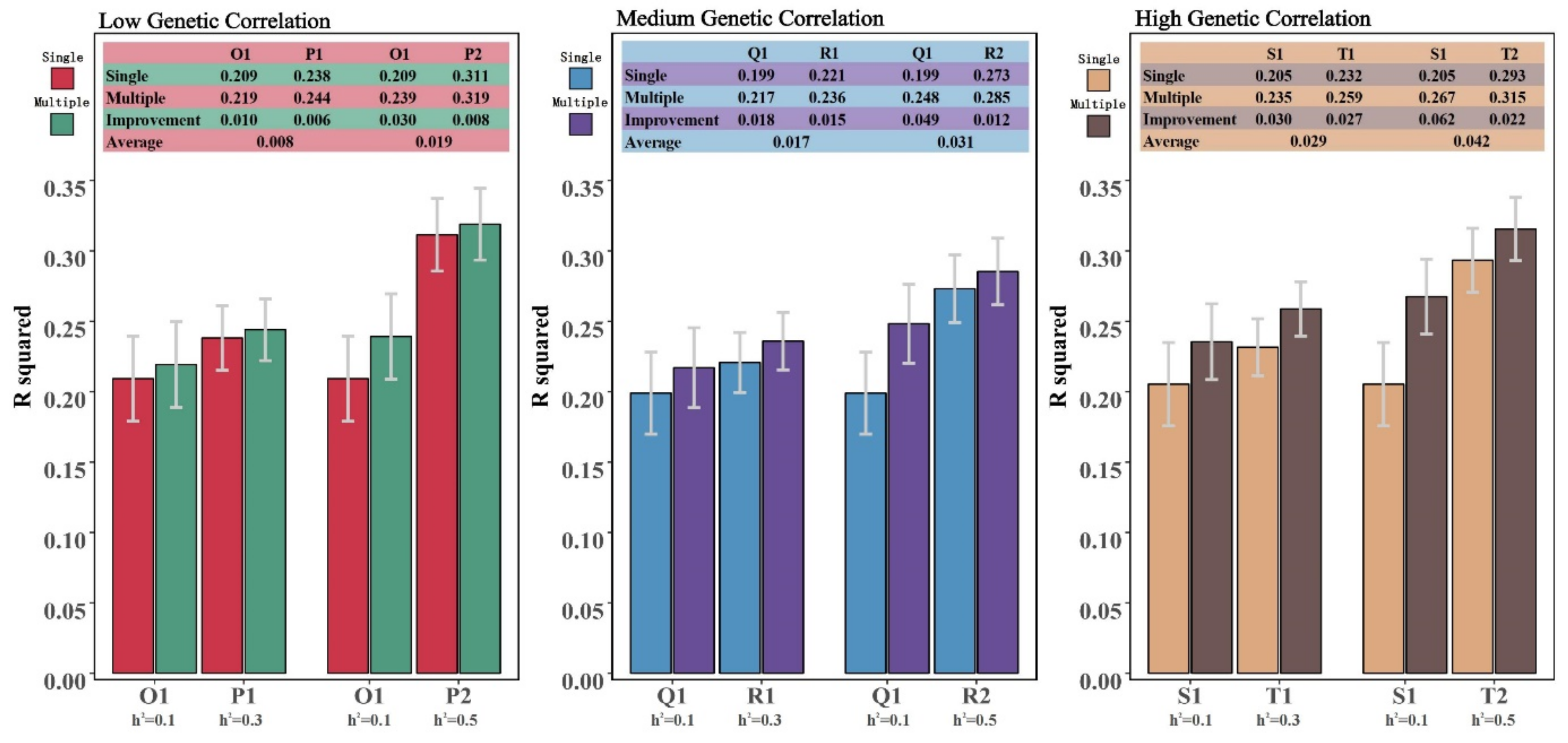
3.2. Genome Prediction Accuracy
3.3. Time Consumption
4. Discussion
4.1. Concerns of Breeders Regarding Multi-Trait Models
4.2. The Role of Heritability and Genetic Correlation in Multi-Trait Models
4.3. Low Heritability Traits Benefit from Correlated High Heritability Traits
4.4. Strengths and Considerations in Simulation Based on Real Sequencing Data
4.5. The Practicality of the Multi-Trait Model Requires Further Investigation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Hermesch, S.; Luxford, B.G.; Graser, H.-U. Genetic parameters for lean meat yield, meat quality, reproduction and feed efficiency traits for Australian pigs. Livest. Prod. Sci. 2000, 65, 249–259. [Google Scholar] [CrossRef][Green Version]
- Hermesch, S.; Luxford, B.G.; Graser, H.-U. Genetic relationships between intramuscular fat content and meat quality, carcase, production and reproduction traits in Australian pigs. Proc. Assoc. Advmt. Anim. Breed. Genet. 1997, 12, 499–502. [Google Scholar] [CrossRef]
- Yang, Y.; Gan, M.; Yang, X.; Zhu, P.; Luo, Y.; Liu, B.; Zhu, K.; Cheng, W.; Chen, L.; Zhao, Y.; et al. Estimation of genetic parameters of pig reproductive traits. Front. Vet. Sci. 2023, 10, 1172287. [Google Scholar] [CrossRef]
- Yu, G.; Wang, C.; Wang, Y. Genetic parameter analysis of reproductive traits in Large White pigs. Anim. Biosci. 2022, 35, 1649–1655. [Google Scholar] [CrossRef]
- Miar, Y.; Plastow, G.S.; Moore, S.S.; Manafiazar, G.; Charagu, P.; Kemp, R.A.; Haandel, B.V.; Huisman, A.E.; Zhang, C.Y.; McKay, R.M.; et al. Genetic and phenotypic parameters for carcass and meat quality traits in commercial crossbred pigs. J. Anim. Sci. 2014, 92, 2869–2884. [Google Scholar] [CrossRef]
- Hirooka, H. Economic selection index in the genomic era. J. Anim. Breed. Genet. 2019, 136, 151–152. [Google Scholar] [CrossRef]
- Hu, H.; Meng, Y.; Liu, W.; Chen, S.; Runcie, D.E. Multi-Trait Genomic Prediction Improves Accuracy of Selection among Doubled Haploid Lines in Maize. Int. J. Mol. Sci. 2022, 23, 14558. [Google Scholar] [CrossRef] [PubMed]
- Mora-Poblete, F.; Maldonado, C.; Henrique, L.; Uhdre, R.; Scapim, C.A.; Mangolim, C.A. Multi-trait and multi-environment genomic prediction for flowering traits in maize: A deep learning approach. Front. Plant Sci. 2023, 14, 1153040. [Google Scholar] [CrossRef]
- Calus, M.P.; Veerkamp, R.F. Accuracy of multi-trait genomic selection using different methods. Genet. Sel. Evol. 2011, 43, 26. [Google Scholar] [CrossRef]
- Jia, Y.; Jannink, J. Multiple-trait genomic selection methods increase genetic value prediction accuracy. Genetics 2012, 192, 1513–1522. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Montesinos-López, A.; Crossa, J.; Toledo, F.H.; Pérez-Hernández, O.; Eskridge, K.M.; Rutkoski, J. A Genomic Bayesian Multi-trait and Multi-environment Model. G3 (Bethesda) 2016, 6, 2725–2744. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Xiao, S.; Tu, J.; Zhang, Z.; Zheng, H.; Huang, L.; Huang, Z.; Yan, M.; Liu, X.; Guo, Y. A further survey of the quantitative trait loci affecting swine body size and carcass traits in five related pig populations. Anim. Genet. 2021, 52, 621–632. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; Bakker, P.I.W.d.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
- Delaneau, O.; Marchini, J.; Zagury, J.-F. A linear complexity phasing method for thousands of genomes. Nat. Methods 2011, 9, 179–181. [Google Scholar] [CrossRef]
- Lourenco, D.; Legarra, A.; Tsuruta, S.; Masuda, Y.; Aguilar, I.; Misztal, I. Single-Step Genomic Evaluations from Theory to Practice: Using SNP Chips and Sequence Data in BLUPF90. Genes 2020, 11, 790. [Google Scholar] [CrossRef]
- Muvunyi, B.P.; Zou, W.; Zhan, J.; He, S.; Ye, G. Multi-Trait Genomic Prediction Models Enhance the Predictive Ability of Grain Trace Elements in Rice. Front. Genet. 2022, 13, 883853. [Google Scholar] [CrossRef]
- Bhatta, M.; Gutierrez, L.; Cammarota, L.; Cardozo, F.; Germán, S.; Gómez-Guerrero, B.; Pardo, M.F.; Lanaro, V.; Sayas, M.; Castro, A.J. Multi-trait Genomic Prediction Model Increased the Predictive Ability for Agronomic and Malting Quality Traits in Barley (Hordeum vulgare L.). G3 (Bethesda) 2020, 10, 1113–1124. [Google Scholar] [CrossRef]
- Sun, J.; Rutkoski, J.E.; Poland, J.A.; Crossa, J.; Jannink, J.-L.; Sorrells, M.E. Multitrait, Random Regression, or Simple Repeatability Model in High-Throughput Phenotyping Data Improve Genomic Prediction for Wheat Grain Yield. Plant Genome 2017, 10, 1–12. [Google Scholar] [CrossRef]
- Misztal, I.; Lourenco, D.; Legarra, A. Current status of genomic evaluation. J. Anim. Sci. 2020, 98, skaa101. [Google Scholar] [CrossRef]
- Moeinizade, S.; Kusmec, A.; Hu, G.; Wang, L.; Schnable, P.S. Multi-trait Genomic Selection Methods for Crop Improvement. Genetics 2020, 215, 931–945. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Montesinos-López, A.; Sandoval, D.A.B.; Mosqueda-Gonzalez, B.A.; Valenzo-Jiménez, M.A.; Crossa, J. Multi-trait genome prediction of new environments with partial least squares. Front. Genet. 2022, 13, 966775. [Google Scholar] [CrossRef]
- Gebreyesus, G.; Lund, M.S.; Buitenhuis, B.; Bovenhuis, H.; Poulsen, N.A.; Janss, L.G. Modeling heterogeneous (co)variances from adjacent-SNP groups improves genomic prediction for milk protein composition traits. Genet. Sel. Evol. 2017, 49, 89. [Google Scholar] [CrossRef] [PubMed]
- Zak, L.J.; Gaustad, A.H.; Bolarin, A.; Broekhuijse, M.L.W.J.; Walling, G.A.; Knol, E.F. Genetic control of complex traits, with a focus on reproduction in pigs. Mol. Reprod. Dev. 2017, 84, 1004–1011. [Google Scholar] [CrossRef] [PubMed]
- Gorssen, W.; Maes, D.; Meyermans, R.; Depuydt, J.; Janssens, S.; Buys, N. High Heritabilities for Antibiotic Usage Show Potential to Breed for Disease Resistance in Finishing Pigs. Antibiotics 2021, 10, 829. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Qin, J.; Yao, T.; Tang, X.; Cui, D.; Chen, L.; Rao, L.; Xiao, S.; Zhang, Z.; Huang, L. Genetic dissection of 26 meat cut, meat quality and carcass traits in four pig populations. Genet. Sel. Evol. 2023, 55, 43. [Google Scholar] [CrossRef]
- Ayalew, W.; Aliy, M.; Negussie, E. Estimation of genetic parameters of the productive and reproductive traits in Ethiopian Holstein using multi-trait models. Asian-Australas J. Anim. Sci. 2017, 30, 1550–1556. [Google Scholar] [CrossRef]
- Makgahlela, M.; Banga, C.; Norris, D.; Dzama, K.; Ngambi, J. Genetic correlations between female fertility and production traits in South African Holstein cattle. S. Afr. J. Anim. Sci. 2007, 37, 180–188. [Google Scholar] [CrossRef]
- Johnsson, M.; Whalen, A.; Ros-Freixedes, R.; Gorjanc, G.; Chen, C.Y.; Herring, W.O.; Koning, D.J.d.; Hickey, J.M. Genetic variation in recombination rate in the pig. Genet. Sel. Evol. 2021, 53, 54. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, T.; Wang, L.; Zhang, L.; Hou, X.; Yan, H.; Wang, L. Optimizing the Construction and Update Strategies for the Genomic Selection of Pig Reference and Candidate Populations in China. Front. Genet. 2022, 13, 938947. [Google Scholar] [CrossRef]
- Cheverud, J.M.; Rutledge, J.J.; Atchley, W.R. Quantitative genetics of development: Genetic correlations among age-specific trait values and the evolution of ontogeny. Evolution 1983, 37, 895–905. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.P.R.d.; Vasconcellos, R.C.d.C.; Pires, L.P.M.; Balestre, M.; Pinho, R.G.V. Inclusion of Dominance Effects in the Multivariate GBLUP Model. PLoS ONE 2016, 11, e0152045. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Lübberstedt, T. Molecular basis of trait correlations. Trends Plant Sci. 2010, 15, 454–461. [Google Scholar] [CrossRef] [PubMed]
- Gebreyesus, G.; Bovenhuis, H.; Lund, M.S.; Poulsen, N.A.; Sun, D.; Buitenhuis, B. Reliability of genomic prediction for milk fatty acid composition by using a multi-population reference and incorporating GWAS results. Genet. Sel. Evol. 2019, 51, 16. [Google Scholar] [CrossRef] [PubMed]



| Group Batch | Breeds | Origins Birthplaces | Breeding Company | Number | Boars | Sows |
|---|---|---|---|---|---|---|
| Group 1 | Duroc | Guangdong Province, China | Wens Foodstuff Group Co., Ltd. | 1919 | 361 | 1558 |
| Group 2 | Landrace | 2328 | 86 | 2242 | ||
| Group 3 | Yorkshire | Jiangxi Province, China | Aonong Biological Technology Group Co., Ltd. | 753 | 53 | 700 |
| Sum | 5000 | 500 | 4500 | |||
| Reference Group (5000) | Mean | Median | Variance | SD | CV | Kurtosis | Skewness | |
|---|---|---|---|---|---|---|---|---|
| TBV | h2 = 0.1 | 2.924 | 2.829 | 45.919 | 6.776 | 0.261 | 0.027 | 0.121 |
| h2 = 0.3 | ||||||||
| h2 = 0.5 | ||||||||
| Phenotype | h2 = 0.1 | 3.112 | 3.195 | 461.185 | 21.475 | 0.794 | −0.024 | 0.002 |
| h2 = 0.3 | 3.020 | 2.950 | 153.826 | 12.403 | 0.471 | 0.001 | 0.013 | |
| h2 = 0.5 | 2.987 | 2.897 | 92.278 | 9.606 | 0.368 | 0.019 | 0.029 | |
| Reference Group Size = 4500 | Genetic Correlation = 0.2 | Genetic Correlation = 0.5 | Genetic Correlation = 0.8 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A1B1 | A2B2 | A3B3 | C1D1 | C2D2 | C3D3 | E1F1 | E2F2 | E3F3 | |
| Single-trait model (mean/sd) | 0.195 (0.028) | 0.240 (0.040) | 0.293 (0.049) | 0.158 (0.059) | 0.241 (0.048) | 0.308 (0.047) | 0.200 (0.029) | 0.272 (0.028) | 0.316 (0.028) |
| Multi-trait model (mean/sd) | 0.198 (0.029) | 0.250 (0.040) | 0.314 (0.049) | 0.161 (0.060) | 0.262 (0.049) | 0.343 (0.049) | 0.204 (0.029) | 0.296 (0.028) | 0.357 (0.033) |
| Improvement | 0.003 | 0.010 | 0.021 | 0.003 | 0.021 | 0.035 | 0.004 | 0.024 | 0.041 |
| Time(s) * | Genetic Correlation | h2 = 0.1 | h2 = 0.3 | h2 = 0.5 | |||
|---|---|---|---|---|---|---|---|
| AIREMLF90 | BLUPF90 | AIREMLF90 | BLUPF90 | AIREMLF90 | BLUPF90 | ||
| Single-trait model | \ | 464.29 | 90.50 | 454.10 | 91.66 | 472.55 | 93.12 |
| Multi-trait model | 0.2 | 1903.51 | 141.16 | 1800.90 | 135.48 | 1856.54 | 133.11 |
| 0.5 | 1660.48 | 136.37 | 1569.59 | 141.61 | 1680.50 | 141.62 | |
| 0.8 | 1557.17 | 136.69 | 1500.12 | 136.39 | 1571.21 | 136.75 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Xiao, S.; Ding, N.; Zhang, Z.; Huang, L. Comparative Study of Single-Trait and Multi-Trait Genomic Prediction Models. Animals 2024, 14, 2961. https://doi.org/10.3390/ani14202961
Tang X, Xiao S, Ding N, Zhang Z, Huang L. Comparative Study of Single-Trait and Multi-Trait Genomic Prediction Models. Animals. 2024; 14(20):2961. https://doi.org/10.3390/ani14202961
Chicago/Turabian StyleTang, Xi, Shijun Xiao, Nengshui Ding, Zhiyan Zhang, and Lusheng Huang. 2024. "Comparative Study of Single-Trait and Multi-Trait Genomic Prediction Models" Animals 14, no. 20: 2961. https://doi.org/10.3390/ani14202961
APA StyleTang, X., Xiao, S., Ding, N., Zhang, Z., & Huang, L. (2024). Comparative Study of Single-Trait and Multi-Trait Genomic Prediction Models. Animals, 14(20), 2961. https://doi.org/10.3390/ani14202961






