Investigating the Ability of Growth Models to Predict In Situ Vibrio spp. Abundances
Abstract
1. Introduction
2. Materials and Methods
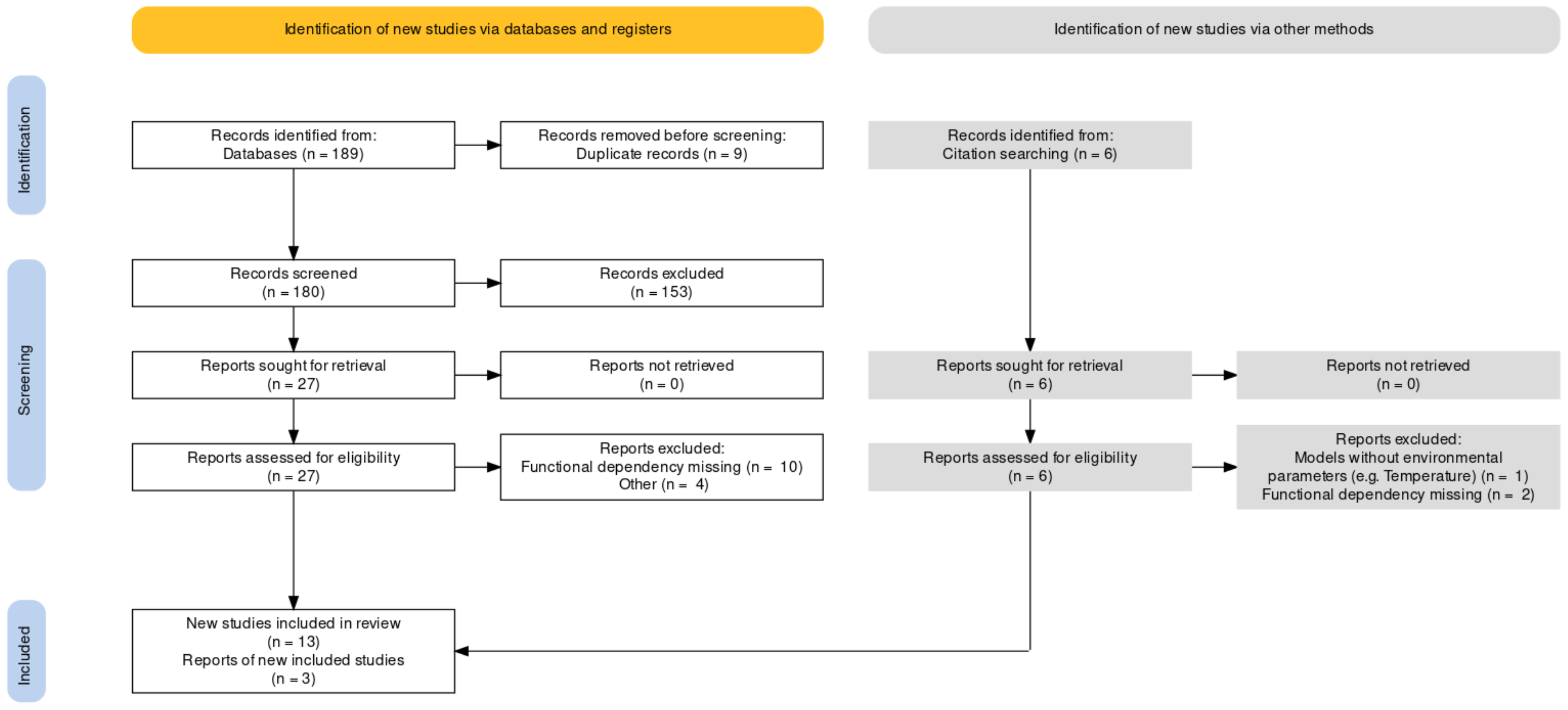
2.1. Literature Search and Model Synthesis
2.2. Data Preparation
2.3. Model Simulations
2.4. Model Performance
3. Results
3.1. Vibrio spp. Growth Models
- Baranyi and modified Gompertz are the most commonly used primary models for describing Vibrio spp. growth over time.
- Square root and Arrhenius-based models are the most frequently applied secondary models for Vibrio spp. growth in dynamic conditions.
- V. cholerae, V. parahaemolyticus, V. harveyi, and V. vulnificus are the species used most often as modeling organisms.
- Vibrio growth was monitored in/on various substrates (free water column, within organisms, in broth substrates, etc.), under different temperature, salinity, and pH conditions. This implies that the aquatic environments and organisms (marine and freshwater), as well as food and water health and safety, are the key areas of research and concern.
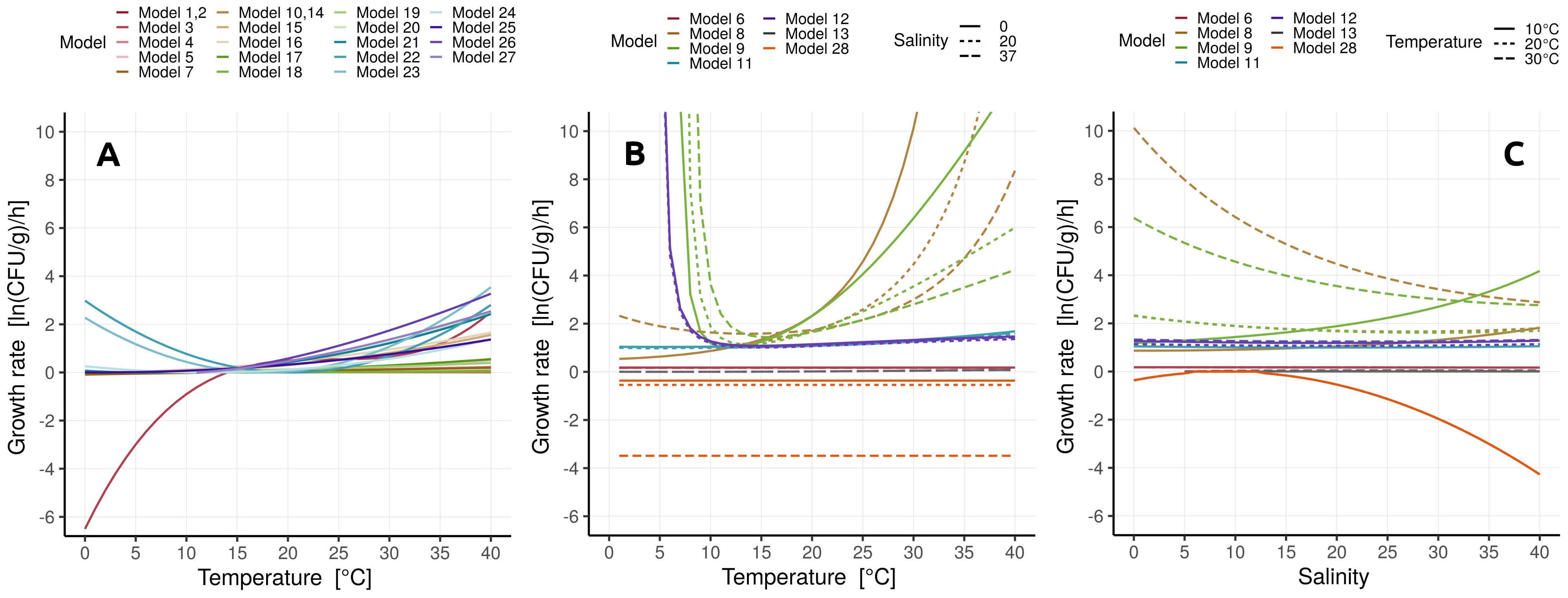
- Temperature was the prevailing environmental parameter used in secondary models, implying a strong effect of temperature on Vibrio spp. abundance. The effect of temperature on the primary model parameters (growth rate and lag time) was most often modeled by the square root or the Arrhenius-based model.
3.2. Vibrio In Situ Datasets
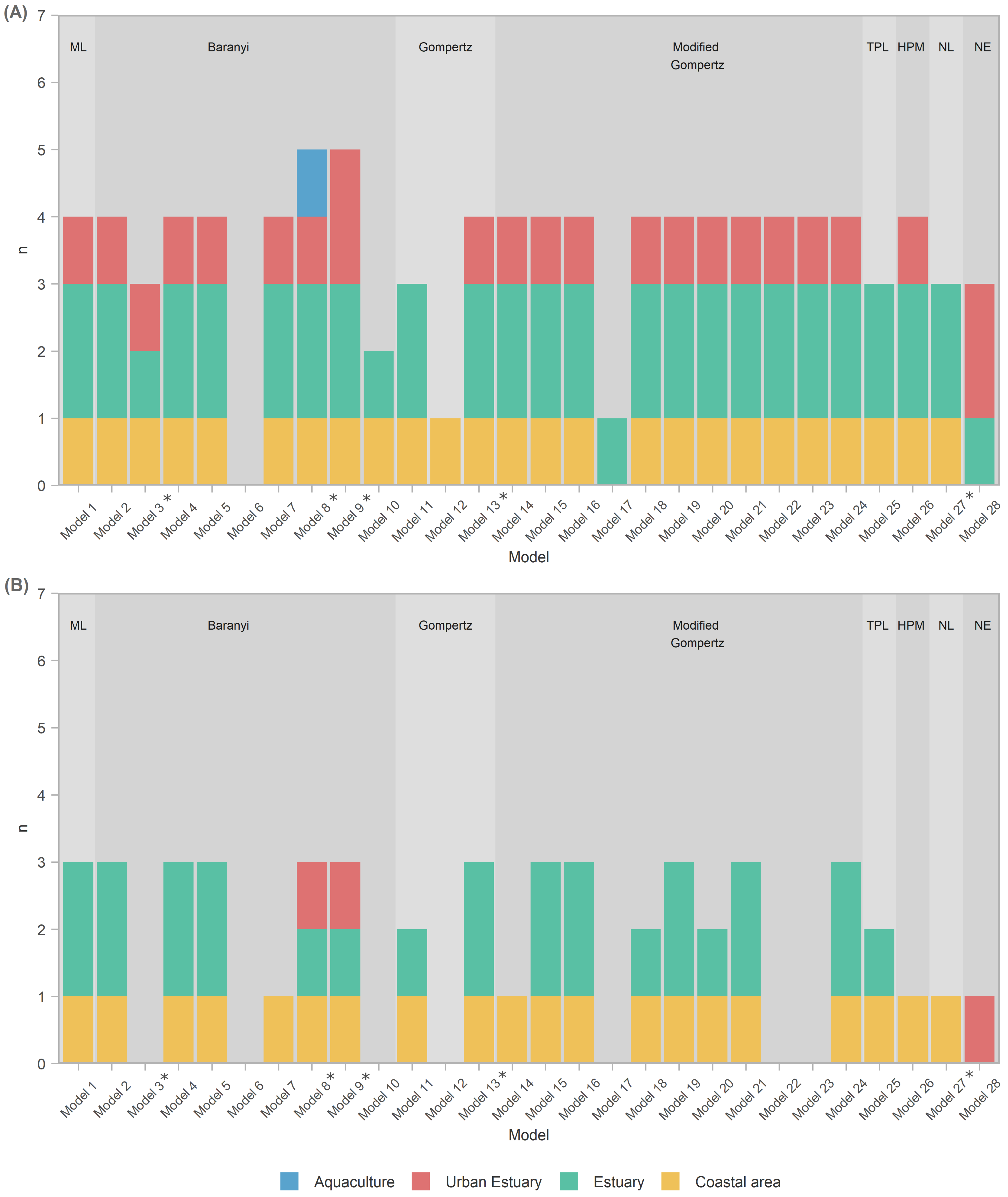
3.3. Model Performance
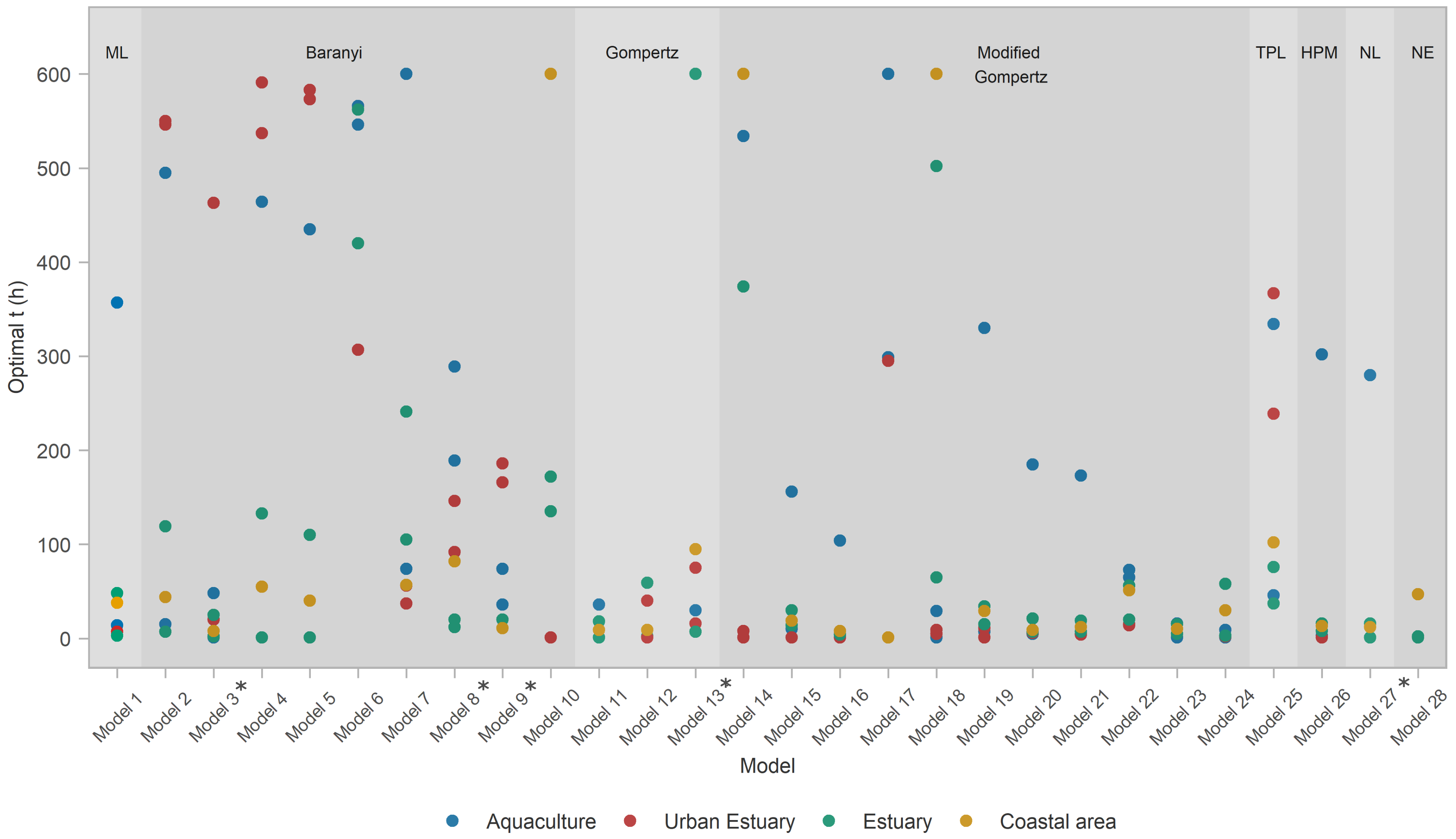
- All models except Model 6 (Baranyi with polinomial pH and salinity secondary models) were able to score above average at least in some habitats, i.e., capture those habitats. Incidentally, Model 6 was the only one not applying a temperature correction
- A total of 93% of models captured the coastal area habitat.
- A total of 93% of all models captured estuary habitat, but only 85% of those (i.e., 79% of all models) captured both estuary datasets; 26 models captured EST1, with 22 of them capturing EST2 as well.
- A total of 75% of models captured an urban habitat, but only two (Models 9 and 28) captured both urban habitat datasets; URB1 was captured by all 20 of them; only 3 models managed to capture URB2.
- Only the Baranyi-type model (Model 8, with temperature and salinity secondary models) captured the AQC1 aquaculture habitat.
- The model with the highest values (Model 28—net exponential, for urban estuary URB2) had low generality, as it captured datasets from only two out of four habitats.
- Of the models that performed well for at least one habitat type, Model 17 had lowest generality as it captured only one EST1 dataset.
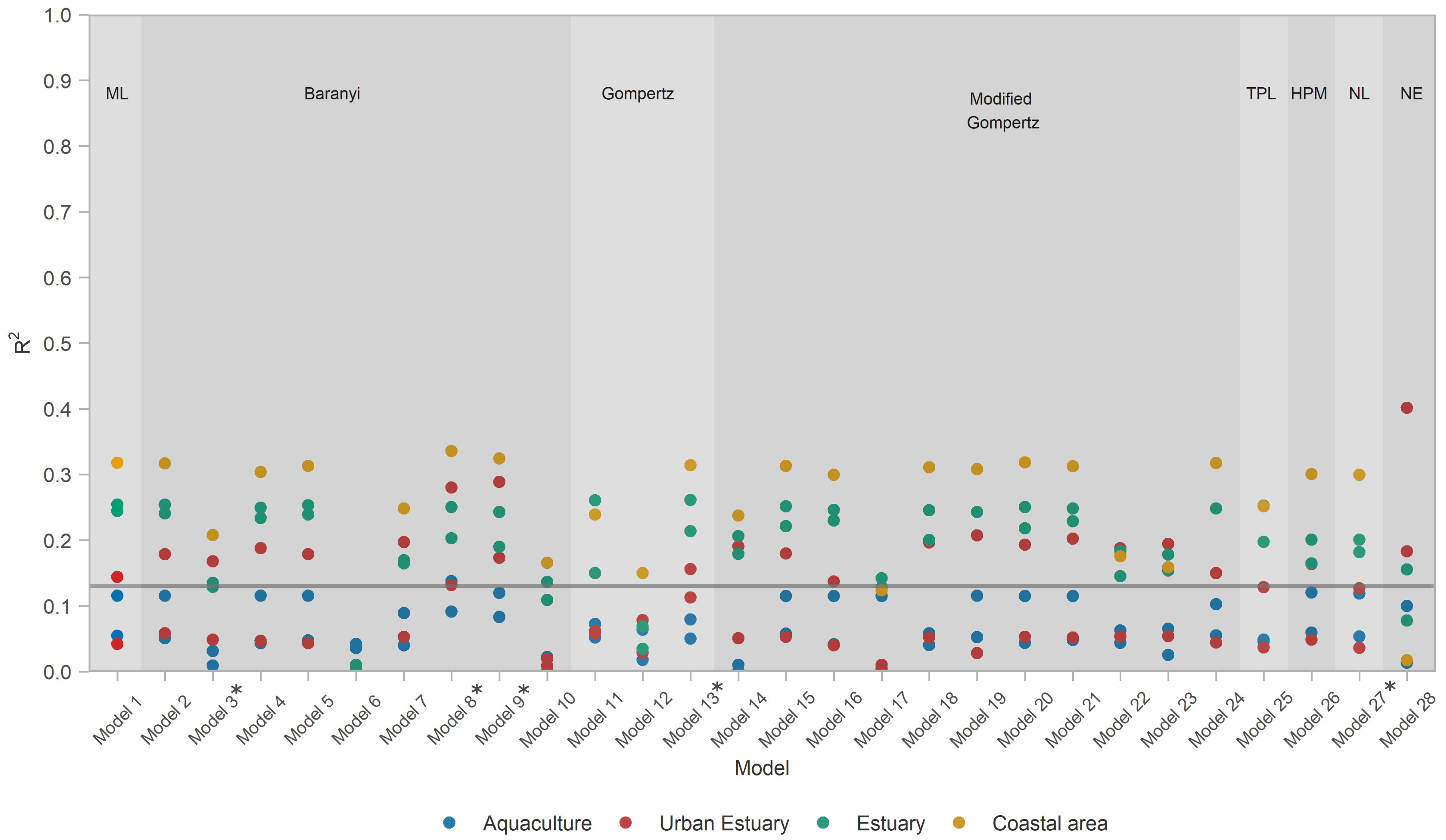
- ≈A total of 72% of the analyzed models had an exceptional ability to capture datasets from the coastal area habitat.
- The ability of models to capture/perform well for estuarine habitats was severely diminished, with only 16/28 (57% of the models) capturing one of the two estuary datasets, and only 10 models (36%) capturing both.
- None of the models were able to capture for the aquaculture habitat datasets, and only three (Models 8, 9, and 28) captured the urban estuary habitat.
- Model 28 seemed even more specialized, as it captured a single urban estuary (URB2)
- Most prolific Baranyi models (Models 8 and 9) remained so by capturing datasets from three habitat types, albeit only a single dataset from each.
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Literature Search
Appendix B. Data Analysis
| Derived Model | A | (C) | ||
|---|---|---|---|---|
| Model 1 [26] | 4 | / | / | 6.4 °C |
| Model 2 [26] | / | Est | Est | 6.4 |
| Model 3 [32] | / | Est | Est | 15 |
| Model 4 [33] | / | Est | Est | 8.3 |
| Model 5 [35] | / | Est | Est | 10.0 |
| Model 6 [36] | / | Est | Est | / |
| Model 7 [34] | / | Est | Est | 8.0 |
| Model 8 [37] | / | Est | Est | 12.9 |
| Model 9 [37] | / | Est | Est | 12.9 |
| Model 10 [31] | / | Est | Est | 15.0 |
| Model 11 [37] | / | Est | Est | 12.9 |
| Model 12 [37] | / | Est | Est | 12.9 |
| Model 13 [38] | / | Est | Est | 8.0 |
| Model 14 [31] | / | Est | / | 15.0 |
| Model 15 [40] | 4 | Est | / | 13.0 |
| Model 16 [40] | 4 | Est | / | 13.0 |
| Model 17 [40] | 4 | Est | / | 13.0 |
| Model 18 [40] | 4 | Est | / | 13.0 |
| Model 19 [40] | 4 | Est | / | 13.0 |
| Model 20 [42] | 6 | Est | / | 10.0 |
| Model 21 [42] | 6 | Est | / | 10.0 |
| Model 22 [42] | 6 | Est | / | 10.0 |
| Model 23 [42] | 6 | Est | / | 10.0 |
| Model 24 [41] | 4 | Est | / | 12.1 |
| Model 25 [45] | / | Est | 9.28 | 12.1 |
| Model 26 [47] | / | Est | 7.64 | 10.8 |
| Model 27 [47] | / | Est | 7.70 | 10.5 |
| Model 28 [49] | / | Est | / | / |
Appendix C. Additional Results
Appendix C.1. Methods Used for Determining Vibrio spp. Abundance
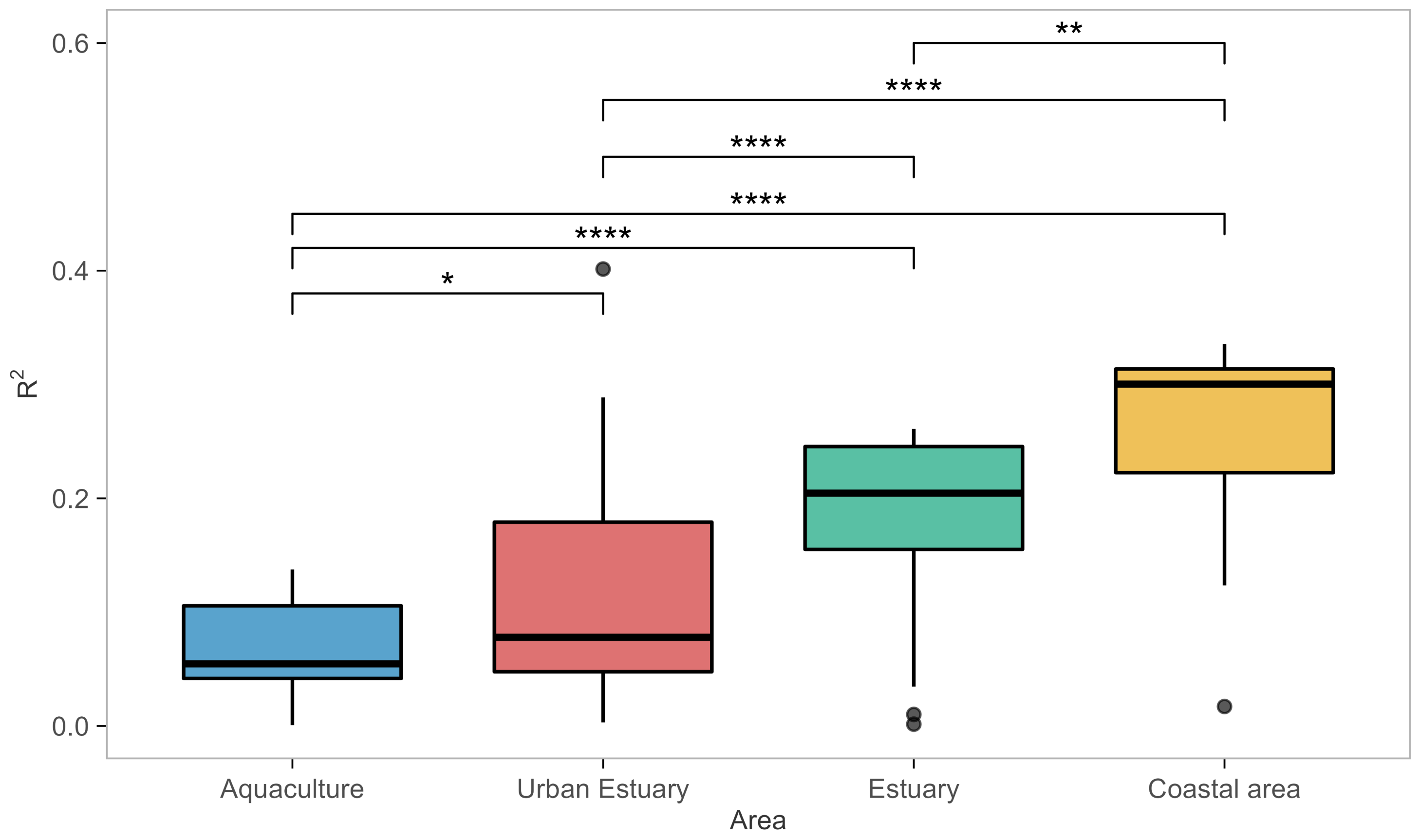
| Function: | t1way (formula = max_r2~Habitat, data = as) |
| Test statistic: | F = 75.561 |
| Degrees of freedom 1: | 3 |
| Degrees of freedom 2: | 49.90 |
| p-value: | 0 |
| Explanatory measure of effect size: | 0.77 |
| Bootstrap CI: | [0.68; 0.84] |
| Formula: | lincon (max_r2~Habitat, data = as) | |||
| Habitat type | psihat | ci.lower | ci. upper | p-value |
| Aquaculture vs. Urban Estuary | −0.03910 | −0.08237 | 0.00417 | 0.01688 |
| Aquaculture vs. Estuary | −0.14203 | −0.17331 | −0.11075 | 0.00000 |
| Aquaculture vs. Coastal Area | −0.21525 | −0.27062 | −0.15989 | 0.00000 |
| Urban Estuary vs. Estuary | −0.10293 | −0.14925 | −0.05662 | 0.00000 |
| Urban Estuary vs. Coastal Area | −0.17616 | −0.23977 | −0.11254 | 0.00000 |
| Estuary vs. Coastal Area | −0.07322 | −0.13069 | −0.01575 | 0.00263 |
Appendix D. Model Evaluation Issues
| Model | Issue | Impacts % of Dataset | Dataset |
|---|---|---|---|
| Model 3 | Negative specific growth rate | 26/99 = 26.26% | AQC1 [54] |
| 16/81 = 19.75% | AQC2 [55] | ||
| 52/223 = 23.32% | EST1 [58] | ||
| 30/127 = 23.62% | EST2 [59] | ||
| 4/72 = 5.56% | COAST [60] | ||
| Model 8 | High values of specific growth rate which generate Inf values | / | / |
| Model 9 | High values of specific growth rate which generate Inf values | 1/81 = 1.23% | AQC2 [55] |
| 6/223 = 2.69% | EST1 [58] | ||
| 4/127 = 3.15% | EST2 [59] | ||
| Model 13 | Salinity, i.e., water activity >0.998 | 80/223 = 35.87% | EST1 [58] |
| 18/240 = 7.50% | URB2 [57] | ||
| Model 27 | Temperature 10.5 °C | 2/81 = 2.47% | AQC2 [55] |
| 29/223 = 13.00% | EST1 [58] | ||
| 16/127 = 12.60% | EST2 [59] | ||
| 1/72 = 1.39% | COAST [60] |
References
- Zhang, X.; Lin, H.; Wang, X.; Austin, B. Significance of Vibrio species in the marine organic carbon cycle—A review. Sci. China Earth Sci. 2018, 61, 1357–1368. [Google Scholar] [CrossRef]
- Sampaio, A.; Silva, V.; Poeta, P.; Aonofriesei, F. Vibrio spp.: Life strategies, ecology, and risks in a changing environment. Diversity 2022, 14, 97. [Google Scholar] [CrossRef]
- Thompson, J.R.; Polz, M.F. Dynamics of Vibrio populations and their role in environmental nutrient cycling. In The Biology of Vibrios; Wiley Online Library: Hoboken, NJ, USA, 2006; pp. 190–203. [Google Scholar]
- Beardsley, C.; Pernthaler, J.; Wosniok, W.; Amann, R. Are readily culturable bacteria in coastal North Sea waters suppressed by selective grazing mortality? Appl. Environ. Microbiol. 2003, 69, 2624–2630. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, D.; Gupta, S.S.; Legros, D. Cholera surveillance and estimation of burden of cholera. Vaccine 2020, 38, A13–A17. [Google Scholar] [CrossRef]
- Gilbert, J.A.; Steele, J.A.; Caporaso, J.G.; Steinbrück, L.; Reeder, J.; Temperton, B.; Huse, S.; McHardy, A.C.; Knight, R.; Joint, I.; et al. Defining seasonal marine microbial community dynamics. ISME J. 2012, 6, 298–308. [Google Scholar] [CrossRef]
- Westrich, J.R.; Ebling, A.M.; Landing, W.M.; Joyner, J.L.; Kemp, K.M.; Griffin, D.W.; Lipp, E.K. Saharan dust nutrients promote Vibrio bloom formation in marine surface waters. Proc. Natl. Acad. Sci. USA 2016, 113, 5964–5969. [Google Scholar] [CrossRef]
- Poloczanska, E.S.; Brown, C.J.; Sydeman, W.J.; Kiessling, W.; Schoeman, D.S.; Moore, P.J.; Brander, K.; Bruno, J.F.; Buckley, L.B.; Burrows, M.T.; et al. Global imprint of climate change on marine life. Nat. Clim. Chang. 2013, 3, 919–925. [Google Scholar] [CrossRef]
- Dore, M.H. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef]
- Bijma, J.; Pörtner, H.O.; Yesson, C.; Rogers, A.D. Climate change and the oceans—What does the future hold? Mar. Pollut. Bull. 2013, 74, 495–505. [Google Scholar] [CrossRef]
- Burge, C.A.; Hershberger, P.K. Climate change can drive marine diseases. In Marine Disease Ecology; Behringer, D.C., Silliman, B.R., Lafferty, K.D., Eds.; Oxford University Press: Oxford, UK, 2020; pp. 83–94. [Google Scholar]
- Martinez-Urtaza, J.; Bowers, J.C.; Trinanes, J.; DePaola, A. Climate anomalies and the increasing risk of Vibrio parahaemolyticus and Vibrio vulnificus illnesses. Food Res. Int. 2010, 43, 1780–1790. [Google Scholar] [CrossRef]
- Da Cunha, D.T. Improving food safety practices in the foodservice industry. Curr. Opin. Food Sci. 2021, 42, 127–133. [Google Scholar] [CrossRef]
- Levallois, P.; Villanueva, C.M. Drinking water quality and human health: An editorial. Int. J. Environ. Res. Public Health 2019, 16, 631. [Google Scholar] [CrossRef]
- Li, H.; Xie, G.; Edmondson, A.S. Review of secondary mathematical models of predictive microbiology. J. Food Prod. Mark. 2008, 14, 57–74. [Google Scholar] [CrossRef]
- Ferrer, J.; Prats, C.; López, D.; Vives-Rego, J. Mathematical modeling methodologies in predictive food microbiology: A SWOT analysis. Int. J. Food Microbiol. 2009, 134, 2–8. [Google Scholar] [CrossRef]
- Peleg, M.; Corradini, M.G. Microbial growth curves: What the models tell us and what they cannot. Crit. Rev. Food Sci. Nutr. 2011, 51, 917–945. [Google Scholar] [CrossRef]
- Perez-Rodriguez, F.; Valero, A. Predictive microbiology in foods. In Predictive Microbiology in Foods; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–10. [Google Scholar]
- Oscar, T. Development and validation of primary, secondary, and tertiary models for growth of Salmonella Typhimurium on sterile chicken. J. Food Prot. 2005, 68, 2606–2613. [Google Scholar] [CrossRef]
- Baranyi, J.; McClure, P.; Sutherland, J.; Roberts, T. Modeling bacterial growth responses. J. Ind. Microbiol. Biotechnol. 1993, 12, 190–194. [Google Scholar] [CrossRef]
- Pirt, S.J. Principles of Microbe and Cell Cultivation; Blackwell Scientific Publications: Hoboken, NJ, USA, 1975. [Google Scholar]
- Ratkowsky, D.; Lowry, R.; McMeekin, T.; Stokes, A.; Chandler, R. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 1983, 154, 1222–1226. [Google Scholar] [CrossRef]
- Davey, K. A predictive model for combined temperature and water activity on microbial growth during the growth phase. J. Appl. Bacteriol. 1989, 67, 483–488. [Google Scholar] [CrossRef]
- Esser, D.S.; Leveau, J.H.; Meyer, K.M. Modeling microbial growth and dynamics. Appl. Microbiol. Biotechnol. 2015, 99, 8831–8846. [Google Scholar] [CrossRef]
- Zwietering, M.; Jongenburger, I.; Rombouts, F.; Van’t Riet, K. Modeling of the bacterial growth curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Shen, J.; Liu, Y.; Chen, K. A predictive model of V ibrio cholerae for combined temperature and organic nutrient in aquatic environments. J. Appl. Microbiol. 2013, 114, 574–585. [Google Scholar] [CrossRef]
- Fu, S.; Liu, Y.; Li, X.; Tu, J.; Lan, R.; Tian, H. A preliminary stochastic model for managing microorganisms in a recirculating aquaculture system. Ann. Microbiol. 2015, 65, 1119–1129. [Google Scholar] [CrossRef]
- Ma, F.; Liu, H.; Wang, J.; Zhang, Z.; Sun, X.; Pan, Y.; Zhao, Y. Behavior of Vibrio parahemolyticus cocktail including pathogenic and nonpathogenic strains on cooked shrimp. Food Control 2016, 68, 124–132. [Google Scholar] [CrossRef]
- Zahaba, M.; Halmi, M.I.E.; Othman, A.R.; Shukor, M.Y. Mathematical modeling of the growth curve of Vibrio sp. isolate MZ grown in Seawater medium. Bioremediation Sci. Technol. Res. 2018, 6, 31–34. [Google Scholar] [CrossRef]
- Baranyi, J.; Roberts, T.A. Mathematics of predictive food microbiology. Int. J. Food Microbiol. 1995, 26, 199–218. [Google Scholar] [CrossRef]
- Boonyawantang, A.; Mahakarnchanakul, W.; Rachtanapun, C.; Boonsupthip, W. Behavior of pathogenic Vibrio parahaemolyticus in prawn in response to temperature in laboratory and factory. Food Control 2012, 26, 479–485. [Google Scholar] [CrossRef]
- Chung, K.H.; Park, M.S.; Kim, H.Y.; Bahk, G.J. Growth prediction and time–temperature criteria model of Vibrio parahaemolyticus on traditional Korean raw crab marinated in soy sauce (ganjang-gejang) at different storage temperatures. Food Control 2019, 98, 187–193. [Google Scholar] [CrossRef]
- Fernandez-Piquer, J.; Bowman, J.P.; Ross, T.; Tamplin, M.L. Predictive models for the effect of storage temperature on Vibrio parahaemolyticus viability and counts of total viable bacteria in Pacific oysters (Crassostrea gigas). Appl. Environ. Microbiol. 2011, 77, 8687–8695. [Google Scholar] [CrossRef] [PubMed]
- Oh, H.; Yoon, Y.; Ha, J.; Lee, J.; Shin, I.S.; Kim, Y.M.; Park, K.S.; Kim, S. Risk assessment of vibriosis by Vibrio cholerae and Vibrio vulnificus in whip-arm octopus consumption in South Korea. Fish. Aquat. Sci. 2021, 24, 207–218. [Google Scholar] [CrossRef]
- Parveen, S.; DaSilva, L.; DePaola, A.; Bowers, J.; White, C.; Munasinghe, K.A.; Brohawn, K.; Mudoh, M.; Tamplin, M. Development and validation of a predictive model for the growth of Vibrio parahaemolyticus in post-harvest shellstock oysters. Int. J. Food Microbiol. 2013, 161, 1–6. [Google Scholar] [CrossRef]
- Posada-Izquierdo, G.D.; Valero, A.; Arroyo-López, F.N.; González-Serrano, M.; Ramos-Benítez, A.M.; Benítez-Cabello, A.; Rodríguez-Gómez, F.; Jimenez-Diaz, R.; García-Gimeno, R.M. Behavior of Vibrio spp. in table olives. Front. Microbiol. 2021, 2021, 1130. [Google Scholar] [CrossRef]
- Zhou, K.; Gui, M.; Li, P.; Xing, S.; Cui, T.; Peng, Z. Effect of combined function of temperature and water activity on the growth of Vibrio harveyi. Braz. J. Microbiol. 2012, 43, 1365–1375. [Google Scholar] [CrossRef]
- Miles, D.W.; Ross, T.; Olley, J.; McMeekin, T.A. Development and evaluation of a predictive model for the effect of temperature and water activity on the growth rate of Vibrio parahaemolyticus. Int. J. Food Microbiol. 1997, 38, 133–142. [Google Scholar] [CrossRef]
- Nishina, T.; Wada, M.; Ozawa, H.; Hara-Kudo, Y.; Konuma, H.; Hasegawa, J.; Kumagi, S. Growth kinetics of Vibrio parahaemolyticus O3: K6 under varying conditions of pH, NaCl concentration and temperature. Food Hyg. Saf. Sci. 2004, 45, 35–37. [Google Scholar] [CrossRef][Green Version]
- Kim, Y.W.; Lee, S.H.; Hwang, I.G.; Yoon, K.S. Effect of temperature on growth of Vibrio paraphemolyticus and Vibrio vulnificus in flounder, salmon sashimi and oyster meat. Int. J. Environ. Res. Public Health 2012, 9, 4662–4675. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Jiao, X.A.; Li, P.; Pan, Z.M.; Huang, J.L.; Gu, R.X.; Fang, W.M.; Chao, G.X. Predictive model of Vibrio parahaemolyticus growth and survival on salmon meat as a function of temperature. Food Microbiol. 2009, 26, 606–614. [Google Scholar] [CrossRef]
- Yoon, K.; Min, K.; Jung, Y.; Kwon, K.; Lee, J.; Oh, S. A model of the effect of temperature on the growth of pathogenic and nonpathogenic Vibrio parahaemolyticus isolated from oysters in Korea. Food Microbiol. 2008, 25, 635–641. [Google Scholar] [CrossRef]
- Van Boekel, M.A. On the use of the Weibull model to describe thermal inactivation of microbial vegetative cells. Int. J. Food Microbiol. 2002, 74, 139–159. [Google Scholar] [CrossRef]
- Buchanan, R.; Whiting, R.; Damert, W. When is simple good enough: A comparison of the Gompertz, Baranyi, and three-phase linear models for fitting bacterial growth curves. Food Microbiol. 1997, 14, 313–326. [Google Scholar] [CrossRef]
- Tang, X.; Zhao, Y.; Sun, X.; Xie, J.; Pan, Y.; Malakar, P.K. Predictive model of Vibrio parahaemolyticus O3: K6 growth on cooked Litopenaeus vannamei. Ann. Microbiol. 2015, 65, 487–493. [Google Scholar]
- Huang, L. Growth kinetics of Listeria monocytogenes in broth and beef frankfurters—Determination of lag phase duration and exponential growth rate under isothermal conditions. J. Food Sci. 2008, 73, E235–E242. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.R.; Hwang, C.A.; Huang, L.; Wu, V.C.; Hsiao, H.I. Kinetic analysis and dynamic prediction of growth of vibrio parahaemolyticus in raw white shrimp at refrigerated and abuse temperatures. Food Control 2019, 100, 204–211. [Google Scholar] [CrossRef]
- Fang, T.; Gurtler, J.B.; Huang, L. Growth kinetics and model comparison of Cronobacter sakazakii in reconstituted powdered infant formula. J. Food Sci. 2012, 77, E247–E255. [Google Scholar] [CrossRef] [PubMed]
- Froelich, B.; Bowen, J.; Gonzalez, R.; Snedeker, A.; Noble, R. Mechanistic and statistical models of total Vibrio abundance in the Neuse River Estuary. Water Res. 2013, 47, 5783–5793. [Google Scholar] [CrossRef]
- Fujikawa, H.; Kai, A.; Morozumi, S. A new logistic model for bacterial growth. Shokuhin Eiseigaku Zasshi. J. Food Hyg. Soc. Jpn. 2003, 44, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Fujikawa, H. Application of the new logistic model to microbial growth prediction in food. Biocontrol Sci. 2011, 16, 47–54. [Google Scholar] [CrossRef][Green Version]
- Ratkowsky, D.A.; Olley, J.; McMeekin, T.; Ball, A. Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 1982, 149, 1–5. [Google Scholar] [CrossRef]
- Huang, L.; Hwang, C.A.; Phillips, J. Evaluating the Effect of Temperature on Microbial Growth Rate—The Ratkowsky and a Bělehrádek-Type Models. J. Food Sci. 2011, 76, M547–M557. [Google Scholar] [CrossRef]
- Kapetanović, D.; Purgar, M.; Gavrilović, A.; Hackenberger, B.K.; Kurtović, B.; Haberle, I.; Pečar Ilić, J.; Geček, S.; Hackenberger, D.K.; Djerdj, T.; et al. AqADAPT: Physiochemical parameters and Vibrio spp. abundance in water samples gathered in the Adriatic Sea. PANGAEA 2022. submitted. [Google Scholar]
- Jug-Dujaković, J.; Gavrilović, A.; Kolda, A.; Žunić, J.; Pikelj, K.; Listeš, E.; Vukić Lušić, D.; Vardić Smrzlić, L.; Perić, L.; El-Matbouli, M.; et al. AQUAHEALTH: Physiochemical parameters and Vibrio spp. abundance in water samples gathered in the Adriatic Sea. PANGAEA 2022. submitted. [Google Scholar]
- Bullington, J.A.; Golder, A.R.; Steward, G.F.; McManus, M.A.; Neuheimer, A.B.; Glazer, B.T.; Nigro, O.D.; Nelson, C.E. Refining real-time predictions of Vibrio vulnificus concentrations in a tropical urban estuary by incorporating dissolved organic matter dynamics. Sci. Total Environ. 2022, 829, 154075. [Google Scholar] [CrossRef] [PubMed]
- Nigro, O.D.; James-Davis, L.I.; De Carlo, E.H.; Li, Y.H.; Steward, G.F. Variable freshwater influences on the abundance of Vibrio vulnificus in a tropical urban estuary. Appl. Environ. Microbiol. 2022, 88, e01884-21. [Google Scholar] [CrossRef] [PubMed]
- Froelich, B.; Gonzalez, R.; Blackwood, D.; Lauer, K.; Noble, R. Decadal monitoring reveals an increase in Vibrio spp. concentrations in the Neuse River Estuary, North Carolina, USA. PLoS ONE 2019, 14, e0215254. [Google Scholar] [CrossRef]
- Urquhart, E.A.; Jones, S.H.; Yu, J.W.; Schuster, B.M.; Marcinkiewicz, A.L.; Whistler, C.A.; Cooper, V.S. Environmental conditions associated with elevated Vibrio parahaemolyticus concentrations in Great Bay Estuary, New Hampshire. PLoS ONE 2016, 11, e0155018. [Google Scholar] [CrossRef]
- Williams, T.C.; Froelich, B.A.; Phippen, B.; Fowler, P.; Noble, R.T.; Oliver, J.D. Different abundance and correlational patterns exist between total and presumed pathogenic Vibrio vulnificus and V. parahaemolyticus in shellfish and waters along the North Carolina coast. FEMS Microbiol. Ecol. 2017, 93, 71. [Google Scholar] [CrossRef] [PubMed]
- Mair, P.; Wilcox, R. Robust statistical methods in R using the WRS2 package. Behav. Res. Methods 2020, 52, 464–488. [Google Scholar] [CrossRef]
- Wilcox, R.R. Introduction to Robust Estimation and Hypothesis Testing, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, PBC: Boston, MA, USA, 2020. [Google Scholar]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Software Artic. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Hamner, B.; Frasco, M.; LeDell, E. Evaluation Metrics for Machine Learning. 2018. Available online: https://cran.r-project.org/web/packages/Metrics/Metrics.pdf (accessed on 25 April 2022).
- Grosjean, P. SciViews–Main Package. 2019. Available online: https://cran.r-project.org/web/packages/SciViews/SciViews.pdf (accessed on 25 April 2022).
- Dowle, M. Package ‘data.table’: Extension of ‘data.frame’. 2021. Available online: https://cran.r-project.org/web/packages/data.table/data.table.pdf (accessed on 25 April 2022).
- Wickham, H. Read Excel Files. 2019. Available online: https://cran.microsoft.com/snapshot/2019-03-09/web/packages/readxl/readxl.pdf (accessed on 25 April 2022).
- Dragulescu, A.; Arendt, C. Read, Write, Format Excel 2007 and Excel 97/2000/XP/2003 Files. 2020. Available online: https://cran.r-project.org/web/packages/xlsx/xlsx.pdf (accessed on 25 April 2022).
- Purgar, M.; Kapetanović, D.; Geček, S.; Marn, N.; Haberle, I.; Hackenberger, K.B.; Gavrilović, A.; Pečar Ilić, J.; Hackenberger K., D.; Djerdj, T.; et al. Codes for Purgar et al. 2022: Investigating the ability of growth models to predict in situ Vibrio spp. abundances. Zenodo 2022. [Google Scholar] [CrossRef]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Martinez-Urtaza, J.; Lozano-Leon, A.; Varela-Pet, J.; Trinanes, J.; Pazos, Y.; Garcia-Martin, O. Environmental determinants of the occurrence and distribution of Vibrio parahaemolyticus in the rias of Galicia, Spain. Appl. Environ. Microbiol. 2008, 74, 265–274. [Google Scholar] [CrossRef]
- Kirchman, D.L. Growth rates of microbes in the oceans. Annu. Rev. Mar. Sci. 2016, 8, 285–309. [Google Scholar] [CrossRef]
- Norris, N.; Levine, N.M.; Fernandez, V.I.; Stocker, R. Mechanistic model of nutrient uptake explains dichotomy between marine oligotrophic and copiotrophic bacteria. PLoS Comput. Biol. 2021, 17, e1009023. [Google Scholar] [CrossRef]
- Trinanes, J.; Martinez-Urtaza, J. Future scenarios of risk of Vibrio infections in a warming planet: A global mapping study. Lancet Planet. Health 2021, 5, e426–e435. [Google Scholar] [CrossRef]
- Ouzzani, M.; Hammady, H.; Fedorowicz, Z.; Elmagarmid, A. Rayyan—A web and mobile app for systematic reviews. Syst. Rev. 2016, 5, 1–10. [Google Scholar] [CrossRef]
- Gekas, V.; Gonzalez, C.; Sereno, A.; Chiralt, A.; Fito, P. Mass transfer properties of osmotic solutions. I. Water activity and osmotic pressure. Int. J. Food Prop. 1998, 1, 95–112. [Google Scholar] [CrossRef]

| Model | Equation | Article |
|---|---|---|
| Modified logistic [25] | [26,27,28,29] | |
| Baranyi [30] | [26,28,29,31,32,33,34,35,36,37] | |
| Gompertz [25] | [37,38,39] | |
| Modified Gompertz [25] | [28,29,31,40,41,42] | |
| Weibull [43] | [28,41] | |
| Three-phase linear [44] | [29,45] | |
| Huang [46] | [29,47] | |
| No-lag phase [48] | [47] | |
| Net exponential | [49] | |
| Modified Richards [25] | [29] | |
| Modified Schnute [25] | [29] | |
| New logistic [50] | [51] |
| Model | Equation | Article |
|---|---|---|
| Square root [52] | [26,33,35,40,41,45] | |
| Polynomial model | [32,34,36,51] | |
| Response surface [37] | [37] | |
| Arrhenius-based [23] | [31,37,40,42] | |
| Modified Ratkovsky [22] | [31] | |
| Suboptimal Huang square root [53] | [47] | |
| Four-parameter square root and water activity [38] | [38] | |
| Net Vibrio growth rate [49] | [49] |
| Parameter | Description | Used in Model |
|---|---|---|
| Logarithm of real-time initial and maximum bacterial counts | All primary models | |
| Maximum specific growth rate | All primary models except Weibull and New logistic All secondary models except Net Vibrio growth rate | |
| Net Vibrio growth rate | Net Vibrio growth rate | |
| Lag time | All primary models except Gompertz, Weibull and New logistic | |
| t | Time | All models |
| Time to reach stationary growth phase | Three-phase linear | |
| A | Maximum increase in microbial cell density | Modified logistic Gompertz Modified Gompertz Modified Richards Modified Schnute |
| B, D | Maximum relative growth rate and time at which the absolute growth rate is maximum | Gompertz |
| Shape parameter | Modified Richards | |
| a, b, c, m, n | Fitted coefficients | Modified Schnute and New logistic model |
| Fitted coefficients | Response surface and Arrhenius-based | |
| T, , | Temperature, minimum and maximum temperature required for growth of the organism | All secondary models |
| , p | Coefficients in the Weibull model | Weibull |
| Optimal, the minimum, and maximum water activity | Four-parameter | |
| Salinity, optimal salinity value, and salinity range for optimal growth | Net Vibrio growth rate |
| Derived Model | Vibrio spp. | Environment | Environmental Conditions | Primary Model | Secondary Model |
|---|---|---|---|---|---|
| Model 1 [26] | V. cholerae | Sea water | Temp | Modified logistic | Square root |
| Model 2 [26] | V. cholerae | Sea water | Temp | Baranyi | Square root |
| Model 3 [32] | V. parahaemolyticus | Soy sauce | Temp | Baranyi | Polynomial |
| Model 4 [33] | V. parahaemolyticus | C. gigas | Temp | Baranyi | Square root |
| Model 5 [35] | V. parahaemolyticus | C. virginica | Temp | Baranyi | Square root |
| Model 6 [36] | V. cocktail 1 | Table Olives | pH and Sal | Baranyi | Polinomial |
| Model 7 [34] | V. cholerae and V. vulnificus | O. minor | Temp | Baranyi | Polinomial |
| Model 8 [37] | V. harveyi | TSYEB 2 | Temp and Sal (w.a.) | Baranyi | Response surface |
| Model 9 [37] | V. harveyi | TSYEB 2 | Temp and Sal (w.a.) | Baranyi | Arrhenius-based |
| Model 10 [31] | V. parahaemolyticus | L. vannamei | Temp | Baranyi | Modified Ratkowsky |
| Model 11 [37] | V. harveyi | TSYEB 2 | Temp and Sal (w.a.) | Gompertz | Response surface |
| Model 12 [37] | V. harveyi | TSYEB 2 | Temp and Sal (w.a.) | Gompertz | Arrhenius-based |
| Model 13 [38] | V. parahaemolyticus | Model broth system | Temp and Sal (w.a.) | Gompertz | The four-parameter square root |
| Model 14 [31] | V. parahaemolyticus | L. vannamei | Temp | Modified Gompertz | Modified Ratkowsky |
| Model 15 [40] | V. parahaemolyticus | Broth | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 16 [40] | V. vulnificus | Broth | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 17 [40] | V. parahaemolyticus | Flounder sashimi | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 18 [40] | V. parahaemolyticus | Salmon sashimi | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 19 [40] | V. vulnificus | Oyster meat | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 20 [42] | V. parahaemolyticus3 | C. gigas broth | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 21 [42] | V. parahaemolyticus4 | C. gigas broth | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 22 [42] | V. parahaemolyticus3 | C. gigas Oyster slurry | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 23 [42] | V. parahaemolyticus4 | C. gigas Oyster slurry | Temp | Modified Gompertz | Square root Arrhenius-based |
| Model 24 [41] | V. parahaemolyticus | Oncorhynchus spp. | Temp | Modified Gompertz, Weibull | Square root |
| Model 25 [45] | V. parahaemolyticus | L. vannamei | Temp | Three-phase linear | Square root |
| Model 26 [47] | V. parahaemolyticus | L. vannamei | Temp | Huang primary | Suboptimal Huang square root |
| Model 27 [47] | V. parahaemolyticus | L. vannamei | Temp | No-lag | Suboptimal Huang square root |
| Model 28 [49] | Vibrio spp. | NR Estuary | Temp and Sal | Net exponential | Net Vibrio growth rate |
| Dataset | Reported Values | Values for validation | Temperature Range (°C) | Salinity Range (ppt) | pH | Habitat TYPE | Collection Site |
|---|---|---|---|---|---|---|---|
| AQC1 [54] | 108 | 99 | 11.1–27.5 | 33.5–39.3 | 8.10–8.61 | Aquaculture | Adriatic Sea, Croatia |
| AQC2 [55] | 88 | 81 | 7.86–25.23 | 24.9–38.2 | 7.56–8.49 | Aquaculture | Adriatic Sea, Croatia |
| URB1 [56] | 213 | 149 | 22.4–31 | 7.98–34.74 | 7.51–8.27 | Urban Estuary | Ala Wai Canal in Honolulu, Hawaii |
| URB2 [57] | 243 | 240 | 19.2–31.8 | 1.0–36.0 | / | Urban Estuary | Ala Wai Canal in Honolulu, Hawaii |
| EST1 [58] | 249 | 223 | 3.1–31.7 | 0.09–18.56 | 6.57–9.17 | Estuary | Neuse River Estuary, North Carolina (USA) |
| EST2 [59] | 133 | 127 | 2.16–25.89 | 9.32–31.86 | 6.82–8.41 | Estuary | Great Bay Estuary, New Hampshire (USA) |
| COAST [60] | 117 | 72 | 8.9–29.4 | 12.0–40.0 | / | Coastal Area | Eastern North Carolina coast (USA) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Purgar, M.; Kapetanović, D.; Geček, S.; Marn, N.; Haberle, I.; Hackenberger, B.K.; Gavrilović, A.; Pečar Ilić, J.; Hackenberger, D.K.; Djerdj, T.; et al. Investigating the Ability of Growth Models to Predict In Situ Vibrio spp. Abundances. Microorganisms 2022, 10, 1765. https://doi.org/10.3390/microorganisms10091765
Purgar M, Kapetanović D, Geček S, Marn N, Haberle I, Hackenberger BK, Gavrilović A, Pečar Ilić J, Hackenberger DK, Djerdj T, et al. Investigating the Ability of Growth Models to Predict In Situ Vibrio spp. Abundances. Microorganisms. 2022; 10(9):1765. https://doi.org/10.3390/microorganisms10091765
Chicago/Turabian StylePurgar, Marija, Damir Kapetanović, Sunčana Geček, Nina Marn, Ines Haberle, Branimir K. Hackenberger, Ana Gavrilović, Jadranka Pečar Ilić, Domagoj K. Hackenberger, Tamara Djerdj, and et al. 2022. "Investigating the Ability of Growth Models to Predict In Situ Vibrio spp. Abundances" Microorganisms 10, no. 9: 1765. https://doi.org/10.3390/microorganisms10091765
APA StylePurgar, M., Kapetanović, D., Geček, S., Marn, N., Haberle, I., Hackenberger, B. K., Gavrilović, A., Pečar Ilić, J., Hackenberger, D. K., Djerdj, T., Ćaleta, B., & Klanjscek, T. (2022). Investigating the Ability of Growth Models to Predict In Situ Vibrio spp. Abundances. Microorganisms, 10(9), 1765. https://doi.org/10.3390/microorganisms10091765








