Linearizing Control of a Distributed Actuation Magnetic Bearing for Thin-Walled Rotor Systems
Abstract
1. Introduction
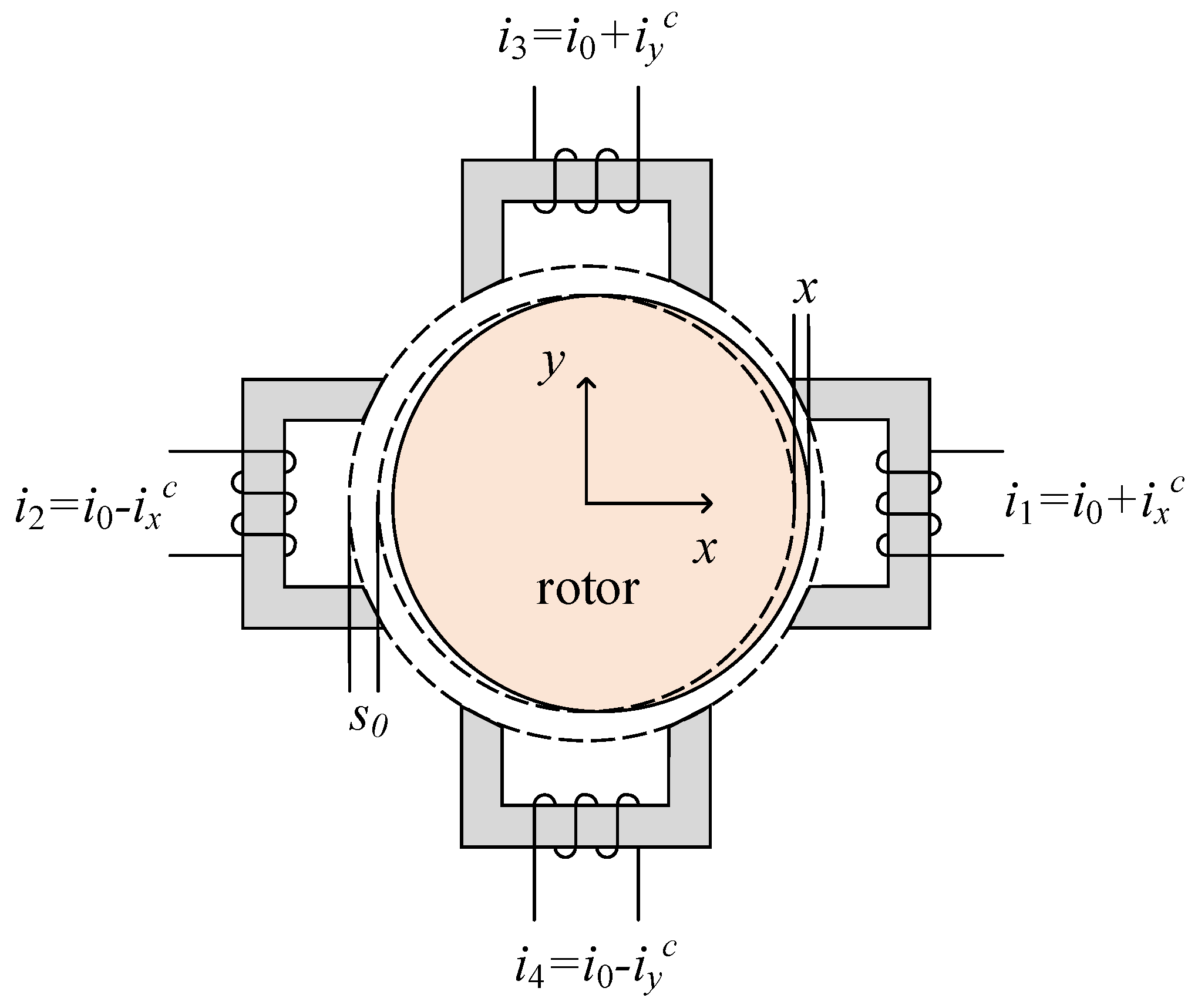
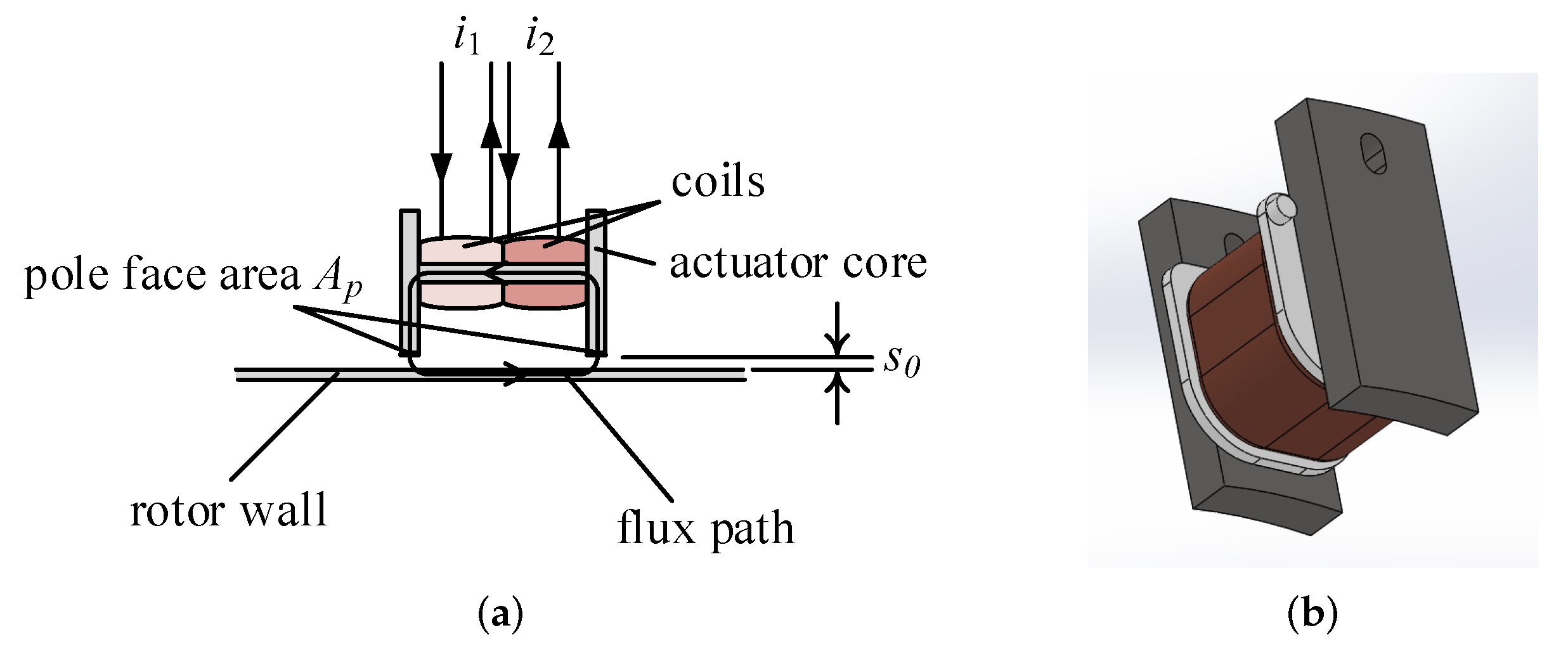
2. DAMB Design and Force Model
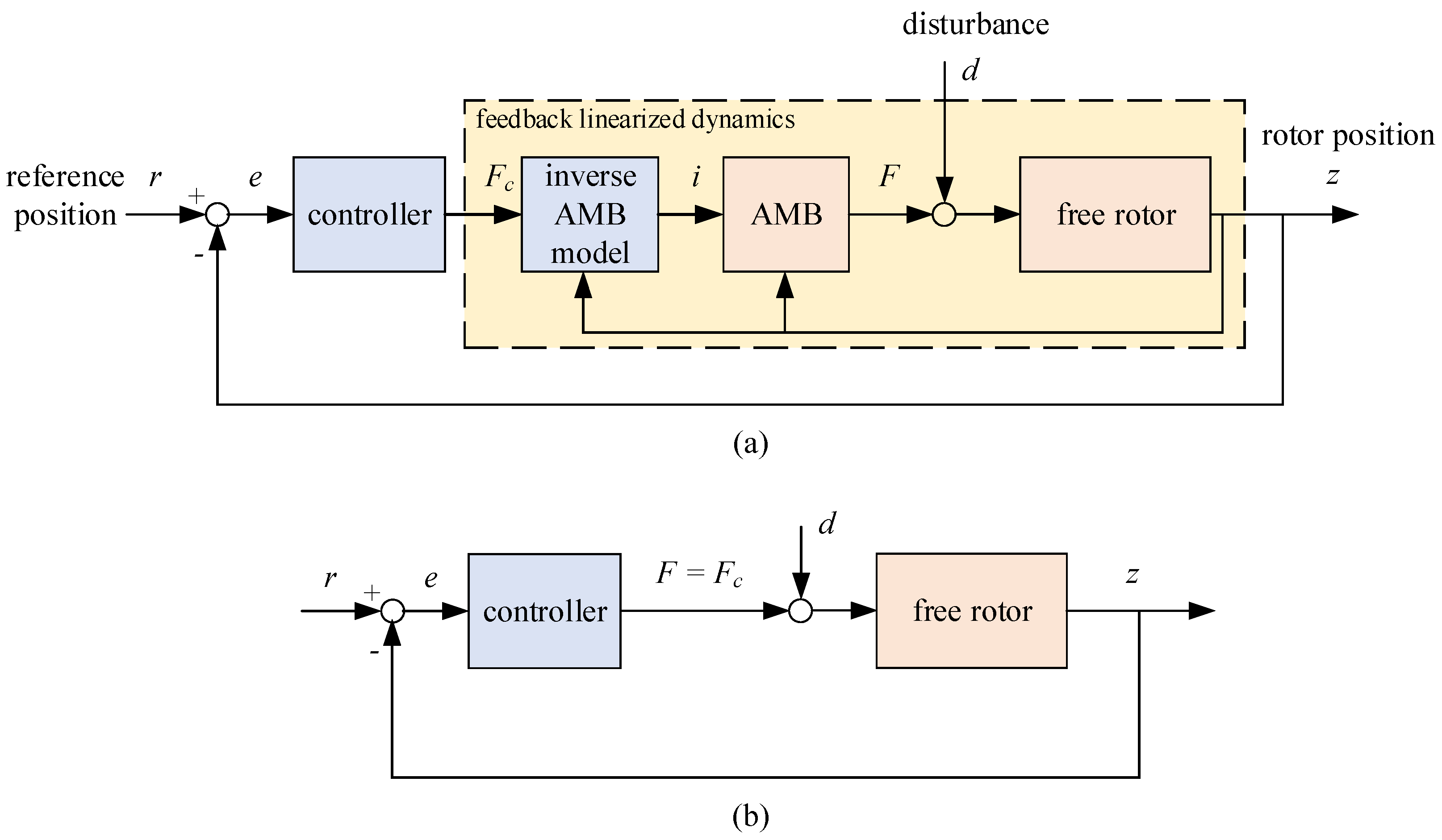
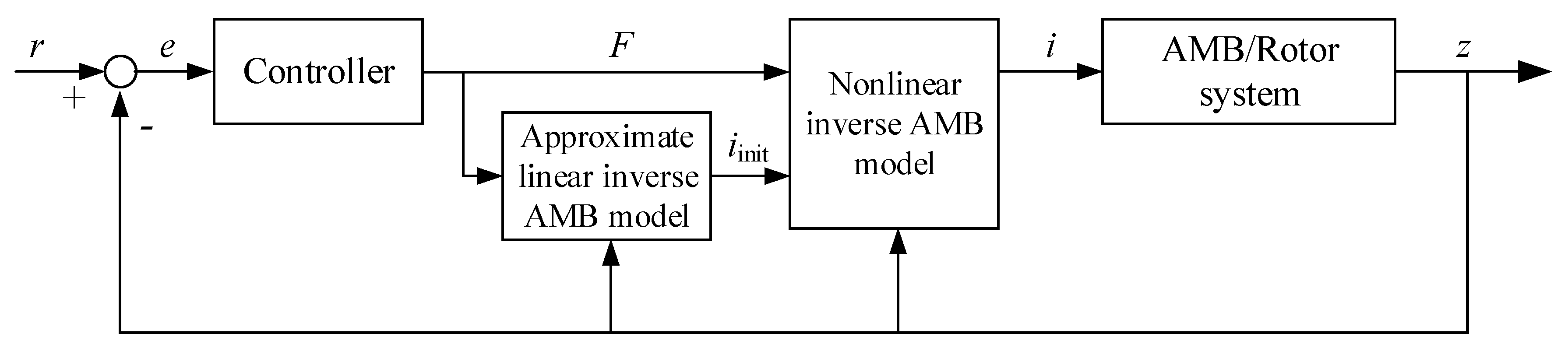
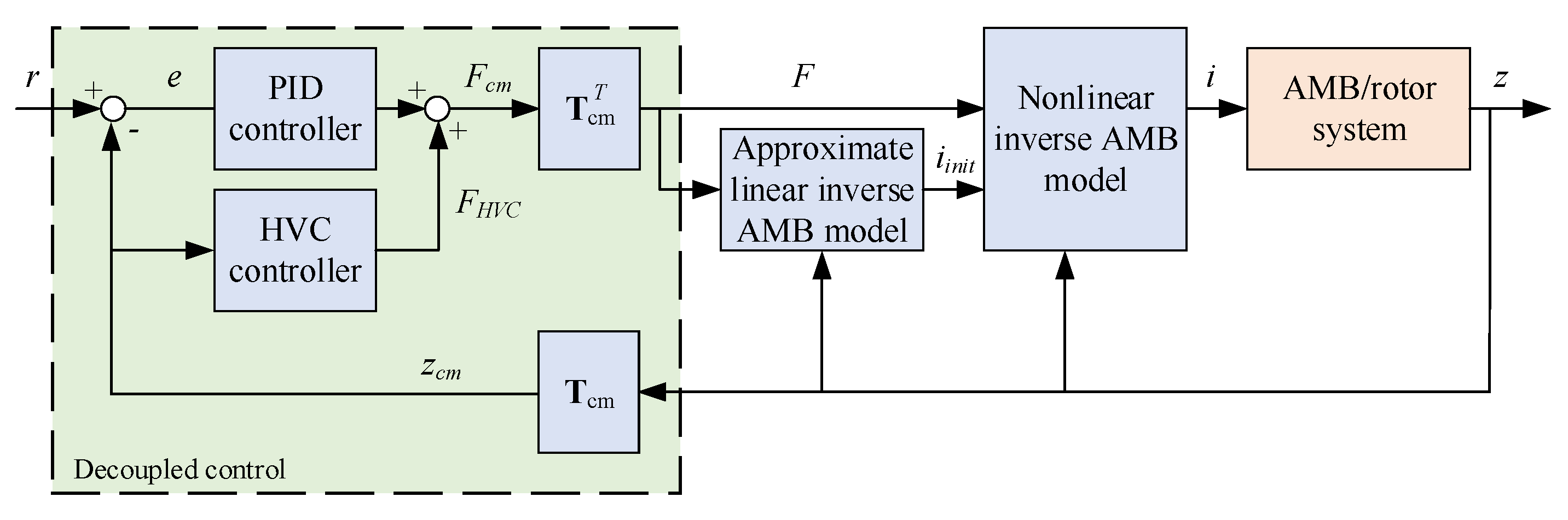
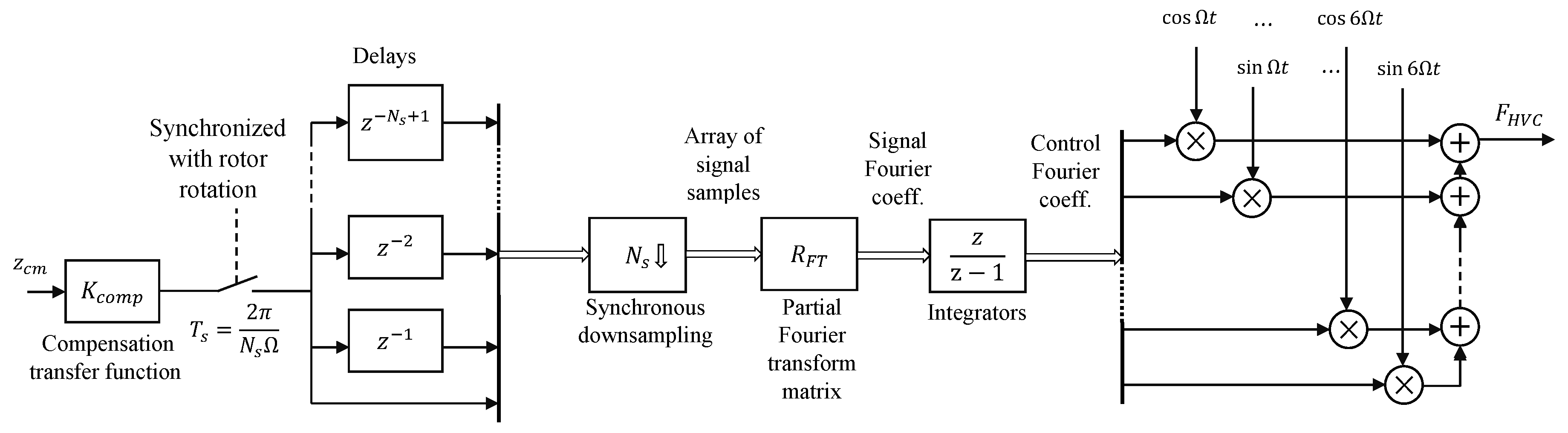
3. Exact Linearizing Control
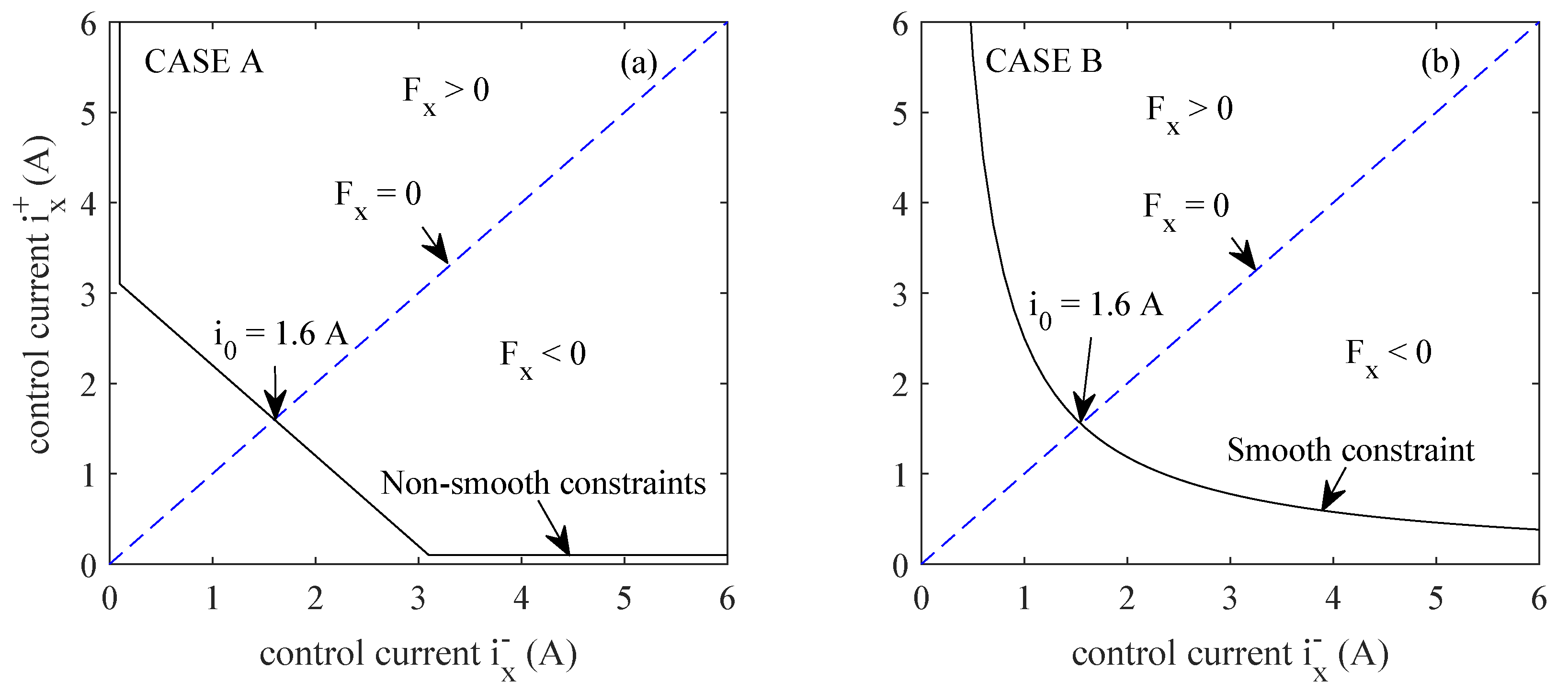
3.1. Gradient-Based Numerical Solution
3.2. Linear Approximation Solution
4. Experiments
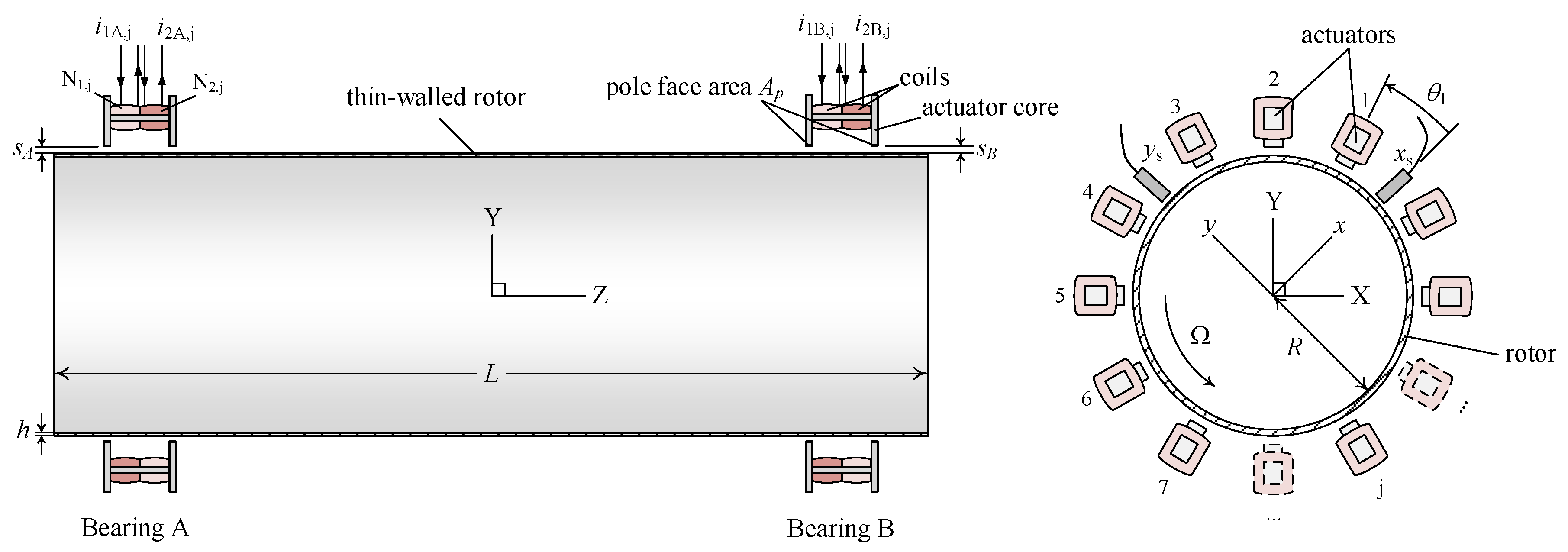
4.1. Thin-Walled Rotor and DAMB Test System
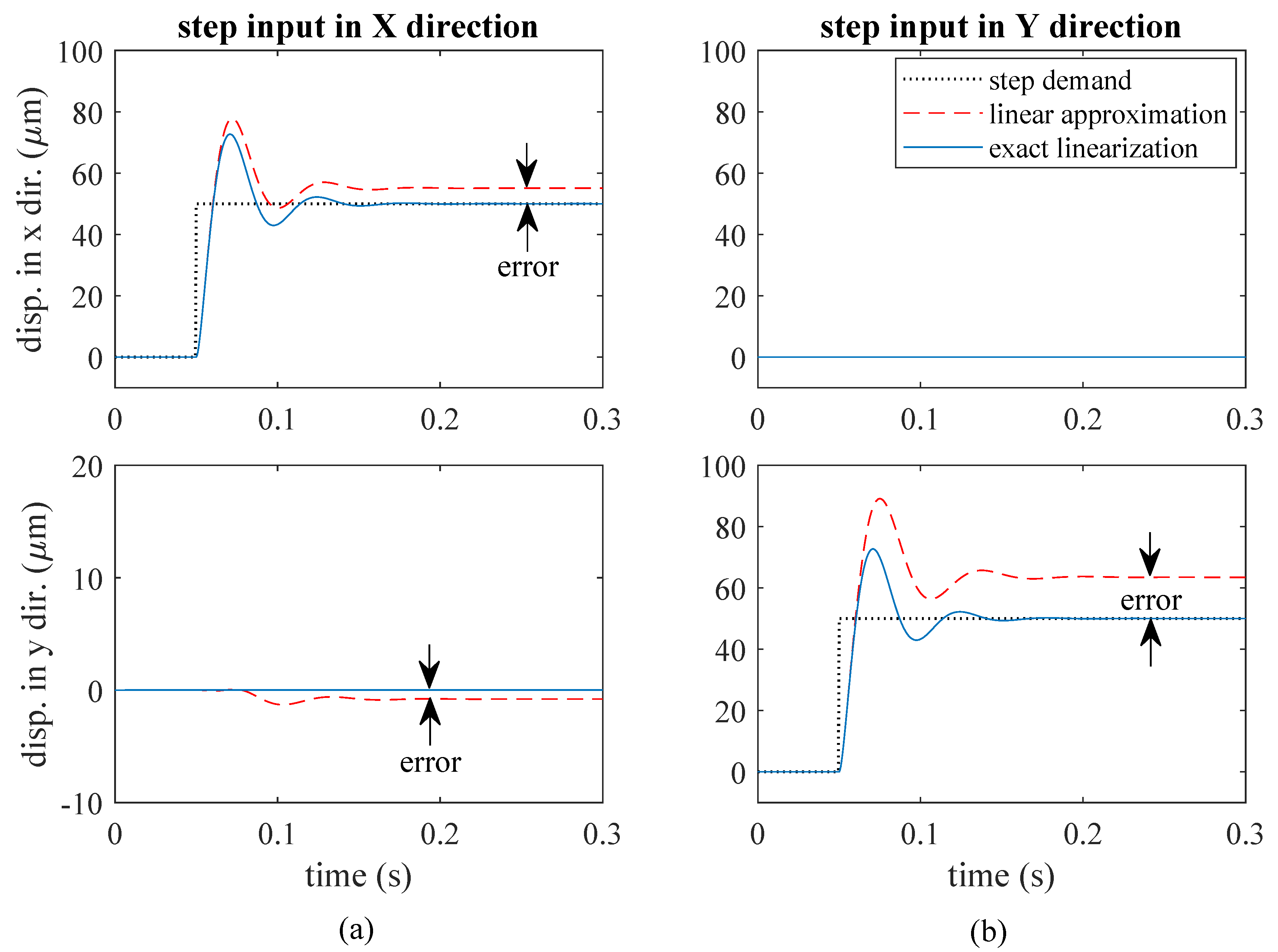
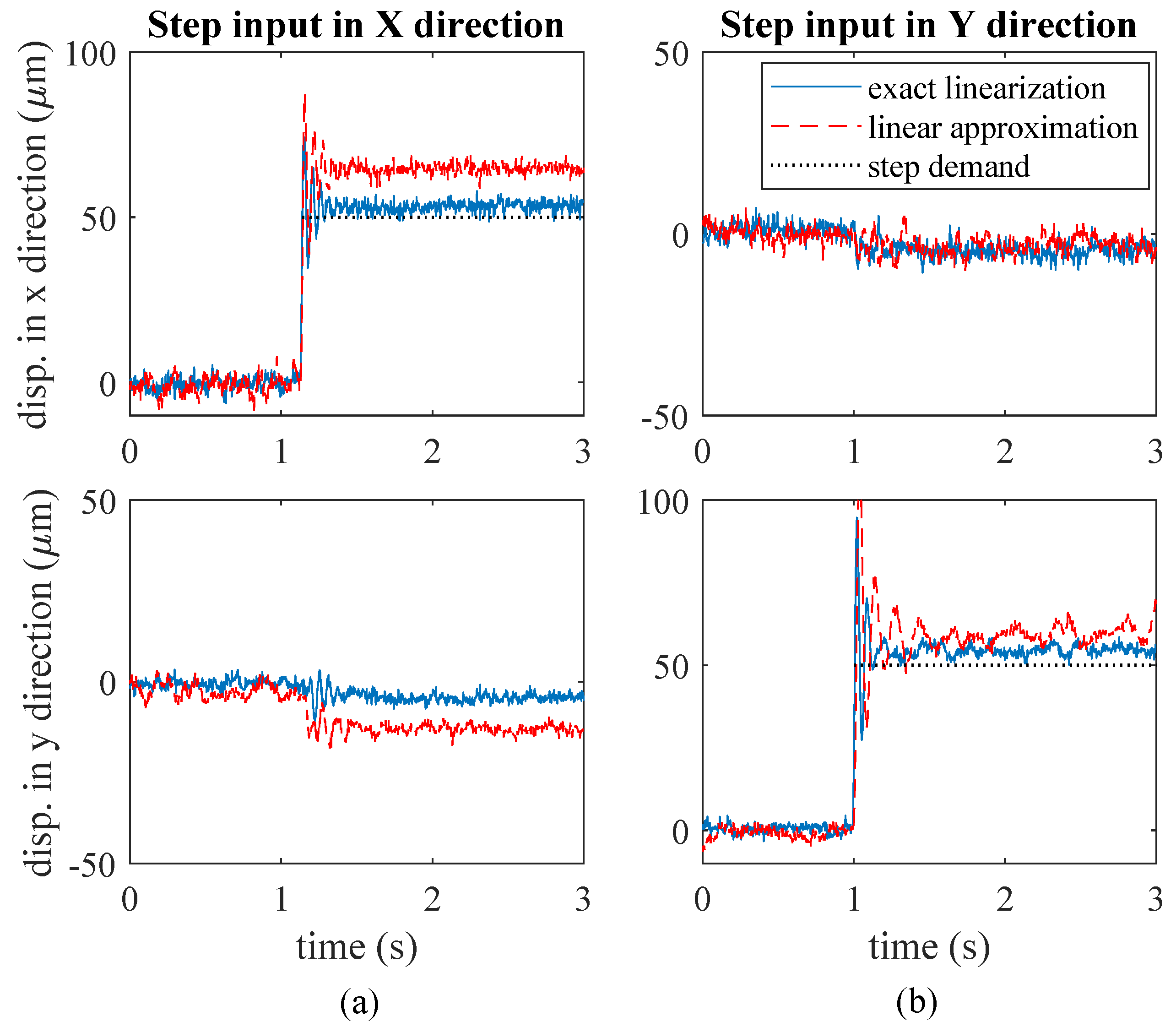
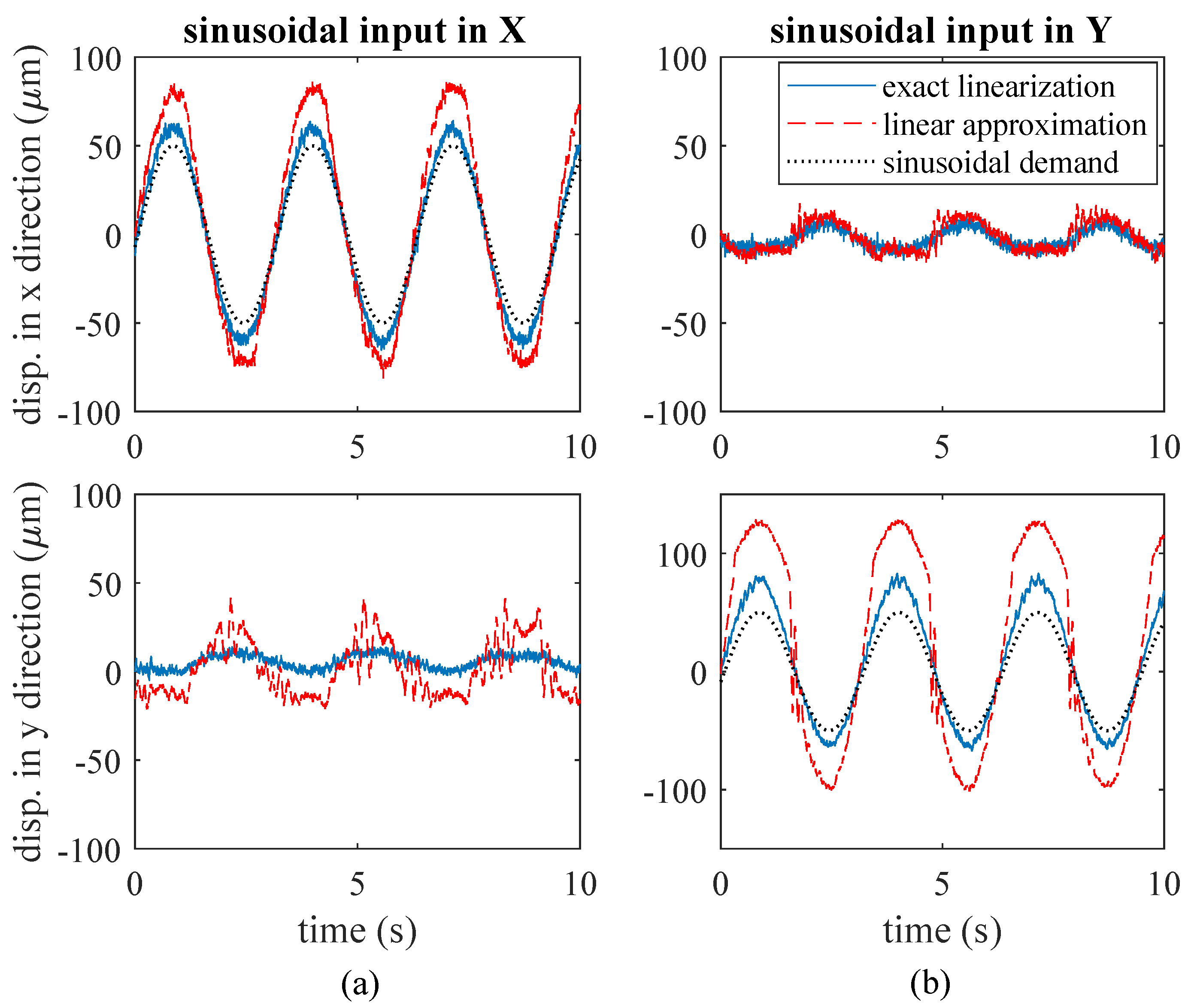
4.2. DAMB Simulations
4.3. Practical Implementation
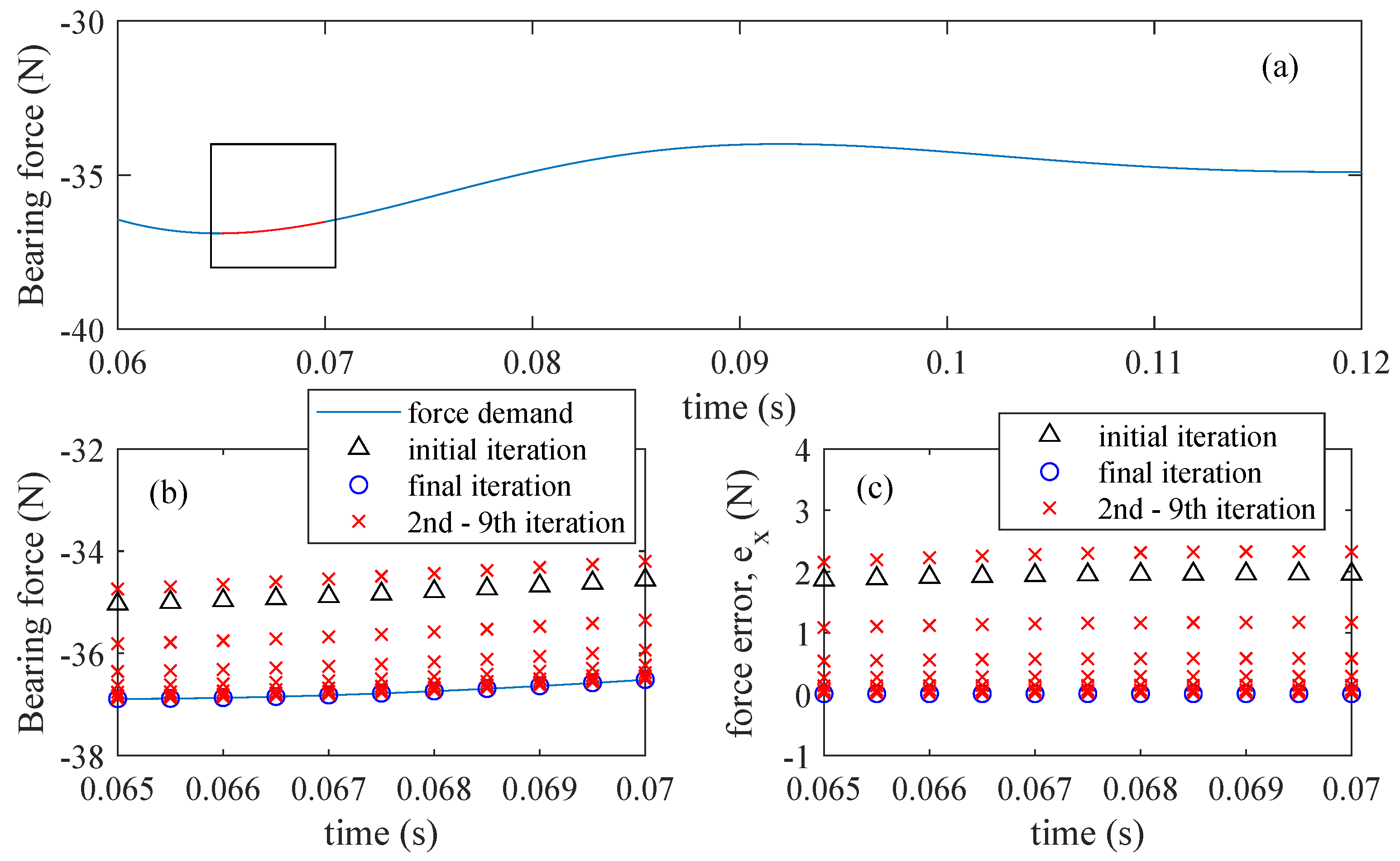
4.4. DAMB Force Control Evaluations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schweitzer, G.; Bleuler, H.; Maslen, E.; Cole, M.; Keogh, P.; Larsonneur, R.; Maslen, E.; Nordmann, R.; Okada, Y. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Berlin/Heidelberg, Germay, 2009. [Google Scholar]
- Xu, X.; Chen, S. Field Balancing and Harmonic Vibration Suppression in Rigid AMB-Rotor Systems with Rotor Imbalances and Sensor Runout. Sensors 2015, 15, 21876–21897. [Google Scholar] [CrossRef] [PubMed]
- Schneeberger, T.; Nussbaumer, T.; Kolar, J.W. Magnetically Levitated Homopolar Hollow-shaft Motor. IEEE/ASME Trans. Mechatron. 2010, 15, 97–107. [Google Scholar] [CrossRef]
- Lusty, C.; Sahinkaya, N.; Keogh, P. A Novel Twin-Shaft Rotor Layout with Active Magnetic Couplings for Vibration Control. Proc. IMechE Part I: J. Syst. Control Eng. 2016, 230, 266–276. [Google Scholar] [CrossRef]
- Cole, M.O.T.; Fakkaew, W. An Active Magnetic Bearing for Thin-Walled Rotors: Vibrational Dynamics and Stabilizing Control. IEEE/ASME Trans. Mechatron. 2018, 23, 2859–2869. [Google Scholar] [CrossRef]
- Chamroon, C.; Cole, M.O.T.; Fakkaew, W. Model and Control System Development for a Distributed Actuation Magnetic Bearing and Thin-Walled Rotor Subject to Noncircularity. ASME J. Vib. Acoust. 2019, 141, 051006. [Google Scholar] [CrossRef]
- Zhou, L.; Li, L. Modeling and Identification of a Solid-Core Active Magnetic Bearing Including Eddy Currents. IEEE/ASME Trans. Mechatron. 2016, 21, 2784–2792. [Google Scholar] [CrossRef]
- Daoud, M.I.; Abdel-Khalik, A.S.; Massoud, A.; Ahmed, S.; Abbasy, N.H. A Design Example of an 8-Pole Radial AMB for Flywheel Energy Storage. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1153–1159. [Google Scholar] [CrossRef]
- Wei, C.; Soffker, D. Optimization Strategy for PID-Controller Design of AMB Rotor Systems. IEEE Trans. Control Syst. Technol. 2016, 24, 788–803. [Google Scholar] [CrossRef]
- Zheng, S.; Li, H.; Han, B.; Yang, J. Power Consumption Reduction for Magnetic Bearing Systems during Torque Output of Control Moment Gyros. IEEE Trans. Power Electron. 2017, 32, 5752–5759. [Google Scholar] [CrossRef]
- Filatov, A.; Hawkins, L.; McMullen, P. Homopolar Permanent-Magnet-Biased Actuators and Their Application in Rotational Active Magnetic Bearing Systems. Actuators 2016, 5, 26. [Google Scholar] [CrossRef]
- Meeker, D.; Maslen, E. A Parametric Solution to the Generalized Bias Linearization Problem. Actuators 2020, 9, 14. [Google Scholar] [CrossRef]
- Mazenc, F.; de Queiroz, M.S.; Malisoff, M.; Gao, F. Further Results on Active Magnetic Bearing Control with Input Saturation. IEEE Trans. Control Syst. Technol. 2006, 14, 914–919. [Google Scholar] [CrossRef]
- Tsiotras, P.; Arcak, M. Low-Bias Control of AMB Subject to Voltage Saturation: State-Feedback and Observer Designs. IEEE Trans. Control Syst. Technol. 2005, 13, 262–273. [Google Scholar] [CrossRef]
- Gerami, A.; Allaire, P.; Fittro, R. Control of Magnetic Bearing with Material Saturation Nonlinearity. J. Dyn. Syst. Meas. Control 2015, 137, 061002. [Google Scholar] [CrossRef]
- Chen, S.; Song, M. Energy-Saving Dynamic Bias Current Control of Active Magnetic Bearing Positioning System Using Adaptive Differential Evolution. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 942–953. [Google Scholar] [CrossRef]
- Trumper, D.L.; Olson, S.M.; Subrahmanyan, P.K. Linearizing Control of Magnetic Suspension Systems. IEEE Trans. Control Syst. Technol. 1997, 5, 427–437. [Google Scholar] [CrossRef]
- Li, L.; Shinshi, T.; Shimokohbe, A. Asymptotically Exact Linearizations for Active Magnetic Bearing Actuators in Voltage Control Configuration. IEEE Trans. Control Syst. Technol. 2003, 11, 185–195. [Google Scholar]
- Chen, M.; Knospe, C.R. Feedback linearization of active magnetic bearings: Current-mode implementation. IEEE/ASME Trans. Mechatron. 2005, 10, 632–639. [Google Scholar] [CrossRef]
- Mystkowski, A.; Kaparin, V.; Kotta, U.; Pawluszewicz, E.; Tõnso, M. Feedback linearization of an active magnetic bearing system operated with a zero-bias flux. Int. J. Appl. Math. Comput. Sci. 2017, 27, 539–548. [Google Scholar] [CrossRef]
- Lindlau, J.D.; Knospe, C.R. Feedback linearization of an active magnetic bearing with voltage control. IEEE Trans. Control Syst. Technol. 2002, 10, 21–31. [Google Scholar] [CrossRef]



| Coefficient | Formula * | Coefficient | Formula * |
|---|---|---|---|
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Length | L | m | |
| Radius | R | m | |
| Wall thickness | h | m | |
| Density | 7850 |
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Pole face area | mm | ||
| Permeability of free space | H/m | ||
| Maximum number of coil-turns | 100 | ||
| Bearing A | |||
| Gap size | mm | ||
| Effective flux path length | mm | ||
| Bearing B | |||
| Gap size | mm | ||
| Effective flux path length | mm |
| Rotational Frequency (rad/s) | Estimated Force (N∠deg) | Estimated Unbalance (kg·m∠deg) |
|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamroon, C.; Cole, M.O.T.; Fakkaew, W. Linearizing Control of a Distributed Actuation Magnetic Bearing for Thin-Walled Rotor Systems. Actuators 2020, 9, 99. https://doi.org/10.3390/act9040099
Chamroon C, Cole MOT, Fakkaew W. Linearizing Control of a Distributed Actuation Magnetic Bearing for Thin-Walled Rotor Systems. Actuators. 2020; 9(4):99. https://doi.org/10.3390/act9040099
Chicago/Turabian StyleChamroon, Chakkapong, Matthew O.T. Cole, and Wichaphon Fakkaew. 2020. "Linearizing Control of a Distributed Actuation Magnetic Bearing for Thin-Walled Rotor Systems" Actuators 9, no. 4: 99. https://doi.org/10.3390/act9040099
APA StyleChamroon, C., Cole, M. O. T., & Fakkaew, W. (2020). Linearizing Control of a Distributed Actuation Magnetic Bearing for Thin-Walled Rotor Systems. Actuators, 9(4), 99. https://doi.org/10.3390/act9040099





