1. Introduction
The continuous evolution of robotics in conjunction with novel techniques for signal processing, control and instrumentation of robots have enabled the widespread of such devices in many applications [
1,
2]. Among many soft robot actuation technologies, as summarized in [
3], tendon-driven actuators are remotely actuated and can lead to a soft robot for continuous operation with low stiffness [
3], making it suitable in different applications [
4,
5,
6], including minimally invasive surgeries [
7]. In addition, such technology enables an optimized mass distribution in conjunction with the possibilities of developing underactuated robotic structures [
8,
9] as well as devices with configurable stiffness [
10]. As tendon-driven robots enable dexterous movements, they are also applied in wearable robots [
11] and bio-inspired robotic devices [
12].
For a better controllability of tendon-driven actuators, the tendon displacement (or strain) provides reliable information regarding the system dynamics and the transmitted movement to robot’s joint or limb in case of tendon-driven wearable robots [
13]. However, the tendon displacement assessment is difficult, due to its large deformation and the difficulty in sensors assembly. Hence, the tendon displacement (and dynamics) is considered a black box model in the modelling and control or is estimated through indirect measurements [
14]. Regarding tendon displacement sensing, some methods were proposed for ex-vivo such as imaging methods and stress-strain tests with universal testing machines [
15]. Both approaches are not able to provide real time measurements in non-structured environments or during the robot operation.
As an emerging sensing technology, optical fiber sensors find many applications on the measurement of mechanical parameters at different scenarios, which includes industrial, healthcare and robotics applications [
16,
17,
18]. Furthermore, optical fiber sensors were employed in ex-vivo tests for strain sensing in Achilles tendons and for tests in knee ligaments [
19,
20]. A sensor embedded in a tendon for stress or strain sensing should present a Young’s modulus close to the one of the tendon to obtain a sensor that does not influence the tendon’s mechanical parameters. However, commercial optical fibers–silica and polymer optical fibers (POFs) have a Young’s modulus of a few GPa (POFs) and tens of GPa (silica optical fiber), which is one order of magnitude higher than the ones of tendons (hundreds of MPa).
This paper presents a POF sensor for real time stress and strain assessment in artificial tendons. The proposed sensor is based on the intensity variation principle [
17], resulting in a compact and low-cost system. A highly stretchable POF was used on the instrumentation, manufactured through the light spinning polymerization process, which results in an optical fiber with a low Young’s modulus and strain limits orders of a magnitude higher than commercial optical fibers [
21]. In order to verify the influence of the POF sensor in the artificial tendon’s properties, tensile tests were performed in the artificial tendon with different optical fibers embedded (i.e., CYTOP, silica fiber and LPS-POF), where the elastic modulus and system stiffness was analyzed for each case. Then, an LPS-POF sensor embedded in an artificial tendon was tested for stress and strain sensing on the tendon.
2. Materials and Methods
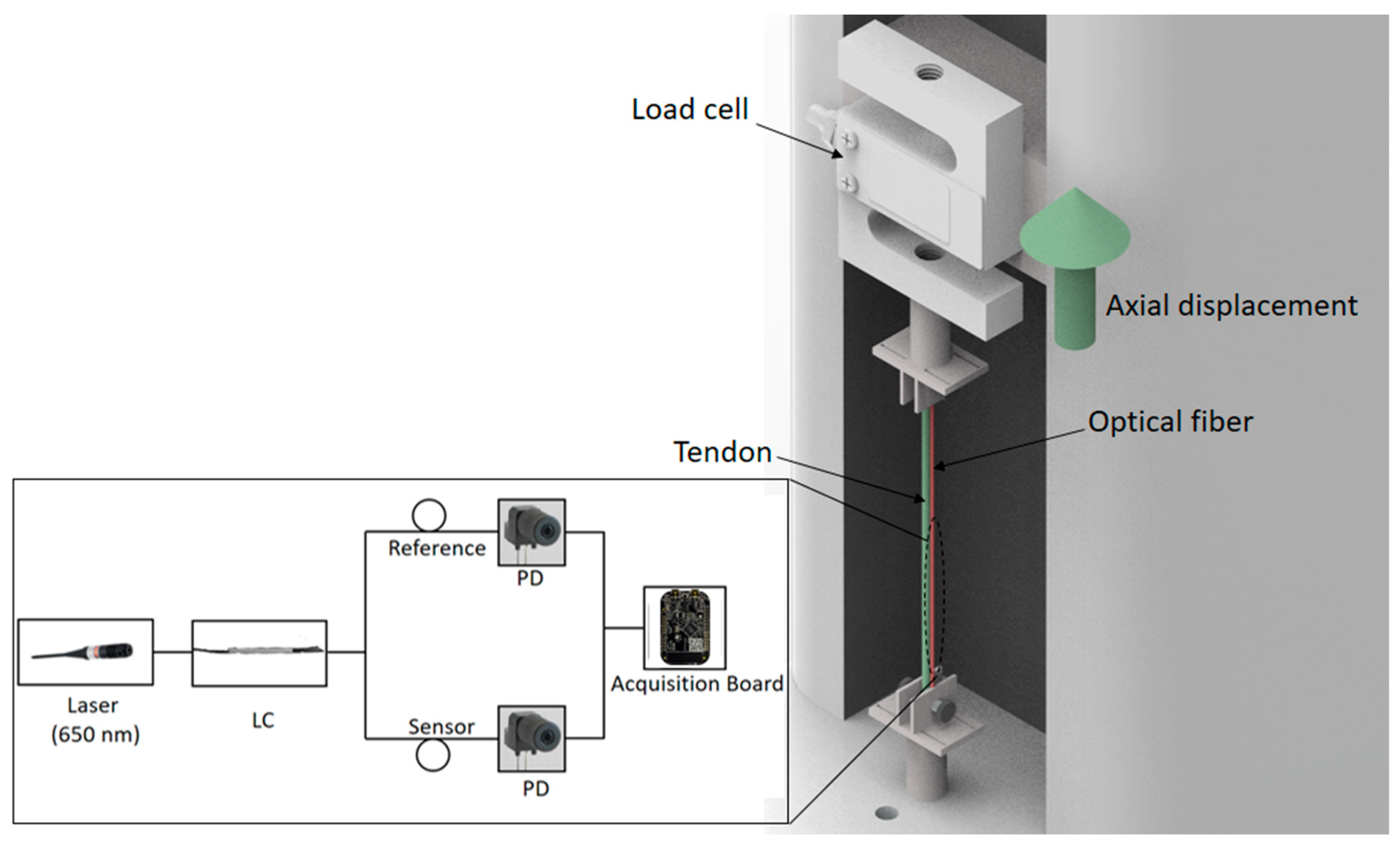
A filament with 2.85 mm diameter made of thermoplastic polyurethane (TPU) model Flex filament (3D Fila, Belo Horizonte, Brazil) was employed to emulate a tendon in the experiments due to its flexibility and low Young’s modulus (tens of MPa). The tests were performed by means of positioning the TPU and/or the fibers in a tensile test machine (Biopdi, São Carlos, Brazil) as show in
Figure 1. The testing machine has a displacement sensor and a load cell to measure position and force, respectively. The tensile tests were performed on TPU and the LPS-POF, where the same strain rate was applied at all tests. The Young’s modulus was estimated as the slope of the stress-strain curve in the linear region, following the ISO 527:2012 standard [
22].
The SMF-28 (Corning, NY, USA) silica optical fiber was used and the CYTOP fiber GIGAPOF® (Chromis Technologies, Warren, NJ, USA) was employed on the performed tests; the fiber has a 0.5 mm diameter made of perfluorinated polymer with a graded refractive index. Then, tests were performed with the tendon combined with the optical fibers (i.e., TPU/LPS-POF, TPU/CYTOP, TPU/silica) to verify which combination has the closest stiffness when compared in the case in which only the tendon was analyzed. The fibers were attached to the tendon using a UV-curing optical adhesive NOA 88 (Norland, Cranbury, NJ, USA).
After the material characterization, one end of the fiber was connected to a laser source (5 mW at 660 nm), whereas the other end was connected to a phototransistor (PD) IF-D92 (Industrial Fiber Optics, Tempe, AZ, USA), as depicted in
Figure 1. The strain on the optical fiber leads was a variation of the fiber refractive index due to the photoelastic effect, resulting in optical power variation on the fiber [
23]. In addition, another fiber, connected to the light source using an optical coupler (LC) IF-562 (Industrial Fiber Optics, USA) and connected to another phototransistor was used to compensate for light source power variations as well as environmental (temperature and humidity) variations. Signals of both phototransistors were acquired by a microcontroller FRDM-KL25Z (NXP, Eindhoven, The Netherlands) with a 16-bits analog-to-digital converter. The sensor response was normalized with respect to the reference arm.
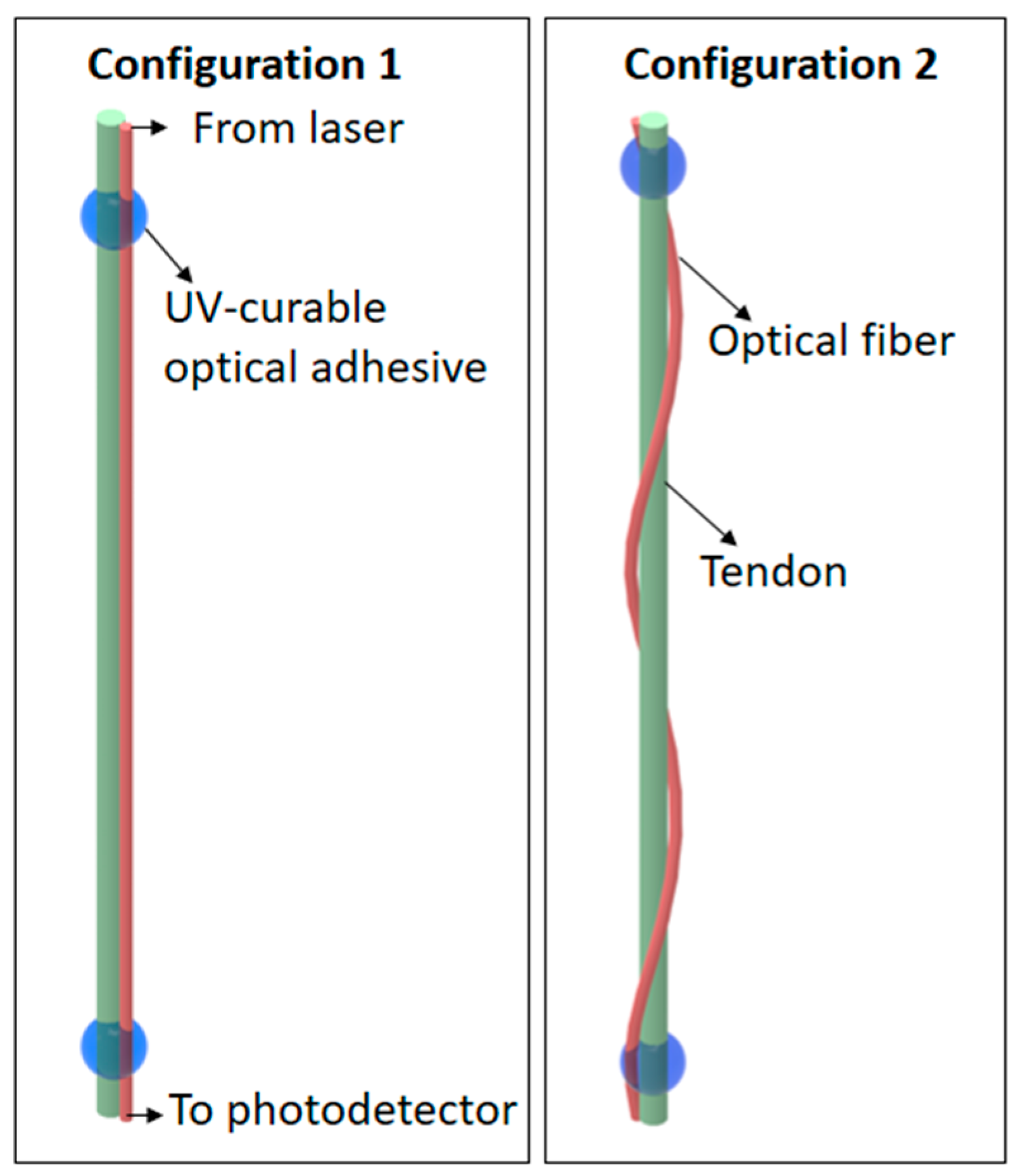
In the sensor application, two configurations were tested as shown in
Figure 2. In the first configuration, the fiber was parallel to the tendon attached to it through two gluing points, which led to the possibility of measuring the strain applied on the tendon, by the fiber stretching. The second configuration the fiber was twisted around the tendon longitudinal axis with two turns (
Figure 2). It was expected that the second configuration would result in a higher sensitivity as a function of the applied force due the stress-optic effect [
23]. It is worth noting that the tests on each configuration were performed only in the axial direction with controlled displacements, where both ends of the fiber were fixed to avoid any torsion or bending in the sensing region.
3. Results and Discussions
3.1. Mechanical Analysis
Figure 3a,b presents the stress-strain curves of TPU and LPS-POF, respectively. From these curves, it is possible to calculate the Young’s modulus of each material, as presented in
Table 1. It also presents the Young’s modulus of silica fiber and CYTOP fiber (characterized in the literature).
The results presented in
Figure 3 show a high linearity of LPS-POF in the 16% strain range, which indicate the suitability of these fibers for tendon strain sensing applications. Since the TPU is used to emulate the tendon, its mechanical behavior was also investigated. For the TPU, the Young’s modulus is about 72 MPa, confirming the high flexibility for the materials chosen. For the TPU and LPS-POF, the tests were made until about 16% strain, but both materials can withstand higher strains [
21,
26]. In addition, LPS-POF Young’s modulus is some orders of magnitude lower than the ones of commercial fibers (silica and CYTOP, in this case).
Then, we combined the TPU with each of the optical fibers presented in
Table 1 in order to verify the resultant mechanical properties of each combination. These experiments were performed as a function of force and displacement, since the cross-sectional area of the combination between tendon and fiber does not present a uniform distribution such as the circular or rectangular cross-sections (fiber diameters show in
Table 1). Thus, instead of the Young’s Modulus of the materials, the experimental characterization was made as function of the stiffness (
k), which is experimentally obtained as the ratio of the force and displacement. In addition, another definition can be made as a function of the material properties and geometry. The stiffness analysis (instead of Young’s modulus evaluation) also shows the influence of the sensor’s length and cross-sectional area on the system’s stiffness, which is an important parameter on the transparent sensor development, since it is desired that the sensor does not change the tendon’s mechanical behavior and higher customizability can be achieved by controlling the length and cross-sectional area of the optical fiber sensor. For an axial loading, the stiffness can be defined as:
where
A is the cross-sectional area of the materials,
E is the Young’s modulus of the material combination and
L is the length.
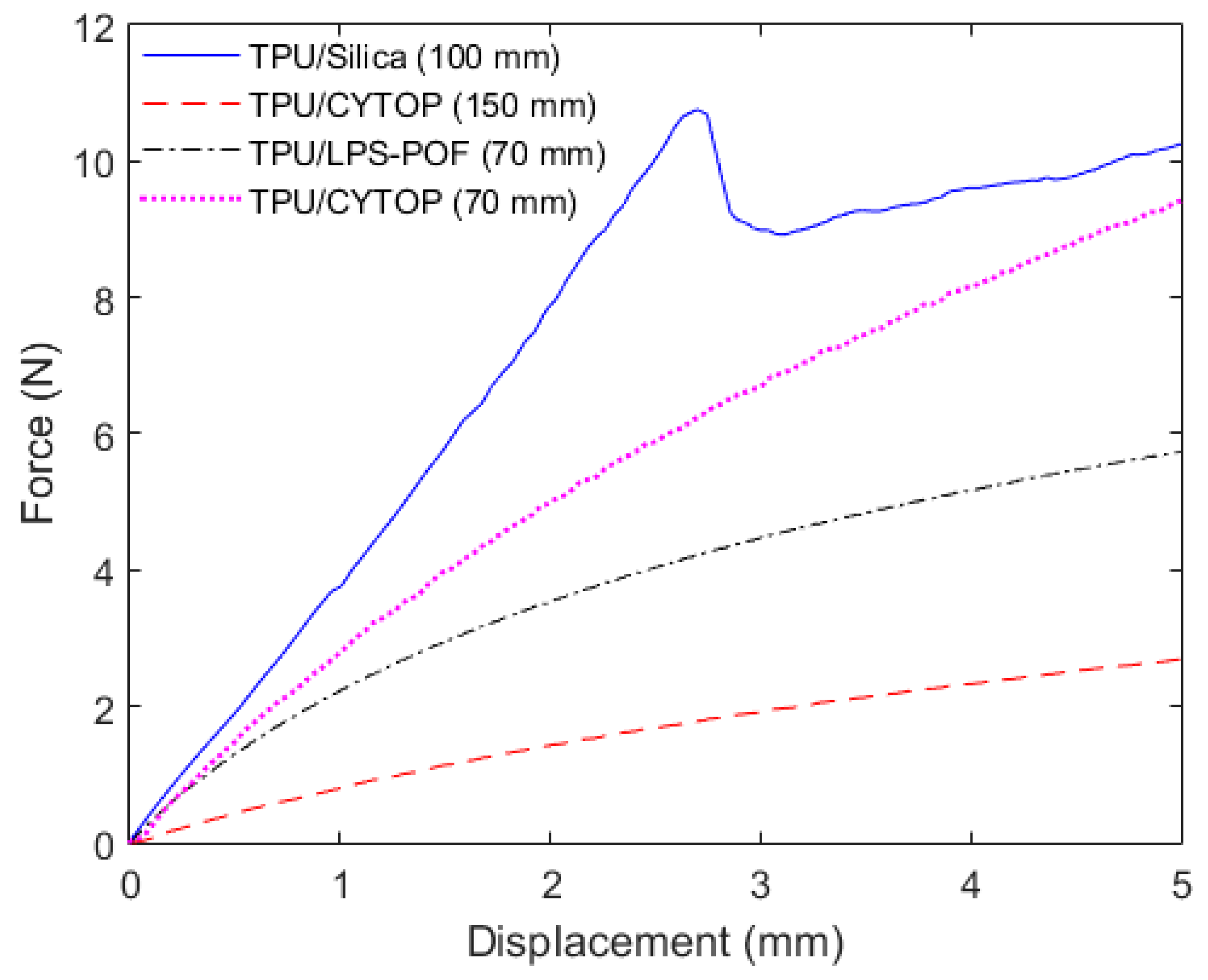
From Equation (1), the stiffness depends on material’s Young’s modulus, cross-sectional area and length of the material, which has to be defined prior to the application. Regarding to the results in
Figure 4, the combination TPU/CYTOP showed the lowest stiffness, which was the combination with the longest length. This shows that even though the CYTOP has the second highest Young’s modulus (among the tested optical fibers), the longer length in combination with the TPU resulted in the lowest stiffness, as anticipated by Equation (1), where longer lengths lead to lower stiffness. For comparison purposes, the TPU/CYTOP combination with 70 mm length was also added, where its higher stiffness than the TPU/LPS-POF can be seen. It is also worth noting that in the TPU/silica fiber combination, the fiber broke at about 2.7 mm displacement due to the brittle nature of the silica fiber. Thus, the results in
Figure 4 show that by using different lengths of material in combination it is possible to provide a large tuning on the material stiffness. For this reason, the maximum and minimum lengths of the sensing region must be known prior to the sensor application in order to obtain a sensor that provides the minimum influence on the tendon stiffness. It also should be noted that the stiffness calculated for the TPU/LPS-POF combination in the experiments was 1783.5 N/m, which is close to the one when only the TPU was tested, 1790.2 N/m. Thus, the LPS-POF does not lead to a significant difference on the material stiffness when the optical fiber and tendon combination is considered.
3.2. Sensor Application
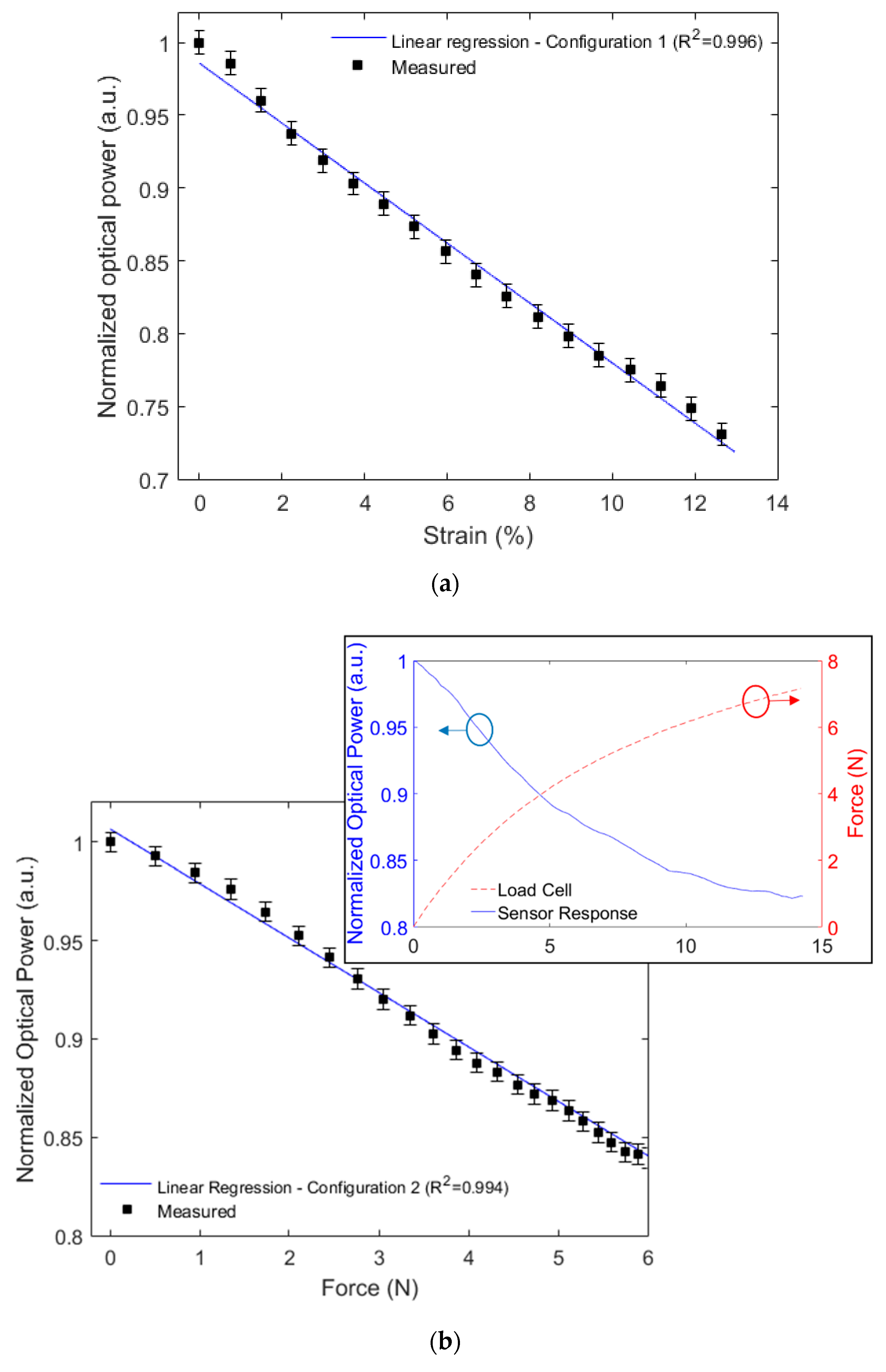
The results in the first configuration (for strain sensing) are shown in
Figure 5a, whereas the ones of the second configuration (force sensing) are presented in
Figure 5b. In configuration 1, the sensor response presented a higher correlation with the strain applied on the tendon, which expected since in this configuration there is the measurement of the displacement in the tendon, the linear regression shown between the sensor response and the strain applied in the tendon has a determination coefficient (R
2) of 0.996. The sensor response and measured force showed a linear correlation with R
2 of 0.994 for the second configuration as depicted in
Figure 5b. Therefore, it is possible to estimate the force on the tendon (and the stress by knowing the tendon cross-sectional area) using the proposed sensor in configuration 2, whereas the strain sensing in the tendon is achieved using configuration 1.
The first configuration presents the fiber in parallel with the tendon, where both elements suffer the same displacement. For this reason, the sensor in configuration 1 shows the pattern of the strain applied in the tendon. If configuration 2 is analyzed, there is not only the axial displacement, but also a bending and torsion in the fiber due to its positioning around the tendon, leading to stress-optic effect. Such effect is related to the applied stress (and force) results in the possibility of the direct force measurement, which was confirmed in the experiments. Therefore, depending on the sensor-mounting configuration, stress or strain can be measured in the tendon and this feature can be used on the control and design of tendon-driven actuators. It is even possible to measure both parameters (stress and strain) in the same time by employing both configurations, which results in the complete dynamic characterization of the tendon responses.
4. Conclusions
In this paper, a POF sensor solution for tendon mechanical applications was presented. The tendon and optical fibers characterizations were performed in a tensile test machine, where each material and their combinations with the TPU were analyzed. The results demonstrated that the combination TPU/LPS-POF presents the closest Young’s Modulus to the TPU material (without any combination). In addition, the high strain limit of LPS-POF is some orders of magnitude higher than the ones of the commercial optical fibers (below 10%) and is within the strain range of tendons. However, when the stiffness was analyzed, the results of material combinations were dependent on the length of the materials. In the sensor application, one configuration was able to estimate the strain applied in the tendon, whereas the other was used for force estimation. Both configurations presented high correlation (R2 higher than 0.99) with the applied strain and force measured by the load cell. These results are encouraging and show the feasibility of the proposed approach on real time stress and strain sensing on artificial tendons, which can be applied in tendon-driven actuators for soft robots at different applications scenarios. Therefore, the proposed system has the advantages of low-cost, portability and capability of measuring the strain directly on the tendon. In addition, the high flexibility of the POF used, in conjunction with its customizability due to the possibility of changing the length and cross-sectional area of the optical fiber, results in a transparent sensor system, since the sensor does not change the artificial tendon stiffness and mechanical behavior. Thus, future researches include the application of the proposed sensor systems in wearable tendon-driven soft robots and even on the assessment of mechanical properties in real tendons of human or animals.
Author Contributions
Conceptualization, A.G.L.-J.; methodology, A.G.L.-J.; formal analysis, A.G.L.-J., C.M., A.F.; validation, W.C.; resources A.G.L.-J., C.M., A.F.; visualization, A.G.L.-J., W.C.; writing—original draft preparation, A.G.L.-J.; writing—review and editing, A.G.L.-J., C.M., A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financed by FAPES (84336650), CNPq (304049/2019-0 and 427054/2018-4). C. Marques acknowledges Fundação para a Ciência e a Tecnologia (FCT) through the CEECIND/00034/2018 (iFish project) and this work was developed within the scope of the project i3N, UIDB/50025/2020 & UIDP/50025/2020, financed by national funds through the FCT/MEC. This work is also funded by national funds (OE), through FCT, I.P., in the scope of the framework contract foreseen in the Numbers 4, 5 and 6 of Article 23, of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19.
Acknowledgments
Authors would like to thank G.B., E.S. and O.P. for providing the LPS-POF used in this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Z.; Wang, X.; Liu, J.; Dai, C.; Sun, Y. Robotic micromanipulation: Fundamentals and applications. Annu. Rev. Control Robot. Auton. Syst. 2019, 2, 181–203. [Google Scholar] [CrossRef]
- Shukla, A.; Karki, H. Application of robotics in offshore oil and gas industry—A review Part II. Robot. Auton. Syst. 2016, 75, 508–524. [Google Scholar] [CrossRef]
- Manti, M.; Cacucciolo, V.; Cianchetti, M. Stiffening in soft robotics: A review of the state of the art. IEEE Robot. Autom. Mag. 2016, 23, 93–106. [Google Scholar] [CrossRef]
- Natale, C.; Pirozzi, S. Minimally invasive torque sensor for tendon-driven robotic hands. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 65–70. [Google Scholar] [CrossRef]
- Bundhoo, V.; Haslam, E.; Birch, B.; Park, E.J. A shape memory alloy-based tendon-driven actuation system for biomimetic artificial fingers, part I: Design and evaluation. Robotica 2009, 27, 131–146. [Google Scholar] [CrossRef]
- Kastor, N.; Mukherjee, R.; Cohen, E.; Vikas, V.; Trimmer, B.A.; White, R.D. Design and manufacturing of tendon-driven soft foam robots. Robotica 2020, 38, 88–105. [Google Scholar] [CrossRef]
- Wang, H.C.; Cui, S.H.; Wang, Y.; Song, C.L. A hybrid electromagnetic and tendon-driven actuator for minimally invasive surgery. Actuators 2020, 9, 92. [Google Scholar] [CrossRef]
- Birouaş, F.I.; Ţarcă, R.C.; Dzitac, S.; Dzitac, I. Preliminary results in testing of a novel asymmetric underactuated robotic hand exoskeleton for motor impairment rehabilitation. Symmetry 2020, 12, 1470. [Google Scholar] [CrossRef]
- Takuma, T. Design of tendon-driven mechanism using geometrical condition. Actuators 2020, 9, 48. [Google Scholar] [CrossRef]
- Choi, J.; Lee, D.-Y.; Eo, J.-H.; Park, Y.-J.; Cho, K.-J. Tendon-driven jamming mechanism for configurable variable stiffness. Soft Robot. 2020, 1–10. [Google Scholar] [CrossRef]
- Kim, B.; Ryu, J.; Cho, K.J. Joint angle estimation of a tendon-driven soft wearable robot through a tension and stroke measurement. Sensors 2020, 20, 2852. [Google Scholar] [CrossRef]
- Lee, G.; Choi, Y. Bio-inspired tendon-driven finger design with isomorphic ligamentous joint. IEEE Access 2020, 8, 18240–18251. [Google Scholar] [CrossRef]
- Wen, L.; Li, Y.; Cong, M.; Lang, H.; Du, Y. Design and optimization of a tendon-driven robotic hand. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 767–772. [Google Scholar] [CrossRef]
- Casas, J.; Leal-Junior, A.; Díaz, C.R.; Frizera, A.; Múnera, M.; Cifuentes, C.A. Large-range polymer optical-fiber strain-gauge sensor for elastic tendons in wearable assistive robots. Materials 2019, 12, 1443. [Google Scholar] [CrossRef] [PubMed]
- Louis-Ugbo, J.; Leeson, B.; Hutton, W.C. Tensile properties of fresh human calcaneal (Achilles) tendons. Clin. Anat. 2004, 17, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Diaz, C.A.R.; Leal-Junior, A.; Marques, C.; Frizera, A.; Pontes, M.J.; Antunes, P.F.C.; Andre, P.S.B.; Ribeiro, M.R.N. Optical Fiber Sensing for Sub-Millimeter Liquid-Level Monitoring: A Review. IEEE Sens. J. 2019, 19, 7179–7191. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Diaz, C.A.R.; Avellar, L.M.; Pontes, M.J.; Marques, C.; Frizera, A. Polymer Optical Fiber Sensors in Healthcare Applications: A Comprehensive Review. Sensors 2019, 19, 3156. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, G.; Guo, Y.; Liu, H. A Three-dimensional fiber bragg grating force sensor for robot. IEEE Sens. J. 2018, 18, 3632–3639. [Google Scholar] [CrossRef]
- Behrmann, G.P.; Hidler, J.; Mirotznik, M.S. Fiber optic micro sensor for the measurement of tendon forces. Biomed. Eng. Online 2012, 11, 1. [Google Scholar] [CrossRef]
- Ren, L.; Song, G.; Conditt, M.; Noble, P.C.; Li, H. Fiber Bragg grating displacement sensor for movement measurement of tendons and ligaments. Appl. Opt. 2007, 46, 6867–6871. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Theodosiou, A.; Frizera-Neto, A.; Pontes, M.J.; Shafir, E.; Palchik, O.; Tal, N.; Zilberman, S.; Berkovic, G.; Antunes, P.; et al. Characterization of a new polymer optical fiber with enhanced sensing capabilities using a Bragg grating. Opt. Lett. 2018, 43, 4799. [Google Scholar] [CrossRef]
- ISO 527-1:2012 Plastics—Determination of Tensile Properties—Part 1: General Principles. Available online: https://www.iso.org/standard/56045.html (accessed on 30 August 2020).
- Leal-Junior, A.G.; Frizera, A.; Pontes, M.J. Analytical model for a polymer optical fiber under dynamic bending. Opt. Laser Technol. 2017, 93, 92–98. [Google Scholar] [CrossRef]
- Antunes, P.; Domingues, F.; Granada, M.; André, P. Mechanical Properties of Optical Fibers; Intech Open Access Publisher: London, UK, 2012; pp. 1–15. [Google Scholar] [CrossRef]
- AGC-Chemicals Amorphous Fluoropolymer CYTOP. Available online: https://www.agcchem.com/documentation/technical-data/cytop/513-cytop-brochure/file (accessed on 6 June 2018).
- Meckel, W.; Goyert, W.; Wieder, W. Thermoplastic polyurethane elastomers. Elastomers A Compr. Rev. 1987, 1, 1–52. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).