Feedforward Plus Feedback Control of an Electro-Hydraulic Valve System Using a Proportional Control Valve
Abstract
1. Introduction
2. Feedforward Control for Nonlinearity Compensation
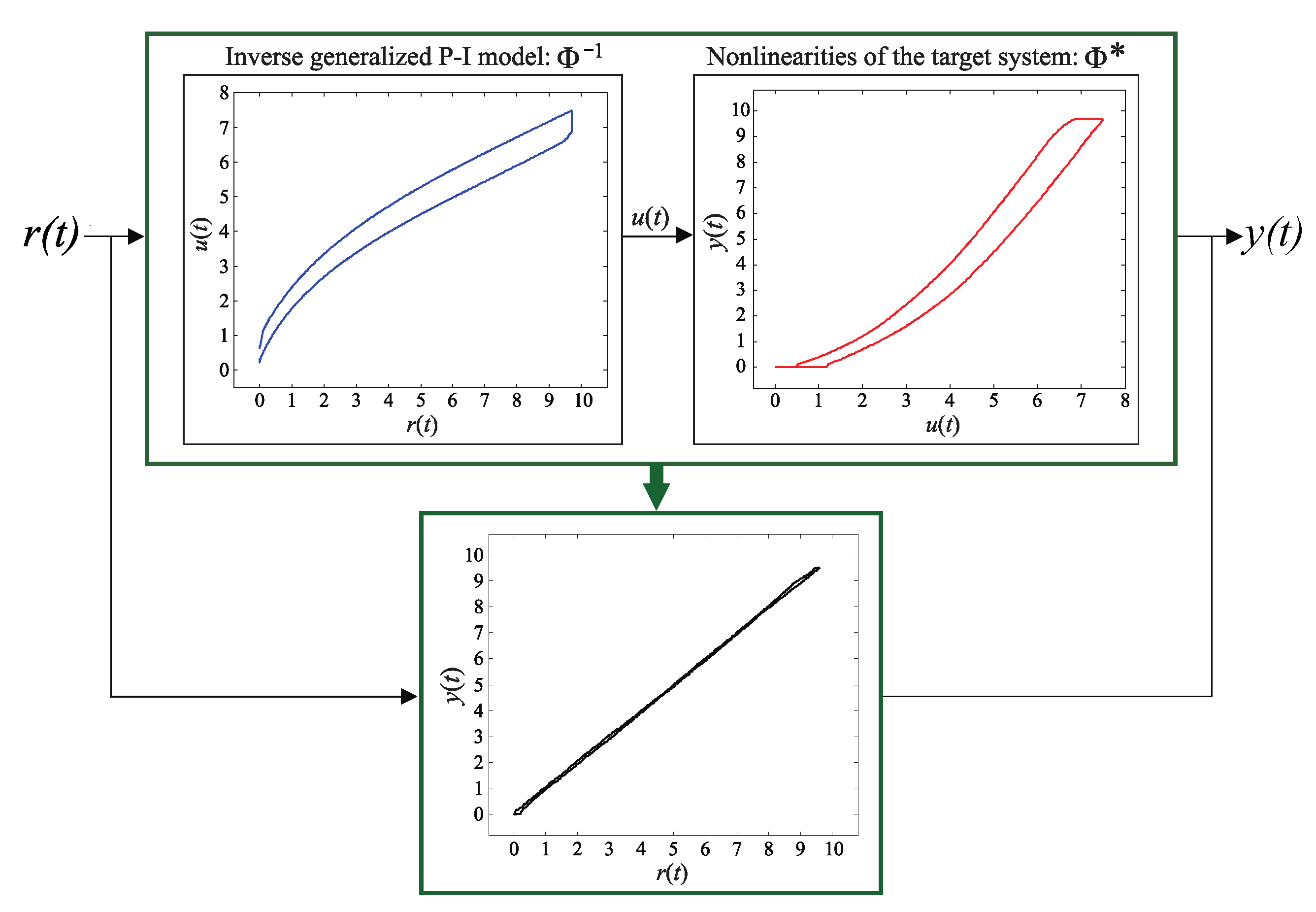
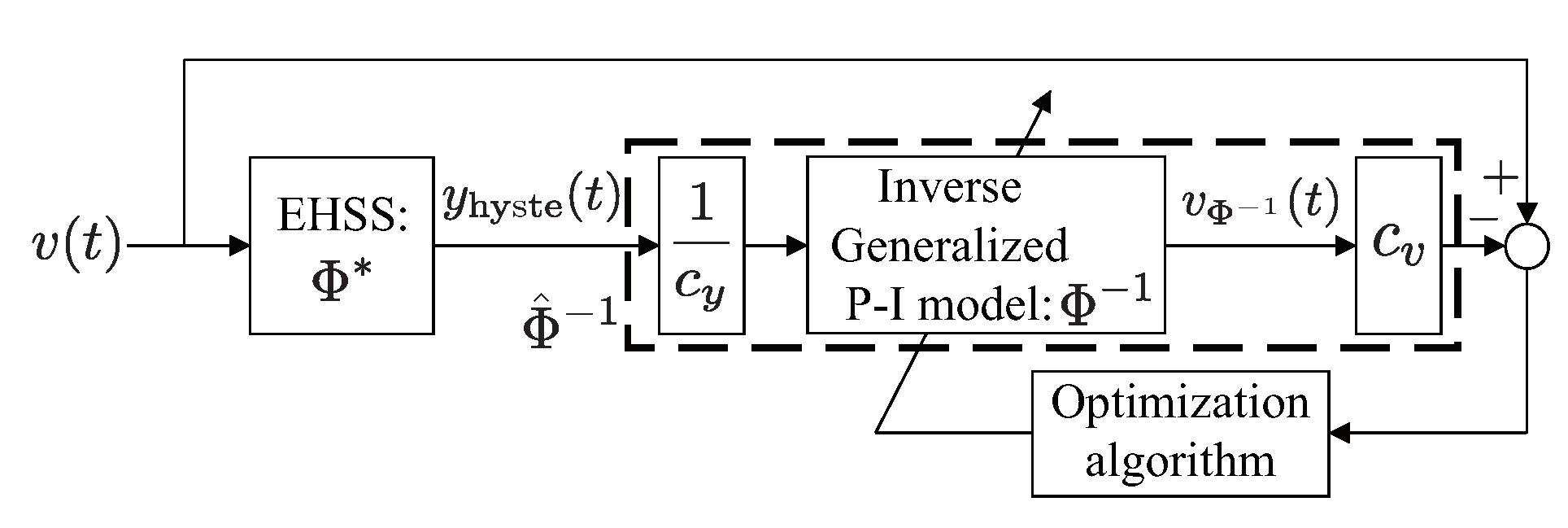
2.1. Inverse Generalized P–I Model
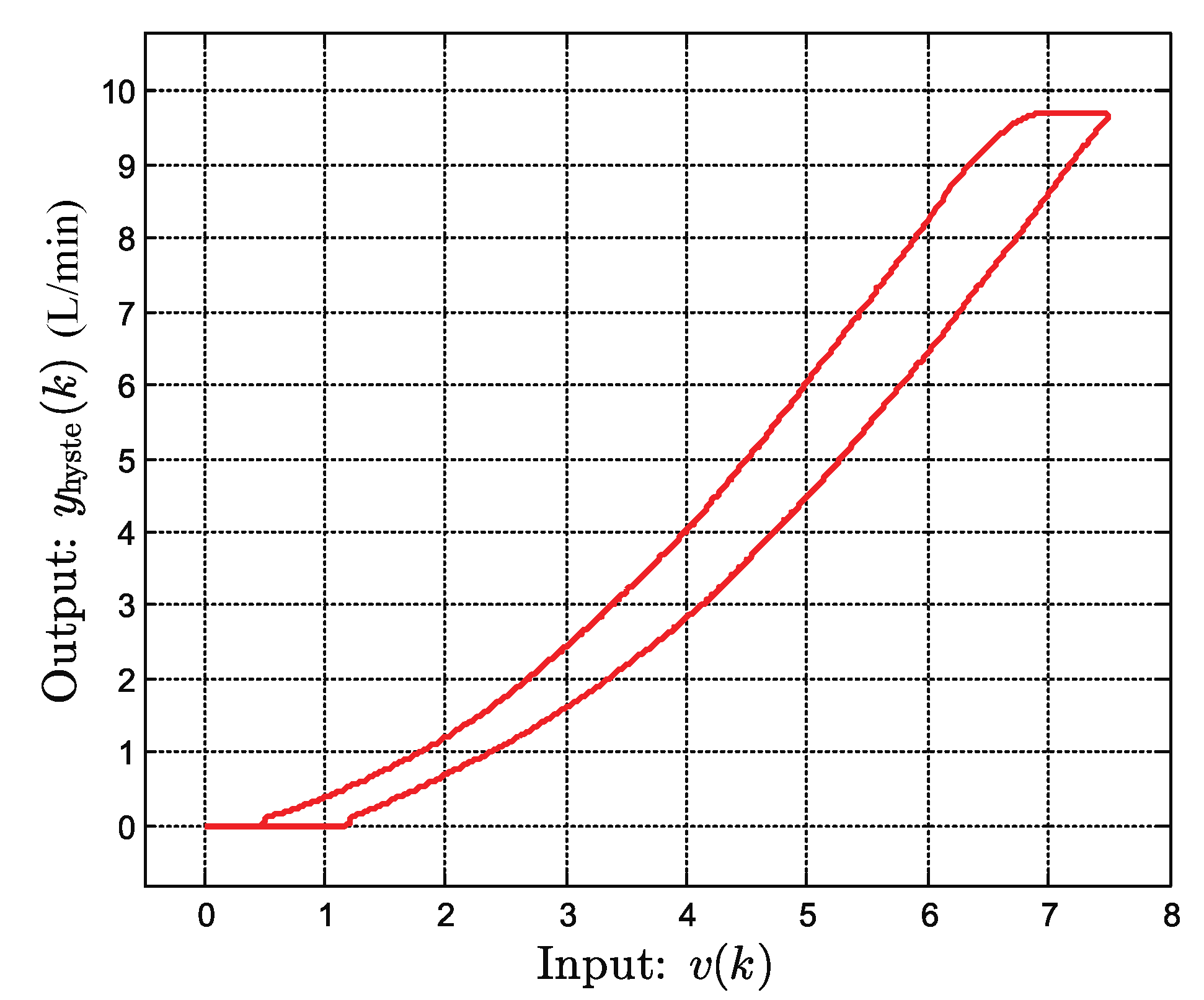
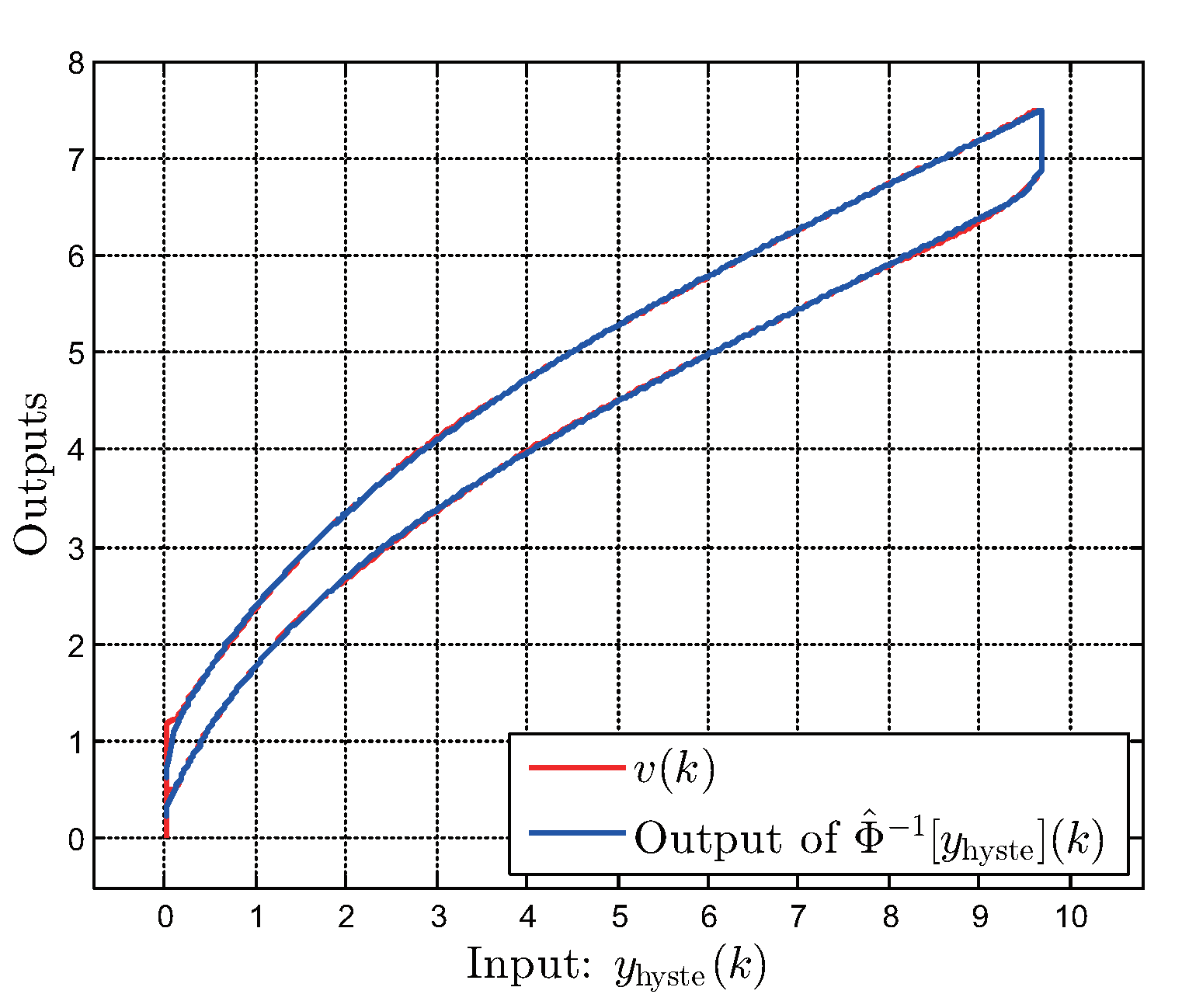
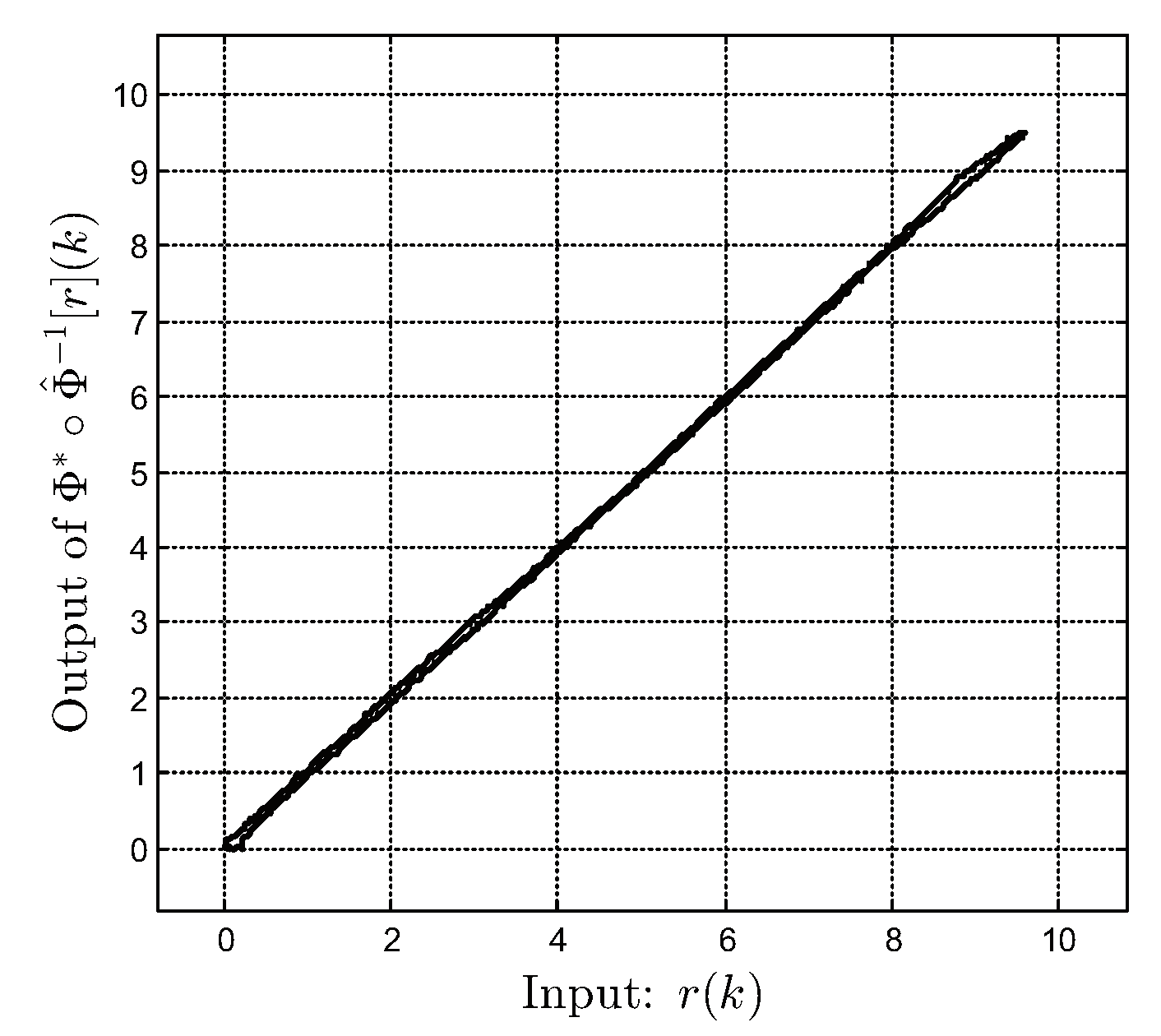
2.2. Parameter Identification and Experimental Validation
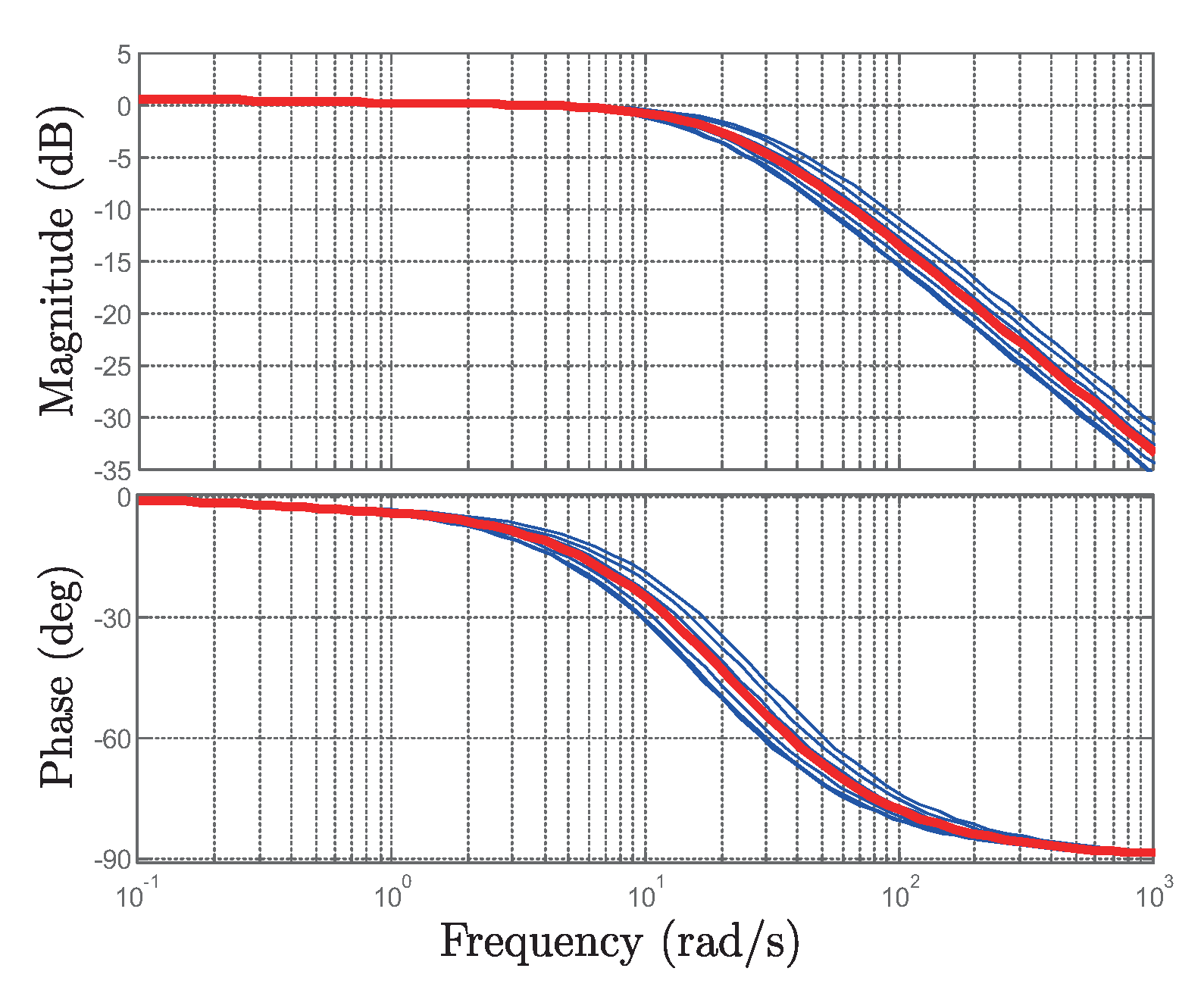
3. Identification of EHVS Linear Dynamics Model
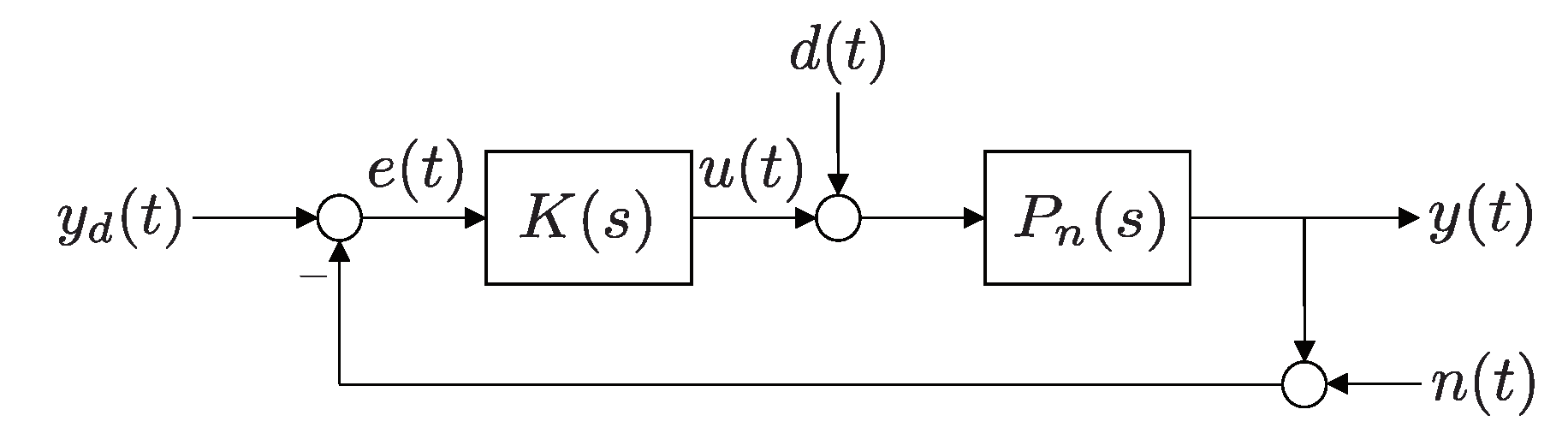
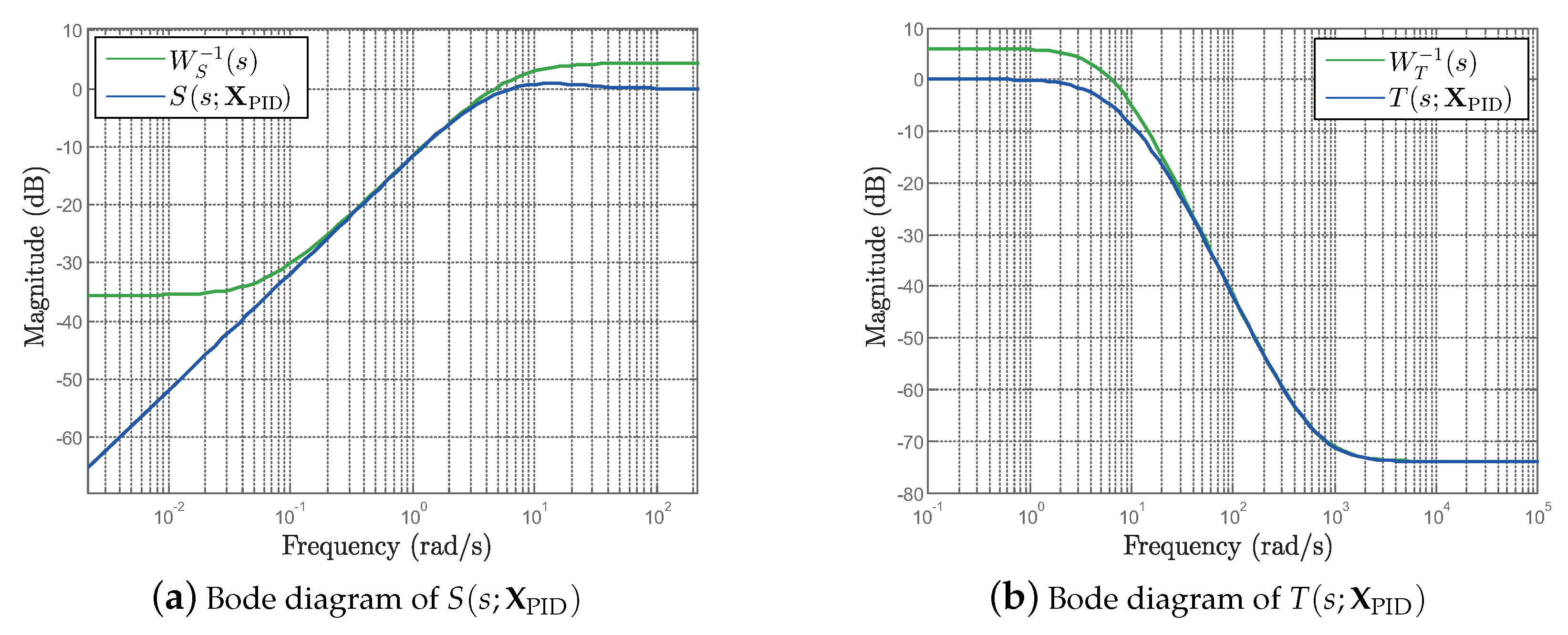
4. EHVS Feedback Controller
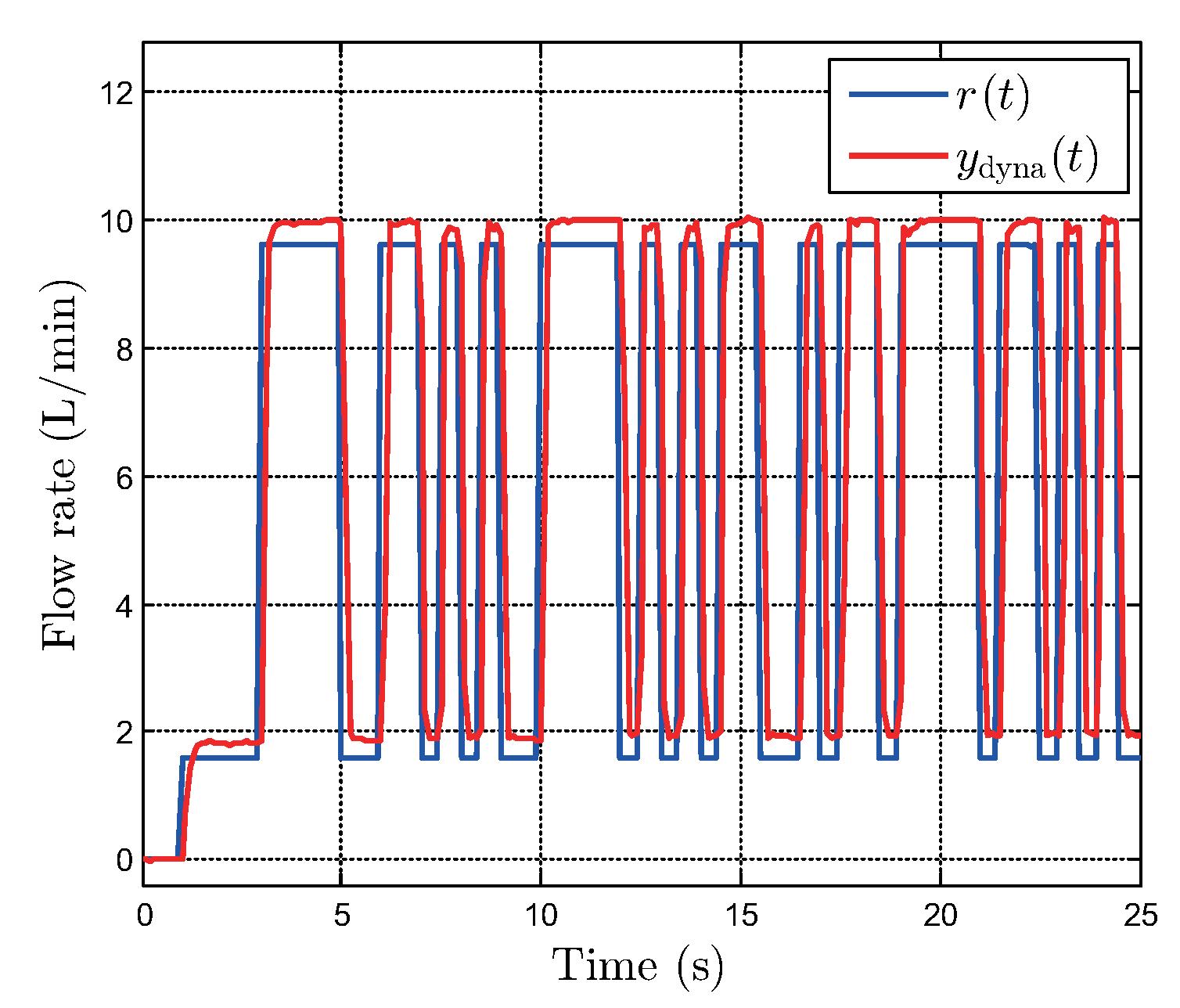
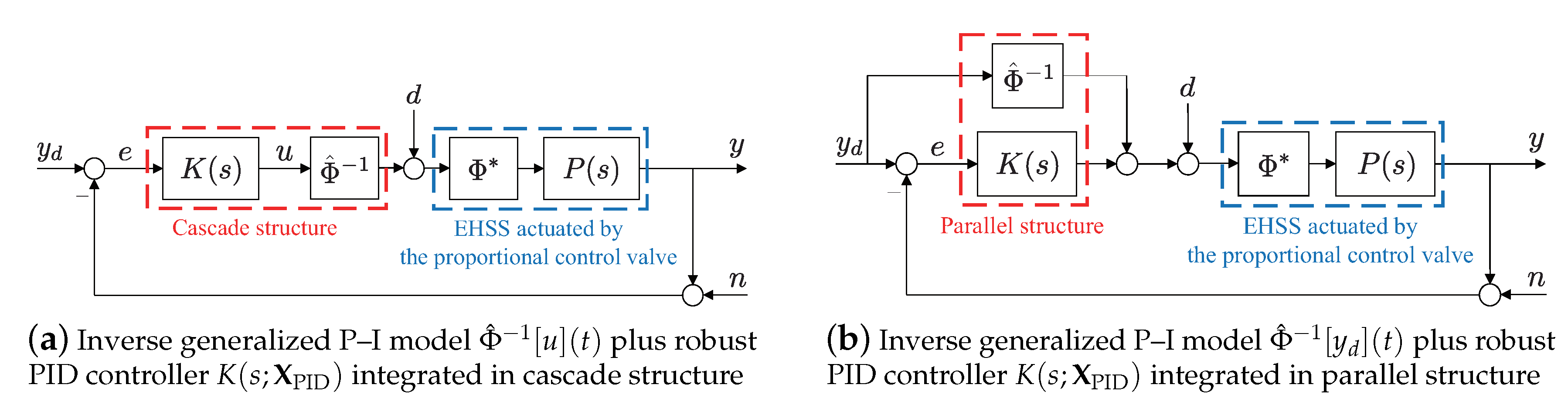
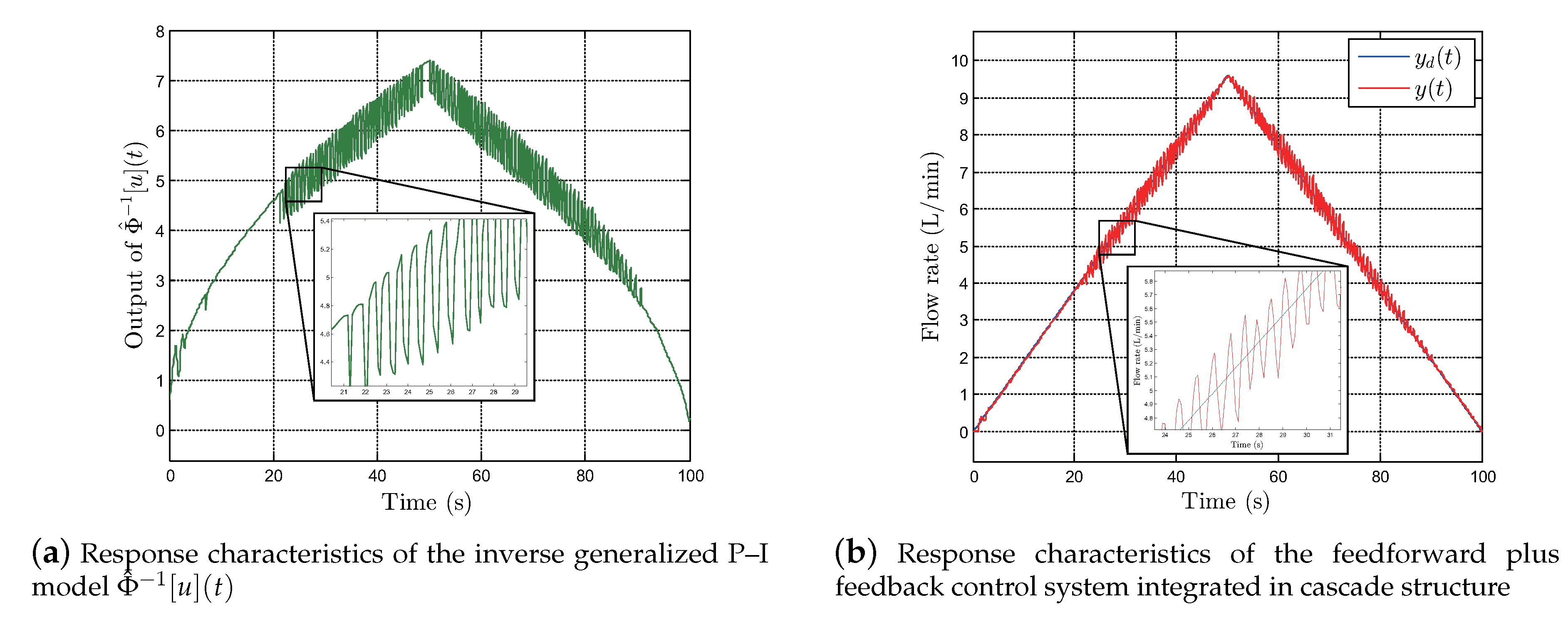
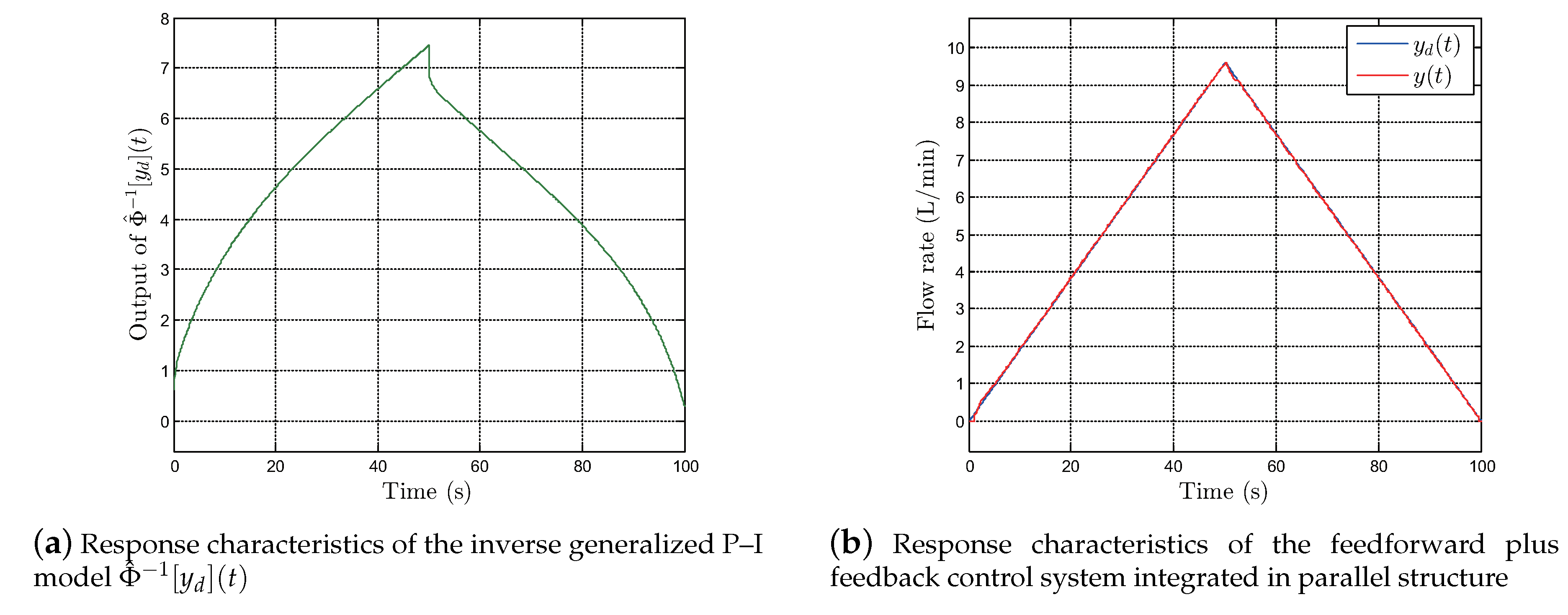
5. Feedforward Plus Feedback Controller and Experimental Validation
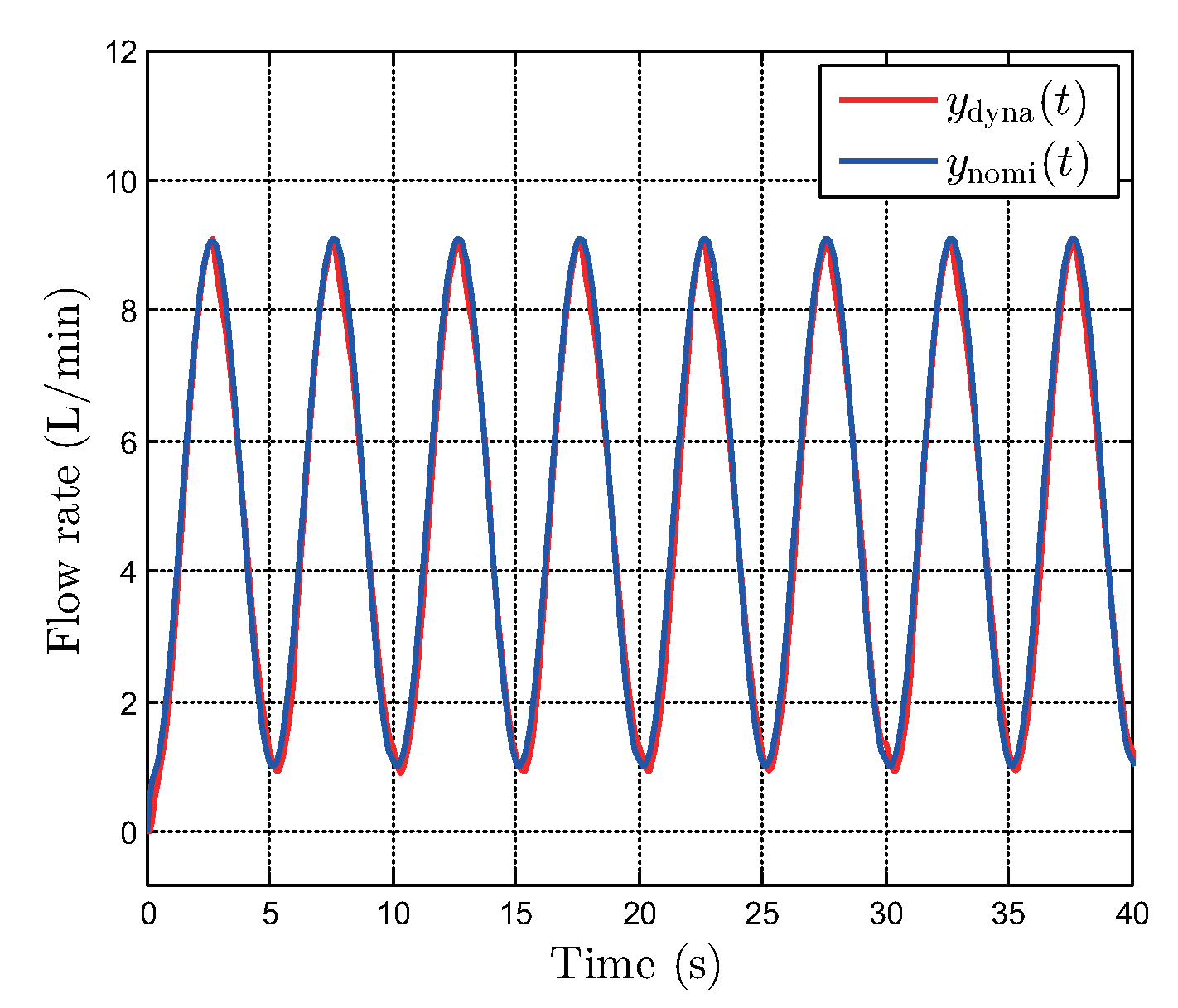
5.1. Tracking Performance Test
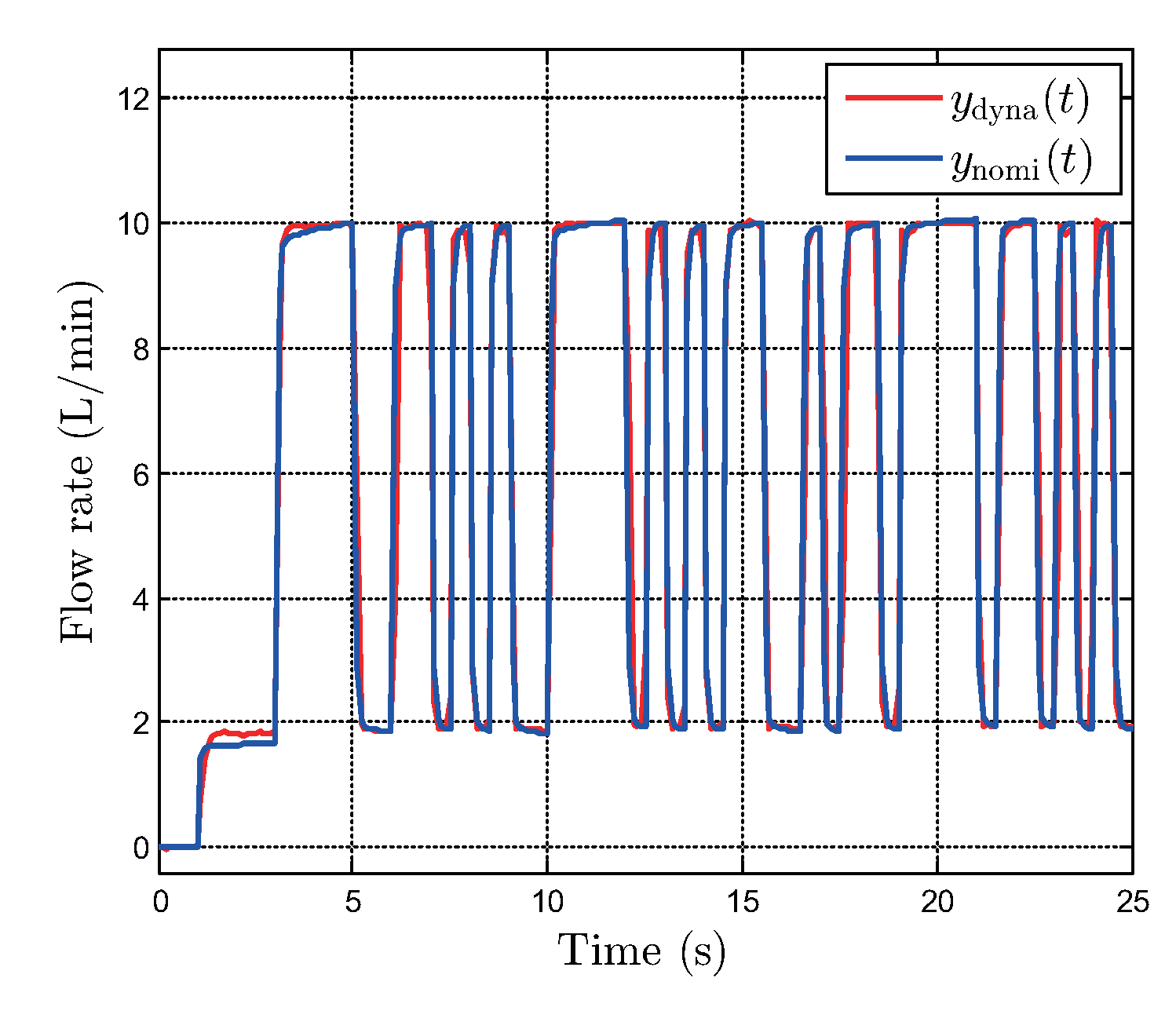
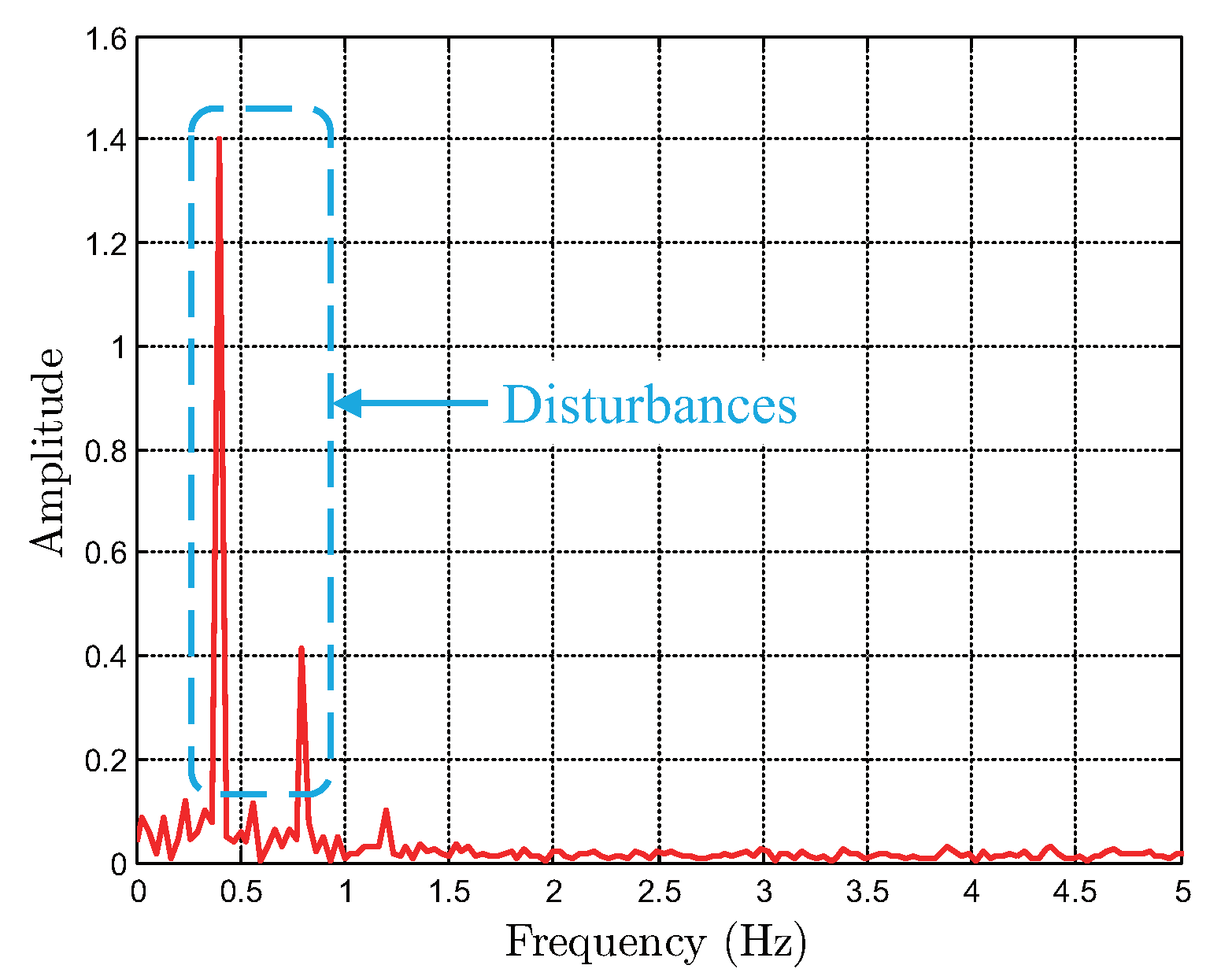
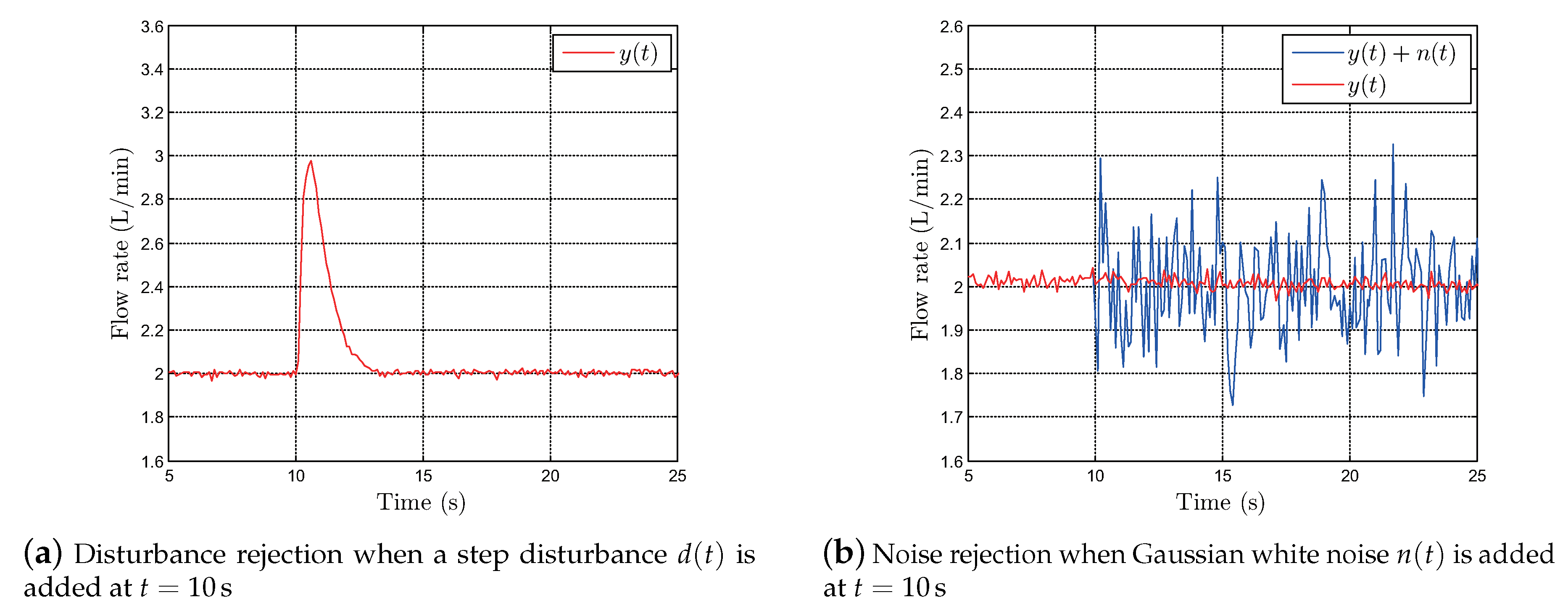
5.2. Robustness Test
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, I.-Y.; Oh, D.-H.; Ji, S.-W.; Yun, S.-N. Control of an overlap-type proportional directional control valve using input shaping filter. Mechatronics 2015, 29, 87–95. [Google Scholar] [CrossRef]
- Milić, V.; Šitum, Ž.; Essert, M. Robust H∞ position control synthesis of an electro-hydraulic servo system. ISA Trans. 2010, 49, 535–542. [Google Scholar] [CrossRef] [PubMed]
- Guo, K.; Wei, J.; Fang, J.; Feng, R.; Wang, X. Position tracking control of electro-hydraulic single-rod actuator based on an extended disturbance observer. Mechatronics 2015, 27, 47–56. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2016, 13, 313–332. [Google Scholar] [CrossRef]
- Yang, Z.; He, Z.; Li, D.; Yu, J.; Cui, X.; Zhao, Z. Direct drive servo valve based on magnetostrictive actuator: Multi-coupled modeling and its compound control strategy. Sen. Actuators Phys. 2015, 235, 119–130. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Yarmohammadi, M.J. Development of a self-tuning PID controller on hydraulically actuated stewart platform stabilizer with base excitation. Int. J. Control. Autom. Syst. 2018, 16, 2990–2999. [Google Scholar] [CrossRef]
- Won, D.; Kim, W. Disturbance observer based backstepping for position control of electro-hydraulic systems. Int. J. Control. Autom. Syst. 2015, 13, 488–493. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, J.; Wang, S. Fractional order control to the electro-hydraulic system in insulator fatigue test device. Mechatronics 2013, 23, 828–839. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakheja, S.; Su, C.-Y. An analytical generalized Prandtl–Ishlinskii model inversion for hysteresis compensation in micropositioning control. IEEE/ASME Trans. Mechatron. 2011, 16, 734–744. [Google Scholar] [CrossRef]
- Ko, Y.-R.; Hwang, Y.; Chae, M.; Kim, T.-H. Direct identification of generalized Prandtl–Ishlinskii model inversion for asymmetric hysteresis compensation. ISA Trans. 2017, 70, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shan, J.; Gabbert, U. Feedback/feedforward control of hysteresis-compensated piezoelectric actuators for high-speed scanning applications. Smart Mater. Struct. 2014, 24, 015012. [Google Scholar] [CrossRef]
- El-Shaer, A.H.; Janaideh, M.A.; Krejci, P.; Tomizuka, M. Robust performance enhancement using disturbance observers for hysteresis compensation based on generalized Prandtl–Ishlinskii model. J. Dyn. Syst. Meas. Control. 2013, 135. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Zakerzadeh, M.R. Position control of shape memory alloy actuator based on the generalized Prandtl–Ishlinskii inverse model. Mechatronics 2012, 22, 945–957. [Google Scholar] [CrossRef]
- Kim, T.-H.; Maruta, I.; Sugie, T. Robust PID controller tuning based on the constrained particle swarm optimization. Automatica 2008, 44, 1104–1110. [Google Scholar] [CrossRef]
- Esbrook, A.; Tan, X.; Khalil, H.K. Control of systems with hysteresis via servocompensation and its application to nanopositioning. IEEE Trans. Control. Syst. Technol. 2013, 21, 725–738. [Google Scholar] [CrossRef]
- Maruta, I.; Kim, T.-H.; Song, D.; Sugie, T. Synthesis of fixed-structure robust controllers using a constrained particle swarm optimizer with cyclic neighborhood topology. Expert Syst. Appl. 2013, 40, 3595–3605. [Google Scholar] [CrossRef]
- Devasia, S. Should model-based inverse inputs be used as feedforward under plant uncertainty? IEEE Trans. Autom. Control. 2002, 47, 1865–1871. [Google Scholar] [CrossRef]
- Fan, Y.; Tan, U.-X. Design of a feedforward-feedback controller for a piezoelectric-driven mechanism to achieve high-frequency nonperiodic motion tracking. IEEE/AMSE Trans. Mechatron. 2019, 24, 853–862. [Google Scholar] [CrossRef]
- Jung, S.; Choi, S.B.; Ko, Y.; Kim, J.; Lee, H. Pressure control of an electro-hydraulic actuated clutch via novel hysteresis model. Control. Eng. Pract. 2019, 91. [Google Scholar] [CrossRef]

| Component | Model | Specifications | Manufacturer |
|---|---|---|---|
| Proportional control valve | D1FBE01CC0NF0016 | P,A,B: 350 bar max., T: 210 bar max. | Parker |
| Flow sensor | QG200 | 0.03-40 L/min | Hydrotechnik |
| CompactRIO real-time controller | NI cRIO-9024 | Real-time controller at 800 MHz | NI |
| w/512 MB DRAM, 4 GB storage | |||
| Analog output module | NI 9263 | Four channels, sampling rate: 100 kS/s, | NI |
| resolution: 16 bits, range: ±10 V | |||
| Analog input module | NI 9223 | Four channels, sampling rate: 1 MS/s, | NI |
| resolution: 16 bits, range: ±10 V |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, Y.-R.; Kim, T.-H. Feedforward Plus Feedback Control of an Electro-Hydraulic Valve System Using a Proportional Control Valve. Actuators 2020, 9, 45. https://doi.org/10.3390/act9020045
Ko Y-R, Kim T-H. Feedforward Plus Feedback Control of an Electro-Hydraulic Valve System Using a Proportional Control Valve. Actuators. 2020; 9(2):45. https://doi.org/10.3390/act9020045
Chicago/Turabian StyleKo, Young-Rae, and Tae-Hyoung Kim. 2020. "Feedforward Plus Feedback Control of an Electro-Hydraulic Valve System Using a Proportional Control Valve" Actuators 9, no. 2: 45. https://doi.org/10.3390/act9020045
APA StyleKo, Y.-R., & Kim, T.-H. (2020). Feedforward Plus Feedback Control of an Electro-Hydraulic Valve System Using a Proportional Control Valve. Actuators, 9(2), 45. https://doi.org/10.3390/act9020045





