Modeling and Compensation of a Bimorph Type Piezoelectric Actuator Exhibiting Odd-Harmonic Oscillation and Frequency-Dependent, Interleaved Hysteresis
Abstract
1. Introduction
2. Hysteresis Modeling with the Play Model
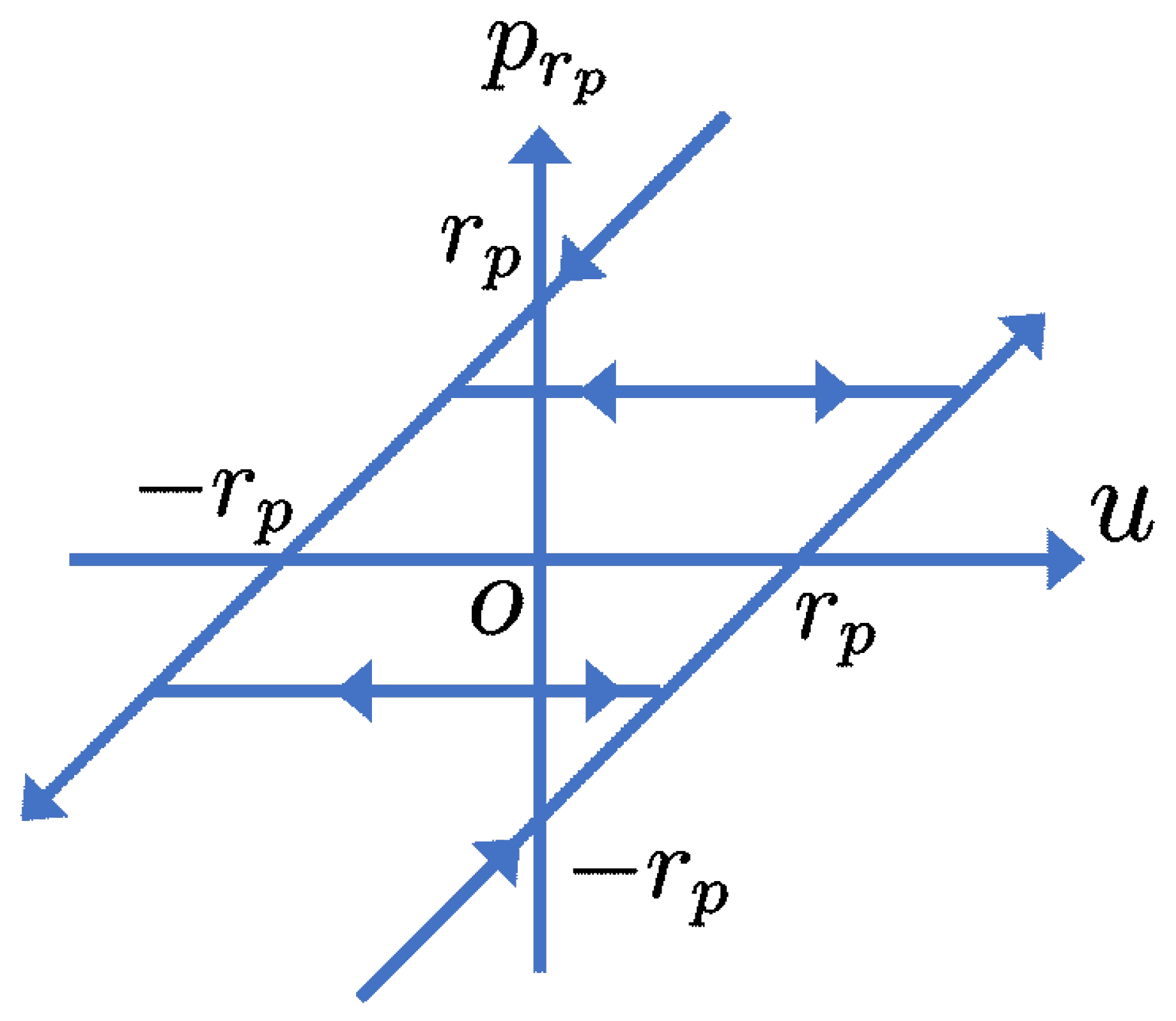
2.1. Play Model
2.2. Modification of the Play Model for Frequency Dependent Hysteresis
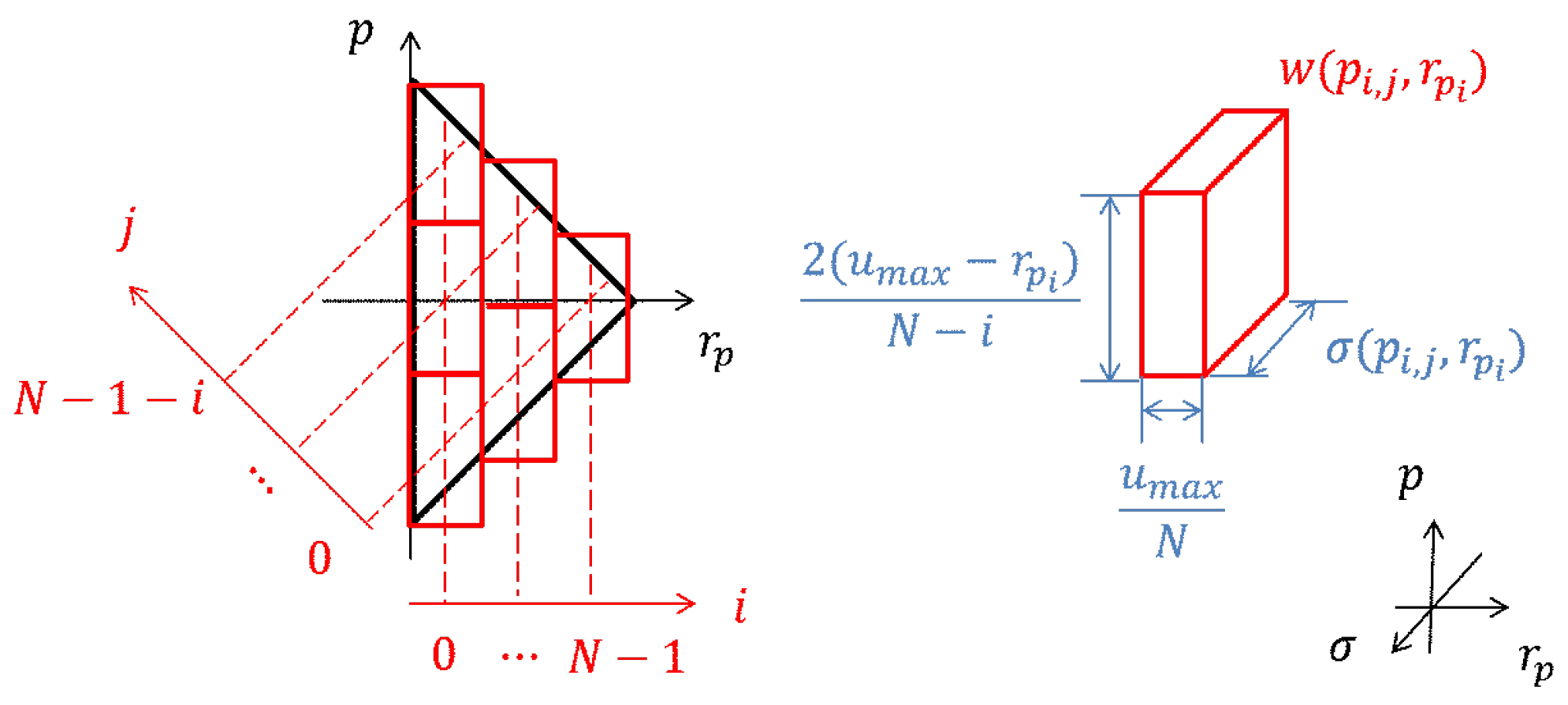
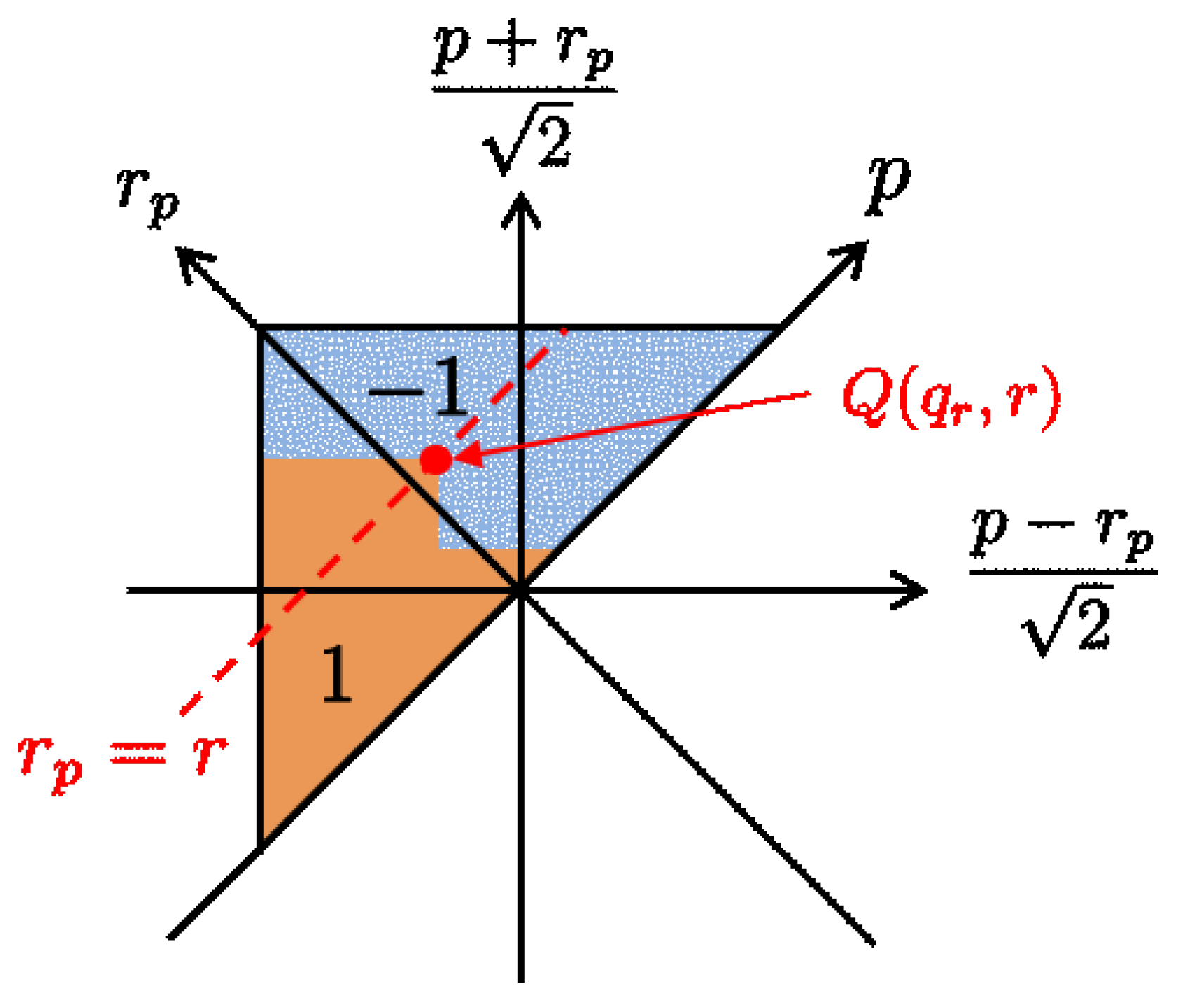
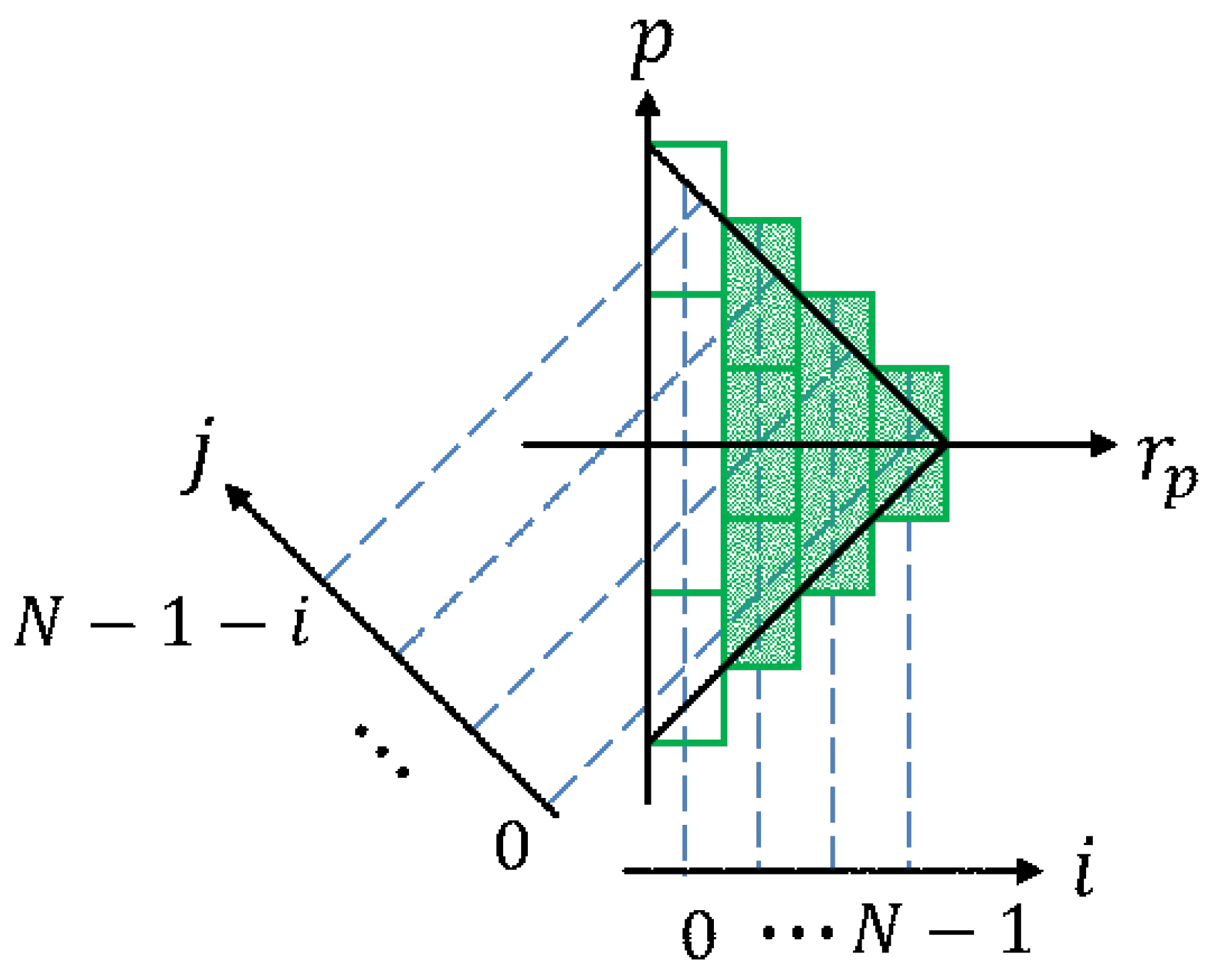
2.3. Discretization of the Play Model
3. Modification of the Play Model to Capture Frequency Dependent Hysteresis
3.1. Modification of the Model Structure to Capture Structural Behavior
3.2. Further Change of the Model Structure to Capture Odd Harmonic Oscillation
3.3. Structural Modification of the Model to Capture Interleaved Hysteresis
4. Controller Design for Hysteresis Compensation
4.1. Synthesis of Control Input
4.2. DIM Controller Synthesis Based on the Proposed Play Model
5. Experiments
5.1. Experimental Apparatus
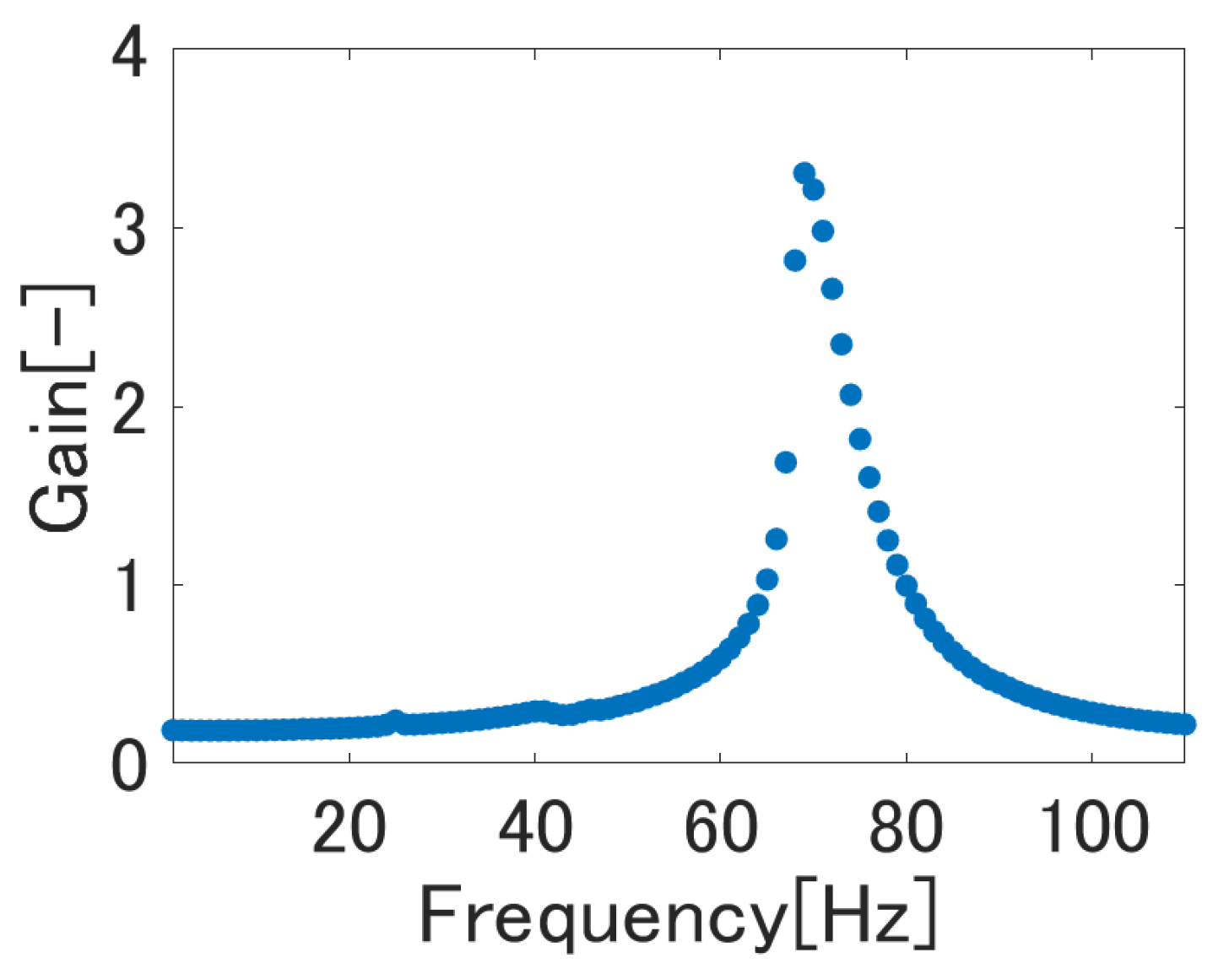
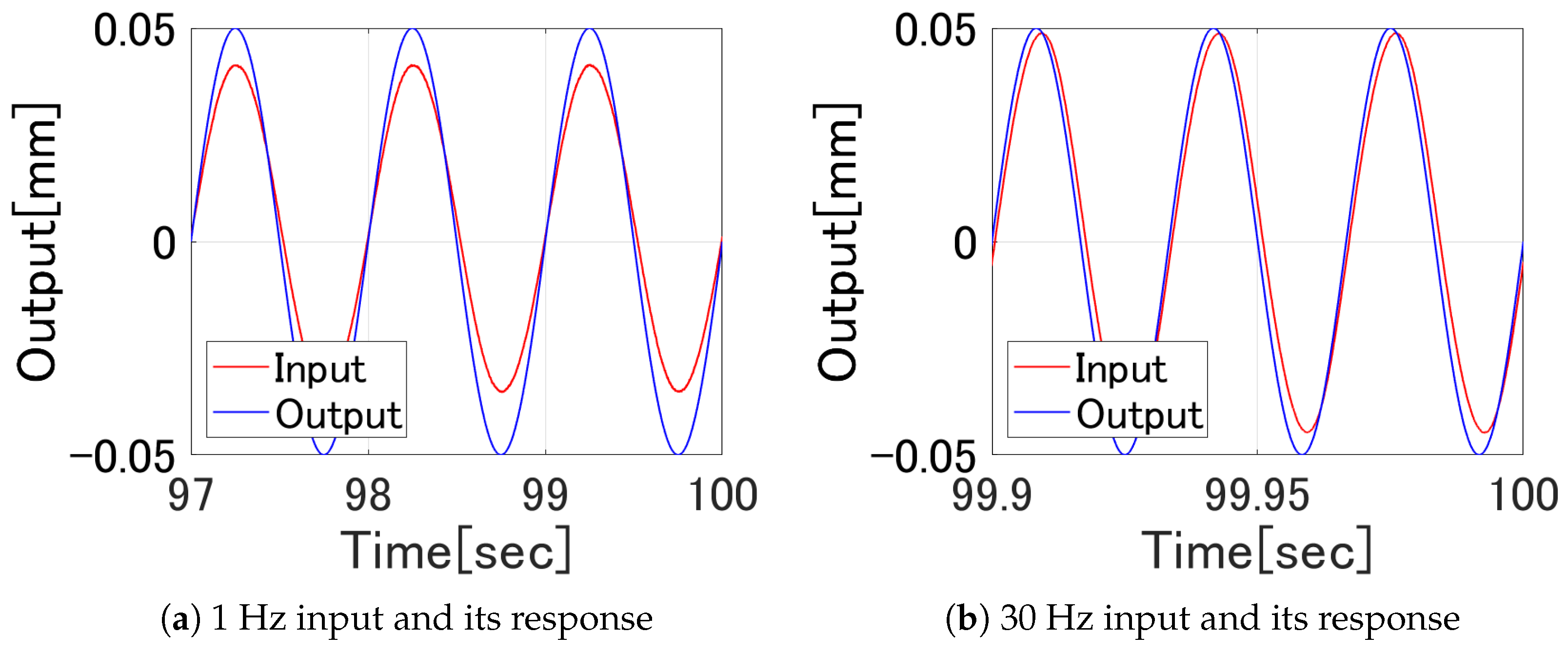
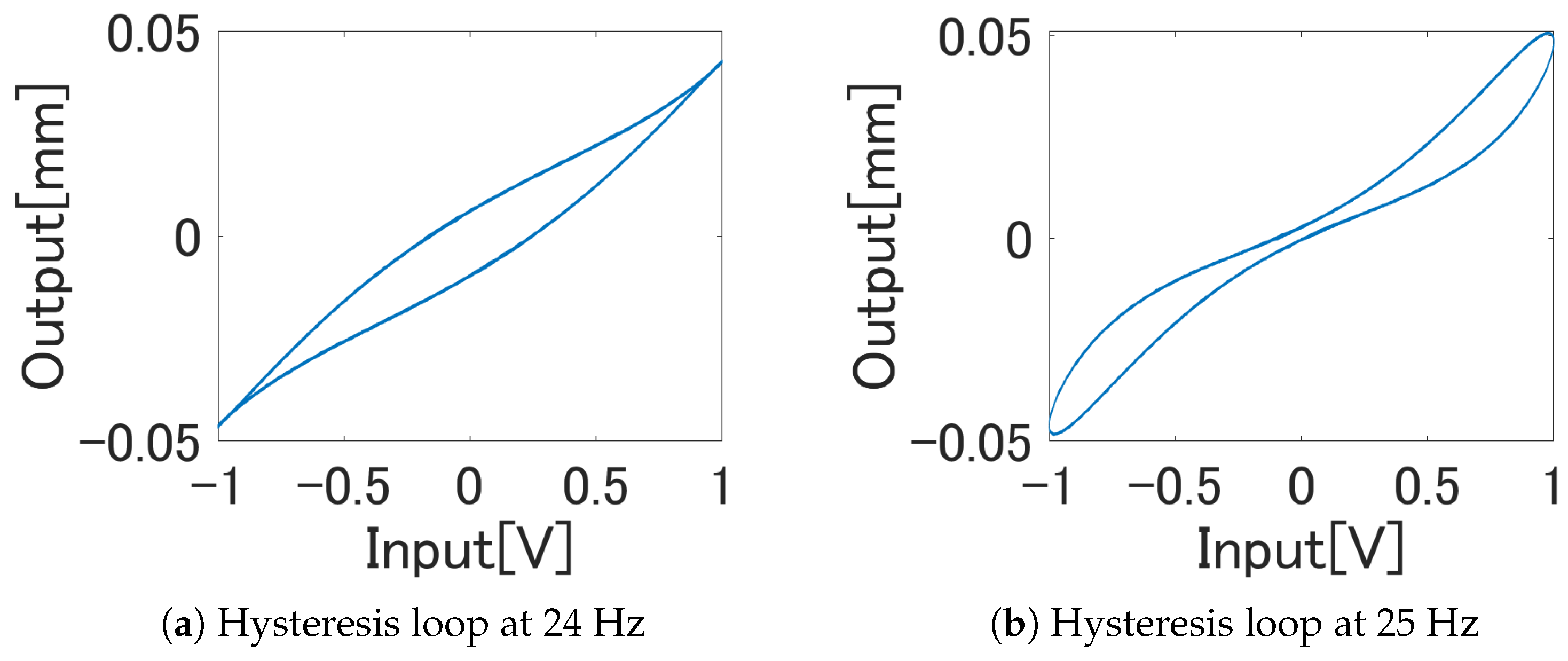
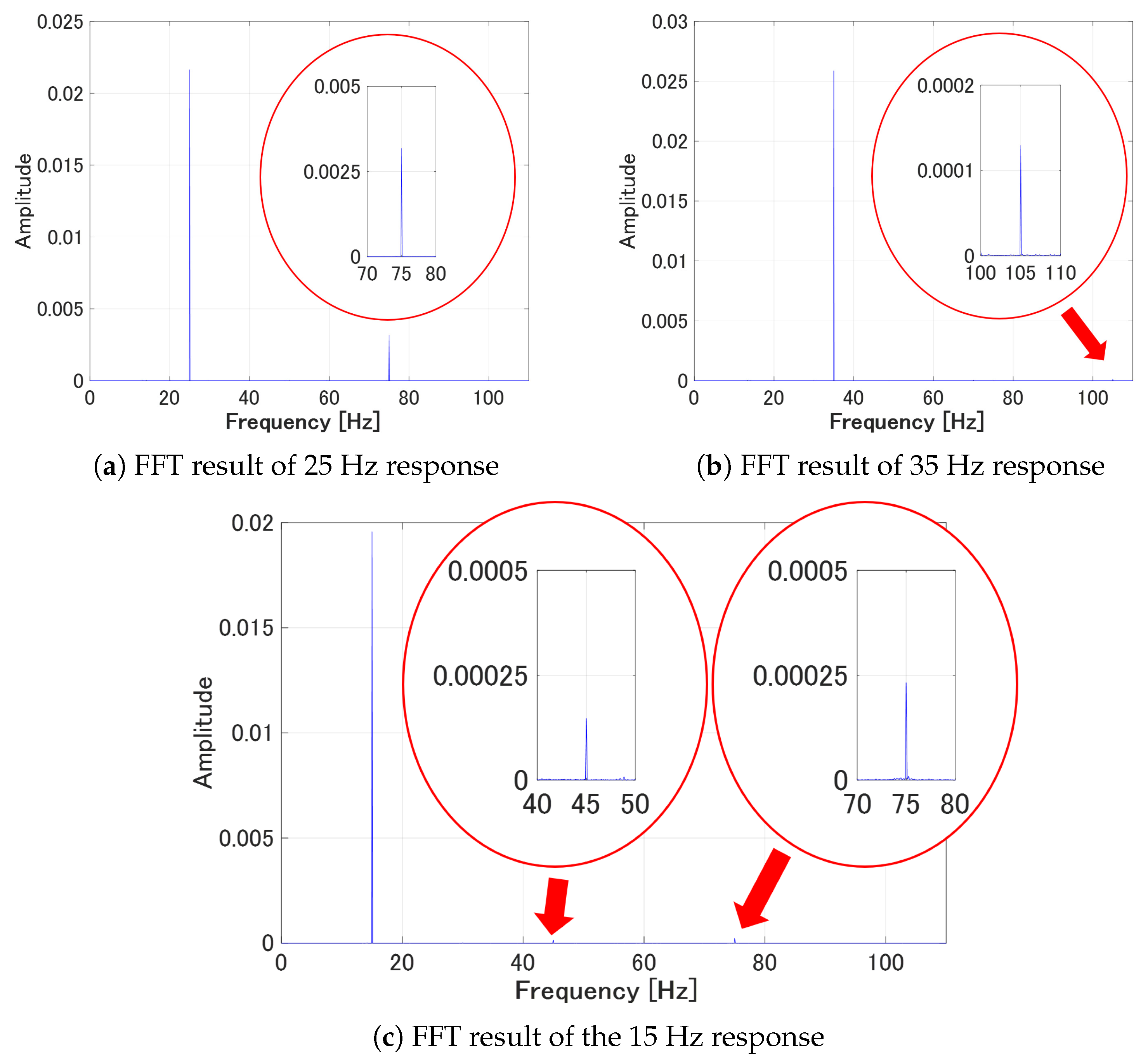
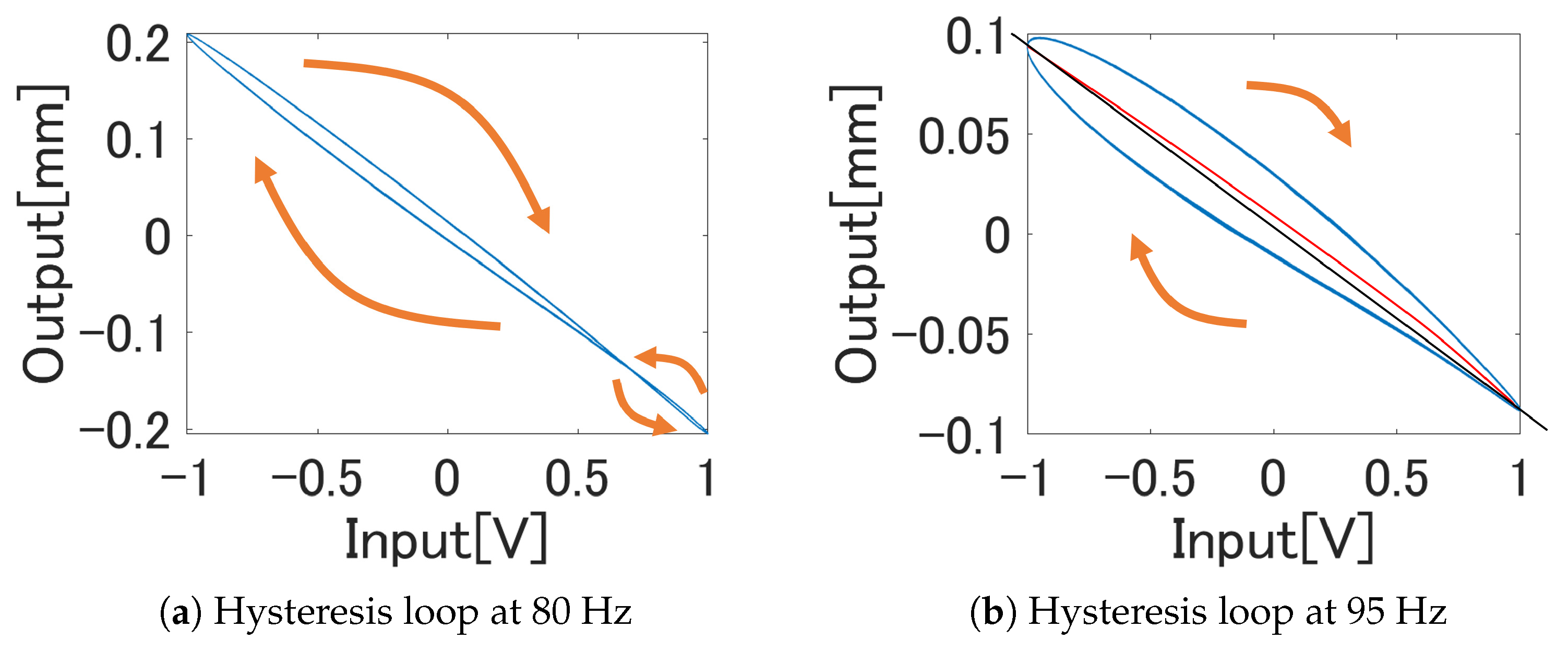
5.2. Identification Experiment
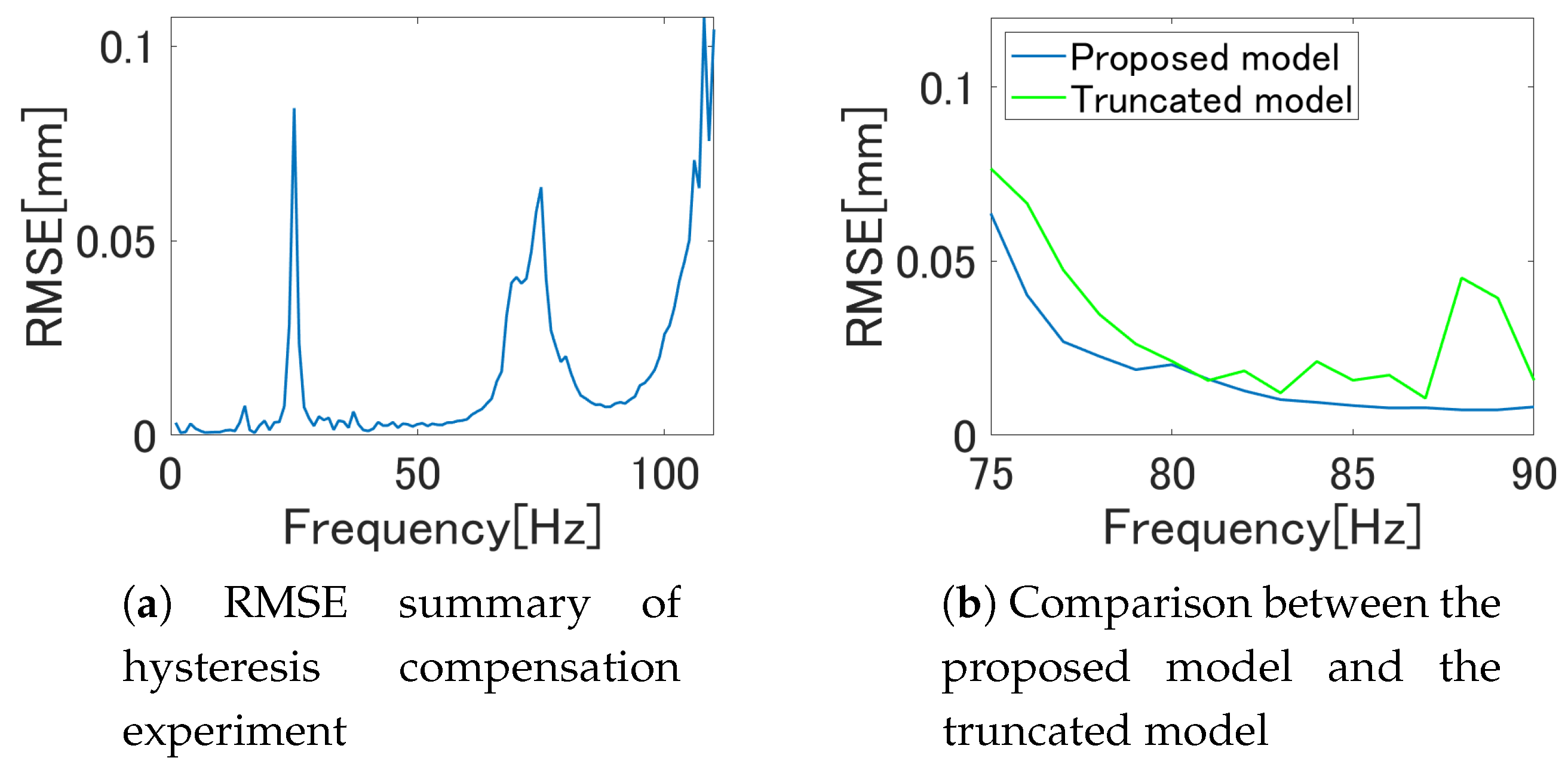
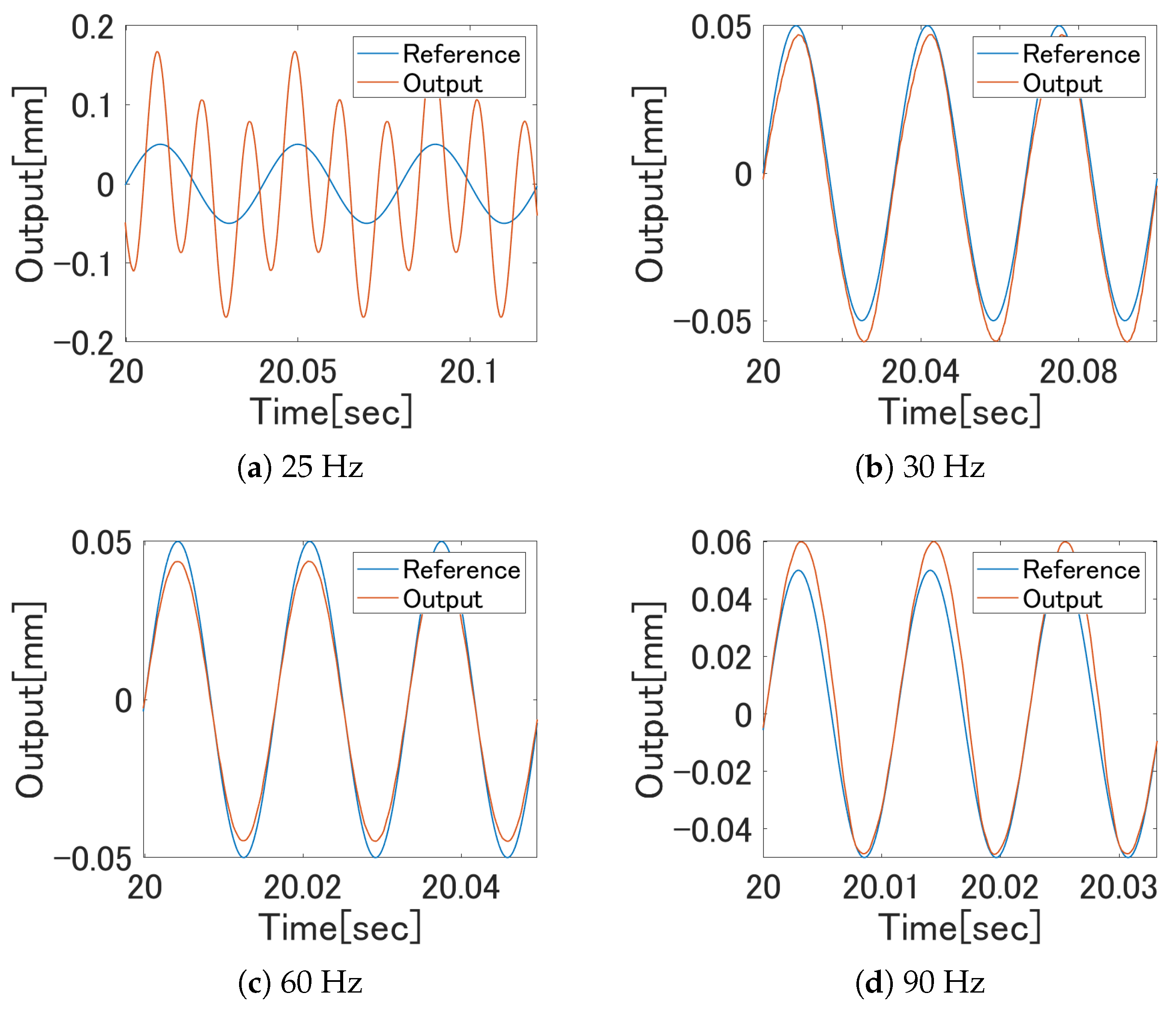
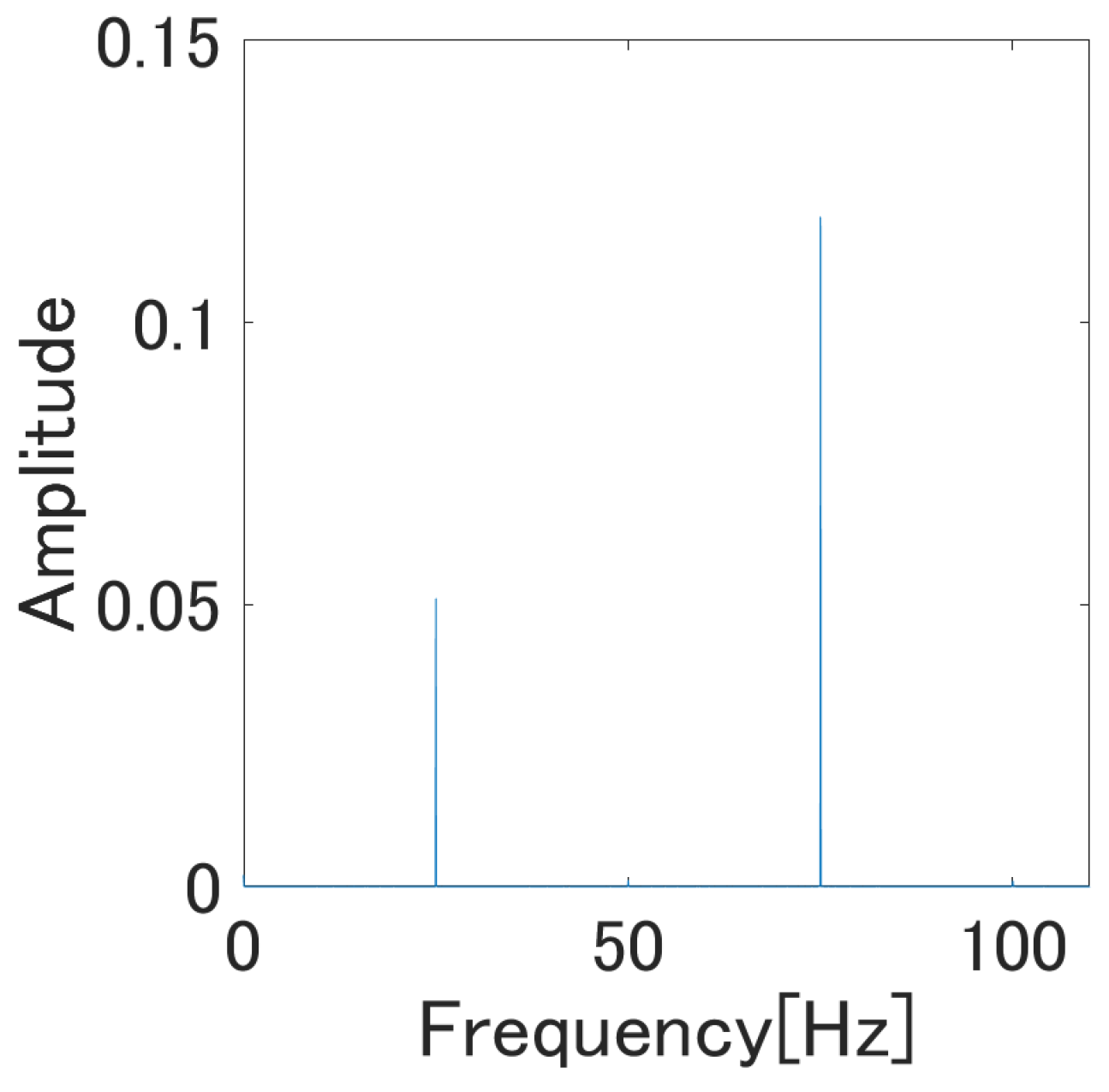
5.3. Hysteresis Compensation Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Idziak, P.; Kowalski, K.; Nowak, L.; Knypiński, K. FE transient analysis of the magnetostrictive actuator. Int. J. Appl. Electromagn. Mech. 2016, 51, S81–S87. [Google Scholar] [CrossRef]
- Shin, D.-M.; Hong, S.W.; Hwang, Y.-H. Recent Advances in Organic Piezoelectric Biomaterials for Energy and Biomedical Applications. Nanomaterials 2020, 10, 123. [Google Scholar] [CrossRef] [PubMed]
- Stefanski, F.; Minorowicz, B.; Persson, J.; Plummer, A.; Bowen, C. Non-linear control of a hydraulic piezo-valve using a generalised Prandtl-Ishlinskii hysteresis model. Mech. Syst. Signal Process. 2017, 82, 412–431. [Google Scholar] [CrossRef]
- Liu, C.; Guo, Y. Modeling and Positioning of a PZT Precision Drive System. Sensors 2017, 17, 2577. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, A.M.; Abo-Ismail, A.; El-Melegy, M.T.; Hamzaid, N.A.; Osman, N.A.A. Development of a Micro-Gripper Using Piezoelectric Bimorphs. Sensors 2013, 13, 5826–5840. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.K.; Majumder, S.; Ghosh, B.; Saha, S. Design and manufacturing of mobile micro manipulation system with a compliant piezoelectric actuator based micro gripper. J. Manuf. Syst. 2015, 35, 76–91. [Google Scholar] [CrossRef]
- Tsai, M.S.; Chen, J.S. Robust Tracking Control of a Piezoacuator Using a New Approximate Hysteresis Model. Trans. ASME J. Dyn. Syst. Meas. Control 2003, 125. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
- Yang, M.J.; Li, C.X.; Gu, G.Y.; Zhu, L.M. Modeling and compensating the dynamic hysteresis of piezoelectric actuators via a modified rate-dependent Prandtl–Ishlinskii model. Smart Mater. Struct. 2015, 24, 125006. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Modeling and High Dynamic Compensating the Rate-Dependent Hysteresis of Piezoelectric Actuators via a Novel Modified Inverse Preisach Model. IEEE Trans. Control Syst. Technol. 2013, 21, 1549–1557. [Google Scholar] [CrossRef]
- Matsuo, T.; Osaka, Y.; Shimasaki, M. Eddy-current analysis using vector hysteresis models with play and stop hysterons. IEEE Trans. Magn. 2000, 36, 1172–1177. [Google Scholar] [CrossRef]
- Matsuo, T.; Shimasaki, M. Representation Theorems for stop and play models with input-dependent shape functions. IEEE Trans. Magn. 2005, 41, 1548–1551. [Google Scholar] [CrossRef]
- Fujii, F.; Tatebatake, K.; Morita, K.; Shiinoki, T. A Bouc-Wen Model-Based Compensation of the Frequency-Dependent Hysteresis of a Piezoelectric Actuator Exhibiting Odd Harmonic Oscillation. Actuators 2018, 7, 37. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J. Research on Hysteresis of Piezoceramic Actuator Based on the Duhem Model. Sci. World J. 2013. [Google Scholar] [CrossRef] [PubMed]
- Janaideh, M.A.; Rakheja, S.; Su, C.Y. Experimental characterization and modeling of rate-dependent hysteresis of a piezoceramic actuator. Mechatronics 2009, 19, 656–670. [Google Scholar] [CrossRef]
- Yang, M.; Li, C.; Gu, G.; Zhu, L. A rate-dependent Prandtl-Ishlinskii model for piezoelectric actuators using the dynamic envelope function based play operator. Front. Mech. Eng. 2015, 10, 37. [Google Scholar] [CrossRef]
- Li, C.X.; Gu, G.Y.; Zhu, L.M.; Su, C.Y. Odd-harmonic repetitive control for high-speed raster scanning of piezo-actuated nanopositioning stages with hysteresis nonlinearity. Sens. Actuators A Phys. 2016, 244, 95–105. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Bouc-Wen Modeling and Inverse Multiplicative Structure to Compensate Hysteresis Nonlinearity in Piezoelectric Actuators. IEEE Trans. Autom. Sci. Eng. 2011, 8, 428–431. [Google Scholar] [CrossRef]
- Alatawneh, N.; Pillay, P. Modeling of the interleaved hysteresis loop in the measurements of rotational core losses. J. Magn. Magn. Mater. 2016, 397, 157–163. [Google Scholar] [CrossRef]
- Morita, K.; Fujii, F. Modeling Bimorph Piezoelectric Actuator Exhibiting Frequency-Dependent Interleaved Hysteresis with Occasional Odd Harmonic Oscillation. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 1548–1554. [Google Scholar] [CrossRef]
- Sprekels, J.; Brokate, M. Hysteresis and Phase Transitions; Sprinver-Verlag: New York, NY, USA, 1996; Volume 121. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Feng, Y.; Rakheja, S.; Tan, Y.; Su, C. Generalized Prandtl-Ishlinskii hysteresis: Modeling and robust control for smart actuators. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 7279–7284. [Google Scholar] [CrossRef]
- Song, X.; Duggen, L.; Lassen, B.; Mangeot, C. Modeling and identification of hysteresis with modified Preisach model in piezoelectric actuator. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM 2017), Munich, Germany, 3–7 July 2017; pp. 1538–1543. [Google Scholar] [CrossRef]
- Li, Z.; Su, C.Y.; Chai, T. Compensation of Hysteresis Nonlinearity in Magnetostrictive Actuators With Inverse Multiplicative Structure for Preisach Model. IEEE Trans. Autom. Sci. Eng. 2014, 11, 613–619. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morita, K.; Fujii, F.; Hosoda, K. Modeling and Compensation of a Bimorph Type Piezoelectric Actuator Exhibiting Odd-Harmonic Oscillation and Frequency-Dependent, Interleaved Hysteresis. Actuators 2020, 9, 36. https://doi.org/10.3390/act9020036
Morita K, Fujii F, Hosoda K. Modeling and Compensation of a Bimorph Type Piezoelectric Actuator Exhibiting Odd-Harmonic Oscillation and Frequency-Dependent, Interleaved Hysteresis. Actuators. 2020; 9(2):36. https://doi.org/10.3390/act9020036
Chicago/Turabian StyleMorita, Kohei, Fumitake Fujii, and Kazune Hosoda. 2020. "Modeling and Compensation of a Bimorph Type Piezoelectric Actuator Exhibiting Odd-Harmonic Oscillation and Frequency-Dependent, Interleaved Hysteresis" Actuators 9, no. 2: 36. https://doi.org/10.3390/act9020036
APA StyleMorita, K., Fujii, F., & Hosoda, K. (2020). Modeling and Compensation of a Bimorph Type Piezoelectric Actuator Exhibiting Odd-Harmonic Oscillation and Frequency-Dependent, Interleaved Hysteresis. Actuators, 9(2), 36. https://doi.org/10.3390/act9020036




