Observer-Based Tracking Control for Polysolenoid Linear Motor with Unknown Disturbance Load
Abstract
1. Introduction
- A novel velocity observer has been proposed such that the observer errors exponentially converge by utilizing the available position sensors attached in PLM. To be specific, based on Lyapunov theorem, the exponential convergence of observer errors has been proofed in a rigorous way. Furthermore, conditions for selecting parameters of the observer are provided as well as delay rate of the observer errors.
- From the observer, a position-velocity and current controllers are designed by Lyapunov direct method. Accordingly, the position or velocity tracking error converge to small arbitrary values by adjusting control parameters.
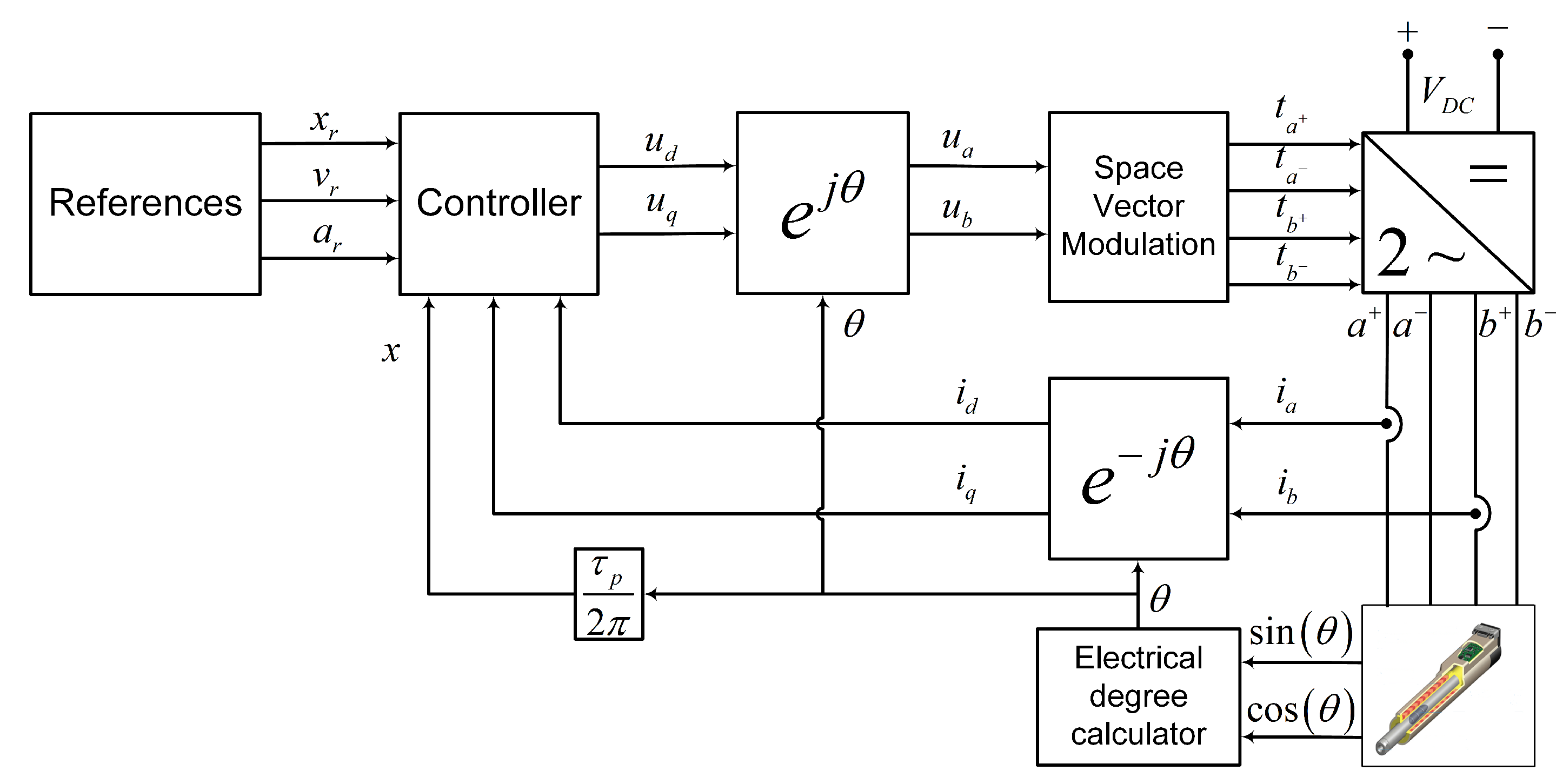
2. Problem Statement
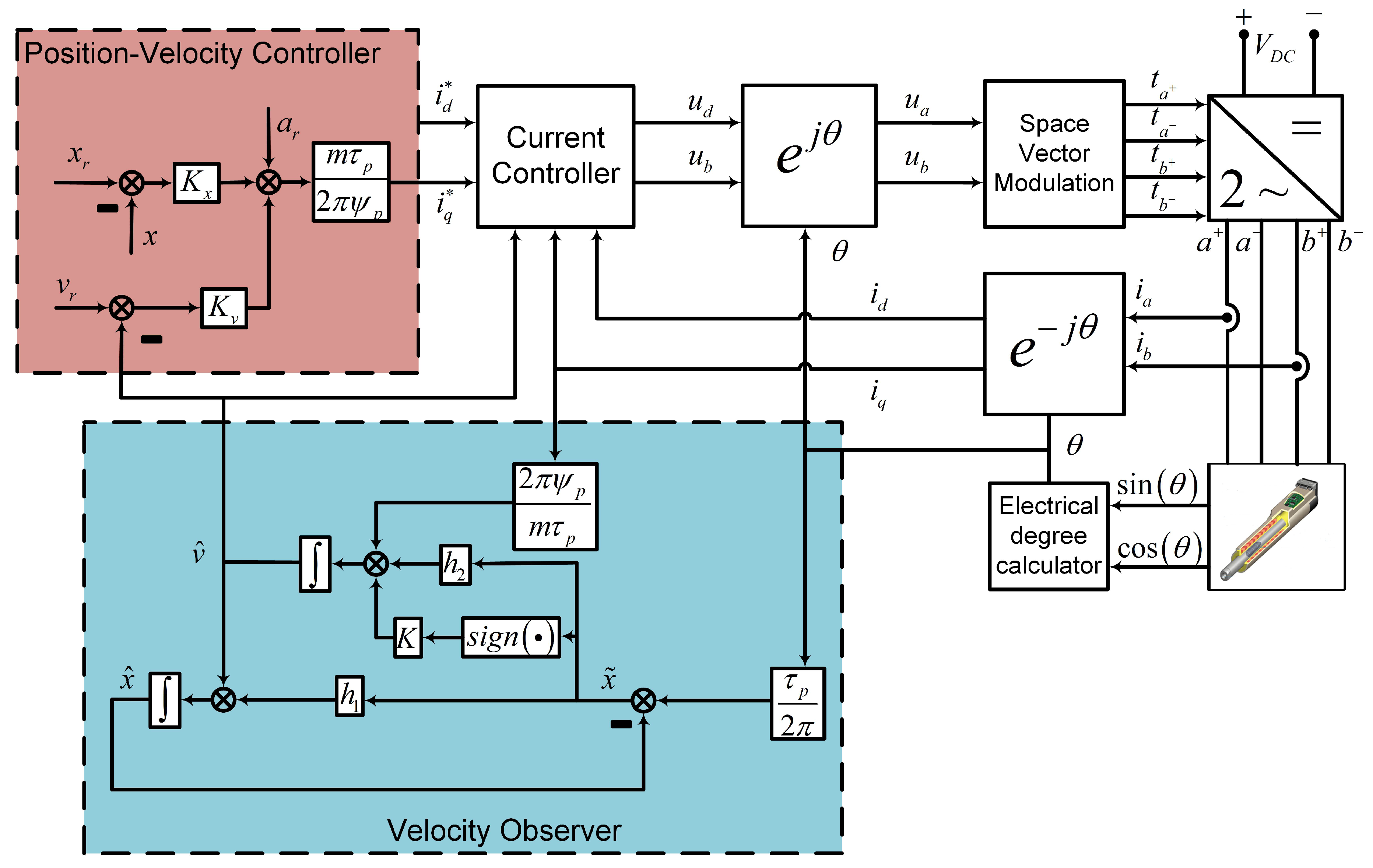
3. Observer Design
4. Controller Design
4.1. Position-Velocity Subsystem
4.2. Current Subsystem
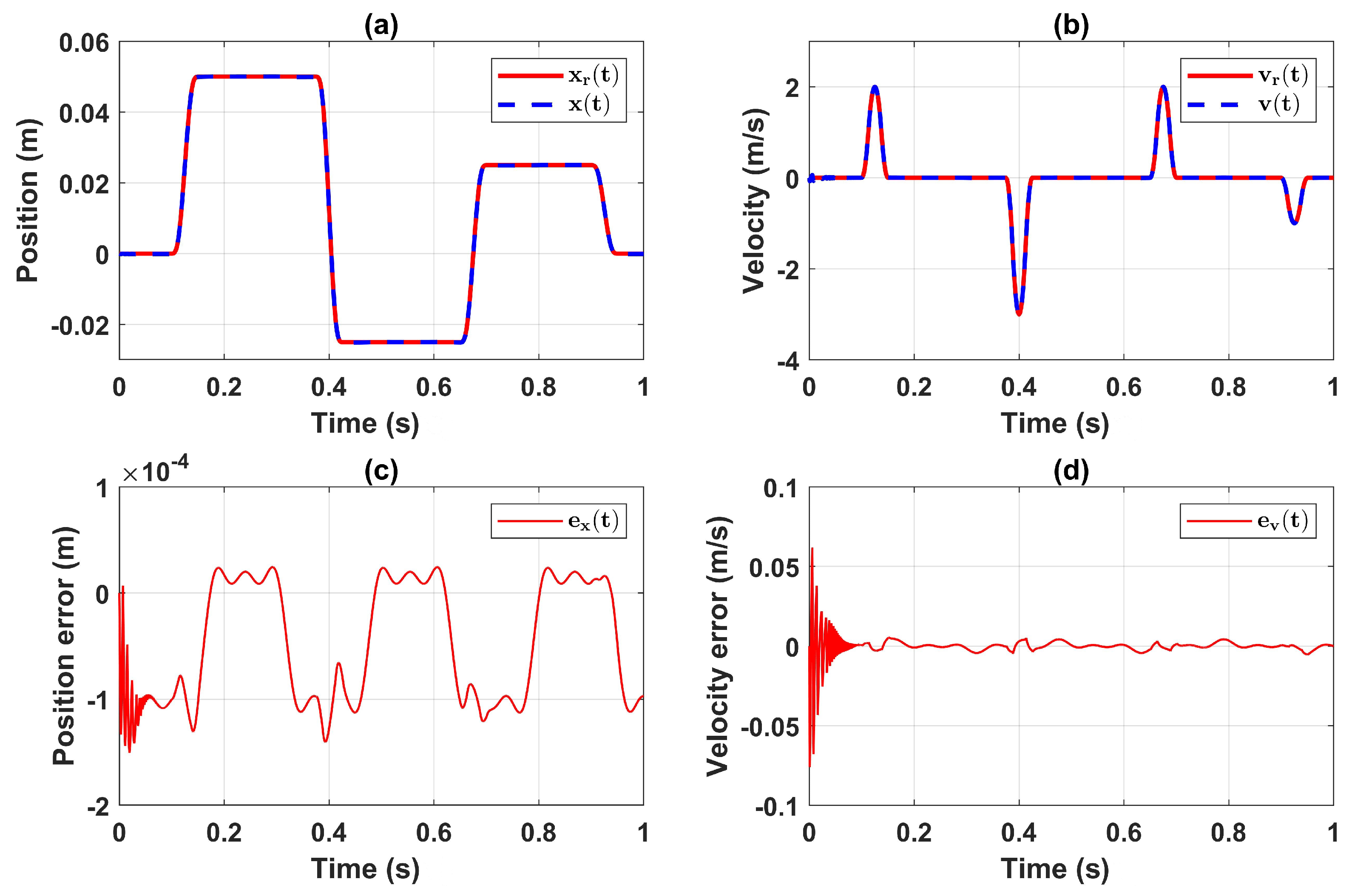
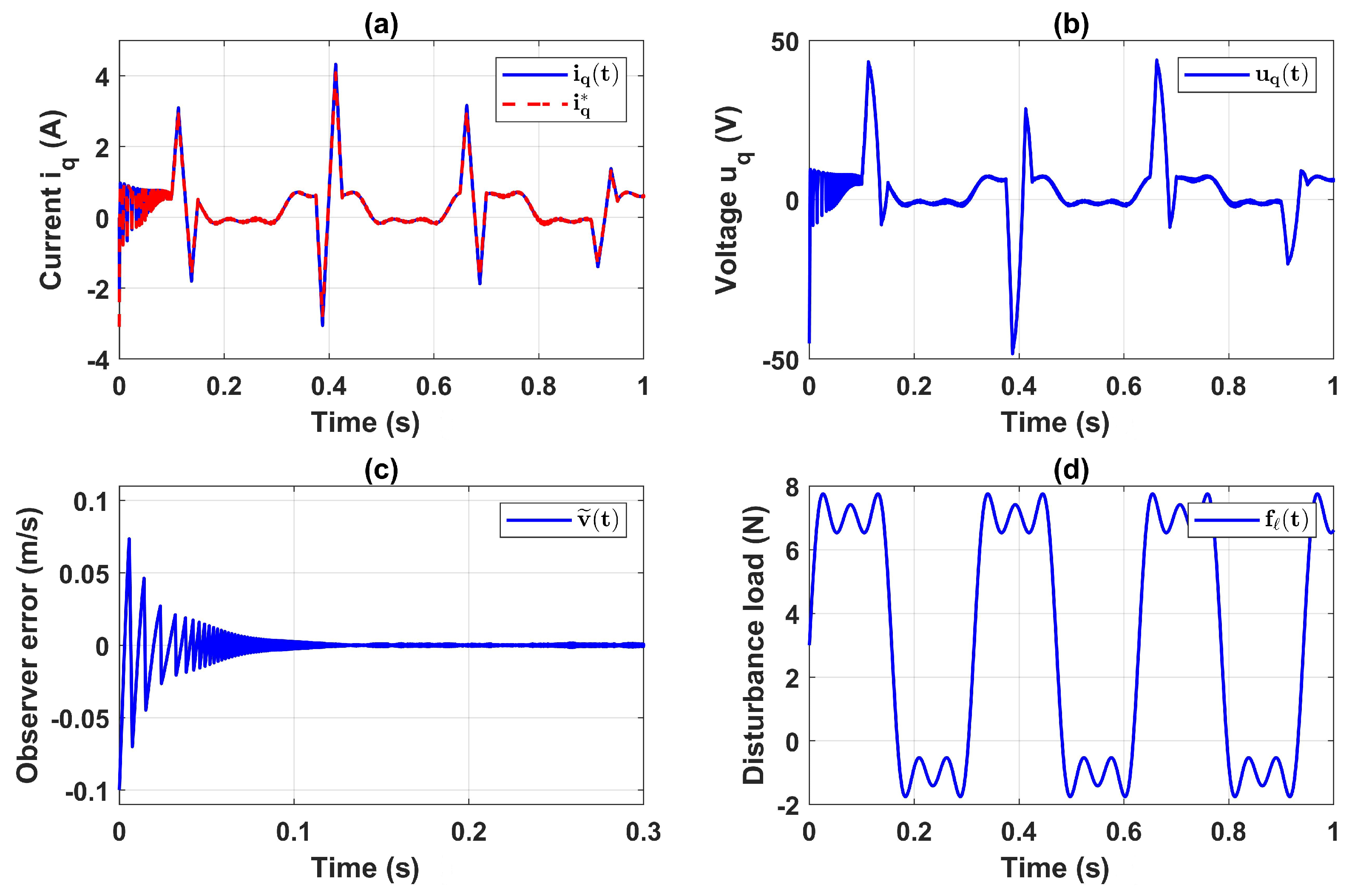
5. Numerical Simulation
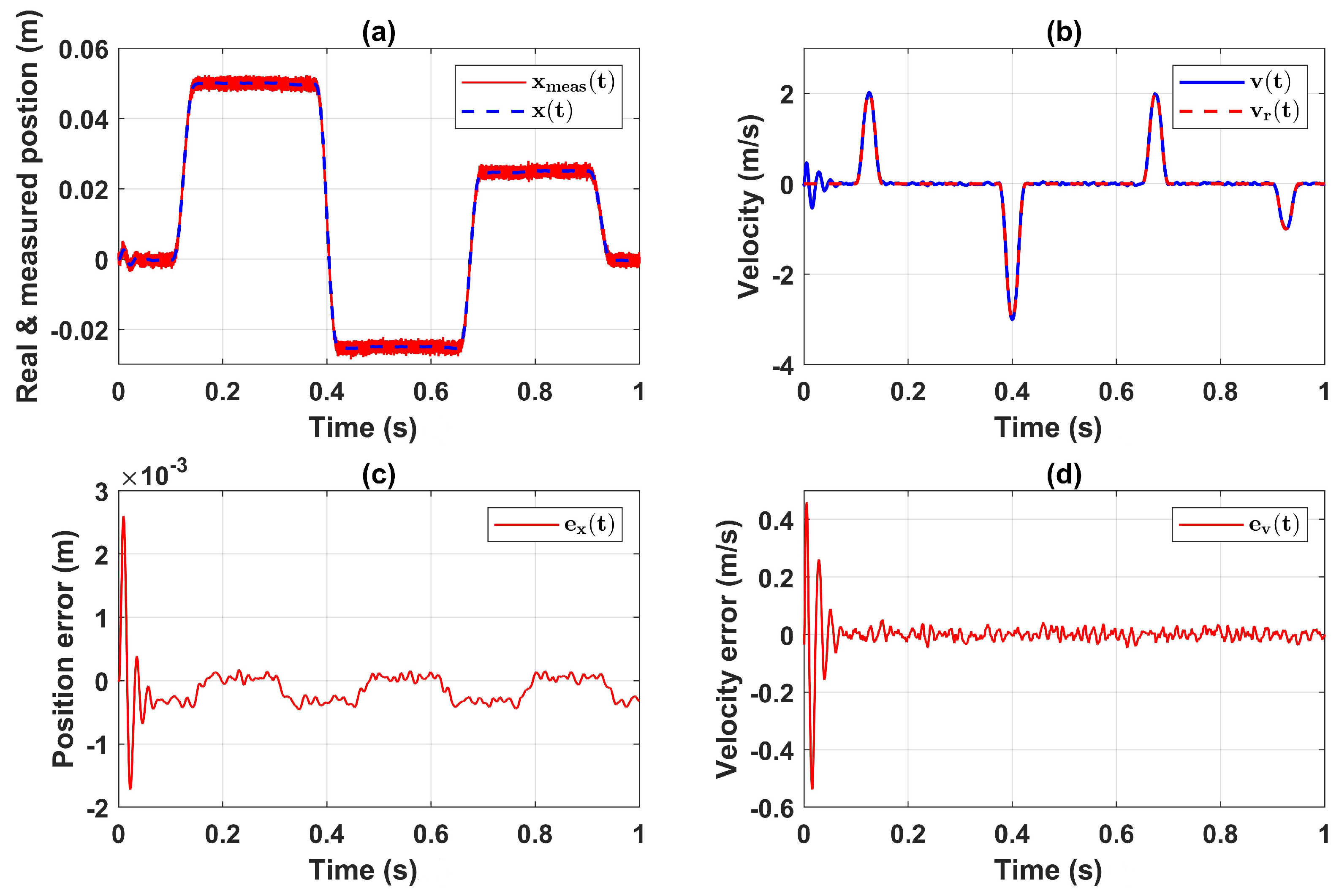
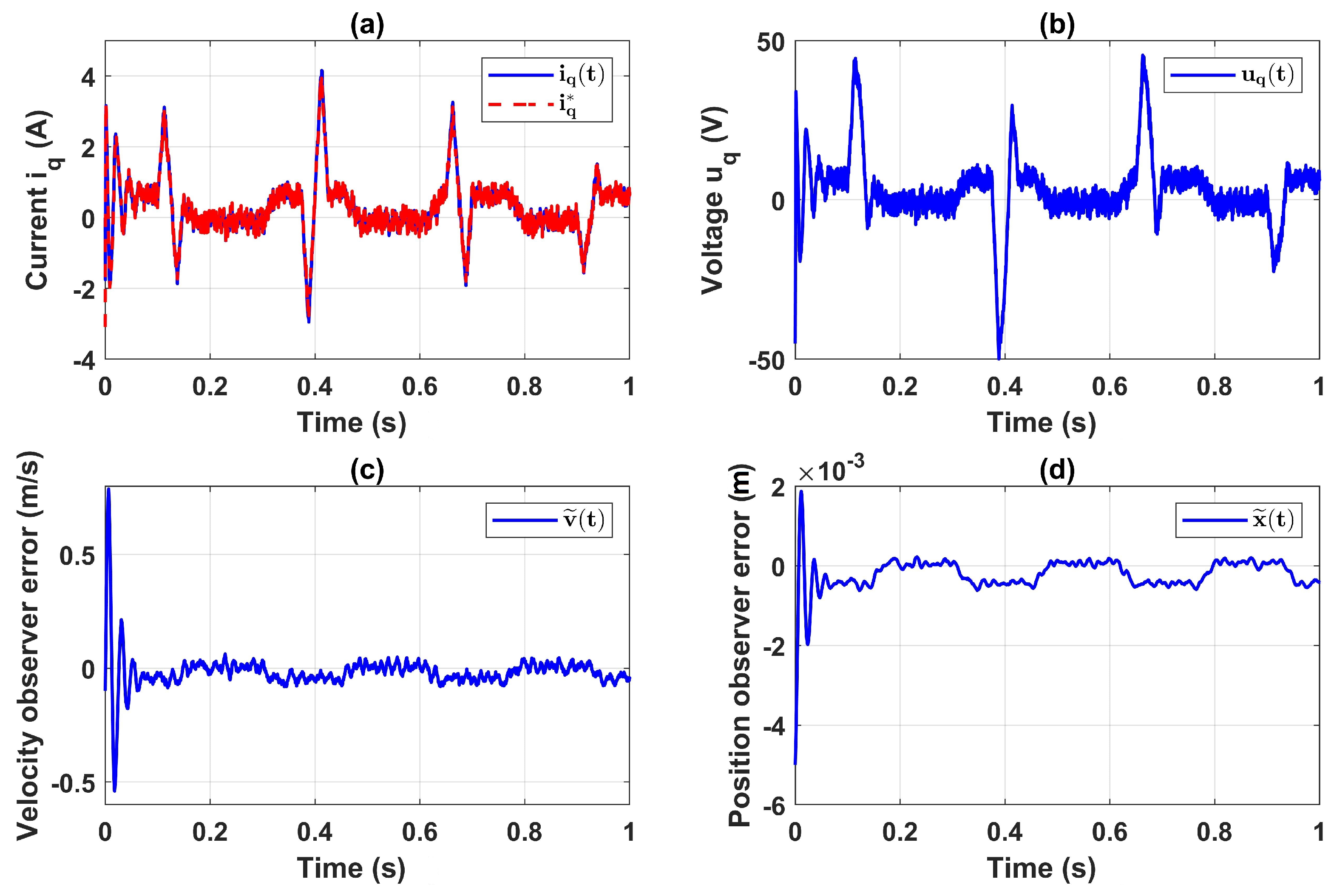
5.1. Simulation Results in Case of None Measurement Noise
5.2. Simulation Results in Presence of Measurement Noise
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gieras, J.F.; Piech, Z.J.; Tomczuk, B. Linear Synchronous Motors: Transportation and Automation Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, Y.; Yu, H.; Che, Z.; Wang, Y.; Zeng, C. Extended state observer-based predictive speed control for permanent magnet linear synchronous motor. Processes 2019, 7, 618. [Google Scholar] [CrossRef]
- Wen, T.; Xiang, B.; Wang, Z.; Zhang, S. Speed control of segmented PMLSM based on improved SMC and speed compensation model. Energies 2020, 13, 981. [Google Scholar] [CrossRef]
- Díaz-Pérez, L.; Torralba, M.; Albajez, J.A.; Yagüe-Fabra, J.A. 2D positioning control system for the planar motion of a nanopositioning platform. Appl. Sci. 2019, 9, 4860. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Z.; Hua, W.; Wang, Z.; Cheng, M. Simplified model predictive current control of primary permanent-magnet linear motor traction systems for subway applications. Energies 2019, 12, 4144. [Google Scholar] [CrossRef]
- Tran, M.S.; Hwang, S.J. Design and experiment of a moving magnet actuator based jetting dispenser. Appl. Sci. 2019, 9, 2911. [Google Scholar] [CrossRef]
- Ausderau, D. Polysolenoid-Linearantrieb Mit Genutetem Stator. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2004. [Google Scholar]
- Boldea, I. Linear Electric Machines, Drives, and MAGLEVs Handbook; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Quang, N.H.; Quang, N.P.; Hien, N.N.; Binh, N.T. Min max model predictive control for polysolenoid linear motor. Int. J. Power Electr. Drive Syst. ISSN 2018, 2088, 1667. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Nguyen, P.Q.; Nam, D.P.; Nguyen, T.B. Multi parametric model predictive control based on laguerre model for permanent magnet linear synchronous motors. Int. J. Electr. Comput. Eng. 2019, 9, 1067. [Google Scholar]
- Nguyen, Q.H.; Dao, N.P.; Nguyen, T.T.; Nguyen, H.M.; Nguyen, H.N.; Vu, T.D. Flatness based control structure for polysolenoid permanent stimulation linear motors. Int. J. Electr. Electron. Eng. 2016, 3, 31–37. [Google Scholar]
- Wang, Z.; Hu, C.; Zhu, Y.; He, S.; Yang, K.; Zhang, M. Neural network learning adaptive robust control of an industrial linear motor-driven stage with disturbance rejection ability. IEEE Trans. Ind. Inf. 2017, 13, 2172–2183. [Google Scholar] [CrossRef]
- Ahn, H.S.; Chen, Y.; Dou, H. State-Periodic Adaptive Compensation of Cogging and Coulomb Friction in Permanent Magnet Linear Motors. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 3036–3041. [Google Scholar]
- Tan, K.; Huang, S.; Lee, T. Robust adaptive numerical compensation for friction and force ripple in permanent-magnet linear motors. IEEE Trans. Magn. 2002, 38, 221–228. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Y.; Zhou, Z.; Ai, W.; Li, X. Robust adaptive motion control of permanent magnet linear motors based on disturbance compensation. IET Electr. Power Appl. 2007, 1, 543–548. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lü, J. Discrete-time fast terminal sliding mode control for permanent magnet linear motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Sun, G.; Ma, Z. Practical tracking control of linear motor with adaptive fractional order terminal sliding mode control. IEEE/ASME Trans. Mechatron. 2017, 22, 2643–2653. [Google Scholar] [CrossRef]
- Cupertino, F.; Giangrande, P.; Pellegrino, G.; Salvatore, L. End effects in linear tubular motors and compensated position sensorless control based on pulsating voltage injection. IEEE Trans. Ind. Electron. 2010, 58, 494–502. [Google Scholar] [CrossRef]
- Hussain, H.A.; Toliyat, H.A. Back-EMF Based Sensorless Vector Control of Tubular PM Linear Motors. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 878–883. [Google Scholar]
- Giangrande, P.; Cupertino, F.; Pellegrino, G. Modelling of Linear Motor End-Effects for Saliency Based Sensorless Control. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3261–3268. [Google Scholar]
- Accetta, A.; Cirrincione, M.; Pucci, M.; Vitale, G. Neural sensorless control of linear induction motors by a full-order Luenberger observer considering the end effects. IEEE Trans. Ind. Appl. 2013, 50, 1891–1904. [Google Scholar] [CrossRef]
- Yu, P.-Q.; Lu, Y.-H.; Wang, Y.; Yang, W.-M.; Chen, Z.-C. Research on permanent magnet linear synchronous motor position sensorless control system. Proc. Chin. Soc. Electr. Eng. 2007, 27, 53–57. [Google Scholar]
- Cupertino, F.; Pellegrino, G.; Giangrande, P.; Salvatore, L. Sensorless position control of permanent-magnet motors with pulsating current injection and compensation of motor end effects. IEEE Trans. Ind. Appl. 2011, 47, 1371–1379. [Google Scholar] [CrossRef]
- Holtz, J. Sensorless control of induction machines—With or without signal injection? IEEE Trans. Ind. Electron. 2006, 53, 7–30. [Google Scholar] [CrossRef]
- Silva, C.; Asher, G.M.; Sumner, M. Hybrid rotor position observer for wide speed-range sensorless PM motor drives including zero speed. IEEE Trans. Ind. Electron. 2006, 53, 373–378. [Google Scholar] [CrossRef]
- LinMot Company Home Page: Products, Linear Motors. Available online: https://linmot.com/products/linear-motors/ (accessed on 1 March 2020).
- Lim, K.C.; Woo, J.K.; Kang, G.H.; Hong, J.P.; Kim, G.T. Detent force minimization techniques in permanent magnet linear synchronous motors. IEEE Trans. Magn. 2002, 38, 1157–1160. [Google Scholar]
- Zhao, W.; Jiao, S.; Chen, Q.; Xu, D.; Ji, J. Sensorless control of a linear permanent-magnet motor based on an improved disturbance observer. IEEE Trans. Ind. Electron. 2018, 65, 9291–9300. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 3. [Google Scholar]
- Atassi, A.; Khalil, H. Separation results for the stabilization of nonlinear systems using different high-gain observer designs. Syst. Control Lett. 2000, 39, 183–191. [Google Scholar] [CrossRef]
- Peng, C.-C.; Li, Y.; Chen, C.-L. A robust integral type backstepping controller design for control of uncertain nonlinear systems subject to disturbance. Int. J. Innov. Comput. Inf. Control 2011, 7, 2543–2560. [Google Scholar]
- Peng, C.-C. Nonlinear integral type observer design for state estimation and unknown input reconstruction. Appl. Sci. 2017, 7, 67. [Google Scholar] [CrossRef]
| Parameter | Notation | Value | Unit |
|---|---|---|---|
| Phase resistance | 10.3 | ohm | |
| Slider (rotor) mass | m | 0.171 | kg |
| Phase inductance | 1.4 | mH | |
| Pairs of poles | 1 | ||
| Pole pitch | 10 | mm | |
| Flux | 0.035 | Wb |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.Q. Observer-Based Tracking Control for Polysolenoid Linear Motor with Unknown Disturbance Load. Actuators 2020, 9, 23. https://doi.org/10.3390/act9010023
Nguyen HQ. Observer-Based Tracking Control for Polysolenoid Linear Motor with Unknown Disturbance Load. Actuators. 2020; 9(1):23. https://doi.org/10.3390/act9010023
Chicago/Turabian StyleNguyen, Hong Quang. 2020. "Observer-Based Tracking Control for Polysolenoid Linear Motor with Unknown Disturbance Load" Actuators 9, no. 1: 23. https://doi.org/10.3390/act9010023
APA StyleNguyen, H. Q. (2020). Observer-Based Tracking Control for Polysolenoid Linear Motor with Unknown Disturbance Load. Actuators, 9(1), 23. https://doi.org/10.3390/act9010023






