Active Control of Bluff-Body Flows Using Plasma Actuators
Abstract
1. Introduction
2. Flow Control Definitions and Preliminary Remarks
3. AFC Local Actuators
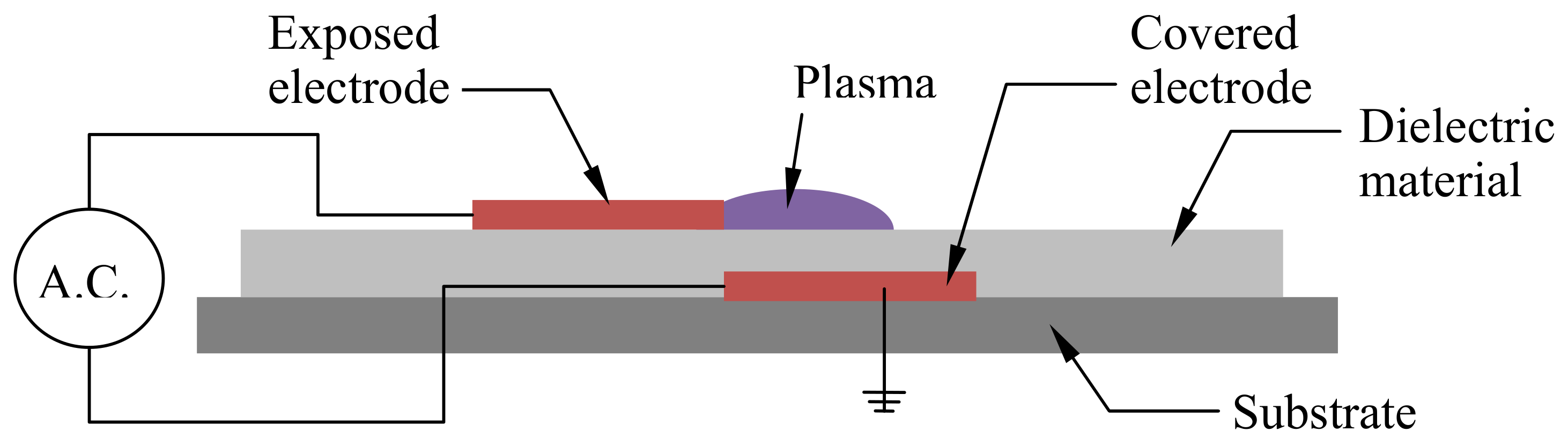
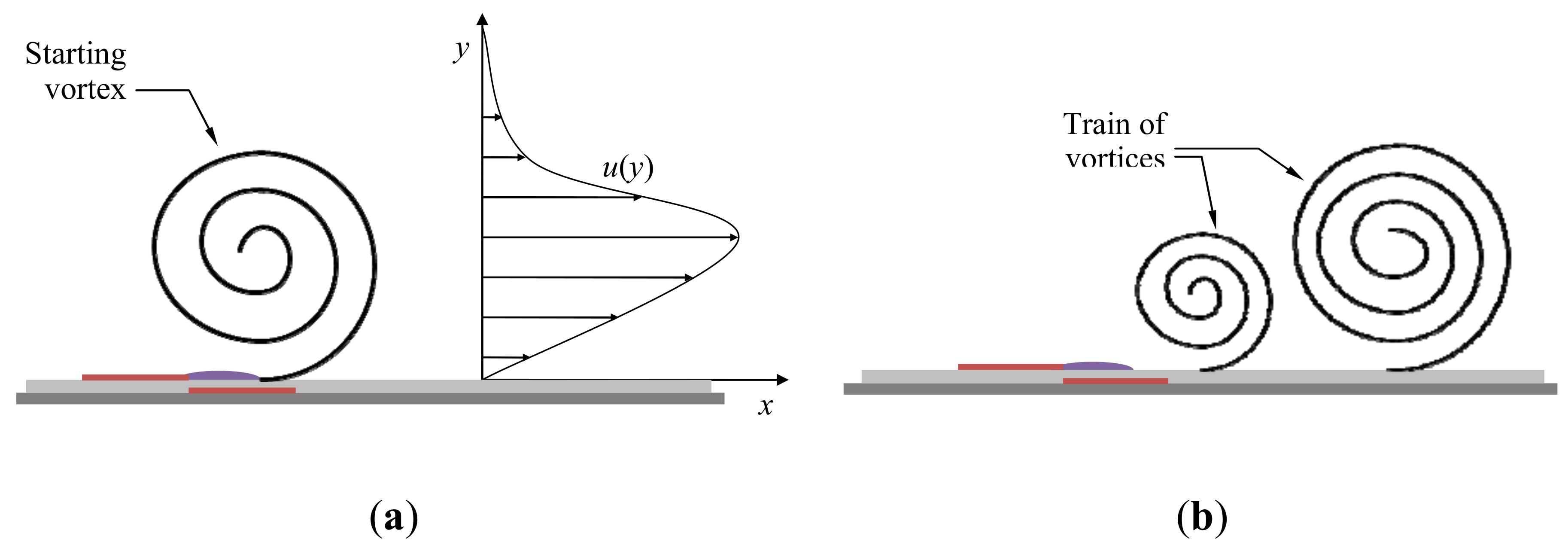
DBD Plasma Actuators
4. Fundamentals of Bluff-Body Flows—The Circular Cylinder
4.1. Stable Regime
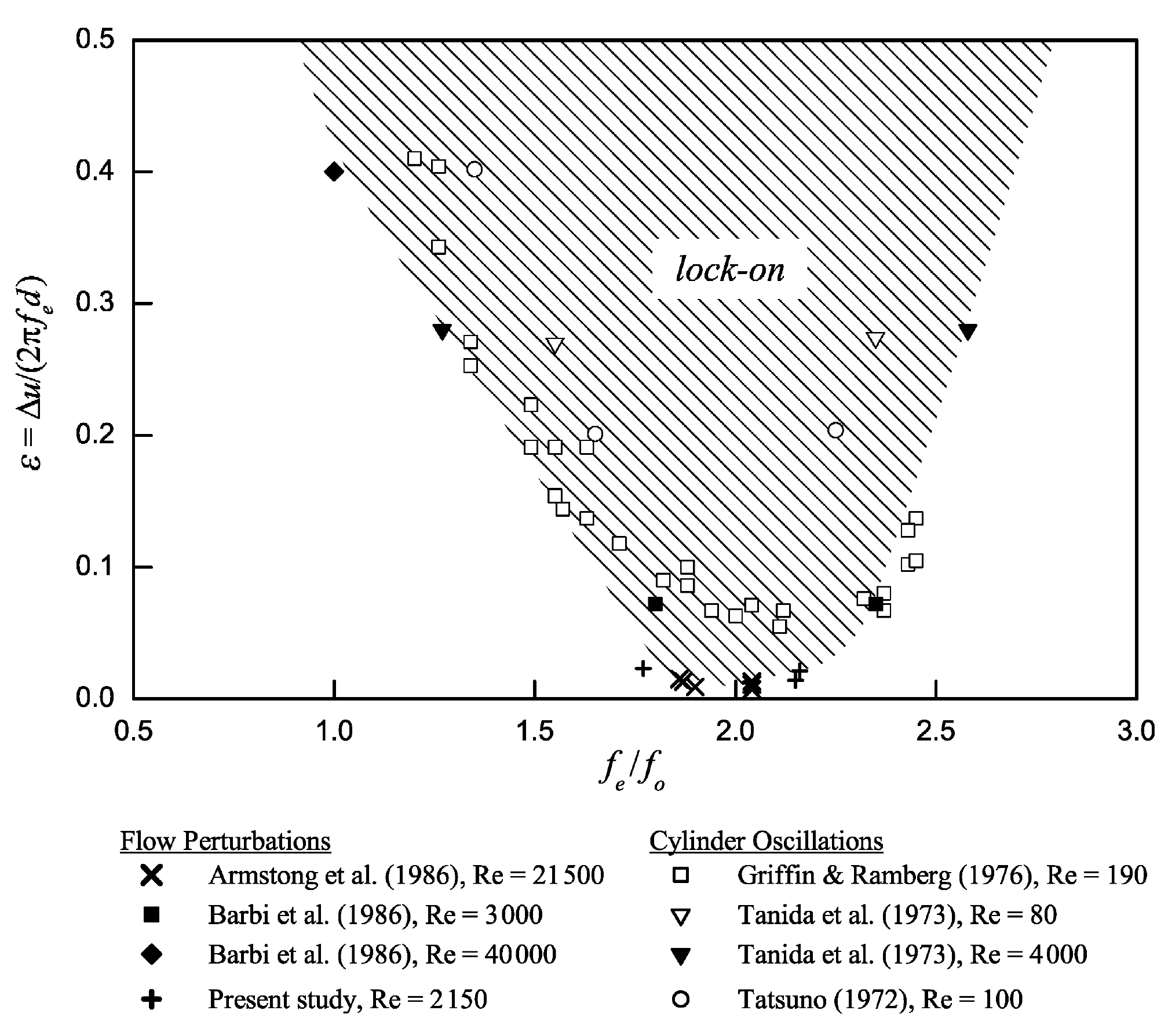
4.2. Flow Instabilities
4.3. Boundary Layer Transition
5. AFC Application on Flows Around Bluff Cylinders
5.1. Symmetric Perturbations
5.1.1. Effect of Actuator Configuration
5.1.2. Effect of Excitation Frequency
5.1.3. Effect of Antisymmetric Perturbations
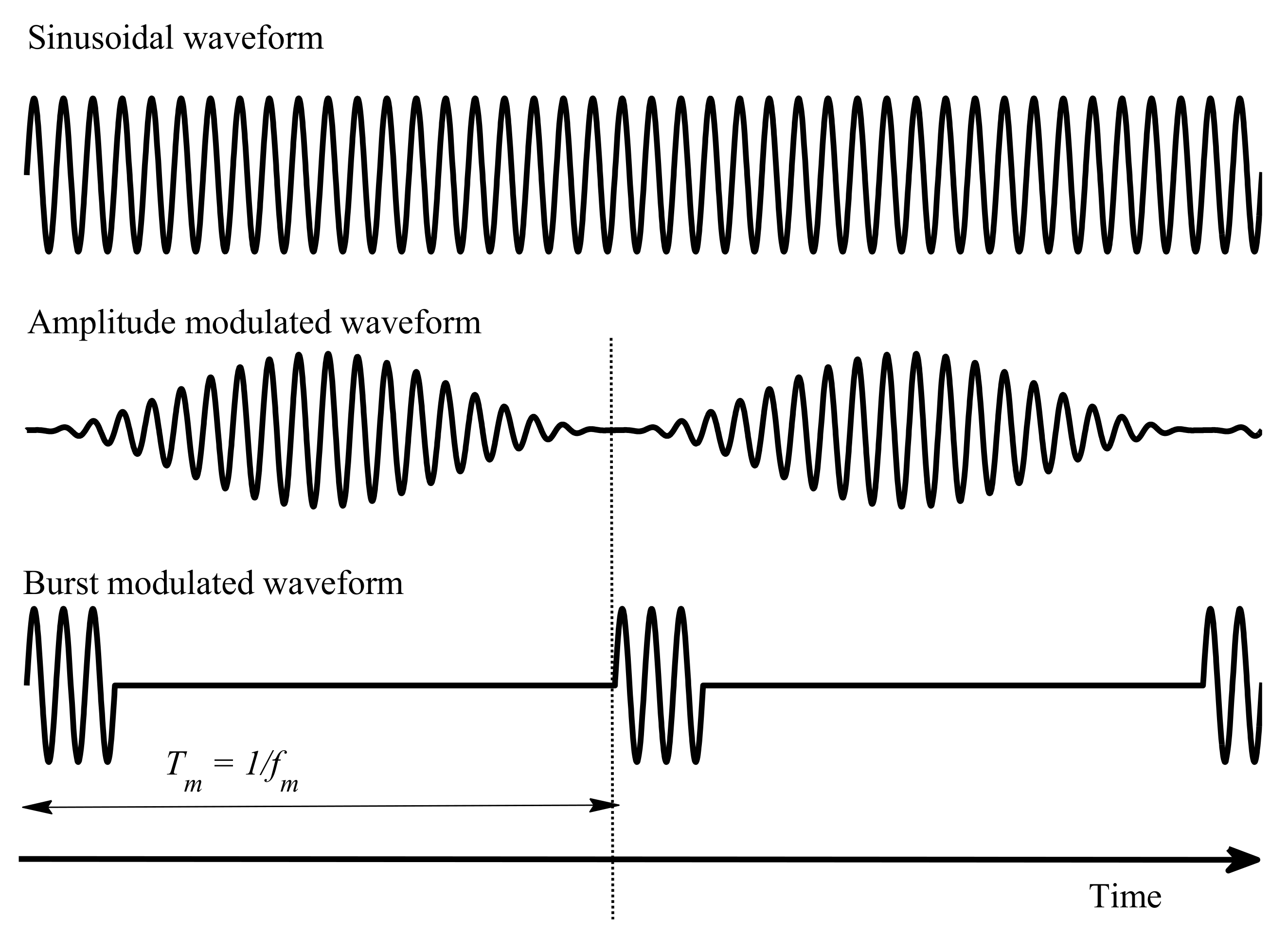
5.1.4. Effect of Waveform Modulation
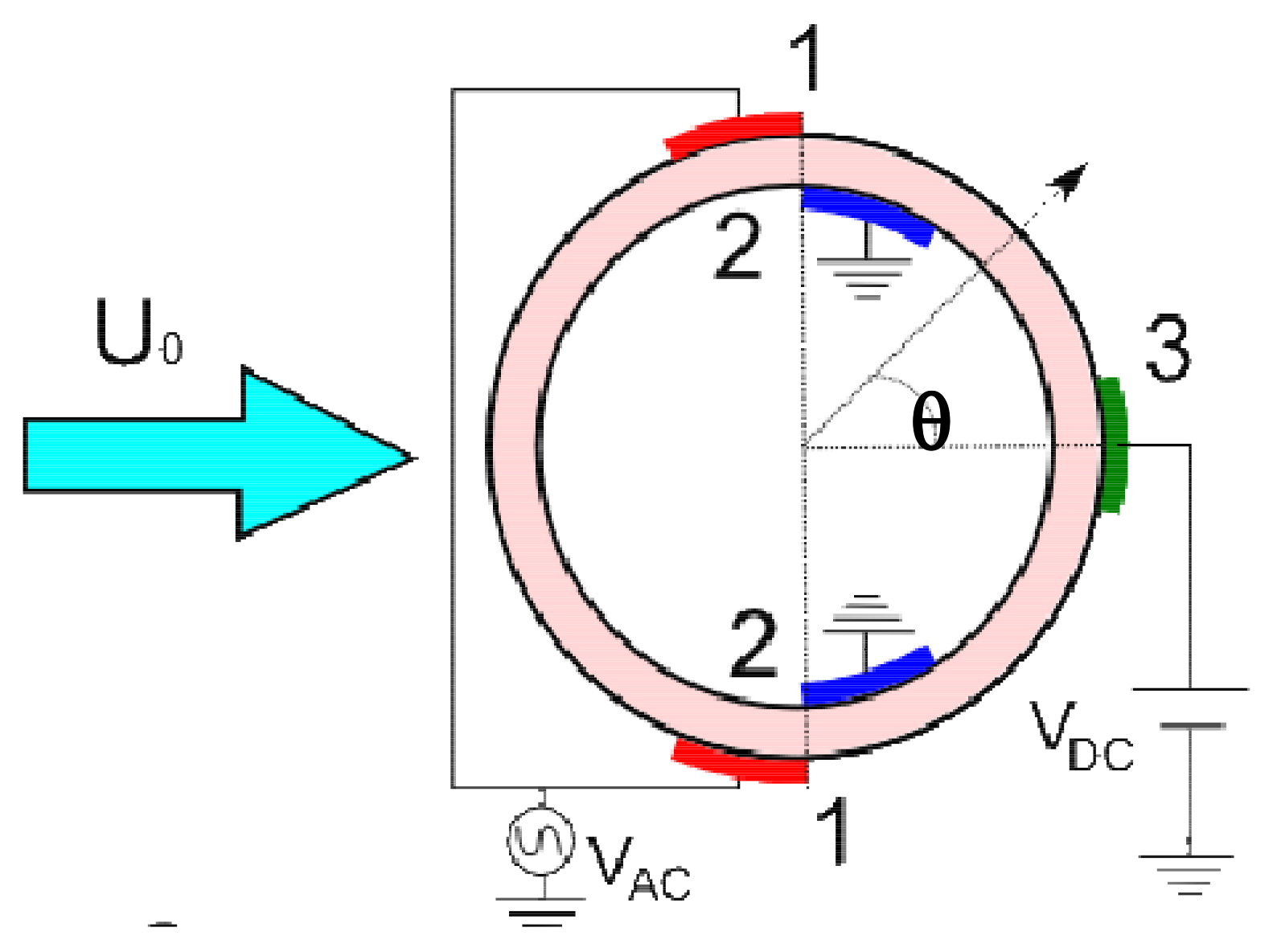
5.2. Asymmetric Perturbations
5.2.1. Continuous and Periodic Excitation
5.2.2. Transient Perturbations
6. Discussion
7. Conclusions
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| AFC | Active Flow Control |
| CFD | Computational Fluid Dynamics |
| DBD | Dielectirc Barrier Discharge |
| EHD | Electrohydrodynamic |
| PIV | Particle Image Velocimetry |
References
- Prandtl, L. Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Proceedings of the Third International Congress of Mathematicians, Heidelberg, Germany, 8–13 August 1904; pp. 484–491. [Google Scholar]
- Gad-el-Hak, M. Flow Control: Passive, Active, and Reactive Flow Management; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Joslin, R.D.; Miller, D.N. (Eds.) Fundamentals and Applications of Modern Flow Control; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2009. [Google Scholar] [CrossRef]
- Corke, T.C.; Enloe, C.L.; Wilkinson, S.P. Dielectric Barrier Discharge Plasma Actuators for Flow Control. Annu. Rev. Fluid Mech. 2010, 42, 505–529. [Google Scholar] [CrossRef]
- Cattafesta, L.N.; Sheplak, M. Actuators for Active Flow Control. Annu. Rev. Fluid Mech. 2011, 43, 247–272. [Google Scholar] [CrossRef]
- Choi, H.; Jeon, W.P.; Kim, J. Control of Flow Over a Bluff Body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef]
- Quen, L.K.; Abu, A.; Kato, N.; Muhamad, P.; Sahekhaini, A.; Abdullah, H. Investigation on the effectiveness of helical strakes in suppressing VIV of flexible riser. Appl. Ocean. Res. 2014, 44, 82–91. [Google Scholar] [CrossRef]
- Resvanis, T.; Rao, Z.; Vandiver, K. Effects of Strake Coverage and Marine Growth on Flexible Cylinder Vortex-Induced Vibrations. J. Offshore Mech. Arct. Eng. 2016, 138, 051801–051801-11. [Google Scholar] [CrossRef]
- Senga, H.; Larsen, C.M. Forced motion experiments using cylinders with helical strakes. J. Fluids Struct. 2017, 68, 279–294. [Google Scholar] [CrossRef]
- Mastrokalos, M.E.; Papadopoulos, C.I.; Kaiktsis, L. Optimal stabilization of a flow past a partially hydrophobic circular cylinder. Comput. Fluids 2015, 107, 256–271. [Google Scholar] [CrossRef]
- Huang, H.; Liu, M.; Gu, H.; Li, X.; Wu, X.; Sun, F. Effect of the slip length on the flow over a hydrophobic circular cylinder. Fluid Dyn. Res. 2018, 50, 025515. [Google Scholar] [CrossRef]
- Hasegawa, M.; Sakaue, H. Microfiber Coating for Drag Reduction by Flocking Technology. Coatings 2018, 8. [Google Scholar] [CrossRef]
- Tombazis, N.; Bearman, P.W. A study of three-dimensional aspects of vortex shedding from a bluff body with a mild geometric disturbance. J. Fluid Mech. 1997, 330, 85–112. [Google Scholar] [CrossRef]
- Shi, X.D.; Feng, L.H. Control of flow around a circular cylinder by bleed near the separation points. Exp. Fluids 2015, 56, 214. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; De Luca, C.; Ficarella, A.; Marra, F. Comparison between synthetic jets and continuous jets for active flow control: Application on a NACA 0015 and a compressor stator cascade. Aerosp. Sci. Technol. 2015, 43, 256–280. [Google Scholar] [CrossRef]
- Chen, W.L.; Li, H.; Hu, H. An experimental study on a suction flow control method to reduce the unsteadiness of the wind loads acting on a circular cylinder. Exp. Fluids 2014, 55, 1707. [Google Scholar] [CrossRef]
- Gao, D.; Chen, G.; Chen, W.; Huang, Y.; Li, H. Active control of circular cylinder flow with windward suction and leeward blowing. Exp. Fluids 2019, 60, 26. [Google Scholar] [CrossRef]
- Blevins, R.D. The effect of sound on vortex shedding from cylinders. J. Fluid Mech. 1985, 161, 217–237. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S.; Yianneskis, M. The effect of flow perturbations on the near wake characteristics of a circular cylinder. J. Fluids Struct. 2003, 18, 367–386. [Google Scholar] [CrossRef]
- Hong, S.; Huang, G.; Yang, Y.; Liu, Z. Introduction of DMD Method to Study the Dynamic Structures of a Three-Dimensional Centrifugal Compressor with and without Flow Control. Energies 2018, 11. [Google Scholar] [CrossRef]
- Chen, J.; Lu, W.; Huang, G.; Zhu, J.; Wang, J. Research on Pulsed Jet Flow Control without External Energy in a Blade Cascade. Energies 2017, 10. [Google Scholar] [CrossRef]
- Williams, J.F.; Zhao, B. The active control of vortex shedding. J. Fluids Struct. 1989, 3, 115–122. [Google Scholar] [CrossRef]
- Roussopoulos, K. Feedback control of vortex shedding at low Reynolds numbers. J. Fluid Mech. 1993, 248, 267–296. [Google Scholar] [CrossRef]
- Muddada, S.; Patnaik, B. An active flow control strategy for the suppression of vortex structures behind a circular cylinder. Eur. J. Mech. Fluids 2010, 29, 93–104. [Google Scholar] [CrossRef]
- Leontini, J.S.; Lo Jacono, D.; Thompson, M.C. Wake states and frequency selection of a streamwise oscillating cylinder. J. Fluid Mech. 2013, 730, 162–192. [Google Scholar] [CrossRef]
- Leontini, J.S.; Lo Jacono, D.; Thompson, M.C. A numerical study of an inline oscillating cylinder in a free stream. J. Fluid Mech. 2011, 688, 551–568. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. Reduction of the loads on a cylinder undergoing harmonic in-line motion. Phys. Fluids 2009, 21, 083103. [Google Scholar] [CrossRef]
- Perdikaris, P.G.; Kaiktsis, L.; Triantafyllou, G.S. Chaos in a cylinder wake due to forcing at the Strouhal frequency. Phys. Fluids 2009, 21, 101705. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.; Lawrence, K.; Kocabiyik, S. Forced streamwise oscillations of a circular cylinder: Locked-on modes and resulting fluid forces. J. Fluids Struct. 2007, 23, 681–701. [Google Scholar] [CrossRef]
- Anagnostopoulos, P. Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 1: Lock-in zone, hydrodynamic forces and wake geometry. J. Fluids Struct. 2000, 14, 819–851. [Google Scholar] [CrossRef]
- Leontini, J.S.; Stewart, B.E.; Thompson, M.C.; Hourigan, K. Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 2006, 18, 067101. [Google Scholar] [CrossRef]
- Carberry, J.; Sheridan, J.; Rockwell, D. Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 2005, 538, 31–69. [Google Scholar] [CrossRef]
- Williamson, C.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Ongoren, A.; Rockwell, D. Flow structure from an oscillating cylinder Part 1. Mechanisms of phase shift and recovery in the near wake. J. Fluid Mech. 1988, 191, 197–223. [Google Scholar] [CrossRef]
- Kumar, S.; Lopez, C.; Probst, O.; Francisco, G.; Askari, D.; Yang, Y. Flow past a rotationally oscillating cylinder. J. Fluid Mech. 2013, 735, 307–346. [Google Scholar] [CrossRef]
- Baek, S.J.; Sung, H.J. Quasi-periodicity in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 2000, 408, 275–300. [Google Scholar] [CrossRef][Green Version]
- Baek, S.J.; Sung, H.J. Numerical simulation of the flow behind a rotary oscillating circular cylinder. Phys. Fluids 1998, 10, 869–876. [Google Scholar] [CrossRef]
- Tokumaru, P.T.; Dimotakis, P.E. Rotary oscillation control of a cylinder wake. J. Fluid Mech. 1991, 224, 77–90. [Google Scholar] [CrossRef]
- Jeon, D.; Gharib, M. On circular cylinders undergoing two-degree-of-freedom forced motions. J. Fluids Struct. 2001, 15, 533–541. [Google Scholar] [CrossRef]
- Ongoren, A.; Rockwell, D. Flow structure from an oscillating cylinder Part 2. Mode competition in the near wake. J. Fluid Mech. 1988, 191, 225–245. [Google Scholar] [CrossRef]
- Baranyi, L. Numerical simulation of flow around an orbiting cylinder at different ellipticity values. J. Fluids Struct. 2008, 24, 883–906. [Google Scholar] [CrossRef]
- Nazarinia, M.; Lo Jacono, D.; Thompson, M.C.; Sheridan, J. Flow behind a cylinder forced by a combination of oscillatory translational and rotational motions. Phys. Fluids 2009, 21, 051701. [Google Scholar] [CrossRef]
- Detemple-Laake, E.; Eckelmann, H. Phenomenology of Kármán vortex streets in oscillatory flow. Exp. Fluids 1989, 7, 217–227. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Liang, C. Dynamic response of a turbulent cylinder wake to sinusoidal inflow perturbations across the vortex lock-on range. Phys. Fluids 2011, 23, 075102. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, J.Y.; Park, N.; Bae, J.H.; Yoo, J.Y. Direct numerical simulation of vortex synchronization due to small perturbations. J. Fluid Mech. 2009, 634, 61–90. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S. Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations. J. Fluids Struct. 2007, 23, 1047–1063. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S.; Yianneskis, M. Bimodal vortex shedding in a perturbed cylinder wake. Phys. Fluids 2007, 19, 011701. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S.; Yianneskis, M. The timing of vortex shedding in a cylinder wake imposed by periodic inflow perturbations. J. Fluid Mech. 2005, 543, 45–55. [Google Scholar] [CrossRef]
- Kim, W.; Yoo, J.Y.; Sung, J. Dynamics of vortex lock-on in a perturbed cylinder wake. Phys. Fluids 2006, 18, 074103. [Google Scholar] [CrossRef]
- Meneghini, J.; Bearman, P. Numerical Simulation of High Amplitude Oscillatory Flow About a Circular Cylinder. J. Fluids Struct. 1995, 9, 435–455. [Google Scholar] [CrossRef]
- Barbi, C.; Favier, D.P.; Maresca, C.A.; Telionis, D.P. Vortex shedding and lock-on of a circular cylinder in oscillatory flow. J. Fluid Mech. 1986, 170, 527–544. [Google Scholar] [CrossRef]
- Gibeau, B.; Koch, C.R.; Ghaemi, S. Active control of vortex shedding from a blunt trailing edge using oscillating piezoelectric flaps. Phys. Rev. Fluids 2019, 4, 054704. [Google Scholar] [CrossRef]
- Saenz-Aguirre, A.; Fernandez-Gamiz, U.; Zulueta, E.; Ulazia, A.; Martinez-Rico, J. Optimal Wind Turbine Operation by Artificial Neural Network-Based Active Gurney Flap Flow Control. Sustainability 2019, 11, 2809. [Google Scholar] [CrossRef]
- Oualli, H.; Hanchi, S.; Bouabdellah, A.; Askovic, R.; Gad-El-Hak, M. Interaction between the near wake and the cross-section variation of a circular cylinder in uniform flow. Exp. Fluids 2008, 44, 807–818. [Google Scholar] [CrossRef]
- Aissa, M.; Bouabdallah, A.; Oualli, H. Radial Deformation Frequency Effect on the Three-Dimensional Flow in the Cylinder Wake. ASME J. Fluids Eng. 2014, 137, 011104–011104-11. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C. Numerical study of flow characteristics behind a stationary circular cylinder with a flapping plate. Phys. Fluids 2011, 23, 073601. [Google Scholar] [CrossRef]
- Shukla, S.; Govardhan, R.; Arakeri, J. Flow over a cylinder with a hinged-splitter plate. J. Fluids Struct. 2009, 25, 713–720. [Google Scholar] [CrossRef]
- Akaydin, H.D.; Elvin, N.; Andreopoulos, Y. The performance of a self-excited fluidic energy harvester. Smart Mater. Struct. 2012, 21, 025007. [Google Scholar] [CrossRef]
- Glezer, A.; Amitay, M. Syntetic Jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y.; Jia, M.; Zong, H.; Cui, W.; Liang, H.; Li, Y. Influence of the discharge location on the performance of a three-electrode plasma synthetic jet actuator. Sens. Actuators Phys. 2015, 235, 71–79. [Google Scholar] [CrossRef]
- Zong, H.; Chiatto, M.; Kotsonis, M.; De Luca, L. Plasma Synthetic Jet Actuators for Active Flow Control. Actuators 2018, 7. [Google Scholar] [CrossRef]
- Woszidlo, R.; Ostermann, F.; Nayeri, C.N.; Paschereit, C.O. The time-resolved natural flow field of a fluidic oscillator. Exp. Fluids 2015, 56, 125. [Google Scholar] [CrossRef]
- Gregory, J.; Tomac, M.N. A Review of Fluidic Oscillator Development. In Proceedings of the 43rd Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L.; Orlov, D.M. Single dielectric barrier discharge plasma enhanced aerodynamics: physics, modeling and applications. Exp. Fluids 2009, 46, 1–26. [Google Scholar] [CrossRef]
- Thomas, F.O.; Corke, T.C.; Iqbal, M.; Kozlov, A.; Schatzman, D. Optimization of Dielectric Barrier Discharge Plasma Actuators for Active Aerodynamic Flow Control. AIAA 2009, 47, 2169–2178. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Sciolti, A.; Campilongo, S.; Ficarella, A. Flame Structure and Chemiluminescence Emissions of Inverse Diffusion Flames under Sinusoidally Driven Plasma Discharges. Energies 2017, 10, 334. [Google Scholar] [CrossRef]
- Pescini, E.; Marra, F.; De Giorgi, M.; Francioso, L.; Ficarella, A. Investigation of the boundary layer characteristics for assessing the DBD plasma actuator control of the separated flow at low Reynolds numbers. Exp. Therm. Fluid Sci. 2017, 81, 482–498. [Google Scholar] [CrossRef]
- Pescini, E.; Martínez, D.; De Giorgi, M.; Ficarella, A. Characterization of the effects of a dielectric barrier discharge plasma actuator on a coaxial jet in a Bunsen burner. Exp. Therm. Fluid Sci. 2018, 91, 292–305. [Google Scholar] [CrossRef]
- Robinson, M. A History of the Electric Wind. Am. J. Phys. 1962, 30, 366–372. [Google Scholar] [CrossRef]
- Whalley, R.D.; Choi, K.S. The starting vortex in quiescent air induced by dielectric barrier discharge plasma. J. Fluid Mech. 2012, 703, 192–203. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I.J. The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Mishra, B.K.; Panigrahi, P.K. Formation and characterization of the vortices generated by a DBD plasma actuator in burst mode. Phys. Fluids 2017, 29, 024104. [Google Scholar] [CrossRef]
- Vernet, J.A.; Örlü, R.; Alfredsson, P.H. Flow separation control by dielectric barrier discharge plasma actuation via pulsed momentum injection. AIP Adv. 2018, 8, 075229. [Google Scholar] [CrossRef]
- Jukes, T.N.; Choi, K.S. Flow control around a circular cylinder using pulsed dielectric barrier discharge surface plasma. Phys. Fluids 2009, 21, 084103. [Google Scholar] [CrossRef]
- Santhanakrishnan, A.; Jacob, J.; Suzen, Y. Flow Control Using Plasma Actuators and Linear/Annular Plasma Synthetic Jet Actuators. In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar] [CrossRef]
- Wang, J.J.; Choi, K.S.; Feng, L.H.; Jukes, T.N.; Whalley, R.D. Recent developments in DBD plasma flow control. Prog. Aerosp. Sci. 2013, 62, 52–78. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Response of a circular cylinder wake to a symmetric actuation by nonthermal plasma discharges. Exp. Fluids 2013, 54, 1467. [Google Scholar] [CrossRef]
- Moreau, E. Airflow control by nonthermal plasma actuators. J. Phys. Appl. Phys. 2007, 40, 605–636. [Google Scholar] [CrossRef]
- Kriegseis, J.; Möller, B.; Grundmann, S.; Tropea, C. Capacitance and power consumption quantification of dielectric barrier discharge (DBD) plasma actuators. J. Electrost. 2011, 69, 302–312. [Google Scholar] [CrossRef]
- Kotsonis, M. Diagnostics for characterization of plasma actuators. Meas. Sci. Technol. 2015, 26, 092001. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1846. [Google Scholar] [CrossRef]
- Soloviev, V.R.; Krivtsov, V.M. Surface barrier discharge modelling for aerodynamic applications. J. Phys. Appl. Phys. 2009, 42, 125208. [Google Scholar] [CrossRef]
- Mertz, B.; Corke, T. Single-dielectric barrier discharge plasma actuator modelling and validation. J. Fluid Mech. 2011, 669, 557–583. [Google Scholar] [CrossRef]
- Kriegseis, J.; Schwarz, C.; Tropea, C.; Grundmann, S. Velocity-information-based force-term estimation of dielectric-barrier discharge plasma actuators. J. Phys. Appl. Phys. 2013, 46, 055202. [Google Scholar] [CrossRef]
- Maden, I.; Maduta, R.; Kriegseis, J.; Jakirlić, S.; Schwarz, C.; Grundmann, S.; Tropea, C. Experimental and computational study of the flow induced by a plasma actuator. Int. J. Heat Fluid Flow 2013, 41, 80–89. [Google Scholar] [CrossRef]
- Kotsonis, M.; Ghaemi, S.; Veldhuis, L.; Scarano, F. Measurement of the body force field of plasma actuators. J. Phys. Appl. Phys. 2011, 44, 045204. [Google Scholar] [CrossRef]
- Debien, A.; Benard, N.; David, L.; Moreau, E. Unsteady aspect of the electrohydrodynamic force produced by surface dielectric barrier discharge actuators. Appl. Phys. Lett. 2012, 100, 013901. [Google Scholar] [CrossRef]
- Cattafesta, L.N. Design of Synthetic Jets. In Syntetic Jets: Fundamentals and Applications; Mohseni, K., Mittal, R., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 49–97. [Google Scholar]
- Feng, L.H.; Wang, J.J.; Pan, C. Effect of novel synthetic jet on wake vortex shedding modes of a circular cylinder. J. Fluids Struct. 2010, 26, 900–917. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J. The virtual aeroshaping enhancement by synthetic jets with variable suction and blowing cycles. Phys. Fluids 2014, 26, 014105. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Bouris, D. The effect of nonharmonic forcing on bluff-body aerodynamics at a low Reynolds number. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 245–252. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Role of the electric waveform supplying a dielectric barrier discharge plasma actuator. Appl. Phys. Lett. 2012, 100, 193503. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Capabilities of the dielectric barrier discharge plasma actuator for multi-frequency excitations. J. Phys. Appl. Phys. 2010, 43, 145201. [Google Scholar] [CrossRef]
- Triantafyllou, G.S.; Kupfer, K.; Bers, A. Absolute instabilities and self-sustained oscillations in the wake of circular cylinders. Phys. Rev. Lett. 1987, 59, 1914–1917. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex Dynamics in the Cylinder Wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Gerrard, J.H. The wakes of cylindrical bluff bodies at low Reynolds number. Math. Phys. Sci. 1978, 288, 351–382. [Google Scholar] [CrossRef]
- Thompson, M.C.; Hourigan, K. The shear-layer instability of a circular cylinder wake. Phys. Fluids 2005, 17, 021702. [Google Scholar] [CrossRef]
- Sosa, R.; Artana, G.; Benard, N.; Moreau, E. Mean lift generation on cylinders induced with plasma actuators. Exp. Fluids 2011, 51, 853–860. [Google Scholar] [CrossRef]
- Artana, G.; Sosa, R.; Moreau, E.; Touchard, G. Control of the near-wake flow around a circular cylinder with electrohydrodynamic actuators. Exp. Fluids 2003, 35, 580–588. [Google Scholar] [CrossRef]
- Hyun, K.T.; Chun, C.H. The wake flow control behind a circular cylinder using ion wind. Exp. Fluids 2003, 35, 541–552. [Google Scholar] [CrossRef]
- Sung, Y.; Kim, W.; Mungal, M.G.; Cappelli, M.A. Aerodynamic modification of flow over bluff objects by plasma actuation. Exp. Fluids 2006, 41, 479–486. [Google Scholar] [CrossRef]
- Kopiev, V.F.; Kazansky, P.N.; Kopiev, V.A.; Moralev, I.A.; Zaytsev, M.Y. HF DBD plasma actuators for reduction of cylinder noise in flow. J. Phys. Appl. Phys. 2017, 50, 475204. [Google Scholar] [CrossRef]
- Sosa, R.; D’Adamo, J.; Artana, G. Circular cylinder drag reduction by three-electrode plasma actuators. J. Phys. Conf. Ser. 2009, 166, 012015. [Google Scholar] [CrossRef]
- D’Adamo, J.; Leonardo, L.; Castro, F.; Sosa, R.; Duriez, T.; Artana, G. Circular Cylinder Drag Reduction By Three-Electrode Plasma Symmetric Forcing. ASME J. Fluids Eng. 2017, 139, 061202–061202-14. [Google Scholar] [CrossRef]
- Zhang, X.; Choi, K.S.; Huang, Y.; Li, H. Flow control over a circular cylinder using virtual moving surface boundary layer control. Exp. Fluids 2019, 60, 104. [Google Scholar] [CrossRef]
- Thomas, F.O.; Kozlov, A.; Corke, T.C. Plasma Actuators for Cylinder Flow Control and Noise Reduction. AIAA 2008, 46, 1921–1931. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Bouris, D. Vortex synchronization in the cylinder wake due to harmonic and nonharmonic perturbations. J. Fluid Mech. 2016, 804, 248–277. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J. Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. J. Fluid Mech. 2010, 662, 232–259. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J. Modification of a circular cylinder wake with synthetic jet: Vortex shedding modes and mechanism. Eur. J. Mech. Fluids 2014, 43, 14–32. [Google Scholar] [CrossRef]
- Ma, L.Q.; Feng, L.H. Vortex formation and evolution for flow over a circular cylinder excited by symmetric synthetic jets. Exp. Therm. Fluid Sci. 2019, 104, 89–104. [Google Scholar] [CrossRef]
- Jukes, T.N.; Choi, K.S. Control of unsteady flow separation over a circular cylinder using dielectric barrier discharge surface plasma. Phys. Fluids 2009, 21, 094106. [Google Scholar] [CrossRef]
- Wang, C.; Tang, H.; Yu, S.C.M.; Duan, F. Lock-on of vortex shedding to a pair of synthetic jets with phase difference. Phys. Rev. Fluids 2017, 2, 104701. [Google Scholar] [CrossRef]
- McLaughlin, T.; Munska, M.; Vaeth, J.; Dauwalter, T.; Goode, J.; Siegel, S. Plasma-Based Actuators for Cylinder Wake Vortex Control. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S. Flow structure in the locked-on wake of a circular cylinder in pulsating flow: Effect of forcing amplitude. Int. J. Heat Fluid Flow 2008, 29, 1567–1576. [Google Scholar] [CrossRef]
- Perrin, R.; Braza, M.; Cid, E.; Cazin, S.; Chassaing, P.; Mockett, C.; Reimann, T.; Thiele, F. Coherent and turbulent process analysis in the flow past a circular cylinder at high Reynolds number. J. Fluids Struct. 2008, 24, 1313–1325. [Google Scholar] [CrossRef]
- Kourentis, L.; Konstantinidis, E. Uncovering large-scale coherent structures in natural and forced turbulent wakes by combining PIV, POD, and FTLE. Exp. Fluids 2012, 52, 749–763. [Google Scholar] [CrossRef]
- Jukes, T.N.; Choi, K.S. Long Lasting Modifications to Vortex Shedding Using a Short Plasma Excitation. Phys. Rev. Lett. 2009, 102, 254501. [Google Scholar] [CrossRef]
- Xu, S.J.; Zhou, Y.; Wang, M.H. A symmetric binary-vortex street behind a longitudinally oscillating cylinder. J. Fluid Mech. 2006, 556, 27–43. [Google Scholar] [CrossRef]
- Kim, K.H.; Choi, J.I. Lock-in regions of laminar flows over a streamwise oscillating circular cylinder. J. Fluid Mech. 2019, 858, 315–351. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J.; Pan, C. Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control. Phys. Fluids 2011, 23, 014106. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J. Synthetic jet control of separation in the flow over a circular cylinder. Exp. Fluids 2012, 53, 467–480. [Google Scholar] [CrossRef]
- Ma, L.; Feng, L. Experimental investigation on control of vortex shedding mode of a circular cylinder using synthetic jets placed at stagnation points. Sci. China Technol. Sci. 2013, 56, 158–170. [Google Scholar] [CrossRef]
- Liu, Y.G.; Feng, L.H. Suppression of lift fluctuations on a circular cylinder by inducing the symmetric vortex shedding mode. J. Fluids Struct. 2015, 54, 743–759. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantinidis, E. Active Control of Bluff-Body Flows Using Plasma Actuators. Actuators 2019, 8, 66. https://doi.org/10.3390/act8030066
Konstantinidis E. Active Control of Bluff-Body Flows Using Plasma Actuators. Actuators. 2019; 8(3):66. https://doi.org/10.3390/act8030066
Chicago/Turabian StyleKonstantinidis, Efstathios. 2019. "Active Control of Bluff-Body Flows Using Plasma Actuators" Actuators 8, no. 3: 66. https://doi.org/10.3390/act8030066
APA StyleKonstantinidis, E. (2019). Active Control of Bluff-Body Flows Using Plasma Actuators. Actuators, 8(3), 66. https://doi.org/10.3390/act8030066




