Structural-Parametric Model and Diagram of a Multilayer Electromagnetoelastic Actuator for Nanomechanics
Abstract
:1. Introduction
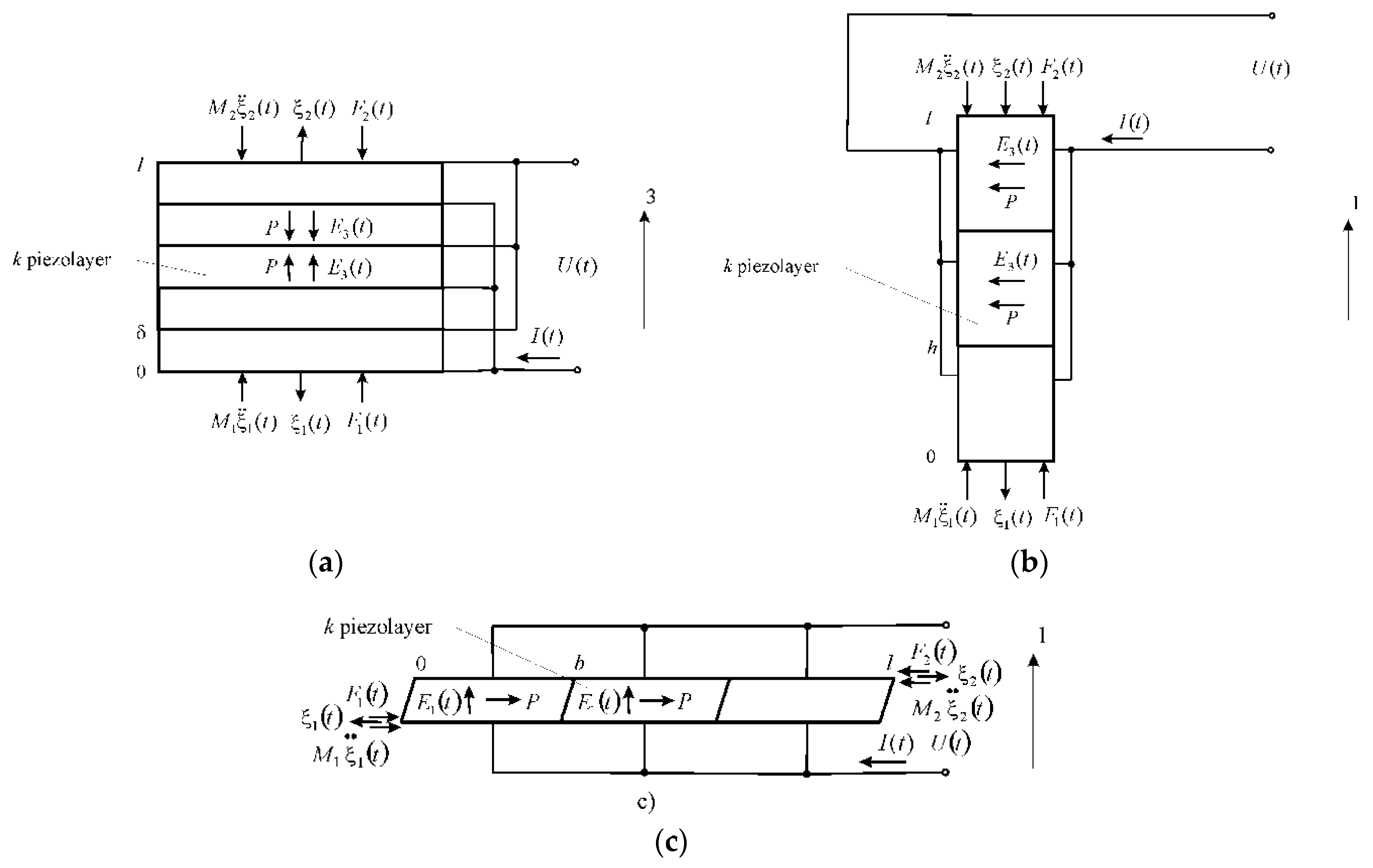
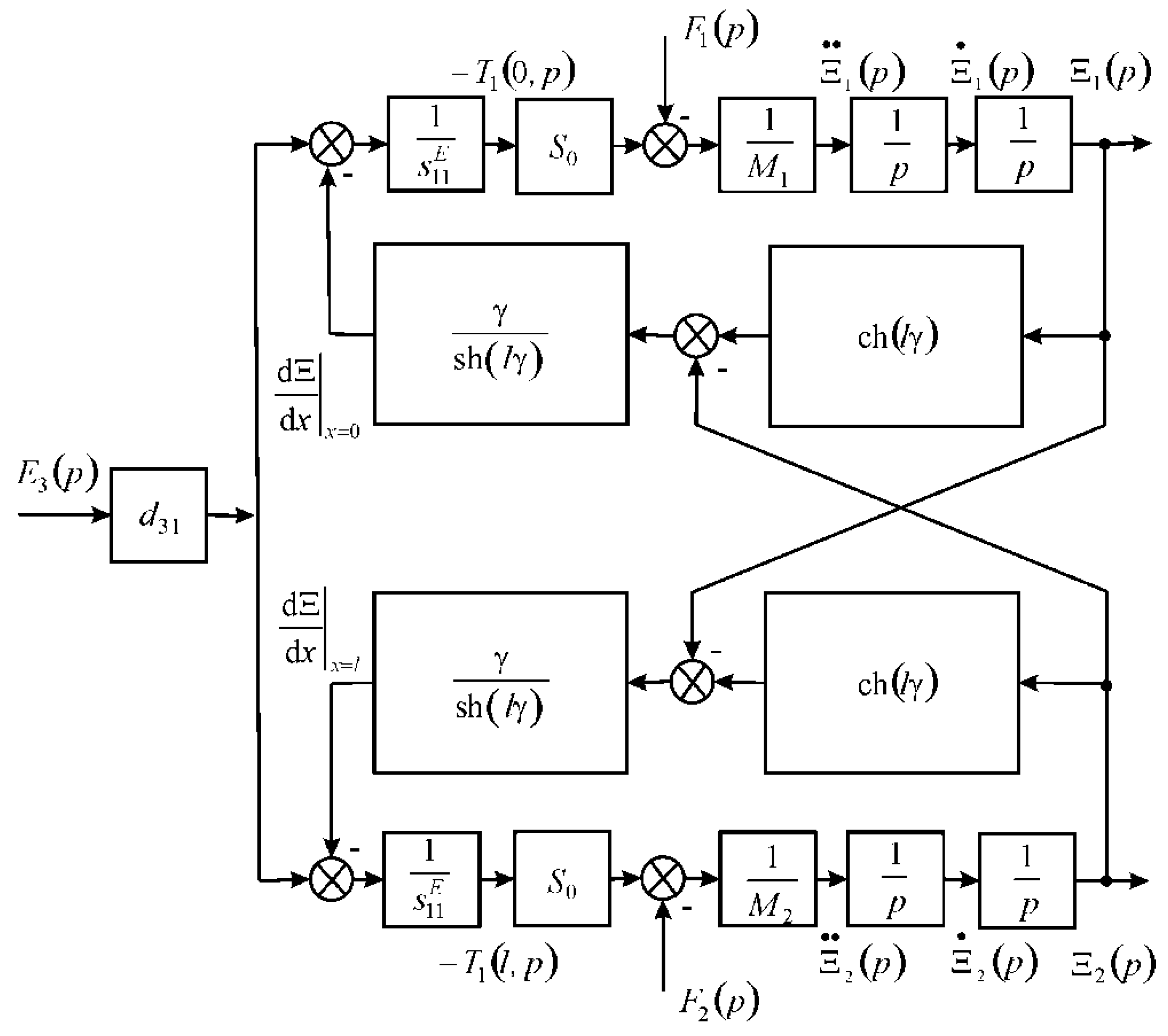
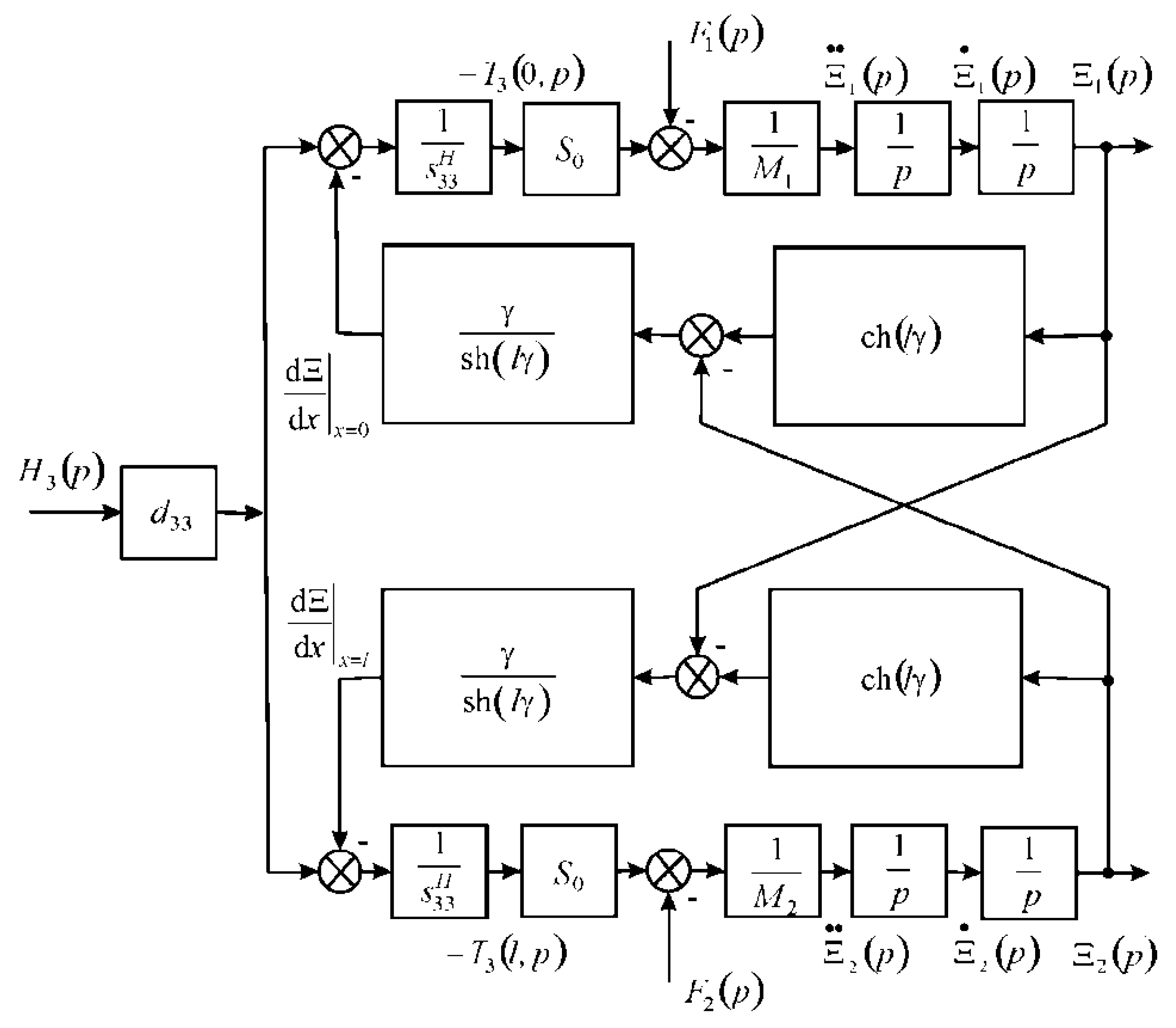
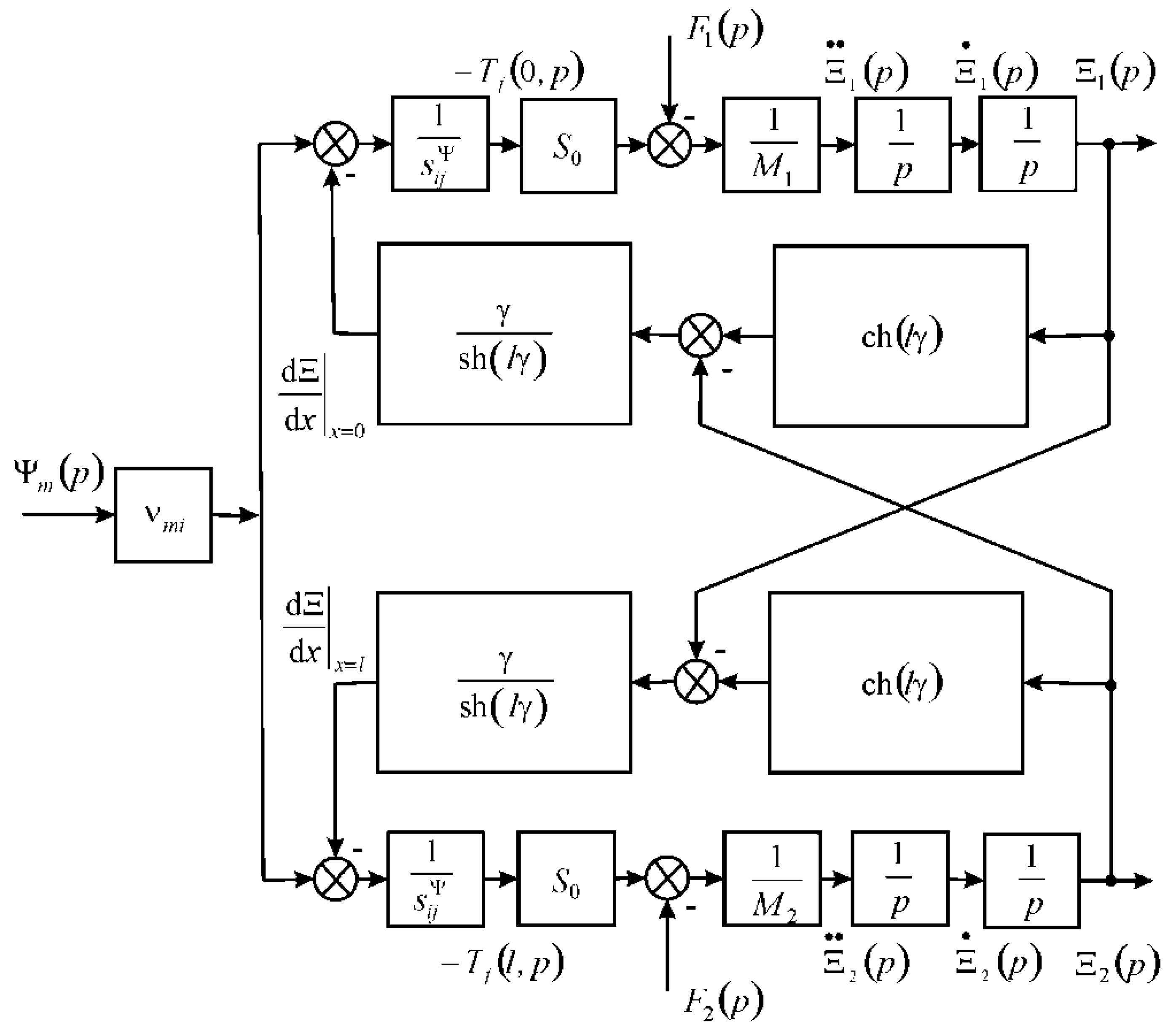
2. Parametric Structural Schematic Diagram of the Multilayer Electromagnetoelastic Actuator
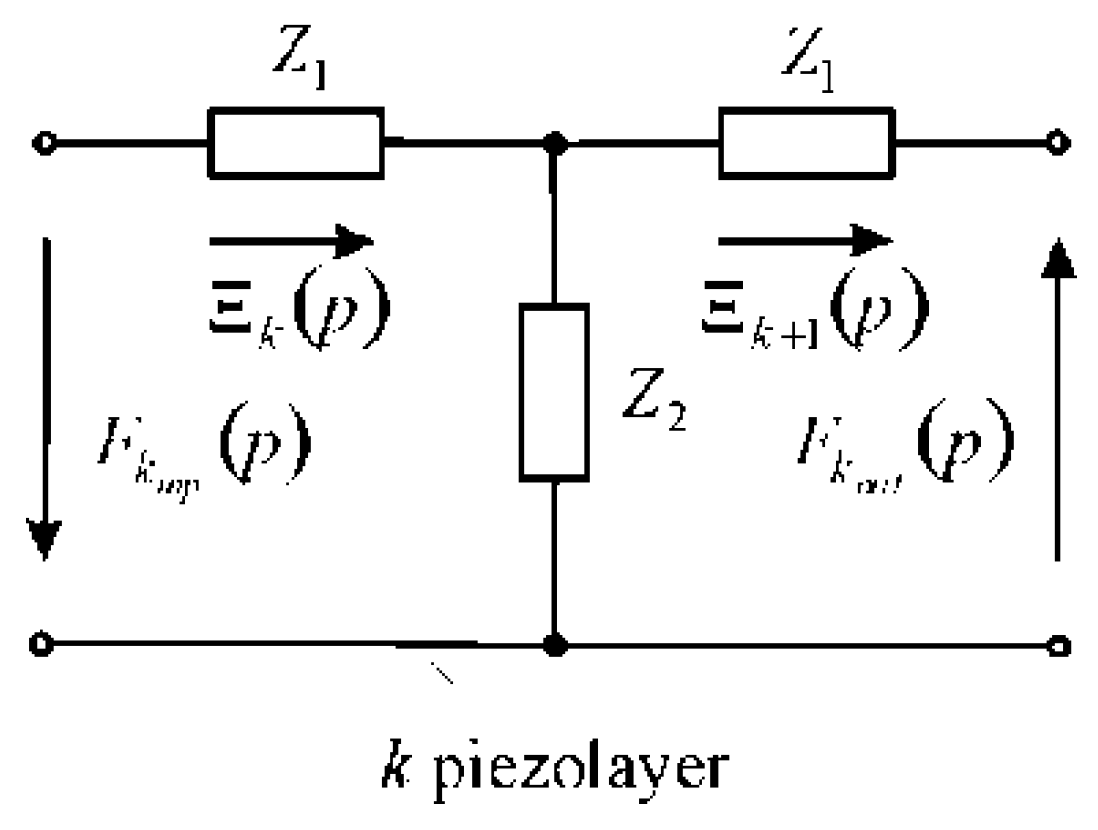
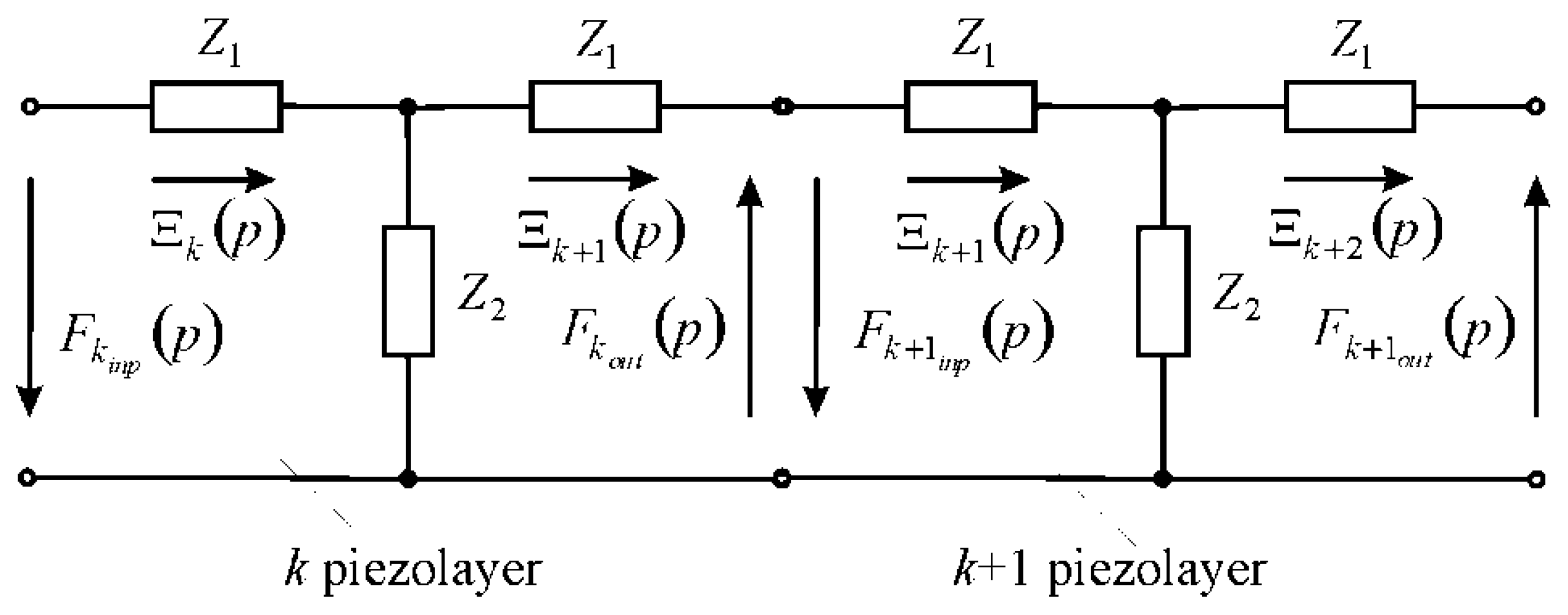
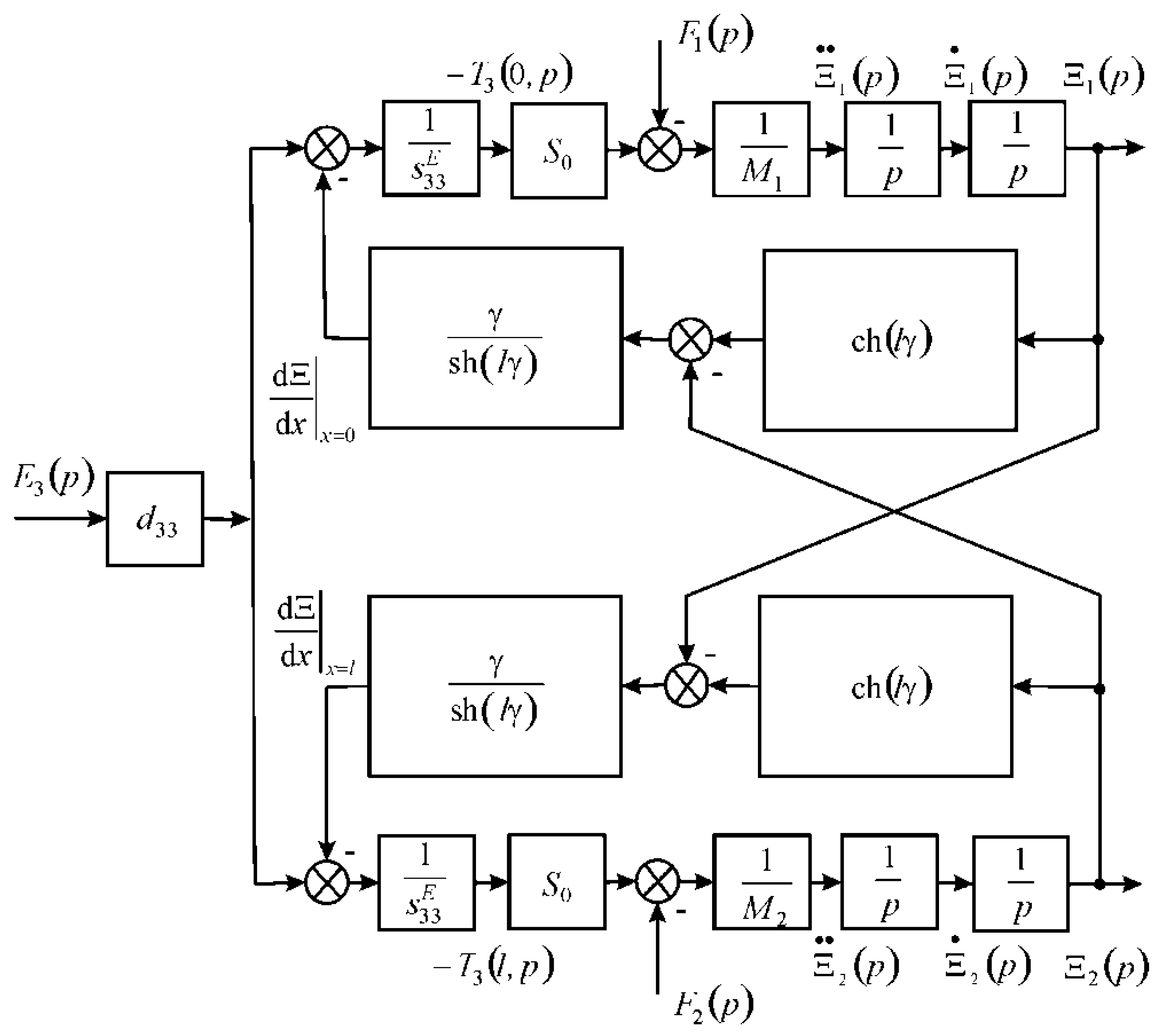
3. Matrix Transfer Function of the Multilayer Electromagnetoelastic Actuator
- ,
- ,
- ,
- ,
- ,
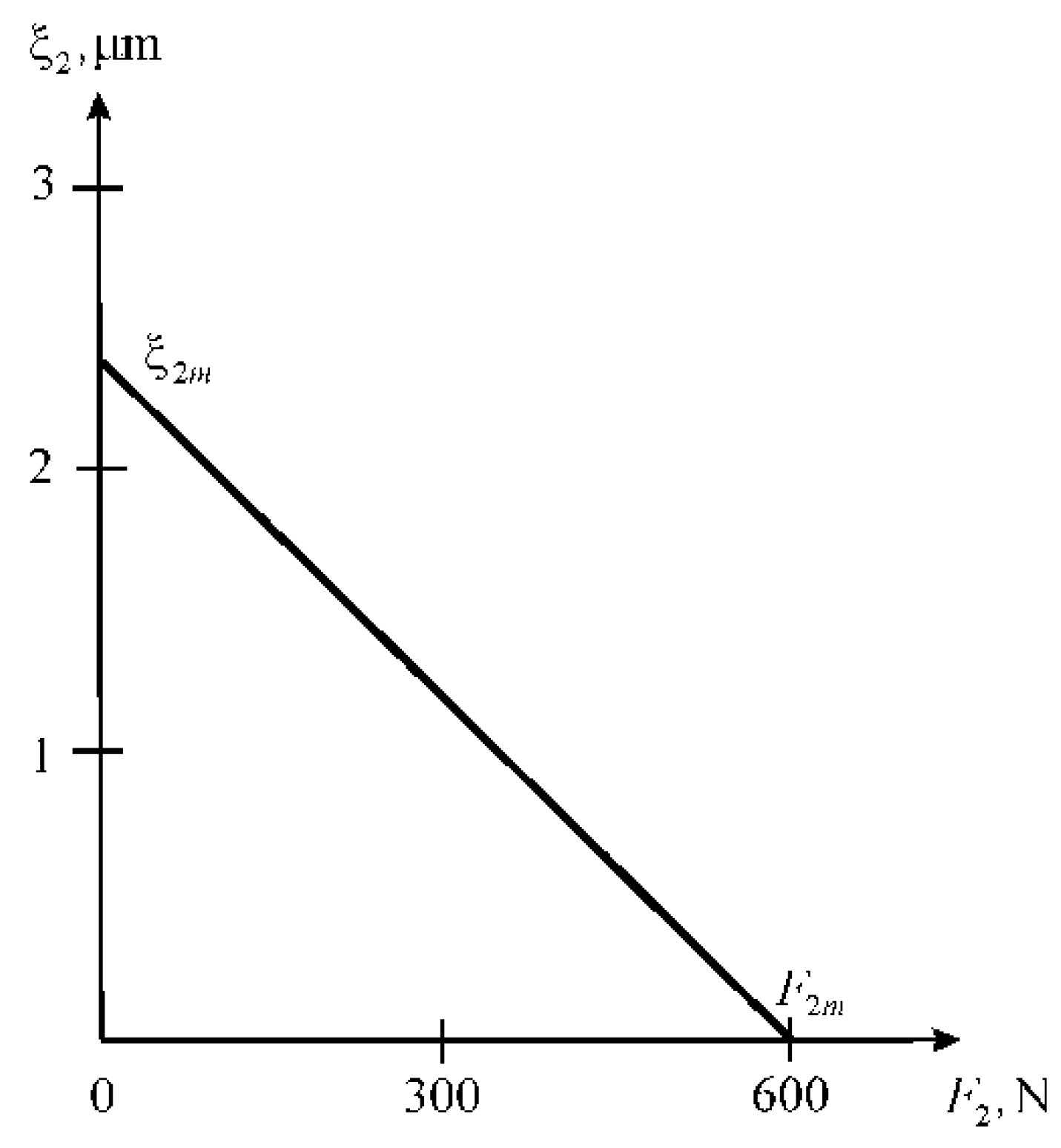
4. Results and Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Schultz, J.; Ueda, J.; Asada, H. Cellular Actuators; Butterworth-Heinemann Publisher: Oxford, UK, 2017; p. 382. [Google Scholar]
- Afonin, S.M. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Dokl. Math. 2006, 3, 943–948. [Google Scholar] [CrossRef]
- Zhou, S.; Yao, Z. Design and optimization of a modal-independent linear ultrasonic motor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 3, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Przybylski, J. Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Eng. Struct. 2015, 84, 140–151. [Google Scholar] [CrossRef]
- Ueda, J.; Secord, T.; Asada, H.H. Large effective-strain piezoelectric actuators using nested cellular architecture with exponential strain amplification mechanisms. IEEE/ASME Trans. Mechatron. 2010, 15, 770–782. [Google Scholar] [CrossRef]
- Karpelson, M.; Wei, G.-Y.; Wood, R.J. Driving high voltage piezoelectric actuators in microrobotic applications. Sens. Actuators A Phys. 2012, 78–89. [Google Scholar] [CrossRef]
- Afonin, S.M. Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. J. Comput. Syst. Sci. Int. 2015, 3, 424–439. [Google Scholar] [CrossRef]
- Afonin, S.M. Structural parametric model of a piezoelectric nanodisplacement transduser. Dokl. Phys. 2008, 3, 137–143. [Google Scholar] [CrossRef]
- Afonin, S.M. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Dokl. Math. 2006, 2, 307–313. [Google Scholar] [CrossRef]
- Cady, W.G. Piezoelectricity: An Introduction to the Theory and Applications of Electromechancial Phenomena in Crystals; McGraw-Hill Book Company: New York, NY, USA; London, UK, 1946; p. 806. [Google Scholar]
- Mason, W. Physical Acoustics: Principles and Methods. Volume I. Part A. Methods and Devices; Academic Press: New York, NY, USA, 1964; Volume 1, p. 515. [Google Scholar]
- Chiatto, M.; Capuano, F.; Coppola, G.; de Luca, L. LEM characterization of synthetic jet actuators driven by piezoelectric element: A Review. Sensors 2017, 17, 1216. [Google Scholar] [CrossRef] [PubMed]
- Afonin, S.M. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. In Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications; Chapter 9; Parinov, I.A., Ed.; Nova Science: New York, NY, USA, 2015; pp. 225–242. [Google Scholar]
- Afonin, S.M. A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. In Advances in Nanotechnology; Chapter 8; Bartul, Z., Trenor, J., Eds.; Nova Science: New York, NY, USA, 2017; Volume 19, pp. 259–284. [Google Scholar]
- Afonin, S.M. Nano- and micro-scale piezomotors. Russ. Eng. Res. 2012, 32, 519–522. [Google Scholar] [CrossRef]
- Afonin, S.M. Generalized parametric structural model of a compound electromagnetoelastic transducer. Dokl. Phys. 2005, 2, 77–82. [Google Scholar] [CrossRef]
- Afonin, S.M. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mech. Solids 2007, 1, 43–49. [Google Scholar] [CrossRef]
- Afonin, S.M. Stability of strain control systems of nano- and microdisplacement piezotransducers. Mech. Solids 2014, 2, 196–207. [Google Scholar] [CrossRef]
- Afonin, S.M. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. Int. J. Phys. 2017, 1, 9–15. [Google Scholar] [CrossRef]
- Afonin, S.M. A block diagram of electromagnetoelastic actuator nanodisplacement for communications Systems. Trans. Netw. Commun. 2018, 3, 1–9. [Google Scholar] [CrossRef]
- Afonin, S.M. Electromagnetoelastic nano- and microactuators for mechatronic systems. Russ. Eng. Res. 2018, 12, 938–944. [Google Scholar] [CrossRef]
- Afonin, S.M. Structural-parametric model of piezoactuator nano- and microdisplacement for nanoscience. AASCIT J. Nanosci. 2017, 3, 12–18. [Google Scholar]
- Afonin, S.M. Wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. Int. J. Math. Anal. Appl. 2016, 4, 31–38. [Google Scholar]
- Afonin, S.M. Structural-parametric model electromagnetoelastic actuator nano and microdisplacement for precision engineering. Eng. Technol. 2016, 6, 110–119. [Google Scholar]
- Afonin, S.M. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators 2018, 1, 6. [Google Scholar] [CrossRef]
- Afonin, S.M. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow, Russia, 29 January–1 February 2018; pp. 1698–1701. [Google Scholar] [CrossRef]
- Bhushan, B. Springer Handbook of Nanotechnology; Springer: Berlin, Germany; New York, NY, USA, 2004; p. 1222. [Google Scholar]
- Uchino, K. Piezoelectric Actuator and Ultrasonic Motors; Kluwer Academic Publisher: Boston, MA, USA, 1997; p. 347. [Google Scholar]
- Nalwa, H.S. Encyclopedia of Nanoscience and Nanotechnology; American Scientific Publishers: Los Angeles, CA, USA, 2004. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afonin, S.M. Structural-Parametric Model and Diagram of a Multilayer Electromagnetoelastic Actuator for Nanomechanics. Actuators 2019, 8, 52. https://doi.org/10.3390/act8030052
Afonin SM. Structural-Parametric Model and Diagram of a Multilayer Electromagnetoelastic Actuator for Nanomechanics. Actuators. 2019; 8(3):52. https://doi.org/10.3390/act8030052
Chicago/Turabian StyleAfonin, Sergey M. 2019. "Structural-Parametric Model and Diagram of a Multilayer Electromagnetoelastic Actuator for Nanomechanics" Actuators 8, no. 3: 52. https://doi.org/10.3390/act8030052
APA StyleAfonin, S. M. (2019). Structural-Parametric Model and Diagram of a Multilayer Electromagnetoelastic Actuator for Nanomechanics. Actuators, 8(3), 52. https://doi.org/10.3390/act8030052




