Variable Preloading Force in an Archetypal Oscillator

Abstract

In this paper, the influence of the time variable preloading force on the vibration of an archetypal oscillator is investigated. The oscillator is modeled as a slider-string system which is mathematically described with a second order nonlinear differential equation with time variable parameters. An approximate procedure for solving the equation is introduced. It is based on the exact solution of the pure nonlinear equation in the form of the Ateb function. The obtained result gives the vibration amplitude and phase variation of the oscillator depending on the preloading force variation. Based on this result, the procedure for regulation of the preloading force as the function of the required vibration amplitude decrease is developed. It is concluded that the preloading force may be used as a control parameter of the oscillator.

1. Introduction

This study is motivated by a growing interest in appropriate regulation of the oscillatory systems built in vibration absorbers. Various types of systems for vibration absorption are already produced, but the problem of their proper regulation is not solved yet. The real systems have nonlinear property and if they are not designed or controlled properly complex dynamic phenomena could be induced. Hence, it is significant to reveal the regularity of motion for such a system. Inspired by the simple shallow arch model of Thompson and Hunt [1], which is widely used in physics and engineering to illustrate the snap-through buckling phenomena, the archetypal oscillator whose properties can be controlled is developed [2]. The model comprises a lumped mass linked by a pair of inclined elastic springs. Each spring of stiffness k is pinned to a rigid support and is capable of resisting both tension and compression. The force in the spring is [3]

$$F=2k\frac{X}{L}\left(1-\frac{1}{\sqrt{{(\frac{l}{L})}^2+{(\frac{X}{L})}^2}}\right),$$

where L is the equilibrium length, X is mass displacement and l is the half distance between rigid supports. Although the springs are assumed to be with linear stiffness, the resulting force on the mass is strongly nonlinear because of changes to the geometric configuration. Depending on the smoothness parameter l/L of the spring force the corresponding oscillator has smooth or discontinue dynamics [4]. (The model is often named ‘smooth and discontinuous’ SD oscillator, too.) In the smooth regime the system bears significant similarities to the Duffing oscillator, but at the discontinuous limit there is a substantial departure in dynamics from the standard one [5]. In the paper [6] the model is extended by introducing of a damper. Smooth dynamics of the oscillator is analyzed. The authors obtained the result that this type of slider-spring-damper system gives benefits of using a nonlinear stiffness in an energy harvesting device. In [4,5,6] it is shown that regulating the smooth parameter the control of the dynamics of the system is possible. The systems are produced and experimental measurements on the real systems are done [7]. The authors obtained the result that there is a difference between measured and analytically calculated values. It is concluded that the difference is due to omitting of the physical nonlinearity in the analytical model [8]. In the aforementioned models the preloading force in the strings is neglected.

However, vibration problems of axially preloaded beams are widely investigated. The natural frequencies of beams under constant compressive [9] and constant tensile [10] axial loads are determined. Various types of beams are considered: free-free, pinned-pinned, pinned-free, clamped-sliding and sliding-sliding ones. Buckling of thin-walled composite beams under axial loads is also investigated [11]. It is shown that the pre-loading of the piezoceramic beams opens the opportunity for increased life time of devices in energy harvesting [12]. In the paper [13] it is reported that the preloading force need not to be constant; in the new types of magnetorheological elastomers for vibration isolators the magnetic attraction force is utilized to change the preloading. A similar result as for beams is obtained for the piano strings loaded with axial force [14]. Various methods are applied for free vibration of axially loaded beams: the corotational finite element formulation [15], the initial values method [16], the Adomian modified decomposition method [17], etc. Methods for solving time-variable dynamics are also developed which are wave-based ones (see [18,19,20,21,22]).

It is noted that the preloading in the studied structures can be considered usually using standard models just by considering an additional force term. In this paper the preloading force will be assumed as an additional axial direction force along the string.

The aim of this paper is to generalize the archetypal oscillator by introducing the physical nonlinearity and of the preloading string force. The dynamics of the smooth archetypal oscillator with and without damping is considered. Special attention is given to the time variable preloading force.

The paper is divided into five sections. In Section 2 the model of the slider-string-damper archetypal oscillator is introduced. Both nonlinearities, geometric and physical, are included. The preloading force is assumed to be time dependent. The mathematical model of the oscillator is a strong nonlinear second order differential equation with slow time variable parameters. In Section 3 an approximate analytic solving procedure based on the exact solution of the pure nonlinear equation with constant parameters is introduced. The amplitude, frequency and phase variation of the system as the function of the order of nonlinearity is obtained. In Section 4, based on the required decrease of amplitude of vibration the procedure for obtaining the preloading force – time variation is developed. The preloading force is suggested as a control parameter. The paper ends with Discussion and Conclusions.

2. Model of the String-Mass System

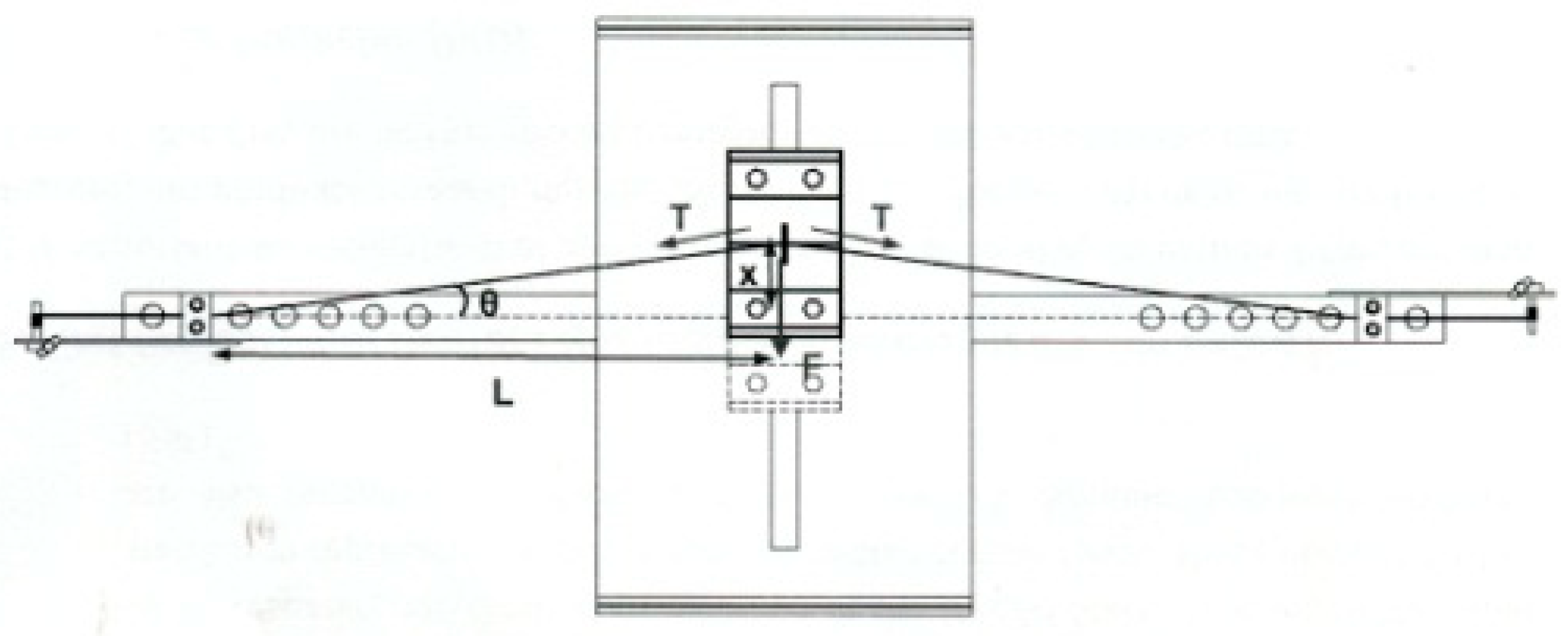
The model of the archetypal oscillator is a slider-string system shown in Figure 1. The slider has the mass m and moves orthogonal to the initial direction of strings.

One end of the string is pinned to a rigid support and the other is connected with the slider. On the fixed end the preloading force in the string is regulated by a turning button. Changing the angle position of the button the preloading force is slowly varied in time.

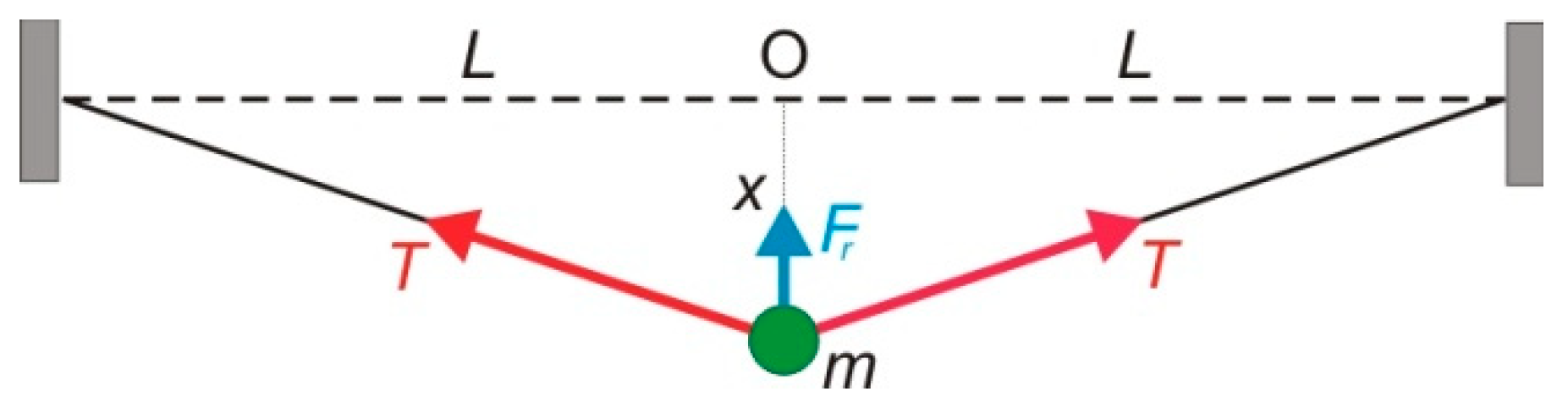
Motion of slider causes deformation of the string (Figure 2). Elongation of the string is

$$\Delta L=\sqrt{L^2+X^2}-L,$$

(1)

where L is the length of the string and X is the displacement. Due to elastic elongation the tension in both parts of the string is

$$T_1=\frac{EA\Delta L}{L},$$

(2)

where E is the Young’s modulus and A is the cross-section of the string. If there is the preloading force T₀ in the string, the total string force is obtained as

$$T=\left(T_0-EA\right)+\frac{EA\sqrt{L^2+X^2}}{L}.$$

(3)

For the angle Θ formed between the initial and deformed position of the string, when

$$sin\mathsf{\Theta }=X/\sqrt{X^2+L^2}$$

the restitution force in x direction is obtained as

$$F=2Tsin\mathsf{\Theta }=2\frac{X}{L}(EA+\frac{T_0-EA}{\sqrt{1+{(\frac{X}{L})}^2}}).$$

(4)

Supposing that the relation (X/L) is small we introduce the series expansion of the function as

$${\left(1+\frac{X^2}{L^2}\right)}^{-1/2}=1-\frac{X^2}{2L^2}+\frac{X^4}{6L^4}+\mathcal{O}\left(\frac{X^6}{L^6}\right).$$

(5)

Assuming the first two terms of (5) the approximate relation for the force (4) is obtained

$$F=2\left(\frac{X}{L}\right)\left(T_0+\frac{EA-T_0}{2}{\left(\frac{X}{L}\right)}^2\right).$$

(6)

The force is the cubic function of the displacement. However, experimental investigation done on the real strings show that the order of nonlinearity differs from 3 (see [7]). The order may be any positive real number of integer or non-integer type. For generalization, the restitution force is assumed as

$$F=2\left(\frac{X}{L}\right)\left(T_0+\frac{EA-T_0}{2}{\left|\frac{X}{L}\right|}^{\alpha -1}\right),$$

(7)

where $\alpha \in ℝ$. Using (7) and the linear damping force the differential equation of the slider motion is

$$m\ddot{X}+2\left(\frac{X}{L}\right)\left(T_0+\frac{EA-T_0}{2}{\left|\frac{X}{L}\right|}^{\alpha -1}\right)+c_d\dot{X}=0$$

(8)

where c_d is the damping coefficient.

Introducing the coefficients of linearity k_la and nonlinearity k_na, and coefficient of damping c

$$k_{la}=\frac{2T_0}{mL},k_{na}=\frac{EA-T_0}{mL},c=\frac{c_d}{m},$$

(9)

the mathematical model (8) is simplified into

$$\frac{d^2}{d{t}^2}\left(\frac{X}{L}\right)+k_{la}\left(\frac{X}{L}\right)+k_{na}\left(\frac{X}{L}\right){\left|\frac{X}{L}\right|}^{\alpha -1}+c\frac{d}{dt}\left(\frac{X}{L}\right)=0,$$

(10)

i.e.,

$$\ddot{x}+k_{la}x+k_{na}x{\left|x\right|}^{\alpha -1}+c\dot{x}=0$$

(11)

where d²/dt² = (^..) and the dimensionless length is

$$x=X/L$$

(12)

In the system due to fatigue the preloading force changes continually in time, but very slowly. The system is very close to its steady state vibration anyway during the operation.

Due to the fact that the force variation is slow, it is usually modelled as a dis-continual step function. Then the system is modelled as a non-time varying one with a constant force acting in a certain period reaching to steady-state response. For the next period, the model has the same form but with the new value of the constant force and the considered initial condition is taken from the previous step.

The model leads to a certain error due to the fact that the real force is not dis-continual but a continual time function. In addition, the solving procedure is complex.

To overcome the lack of the model and to minimize the error, we assume the real physical form of the force as a continual time function. If the perturbation parameter ε to the steady state vibration is small, i.e., ε <<1, the time variation τ is slow and defined as the ‘slow time’ where $\tau =\epsilon t$. (Usually, the value of the small parameter is up to 0.1 (see [24])). Assuming that the preloading force is varying in slow time τ, the mathematical model of the system is

$$\ddot{x}+k_{la}\left(\tau \right)x+k_{na}\left(\tau \right)x{\left|x\right|}^{\alpha -1}+c\dot{x}=0,$$

(13)

where

$$k_{la}\left(\tau \right)=\frac{2T_0\left(\tau \right)}{mL},k_{na}\left(\tau \right)=\frac{EA-T_{0\left(\tau \right)}}{mL}.$$

Due to the fact that EA >> T₀ in the Equation (13) the coefficient of nonlinearity is much higher than the coefficient of the linear term, i.e., k_na >> k_la. If the damping is small the Equation (13) is written as

$$\ddot{x}+k_{na}\left(\tau \right)x{\left|x\right|}^{\alpha -1}=-\epsilon k_{la}\left(\tau \right)x-\epsilon c\dot{x},$$

(14)

where ε << 1 is a small parameter. The Equation (14) is a strong nonlinear equation with ‘slow’ time variable coefficients and small perturbation terms of the order ε.

3. Analytic Solving Procedure

Assuming that the small parameter is zero, i.e., ε = 0 and τ = 0, the expression (14) transforms into a pure nonlinear equation with constant coefficient

$$\ddot{x}+k_{na}x{\left|x\right|}^{\alpha -1}=0.$$

(15)

The exact solution of (15) is [25]

$$x=Cca(sa\left(\alpha ,1,\mathsf{\Omega }t+\theta \right)),$$

(16)

where ca is the cosine Ateb (inverse Beta) function, Ω is the frequency of the function, C is the arbitrary amplitude and θ is the arbitrary phase. The first and the second time derivatives of (16) are [26]

$$\dot{x}=-C\frac{2\mathsf{\Omega }}{\alpha +1}sa\left(1,\alpha ,\mathsf{\Omega }t+\theta \right)$$

(17)

$$\ddot{x}=-C\frac{2{\mathsf{\Omega }}^2}{\alpha +1}c{a}^{\alpha }\left(\alpha ,1,\mathsf{\Omega }t+\theta \right)$$

(18)

where sa is the sine Ateb function. The solution (16) and the derivative (18) satisfy the relation (15) for

$${\mathsf{\Omega }}^2=k_{na}\frac{\alpha +1}{2}{\left|C\right|}^{\alpha -1}$$

(19)

To solve the Equation (14) we introduce the solution and its time derivative in the form (16) and (17) but with time variable amplitude and phase [27]. It is also assumed that the frequency of the function (19) depends on the amplitude of vibration and on the slow time. Thus, we have

$$x=C\left(t\right)ca(\alpha ,1,\psi \left(t\right)),$$

(20)

$$\dot{x}=-C\left(t\right)\mathsf{\Omega }\left(C,\tau \right)\frac{2}{\alpha +1}sa\left(1,\alpha ,\psi \left(t\right)\right),$$

(21)

where C(t) is the time variable amplitude, ψ(t) is the time variable phase that satisfies the relation

$$\dot{\psi }\left(t\right)=\Omega +\dot{\theta }\left(t\right).$$

(22)

Comparing the time derivative of (20) with the assumed relation (21) the following expression is obtained

$$\dot{C}ca-C\dot{\theta }\frac{2}{\alpha +1}sa=0,$$

(23)

where ca = ca $\alpha ,1,\psi \left(t\right),$ $sa=sa\left(1,\alpha ,\psi \left(t\right)\right),C=$C(t) and $\theta =\theta \left(t\right).$ Substituting (20), (21) and the time derivative of (21) into (14) we have

$$\dot{C}\frac{2\mathsf{\Omega }}{\alpha +1}sa+C\mathsf{\Omega }\dot{\theta }\frac{2}{\alpha +1}c{a}^{\alpha }=\epsilon k_{la}Cca-\epsilon cC\mathsf{\Omega }\frac{2}{\alpha +1}sa,$$

(24)

where Ω = Ω(C,τ). Equations (23) and (24) are two first order differential equations which represent the rewritten version of (14) in new variables C and ψ, i.e., θ. After some transformation and using (19) it is

$$\dot{C}\mathsf{\Omega }=\epsilon k_{la}Csaca-\epsilon cC\mathsf{\Omega }\frac{2}{\alpha +1}s{a}^2,$$

(25)

$$C\mathsf{\Omega }\frac{2}{\alpha +1}\dot{\theta }=\epsilon k_{la}Cc{a}^2-\epsilon cC\mathsf{\Omega }\frac{2}{\alpha +1}saca.$$

(26)

It is not an easy task to solve the system of Equations (25) and (26). It is at this moment the averaging over the period of Ateb functions is introduced. The averaged equations are

$$\dot{C}=-\epsilon C\left(\frac{1}{\mathsf{\Omega }}\frac{\partial \mathsf{\Omega }}{\partial \tau }+c\right)\frac{2}{\alpha +1}\langle s{a}^2\rangle ,$$

(27)

$$\dot{\theta }=\frac{\epsilon k_{la}}{\mathsf{\Omega }}\langle c{a}^2\rangle \frac{\alpha +1}{2}.$$

(28)

For the initial condition C(0) = C₀ when Ω(0) = Ω₀, the solution of (27) is

$$ln\frac{C}{C_0}=\frac{2}{\alpha +1}\left(ln\frac{{\mathsf{\Omega }}_0}{\mathsf{\Omega }}-\epsilon ct\right)\langle s{a}^2\rangle .$$

(29)

After some calculation the value of the averaged Ateb function is obtained in the form [26]

$$\langle s{a}^2\rangle =\frac{\alpha +1}{\alpha +3}.$$

(30)

Substituting (19) and the corresponding initial value into (29) and after some transformation the averaged amplitude variation is

$${\left(\frac{C}{C_0}\right)}^{\alpha }={\left(\frac{k_{na0}}{k_{na}\left(\tau \right)}\right)}^{\frac{1}{\alpha +3}}exp\left(-\frac{2\epsilon ct}{\alpha +3}\right).$$

(31)

According to (9) and

$$k_{na0}=\frac{EA-T_0\left(0\right)}{mL},k_{na}\left(\tau \right)=\frac{EA-T_0\left(\tau \right)}{mL},$$

(32)

the amplitude of vibration follows as

$$\frac{C}{C_0}={\left(\frac{EA-T_0\left(0\right)}{EA-T_0\left(\tau \right)}\right)}^{\frac{1}{\alpha \left(\alpha +3\right)}}exp\left(-\frac{2\epsilon ct}{\alpha \left(\alpha +3\right)}\right),$$

(33)

where T₀(0) is the initial string force and T₀(τ) is the time variable preloading force.

3.1. Preloading Force is Constant

If the preloading force is constant, the relation (33) simplifies into

$$C=C_{0}exp\left(-\frac{2\epsilon ct}{\alpha \left(\alpha +3\right)}\right).$$

(34)

The amplitude of vibration depends on the damping coefficient and on the order of nonlinearity.

3.2. Damping is Neglected

For the case when the damping is neglected, the Equation (29) simplifies into

$$C=C_0{\left(\frac{\mathsf{\Omega }}{{\mathsf{\Omega }}_0}\right)}^{-\frac{2}{\alpha +3}}.$$

(35)

For the linear case, when α = 1, the amplitude variation is

$$C=C_0{\left(\frac{\mathsf{\Omega }}{{\mathsf{\Omega }}_0}\right)}^{-\frac{1}{2}}.$$

(36)

where Ω is the frequency of vibration of the linear oscillator. The obtained result (36) corresponds to the already published one [28].

Substituting (9) and (19) into (36) it is

$$C=C_0{\left(\frac{EA-T_0\left(0\right)}{EA-T_0\left(\tau \right)}\right)}^{\frac{1}{\alpha \left(\alpha +3\right)}}$$

(37)

The expression (37) gives the explicit dependence of the amplitude of vibration on the variation of the string force. However, the influence of the order of nonlinearity is also evident.

4. Control of Vibration with Preloading String Force

Let us rewrite the relation (37) as

$$T_0\left(\tau \right)=EA-\left(EA-T_0\left(0\right)\right){\left(\frac{C_0}{C\left(\tau \right)}\right)}^{\alpha \left(\alpha +3\right)}.$$

(38)

Equation (38) is the expression of the string force variation as the function of the amplitude of vibration. For the known or required amplitude of vibration the string force is computed. The force in the string is controlled by turning the button on the fixed ends of the string (see Figure 1). Analyzing the relation (38) it is evident that the decrease of the amplitude of vibration requires decrease of the loading force in the string, too.

Thus, for example, if it is required that the amplitude of vibration has to be eliminated according to the function

$$C\left(\tau \right)=C_0\exp \left(-\epsilon t\right),$$

(39)

the force in the string (38) has to be changed according to

$$T_0\left(\tau \right)=EA-\left(EA-T_0\left(0\right)\right)\exp \left(2\epsilon t\left(\alpha +1\right)\right).$$

(40)

The string force decreases to zero. This value is obtained after the time

$$t_0=\frac{1}{2\epsilon \left(\alpha +1\right)}ln\frac{EA}{EA-T_0\left(0\right)},$$

(41)

which depends on the order of nonlinearity and initial string force. Unfortunately, there is the remained amplitude of vibration

$$C\left(t_0\right)=C_0{\left(1-\frac{T_0\left(0\right)}{EA}\right)}^{\frac{1}{2\left(\alpha +1\right)}}.$$

(42)

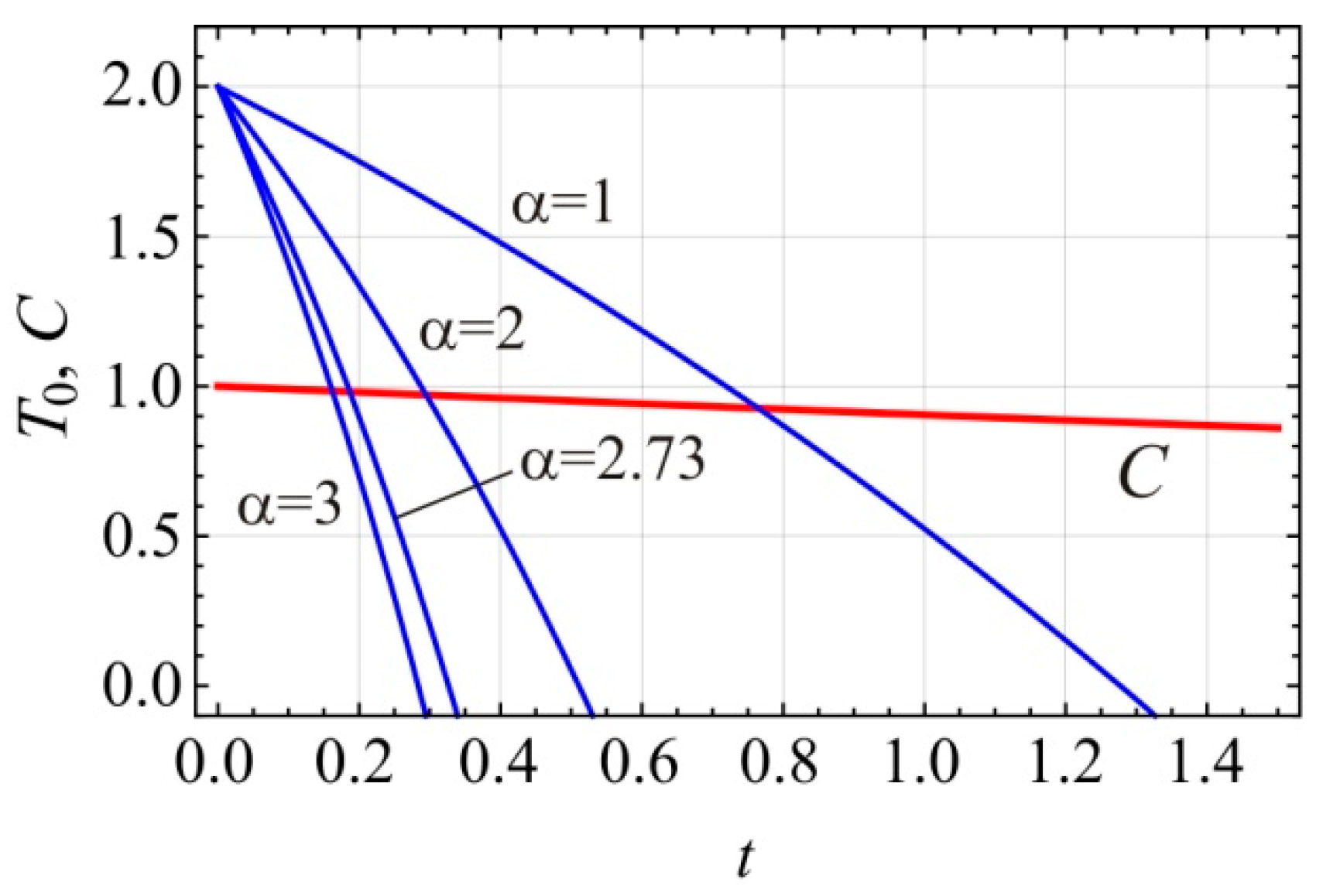
In Figure 3 a numerical example is considered. Parameters of the system are: EA = 5 N, T₀(0) = 2 N, C₀ = 1 mm and ε = 0.1. For the exponential amplitude function (39) the preloading string force (40) for various order of nonlinearity (α = 1, 2, 2.73, 3) is computed and plotted. Analyzing the curves in Figure 3 it can be concluded that if the amplitude of vibration decreases it requires the decrease of the force in the string. The higher is the order of the nonlinearity, the faster is the decrease of the string force for the same amplitude variation.

In

Table 1. Absorption parameters versus nonlinearity.

α	1	2	2.73	3
t0	1.2771	0.5108	0.3265	0.2838
C(t0)	0.8801	0.9502	0.9678	0.9720

absorption time and the residual amplitude of vibration versus α is presented. Using the values given in the Table 1, it can be seen that the time of vibration absorption strongly depends on the order of nonlinearity.

The order of nonlinearity has the quantitative influence on the dynamics of the system, but qualitatively the behavior is the same as for the cubic nonlinearity. Thus, if the initial preloading force is constant the amplitude of vibration decreases faster for smaller than for the higher order of nonlinearity. The amplitude decrease is the fastest for the linear case.

For the system where the damping is omitted and the preloading force is decreasing, the amplitude of vibration is also decreasing. However, if the preloading force is increasing, the amplitude of vibration is increasing in time. Thus, for elimination of the vibration the relaxation of the preloading force in time is necessary.

If the vibration amplitude decrease is required to be an exponential time function, then the relaxation of the preloading force has to be the function of the same type. The decrease of the preloading force is faster for the system with higher order of nonlinearity. The vibration absorption time is much longer for the linear case than for nonlinear one. If the order of nonlinearity is higher, the vibration absorption time is shorter. However, the residual amplitude of vibration after preloading force relaxation is higher for nonlinear system than for linear one. In spite of that, we recommend the use of nonlinear absorption system with high order of nonlinearity to give the shortest time for vibration absorption.

5. Conclusions

In this paper, the influence of the time-variable preloading force on the vibration of the oscillator of archetypal type is considered. The obtained results show that there is a significant influence of the order of nonlinearity and of the initial preloading force on the dynamics of the oscillator. In addition, it is concluded that the required amplitude of vibration in the system can be obtained by regulating of the preloading force in the string during the time. The preloading force may be used as a control parameter of the oscillator.