A Novel, Low-Cost and Reliable Workbench for Optimal Voltage Distribution on Piezoelectric Array Actuators
Abstract
1. Introduction
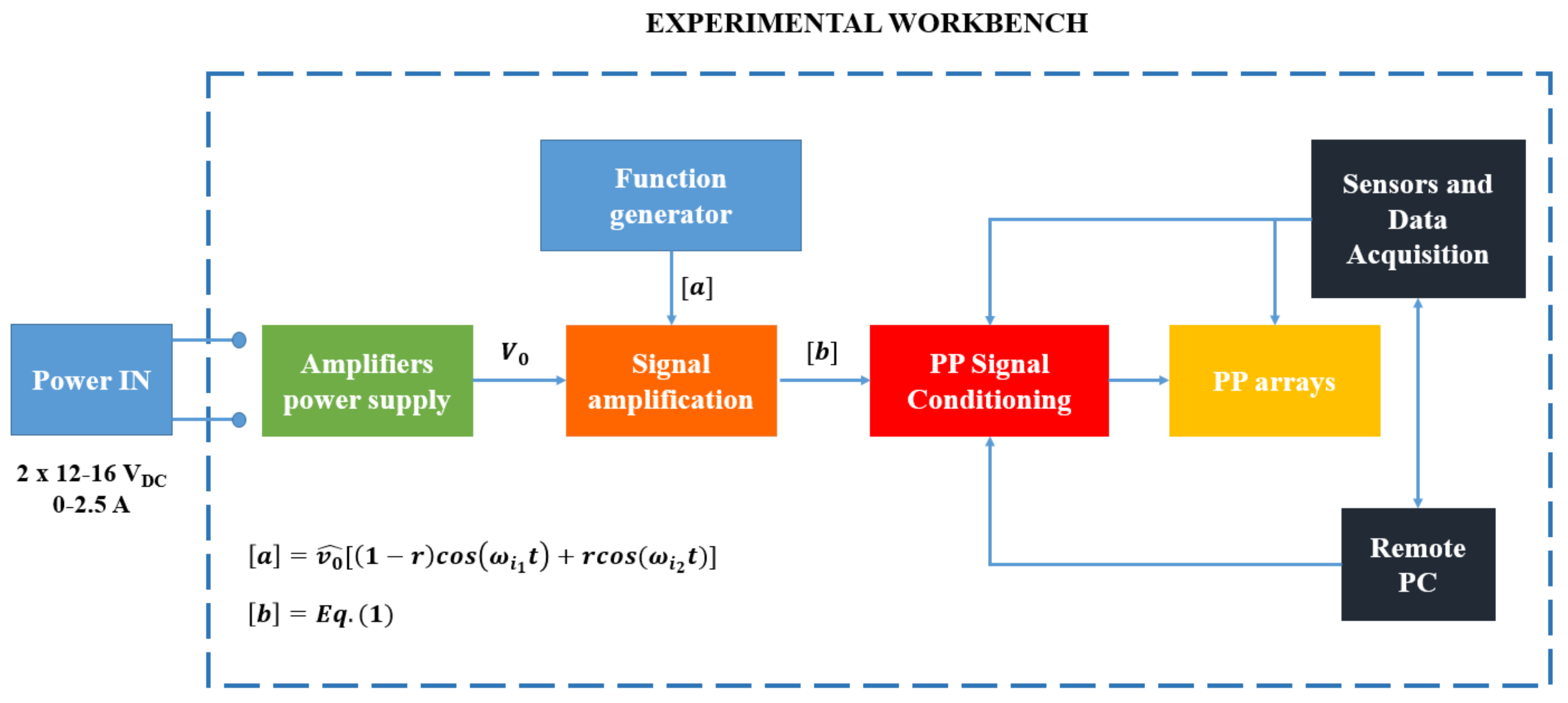
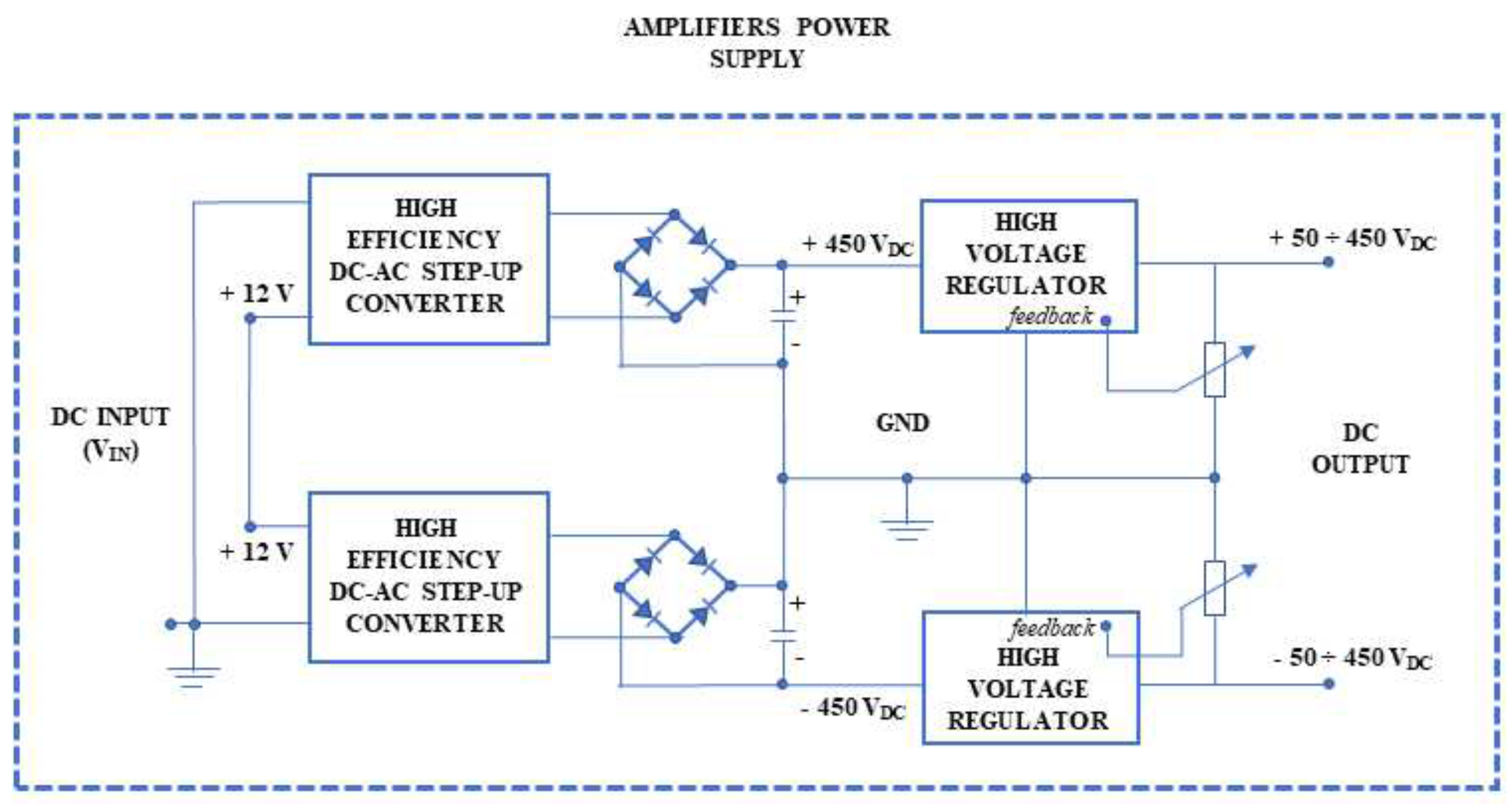
- the workbench must be powered by a dual-channel DC power source (12–16 , 0–2.5 A for each channel);
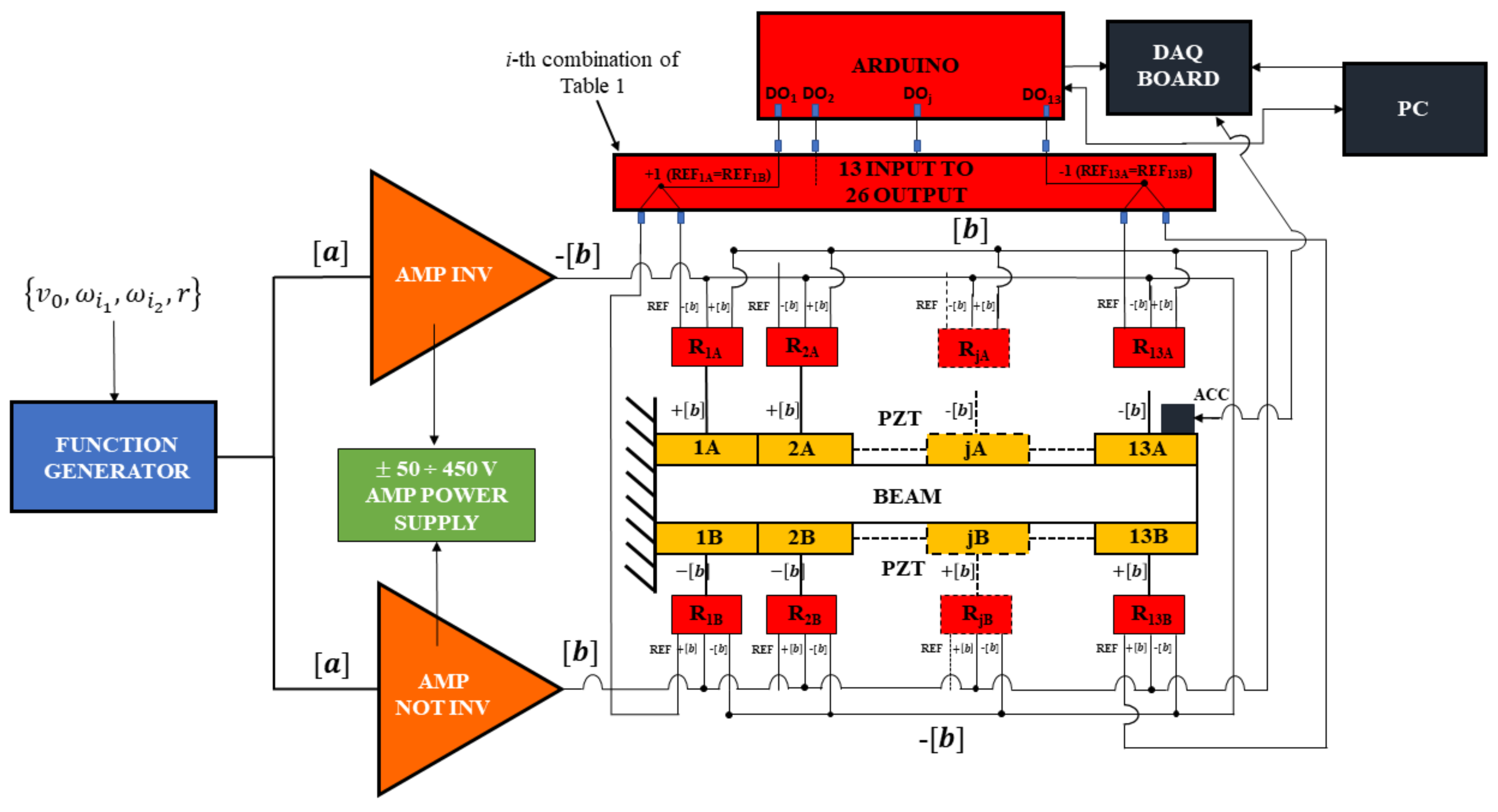
- according to the Pin Force model [6] each PP couple (upper and lower plate) must be driven by the same signal (single or dual–tone), but one must be in opposition phase with respect to the other;
- the PP driving signal must be adjustable in frequency (range 10 Hz–2 kHz) and tone amplitude (up to 450 V);
- two operating modes of the PPs couples must be included;
- the PP signal must be unaffected by the number of activated PP couples;
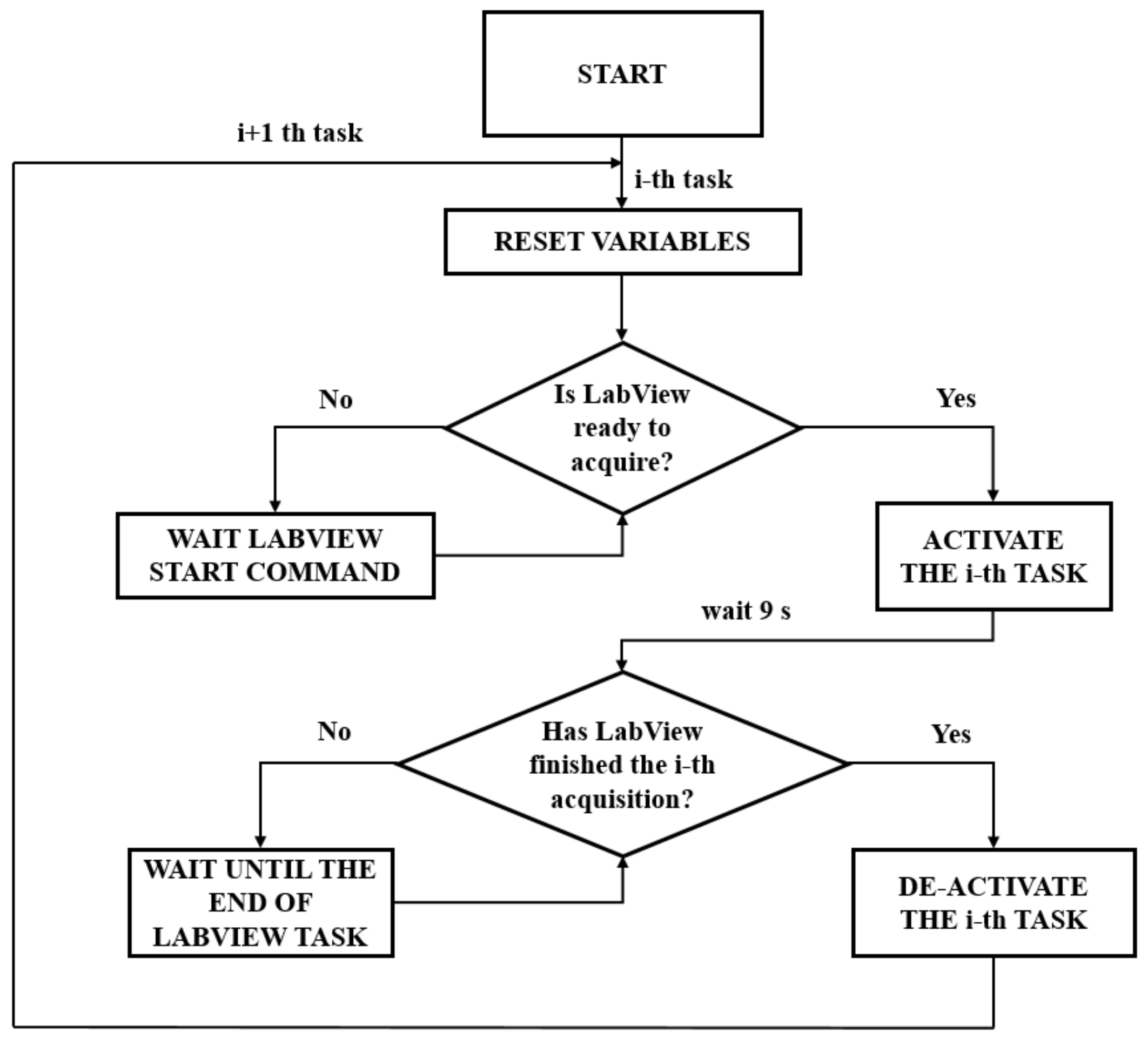
- the PP couples operating modes must be managed by a remote PC.
2. Materials and Methods
3. Results
- the FUNCTION GENERATOR;
- the AMP INV;
- the AMP NOT INV.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weber, F.; Distl, H.; Fischer, S.; Braun, C. MR Damper Controlled Vibration Adsorber for Enhanced Mitigation of Harmonic Vibrations. Actuators 2016, 5, 27. [Google Scholar] [CrossRef]
- Botta, F.; Marx, N.; Schwingshackl, C.; Cerri, G.; Dini, D. A Wireless Vibration Control Technique for Gas Turbine Blades Using Piezoelectric Plates and Contactless Energy Transfer. ASME 2013. [Google Scholar] [CrossRef]
- Herold, S.; Mayer, D. Adaptive Piezoelectric Absorber for Active Vibration Control. Actuators 2016, 5, 7. [Google Scholar] [CrossRef]
- Botta, F.; Toccaceli, F. Piezoelectric Plates Distribution for Active Control of Torsional Vibrations. Actuators 2018, 7, 23. [Google Scholar] [CrossRef]
- Mokrani, B.; Bastaits, R.; Romanescu, I.; Horodinca, M.; Burda, I.; Preumont, A. Passive Damping of Rotationally Periodic Structures with Tuned Piezoelectric Inductive Shunt. Actuators 2018, 7, 41. [Google Scholar] [CrossRef]
- Crawley, E.F.; de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA J. 1987, 25, 1373–1385. [Google Scholar] [CrossRef]
- Gupta, V.; Sharma, M.; Nagesh, T. Optimization Criteria for Optimal Placement of Piezoelectric Sensors and Actuators on a Smart Structure: A Technical Review. J. Intell. Mater. Syst. Sruct. 2010, 21, 1227–1243. [Google Scholar] [CrossRef]
- Frecker, M.I. Recent Advances in Optimization of Smart Structures and Actuators. J. Intell. Mater. Syst. Sruct. 2003, 14, 207–216. [Google Scholar] [CrossRef]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Belfiore, N.P.; Sciuto, S.A. A review on parametric dynamic models of magnetorheological dampers and their characterization methods. Actuators 2018, 7, 16. [Google Scholar] [CrossRef]
- Poursaeidi, E.; Salavatian, M. Fatigue grow simulation in a generator fan blade. Eng. Fail. Anal. 2009, 16, 888–898. [Google Scholar] [CrossRef]
- Witek, L. Experimental crack propagation and failure analysis of the first stage compressor blade subject to vibration. Eng. Fail. Anal. 2009, 16, 2163–2170. [Google Scholar] [CrossRef]
- Rafiee, M.; Nitzsche, F.; Labrosse, M. Dynamics, vibration and control of rotating composite beams and blades: A critical review. Thin-Walled Struct. 2017, 119, 795–819. [Google Scholar] [CrossRef]
- Ehrich, F.F. Observed Rotordynamic Phenomena in Aircraft Gas Turbine Development. In Proceedings of the 27th Conference on Mechanical Vibration and Noise International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Lourenco, N.J.; Graca, M.L.A.; Franco, L.A.L.; Silva, O.M.M. Fatigue failure of a compressor blade. Eng. Fail. Anal. 2008, 15, 1150–1154. [Google Scholar] [CrossRef]
- Kermanpur, A.; Sepehri, A.H.; Ziaei-Rad, S.; Nourbakhshnia, N.; Mosaddeghfar, M. Failure analysis of Ti6Al4V gas turbine compressor blades. Eng. Fail. Anal. 2008, 15, 1052–1064. [Google Scholar] [CrossRef]
- Witek, L. Simulation of crack growth in the compressor blade subjected to resonant vibration using hybrid method. Eng. Fail. Anal. 2015, 49, 57–66. [Google Scholar] [CrossRef]
- Witek, L. Fatigue Investigations of the Compressor Blades with Mechanical Defects. Key Eng. Mater. 2014, 598, 269–274. [Google Scholar] [CrossRef]
- Botta, F.; Dini, D.; Schwingshackl, C.; di Mare, L.; Cerri, G. Optimal placement of piezoelectric plates to control multimode vibrations of a beam. Adv. Acoust. Vib. 2013, 2013, 905160. [Google Scholar] [CrossRef]
- Botta, F.; Marx, N.; Gentili, S.; Schwingshackl, C.W.; Di Mare, L.; Cerri, G.; Dini, D. Optimal placement of piezoelectric plates for active vibration control of gas turbine blades: Experimental results. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 3 April 2012. [Google Scholar]
- Botta, F.; Rossi, A.; Schinaia, L.; Scorza, A.; Orsini, F.; Sciuto, S.A.; Belfiore, N.P. Experimental Validation on Optimal Placement of PZT Plates for Active Beam Multimode Vibrations Reduction. In Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics, Salerno, Italy, 4 September 2017. [Google Scholar]
- Rossi, A.; Botta, F.; Maiozzi, R.; Scorza, A.; Sciuto, S.A. Experimental results for active control of multimodal vibrations by optimally placed piezoelectric actuators. MATEC Web Conf. 2018, 211, 20001. [Google Scholar] [CrossRef]
- Botta, F.; Scorza, A.; Rossi, A. Optimal piezoelectric potential distribution for controlling multimode vibrations. Appl. Sci. 2018, 8, 551. [Google Scholar] [CrossRef]
- Zhao, J.J.; Zhao, X.B.; Li, X.H.; Zhang, B.; Wang, B.; Zhang, W. Fasteners State Detection System Based on Wireless Data Transfer Module. Appl. Mech. Mater. 2014, 513, 3924–3927. [Google Scholar] [CrossRef]
- Orsini, F.; Rossi, A.; Scorza, A.; Sciuto, S.A. Development and preliminary characterization of a novel system for the force platforms dynamic calibration. In Proceedings of the IEEE International Instrumentation and Measurement Technology, Torino, Italy, 22–25 May 2017. [Google Scholar]
- Adamo, F.; Attivissimo, F.; Marracci, M.; Tellini, B. Characterization of a system for measurements on soft ferrites. Meas. Sci. Technol. 2012, 23, 085602. [Google Scholar] [CrossRef]
- Wiberg, A.O.J.; Bres, C.S.; Danicic, A.; Myslivets, E.; Radic, S. Performance of Self-Seeded Parametric Multicasting of Analog Signals. IEEE Photonics Technol. Lett. 2011, 23, 1570–1572. [Google Scholar] [CrossRef]
- Šaliga, J.; Kollár, I.; Michaeli, L.; Buša, J.; Lipták, J.; Virosztek, T. A comparison of least squares and maximum likelihood methods using sine fitting in ADC testing. Measurement 2013, 46, 4362–4368. [Google Scholar] [CrossRef]
- Rapuano, S. Preliminary considerations on ADC standard harmonization. IEEE Trans. Instrum. Meas. 2008, 57, 386–394. [Google Scholar] [CrossRef]
- Ciufu, L.; Popescu, C.L.; Popescu, M.O. Experimental mitigation techniques to reduce the Total Harmonic Distortion of low voltage non-linear power sources. In Proceedings of the 10th International Symposium on Advanced Topics in Electrical Engineering, Bucharest, Romania, 23–25 March 2017. [Google Scholar]
- Dwivedi, V.; Singh, D. Electric Power Quality Monitoring (PQM) using Virtual Instrumentation. In Proceedings of the International Symposium on Power Electronics Electrical Drives Automation and Motion, Pisa, Italy, 14–16 June 2010. [Google Scholar]
- Shmilovitz, D. On the definition of total harmonic distortion and its effect on measurement interpretation. IEEE Trans. Power Deliv. 2005, 20, 526–528. [Google Scholar]
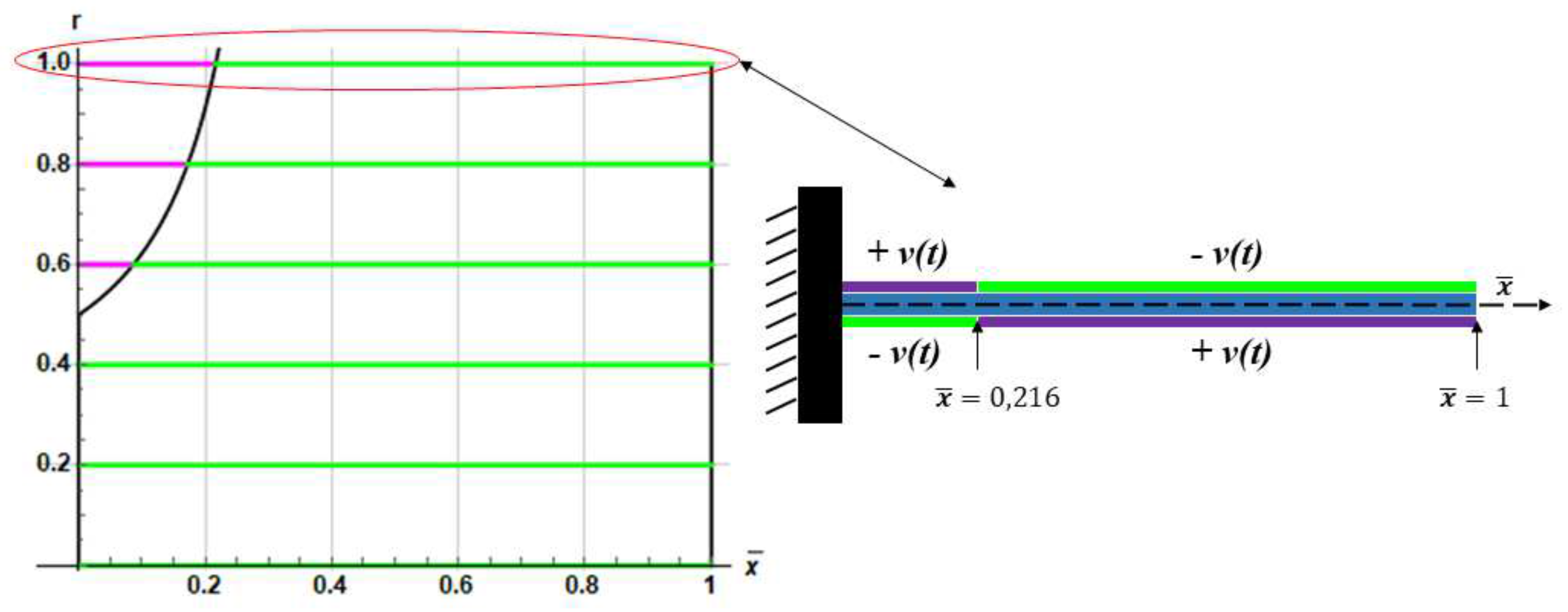
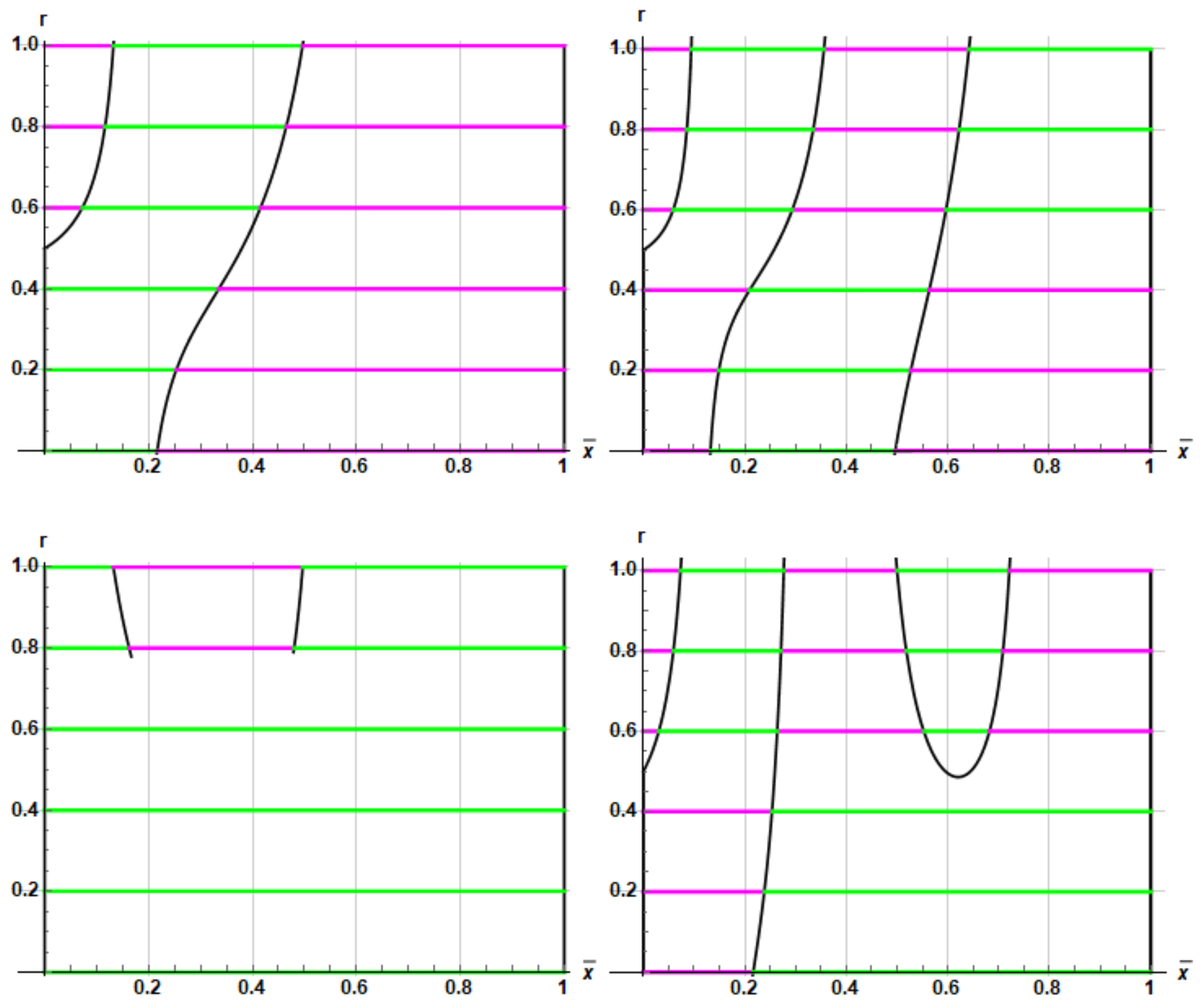
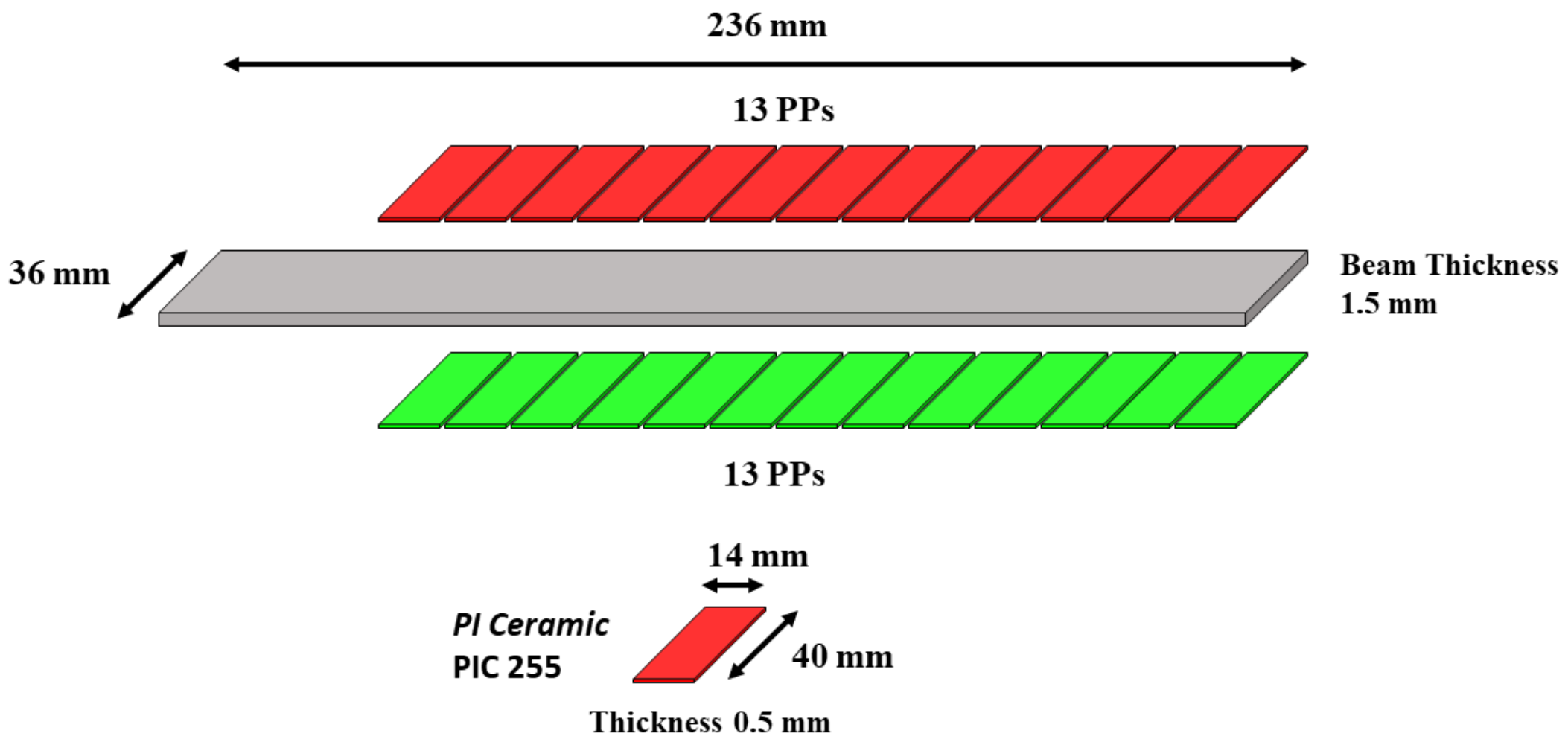
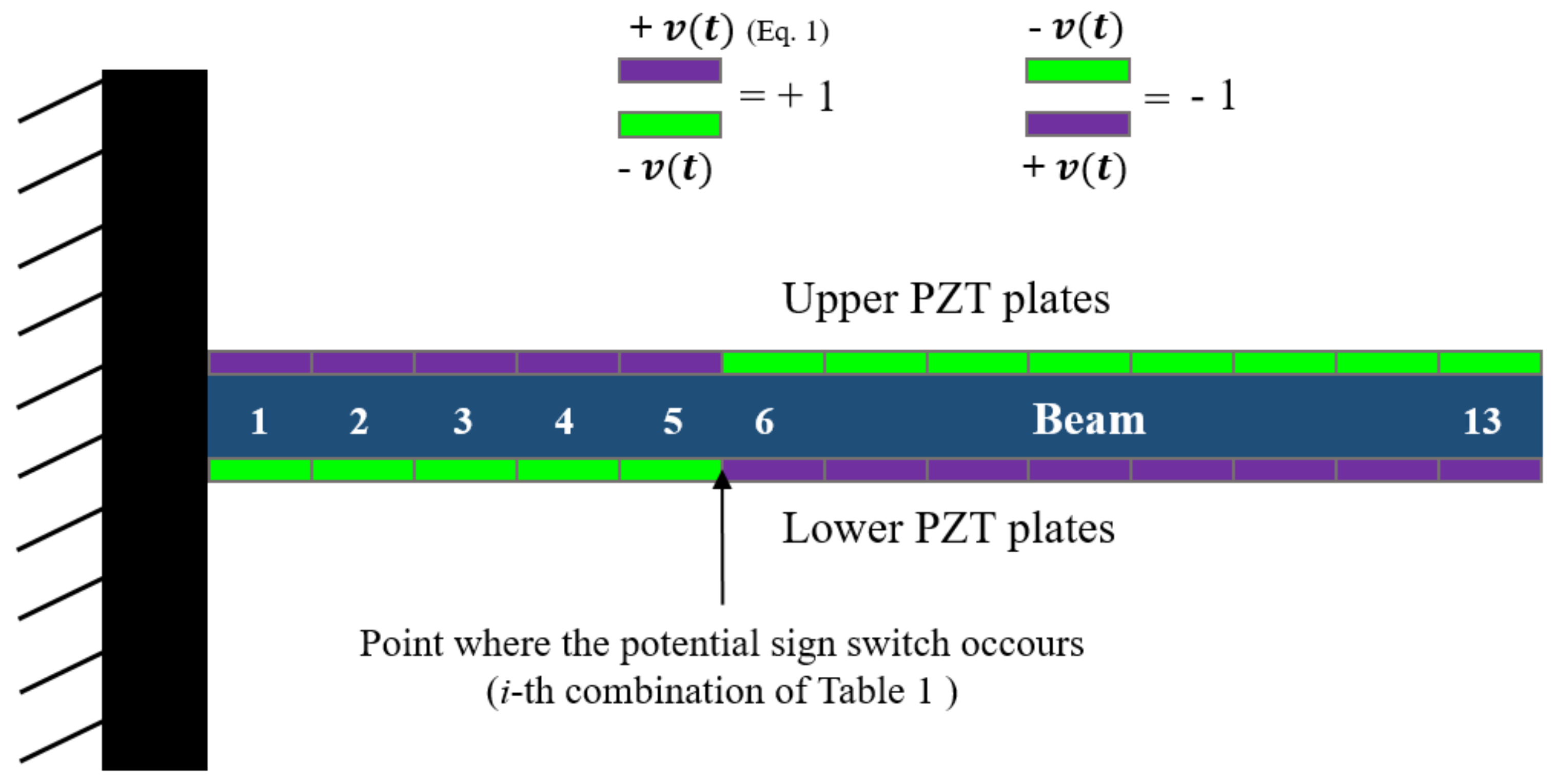


| Combination\Plates Couple | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 2 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 |
| 3 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | +1 |
| 4 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | −1 |
| 5 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | +1 | +1 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| i | +1 | +1 | +1 | +1 | +1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 8192 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 |
| SINAD (dB) | THDF (%) | |
|---|---|---|
| FUNCTION GENERATOR | 66.46 ± 0.07 | 0.013580 ± 1.62 |
| AMP INV | 34.32 ± 0.03 | 0.03 ± 0.01 |
| AMP Not INV | 33.70 ± 0.21 | 0.03 ± 0.01 |
| PPs Couple | SINAD (dB) | THDF (%) | ||
|---|---|---|---|---|
| 1 | 20.87 ± 0.36 | 20.76 ± 0.11 | 1.61 ± 0.18 | 1.35 ± 0.16 |
| 2 | 19.93 ± 2.01 | 19.64 ± 1.95 | 2.05 ± 0.15 | 1.65 ± 0.20 |
| 3 | 20.77 ± 0.30 | 20.47 ± 0.18 | 1.95 ± 0.16 | 1.63 ± 0.21 |
| 4 | 21.30 ± 0.38 | 21.04 ± 0.16 | 1.84 ± 0.16 | 1.50 ± 0.09 |
| 5 | 21.10 ± 0.07 | 20.78 ± 0.10 | 2.06 ± 0.07 | 1.51 ± 0.08 |
| 6 | 20.44 ± 0.17 | 21.21 ± 0.14 | 1.51 ± 0.23 | 2.19 ± 0.09 |
| 7 | 20.70 ± 0.18 | 21.35 ± 0.33 | 1.56 ± 0.17 | 1.85 ± 0.15 |
| 8 | 20.89 ± 0.16 | 21.64 ± 0.14 | 1.53 ± 0.18 | 2.09 ± 0.08 |
| 9 | 20.63 ± 0.23 | 21.21 ± 0.69 | 1.53 ± 0.16 | 1.84 ± 0.14 |
| 10 | 20.60 ± 0.12 | 21.30 ± 0.10 | 1.45 ± 0.14 | 2.04 ± 0.09 |
| 11 | 15.92 ± 1.13 | 20.55 ± 1.56 | 5.61 ± 0.37 | 2.29 ± 0.76 |
| 12 | 20.65 ± 0.12 | 21.42 ± 0.11 | 1.47 ± 0.18 | 2.14 ± 0.06 |
| 13 | 20.66 ± 0.12 | 21.35 ± 0.10 | 1.50 ± 0.14 | 2.03 ± 0.08 |
| PPs Couple | SINAD (dB) | THDF (%) | ||
|---|---|---|---|---|
| 1 | 23.71 ± 0.21 | 19.91 ± 0.49 | 0.32 ± 0.13 | 1.27 ± 0.32 |
| 2 | 24.32 ± 0.03 | 21.00 ± 0.05 | 0.30 ± 0.04 | 1.23 ± 0.10 |
| 3 | 24.29 ± 0.47 | 21.53 ± 0.08 | 0.36 ± 0.14 | 1.20 ± 0.10 |
| 4 | 24.64 ± 0.01 | 21.84 ± 0.02 | 0.38 ± 0.19 | 1.20 ± 0.18 |
| 5 | 24.14 ± 0.37 | 21.23 ± 0.86 | 0.36 ± 0.06 | 1.20 ± 0.21 |
| 6 | 24.65 ± 0.03 | 21.49 ± 0.04 | 0.37 ± 0.04 | 1.34 ± 0.10 |
| 7 | 24.86 ± 0.01 | 21.88 ± 0.04 | 0.43 ± 0.07 | 1.28 ± 0.10 |
| 8 | 24.90 ± 0.01 | 22.01 ± 0.02 | 0.39 ± 0.15 | 1.24 ± 0.11 |
| 9 | 24.98 ± 0.02 | 21.26 ± 0.04 | 0.38 ± 0.11 | 1.26 ± 0.14 |
| 10 | 25.12 ± 0.02 | 24.49 ± 0.12 | 0.31 ± 0.04 | 1.22 ± 0.03 |
| 11 | 25.56 ± 0.23 | 21.58 ± 0.76 | 0.76 ± 0.05 | 1.26 ± 0.45 |
| 12 | 25.46 ± 0.05 | 21.61 ± 0.12 | 0.43 ± 0.04 | 2.01 ± 0.23 |
| 13 | 25.52 ± 0.02 | 21.66 ± 0.13 | 0.50 ± 0.16 | 1.72 ± 0.17 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schinaia, L.; Scorza, A.; Botta, F.; Rossi, A.; Maiozzi, R.; Orsini, F.; Sciuto, S.A. A Novel, Low-Cost and Reliable Workbench for Optimal Voltage Distribution on Piezoelectric Array Actuators. Actuators 2019, 8, 6. https://doi.org/10.3390/act8010006
Schinaia L, Scorza A, Botta F, Rossi A, Maiozzi R, Orsini F, Sciuto SA. A Novel, Low-Cost and Reliable Workbench for Optimal Voltage Distribution on Piezoelectric Array Actuators. Actuators. 2019; 8(1):6. https://doi.org/10.3390/act8010006
Chicago/Turabian StyleSchinaia, Lorenzo, Andrea Scorza, Fabio Botta, Andrea Rossi, Roberto Maiozzi, Francesco Orsini, and Salvatore Andrea Sciuto. 2019. "A Novel, Low-Cost and Reliable Workbench for Optimal Voltage Distribution on Piezoelectric Array Actuators" Actuators 8, no. 1: 6. https://doi.org/10.3390/act8010006
APA StyleSchinaia, L., Scorza, A., Botta, F., Rossi, A., Maiozzi, R., Orsini, F., & Sciuto, S. A. (2019). A Novel, Low-Cost and Reliable Workbench for Optimal Voltage Distribution on Piezoelectric Array Actuators. Actuators, 8(1), 6. https://doi.org/10.3390/act8010006






