Design and Analysis of Novel Actuation Mechanism with Controllable Stiffness
Abstract
:1. Introduction
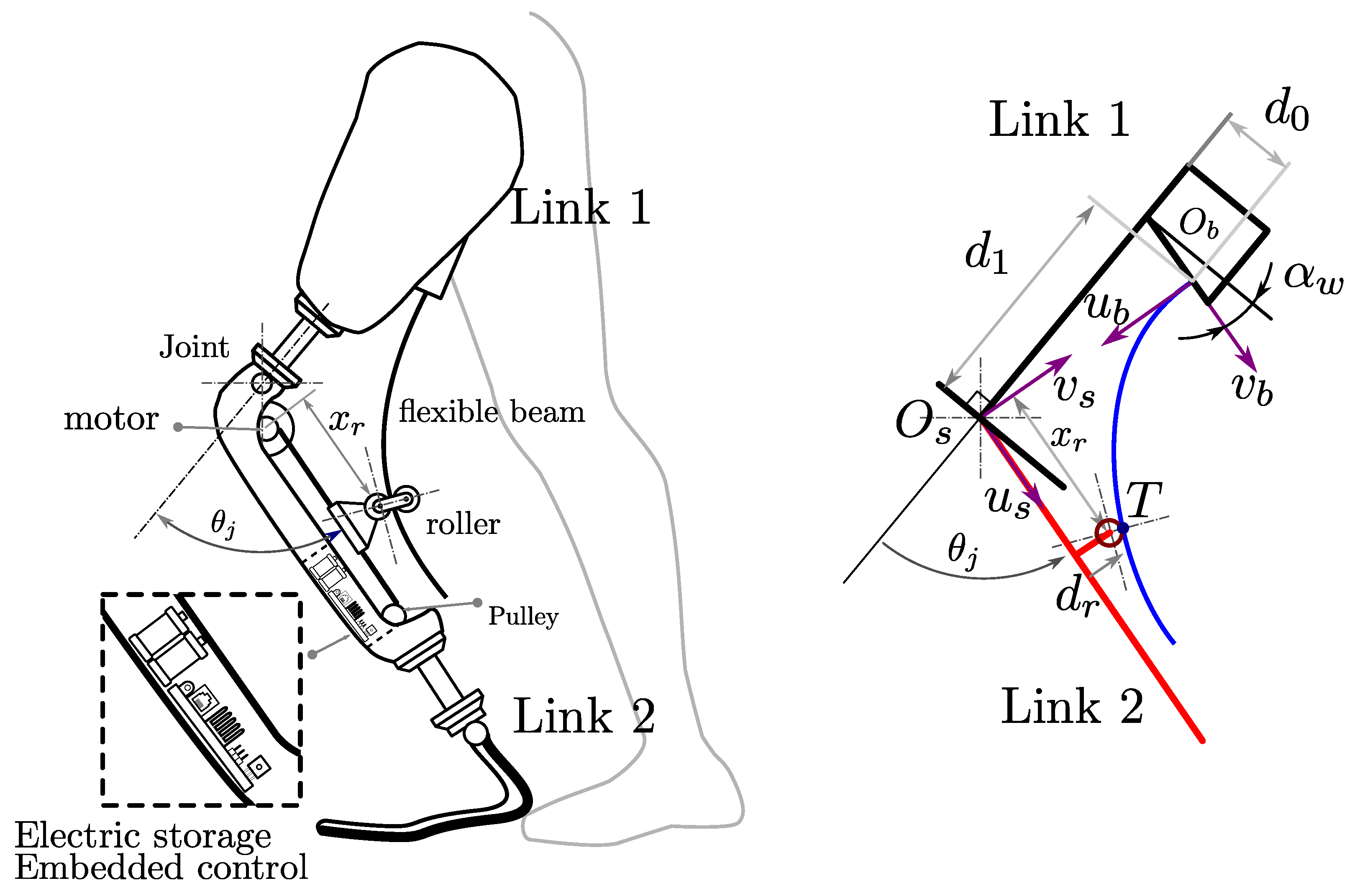
2. Design Concept
3. Geometry and Beam Deflection Statics
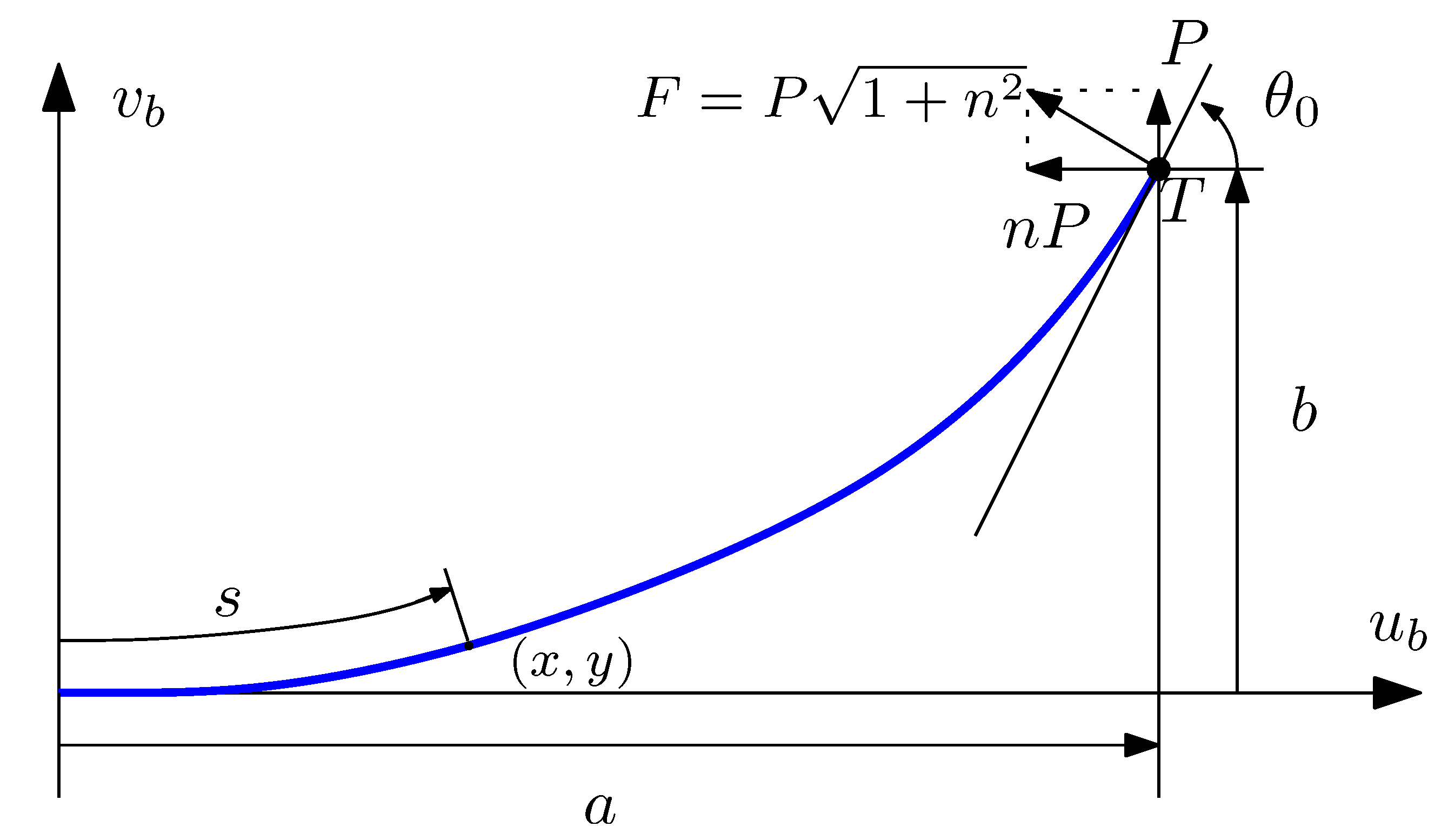
3.1. Large Beam Deflection Formulation
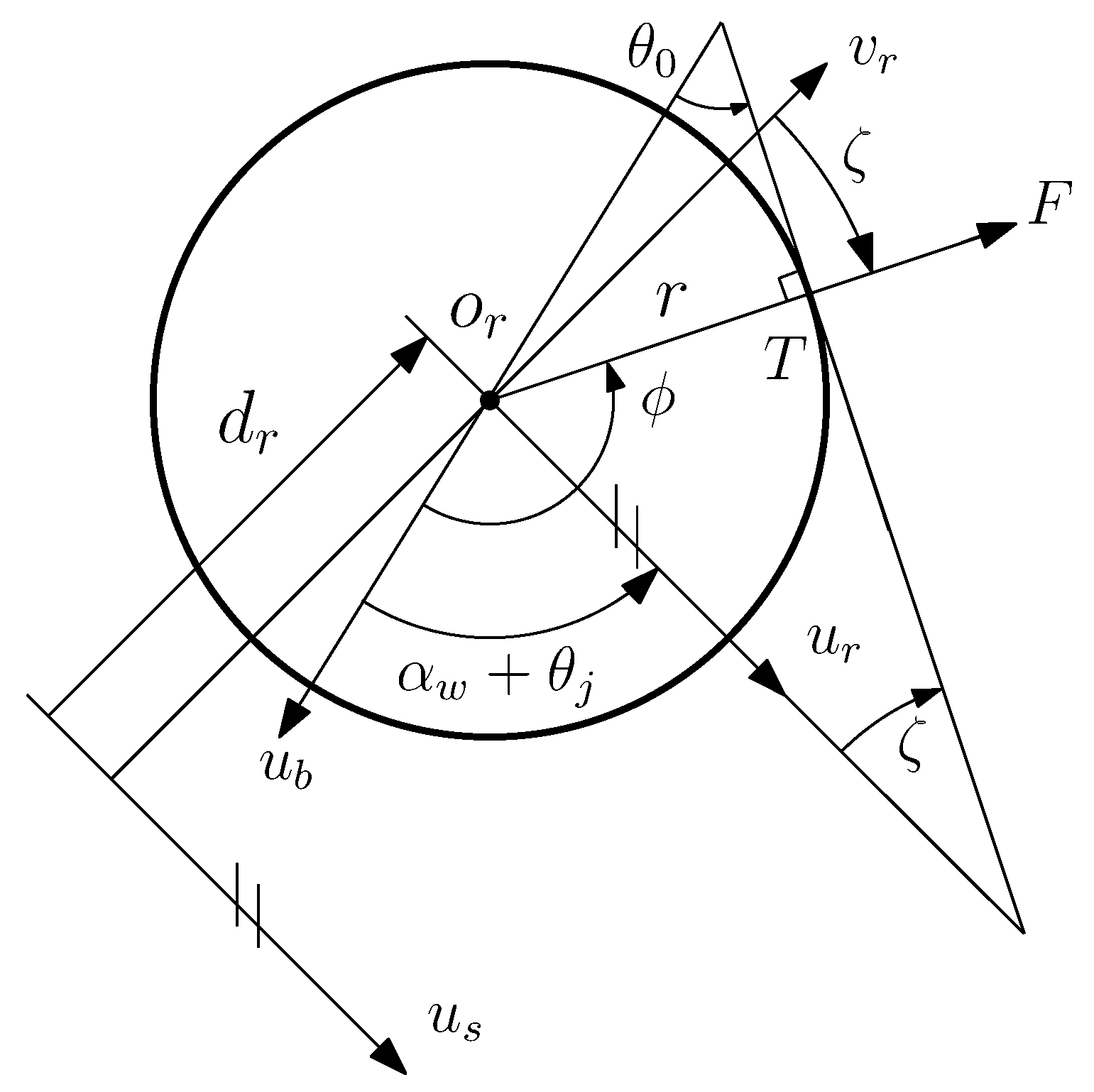
3.2. Rolling Contact Constraints
3.3. Numerical Solution Method
| Algorithm 1Solvebeam script. |
| Require:, , parameters of the beam and actuator. |
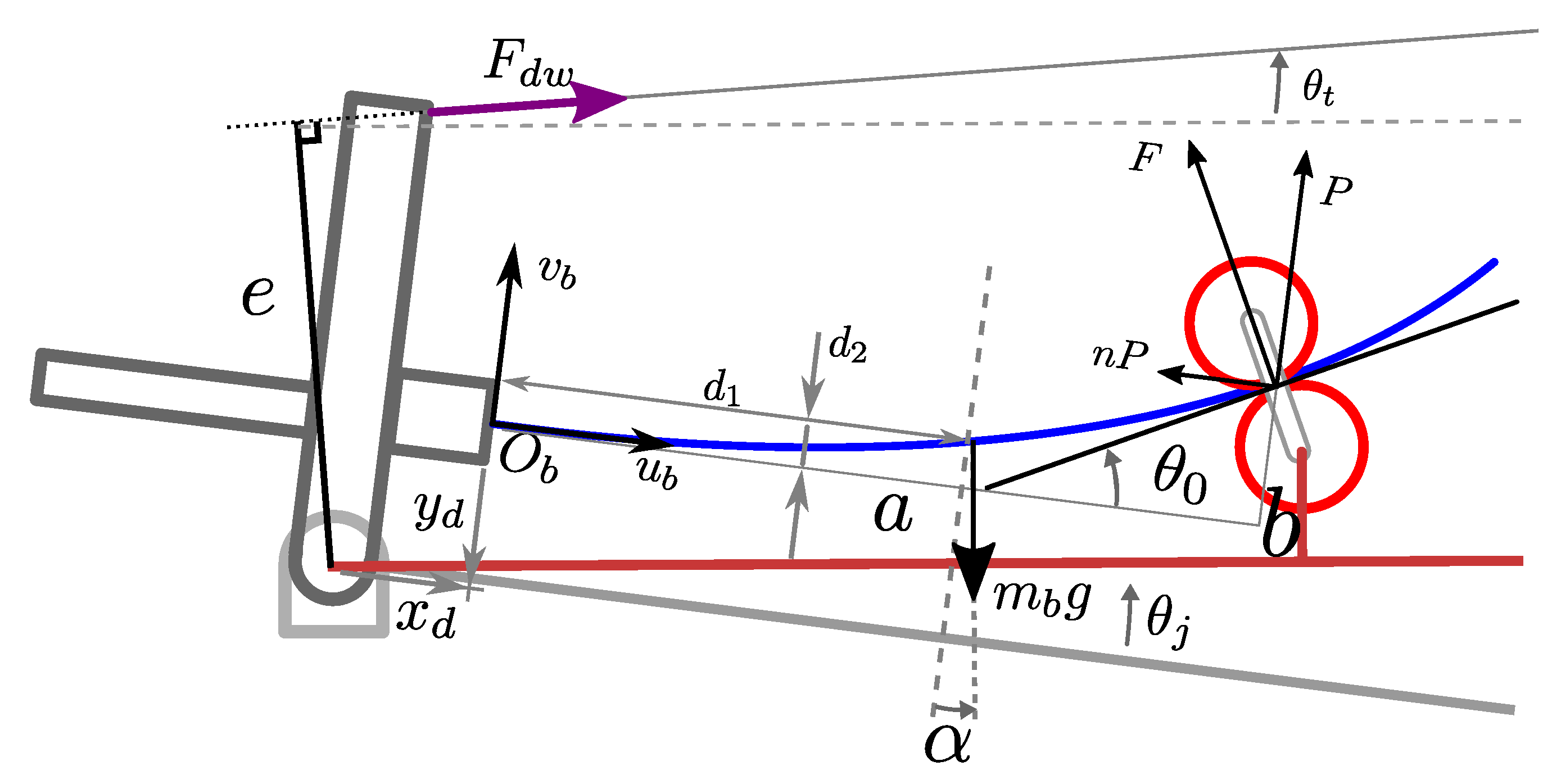
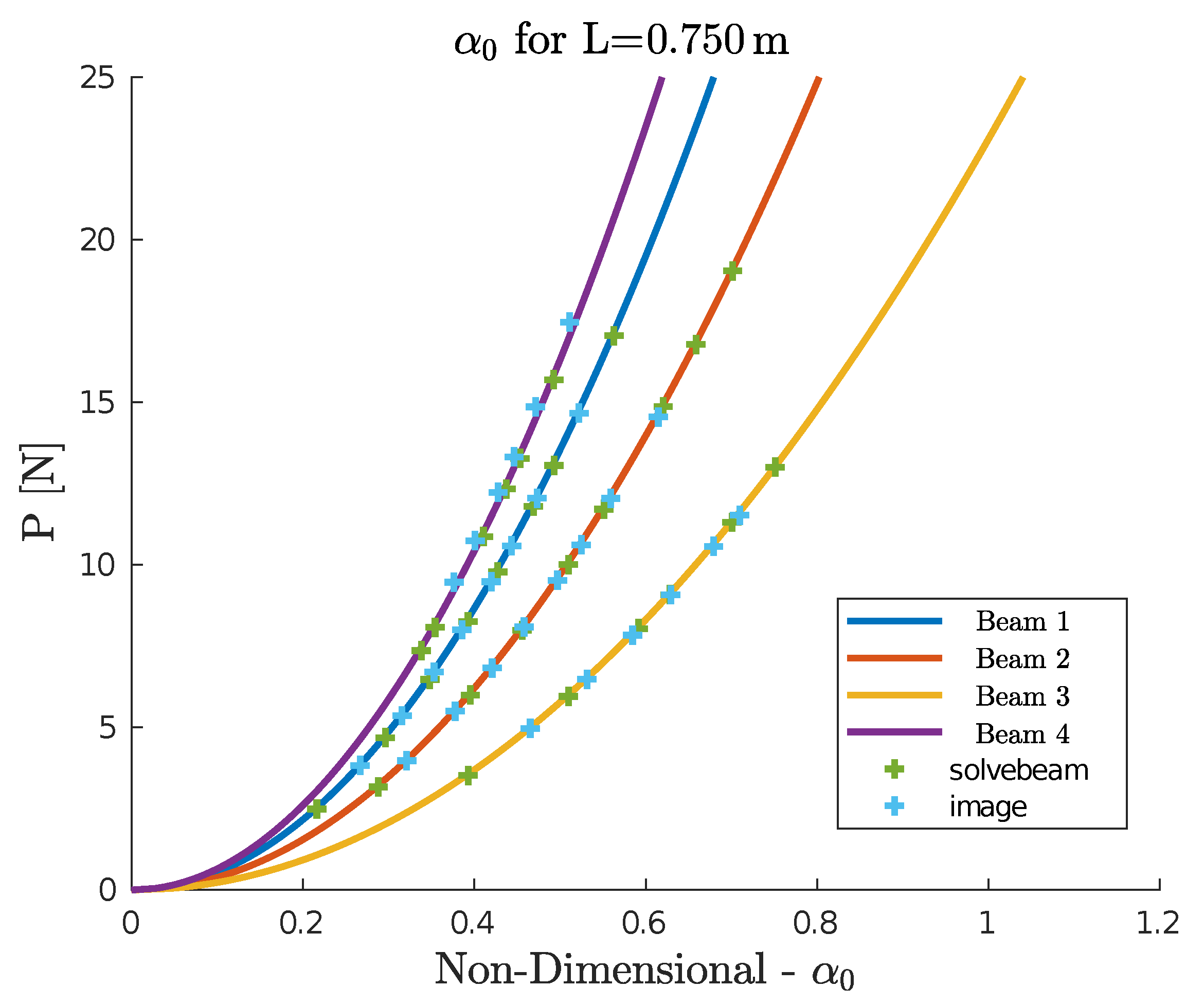
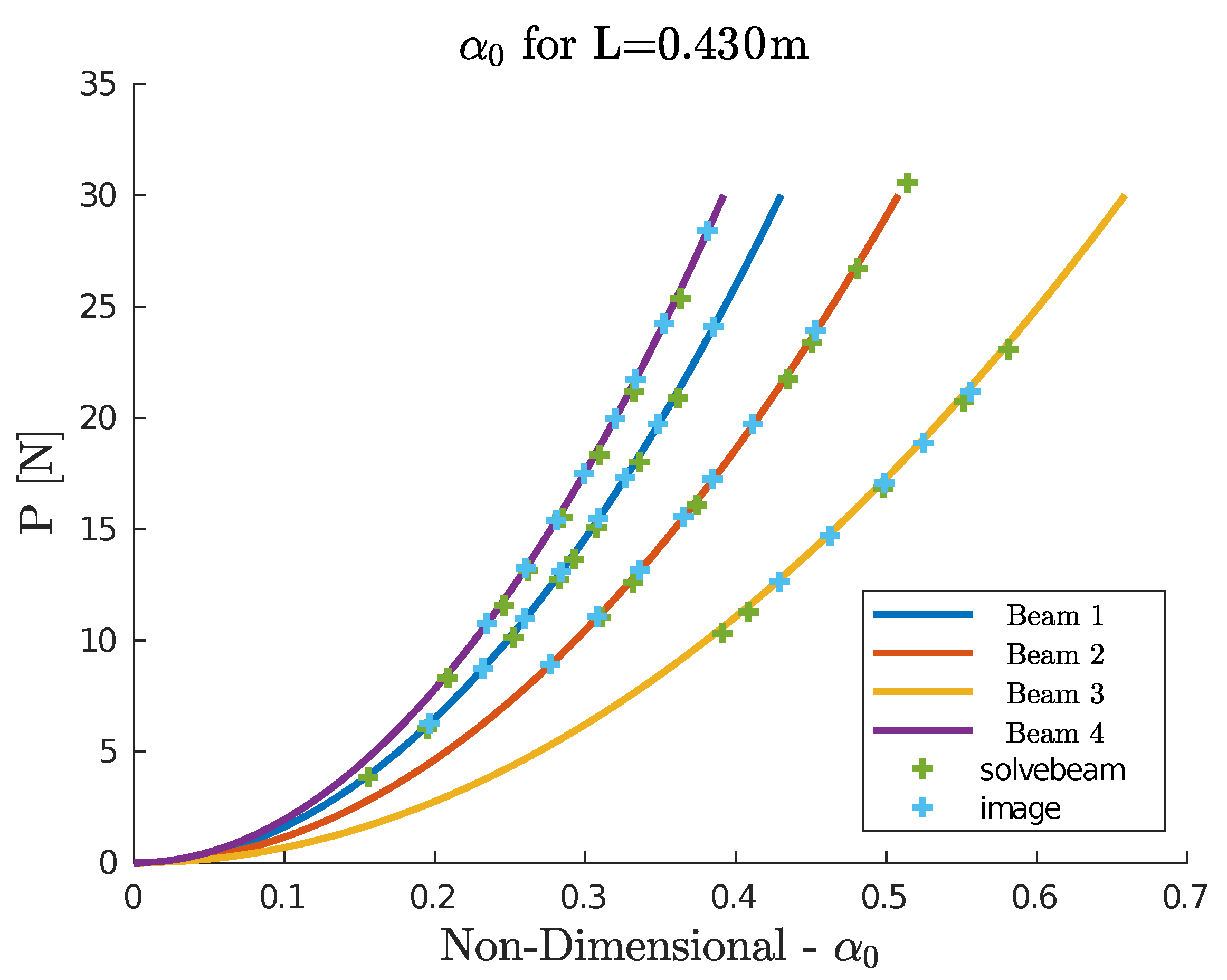
4. Experimental Validation
Experiment Methodology
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| VSA | Variable Stiffness Actuator |
| SEA | Series Elastic Actuation |
| DOF | Degree of Freedom |
| MIA | Mechanical Impedance Adjuster |
| LWR | Lightweight Robot |
| FEA | Finite-Element Analysis |
| PRBM | Pseudorigid-Body Model |
Appendix A
Appendix A.1. Transformations in Homogeneous Coordinates
References
- Zinn, M.; Khatib, O.; Roth, B.; Salisbury, J.K. Playing it safe [human-friendly robots]. IEEE Rob. Autom Mag. 2004, 11, 12–21. [Google Scholar] [CrossRef]
- Van Ham, R.; Sugar, T.G.; Vanderborght, B.; Hollander, K.W.; Lefeber, D. Compliant actuator designs. IEEE Rob. Autom. Mag. 2009, 16, 81–94. [Google Scholar]
- Wolf, S.; Grioli, G.; Eiberger, O.; Friedl, W.; Grebenstein, M.; Höppner, H.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.G.; et al. Variable stiffness actuators: Review on design and components. IEEE/ASME Trans. Mechatron. 2016, 21, 2418–2430. [Google Scholar] [CrossRef]
- Vanderborght, B.; Albu-Schäffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Rob. Autom. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Morita, T.; Sugano, S. Design and development of a new robot joint using a mechanical impedance adjuster. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 3, pp. 2469–2475. [Google Scholar]
- Morita, T.; Sugano, S. Development of 4-DOF manipulator using mechanical impedance adjuster. In Proceedings of the 1996 IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 2902–2907. [Google Scholar]
- Morita, T.; Sugano, S. Development and evaluation of seven DOF MIA ARM. In Proceedings of the 1997 IEEE International Conference on Robotics and Automation, Monterey, CA, USA, 10–11 July 1997; Volume 1, pp. 462–467. [Google Scholar]
- Petit, F.; Albu-Schäffer, A. State feedback damping control for a multi DOF variable stiffness robot arm. In Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; pp. 5561–5567. [Google Scholar]
- Verstraten, T.; Beckerle, P.; Furnémont, R.; Mathijssen, G.; Vanderborght, B.; Lefeber, D. Series and parallel elastic actuation: Impact of natural dynamics on power and energy consumption. Mech. Mach. Theory 2016, 102, 232–246. [Google Scholar] [CrossRef]
- Nasiri, R.; Khoramshahi, M.; Shushtari, M.; Ahmadabadi, M.N. Adaptation in variable parallel compliance: Towards energy efficiency in cyclic tasks. IEEE/ASME Trans. Mechatron. 2017, 22, 1059–1070. [Google Scholar] [CrossRef]
- Verstraten, T.; Geeroms, J.; Mathijssen, G.; Convens, B.; Vanderborght, B.; Lefeber, D. Optimizing the power and energy consumption of powered prosthetic ankles with series and parallel elasticity. Mech. Mach. Theory 2017, 116, 419–432. [Google Scholar] [CrossRef]
- Geeroms, J.; Flynn, L.; Jimenez-Fabian, R.; Vanderborght, B.; Lefeber, D. Energetic analysis and optimization of a MACCEPA actuator in an ankle prosthesis. Auton. Robots 2018, 42, 147–158. [Google Scholar] [CrossRef]
- Salisbury, J.K. Active stiffness control of a manipulator in cartesian coordinates. In Proceedings of the 1980 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980; Volume 19, pp. 95–100. [Google Scholar]
- Takakura, S.; Murakami, T.; Ohnishi, K. An approach to collision detection and recovery motion in industrial robot. In Proceedings of the 15th Annual Conference of IEEE Industrial Electronics Society (IECON’89), Philadelphia, PA, USA, 6–10 November 1989; pp. 421–426. [Google Scholar]
- Shetty, B.R.; Ang, M.H. Active compliance control of a PUMA 560 robot. In Proceedings of the 1996 IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 3720–3725. [Google Scholar]
- Burger, R.; Haddadin, S.; Plank, G.; Parusel, S.; Hirzinger, G. The driver concept for the DLR lightweight robot III. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 5453–5459. [Google Scholar]
- Bischoff, R.; Kurth, J.; Schreiber, G.; Koeppe, R.; Albu-Schäffer, A.; Beyer, A.; Eiberger, O.; Haddadin, S.; Stemmer, A.; Grunwald, G.; et al. The KUKA-DLR Lightweight Robot arm—A new reference platform for robotics research and manufacturing. In Proceedings of the 2010 41st International Symposium on Robotics (ISR) and 2010 6th German Conference on Robotics (ROBOTIK), Munich, Germany, 7–9 June 2010; pp. 1–8. [Google Scholar]
- De Luca, A.; Albu-Schaffer, A.; Haddadin, S.; Hirzinger, G. Collision Detection and Safe Reaction with the DLR-III Lightweight Manipulator Arm. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1623–1630. [Google Scholar]
- Fuchs, S.; Haddadin, S.; Keller, M.; Parusel, S.; Kolb, A.; Suppa, M. Cooperative bin-picking with time-of-flight camera and impedance controlled DLR Lightweight Robot III. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 4862–4867. [Google Scholar]
- Wang, W.; Loh, R.N.; Gu, E.Y. Passive compliance versus active compliance in robot-based automated assembly systems. Ind. Robot 1998, 25, 48–57. [Google Scholar] [CrossRef]
- Dahiya, A.; Braun, D.J. Efficiently tunable positive–negative stiffness actuator. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1235–1240. [Google Scholar]
- Braun, D.J.; Apte, S.; Adiyatov, O.; Dahiya, A.; Hogan, N. Compliant actuation for energy efficient impedance modulation. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 636–641. [Google Scholar]
- Khalaf, P.; Warner, H.; Hardin, E.; Richter, H.; Simon, D. Development and experimental validation of an energy regenerative prosthetic knee controller and prototype. In Proceedings of the ASME 2018 Dynamic Systems and Control Conference, Atlanta, GA, USA, 27–29 June 2018. [Google Scholar]
- Shepherd, M.K.; Rouse, E.J. The VSPA foot: A quasi-passive ankle-foot prosthesis with continuously variable stiffness. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2375–2386. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, M.K.; Rouse, E.J. Design of a quasi-passive ankle-foot prosthesis with biomimetic, variable stiffness. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6672–6678. [Google Scholar]
- Bisshopp, K.; Drucker, D. Large deflection of cantilever beams. Q. Appl. Math. 1945, 3, 272–275. [Google Scholar] [CrossRef]
- Zhang, A.; Chen, G. A comprehensive elliptic integral solution to the large deflection problems of thin beams in compliant mechanisms. J. Mech. Rob. 2013, 5, 021006. [Google Scholar] [CrossRef]
- Campanile, L.; Hasse, A. A simple and effective solution of the elastica problem. Proc. Ins. of Mech. Eng. C J. Mech. Eng. Sc. 2008, 222, 2513–2516. [Google Scholar] [CrossRef]
- Mattiasson, K. Numerical results from large deflection beam and frame problems analysed by means of elliptic integrals. Int. J. Numer. Methods Eng. 1981, 17, 145–153. [Google Scholar] [CrossRef]
- Saxena, A.; Kramer, S. A simple and accurate method for determining large deflections in compliant mechanisms subjected to end forces and moments. J. Mech. Des. 1998, 120, 392–400. [Google Scholar] [CrossRef]
- Banerjee, A.; Bhattacharya, B.; Mallik, A. Large deflection of cantilever beams with geometric non-linearity: Analytical and numerical approaches. Int. J. Non Linear Mech. 2008, 43, 366–376. [Google Scholar] [CrossRef]
- dos Santos, E.G.; Richter, H. Modeling and Control of a Novel Variable-Stiffness Regenerative Actuator. In Proceedings of the ASME 2018 Dynamic Systems and Control Conference, Atlanta, GA, USA, 27–29 June 2018. V002T24A003. [Google Scholar]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley & Sons, Inc.: New York, NT, USA, 2006; Volume 3. [Google Scholar]
- Bauchau, O.A.; Craig, J.I. Structural Analysis: With Applications to Aerospace Structures; Volume 163, Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Troughton, M. Handbook of Plastics Joining: A Practical Guide; William Andrew: Norwich, NY, USA, 2008. [Google Scholar]
- Genta, G.; Delprete, C. Some considerations on the experimental determination of moments of inertia. Meccanica 1994, 29, 125–141. [Google Scholar] [CrossRef]


| Material | Cross-Section () (mm) | Mass (kg) | E (MPa) |
|---|---|---|---|
| 6061 aluminum | 5.46 × 31.70 | 0.3823 | 70.8 |
| 6061 aluminum | 5.46 × 25.49 | 0.4044 | 63.1 |
| 1075 spring steel | 3.16 ×25.45 | 0.5646 | 194.0 |
| Low-carbon steel | 4.69 × 25.20 | 0.8440 | 169.2 |
| Material | ||||
|---|---|---|---|---|
| 6061 aluminum | 23.7 | 137.4 | 13.6 | 78.8 |
| 6061 aluminum | 29.4 | 137.4 | 16.9 | 78.8 |
| 1075 spring steel | 29.5 | 237.3 | 16.9 | 136.1 |
| Low-carbon steel | 29.8 | 159.9 | 17.1 | 91.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos, E.G.; Richter, H. Design and Analysis of Novel Actuation Mechanism with Controllable Stiffness. Actuators 2019, 8, 12. https://doi.org/10.3390/act8010012
dos Santos EG, Richter H. Design and Analysis of Novel Actuation Mechanism with Controllable Stiffness. Actuators. 2019; 8(1):12. https://doi.org/10.3390/act8010012
Chicago/Turabian Styledos Santos, Erivelton Gualter, and Hanz Richter. 2019. "Design and Analysis of Novel Actuation Mechanism with Controllable Stiffness" Actuators 8, no. 1: 12. https://doi.org/10.3390/act8010012
APA Styledos Santos, E. G., & Richter, H. (2019). Design and Analysis of Novel Actuation Mechanism with Controllable Stiffness. Actuators, 8(1), 12. https://doi.org/10.3390/act8010012






