Abstract
When an ultrathin and flexible steel plate is to be levitated, levitation control becomes difficult because the ultrathin steel plate undergoes increased flexure. We herein propose a levitation method for an ultrathin steel plate that is bent to an extent that does not induce plastic deformation. In this study, to investigate the levitation stability of an ultrathin steel plate, we applied disturbance cancellation control in the bending levitation system. The object of electromagnetic levitation was a rectangular zinc-coated ultrathin steel plate (SS400) of length 800 mm, 600 mm, and thickness 0.19 mm. The vibrator was attached below the three frames, in which the electromagnet unit was installed so that the frames could be vibrated up and down. We conducted experiments on the levitation performance when the electromagnet was displaced by the frame vibration in the bending levitation system. The results showed that a stable levitation can be achieved even with an input of external disturbance when levitating at the optimum bending angle.
1. Introduction
Recently, magnetic levitation technology that is capable of gripping and conveying objects in a non-contact manner has attracted attention, and active studies that use the characteristics of magnetic force, such as the electromagnetic suspension and induction repulsion methods, have been performed [1,2,3,4]. Thin steel plates are widely used as materials for automobiles, electric appliances, cans, and other products in current industries. With various industrial demands, the surface quality of steel plates continues to be enhanced. However, since a contact conveyance using rollers is mainly adopted in the process of a thin-steel-plate production line, the problem of surface quality deterioration still remains. It is expected that magnetic levitation technology can be applied to thin steel plate production processes, which require high surface quality. However, elastic vibration is induced because of the flexibility arising from the plate thickness and area; therefore, the stability at the time of levitation is significantly impaired. Prior research has indicated the size of the objective steel plate to be relatively small, and no successful report has been made on a stable noncontact conveyance system of a very thin steel plate, despite the increasing demand in the recent years [5,6]. In the past, our research group has constructed an electromagnetic levitation control system in which the relative distance between the electromagnet and a steel plate was maintained, aimed to prevent the steel plate from falling from the conveyor or contacting the electromagnet during electromagnetic levitation conveyance. Furthermore, we have proposed a method of levitating a thin steel plate with a thickness of less than 0.3 mm by moderately bending it beforehand [7,8,9]. This levitation method is a way of bending levitation within a range, not to plastically deform the steel plate, and the steel plate used in the experiment is a flat steel plate. The levitation stability was improved by bending and this subsequent stability was maintained through the input of external disturbances, such as control current or vibrating the frame where the electromagnet unit was installed [10]. However, the bending levitation system cannot obtain the same levitation stability as when no disturbance is present. In this study, we experimentally examine the bending levitation performance, in which disturbance cancellation control is applied to the bending levitation system.
2. System for Control Experiment
Figure 1 shows the electromagnetic levitation control system. Figure 2 shows a schematic illustration of the experimental apparatus. Figure 3 shows a photograph of the electromagnet. Figure 4 shows an electromagnet angle θ. Figure 5 shows a photograph of the experimental apparatus.
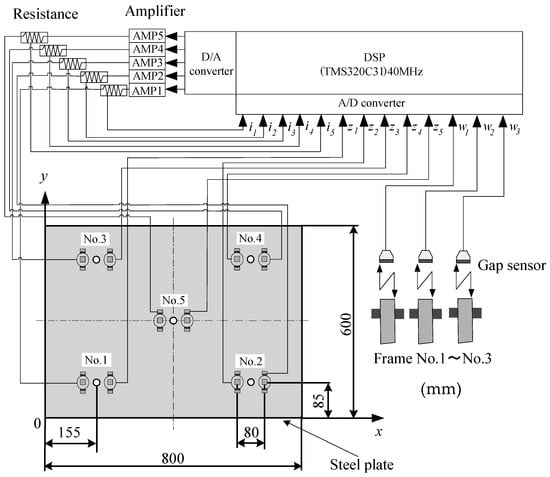
Figure 1.
Electromagnetic levitation control system.
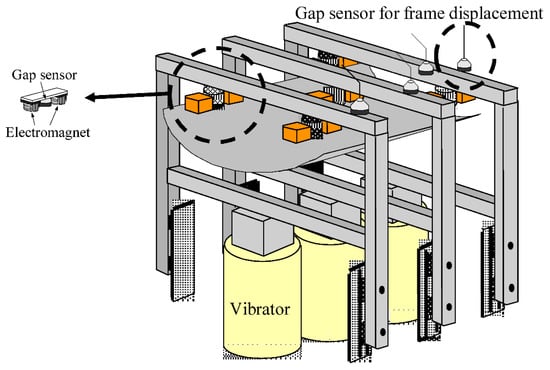
Figure 2.
Schematic illustration of the experimental apparatus.

Figure 3.
Photograph of an electromagnet.

Figure 4.
Electromagnet angle.
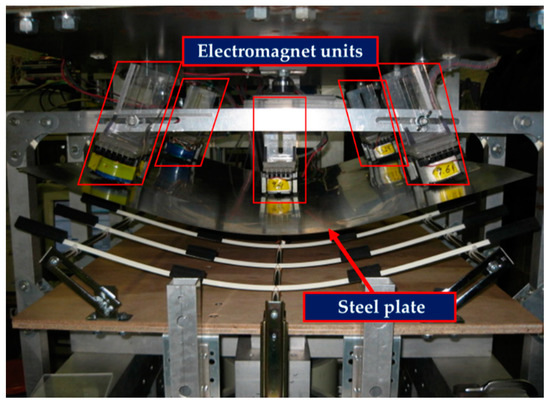
Figure 5.
Photograph of the experimental apparatus.
Table 1 shows eddy-current gap sensors. Table 2 shows the specifications of A/D and D/A converters used for experiments. Table 3 shows the specifications of amplifier. The object of electromagnetic levitation is a rectangular zinc-coated steel plate (SS400) of length a = 800 mm, width b = 600 mm, and thickness h = 0.19 mm. To accomplish the noncontact support of a rectangular ultrathin steel plate using five pairs of electromagnets (Nos. 1–5), as if the plate were hoisted by strings, the displacement of the steel plate (z1–z5) was measured by five eddy-current gap sensors. Among the five pairs of electromagnets, four pairs at the corners were inclined and a central electromagnet was moved in the vertical direction. In addition, the distance between the surface of the electromagnets and the steel plate was controlled at 5 mm, even when θ was changed. Thus, by moving the five electromagnets, the bending magnetic levitation of the steel plate was possible. Here, θ is defined as an electromagnet angle. The coil current (i1–i5) is detected from the external resistance for measurement.

Table 1.
The specification of five eddy-current gap sensors.

Table 2.
The specification of A/D converter and D/A converter.

Table 3.
The specification of an amplifier.
The vibrator shown in Figure 6 was attached below the three frames on which the electromagnet unit was installed, such that the frame could be vibrated up and down. Table 4 shows the specifications of the vibrator. After adjusting the amplitude and the phase of the frame to be constant using a sine wave of constant frequency, the steel plate was levitated while the frame was vibrating. In each frame, an eddy-current gap sensor was installed and the displacement of the frame during excitation was measured as (w1–w3). In this system, the sampling frequency was 1000 Hz.

Figure 6.
Photograph of the vibrator.

Table 4.
Specifications of the vibrator.
3. Equation of Motion
The vibrations of the steel plate include translation, roll, pitch, twist and elastic vibration. It is considered that these vibrations affect displacement of the steel plate at the sensor position. In this study, we considered that it was enough to levitate the steel plate when each electromagnet units controlled the gap exactly. Therefore, we adopted a one degree-of-freedom model. Figure 7 shows one degree-of-freedom model of levitation control of the steel plate. In this model, independent control is performed, in which the information on the detected values of displacement, velocity and coil current of the electromagnets under study at one position is fed back only to the same electromagnet. The steel plate is divided into five hypothetical masses and each part is modeled as a lumped constant system. In an equilibrium levitation state, the magnetic forces are determined to balance with gravity. The equation of motion around the equilibrium state of the steel plate subjected to magnetic forces is expressed as:
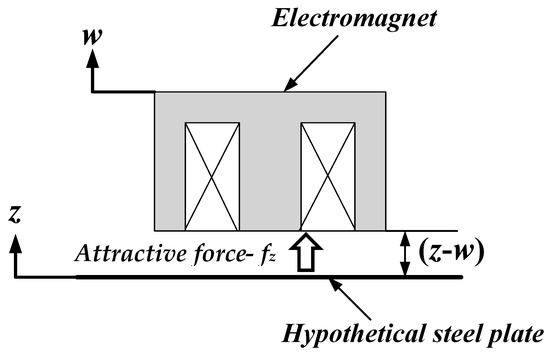
Figure 7.
One degree-of-freedom model of levitation control of the steel plate.
Here, mz: mass obtained by dividing the steel plate virtually into five [kg], z: displacement from the equilibrium levitation position of the steel plate [m], and fz: variation value of the attractive force per electromagnet [N].
The distance between the electromagnet and the steel plate is defined as Z = z(t) − w(t). Then, a component Leff/Z in inverse proportion to the distance Z and a component Llea corresponding to the leakage of the magnetic flux are added and approximated to obtain an inductance L per electromagnet as shown in the following equation:
The relational expression between the voltage applied to the electromagnet Vz and the current Iz flowing through the coil is expressed by the following equation when the resistance of the electromagnet coil is Rz.
When Taylor expansion is performed in the vicinity of the equilibrium point (Z0, Iz), the fluctuation value vz from the stationary voltage applied to the electromagnet coil is expressed by the following equation:
However, Lz is the inductance of the electromagnetic coil in the equilibrium levitation state, and it is assumed that it can be expressed by the following equation:
The equations relating to the electromagnet attractive force and the current concerning the current flowing in the electromagnet coil, which have undergone the linearization approximation, are as follows:
Here, Fz: total value of the static attractive forces generated from both electromagnets pairs in the equilibrium levitation state [N], Z0: gap between the electromagnet surface and the steel plate surface in the equilibrium levitation state [m], w: displacement of the frame, Iz: steady state current for obtaining static attraction force [A], iz: variation value of the current flowing through the electromagnet coil [A], Leff/Z0: effective inductance per electromagnet [H], Llea: leakage inductance per electromagnet [H], Lz: inductance of the electromagnetic coil in the equilibrium levitation state [H], Rz: total resistance value of the electromagnet coil of the pair [Ω], vz: fluctuation value from the stationary voltage applied to the electromagnet of the pair [V].
4. State Equation
The absolute displacement of the steel plate, absolute speed, the current flowing in the electromagnet coil, displacement of frame and speed are adopted as state variables. Subsequently, we summarize Equations (1) and (5)–(7) and obtain the following state equation:
However,
5. Control Theory
5.1. Optimal Control
In this study, a control system is constructed using a discrete time system; therefore, the evaluation function of a continuous system is digitized, and the control law is obtained based on the optimal control of the discrete time system [11].
where Q is a semi-regular matrix and H is a regular matrix. The feedback control input at this time is as follows:
where , , and are the feedback gains for the displacement, speed, and current, respectively, in the levitation control. Weighting coefficients are as follows.
The weighting factor at the time of creating the feedback gain was searched by trial and error and determined so that the displacement standard deviation for each control theory is equal when the electromagnetic angle θ = 0° in a state where without disturbance.
5.2. Disturbance Cancellation Control
Because the current feedback is performed, it is assumed that the temporary delay characteristic of the electromagnet coil is almost negligible. When the delay of the current due to the inductance is small, Equation (7) can be approximately expressed by the following equation.
Here, for the vibration isolation of the frame displacement w(t) in Equation (6), the control input of the disturbance cancellation control using the optimum control is obtained by the following equation:
Because the control voltage (t) is equal to (t) in the equilibrium levitation state, the control current (t) can be expressed by Equations (16) and (17), expressed cumulatively as follows:
By substituting Equation (18) into Equation (6), the fluctuation component , the absolute displacement z(t) of the steel plate, and the absolute velocity of the attractive force applied to the steel plate in the equilibrium state as the control object, are 0, and the feedforward gain is expressed by the following equation:
6. Levitation Experiment
We conducted preliminary experiments as a set of disturbances, assuming actual usage environment. We measured the resonance frequency of the steel plate as the most severe to the steel plate. Additionally, we set the vibration of the disturbance to be the band containing the resonance frequency (0–10 Hz) of the steel plate. We conducted experiments to make the steel plate (thickness 0.19 mm) bending levitation under disturbance conditions [10]. As a result, it was found that the levitation performance is the best at the electromagnet angle of 13°. In this report, to compare the control method with previous studies, the experiment was conducted at the electromagnet angle of 0° and 13°.
A random external disturbance in the frequency range between 0 and 10 Hz was added to all frames, and the levitation performance was evaluated by comparing the standard deviation of the displacement and levitation probability for each electromagnet angle. The standard deviation of the displacement was measured 10 times for each electromagnet angle, and the average values of these results were used as the experimental value. To eliminate the influence of the transient state, measurements were performed approximately 10 s after the start of levitation. The levitation probability is considered successful when it continues for at least 30 s and the levitation performance is calculated as a percentage of successful levitations among 50 trials.
Figure 8 shows the time history of displacement and amplitude spectral of the vibrating frames by the random disturbance. Figure 9 shows the time history of displacements and amplitude spectrums of the bending levitation resulting when vibrating the frames by the random disturbance: (a) optimum control (b) disturbance cancellation control. From Table 5, although the standard deviation of displacement of the steel plate was 0.129 mm when using the optimum control, it was 0.092 mm when using the disturbance cancellation control, a reduction of approximately 30%. Figure 9 shows that the peak near 10 Hz in the optimum control was significantly reduced by using the disturbance cancellation control. Table 6 shows that the levitation probability is 86% when using the optimal control and 96% when using the disturbance cancellation control. Thus, the levitation probability was improved. The results above show that by controlling the vibration transmitted to the electromagnets using the disturbance cancellation control, the elastic vibration can be suppressed and a stable magnetic levitation control can be performed.
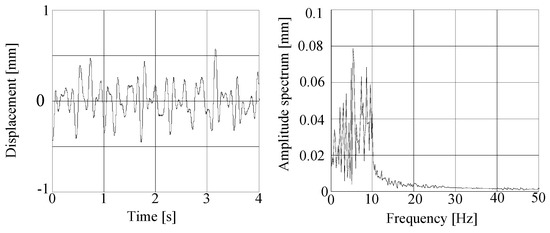
Figure 8.
Time histories of displacement and amplitude spectrums of vibrating frames by random disturbance.
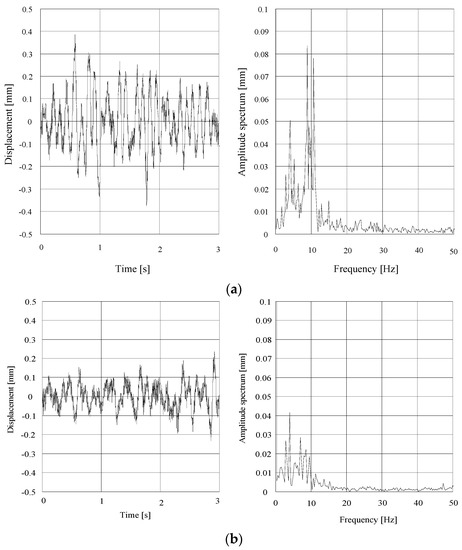
Figure 9.
Bending levitation result when vibrating frames by the random disturbance (θ = 13°). (a) Optimal control; (b) Optimal control with disturbance cancellation control.

Table 5.
Standard deviation of displacement.

Table 6.
Levitation probability when vibrating frames by the random disturbance (θ = 13°).
7. Conclusions
In this study, we conducted experiments on the levitation performance when the electromagnet was displaced by the frame vibration in the bending levitation system. The results showed that a stable levitation can be established even with an input external disturbance when using the disturbance cancellation control. In the future, we intend to conduct bending levitation experiments to verify the effectiveness of the bending levitation system when using other plate thicknesses and different control methods in the vibrating frame.
Author Contributions
K.O., M.T., T.N. and H.K. Wrote the paper; K.O. carried out the experiments; M.T. contributed the analyses of the data; T.N. and H.K. contributed the design of the controller and electric circuit. T.N. did project administration. H.K. did supervision.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carl, R.K.; Samir, M.T. Robust Adaptive Control of Unbalance Response for a Flexible Rotor. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1997, 40, 599–606. [Google Scholar]
- Kim, C.; Kim, K.; Yu, J.; Cho, H. Dynamic performance evaluation of 5-DOF magnetic levitation and guidance device by using equivalent magnetic circuit model. IEEE Trans. Magn. 2013, 49, 4156–4159. [Google Scholar] [CrossRef]
- Perini, E.; Giunchi, G.; Geri, M.; Morandi, A. Experomental and Numerical Investigation of the Levitaton Force between Bilk Permanent Magnet and Mg B2 Disk. IEEE Trans. Appl. Supercond. 2009, 19, 2124–2128. [Google Scholar] [CrossRef]
- Javed, A.; Mizuno, T.; Takasaki, M.; Ishino, Y.; Hara, M.; Yamaguchi, D. Lateral Vibration Suppression by Varying Stiffness Control in a Vertically Active Magnetic Suspension System. Actuators 2018, 7, 21. [Google Scholar] [CrossRef]
- Matsumoto, S.; Arai, Y.; Nakagawa, T. Noncontact Levitation and Conveyance Characteristics of a very Thin Steel Plate Magnetically Levitated by a LIM-Driven Cart. IEEE Trans. Magn. 2014, 50, 8600304. [Google Scholar] [CrossRef]
- Namerikawa, T.; Mizutani, D.; Kuroki, S. Robust H.INF. DIA Control of Levitated Steel Plates. IEEJ Trans. Ind. Appl. 2016, 126, 1319–1324. [Google Scholar] [CrossRef]
- Yonezawa, H.; Marumori, H.; Narita, T.; Hasegawa, S.; Oshinoya, Y. Bending Magnetic Levitation Control for Thin Steel Plate (Experimental Consideration Using Sliding Mode Control). In Proceedings of the International Power Electronics Conference -ECCE ASIA-, Hiroshima, Japan, 18–21 May 2014. [Google Scholar]
- Tada, M.; Yonezawa, H.; Marumori, H.; Narita, T.; Kato, H. Evaluation of levitation performance of bending flexible steel plate considering elastic mode. Trans. Magn. Soc. Jpn. (Spec. Issues) 2017, 1, 70–75. [Google Scholar]
- Tada, M.; Yonezawa, H.; Marumori, H.; Narita, T.; Kato, H. Integrated control of bending levitation for flexible steel plate using sliding mode control. J. Jpn. Soc. Appl. Electromagn. Mech. 2017, 25, 82–87. [Google Scholar] [CrossRef]
- Tada, M.; Yonezawa, H.; Marumori, H.; Narita, T.; Kato, H.; Moriyama, H. Basic Study on Maglev System for Flexible Steel Plate with Curvature: Effect on Levitation Performance under Disturbance. In Proceedings of the 18th International Symposium on Applied Electromagnetics and Mechanics, Chamonix Mont Blanc, France, 3–6 September 2017. [Google Scholar]
- Hasegawa, S.; Ohta, N.; Oshinoya, Y.; Ishibashi, K. Disturbance Cancellation Control of Electromagnetic Levitation System for Thin Steel Plate (Basic Research on Rigid Steel Plate). Proc. Sch. Eng. Tokai Univ. Ser. E 2004, 44, 67–73. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).