1. Introduction
In the biological body, different muscles have similar general functionality but vary in contraction properties (e.g., maximum contraction speed and maximum isometric force). In robotics, we may replicate this by different actuator types (e.g., electric motors, and pneumatic and hydraulic actuators). Electric motors (EM) are widely utilized in legged robots (e.g., Asimo [
1] and HRP-4 [
2]). These actuators are able to achieve the precise position or torque control. Because of their high torque-velocity range, high performance in continuous operation with constant speeds and precision in position (torque) control, they are suitable for manipulation (e.g., in industrial robots). However, in a hybrid task of legged locomotion suffering from impacts, requiring efficient actuation in a wide range of torque/velocity and having close interaction with uncertain environment, EMs loose part of their fortes. In addition, steady gaits as rhythmic movements, comprise combinations of periodic motions. Therefore, employing compliant actuators that can easily change their natural frequency in legged robots facilitate locomotion.
Serial elastic actuators (SEAs, [
3]) provide the first requirement of artificial legged locomotory systems by adding flexibility to EMs [
4,
5,
6]. Furthermore, compared to a direct drive (rigid) EM, the SEA has lower impedance, higher impact resistance and higher energy efficiency [
7,
8,
9]. These advantages are achieved by storing and returning elastic energy during the loading/unloading cycle (mimicking the stretch-shortening cycles in human muscles, [
10]). Nevertheless, this is not sufficient for adapting to different gait conditions (e.g., speed) while keeping performance, efficiency and robustness against uncertainties and perturbations. In contrast to SEAs, human muscles can adapt compliance to cope with challenges such as changing ground conditions (e.g., damping, stiffness [
11], rough terrains [
12], recovering from perturbations [
13]) and changing the motion speed [
14].
To overcome this limitation of SEAs, stiffness adjustment was introduced in variable impedance actuators (VIA) [
15]. VIAs are usually constructed by adding another EM (e.g., a direct drive servo motor) to the actuator design to control spring stiffness (e.g., via changing the lever arm or preloading of the spring) [
16]. It improves the controllability of the output which is useful for enabling legged robots to cope with changing ground conditions and changing the motion speed efficiently. However, the controller and the mechanical design are necessarily much more complex [
15,
16] than EM and SEA. Furthermore, in such designs, the second actuator of VIA usually has low power and low bandwidth in order to permit spring stiffness adjustment. Hence, the second actuator of VIA is not designed to be employed as a power generator. In addition, both EMs continuously consume power during all movements when they are back-drivable (e.g., as in the humanoid robot Veronica [
16]), and hence are not energy efficient. Therefore, VIAs can reduce the required power, but not the torque [
8,
17]. We need an actuator which can overcome these disadvantages of VIAs.
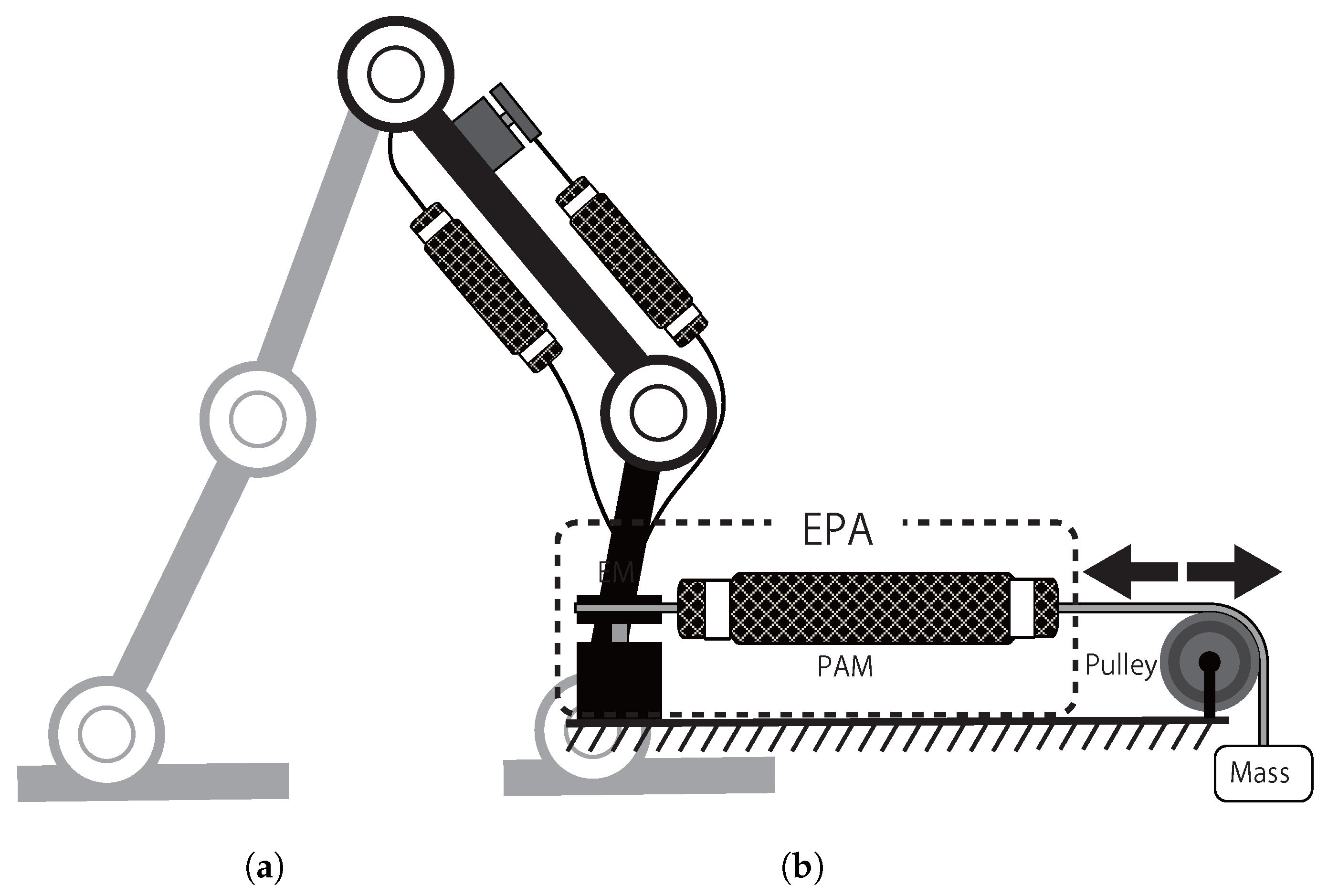
Our solution is a new hybrid Electric-Pneumatic Actuator (EPA) which combines pneumatic artificial muscles (PAM) with electric motors (EM) (e.g., as shown in
Figure 1a). In contrast to EMs, pneumatic actuators are well-suited to mimic compliant behavior, but they fail in accurate control (e.g., position control) [
18,
19]. PAMs are similar to biological muscles [
20] having nonlinear force-length relationship. Hence, PAMs can be considered as the adjustable stiffness (like a preloaded spring [
15]) beside EM to develop a new variable impedance actuator. Compared to EMs, PAMs are compliant, cheap and lightweight, but they have low bandwidth. As both EM and PAM individually cannot well replicate biological actuation, we propose combining them to better match the requirements for legged locomotion. In EPA, the PAM can be used: (i) as a fixed adjustable compliance; (ii) for energy management as a separate actuator to inject or absorb energy; and (iii) a passive nonlinear spring with muscle-like force-length relationship. It is noticeable that based on the actuators’ properties and with inspiration from human motor control, we can avoid increasing control complexity which might be expected from combining two different actuators.
In the first case, changing the stiffness can be used for two targets: (1) presetting of the actuator impedance for a fixed periodic motion with a determined gait characteristic (e.g., frequency); and (2) adapting the compliance during each step. For the first target, required energy in PAMs are ignorable. For the second target, an optimal solution can be found to compromise between energy expenditure in PAM and EM to minimize the total energy. In this paper, we show the advantages of the EPA regarding the first target both in the simulations and experiments. When we close the valves energy consumption in the PAM is minor. Thus, with a pressurized air tank, we just need to open and close the valves once for each frequency. Suppose that the actuator is used for steady walking (e.g., at regular speed). We only need to set the pressure of each muscle to a predefined value which is optimal for the periodic motion at that frequency. Hence, for steady state movement at a certain frequency the required energy to switch the valves is ignorable compared to the total energy required during that gait (e.g., 10 min walking).
To develop the new actuator, first we need a precise dynamic model of PAMs and EMs. Electric motors have well-accepted precise models, while PAMs are not well studied in the literature. In this paper, we examined two different static and dynamic models and presented a new model to identify our PAM dynamic behavior to be employed in EPA. An experimental setup was built to provide data for developing a dynamic model of EPA. Then, simulation studies were performed to verify the capabilities of the new actuator in producing periodic movement, required for legged locomotion. Finally, we tested how PAM compliance adjustment (by setting the air pressure) can reduce energy consumption in periodic movement required in legged locomotion. This last experiment was performed in a knee joint of a bioinspired bipedal robot (BioBiped3 [
21]).
2. Electric-Pneumatic Actuator
In this section, we present the concept, model and implementation of the EPA, the hybrid Electric-Pneumatic Actuator. As mentioned in
Section 1, the goal of combining the two actuators is to benefit from the advantages of both actuators without increasing control complexity and probable side effects, as much as possible. Therefore, we take the following steps: (i) developing a hardware setup and doing identification experiments; (ii) developing a model of EPA based on hardware experiments; (iii) simulation analysis using the model developed in Step ii; and (iv) doing some preliminary hardware experiments with BioBiped3 robot as a proof of concept. For simplifying control of periodic movements in locomotion, we divide motion control into two sub-tasks performing the periodic movement (position control) and tuning the natural frequency (with impedance control). This task distribution is a base for determining the role of EM and PAM in our actuation mechanism both in simulations and hardware experiments. Therefore, the PAM is mainly used for impedance (stiffness) adjustment while the EM is employed for position control. With this hybrid control, we can do both position, impedance, and consequently, force control in a simple way.
2.1. PAM Identification Setup
EPA is composed of electric motor (EM) and pneumatic air muscle (PAM). Since there is a well accepted model of the EM, here we focus on the PAM. A pneumatic artificial muscle is a membrane that expands radially and contracts axially when inflated. Accordingly, it can generate high pulling forces along the longitudinal axis [
22]. In this paper, we employ Mckibben type pneumatic artificial actuator which can control mechanical compliance by tuning air pressure. If the optimal pressure is supplied in advance, closed valves do not require energy during movement. In addition, if the robot is equipped with a filled air tank, there will be no energy loss during conducting task, except air leakage which is minor if the time and speed of the gait are moderate (e.g., walking at normal speed for 10 min).
In contrast to EM, there is no comprehensive dynamic model of PAM predicting relation between the muscle force, position and pressure [
20,
23,
24,
25,
26,
27,
28]. Chou et al. [
23] proposed an experiment-based static model containing only position and pressure term which is not suitable for a dynamic motion. To overcome the limitations of the static model, few dynamic models were introduced which are usually represent the best the studied setup. For example, Tang et al. [
26] proposed a dynamic model extending the static one by adding viscous damping and coulomb friction. Such models are reasonably fitted to their experimental setup, but applying it to our different setup is not preferred. To derive a precise model of EPA, we have developed our experimental setup including an EM in series with a PAM. First, we introduce a new dynamic model of PAM and then combine it with the model of EM to generate the EPA model. The goal is not developing a new general model for PAM, but a more precise simulation model of our EPA setup.
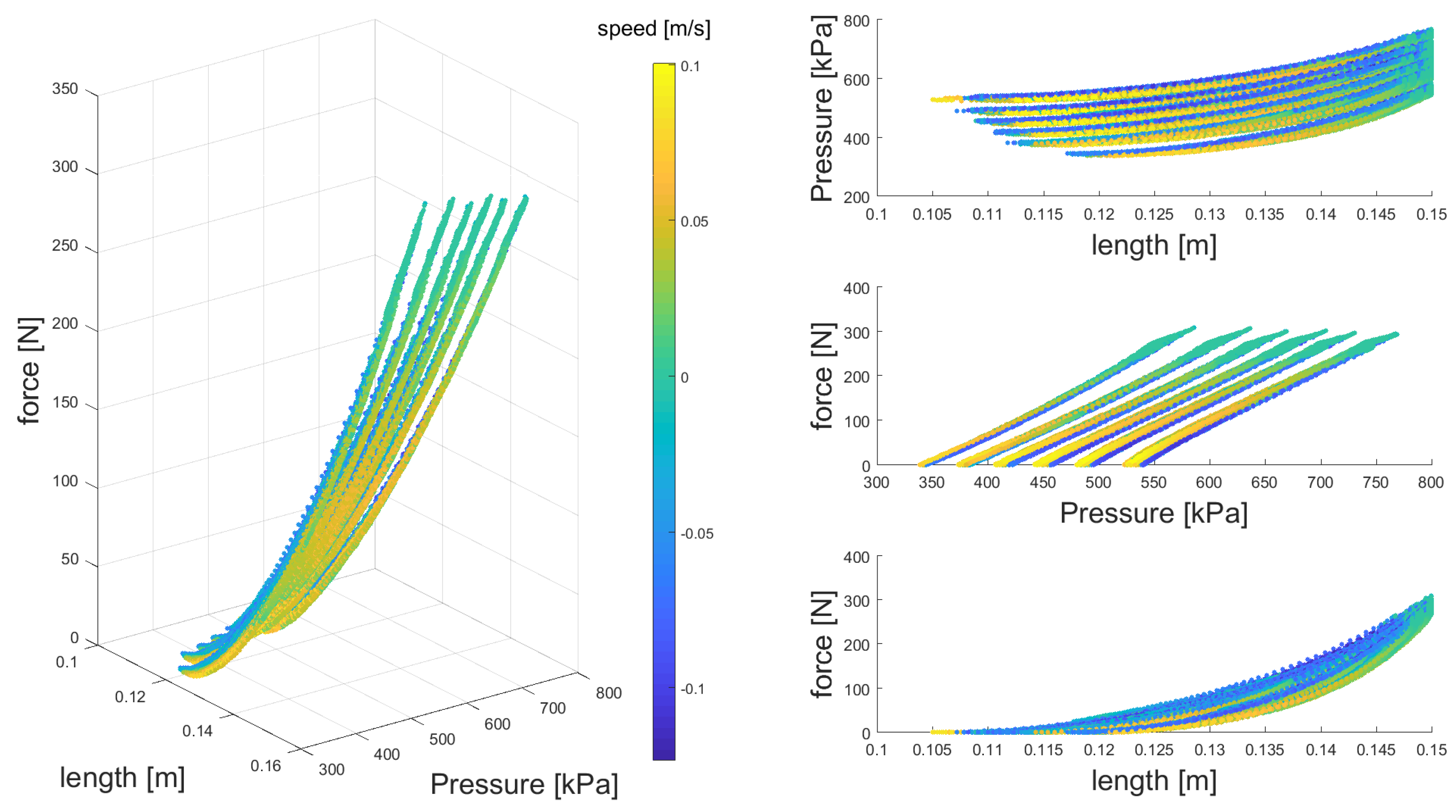
Our experimental setup to identify the PAM dynamic model included a brushless DC motor (120 W; Maxon, Sachseln, Switzerland), a force sensor (ALM-170; AMOS, Mannheim, Germany), and a self-made PAM connected by very stiff bylon straps (called non-stretchable nylon straps [
29]). We measured muscle force, displacement and pressure in a periodic movement with different magnitudes and frequencies. The PAM elongation was computed by the motor joint angle. The pressure inside the PAM was measured by an air pressure sensor (PSE 530; SMC, Tokyo, Japan). A set of Beckhoff EtherCAT terminals (EK1100, EL2124, EL3004, EL4034, and EL9011; Beckhoff, Verl, Germany) were used for controlling the motor and collecting data. A Matlab (MathWorks, Natick, MA, USA) xPC Target machine programmed by Matlab 2015b Simulink was used for the real time control of the setup.
The PAM was inflated with a certain amount of air in no load condition before each experiment. These initial pressure values were distributed uniformly between 460 kPa and 640 kPa (every 30 kPa). During each experiment, the motor speed was controlled with a randomized profile for 200 s. Except the motor encoder data, collected with a sampling rate of 500 Hz, all other sensors’ sampling rate were 1000 Hz. After data normalization, nonlinear regression analysis and curve fitting are employed to identify the PAM dynamic model.
2.2. Dynamic Model of PAM
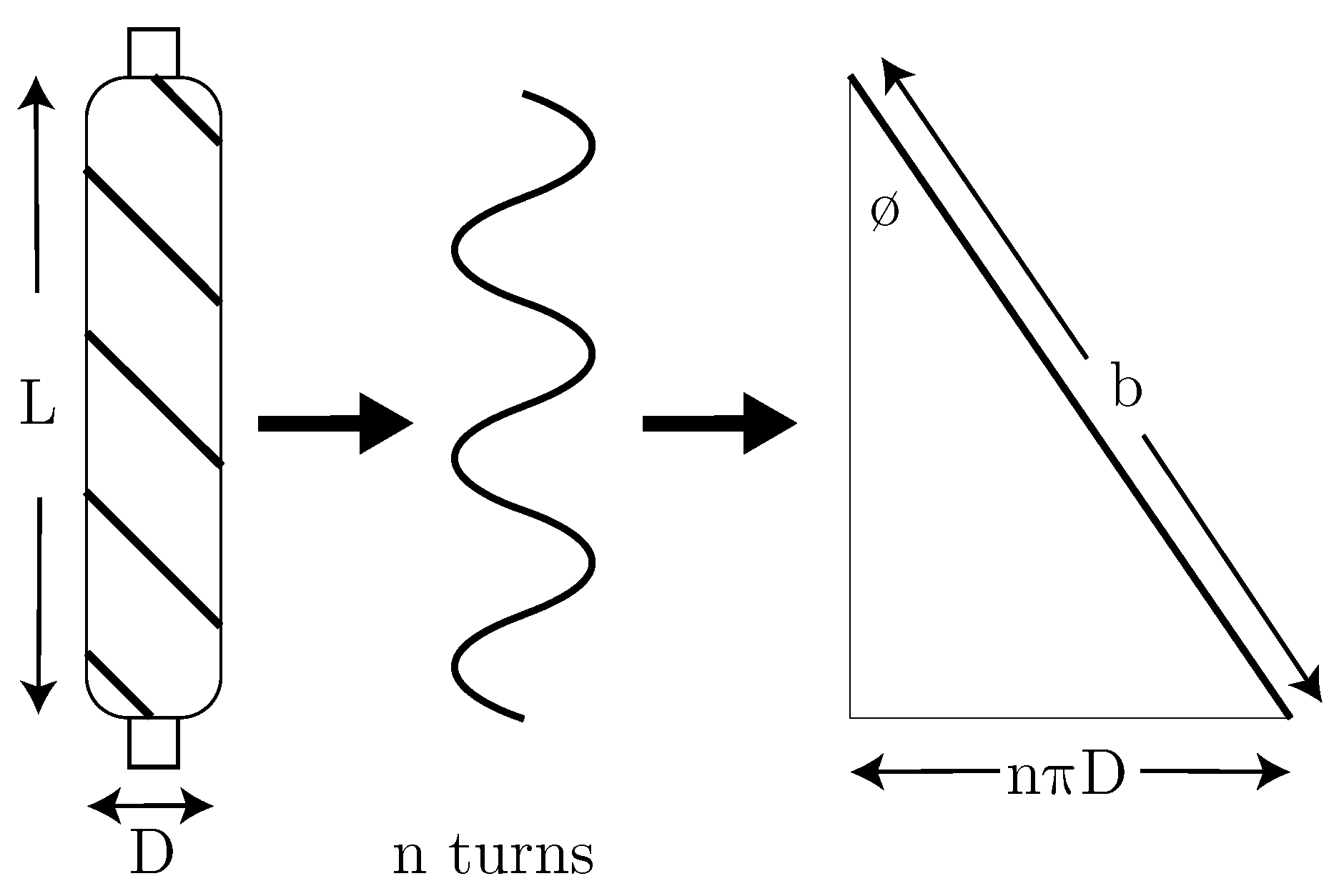
The simplest and most common model of PAM is the static one which uses the PAM length
L and pressure
P, to estimate the muscle force
.
in which
b and
n are the thread length and the number of turns for a single thread, respectively, as shown in
Figure 2. With a fixed thread length, the volume of the air muscle (
V) is calculated based on the muscle length as follows.
With a fixed amount of the air mass, changing the muscle length (from
to
) results in a different pressure (
) from the initial one (
). This can be calculated by the Boyle’s law:
Therefore, if the air mass is fixed, and the muscle length is changing, e.g., with an electric motor (see
Section 2.1) a unique relationship between the muscle force, pressure and length can be found using Equations (
1) to (
3). In this model, the effect of length changing speed (
) is not considered.
In [
26], a dynamic model presented including the static model, viscous damping and coulomb friction.
in which, Coulomb friction
is velocity-irrelevant and viscous damping
is dependent on velocity. Here,
and
are calculated by the following equations
where
,
,
and
(for
) are the coefficients to be determined and the
is contraction length. In addition,
is introduced as a correction term which is empirically approximated by
m as the constant hanging mass (see [
26] for details).
In this model, static part is different from the first model and different combinations of pressure, length and speed with various powers are multiplied to each other. This model might be overtuned to the specific experiments presented in [
26]. Inspired by this model, we have defined a new model. In our dynamic model, we employed a 3D order polynomial to approximate the PAM force as a function of muscle pressure, length and speed. First, we consider all possible multiplication of inputs (all terms of the 3D order polynomial) which will be 64 elements. Then, the smallest coefficient was removed and the approximation error is evaluated. If the error is below a threshold, this reduction procedure is repeated. This algorithm results in the following formulation for approximating muscle force.
in which
to
are the constant coefficients. Here, we found that all terms in the dynamic model of Tang et al. is not required, while two additional terms (
and
) are added. These two terms show a pressure dependent nonlinear damping behavior of the muscle. This could result in the hysteresis observed in actuation with PAMs.
Our model comprises the dynamic Equation (
8) besides Equations (
2) and (
3). We compared this model with the two aforementioned ones to find the most precise approximation to develop EPA model. The static model was selected because it is the most common model in the literature. The dynamic model of Tang et al. was chosen for its acceptable description of the physical phenomenon in PAM by employing viscous damping and coulomb friction terms. To evaluate the correlation between the model and the experimental results, the
coefficient was utilized. The results show that our method gives better approximation (higher
correlation) compared to the other two methods.
2.3. EPA Evaluation
Locomotion can be developed by a combination of oscillatory movements for different locomotor sub-functions. For any active oscillating mechanism (e.g., actuated spring-mass system), there exists a natural frequency, which needs the minimum effort to move. As mentioned before, our control strategy is splitting control of the oscillatory movement to position control by EM and tuning the natural frequency by the PAM. We test this idea in simulations and hardware experiments. The focus of the simulation study is on serial configuration while in the hardware experiment, the emphasis is on benefits of the parallel PAM.
2.3.1. Simulation Study
Considering an SEA controlled robot joint, it is shown that for a periodic movement (e.g., mimicking bouncing in locomotion), one optimal stiffness exists for each frequency. By adjusting the spring stiffness to this optimal value, the actuator can move the system states from any initial condition to the desired limit cycle and just compensate losses afterward. In the ideal case (without losses), the motor may rest after reaching the limit cycle. With SEA it is not possible to change the stiffness. However, in EPA, PAM air pressure can be used to adjust the actuator stiffness and consequently the impedance. Using the new model of PAM, we developed an EPA simulation model with serial configuration and showed how fine-tuning of PAM results in an efficient control by EM. For example, in a bouncing gait, the optimal muscle stiffness for different hopping conditions (e.g., frequency) can be identified with this approach. Note that the additional energy for adjusting the PAM (compared to SEA) is required just once for each hopping condition and, after reaching the limit cycle, PAM does not spend any extra energy with closing the valves. Still, the control complexity of the EPA is similar to that of an SEA.
The serial EPA (PAM in series with EM) model is simulated in MATLAB using the proposed dynamic model of the PAM. In this study, we investigate how this arrangement can increase efficiency of the periodic movement. In this simulation a mass is connected to the EPA (
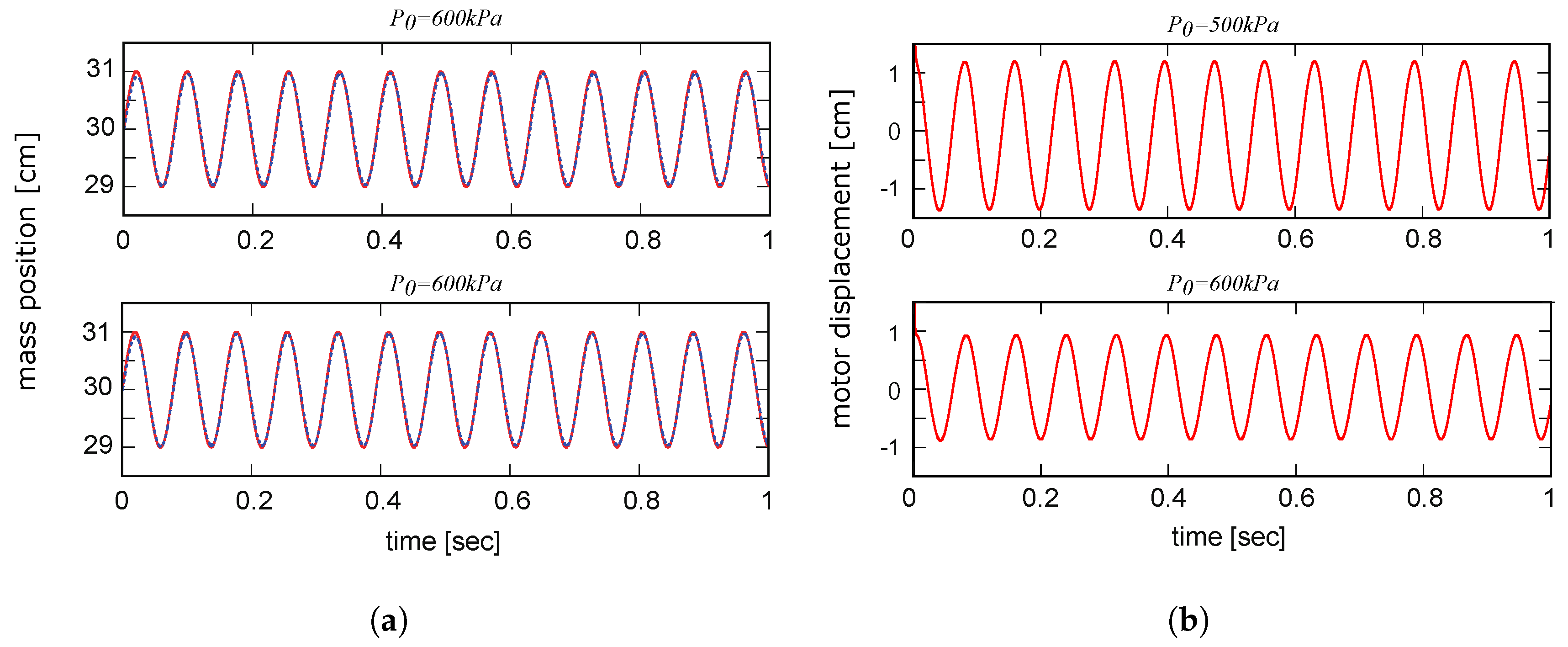
Figure 1b) which should track a desired sinusoidal motion with a certain frequency. The movement amplitude and frequency are changed and the effect of different values of muscle pressure in EM position control and required power is investigated.
In the simulation, a PAM with 15 cm unloaded length is filled with a specific amount of air (fixed air mass). The amount of inflated air pressure in PAM is not added during motion meaning the valves are closed and the desired unloaded pressure is adjusted beforehand. Indeed, the PAM pressure is changing during experiment due to variation of the muscle length, but the amount of air is fixed by closing the valves as mentioned before. To follow the desired sinusoidal movement of the mass, the EM is controlled with a PID controller. The amplitude of the periodic movements is 1 cm and the bias of sine wave is 30 cm. The range of mass displacement (2 cm) is resulted from the EPA actuator movement. This number is comparable to human muscle length changes in walking and is also higher than the motion range in BioBiped3 experiments (see
Section 2.3.2). Another reason for defining this motion range is because of the PAM length. Due to the PAM contraction, which is 20–25% of the muscle length, for a 15 cm length PAM, the maximum contraction will be less than 4 cm. We considered half of this number to assure that the EPA works on the identified range of the PAM. To apply such an actuator for locomotion, tuning lever arm helps increase joint movement range.
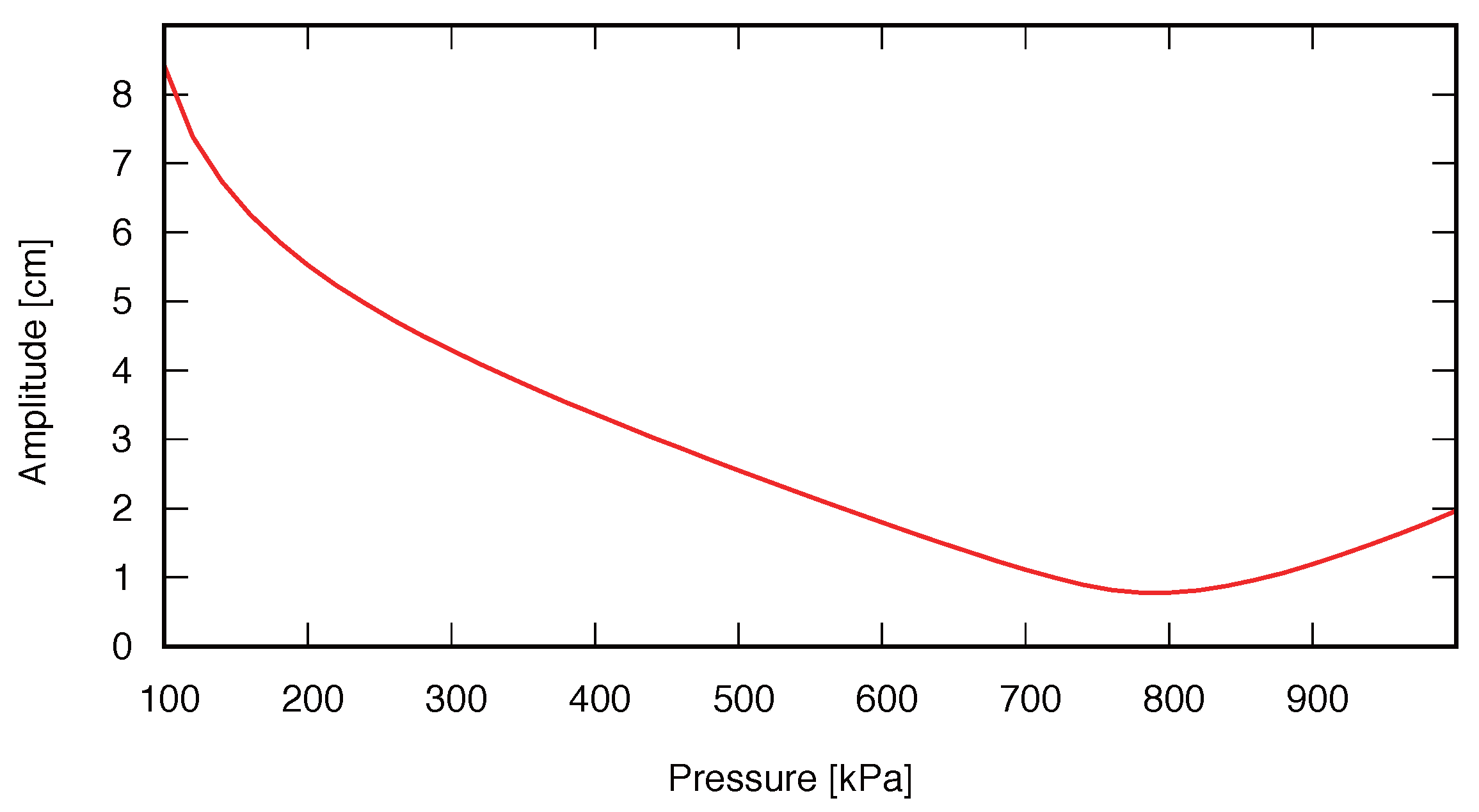
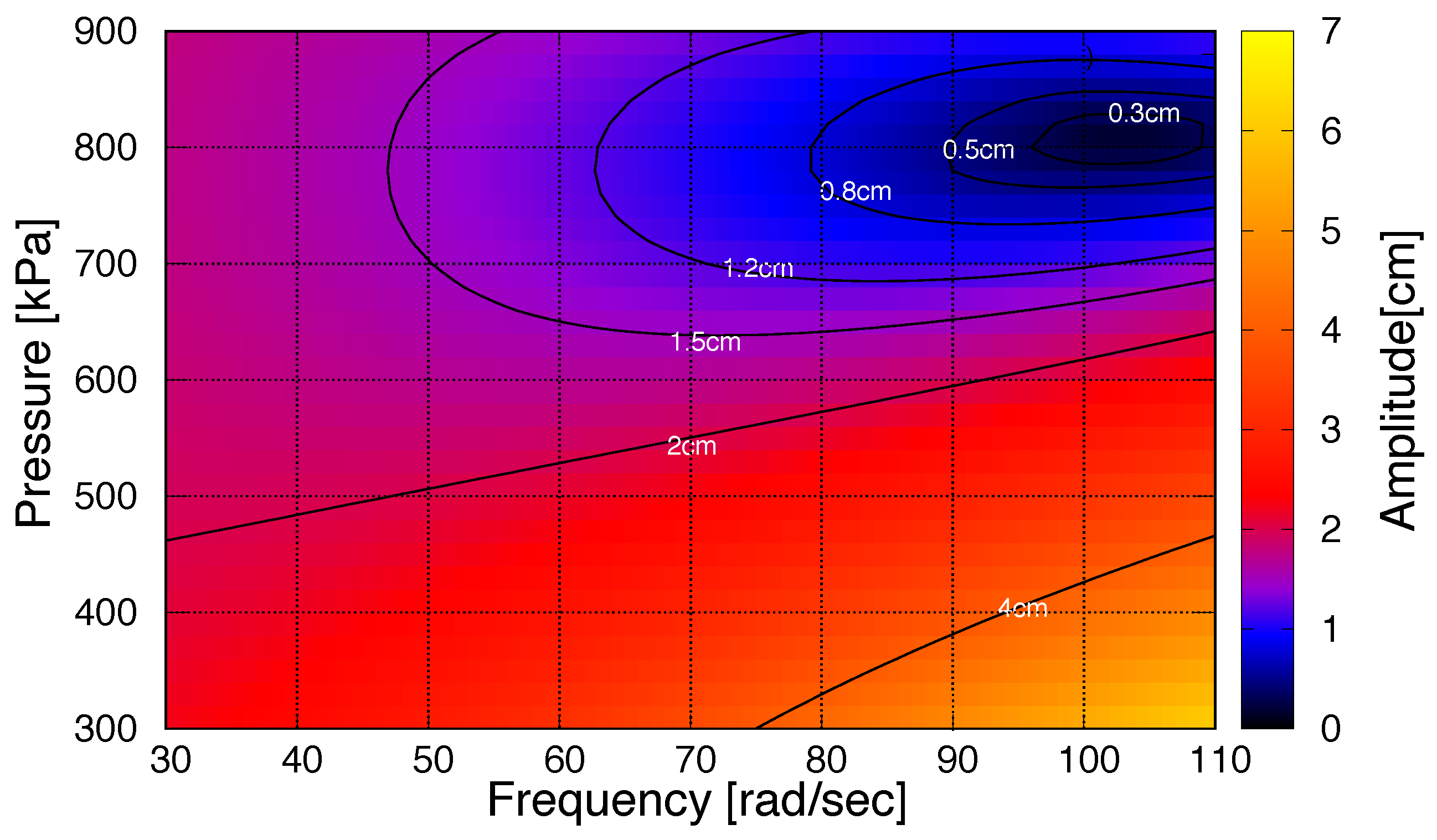
The periodic movement is characterized by the frequency of the reference sinusoidal signal (ranging from 20 rad/s to 110 rad/s). At each motion frequency, the optimal pressure is found by minimizing the motor movement. Therefore, by adjusting the PAM pressure to its optimal value, the least EM movement can be applied to control the robot joint at each frequency. The simulation results of the EPA model are described in
Section 3.2.
2.3.2. Hardware Experiment
The concept of EPA is not constrained to a specific arrangement of actuators. The PAM can be attached to the EM in both serial, parallel or antagonistic arrangement. Recently, studies on considering parallel stiffness to the SEA (called SPEA) address the issues existing in SEAs (e.g., SEA cannot reduce the consumed torque [
8,
17]). Effects of parallel stiffness on reducing peak power and energy consumption of the actuator in prosthesis were described and compared with serial stiffness in [
12]. Thus, we investigate the effect of PAM compliance adjustment in energy consumption of the EPA.
In
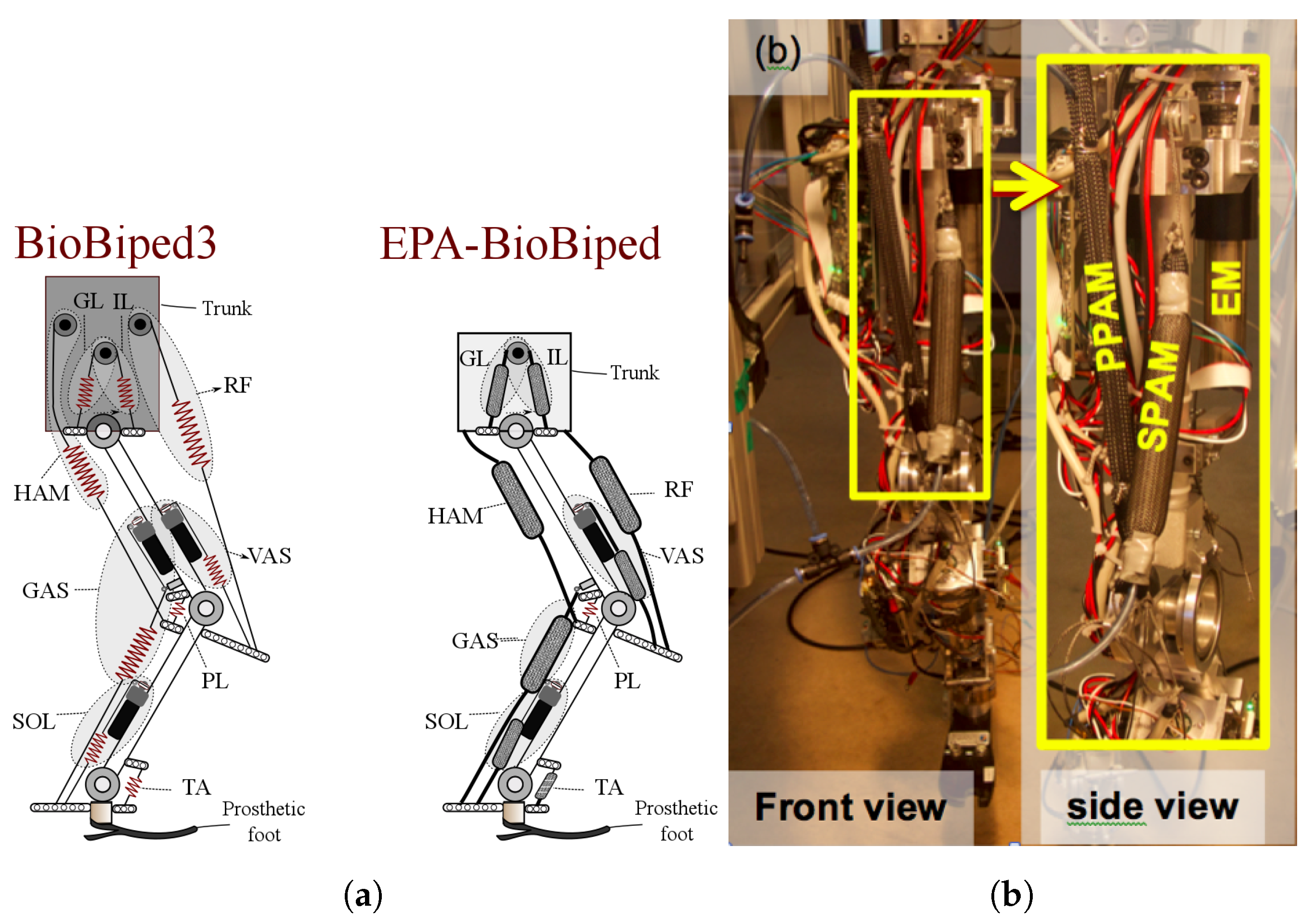
Figure 3a, the schematic of Biobiped3 robot ([
21] and the concept of EPA-instrument BioBiped robot (
http://www.biobiped.de) are illustrated. In
Figure 3b, the SEA for the vastus muscle is replaced by an EPA in which two PAMs are applied in series (SPAM) and in parallel (PPAM) to the actuator. In
Section 3.3, we show that different arrangements and stiffness adjustment through tuning the PAM pressure yield more efficient motion control. In this experiment, we fixed the robot trunk and employed the knee actuator to generate a periodic movement at different frequencies. The desired joint position was given by a sinusoidal signal, in which the frequency was increasing linearly from 0.5 Hz to 2 Hz in 5 min. Here, the knee movement is
which mimics human knee movement during stance phase of walking at 1 m/s [
30]. In our experiment, this results in 7.5 cm movement in the foot, as the hip is fixed. This motion requires about 1 cm variation in the SEA length which is in the motion range defined in simulations.
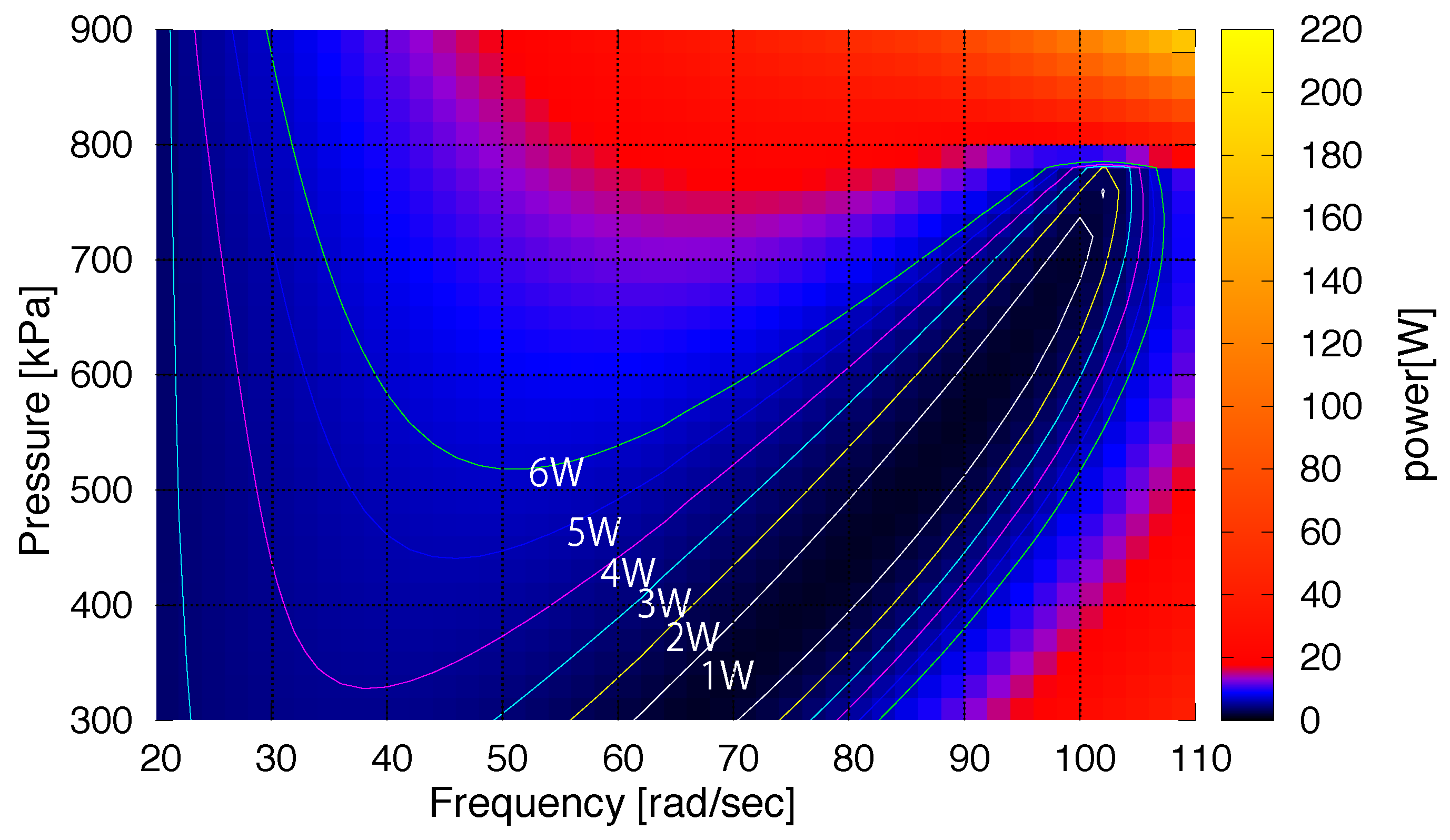
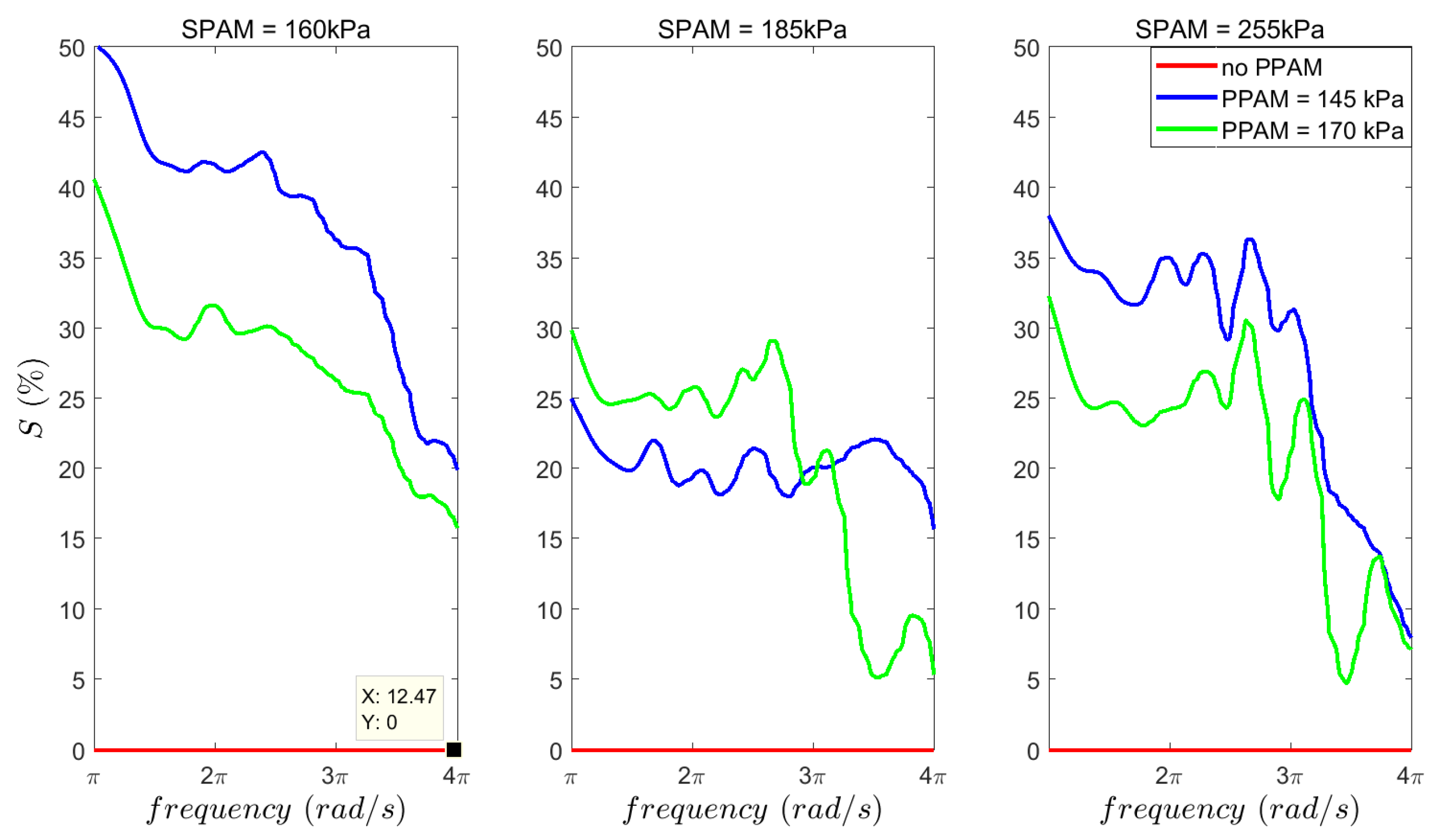
In our experiments, the effects of SPAM and PPAM pressures on energy consumption at different frequencies are considered to analyze the effect of the PAM on efficiency of the actuator. The integrated current square was used as a measure of energy consumption.
in which
I is the motor current and
T is the period of the sinusoidal signal. The computed term
E based on the consumed current can be used as a measure for electric energy while the movement patterns are kept fixed. This parameter is computed for different values of PPAM and SPAM stiffness (air pressure) to investigate the effectiveness of EPA concept. It is shown that by tuning PAM’s air pressure, more efficiency at each frequency can be achieved. Therefore, in order to control locomotion that can be described by combinations of different oscillatory movements, the optimal stiffness (equivalently air pressure) should be found to work in a range of optimal solutions.
4. Discussion
Muscles are arguably the best-known actuation technology that approaches a perfect force source i.e., one with extremely low impedance (perfectly back-drivable) and stiction, although with only moderate bandwidth [
7]. Inspired by the functional performance and neuromechanical control of biological muscles [
31], appropriate design of the actuator and control strategies can largely enhance the locomotor function. If a robot without any passive compliance jumps or runs, even with precise force feedback control to have active compliance [
32,
33], it has to cope with energy losses and compensate delay effects [
34]. Adaptable compliances as found in biological systems provide significant advantages over traditional actuation for legged robots and assistive devices (e.g., orthoses, prostheses). Although VIAs are rapidly developing with a wide range of different actuators, there is no “winning” design, but rather application-dependent optimal solutions [
15]. In this paper, we address this problem by developing a novel actuator namely EPA, comprised of electric motors and pneumatic air muscles. Preliminary simulation and experimental results presented in the previous sections support the idea of approaching human muscle features with the EPA.
PAM-driven biped robots can walk stably and perform efficient hopping and running steps without any feedback [
34]. PAMs also provide adjustable compliance supporting periodic movements [
22]. However, due to difficulties in force control and nonlinear air pressure–force behavior in PAMs, providing an analytical approach for stabilizing PAM-actuated legged systems is problematic. In these systems, stability is usually obtained by hand tuning of control parameters and is rarely investigated analytically. Combining the EM and PAM into an EPA may help improve controllability and overcome the drawbacks of each actuator type (e.g., increasing the bandwidth of PAMs by adding parallel EM in Macro-Mini scheme [
35]). The main hypothesis that is investigated in this paper was as follows:
The combination of PAM and EM permits a variety of arrangements which may enable this hybrid actuator to outperform existing actuators in efficiency over the operational region required for human-like locomotion which is a combination of periodic tasks in the steady state. To verify this hypothesis and benefit from properties of different actuators (PAM and EM) in EPA, first we need to have better understanding of their dynamical behavior. In human muscle-tendon-complex (MTC), actuation comes from the muscle during activation, while passive behavior is resulted from both tendon and muscle properties. In EPA, we consider EM to develop force as an active part, while the PAM is used as an adjustable compliance (passive). Although in future application of EPA, PAM can be also used to inject energy to the system as an actuators, here we did not investigate this property of PAMs. In order to enhance our understanding or PAM, a new dynamic model was developed which was used in simulation studies. In spite of the nonlinear and complex dynamical behavior of PAMs together with hysteresis, impedance (or stiffness) adjustment can be easily implemented by changing the PAM pressure. This is a simple approach to adapt the passive behavior of the EPA. Therefore, in our simulations and experiments we did not control PAM pressure continuously. In that sense, the control complexity is similar to that of SEA. Definitely, if we need continuous adaptation of PAM pressure, we need another control layer. However, the idea can be extended by identifying different behavioral regimes corresponding to muscle stiffness and using the same control architecture for continuous impedance adjustment. Hence, the higher complexity of EPA control compared to SEA relates to selecting the optimal stiffness for the targeted task (gait). For example if a linear relation between frequency and optimal pressure can be found (as shown by black region in
Figure 8), the control rule for selecting optimal pressure of PAM will be also very simple. This shows that, the nonlinearity of the PAM model and dependence to muscle length change (speed
) does not necessarily affect the control principle, significantly. As a result, using PAM as an adjustable stiffness is a practical solution for optimizing actuator dynamics for locomotion without significant increase of control complexity.
Based on the simulation results in
Section 3.2, for a repetitive motion in a certain time, the PAM in EPA is able to supply optimal compliance for producing desired periodic movements with low energy and simple design (in comparison to other VIAs [
22]). Supposed to the insignificance of air leakage on the valves, the longer the executing time of such a repetitive movement, the more efficiency obtained with the EPA actuation mechanism. This results from event based adjustment of the PAM muscle to provide the required compliance for the corresponding motion time.
As shown in this paper, using PAM instead of springs in a SEA configuration allows us to adjust the compliance as in VIAs. This makes the system more efficient (compared to EM) and more robust against impacts (not shown). In the future, we will compare this actuator with other VIAs regarding performance, efficiency and robustness against perturbations. The addition of a parallel PAM to this design (as an adjustable passive compliance) can also reduce EM torque when not all of the torque passes through the motor. Studies on parallel stiffness show that this resolves a main drawback of compliant actuators with series compliance [
8,
9] which are in line with our findings in experiments with BioBiped3 robot. To examine the applicability of the actuator for legged locomotion, our next step is implementing the EPA on the 1D hopper robot (MARC-Hopper-II, [
36]) to perform robust and efficient hopping and compare it with other compliant actuators. Furthermore, with this new combination, we can also benefit from muscle-like properties of lightweight PAMs [
20], e.g., using compliance control techniques [
22]. As different (biological) muscles may have different functions during a specific task (e.g., operating as spring, drives or brakes), this can be represented by a muscle-specific design of EPA, as combinations of PAM and EM (e.g., with series, parallel, antagonistic arrangements).
Based on its mechanical properties and its flexible arrangement in multi-segment-systems, the EPA provides a novel actuator, which mimics human muscle function and is able to mechanically adapt to different gaits and conditions (e.g., locomotion speed). With EPA technology, new versatile and efficient locomotor systems for a wide range of applications can be designed.