MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations
Abstract
:1. Introduction
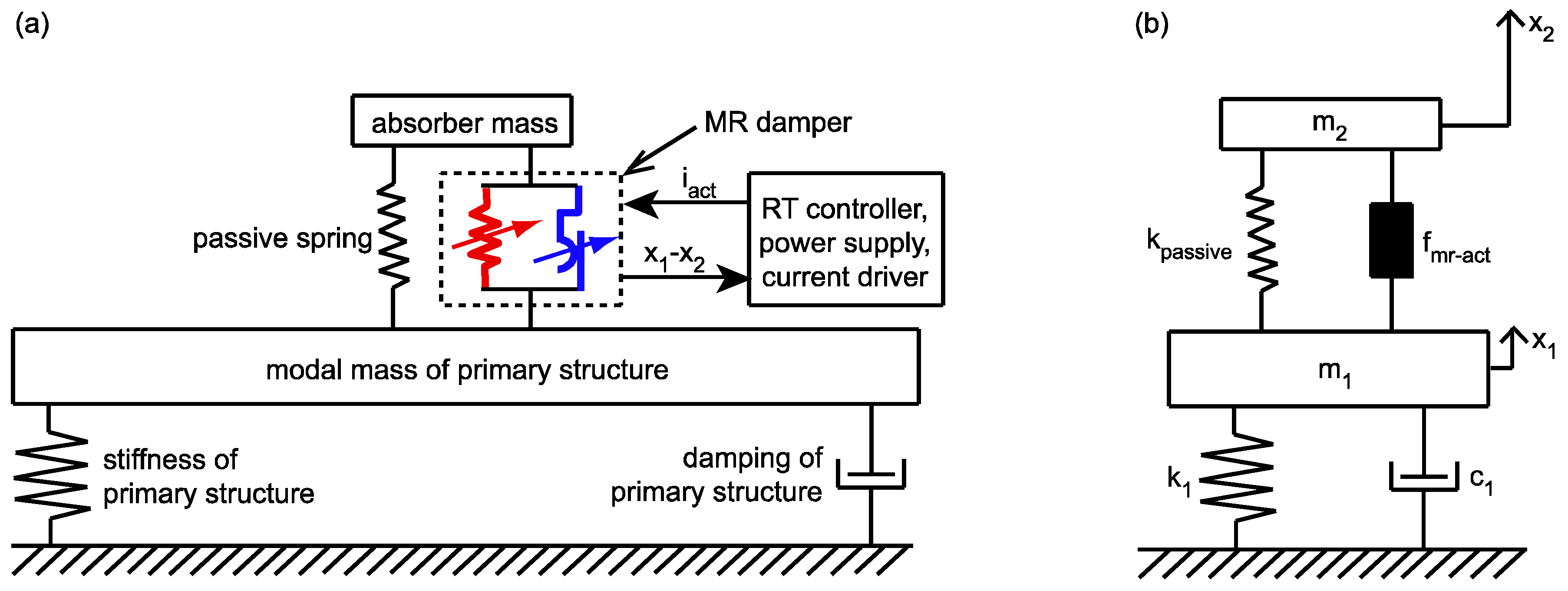
2. Concept of MR-SVA
2.1. Control Objectives
- its controlled frequency is equal to the actual frequency of vibration at all instants, and
- its controlled damping is minimized under the constraint that the relative motion amplitude of the absorber mass must not be greater than its maximum tolerable value.
2.2. Real-Time Frequency and Damping Controls with MR Damper
- a controllable stiffness force to tune the controllable frequency of the MR-SVA to the actual frequency of vibration, and
- a controllable damping force to minimize the damping and control the relative motion amplitude of the absorber mass.
- zero stiffness when the disturbing frequency is equal to the targeted eigenfrequency of the primary structure, i.e., , whereby the controlled frequency of the MR-SVA is equal to , i.e., .
- positive stiffness if in order to augment the total stiffness of the MR-SVA that is the sum of the passive spring stiffness and the controlled stiffness emulated by the MR damper to generate .
- negative stiffness if in order to diminish the total stiffness of the MR-SVA to produce .
2.3. Control Based on Measured Collocated Displacement
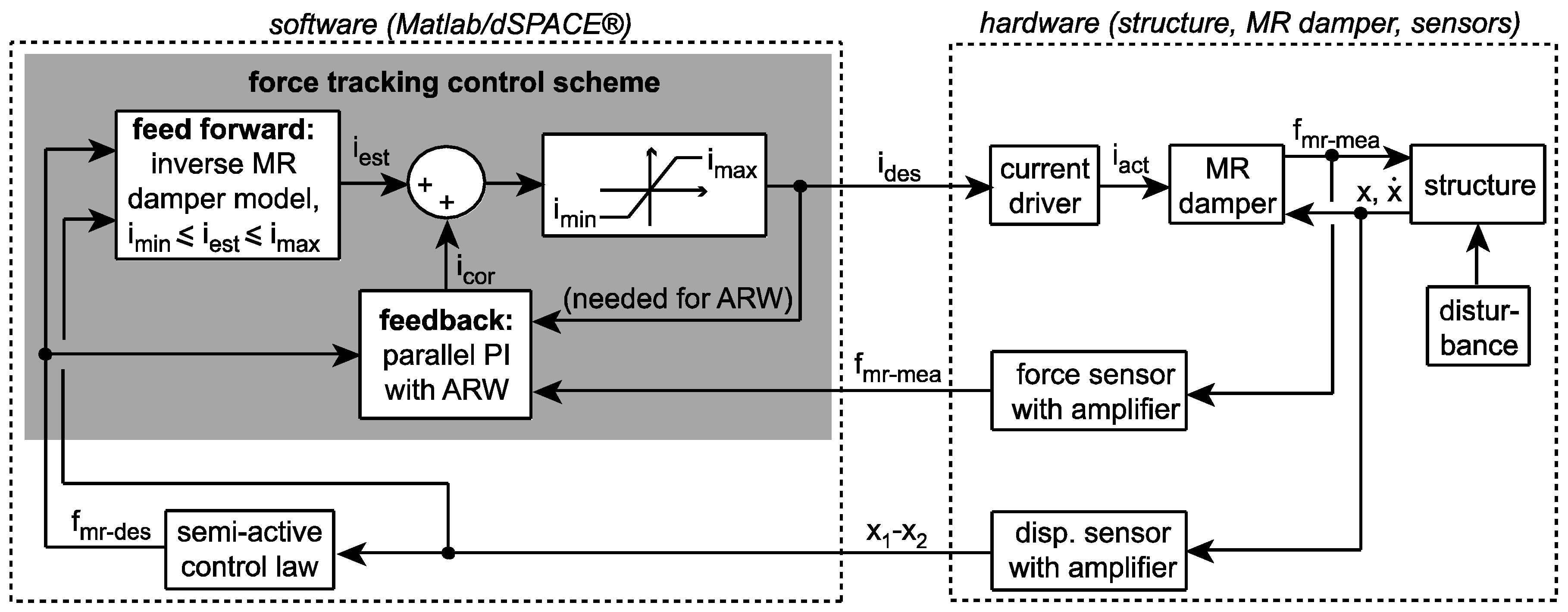
2.4. MR Damper Force Tracking Control Scheme
3. Control Algorithm
3.1. Stiffness of Passive Spring
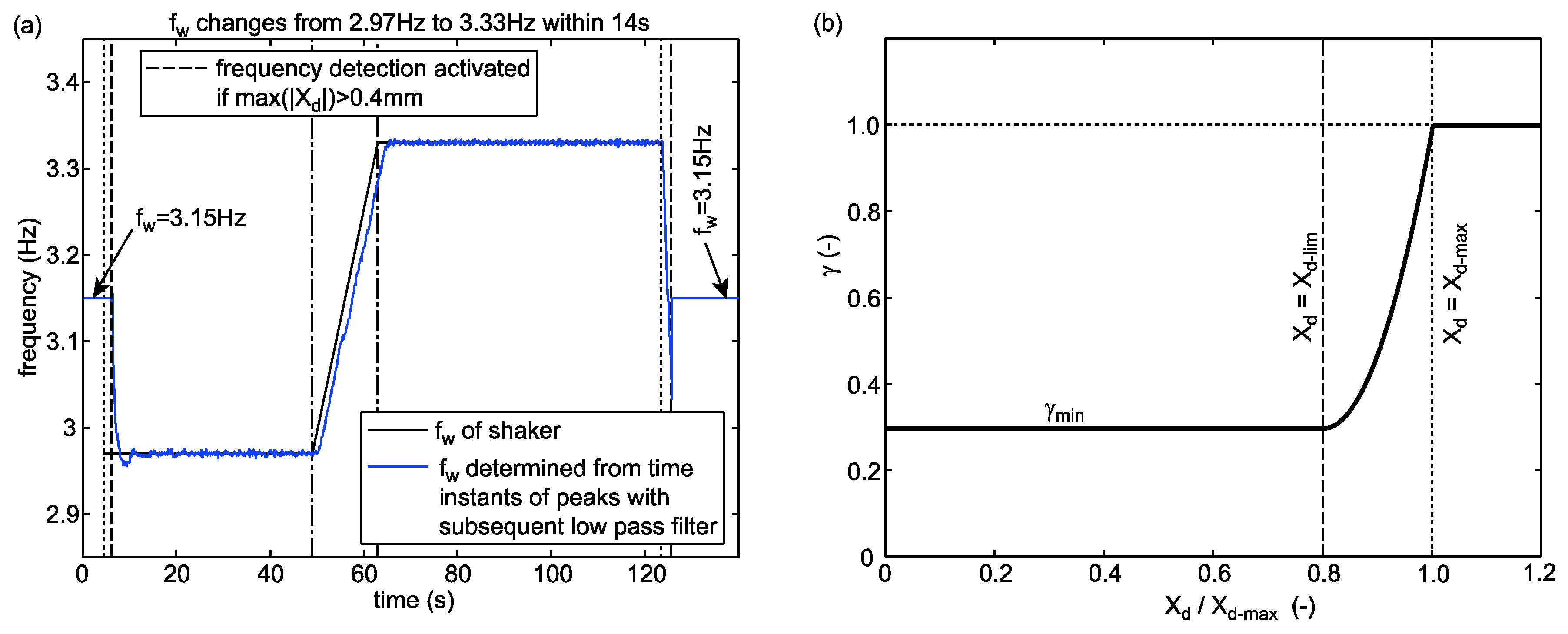
3.2. Controlled Frequency
3.3. Controlled Adaptive Damping
3.4. Desired Semi-Active Control Force
3.5. Actual Semi-Active Control Force
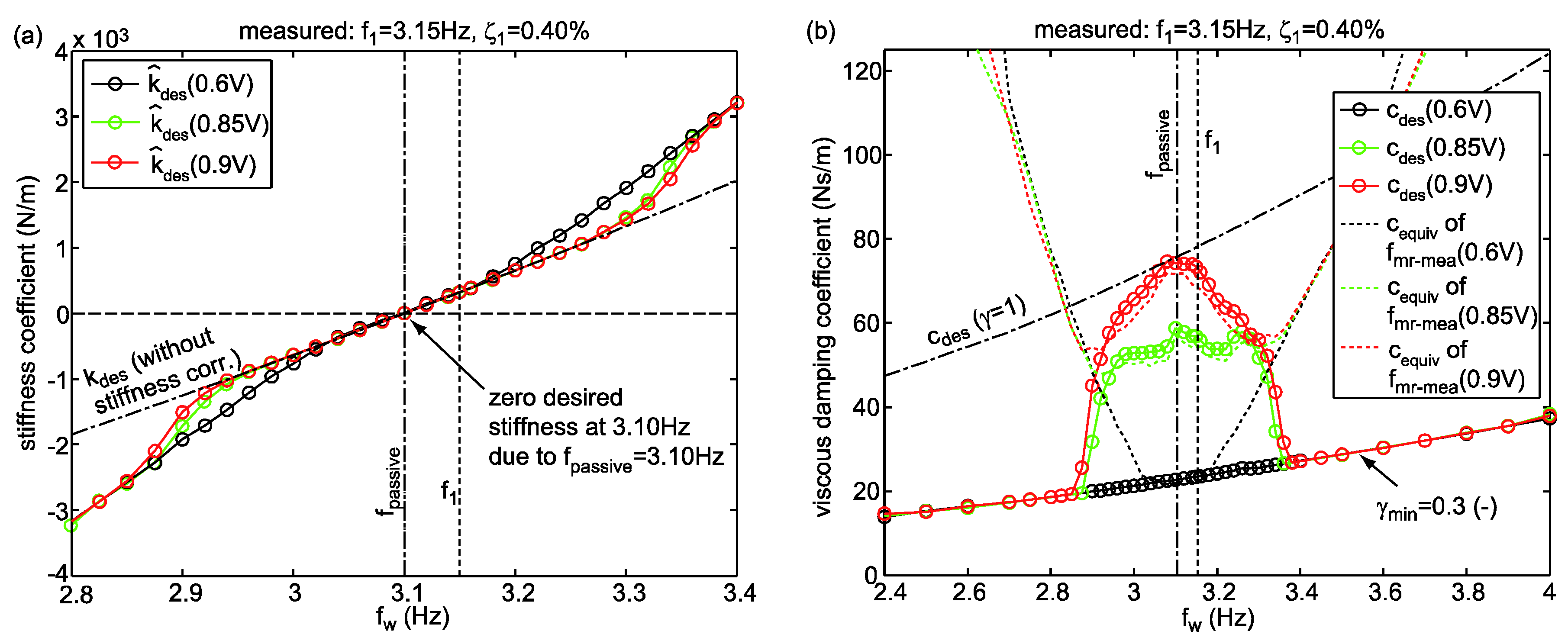
3.6. Stiffness Correction Method For Precise Frequency Control
3.7. Compromise Solution for Stiffness Correction Method
4. Numerical Validation
4.1. Assessment Criterion
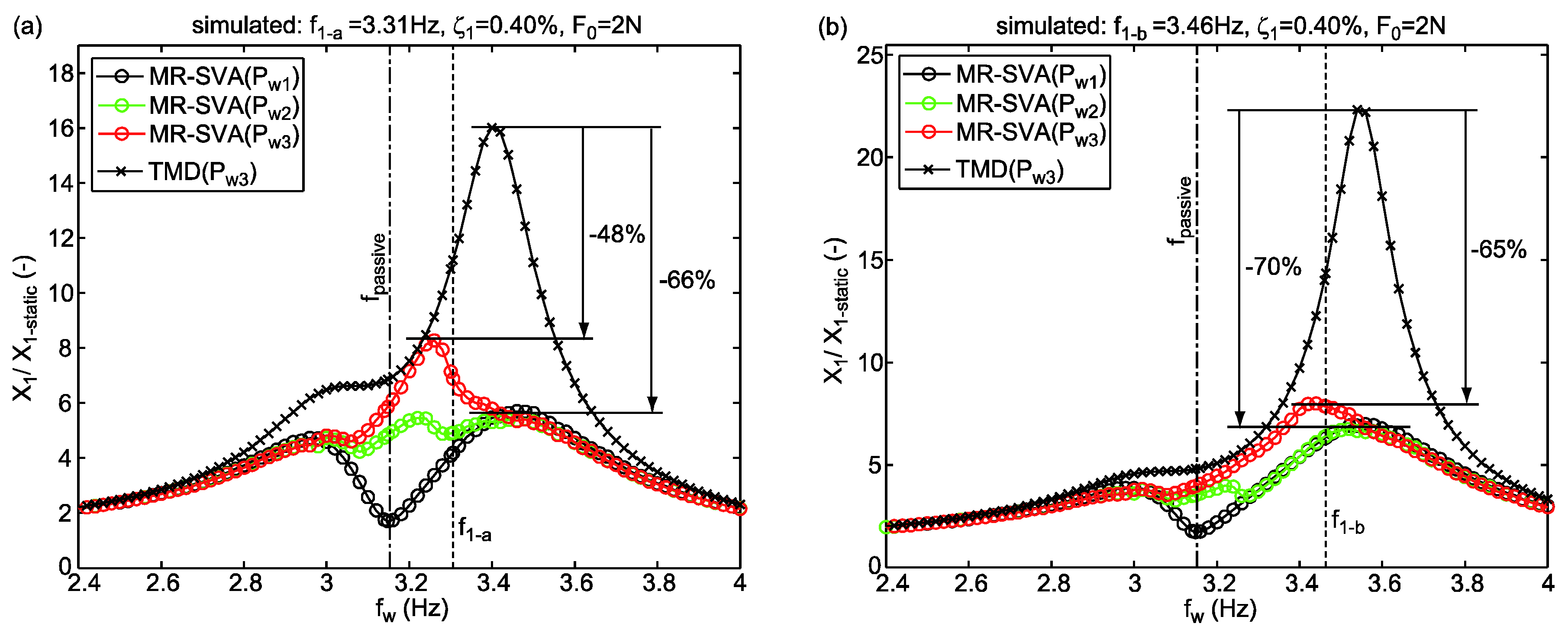
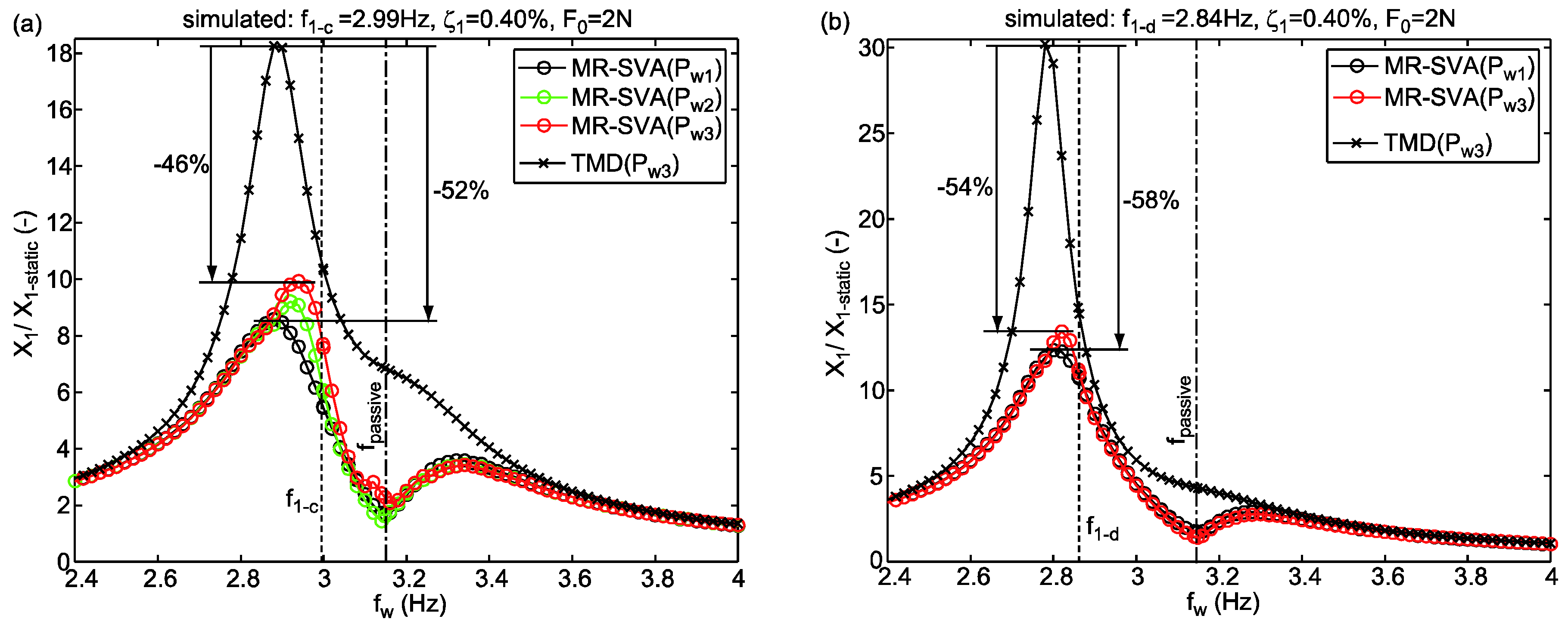
4.2. Assessment of MR-SVA for Tuned and De-Tuned Cases
- The prototype MR-SVA is a mock-up MR-SVA that is designed for a laboratory scale bridge which explains that and are small while and are high compared to values of real mass dampers in big structures. Detailed information on the mock-up MR-SVA and the laboratory scale bridge is available in Section 5.1.
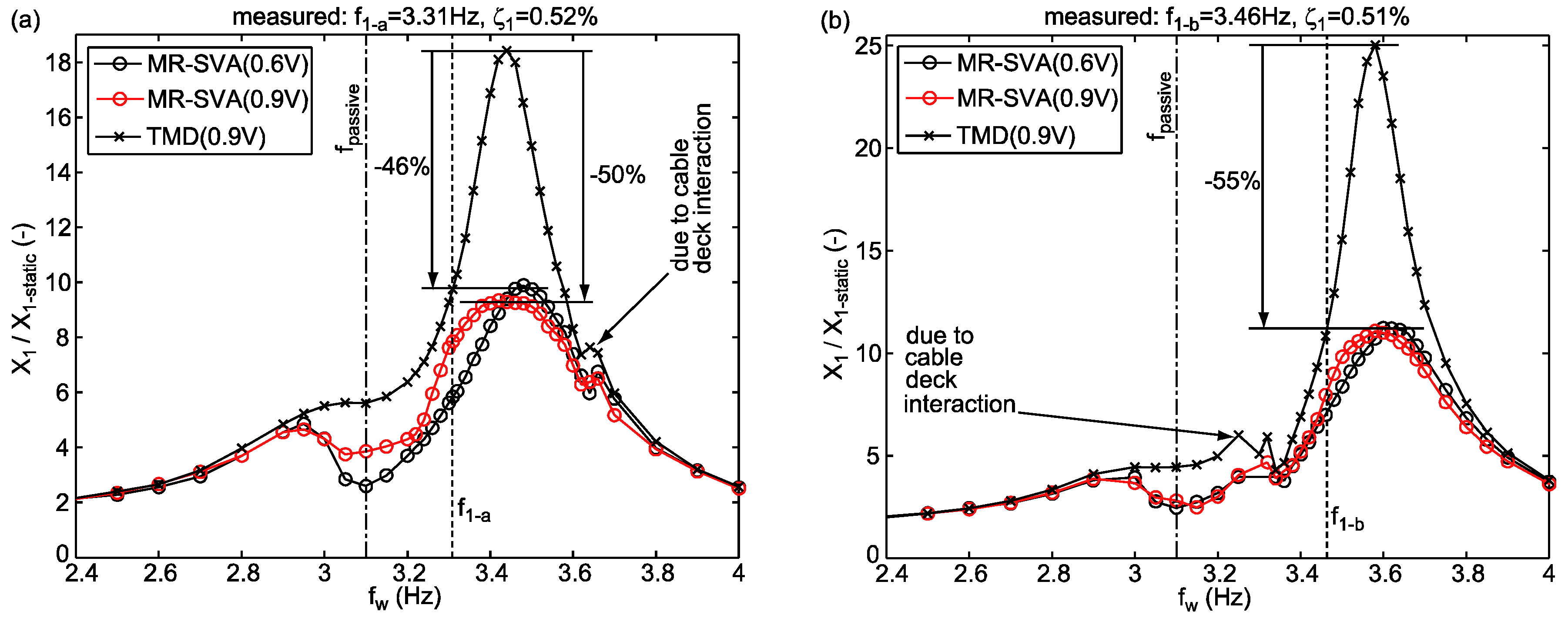
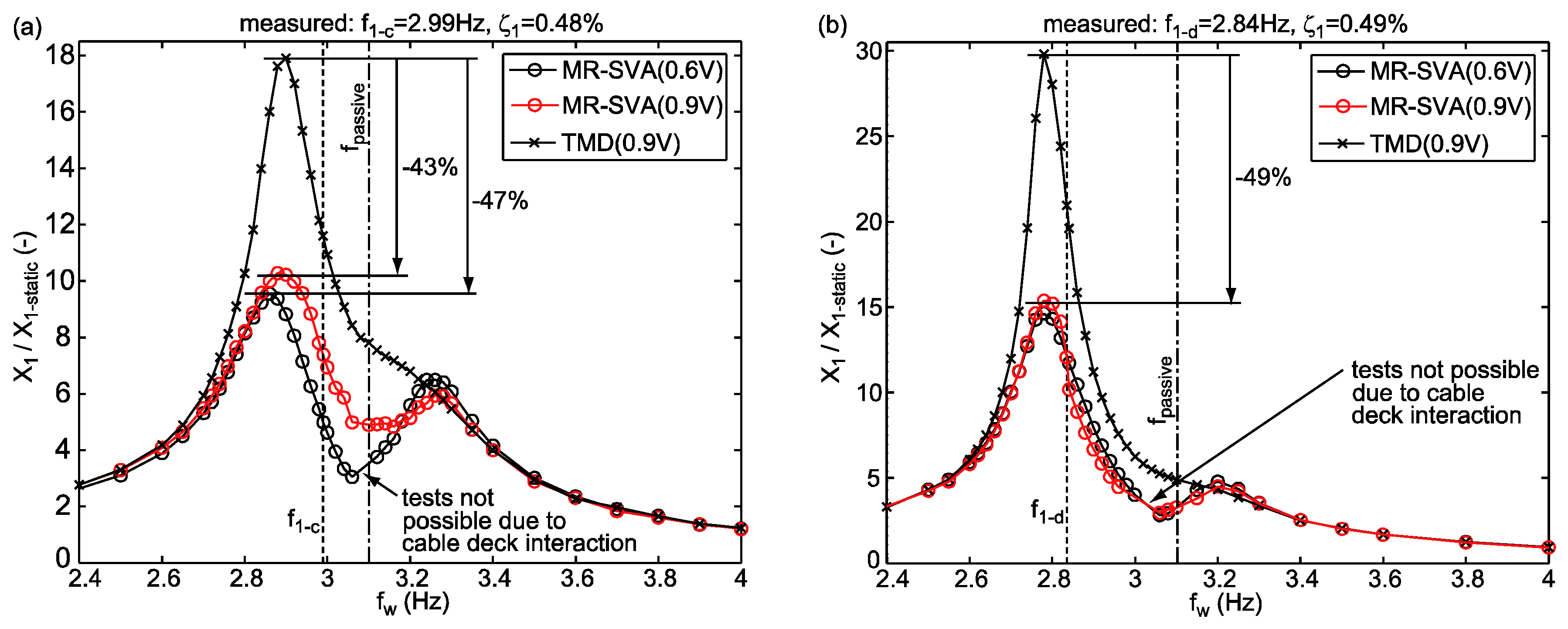
- The experimental validation of the prototype MR-SVA is performed with a suboptimally tuned as the passive mass spring packet of the MR-SVA was originally designed to assess the semi-active TMD concept of the Volgograd Bridge, Russia [2,3,18,21], which required to design according to the design of TMDs for minimum structural displacement [6], i.e., .
4.3. Levels of Excitation
- Maximum excitation : The maximum excitation force amplitude evokes whereby the desired damping of the MR-SVA is equal to its nominal value . For higher levels of excitation, i.e., , the normalized displacement response given by Equation (16) does not change since the damping gain = 1 for does not change the desired damping, see Equation (9).
- Excitation : The excitation force amplitude results in whereby the desired damping of the MR-SVA is equal to its minimum value . For lower levels of excitation, i.e., , the normalized displacement response given by Equation (16) does not change as the damping gain for is constant, see Equation (9).
- Excitation : The excitation force amplitude is selected to be slightly smaller than the worst-case excitation , i.e., , to show the significant vibration reduction improvement when the excitation is approx. 80% to 90% of worst case excitation .
4.4. Benchmark
4.5. Dynamic Simulation
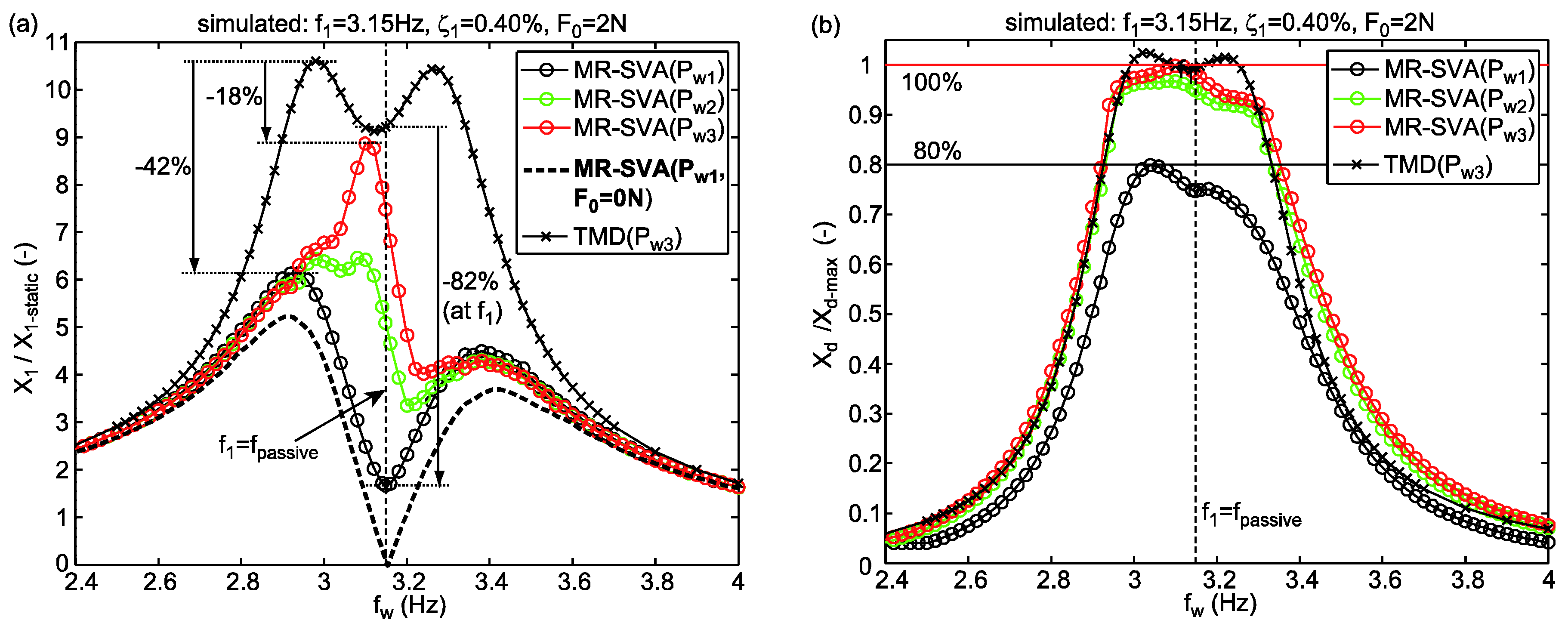
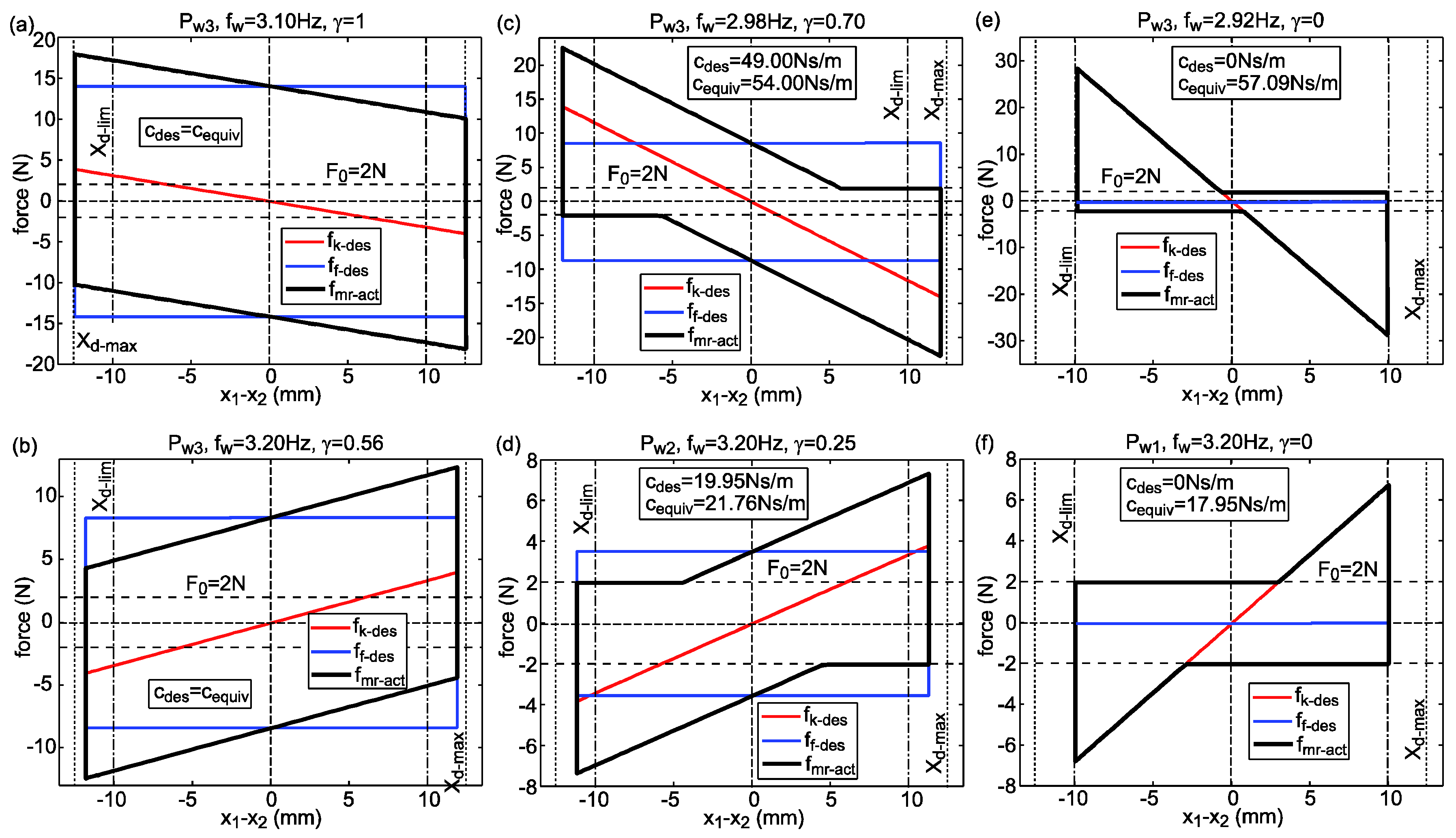
4.6. Numerical Results
- : If the damping of the MR-SVA cannot be reduced by the adaptive nonlinear damping control approach Equations (5)–(9) because the relative motion amplitude of the damper mass is equal to the normalized displacement due to the MR-SVA is equal to that of the passive TMD; this occurs at equal to the natural frequency of the TMD, i.e., , since then the frequency tunings and—because of —also the damping tunings of the TMD and MR-SVA are the same.
- : If the damping of the MR-SVA can be reduced by the adaptive nonlinear damping control approach Equations (5)–(9) due to the MR-SVA leads to significantly smaller normalized displacements than the passive TMD because
- the reduced damping augments and thereby increases the amplitude of the MR-SVA stiffness force, and
- the frequency control generates the targeted phase shift of 180 degrees between the MR-SVA stiffness force and the excitation force,
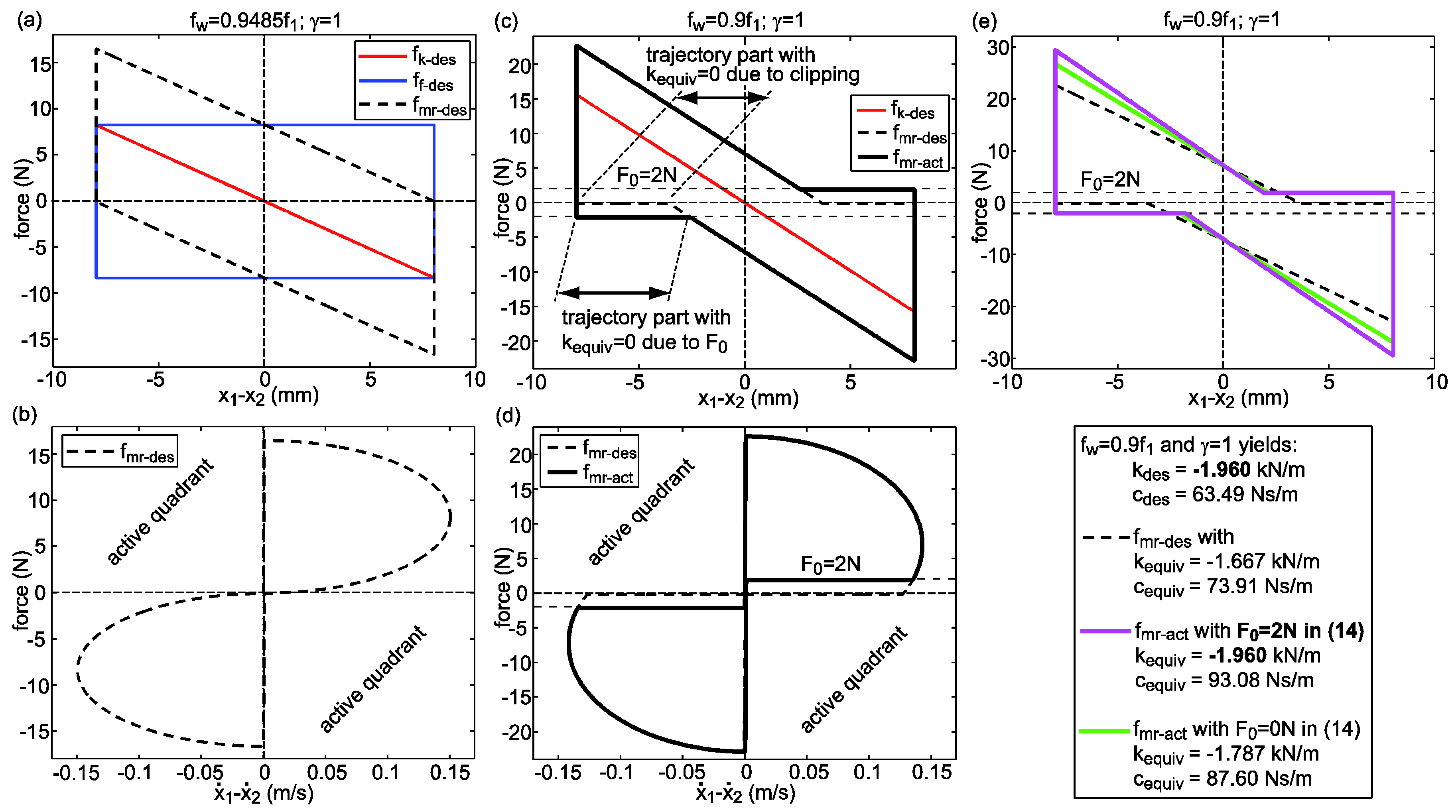
- The normalized displacement response due to the MR-SVA with = 2 N and for shows two maxima at approx. 2.9 Hz and 3.4 Hz because the actual, i.e., energy equivalent viscous damping coefficient is greater than its desired counterpart at these frequencies which diminishes the stiffness force amplitude of the MR-SVA and, as a result, lowers the compensation of the disturbing force.
- The simulation of the MR-SVA with negligible small residual force ( = 0 N) of the MR damper representing an ideal semi-active control force range cancels the oscillations of the primary structure at since then the MR-SVA precisely emulates the behaviour of the undamped dynamic vibration absorber. For excitation frequencies the MR-SVA cannot generate the behaviour of the undamped dynamic vibration absorber because the stiffness emulation by the MR damper force to generate the frequency control of the MR-SVA can only be realized in combination with a dissipative force whereby undesired damping is generated. Only with active vibration absorbers it is possible to emulate the behaviour of the undamped dynamic vibration absorber for any disturbing frequency [31].
5. Experimental Validation
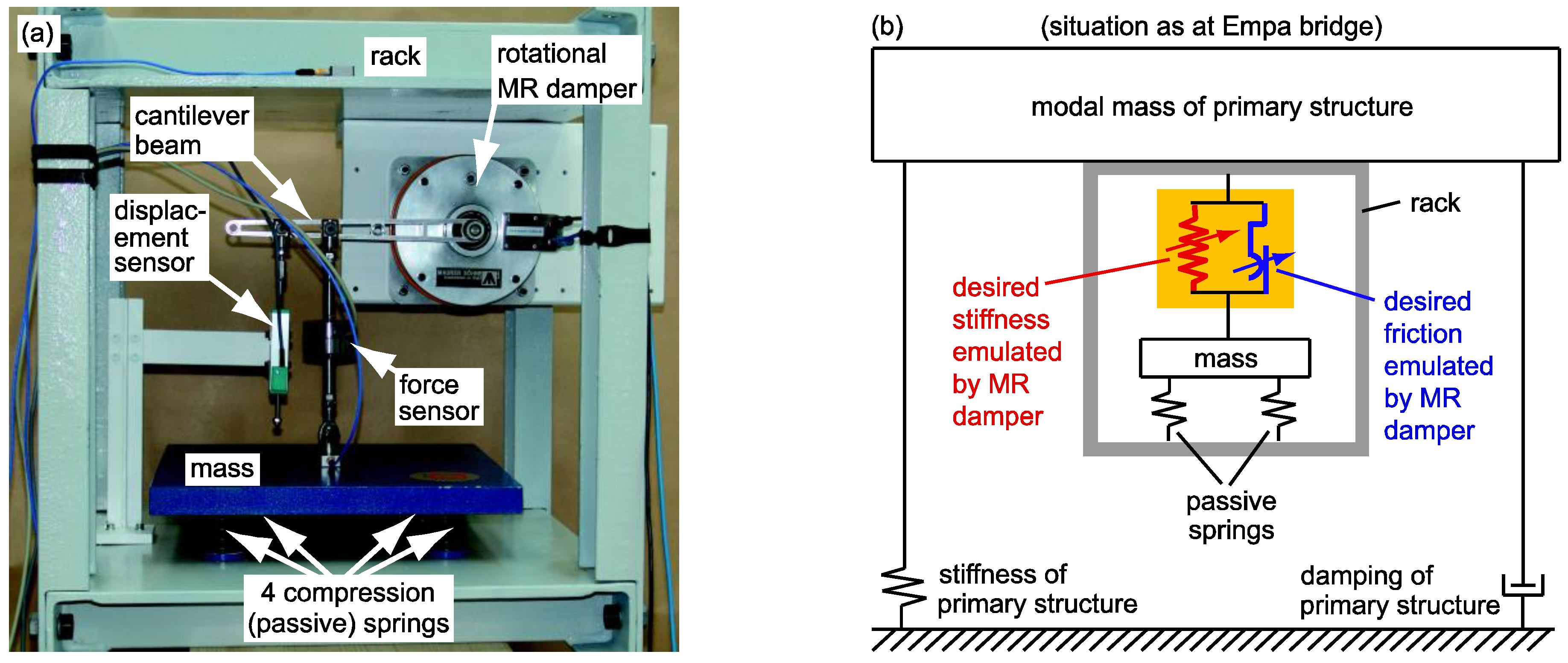
5.1. Test Set-Up
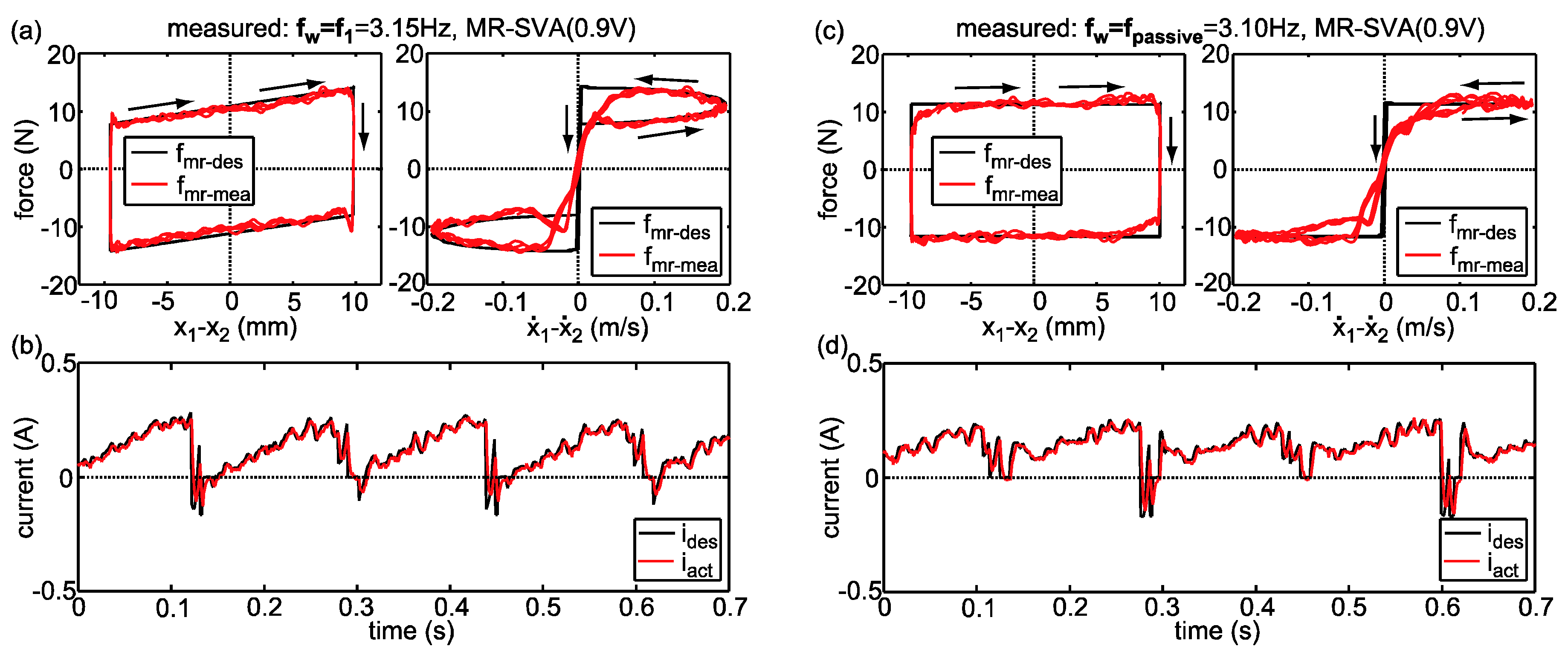
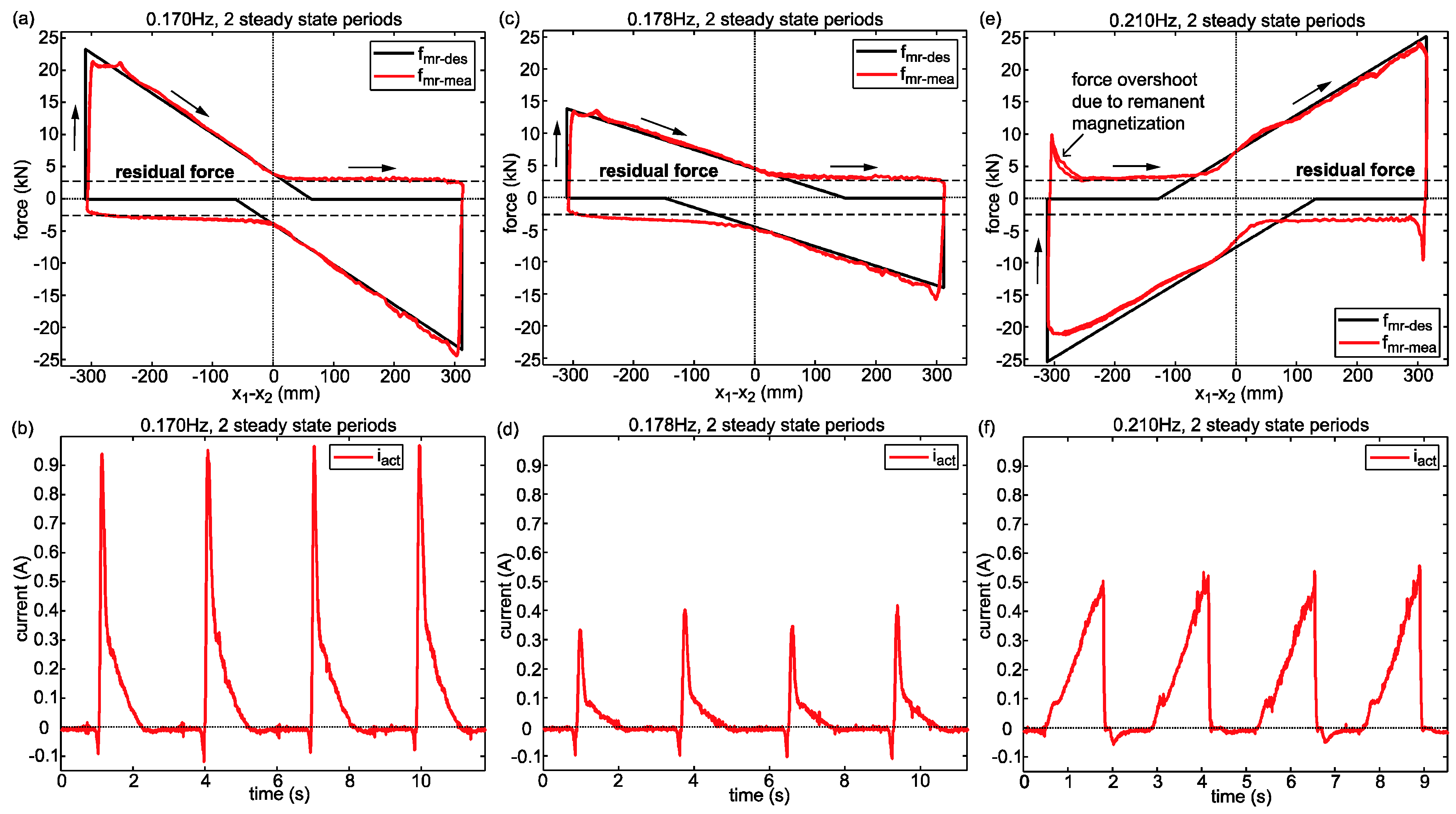
5.2. Force Tracking Control Scheme
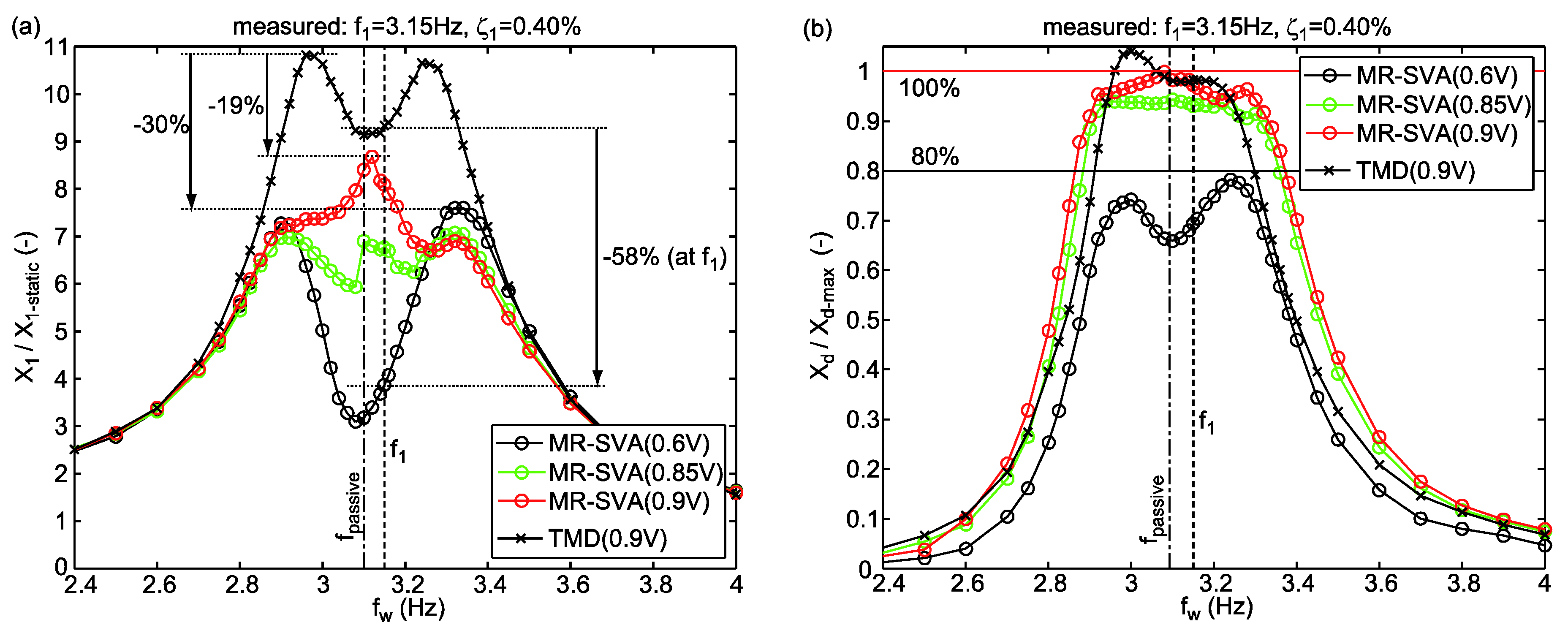
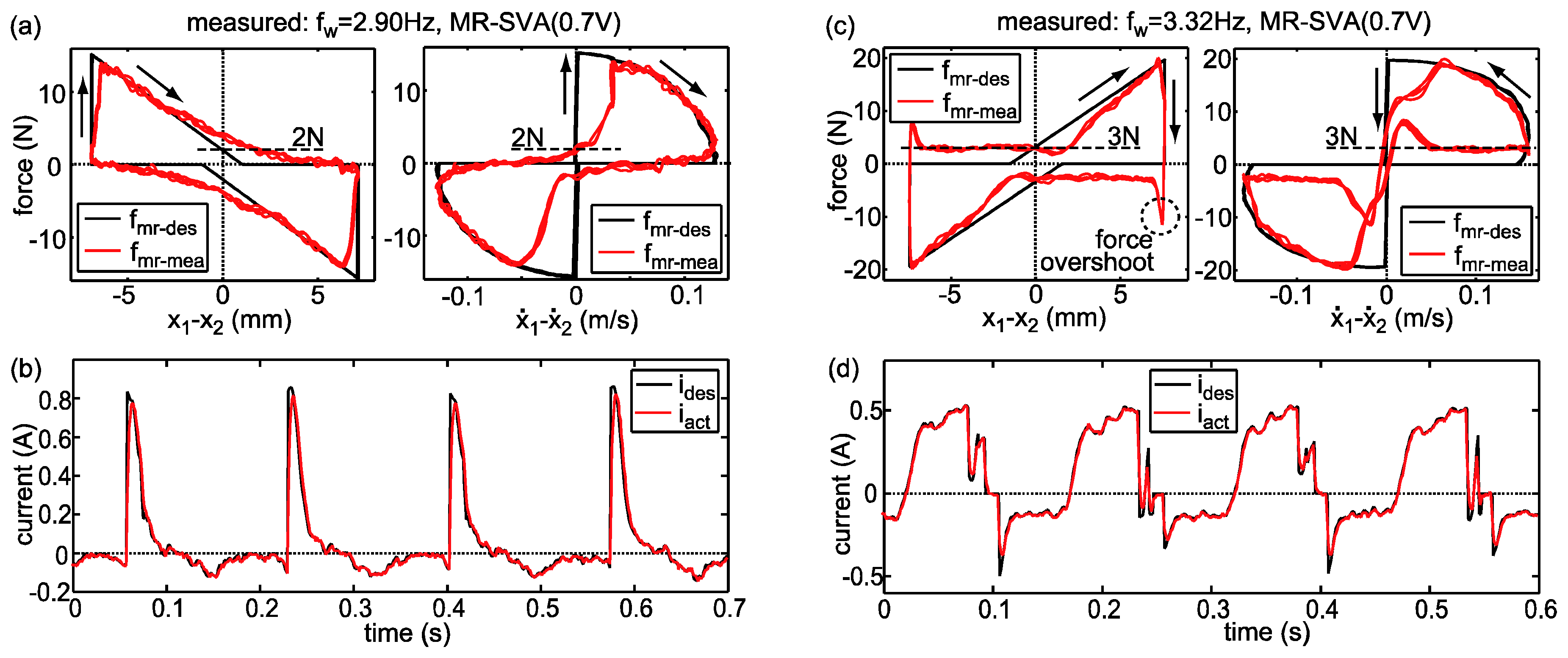
5.3. Experimental Results
6. MR-SVA of Danube City Tower in Vienna
6.1. Project Description
6.2. Hybrid Testing
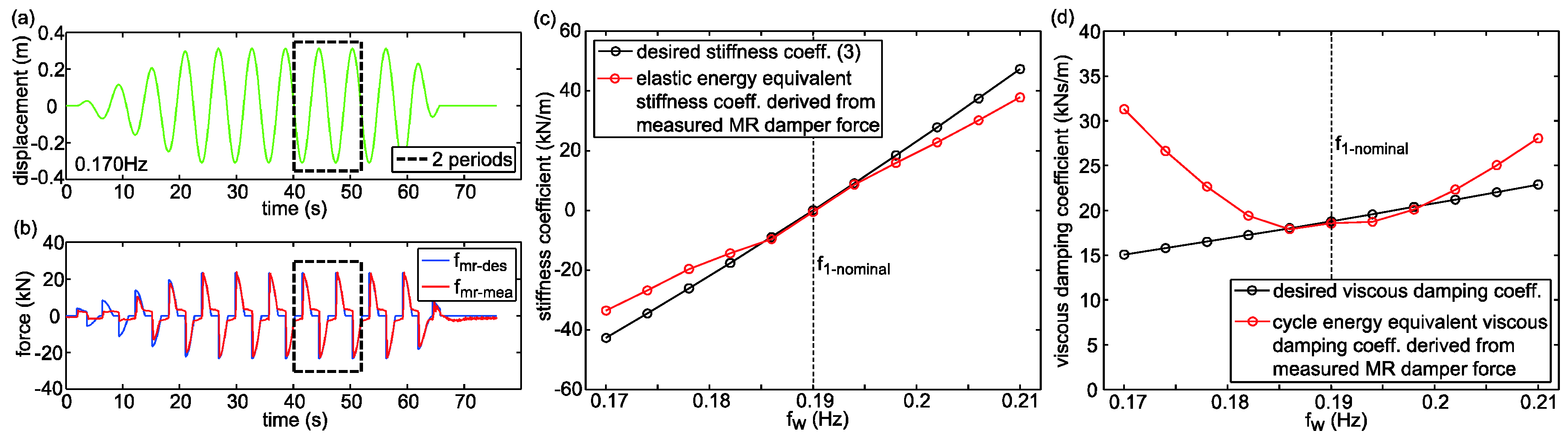
6.3. Accurate Force Tracking Control within 1 Day
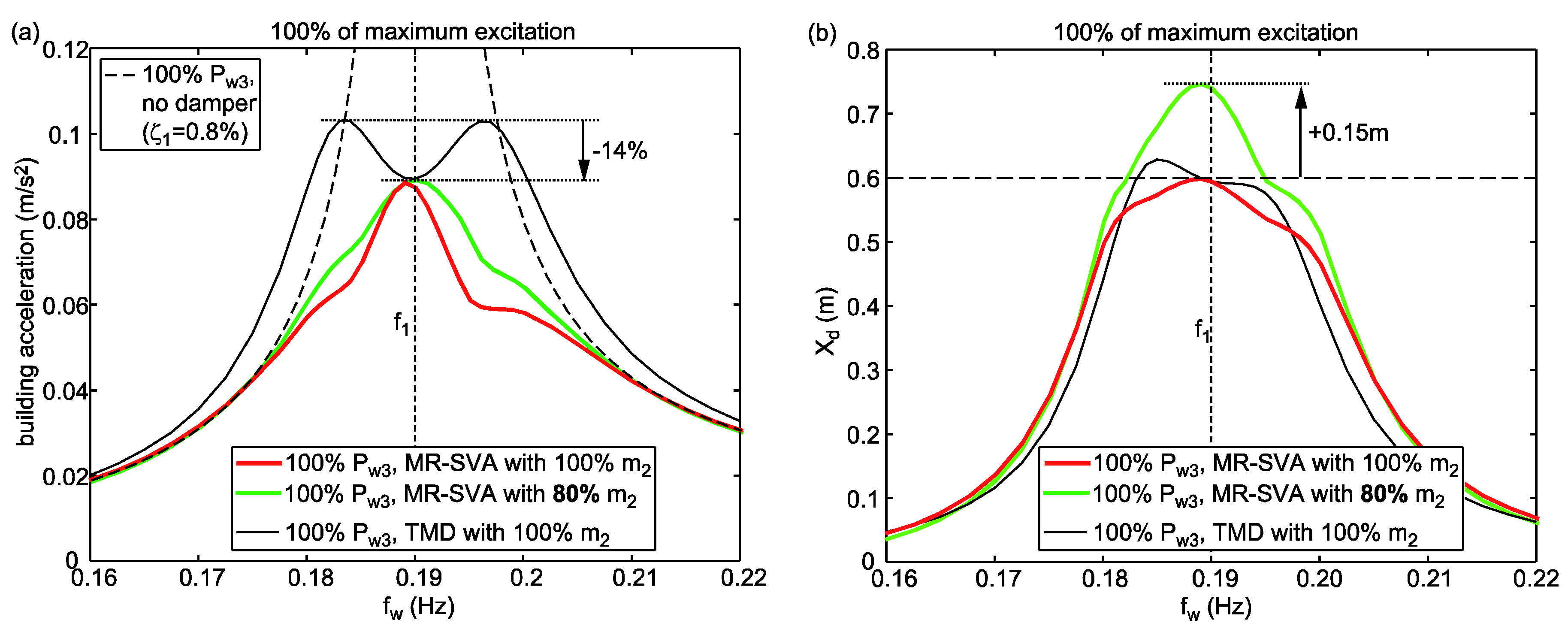
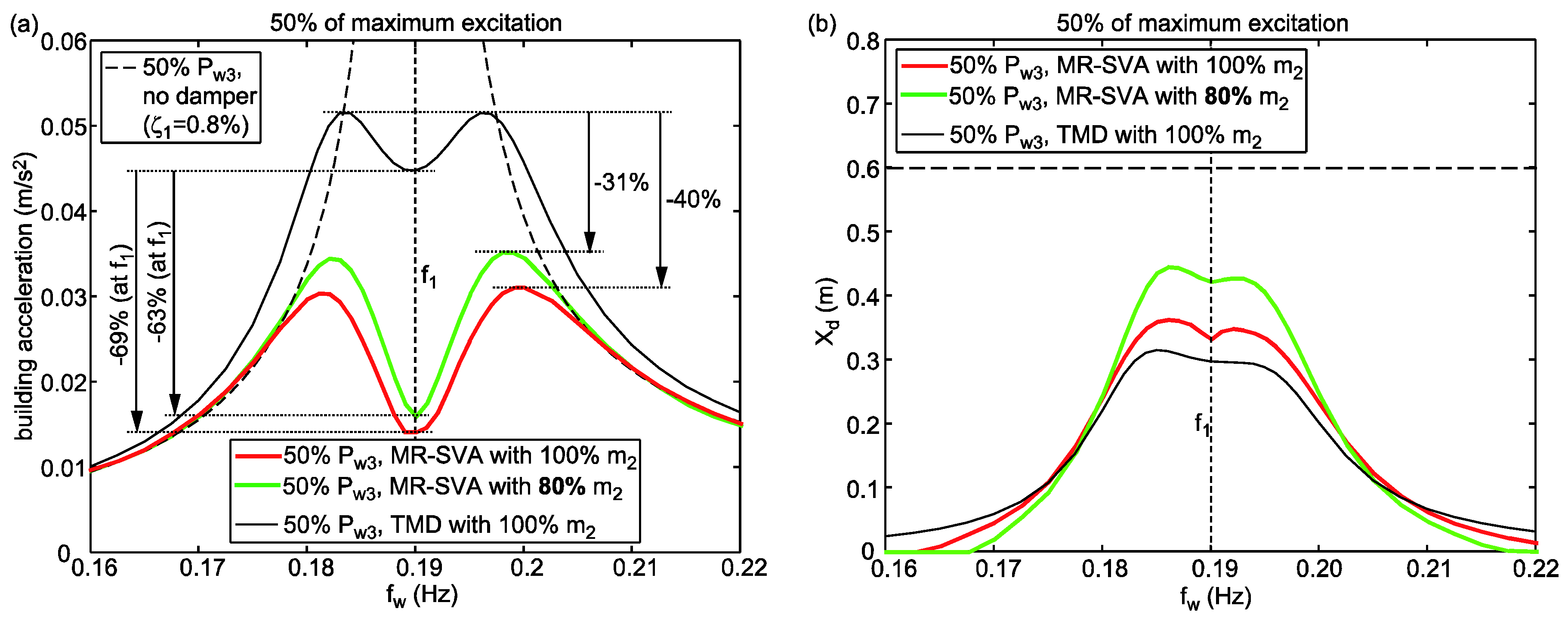
6.4. MR-SVA with Reduced Mass
7. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Structurae. Volgograd Bridge. Available online: https://structurae.net/structures/volgograd-bridge/videos (accessed on November 2016).
- Weber, F.; Distl, H. Real-time controlled tuned mass dampers for Wolgograd Bridge. Beton-Und Stahlbetonbau 2013, 108, 362–372. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H.; Maślanka, M. Semi-active TMD Concept for Volgograd Bridge. Top. Dyn. Civ. Struct. 2013, 4, 79–88. [Google Scholar]
- Thornton Tomasetti. Taipei 101’s TMD Explained. Available online: https://www.thorntontomasetti.com/taipei-101s-tmd-explained/ (accessed on November 2016).
- Holmes, J.D. Wind Loading of Structures, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; McGraw-Hill Book Company: New York, NY, USA; The Maple Press Company: York, PA, USA, 1934. [Google Scholar]
- Asami, T.; Nishihara, O. Closed-Form Exact Solution to H∞ Optimization of Dynamic Vibration Absorbers (Application to Different Transfer Functions and Damping Systems). Tech. Briefs J. Vib. Acoust. 2003, 125, 398–411. [Google Scholar] [CrossRef]
- Weber, F. Semi-active vibration absorber based on real-time controlled MR damper. Mech. Syst. Signal Process. 2014, 46, 272–288. [Google Scholar] [CrossRef]
- Pinkaew, T.; Fujino, Y. Effectiveness of semi-active tuned mass dampers under harmonic excitation. Eng. Struct. 2001, 23, 850–856. [Google Scholar] [CrossRef]
- Lin, P.Y.; Chung, L.L.; Loh, C.H. Semiactive control of building structures with semiactive tuned mass damper. Comput. Aided Civ. Infrastruct. Eng. 2005, 20, 35–51. [Google Scholar] [CrossRef]
- Cai, C.S.; Wu, W.J.; Araujo, M. Cable vibration control with a TMD-MR damper system: Experimental exploration. J. Struct. Eng. ASCE 2007, 133, 629–637. [Google Scholar] [CrossRef]
- Casado, C.M.; Poncela, A.V.; Lorenzana, A. Adaptive Tuned Mass Damper for the Construction of Concrete Piers. Struct. Eng. Int. 2007, 17, 252–255. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Sonmez, E. Structures with semiactive variable stiffness single/multiple tuned mass dampers. J. Struct. Eng. 2007, 133, 67–77. [Google Scholar] [CrossRef]
- Kang, J.; Kim, H.-S.; Lee, D.-G. Mitigation of wind response of a tall building using semi-active tuned mass dampers. Struct. Des. Tall Spec. Build. 2011, 20, 552–565. [Google Scholar] [CrossRef]
- Weber, F.; Boston, C.; Maślanka, M. Adaptive TMD based on the emulation of positive and negative stiffness with MR damper. Smart Mater. Struct. 2011, 20, 015012. [Google Scholar] [CrossRef]
- Zemp, R.; de la Llera, J.C.; Roschke, P. Tall building vibration control using a TM-MR damper assembly: Experimental results and implementation. Earthq. Eng. Struct. Dyn. 2011, 40, 257–271. [Google Scholar] [CrossRef]
- Woo, S.S.; Lee, S.H.; Chung, L. Seismic response control of elastic and inelastic structures by using passive and semi-active tuned mass dampers. Smart Struct. Syst. 2011, 8, 239–252. [Google Scholar] [CrossRef]
- Weber, F.; Maślanka, M. Frequency and damping adaptation of a TMD with controlled MR damper. Smart Mater. Struct. 2012, 21, 055011. [Google Scholar] [CrossRef]
- Chung, L.-L.; Lai, Y.-A.; Yang, C.-S.W.; Lien, K.-H.; Wu, L.-Y. Semi-active tuned mass dampers with phase control. J. Sound Vib. 2013, 332, 3610–3625. [Google Scholar] [CrossRef]
- Mishra, S.K.; Gur, S.; Chakraborty, S. An improved tuned mass damper (SMA-TMD) assisted by a shape memory alloy spring. Smart Mater. Struct. 2013, 22, 095016. [Google Scholar] [CrossRef]
- Weber, F. Dynamic characteristics of controlled MR-STMDs of Wolgograd Bridge. Smart Mater. Struct. 2013, 22, 095008. [Google Scholar] [CrossRef]
- Frahm, H. Devices for Damping Vibrations of Bodies. U.S. Patent 989,958,1911, 30 October 1909. [Google Scholar]
- Fang, S.; Liu, S.; Liang, J. The Design of Dynamic Vibration Absorber on the Engine of Fire Smoke Exhausting Robot. Appl. Mech. Mater. 2012, 105–107, 180–184. [Google Scholar] [CrossRef]
- Koo, J.H.; Ahmadian, M.; Setareh, M. Experimental robustness analysis of magneto-rheological tuned vibration absorbers subject to mass off-tuning. J. Vib. Acoust. 2006, 128, 126–131. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, A.; You, X.; Shi, L. Theoretical Research of the Active-type Dynamic Vibration Absorbers. Adv. Mater. Res. 2011, 255–260, 1820–1824. [Google Scholar] [CrossRef]
- Kim, Y.K.; Koo, J.H.; Kim, K.S.; Kim, S.H. Suppressing harmonic vibrations of a miniature cryogenic cooler using an adaptive tunable vibration absorber based on magneto-rheological elastomers. Rev. Sci. Instrum. 2011, 82, 035103. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-M.; Wang, S.; Brennan, M.J. Optimal and robust modal control of a flexible structure using an active dynamic vibration absorber. Smart Mater. Struct. 2011, 20, 045003. [Google Scholar] [CrossRef]
- Liao, G.J.; Gong, X.L.; Kang, C.J.; Xuan, S.H. The design of an active-adaptive tuned vibration absorber based on magnetorheological elastomer and its vibration attenuation performance. Smart Mater. Struct. 2011, 20, 075015. [Google Scholar] [CrossRef]
- Xu, Z.B.; Gong, X.L.; Chen, X.M. Development of a Mechanical Semi-Active Vibration Absorber. Adv. Vib. Eng. 2011, 10, 229–238. [Google Scholar]
- Acar, M.A.; Yilmaz, C. Design of an adaptive-passive dynamic vibration absorber composed of a string-mass system equipped with negative stiffness tension adjusting mechanism. J. Sound Vib. 2013, 332, 231–245. [Google Scholar] [CrossRef]
- Weber, F. Optimal semi-active vibration absorber for harmonic excitation based on controlled semi-active damper. Smart Mater. Struct. 2014, 23, 095033. [Google Scholar] [CrossRef]
- Weber, F.; Baader, J.; Bitterli, K.; Rufer, P. Actively controlled vibration absorbers for long span belt conveyor bridges. Stahlbau 2015, 84, 246–251. [Google Scholar] [CrossRef]
- Weber, F.; Boston, C. Energy Based Optimization of Viscous-Friction Dampers on Cables. Smart Mater. Struct. 2010, 19, 045025. [Google Scholar] [CrossRef]
- Weber, F.; Boston, C. Clipped viscous damping with negative stiffness for semi-active cable damping. Smart Mater. Struct. 2011, 20, 045007. [Google Scholar] [CrossRef]
- Weber, F.; Maślanka, M. Precise Stiffness and Damping Emulation with MR Dampers and its Application to Semi-active Tuned Mass Dampers of Wolgograd Bridge. Smart Mater. Struct. 2014, 23, 015019. [Google Scholar] [CrossRef]
- Weber, F. Robust force tracking control scheme for MR dampers. Struct. Control Health Monit. 2015, 22, 1373–1395. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Yang, J.; Kim, J.; Agrawal, A. Resetting Semiactive Stiffness Damper for Seismic Response. Control. J. Struct. Eng. 2000, 126, 1427–1433. [Google Scholar] [CrossRef]
- Boston, C.; Weber, F.; Guzzella, L. Modeling of a disk-type magnetorheological damper. Smart Mater. Struct. 2010, 19, 045005. [Google Scholar] [CrossRef]
- Weber, F. Working Behaviour and Control of Magnetorheological Dampers. In New Trends in Smart Technologies; Boller, C., Janocha, H., Eds.; Fraunhofer Verlag: Saarbrücken, Germany, 2013. [Google Scholar]
- Weber, F.; Huber, P.; Distl, H.; Braun, C. Real-time controlled TMD of Danube City Tower. In Proceedings of the CTBUH (Council on Tall Buildings and Urban Habitat) International Conference 2016, Shenzhen, Guangzhou, Hong Kong, China, 16–21 October 2016.




| Tuned Case | De-Tuned Cases | |||
|---|---|---|---|---|
| Prototype MR-SVA | Nominal Primary Structure | Eigenfrequency Change | Eigenfrequency | DampingRatio |
| = 3.15 Hz (simulation) | = 3.15 Hz | +5% | = 3.31 Hz | 0.52% |
| = 3.10 Hz (tests) | = 1680 kg | +10% | = 3.46 Hz | 0.51% |
| = 26.325 kg | = 658.1 kN/m | −5% | = 2.99 Hz | 0.48% |
| = 2 N (simulation) | = 0.40% | −10% | = 2.84 Hz | 0.49% |
| 2, …, 4 N (tests) | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, F.; Distl, H.; Fischer, S.; Braun, C. MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations. Actuators 2016, 5, 27. https://doi.org/10.3390/act5040027
Weber F, Distl H, Fischer S, Braun C. MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations. Actuators. 2016; 5(4):27. https://doi.org/10.3390/act5040027
Chicago/Turabian StyleWeber, Felix, Hans Distl, Sebastian Fischer, and Christian Braun. 2016. "MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations" Actuators 5, no. 4: 27. https://doi.org/10.3390/act5040027
APA StyleWeber, F., Distl, H., Fischer, S., & Braun, C. (2016). MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations. Actuators, 5(4), 27. https://doi.org/10.3390/act5040027







