Abstract
In this paper, we have developed a new thermoacoustic model for predicting the resonance frequency and quality factors of one-dimensional (1D) nanoresonators. Considering a nanoresonator as a fix-free Bernoulli-Euler cantilever, an analytical model has been developed to show the influence of material and geometrical properties of 1D nanoresonators on their mechanical response without any damping. Diameter and elastic modulus have a direct relationship and length has an inverse relationship on the strain energy and stress at the clamp end of the nanoresonator. A thermoacoustic multiphysics COMSOL model has been elaborated to simulate the frequency response of vibrating 1D nanoresonators in air. The results are an excellent match with experimental data from independently published literature reports, and the results of this model are consistent with the analytical model. Considering the air and thermal damping in the thermoacoustic model, the quality factor of a nanowire has been estimated and the results show that zinc oxide (ZnO) and silver-gallium (Ag2Ga) nanoresonators are potential candidates as nanoresonators, nanoactuators, and for scanning probe microscopy applications.
1. Introduction
Human-made mechanical resonators have been around for a thousand years [1]. Early applications included musical instruments and chronographs operating in millihertz to kilohertz frequencies, while more recent interest has turned to ultra-high frequency resonators and oscillators suitable for wireless technologies, mass sensing and even biological applications [2,3,4,5,6,7,8,9]. The trend has leaned towards small, stiff and low-mass micro-electro-mechanical systems (MEMS), and further towards nano-electro-mechanical systems (NEMS). There have been examples of reports of using nano-mechanical resonators for myriad applications including mass sensing, charge detection, biosensing and radio frequency (RF) communications [2,5,8,9,10,11,12,13]. While there has been impressive progress in MEMS and NEMS resonators, these resonators are mostly chip-based and in-plane and are fabricated using silicon micro and nano-fabrication processes. The development of nanometer scale out-of-plane high aspect ratio resonators have been slow; an example includes the carbon nanotubes reported in the past for scanning probe microscopy (SPM) applications [6,14,15,16,17].
Atomic force microscopy (AFM) is the most successful SPM technique for characterization and manipulation of materials at the nanoscale. Since the invention of AFM, it has had tremendous impact on various disciplines including life sciences [18], molecular metrology and material science [19], nanolithography [20], semiconductor manufacturing [21] and nanomechanics [22] to name a few. The AFM vertical resolution is outstanding, limited to 0.1 nm because of electronic noise from the detection system and cantilever thermal fluctuations [23]. The in-plane, or lateral, resolution has instead long been recognized as crucial because of the non-vanishing size of the probe so that a convolution of tip shape on sample topography has to be expected at large magnifications. This phenomenon lowers the resolution, i.e., the possibility of distinguishing two points far apart from each other [23]. The final result is that the AFM broadens peaks and shrinks holes, thereby introducing gross artefacts. Tentative attempts to overcome this limitation include, for example, the use of single-walled carbon nanotubes (SWNT) as imaging tip in order to minimize the tip convolution [23,24,25]. However, manipulation of SWNT as AFM tips has been difficult due to the flexible nature of the nanotubes and the van der Wals interaction between tubes resulting in adhesion. To overcome these obstacles, one needs to use chemical vapor deposition or other techniques to make rigid nanotube probes at the loss of mechanical properties. New materials that are rigid and have high aspect ratio structures, such as Ag2Ga metallic nanoneedles [7] and ZnO nanowires and nanobelts [26], may enable better materials for nano-actuation and SPM applications. While many experiments have reported such nanoresonators, only a few theoretical reports exist on the modeling and characterization of nanoresonators’ natural frequency and loss mechanisms [3,27,28,29,30].
Bhiladvala et al. suggested two different mechanisms for the interaction between air molecules and nanoresonator depending on the diameter of nanoresonator and the air pressure [5]. As the cantilever diameter or width approaching sub-micron size, the size of beam itself is comparable to air molecules’ mean free path [5]. The Knudsen number (Kn) is the ratio of mean free path of air molecules to the lateral size of the resonator and it depends on the pressure of the air. Three different regimes based on the Knudsen number (Kn) were defined [5]. For Kn smaller than 0.01, continuum regime for air and fluid mechanics equations can be used. For Kn larger than 10, one can use the free molecular flow regime. A cross-over regime where 0.01 < Kn < 10 was also defined as transient between the continuum and molecular flow regimes [5]. Variations on the cross-flow regime has also been reported in the literature [31,32]. For Kn < 10, reports have also used simple continuum models even for the cross-flow regime [27,33,34].
Based on this initial paper in reference [5], Biedermann et al. developed a model for calculating the nanoresonator Q factor. Although they used the same concept and definition for free molecular flow, crossover and continuum regime, they considered the Ag2Ga nanowire in the free molecular regime and suggested an equation for Q factor estimation as [8,35], where (i) represents different modes for the lateral vibration of the beam, is the angular natural frequency of nanoresonator at different modes; is the density of nanoresonator; A is the cross-sectional area of the nanoresonator; b is the effective area for damping per unit length; P is the pressure; Ro is the universal gas constant; T is the temperature; and Mm is the molecular weight. Unfortunately, the results of this equation are not consistent with their experimental Q factor findings using laser Doppler vibrometry resulting in a large error in estimated Q factors [8,35]. For the first mode, the experimental Q factors were 1.2, whereas the Q factor using the above-estimated equation was only 0.49, creating an almost 58% difference between the estimated and the experimental values. The errors are similar in other modes.
There are also other reports that have estimated the Q factor for nanoresonators [5,27]. Yum et al. defined the normalized dimension parameter () to include nanoresonator geometry and properties along with fluid viscosity [27], where µ is the viscosity and surrounding medium; W is the width; and h is the height of nanoresonator. They showed a linear relationship between Dn and damping coefficient (inverse of quality factor). This equation is just for resonators with a rectangular cross-section and it is not applicable on cylindrical geometries. Also, this theory is only tested on ZnO nanobelts and it has not been confirmed for other materials and geometries. The other limitation of this theory is that it is only for the first mode. It should be noted that while Biedermann et al. claim that there is a linear relationship between the resonance frequency and Q factor, Yum et al. report, and our results presented here, show a nonlinear relationship between these two parameters. While these methods are interesting, a new model that accurately describes the theoretical and experimental values of Q factor is in need of further development.
A finite element model (FEM) was previously developed to simulate the behavior of the nanoresonator using experimental Q factor [36]. However, in this paper, we investigate a new theoretical and FEM approach based on thermoacoustic modeling (integrating Navier-Stokes equation, continuity equation, and energy equation) to understand the behavior of nanoresonators and it can predict the Q factor of vibrating nanoresonator in air. The effect of density, bending modulus, length and diameter of 1D nanoresonator on the stress at its clamp end and strain energy are presented. In this thermoacoustic model, we have considered continuum flow for air Kn < 10 and our simulations show excellent agreement with experimental data. Figure 1 shows the Knudsen number, continuum and free molecular flow for two resonators that are simulated in COMSOL.
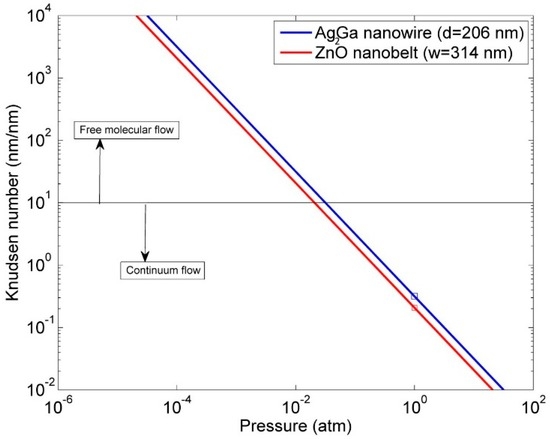
Figure 1.
Effect of nanoresonator size and its surrounding pressure in air on the Knudsen number at 300 °·K. The squares show the condition of nanoresonators that are tested in the thermoacoustic model.
2. Analytical Model
This section discusses the lateral vibration of a high aspect ratio nanoresonator without any damping. The effect of damping has been presented in the next section. Figure 2 presents the schematic of the base motion of the nanoresonator. In practice, a nanoresonator can be used as a standing wave stylus for SPM in non-contact mode and it is necessary to avoid any contact forces. Here, the contact forces on the tip of resonator are neglected to simplify the model. The aim of this section is to investigate the effect of material properties and geometry of a 1D nanoresonator on its mechanical behavior. Because of its high aspect ratio, a 1D nanoresonator can be considered as a Bernoulli-Euler beam, and its natural frequencies at different modes for transverse vibration are [37]:
where ki is the constant coefficient of natural frequency for different modes; L is the length; E is the elastic modulus; and I is the planar second moment of area of the nanoresonator. Figure 2 shows loading, mechanical properties and free body diagram of a nanoresonator when it is actuated by transverse base motion. Working in the steady state, the actuator applies constant vibration amplitude on the clamping end of a nanoresonator. Therefore, a base harmonic mechanical displacement is considered as the actuation input (E = D·Sin(t)) of nanoresonator instead of force actuation. D is the input vibration amplitude. This model does not include air damping and it is applicable to high vacuum conditions. Assuming the nanoresonator as a Bernoulli-Euler beam [38], the equation of motion is given by:
where x is the spatial coordinate; y is the lateral displacement of a nanoresonator; and t represents time. Considering constant EI, B as the vibration amplitude along the nanoresonator length, and as the response of harmonic excitation, the deflection of the nanoresonator at the free end would be:
where λ is eigenvalues:
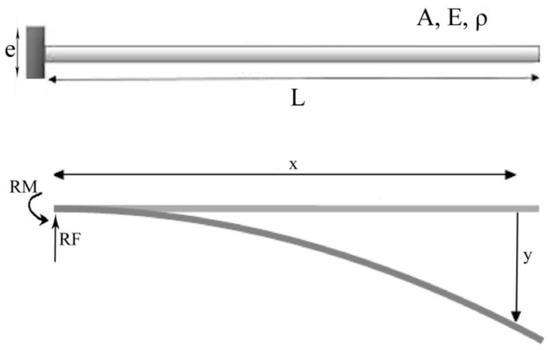
Figure 2.
Schematic figure of base motion of a nanoresonator.
Since Ci are the constants applying the boundary conditions as a clamp-free beam, C1 to C4 will be:
Because of the nanoresonator’s high aspect ratio, the reaction force and shear stress at the clamp end is negligible in comparison to the normal stress of bending. For the reaction moment at the clamp end of the nanoresonator for a cylindrical shape resonator (nanowire) we have:
The stress at the clamped end of the nanowire is:
where d is the diameter of nanowire. The strain energy because of elastic deformation of vibrating nanowire is:
Bending modulus of nanoresonators should be used in these simulations. In all of above equations, the dependent variable of harmonic and hyperbolic functions is λL. For the natural frequencies, considering Equations (1) and (4), we have:
Equation (9) means that for a specific natural frequency, the value of λL is constant. In the present model, damping and energy loss have not been considered. Consequently, the value of (2 + 2cos (λL)cosh(λL)) at the resonance frequencies is zero at the denominator of C1 and the values of C1 to C4 are infinite.
Considering Equation (1), the natural frequencies of a cylindrical nanoresonator with constant diameter are:
The normal stress at the clamp end of a cylindrical nanoresonator for a specific vibration mode can be calculated using Equations (1), (4), (6), (7) and (9):
C is a constant as a result of the integral in Equation (7), where λL is constant at a vibration mode (Equation (9)). For the strain energy, considering constant λL for a vibration mode in Equations (1), (4), and (8), we have:
C’ is a constant for each mode equal to the integral of Equation (8).
In practice, there is an actuator with a specific working frequency to oscillate the nanoresonator. If the resonator has smaller natural frequency, it will be easier to actuate it with sufficient vibration amplitude. High vibration amplitude makes the virtual tip bigger and it would be easier to move the nanoresonator close to the target surface in SPM. Another important note is that after the third mode, the values of normal stress and strain energy for each mode are increased linearly in logarithmic scale. Also it should be mentioned that changing the geometric parameters of the needle has more effect on the characteristics of the resonator rather than its material properties.
Selecting the proper characteristics for the nanoresonator is tricky and it is all about compromising between parameters. Working in higher modes increases the stored energy and vibration amplification, but it also increases the stress at the clamp end, which could lead to failure of bonding between the nanoresonator and its actuator. Higher density decreases the natural frequency but does not influence the vibration amplitude, stress and stored elastic energy.
3. Thermoacoustic Finite Element Model (FEM)
There are different loss mechanisms that limit the performance of nanoresonators, including clamping, thermal effects, electrostatic forces, surrounding medium hydrodynamic loading, van der Waals force, Casmir force and other type of forces depending on the nanoresonator application [39,40,41]. Thus far, there have been various models for estimating the Q factor of micro and nanoresonators [5,28,29,42,43,44]. Whether or not considering all of these energy loss mechanisms in the model is necessary depends on the size and environment conditions of the resonator. As an example, in most of the reported models, in calculating the damping of micro-scale resonators and MEMS resonators, the thermal loss was not been considered and the model is mostly about viscous damping [28,39,43,45]. Most of these models are focused on AFM probes. These models have incorporated the viscous damping as the only mechanism affecting energy loss and, in considering the inertial forces, these models have calculated the quality factors of the microscale resonators [28,46,47,48]. However, these models cannot estimate the quality factor and damping of the nanoresonators precisely. The reason for the inaccuracy is that when one scales down from micro to nanoresonators, the inertial forces become less important and the thermal loss becomes more important.
Fabricating an individual nanoresonator from different materials and recording its frequency response function is often time consuming and not practicable. Therefore, collecting experimental data on damping of the nanoresonators is an expensive and hard way to go; we thus present here a model to calculate the Q factor of nanoresonators using thermoacoustic simulations for different geometries and mechanical properties. Thermoacoustic modeling has not been employed to study the mechanical resonance frequency and quality factor of nanoresonators before and is thus a new tool for high aspect ratio nanostructures.
Thermoacoustic modeling is a method to investigate energy loss in the viscous, acoustic, and thermal boundary layers around the nanoresonators. The small fluctuations of air pressure on top of atmosphere (stationary) pressure due to the vibrations of nanoresonators are acoustic waves. The wave equation of Helmholtz equation is derived by linearization of fundamental equations of fluid dynamics including Navier-Stokes equation, continuity equation, and energy equation. Of course the conservation equations for momentum, mass and energy for the acoustic perturbation has to be considered. Computational methods can be used to solve these equations numerically while they are coupled with thermal field. Here a FEM thermoacoustic model is developed using COMSOL Multiphysics software package (COMSOL Inc., Burlington, MA, USA) to simulate the frequency response function of 1D nanoresonators vibrating in the air.
In COMSOL, air is considered as a continuous gaseous medium and by defining air properties, COMSOL can simulate its effect on the vibration of nanoresonators. We have three sets of equations, one set that applies on the resonator as an elastic solid, one set that applies on the air as a fluid, and one set that links the solid displacement and stress to the surrounding fluid as an acoustic interaction on the element nodes that are defined as the contact surface. The vibration of the nanoresonator will create a harmonic displacement in thermoacoustic sphere:
where I is the square root of −1 and usolid is the velocity field of solid elements at the interface. For the continuity equation we have:
where ρ is the density of air and ρ0 is the background (initial) density. The momentum equation for thermoacoustic region would be:
µ is the dynamic viscosity and µB is the bulk viscosity. The energy conservation would be:
Cp represents the heat capacity at constant pressure, k the thermal conductivity, α0 the coefficient of thermal expansion. And finally the equation of state connects these parameters together:
βT is the isothermal compressibility. Thermoacoustic model only considers the conduction for temperature variation. Temperature variation can change the air properties including density, coefficient of thermal expansion and isothermal compressibility. These values can affect the condition of acoustic interaction and that is why the local temperature variation around the resonator is important. Other studies have estimated the thickness of thermal and viscous layer as a function of frequency [50]. For all of the frequencies, the stationary temperature is assumed room temperature (20 °C). If the temperature variation is large, there might be some convective heat transfer outside of thermoacoustic layer which in long term may cause a change in stationary temperature.
The model consists of a thin cantilever beam with high aspect ratio and there are two spheres around the beam (Figure 3). The smaller sphere is the thermoacoustic layer that calculates the fluid dynamics and thermal energy transfer of the nanoresonator. The bigger sphere is transferring the acoustic field of air in the thermoacoustic layer to the outside boundary. In this way, we can radiate the loss energy out of medium and consider an infinite volume of air around the resonator as it is. In some cases, there is a wall or another nanoresonator near the target resonator that will affect the acoustic field, but for our model, we consider only an individual resonator that is surrounded by air.
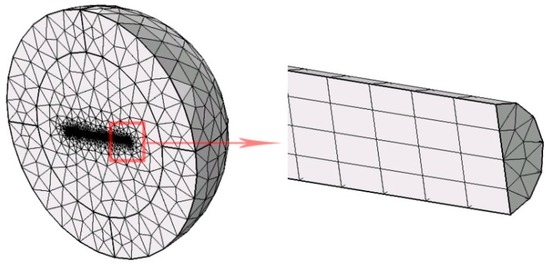
Figure 3.
Thermoacoustic model of nanoresonators. Triangular prism element for the resonator and tetrahedron for surrounding medium.
The model has a symmetry plane parallel to the lateral vibrations and resonator axis. For meshing, a triangular prism element for the resonator and tetrahedron for the surrounding medium have been considered. To have accurate results, the maximum size of the elements was determined as 20% of the wavelength. It should be mentioned that there is a boundary viscous and thermal thin layer around the resonator; the gradients of velocity and temperature are large, and the mesh size in this region should be smaller than the thickness of the acoustic boundary layer [49]. Figure 3 presents the meshed model in COMSOL. Frequency domain analysis was used to develop a frequency response function (FRF) for the nanoresonator. Clamp-free was considered as the boundary conditions of the beam, and base motion vibration with ~500 nm amplitude was applied as a mechanical input. The vibration amplitude at the free end is plotted for different frequencies and the width of the half power point of experimental and simulated graphs is calculated as the Q factor.
4. Results
To check the accuracy of the model, the results of the FEM model are compared to the results of reported experimental data on nanoresonators. Based on the results of Section 2, nanoresonators have been selected as the candidates for a 1D nanomechanical tool: a Ag2Ga nanowire (cylindrical shape with high density and bending modulus) [35,51] and a zinc oxide (ZnO) nanobelt (square cross-section) [26,27].
Table 1 shows the properties of the selected nanoresonators. Figure 4 presents the frequency response function (FRF) resulting from experimental data and thermoacoustic simulations. It should be mentioned that experimental data has an arbitrary unit and, in Figure 4, each experimental graph peak has been normalized to the maximum of relative simulated data.

Table 1.
Properties of ZnO nanobelt and Ag2Ga nanowire.

Figure 4.
Frequency response function of Ag2Ga nanowire and ZnO nanobelt resulted from experimental data and thermoacoustic model. The results of experimental data and thermoacoustic model match.
Table 2 compares the experimental and simulated results for the selected nanoresonators. The simulated values of resonance frequency f and Q factor are very close to their experimental values [35]. The last column in Table 2 shows the calculated Q factors based on an equation in reference [35]. The error in the results of the thermoacoustic model is much lower than the estimation in reference [35] and it shows the effectiveness of COMSOL multiphysics simulation (thus the physics is right!).

Table 2.
Comparing natural frequencies and Q factors of nanoresonators from experiments and simulations.
Equation (1) calculates the natural frequencies of a nanoresonator when there is no loss. Having any kind of loss, including viscous and thermal, is like adding a mass to the vibrating system—it can cause a downshift in resonance frequencies. In other words, the peak frequency in the damped system is definitely smaller than the natural frequency. The resonance frequency resulted from simulation and experiments are very close for ambient conditions. However, when that small nanowire is working in vacuum, we can no longer simulate the air as a continuum fluid (as it is in free molecular flow regime) with the thermoacoustic model.
Table 3 compares the mechanical response of the Ag2Ga nanowire and ZnO nanobelt. The first resonance frequency of ZnO nanobelt is close to the second mode of Ag2Ga and the stress at the clamp end for these two modes are close. However, the vibration amplitude and strain energy for the ZnO nanobelt is much higher than for the Ag2Ga nanowire, suggesting ZnO nanowires can be better choices for SPM as a tip. However, there are other deliberations including the fabrication process that should be considered before final selection.

Table 3.
The mechanical response of the Ag2Ga nanowire and Zno nanobelt from a thermoacoustic model.
Figure 5 shows the mode shapes and temperature variation for the first four modes of the Ag2Ga nanoneedle. As is shown, the radius of the thermal boundary layer decreases as the frequency increases. For example, the diameter of temperature variation for the fourth mode is in the same scale of the nanoresonator length, but for the first mode, the diameter of temperature variation is almost twice the length of the nanoresonator. Based on the acoustic effects of MEMS resonators that led to improved performance [50], we used a similar concept to define the radius of the thermoacoustic sphere. A smaller thermoacoustic sphere can be used for high frequency modes to make the computations faster and less expensive. In these simulations, the radius of the thermoacoustic sphere (R) for the first mode is 50% larger than the resonator’s length (L), but in higher modes, the radius of the thermoacoustic model and the length of the nanoresonator are equal. Figure 6 compares the results of the thermoacoustic model for the first resonance mode with different thermoacoustic sphere size. The results are different when R = L, R = 1.5 L. However, there are no differences between the results of simulations when R = 1.5 L and R = 2 L. Therefore, if the sphere is large enough that the temperature variation at outer regions of sphere is zero, the size of sphere is optimum and making the sphere bigger will not affect the results. Based on these observations for the final results, R = 1.5 L was selected for the first mode but for modes 2, 3, and 4, R = L was selected as the size of sphere.
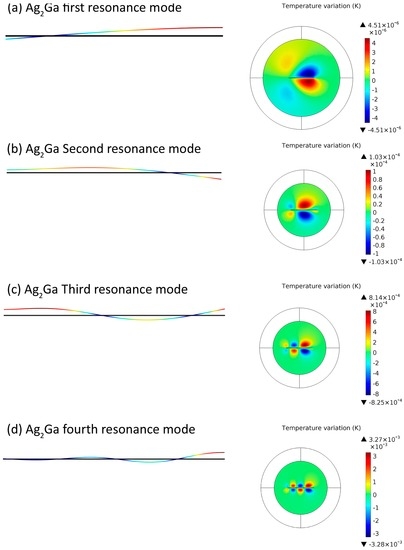
Figure 5.
Mode shape and temperature variation for different modes of AgGa nanoneedle.
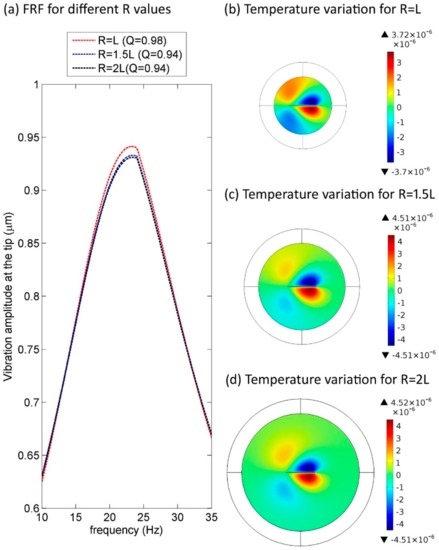
Figure 6.
The effect of thermoacoustic sphere radius (R) on the temperature variation distribution and Q factor for the first mode of Ag2Ga nanowire.
In these simulations, the temperature variation is small and local, but if this is not the case in a simulation, higher initial temperature should be utilized for the interaction. In Figure 5, as the vibrating mode is increased, the temperature variation increases and it becomes more local. It should be noted that, in the frequency domain, the results are for a steady-state situation, and transient conditions are not available.
Although thermoacoustic simulation works very well at the continuum regime, its results are not as precise in the free molecular flow regime, low-vacuum conditions, and very small diameter beams; thermoacoustic simulation can’t predict the Q factor correctly. This suggests that the physics at the molecular flow regime needs new equations which COMSOL currently does not offer.
Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 show the effect of diameter, length, bending modulus, and density on the maximum stress at the clamp end and elastic stored energy of nanowire in an ambient condition for each mode. In each figure, the fitted curve on the thermoacoustic results is shown. Except for the relationship between the diameter and normal stress, the simulated results corroborate the findings of the analytical model.
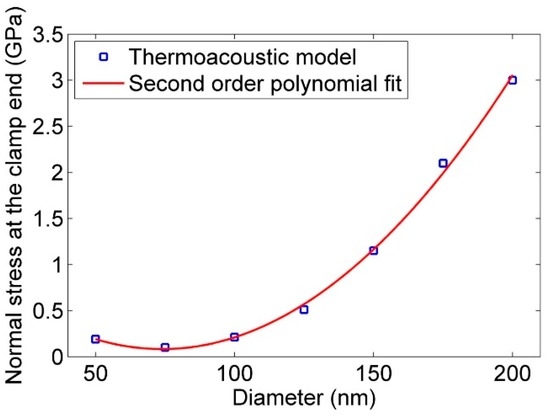
Figure 7.
Effect of diameter on the normal stress at the clamp end of nanowire. Theoretical model suggested a linear fit while the thermoacoustic model shows a second-order polynomial fit for the relationship of diameter and normal stress at the clamp end.
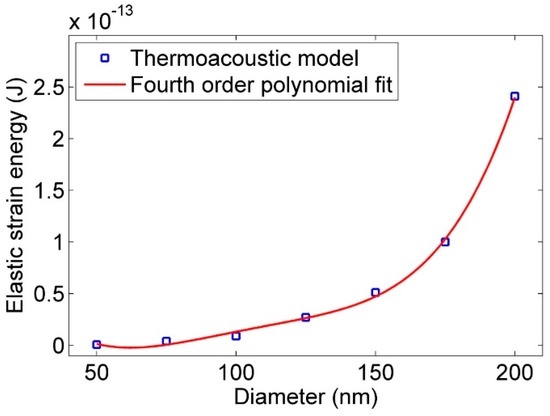
Figure 8.
Effect of diameter on the stored strain energy of nanowire. The analytical model matches with the results of the thermoacoustic model ().
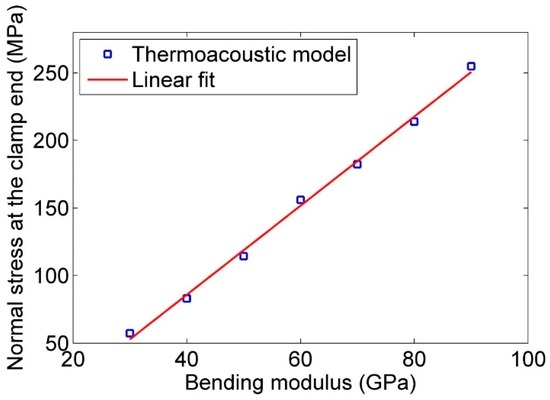
Figure 9.
Effect of bending modulus on the normal stress at the clamp end of a nanowire. The analytical model corresponds to the results of the thermoacoustic model ().
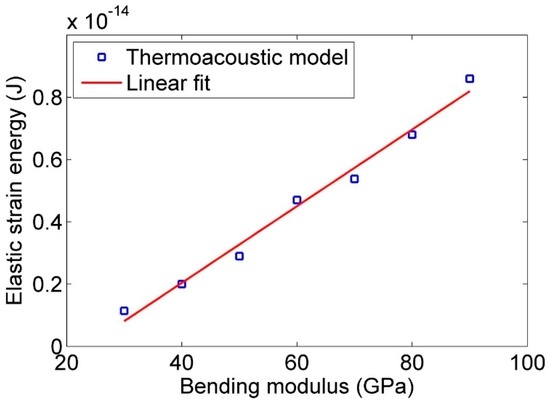
Figure 10.
Effect of bending modulus on the elastic strain energy of nanowire. The analytical model matches with the results of a thermoacoustic model ().
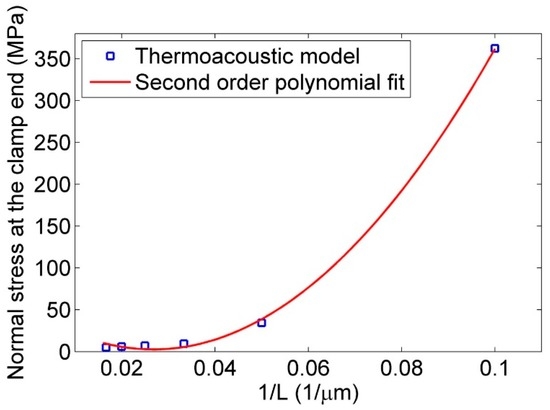
Figure 11.
Effect of length on the normal stress at the clamp end of nanowire. The analytical model’s findings match the results of the thermoacoustic model ().
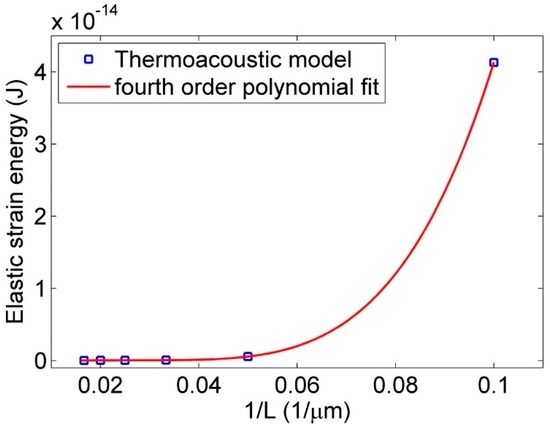
Figure 12.
Effect of length on the elastic strain energy of nanowire. The analytical model matches the results of the thermoacoustic model ().
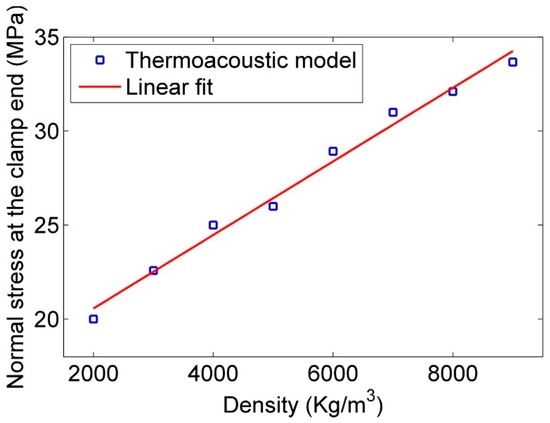
Figure 13.
Effect of density on the normal stress at the clamp end of nanowire.
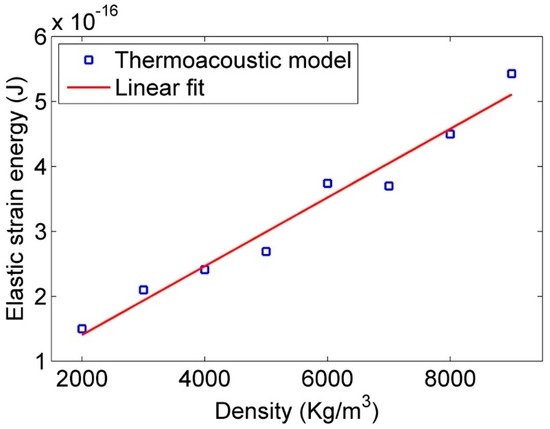
Figure 14.
Effect of density on the elastic strain energy of nanowire.
Figure 7 and Figure 8 show the effect of diameter on the normal stress at the clamp end and strain energy of the nanoresonator. In these simulations, 10 µm as length, 90 GPa as bending modulus, and 9000 kg/m3 as the density of the nanoresonator were kept constant, and the results are plotted for different diameters. While the analytical model (Equation (11)) suggests linear behavior between the diameter and normal stress, the simulation results show a second-order polynomial fit. As the diameter of the nanoresonator decreases, it gets closer to the free molecular regime and the thermoacoustic model fails to simulate the vibration of nanoresonator in this regime accurately. However, Figure 8 shows a fourth-order polynomial fit for strain energy which is consistent with what is suggested in Equation (12).
Figure 9 shows a linear relationship between bending modulus and stress for the nanoresonators. Figure 10 also shows the linear effect of bending modulus on strain energy. In these simulations, the selected measurements for defining the properties of the nanoresonator are: 20 µm length, 200 nm diameter, and 9000 kg/m3 as density. Equations (11) and (12) confirm the same effect for the bending modulus.
For investigating the effect of length, 200 nm diameter, 20 GPa bending modulus, and 9000 kg/m3 density were kept constant, and length was changed from 10 to 60 µm. The analytical model as well as Figure 11 shows a second-order fit for stress versus the inverse of length. Figure 12 and Equation (12) show a fourth-order fit for strain energy versus the inverse of length. Figure 13 and Figure 14 also show the negligible effect of density on stress and strain energy as it was suggested in Equation (11) and (12).
Now that we are sure that the simulation results are consistent with the experiments, we can use this model to investigate the effect of nanoresonator properties on its Q factor. Therefore, a series of simulations were designed to show the effect of the length, diameter, density, and elastic modulus of a vibrating resonator in air on its Q factor. Equation (18) has been developed based on the results of simulations.
ki is the constant coefficient of natural frequency for different modes, d the diameter, L length, E elastic modulus, and ρ the density of nanowire. This equation is for an individual nanoresonator as a fix-free cantilever vibrating in air and it looks like this equation is similar to the one that has been suggested by Yum et al. [27]. However, by adding the thermal damping, the power of parameters has been modified in Equation 18 and is more accurate.
5. Discussion and Conclusions
A scanning probe microscopy (SPM) typically employs probe tips of various shapes attached to short beams that limit the geometry of features that can be probed [52]. In recent efforts to overcome this, researchers have added a carbon nanotube to the end of an atomic force microscope (AFM) tip [53]. New materials such as Ag2Ga and ZnO nanowires and nanobelts have also been used. In carbon nanotubes, the shank lengths are only in a region of a few micrometers long and also cause adhesive effects due to van der Wals forces which can be overcome by using resonating probes. To minimize this influence, different techniques have been evaluated such as: torsional [54], longitudinal [55], and lateral vibrations in SPM and AFM [56]. Compared to carbon nanotubes, the Ag2Ga offers a versatile probe, room temperature probe fabrication and also an ability to grow probes of any length with high rigidity [7]. These could be useful in places like probing inside a via. In general, these methods employ a 1D probe tip that is oscillated below the natural frequency of the probe’s shank. Once the work piece is contacted by the vibrating free end of the probe tip, it causes a shift in the phase and natural frequency of the probe system [57,58]. All of the earlier solutions do not provide the capability of rapidly and accurately measuring even high aspect ratio micro-scale features such as vias, micro-cooling channels, and fiber optic couplers. In particular, for micro scale probes with spherical contact tips, tip diameters in many cases are larger than 100 μm, which is not effective for holes with less than 200 μm diameter. Second, probe tips smaller than 100 μm in diameter are relatively short and still large compared to the targeted hole diameters such as fuel injector nozzles, chip vias, or micro cooling channels. Furthermore, the measurement speed is low and probes often function only in the touch trigger mode. These probes are susceptible to adhesion and thus, after contacting the work piece, they stick to the measured surface. Procedures to overcome adhesion effects often reduce repeatability and increased time needed to perform the measurement. Using nanoresonators with high strain energy to avoid sticking to the target surface is a feature that is desired. The high frequency vibration can apply large stress at its bonding section to the actuator and make the bonding break. High amplification can act as a virtual tip to move the nanoresonator close to the target surface.
Table 4 summarizes the effect of material and geometrical parameters on the mechanical response of a vibrating nanowire. Among these parameters, length is the most influential parameter and density is the least influential one. To simulate the behavior of vibrating nanoresonator in air, a thermoacoustic multiphysics model is presented in this report and the results match the experimental data accurately. A thermoacoustic model only works in the continuum regime, and its results in the free molecular regime need new physics to describe them in COMSOL. Ag2Ga nanowire and ZnO nanobelt were selected as the potential candidates due to their use as a stylus in SPM. This model is the first of its kind and has excellent agreement with the experimental reports in the literature and thus is useful for predicting the mechanical properties of such 1D nanomaterials. Future developments in this area could be development of a package in COMSOL to describe the molecular flow regime that can accurately predict the resonance frequency and quality factors of nanoresonators. New 2D nanomaterials such as transition metal dichalgogenides (TMDs) with their layered structure and ultra-high strength and ability to withstand deformation up to 25% could be simulated for their resonance frequency and quality factors using this model rather than doing expensive experiments in the future.

Table 4.
The effect of material and geometrical properties of a vibrating nanoresonator in vacuum on its mechanical response.
Acknowledgments
Funding for this work was partially provided by the National Science Foundation (ECCS 1463987; CMMI: 1463869 and DMR: 1410678) for B.P.
Author Contributions
B.P. conceived the original study, M.S.L. developed, performed and interpreted the simulations. B.P. and R.W.C. reviewed and provided additional interpretations of the simulations. All three authors contributed to the writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Nomenclature
| Angular natural frequency of nanoresonator at different modes | |
| Density of nanoresonator | |
| Cross-section of nanoresonator | |
| Pressure | |
| Molecular weight | |
| Temperature | |
| Universal gas constant | |
| Effective area for damping per unit length | |
| The constant coefficient of natural frequency for different modes | |
| Elastic modulus of nanoresonator | |
| Length of nanoresonator | |
| Width of nanoresonator | |
| Height of nanoresonator | |
| Planar second moment of nanoresonator area | |
| Special coordinates of nanoresonator | |
| Lateral displacement of vibrating nanoresonator in time domain | |
| Time | |
| Deflection of nanoresonator in special coordinates | |
| Base excitement of nanoresonator | |
| Actuating angular frequency | |
| Amplitude of base excitation | |
| , , , , , | Constant |
| Eigenvalue | |
| Reaction moment at clamp end of nanoresonator | |
| Stress | |
| Diameter of nanowire | |
| Elastic strain energy |
References
- Jensen, K.; Peng, H.B.; Zettl, A. Limits of nanomechanical resonators. In Proceedings of the IEEE International Conference on Nanoscience and Nanotechnology, Brisbane, Australia, 3–7 July 2006.
- Erbe, A.; Blick, R.H. Nanomechanical resonators operating at radio frequencies. Phys. B Condens. Matter 1999, 272, 575–577. [Google Scholar] [CrossRef]
- Kiracofe, D.R.; Yazdanpanah, M.M.; Raman, A. Mass and stiffness calibration of nanowires using thermally driven vibration. Nanotechnology 2011, 22, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, P.; Harrington, D.A.; Ekinci, K.L.; Yang, Y.T.; Murphy, M.J.; Roukes, M.L. Intrinsic dissipation in high-frequency micromechanical resonators. Phys. Rev. B 2002, 66, 1–15. [Google Scholar] [CrossRef]
- Bhiladvala, R.B.; Wang, Z.J. Effect of fluids on the Q factor and resonance frequency of oscillating micrometer and nanometer scale beams. Phys. Rev. E 2004, 69, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Yazdanpanah, M.M.; Hosseini, M.; Pabba, S.; Berry, S.M.; Dobrokhotov, V.V.; Safir, A.; Keynton, R.S.; Cohn, R.W. Micro-Wilhelmy and related liquid property measurements using constant-diameter nanoneedle-tipped atomic force microscope probes. Langmuir 2008, 24, 13753–13764. [Google Scholar] [CrossRef] [PubMed]
- Jalilian, R.; Rivera, J.; Askari, D.; Arva, S.; Rathfon, J.M.; Cohn, R.W.; Yazdanpanah, M.M. Toward wafer-scale patterning of freestanding intermetallic nanowires. Nanotechnology 2011, 22, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Biedermann, L.B. Vibrational Spectra of Nanowires Measured Using Laser Doppler Vibrometry and STM Studies of Epitaxial Graphene: An LDRD Fellowship Report; Sandia National Laboratories: Livermore, CA, USA, 2009. [Google Scholar]
- Fischer, L.M.; Wright, V.A.; Guthy, C.; Yang, N.; McDermott, M.T.; Buriak, J.M.; Evoy, S. Specific detection of proteins using nanomechanical resonators. Sens. Actuators B Chem. 2008, 134, 613–617. [Google Scholar] [CrossRef]
- Arcamone, J.; Rius, G.; Abadal, G.; Teva, J.; Barniol, N.; Perez-Murano, F. Micro/nanomechanical resonators for distributed mass sensing with capacitive detection. Microelectron. Eng. 2006, 83, 1216–1220. [Google Scholar] [CrossRef]
- Blick, R.H.; Erbe, A.; Krommer, H.; Kraus, A.; Kotthaus, J.P. Charge detection with nanomechanical resonators. Phys. E Low Dimens. Syst. Nanostruct. 2000, 6, 821–827. [Google Scholar] [CrossRef]
- Hutchinson, A.B.; Truitt, P.A.; Schwab, K.C.; Sekaric, L.; Parpia, J.M.; Craighead, H.G.; Butler, J.E. Dissipation in nanocrystalline-diamond nanomechanical resonators. Appl. Phys. Lett. 2004, 84, 972–974. [Google Scholar] [CrossRef]
- Eom, K.; Kwon, T.Y.; Yoon, D.S.; Lee, H.L.; Kim, T.S. Dynamical response of nanomechanical resonators to biomolecular interactions. Phys. Rev. B 2007, 76, 1–4. [Google Scholar] [CrossRef]
- Wilson, N.R.; Macpherson, J.V. Carbon nanotube tips for atomic force microscopy. Nat. Nanotechnol. 2009, 4, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; Cassell, A.M.; Liu, H.B.; Chao, K.J.; Han, J.; Meyyappan, M. Large-scale fabrication of carbon nanotube probe tips for atomic force microscopy critical dimension Imaging applications. Nano Lett. 2004, 4, 1301–1308. [Google Scholar] [CrossRef]
- Yenilmez, E.; Wang, Q.; Chen, R.J.; Wang, D.W.; Dai, H.J. Wafer scale production of carbon nanotube scanning probe tips for atomic force microscopy. Appl. Phys. Lett. 2002, 80, 2225–2227. [Google Scholar] [CrossRef]
- Jalilian, R.; Jauregui, L.A.; Lopez, G.; Tian, J.F.; Roecker, C.; Yazdanpanah, M.M.; Cohn, R.W.; Jovanovic, I.; Chen, Y.P. Scanning gate microscopy on graphene: Charge inhomogeneity and extrinsic doping. Nanotechnology 2011, 22, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Parot, P.; Dufrene, Y.F.; Hinterdorfer, P.; le Grimellee, C.; Navajas, D.; Pellequer, J.L.; Scheuring, S. Past, present and future of atomic force microscopy in life sciences and medicine. J. Mol. Recognit. 2007, 20, 418–431. [Google Scholar] [CrossRef] [PubMed]
- Jalili, N.; Laxminarayana, K. A review of atomic force microscopy imaging systems: Application to molecular metrology and biological sciences. Mechatronics 2004, 14, 907–945. [Google Scholar] [CrossRef]
- Xie, X.N.; Chung, H.J.; Sow, C.H.; Wee, A.T.S. Nanoscale materials patterning and engineering by atomic force microscopy nanolithography. Mater. Sci. Eng. R Rep. 2006, 54, 1–48. [Google Scholar] [CrossRef]
- Minne, S.C.; Soh, H.T.; Flueckiger, P.; Quate, C.F. Fabrication of 0.1-µm metal-oxide-semiconductor field-effect transistors with the atomic-force microscope. Appl. Phys. Lett. 1995, 66, 703–705. [Google Scholar] [CrossRef]
- Li, H.B.; Rief, M.; Oesterhelt, F.; Gaub, H.E.; Zhang, X.; Shen, J.C. Single-molecule force spectroscopy on polysaccharides by AFM-nanomechanical fingerprint of alpha-(1,4)-linked polysaccharides. Chem. Phys. Lett. 1999, 305, 197–201. [Google Scholar] [CrossRef]
- Tranchida, D.; Piccarolo, S.; Deblieck, R.A.C. Some experimental issues of AFM tip blind estimation: The effect of noise and resolution. Meas. Sci. Technol. 2006, 17, 2630–2636. [Google Scholar] [CrossRef]
- Martinez, J.; Yuzvinsky, T.D.; Fennimore, A.M.; Zettl, A.; Garcia, R.; Bustamante, C. Length control and sharpening of atomic force microscope carbon nanotube tips assisted by an electron beam. Nanotechnology 2005, 16, 2493–2496. [Google Scholar] [CrossRef]
- Dai, H.J.; Hafner, J.H.; Rinzler, A.G.; Colbert, D.T.; Smalley, R.E. Nanotubes as nanoprobes in scanning probe microscopy. Nature 1996, 384, 147–150. [Google Scholar] [CrossRef]
- Wang, Z.L. Zinc oxide nanostructures: Growth, properties and applications. J. Phys. Condens. Matter 2004, 16, R829–R858. [Google Scholar] [CrossRef]
- Yum, K.; Wang, Z.Y.; Suryavanshi, A.P.; Yu, M.F. Experimental measurement and model analysis of damping effect in nanoscale mechanical beam resonators in air. J. Appl. Phys. 2004, 96, 3933–3938. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Vancura, C.; Dufour, I.; Heinrich, S.M.; Josse, F.; Hierlemann, A. Analysis of resonating microcantilevers operating in a viscous liquid environment. Sens. Actuators A Phys. 2008, 141, 43–51. [Google Scholar] [CrossRef]
- Herrera-May, A.L.; Garica-Ramirez, P.J.; Aguilera-Cortes, L.A.; Plascencia-Mora, H.; Garcia-Gonzalez, L.; Manjarrez, E.; Narducci, M.; Figueras, E. Analytical modeling for the bending resonant frequency of sensors based on micro and nanoresonators with complex structural geometry. IEEE Sens. J. 2011, 11, 1361–1374. [Google Scholar] [CrossRef]
- Li, M.W.; Bhiladvala, R.B.; Morrow, T.J.; Sioss, J.A.; Lew, K.K.; Redwing, J.M.; Keating, C.D.; Mayer, T.S. Bottom-up assembly of large-area nanowire resonator arrays. Nat. Nanotechnol. 2008, 3, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Verbridge, S.S.; Craighead, H.G.; Parpia, J.M. A megahertz nanomechanical resonator with room temperature quality factor over a million. Appl. Phys. Lett. 2008, 92, 1–3. [Google Scholar] [CrossRef]
- Belov, M.; Quitoriano, N.J.; Sharma, S.; Hiebert, W.K.; Kamins, T.I.; Evoy, S. Mechanical resonance of clamped silicon nanowires measured by optical interferometry. J. Appl. Phys. 2008, 103, 1–7. [Google Scholar] [CrossRef]
- Zhou, J.; Lao, C.S.; Gao, P.X.; Mai, W.J.; Hughes, W.L.; Deng, S.Z.; Xu, N.S.; Wang, Z.L. Nanowire as pico-gram balance at workplace atmosphere. Solid State Commun. 2006, 139, 222–226. [Google Scholar] [CrossRef]
- Biedermann, L.B.; Tung, R.C.; Raman, A.; Reifenberger, R.G.; Yazdanpanah, M.M.; Cohn, R.W. Characterization of silver-gallium nanowires for force and mass sensing applications. Nanotechnology 2010, 21, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Loeian, S.M.; Panchapakesan, B. High Frequency Resonators using Exotic Nanomaterials. In Proceedings of the COMSOL Conference, Boston, MA, USA, 8–10 October 2014.
- Timoshenko, S.; Young, D.H.; Weaver, W. Vibration Problems in Engineering, 4th ed.; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Harris, C.M.; Piersol, A.G. Harris' Shock and Vibration Handbook, 5th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Lee, J.W.; Tung, R.; Raman, A.; Sumali, H.; Sullivan, J.P. Squeeze-film damping of flexible microcantilevers at low ambient pressures: Theory and experiment. J. Micromech. Microeng. 2009, 19, 1–14. [Google Scholar] [CrossRef]
- Gusso, A. Energy loss mechanism for suspended micro- and nanoresonators due to the Casimir force. Phys. Rev. B 2010, 81, 1–7. [Google Scholar] [CrossRef]
- Rieger, J.; Isacsson, A.; Seitner, M.J.; Kotthaus, J.P.; Weig, E.M. Energy losses of nanomechanical resonators induced by atomic force microscopy-controlled mechanical impedance mismatching. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Blom, F.R.; Bouwstra, S.; Elwenspoek, M.; Fluitman, J.H.J. Dependence of the quality factor of micromachined silicon beam resonators on pressure and geometry. J. Vac. Sci. Technol. B 1992, 10, 19–26. [Google Scholar] [CrossRef]
- Pandey, A.K.; Pratap, R. Effect of flexural modes on squeeze film damping in MEMS cantilever resonators. J. Micromech. Microeng. 2007, 17, 2475–2484. [Google Scholar] [CrossRef]
- Chon, J.W.M.; Mulvaney, P.; Sader, J.E. Experimental validation of theoretical models for the frequency response of atomic force microscope cantilever beams immersed in fluids. J. Appl. Phys. 2000, 87, 3978–3988. [Google Scholar] [CrossRef]
- Zhang, W.; Turner, K. Frequency dependent fluid damping of micro/nano flexural resonators: Experiment, model and analysis. Sens. Actuators A Phys. 2007, 134, 594–599. [Google Scholar] [CrossRef]
- Leveque, G.; Girard, P.; Belaidi, S.; Solal, G.C. Effects of air damping in noncontact resonant force microscopy. Rev. Sci. Instrum. 1997, 68, 4137–4144. [Google Scholar] [CrossRef]
- Salapaka, M.V.; Bergh, H.S.; Lai, J.; Majumdar, A.; McFarland, E. Multi-mode noise analysis of cantilevers for scanning probe microscopy. J. Appl. Phys. 1997, 81, 2480–2487. [Google Scholar] [CrossRef]
- Green, C.P.; Sader, J.E. Torsional frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 2002, 92, 6262–6274. [Google Scholar] [CrossRef]
- Comsol, A.B. COMSOL Multiphysics User’s Guide; COMSOL Inc.: Burlington MA, USA, 2014. [Google Scholar]
- Czarny, J.; Walther, A.; Desloges, B.; Robert, P.; Redon, E.; Verdot, T.; Ege, K.; Guianvarc'h, C.; Guyader, J.L. New Architecture of MEMS Microphone for Enhanced Performances. In Proceedings of the IEEE International Semiconductor Conference Dresden Grenoble (ISDSG 2013), Dresden, Germany, 26–27 September 2013.
- Yazdanpanah, M.M.; Harfenist, S.A.; Safir, A.; Cohn, R.W. Selective self-assembly at room temperature of individual freestanding Ag2Ga alloy nanoneedles. J. Appl. Phys. 2005, 98, 1–7. [Google Scholar] [CrossRef]
- zurMuhlen, E.; Munoz, M.; Gehring, S.; Reineke, F. Metrology in scanning probe microscopy with atomic force microscopy and near-field scanning optical microscopy. Eur. J. Cell Biol. 1997, 74, 72. [Google Scholar]
- Hafner, J.H.; Cheung, C.L.; Lieber, C.M. Direct growth of single-walled carbon nanotube scanning probe microscopy tips. J. Am. Chem. Soc. 1999, 121, 9750–9751. [Google Scholar] [CrossRef]
- Lee, D.W.; Ono, T.; Esashi, M. Cantilever with integrated resonator for application of scanning probe microscope. Sens. Actuators A Phys. 2000, 83, 11–16. [Google Scholar] [CrossRef]
- Kanda, T.; Morita, T.; Kurosawa, M.K.; Higuchi, T. A flat type touch probe sensor using PZT thin film vibrator. Sens. Actuators A Phys. 2000, 83, 67–75. [Google Scholar] [CrossRef]
- Kim, B.; Masuzawa, T.; Bourouina, T. The vibroscanning method for the measurement of micro-hole profiles. Meas. Sci. Technol. 1999, 10, 697–705. [Google Scholar] [CrossRef]
- Bar, G.; Delineau, L.; Brandsch, R.; Ganter, M.; Whangbo, M.H. Hysteresis in the distance-sweep curves of elastomers and its implications in tapping mode atomic force microscopy. Surf. Sci. 2000, 457, L404–L412. [Google Scholar] [CrossRef]
- Rabe, U.; Amelio, S.; Kopycinska, M.; Hirsekorn, S.; Kempf, M.; Goken, M.; Arnold, W. Imaging and measurement of local mechanical material properties by atomic force acoustic microscopy. Surf. Interface Anal. 2002, 33, 65–70. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).