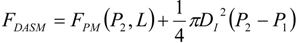In the section, the working principle of pneumatic muscle is analyzed to form the theoretic basis and inspiration for incorporating the cylindrical insert to eliminate the central volume of pneumatic muscle. As a result, the initial sleeve muscle concept is established, which provides an enhanced force capacity and reduced energy consumption compared with the traditional pneumatic muscle. Subsequently, the concept of DA sleeve muscle is introduced, which provides a unique bi-directional actuation capability by isolating the central volume into an additional chamber and leveraging the resultant extension force.
2.1. Sleeve Muscle: Inspired by the Force Analysis of Pneumatic Muscle
As a muscle-like actuator, the pneumatic muscle simulates the function of biological skeletal muscle by generating a contraction force to the external load. Specifically, the flexible membrane of the muscle actuator contracts under the internal gas pressure. In this process, the membrane also expands radially, enlarging the internal volume of the actuator. Understanding the volume change is critical in the study of the pneumatic muscle’s functioning mechanism, as demonstrated by the following derivation of its pressure-force relationship.
Neglecting the strain energy in the membrane, the following equation can be obtained by applying the principle of virtual work:
where
Wout and
Win are the input work and output work, respectively.
dWout can be expressed as:
where
F is the actuator contraction force, and
L the length of the pneumatic muscle.
dWin can be expressed as:
where
P is the actuator internal pressure,
Patm is the atmosphere pressure, and
V is the actuator internal volume. Combining the three equations above, the force output can be expressed as:
As indicated by this equation, the contraction force F is proportional to the gauge pressure (P − Patm), with the coefficient of proportionality as (− dV/dL). Therefore, in order to generate a contraction force output, the internal volume V needs to expand when the muscle length L shortens, resulting in a positive value of (− dV/dL). This is always true for a regular pneumatic muscle in its normal operation, until the maximum contraction is reached.
Figure 3.
Dividing the internal volume into two parts: V1 and V2. Note that V2 is negligible at the equilibrium state.
Figure 3.
Dividing the internal volume into two parts: V1 and V2. Note that V2 is negligible at the equilibrium state.
In the analysis above, the volume inside the pneumatic muscle is treated as a whole. However, one can gain further insight of the force-generating process by hypothetically dividing the internal volume into two portions, including
V1, a cylindrical volume at the center of the muscle, whose diameter is equal to that of the muscle’ end connectors; and
V2, a ring-shaped volume surrounding
V1 (
Figure 3).
At the equilibrium state, the pneumatic muscle’s internal volume is close to a cylinder, and thus
V2 is negligible at this state. Both
V1 and
V2 change with the length of the actuator, and, thus, the total contraction force can be expressed as the sum of
F1 and
F2:
where
F1 and
F2 are the contributions of the changes of
V1 and
V2, respectively:
To analyze the contributions of these volume changes,
V1 can be expressed as the product of the fixed cross-sectional area
![Actuators 02 00129 i009]()
(
D is the diameter of the muscle end connector) and the muscle length
L, and, thus, decreases with the shortening of the muscle. Consequently, the contribution of
V1 to the contraction force is always negative, as indicated by the following equation:
On the other hand,
V2 expands as the pneumatic muscle contracts, and thus contributes positively to the generation of the output force:
Based on these two equations, it can be inferred that the total contraction force
F is always less than
F2, due to the fact that the negative
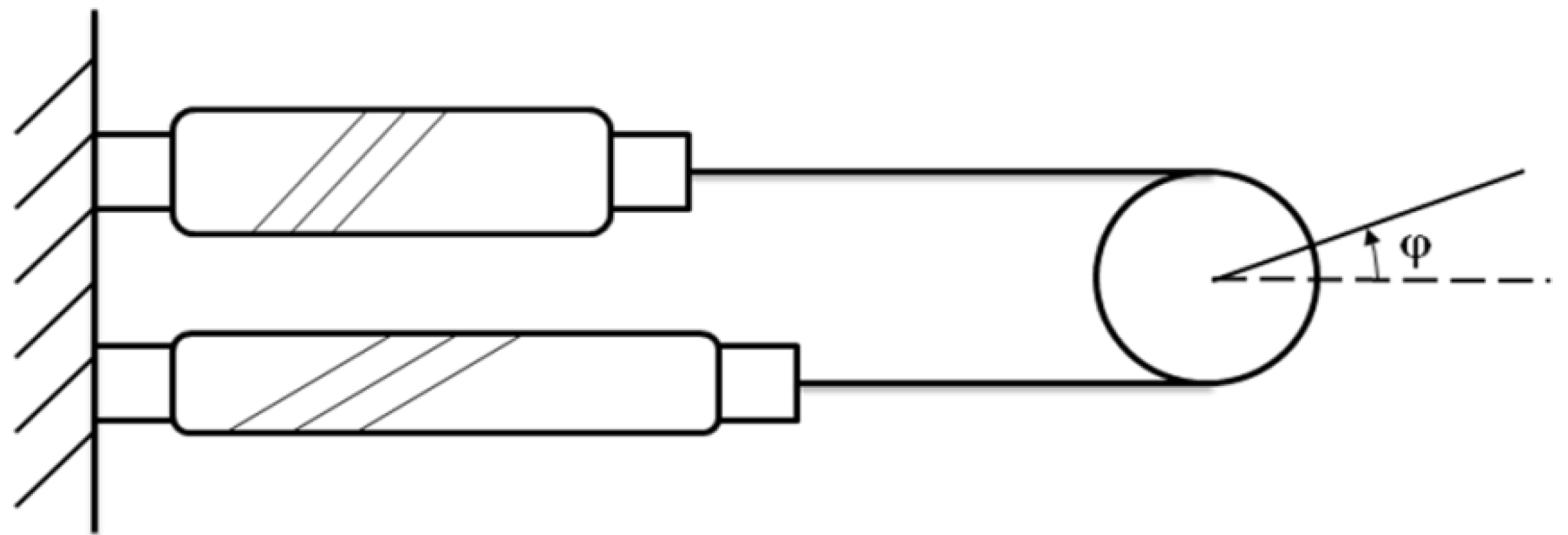
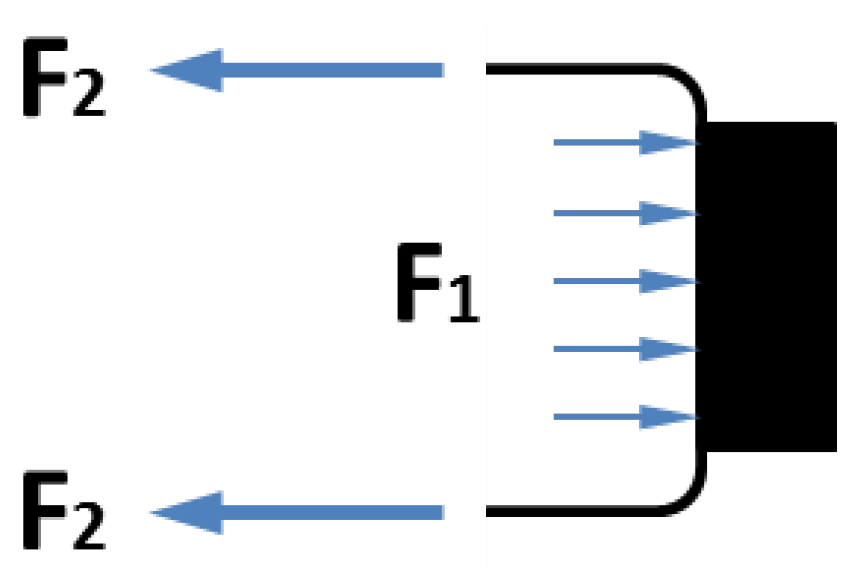
F1 reduces the total force output. This conclusion can be better explained with a simple force analysis as shown in
Figure 4. Among the two forces applied to the moving end of the pneumatic muscle,
F2 is the contraction force generated by the membrane, while
F1 is the extension force applied to the end connector due to the internal air pressure. When these forces are applied simultaneously,
F1 partially cancels out
F2, resulting in a loss of the actuator force capacity.
Figure 4.
Contributions of V1 and V2 to the contraction force: F1 is extension force applied to the end connector due to the internal pressure, and F2 is extension force by the membrane.
Figure 4.
Contributions of V1 and V2 to the contraction force: F1 is extension force applied to the end connector due to the internal pressure, and F2 is extension force by the membrane.
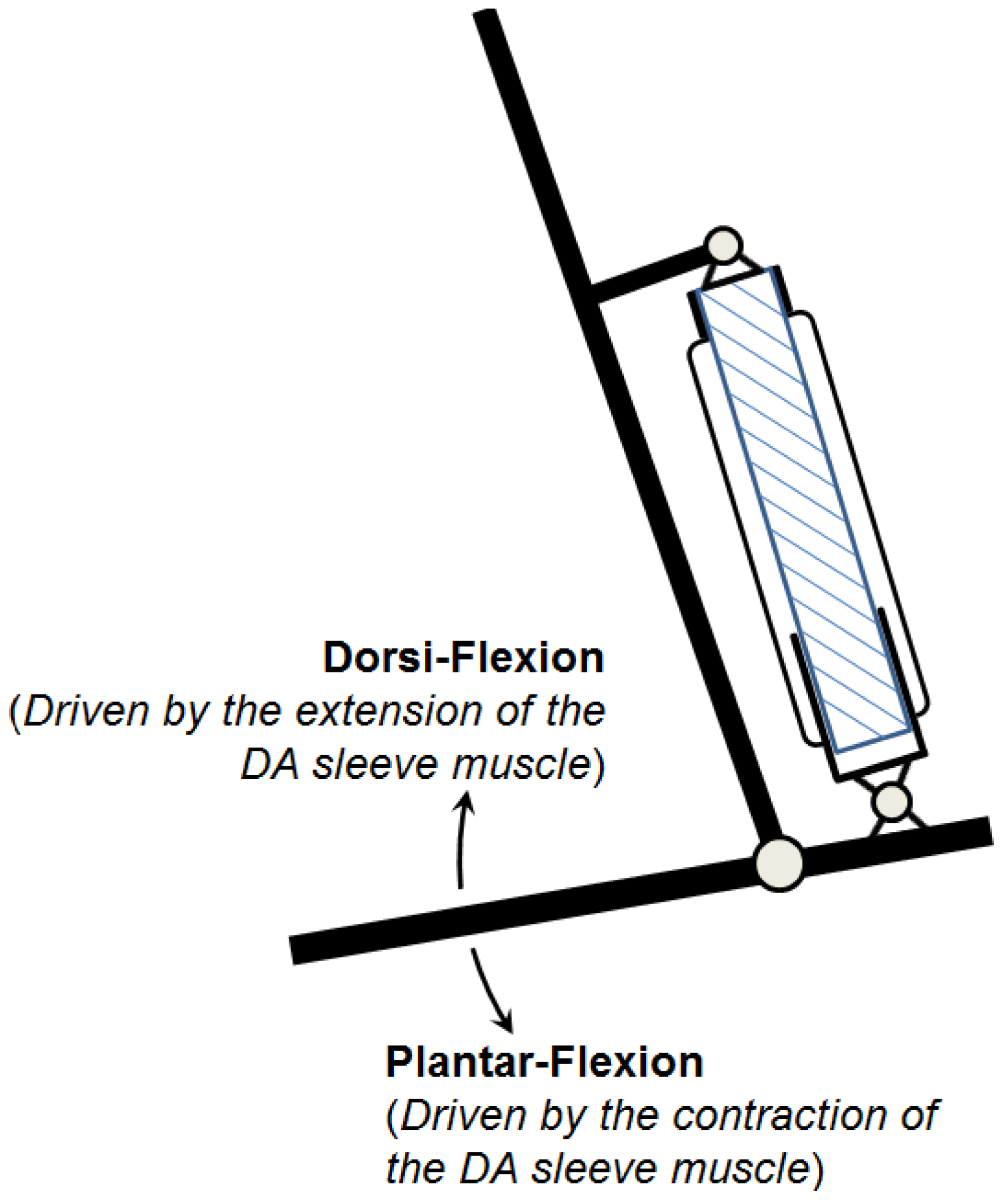
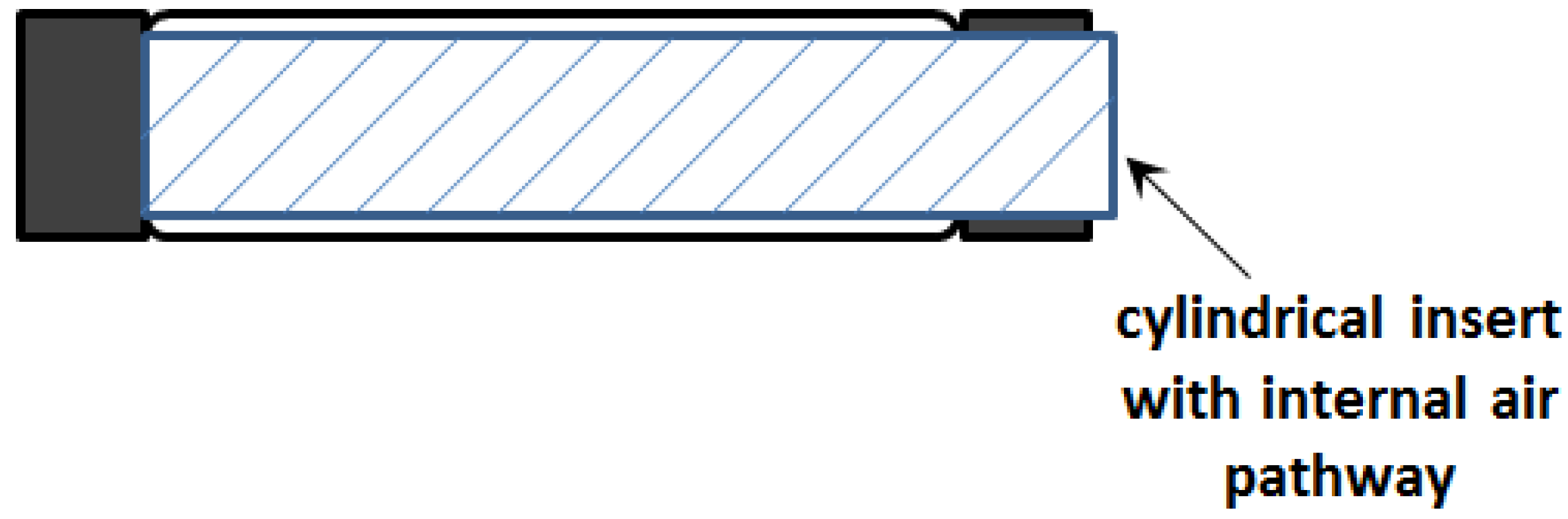
This observation inspired the concept of the initial sleeve muscle concept, in which a rigid cylindrical bar or tube is inserted into the center of the muscle actuator (
Figure 5).
Figure 5.
Schematic of the initial sleeve muscle actuator.
Figure 5.
Schematic of the initial sleeve muscle actuator.
Note that the cylindrical insert incorporates a built-in air pathway to enable the access to the volume between the insert and the membrane. As such, the membrane is still able to generate the desired contraction force to the moving end, which now slides on the smooth outer surface of the insert. More importantly, with the central space occupied by the insert, the volume
V1 is largely eliminated, which in turn eliminates the corresponding extension force
F1. Correspondingly, an increase in the actuator force capacity can be obtained:
where
DI is the outer diameter of the insert, which needs to be slightly less than the muscle end-connector diameter
D to ensure the structural strength of the moving end. From Equation (10), it can be deduced that, under a certain internal pressure, the magnitude of force increase is a constant,
i.e., not affected by the contraction of the muscle. As such, this effect is especially important in the large-contraction region, where the contraction force is much less than that at the equilibrium state.
In addition to the greater force capacity, the sleeve muscle also features a substantial reduction in energy consumption compared with the traditional pneumatic muscle. This can be primarily attributed to two factors: (1) The internal volume has been significantly reduced after incorporating the insert; and (2) With the greater force capacity, the sleeve muscle requires a lower internal air pressure to generate the desired force output, also contributing to the energy saving. Experiments conducted on a sleeve muscle prototype demonstrated that, depending on the percentage of muscle contraction, the energy consumption can be lowered by 20%~37% compared with an identical pneumatic muscle without the insert [
16].
2.2. DA Sleeve Muscle: Making Full Use of the Potential Provided by Sleeve Muscle
In the theoretical analysis supporting the inception of the sleeve muscle, a key observation is the totally opposite contributions from the volumes V1 and V2. Pressurizing V1 generates an extension force, while pressurizing V2 generates a contraction force. In the traditional pneumatic muscle, V1 and V2 are inseparable, causing the extension force to partially offset the contraction force and resulting in a total force output lower than the contraction force. In the initial sleeve muscle as described above, V1 (along with the corresponding extension force) is largely eliminated with the insert, generating a greater force output under the same internal pressure.
Despite the successful performance enhancement with the initial sleeve muscle, eliminating
V1 only makes partial use of the potential provided by the approach of incorporating an insert into the muscle actuator. Since the contributions from
V1 and
V2 are totally opposite, what if we separate them and let them contribute separately and independently to the actuation effort, as in
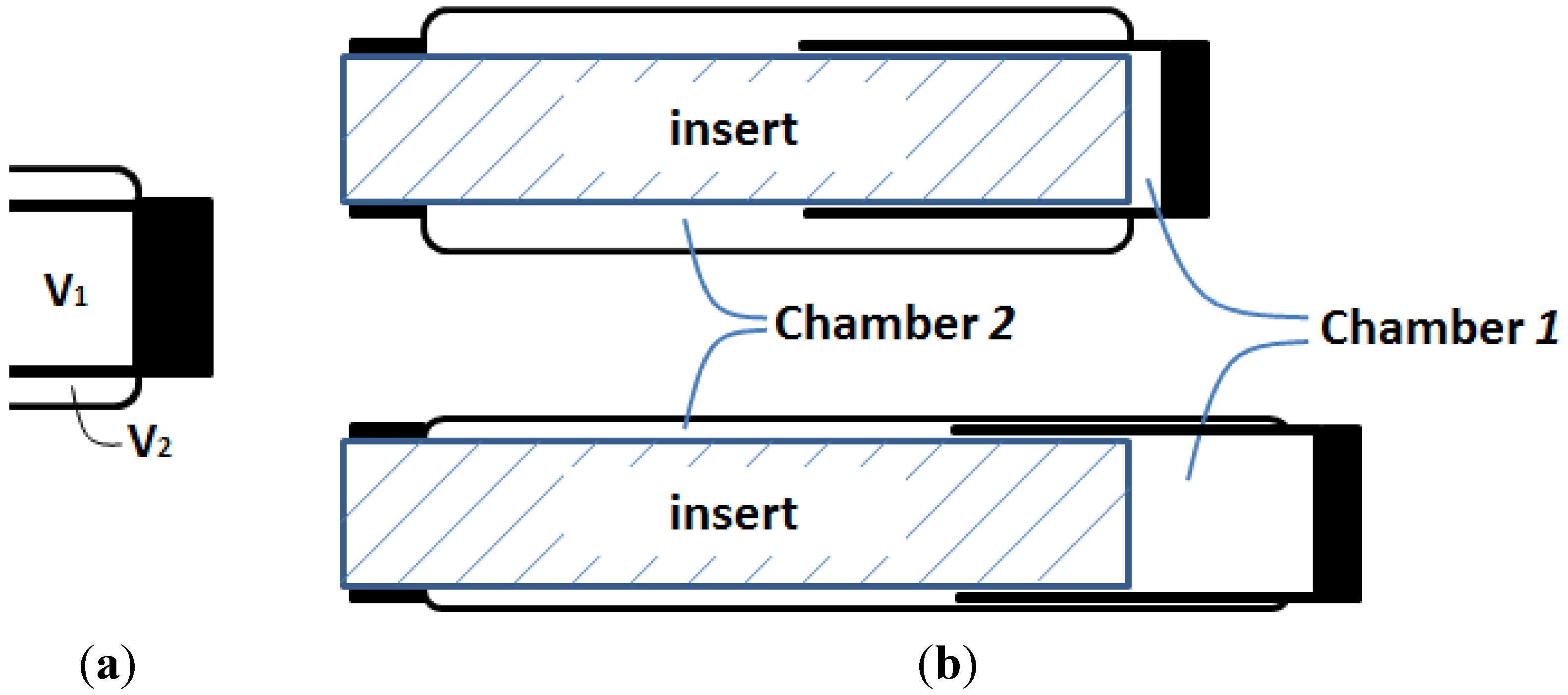
Figure 6a? If this hypothetical structural change can be realized, the resultant muscle actuator can not only generate a greater contraction force, but also generate an extension force for bi-directional actuation.
Figure 6.
Oncept of the DA sleeve muscle: (a) Separating V1 and V2 with a rigid shell, and (b) the resulting DA sleeve muscle structure.
Figure 6.
Oncept of the DA sleeve muscle: (a) Separating V1 and V2 with a rigid shell, and (b) the resulting DA sleeve muscle structure.
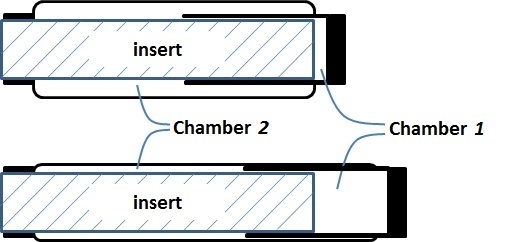
The research inspired by the hypothetical question above leads to a new double-acting sleeve muscle actuator, as shown in
Figure 6b. Instead of simply eliminating
V1, this new actuator introduces an additional pressurizable chamber (Chamber 1) over the moving end of the sleeve muscle. This additional chamber essentially isolates the portion of the original
V1 that is unaffected by the motion of the moving end, and thus retains the extension force associated with the volume
V1. With this unique structure, the DA sleeve muscle features two separate chambers that can be individually pressurized or exhausted for contraction and extension, providing a truly bi-directional robotic actuator. Note that the structure in
Figure 6b is similar to a U.S. patent filed by Sato [
17], in which a telescoping structure is incorporated at the center of the traditional pneumatic muscle. However, there is a fundamental difference: The actuator in the Sato patent is a single-acting actuator, and its central structure is introduced to reduce the inner volume of the actuator. In comparison, the DA sleeve muscle is double-acting, with the central structure being able to generate an extension force to the external load. This bi-directional actuation capability is unique.
A few details in the schematic in
Figure 6b are worth elaborating. First, the two separate chambers can be independently controlled with respect to their internal pressures, and thus a significant pressure differential may be applied to the rigid shell that separates the chambers. As such, a thin-wall shell with sufficient strength, such as those used in pneumatic cylinders, is required. The shell must be rigidly connected to the moving end of the muscle actuator with proper sealing to provide the required airtightness. In addition, the shell slides on the outer surface of the stationary insert during operation, which requires proper moving seal at the surface of contact. U-Cup is the seal of recommendation, since this type of seal does not rely on the initial compression to seal, and thus generates lower friction in sliding. Note that the pressure differential across the seal is undetermined,
i.e., the Chamber 1 pressure can be higher or lower than the Chamber 2 pressure in operation. Therefore, two antagonistically placed U-Cups are needed to provide the desired sealing effect under any arbitrary pressure differential.
Based on the schematic in
Figure 6b, the force output can be expressed as a function of the pressures in the chambers. For the membrane pulling force, various theoretical or empirical models have been established with different levels of complexity and accuracy. Please see the review paper by Zhang and Philen [
13] for more details. To avoid losing generality in force calculation, assume the membrane force model takes the following form:
in which
P is the internal air pressure and
L is the length of the actuator. For the DA sleeve muscle, the pressure applied to the membrane is the Chamber 2 pressure
P2. Also, compared with the pneumatic muscle, the DA sleeve muscle provides an increase in the force output as expressed by Equation (10). As such, the contraction force of the DA sleeve muscle
FC can be expressed as:
For the extension force, the cross-sectional area is a constant
![Actuators 02 00129 i009]()
. As such, the extension force can be expressed as:
in which
P1 is the Chamber 1 pressure. Combining Equations (12) and (13), the force output of the DA sleeve muscle is:
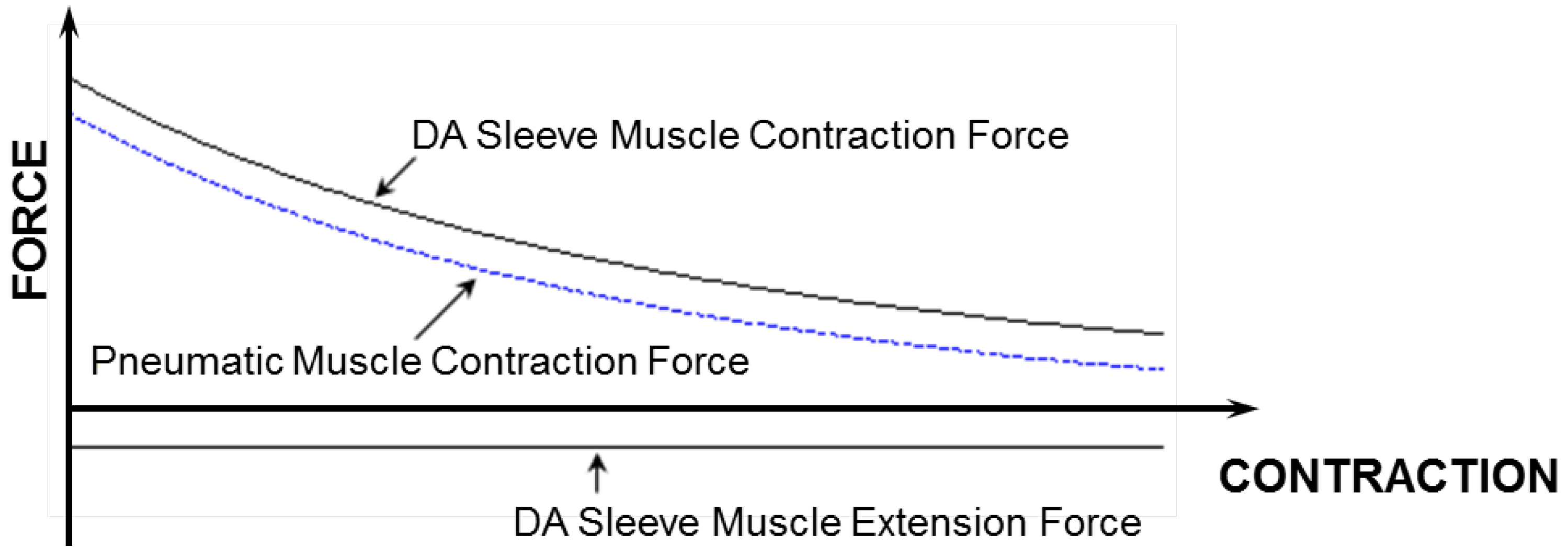
for which the contraction force is considered as positive. Based on this equation, a comparison of the force capacity of the DA sleeve muscle versus the traditional pneumatic muscle is shown in
Figure 7. From this figure, one can clearly see the increased contraction force capacity (positive) and the newly added extension force capacity (negative) provided by the DA sleeve muscle, indicating the significant performance enhancement of this new muscle actuator. Note that the simple analysis in this section is intended to quantify the DA sleeve muscle’s performance enhancement in comparison with the corresponding pneumatic muscle (with the identical membrane). The performance enhancement results from the structural modification, whose effect on the actuation force is relatively easy to analyze (compared with the contraction force of the membrane). Therefore, the simple analysis above can provide a satisfactory result in determining the DA sleeve muscle’s actuation force, which has been experimentally demonstrated, as summarized in the subsequent section. To use the result (Equation (14)), any pneumatic muscle force model with acceptable accuracy can be used to determine
FPM, and the actuation force of the corresponding DA sleeve muscle can be calculated accordingly.
Figure 7.
The force capacity of the DA sleeve muscle in comparison with that of the traditional pneumatic muscle.
Figure 7.
The force capacity of the DA sleeve muscle in comparison with that of the traditional pneumatic muscle.

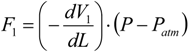
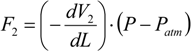
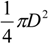 (D is the diameter of the muscle end connector) and the muscle length L, and, thus, decreases with the shortening of the muscle. Consequently, the contribution of V1 to the contraction force is always negative, as indicated by the following equation:
(D is the diameter of the muscle end connector) and the muscle length L, and, thus, decreases with the shortening of the muscle. Consequently, the contribution of V1 to the contraction force is always negative, as indicated by the following equation:
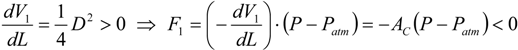
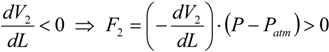
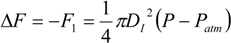
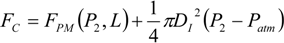
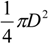 . As such, the extension force can be expressed as:
. As such, the extension force can be expressed as: