Global-Initialization-Based Model Predictive Control for Mobile Robots Navigating Nonconvex Obstacle Environments
Abstract
1. Introduction
- An MPC framework that incorporates global optimization techniques to improve the trajectory tracking performance in environments with nonconvex obstacles is proposed.
- A selective activation strategy is implemented in the proposed framework to invoke global optimization only when the robot is at risk of becoming trapped, thereby preserving computational efficiency.
- The effectiveness of the proposed framework is demonstrated through real-time simulations in nonconvex obstacle environments, and the results demonstrate successful obstacle avoidance and recovery from local minima.
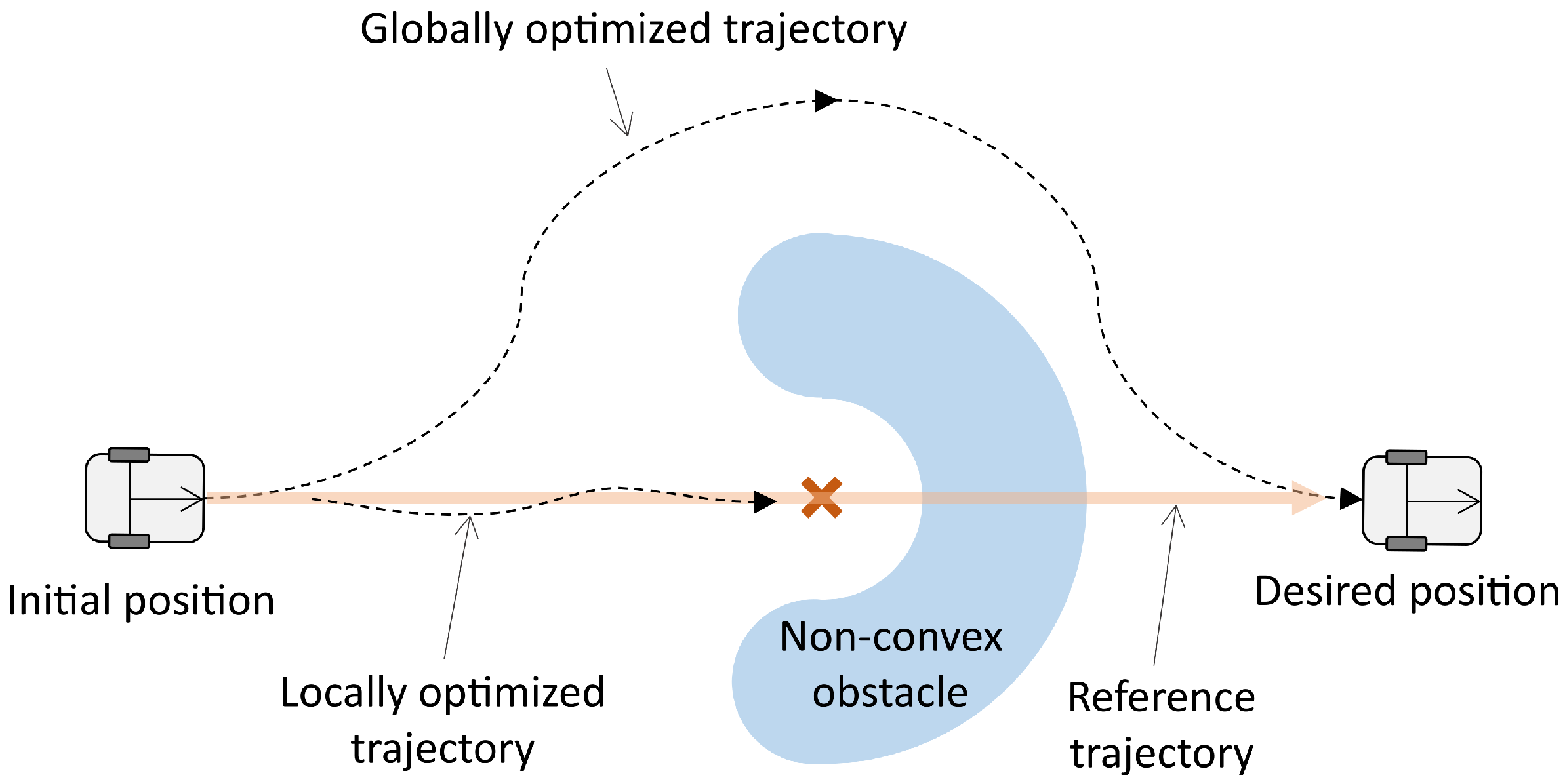
2. Nonconvex Obstacle Avoidance Problem in the MPC Framework
3. Proposed Method
3.1. Nonlinear MPC Formulation for Trajectory Tracking
3.2. Global Search-Based Initial Guess Selection
| Algorithm 1: Pseudocode of IG-PSO Initializer |
 |
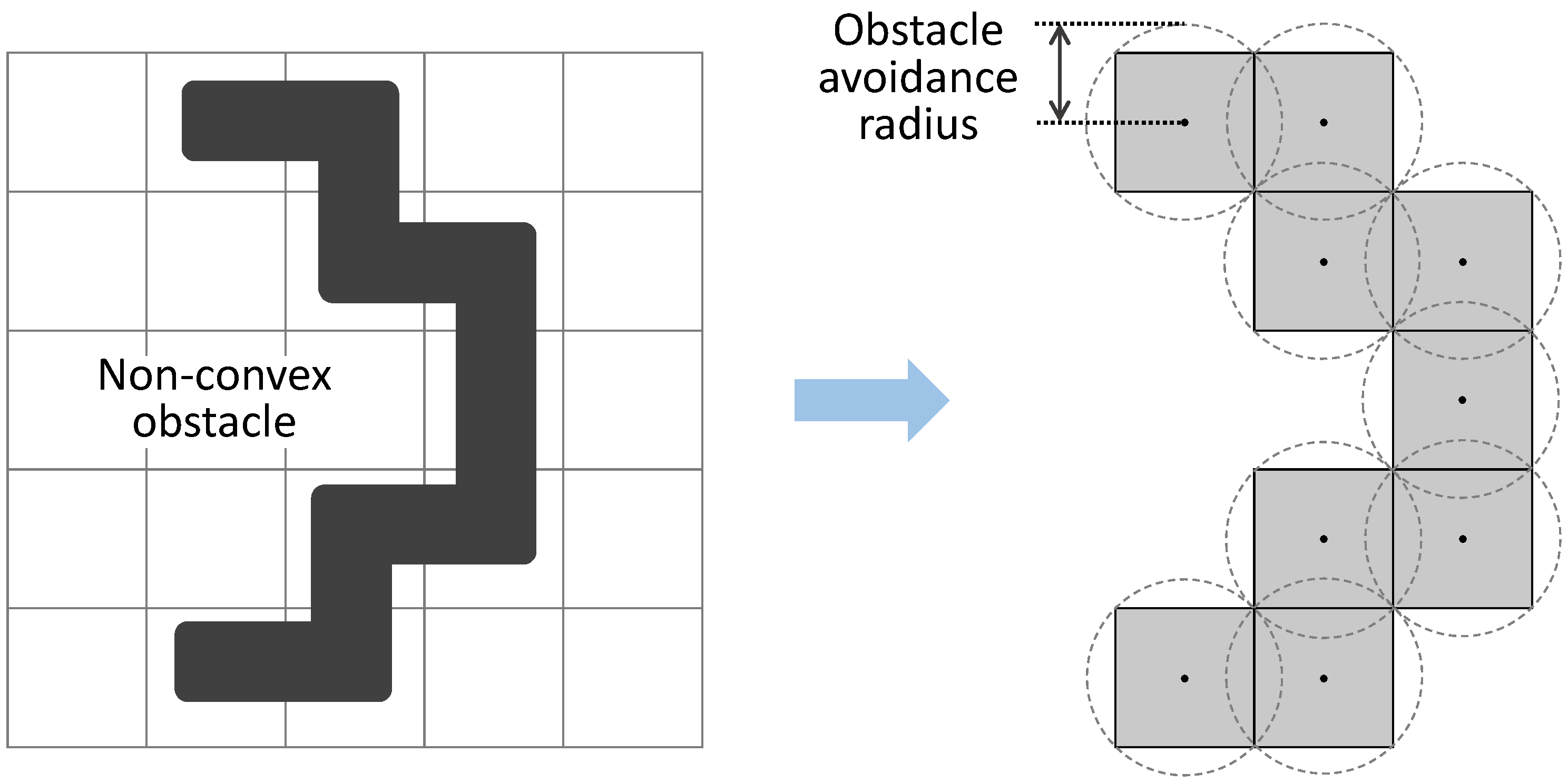
3.3. Grid-Based Representation of Nonconvex Obstacles for Collision Avoidance Constraints
3.4. IG-PSO-Initialized MPC Framework with Nonconvex Obstacle Avoidance
| Algorithm 2: Pseudocode of IG-PSO-initialized MPC Framework |
 |
4. Real-Time Simulation with Gazebo and ROS
4.1. Simulation Setup
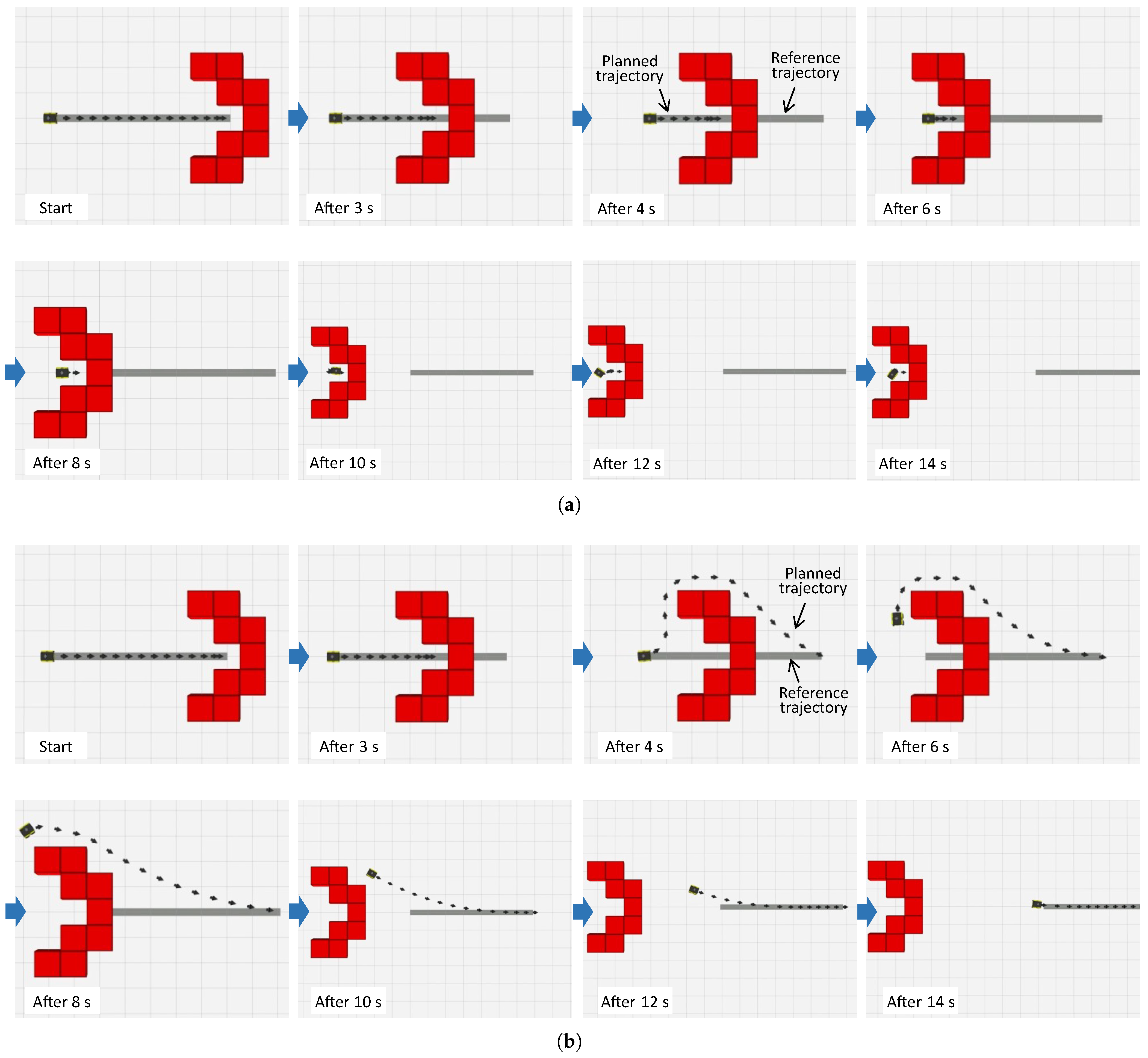
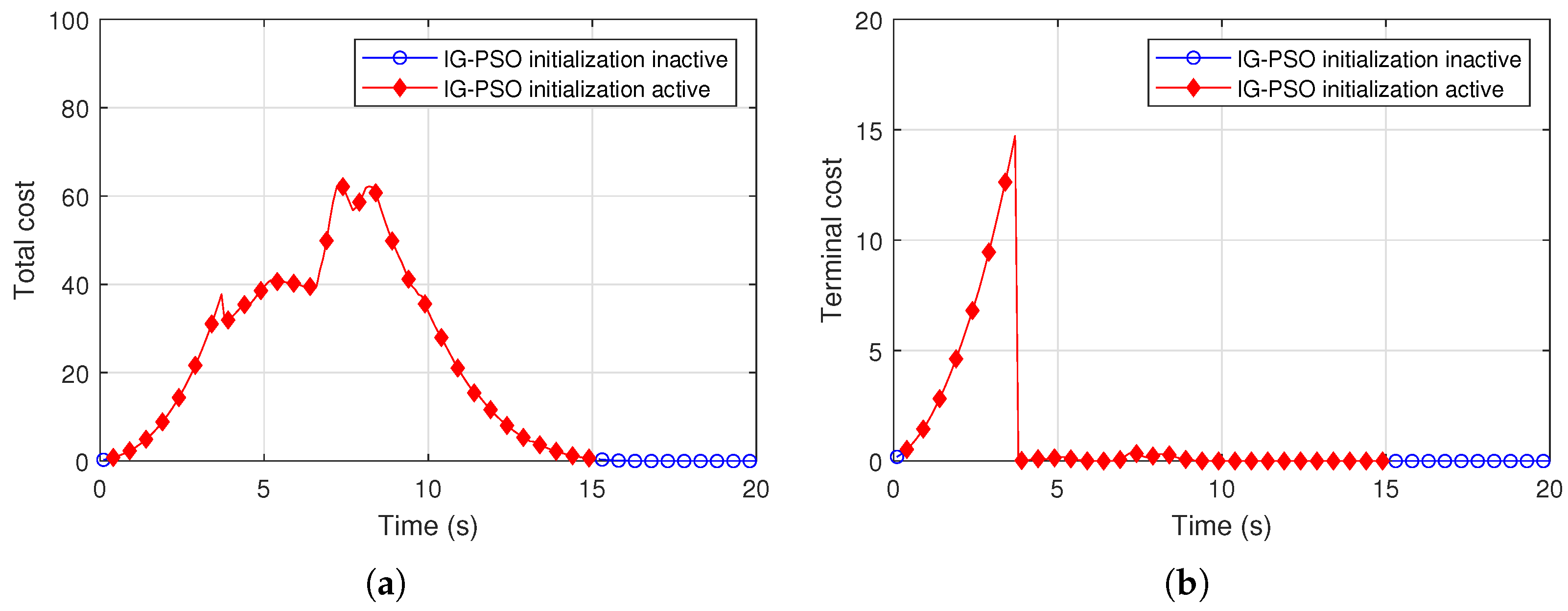
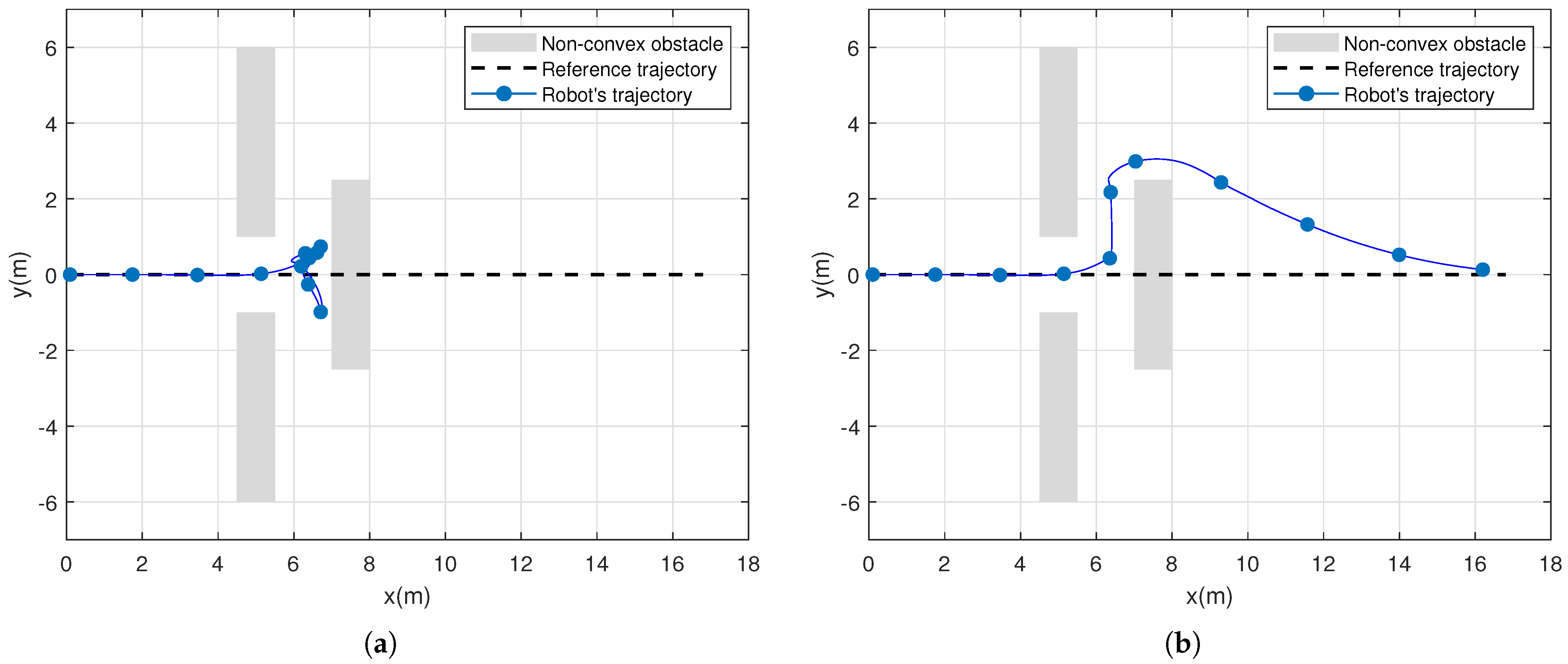
4.2. Results
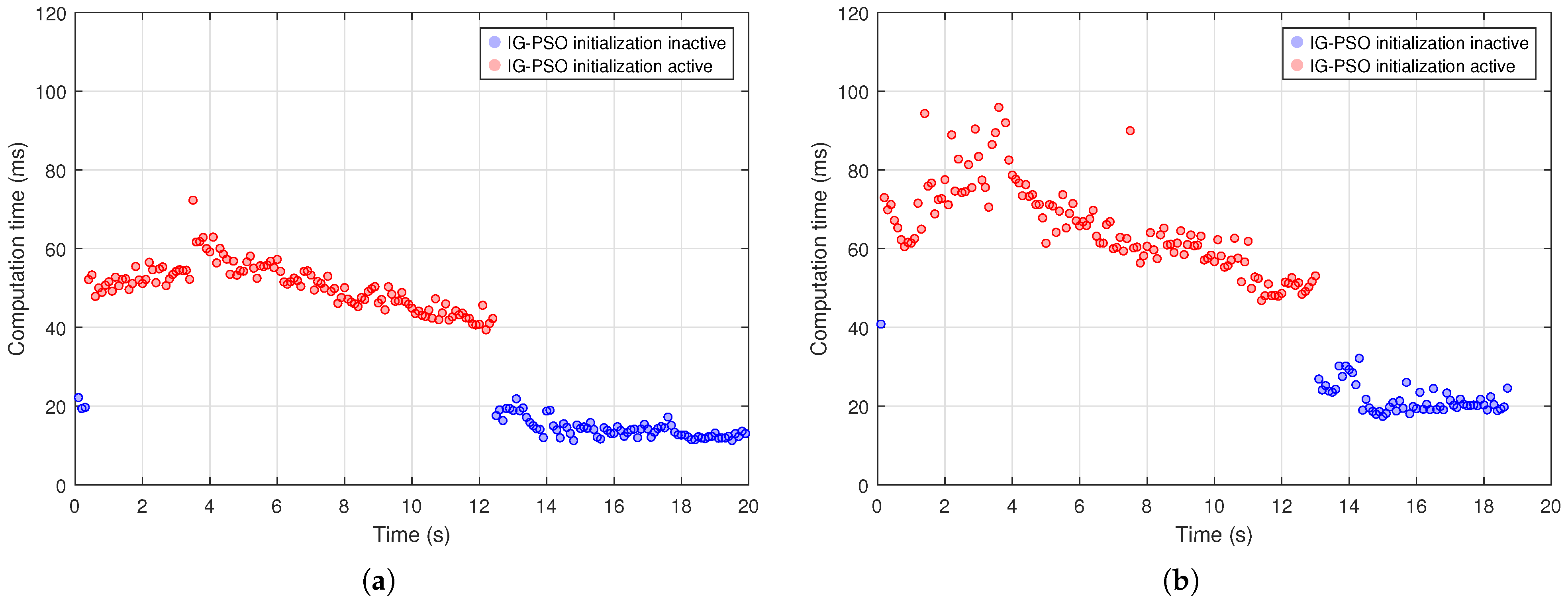
4.3. Discussion on Map Complexity and Computational Performance
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| IG-PSO | Initial-Guess Particle Swarm Optimization |
| IPOPT | Interior Point OPTimizer |
| MGMM-ACO | Multivariate Gaussian Mixture Model-Ant Colony Optimization |
| MPC | Model Predictive Control |
| PSO | Particle Swarm Optimization |
| ROS | Robot Operating System |
| RViz | ROS Visualization |
References
- Sun, Z.; Dai, L.; Liu, K.; Xia, Y.; Johansson, K.H. Robust MPC for tracking constrained unicycle robots with additive disturbances. Automatica 2018, 90, 172–184. [Google Scholar] [CrossRef]
- Tang, J.; Wu, S.; Lan, B.; Dong, Y.; Jin, Y.; Tian, G.; Zhang, W.A.; Shi, L. GMPC: Geometric model predictive control for wheeled mobile robot trajectory tracking. IEEE Robot. Autom. Lett. 2024, 9, 4822–4829. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Guan, X.; Wang, Y.; Zhang, B.; Wang, Y.; Li, G. Adaptive MPC-based multi-terrain trajectory tracking framework for mobile spherical robots. IEEE/ASME Trans. Mechatron. 2025, 1–13. [Google Scholar] [CrossRef]
- El-Sayyah, M.; Saad, M.R.; Saad, M. Nonlinear model predictive control for trajectory tracking of omnidirectional robot using resilient propagation. IEEE Access 2025, 13, 112642–112653. [Google Scholar] [CrossRef]
- Li, B.; Ji, Z.; Zhao, Z.; Yang, C. Model Predictive Optimization and Terminal Sliding Mode Motion Control for Mobile Robot With Obstacle Avoidance. IEEE Trans. Ind. Electron. 2025, 72, 9293–9303. [Google Scholar] [CrossRef]
- Tiriolo, C.; Franzè, G.; Lucia, W. A receding horizon trajectory tracking strategy for input-constrained differential-drive robots via feedback linearization. IEEE Trans. Control. Syst. Technol. 2023, 31, 1460–1467. [Google Scholar] [CrossRef]
- Tang, M.; Lin, S.; Luo, Y. Mecanum wheel AGV trajectory tracking control based on efficient MPC algorithm. IEEE Access 2024, 12, 13763–13772. [Google Scholar] [CrossRef]
- Wijayathunga, L.; Rassau, A.; Chai, D. Challenges and solutions for autonomous ground robot scene understanding and navigation in unstructured outdoor environments: A review. Appl. Sci. 2023, 13, 9877. [Google Scholar] [CrossRef]
- Nowakowski, M.; Kurylo, J.; Braun, J.; Berger, G.S.; Mendes, J.; Lima, J. Using LiDAR data as image for AI to recognize objects in the mobile robot operational environment. In Proceedings of the Optimization, Learning Algorithms and Applications; Pereira, A.I., Mendes, A., Fernandes, F.P., Pacheco, M.F., Coelho, J.P., Lima, J., Eds.; Springer: Cham, Switzerland, 2024; pp. 118–131. [Google Scholar]
- Cognominal, M.; Patronymic, K.; Wańkowicz, A. Evolving field of autonomous mobile robotics: Technological advances and applications. Fusion Multidiscip. Res. Int. J. 2021, 2, 189–200. [Google Scholar] [CrossRef]
- Zinage, V.; Khalil, A.; Bakolas, E. TransformerMPC: Accelerating model predictive control via transformers. arXiv 2024, arXiv:2409.09266. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Chen, L.; Paleja, R.; Nageshrao, S.; Gombolay, M. Faster model predictive control via self-supervised initialization learning. arXiv 2025, arXiv:2408.03394. [Google Scholar]
- Schwenkel, L.; Gharbi, M.; Trimpe, S.; Ebenbauer, C. Online learning with stability guarantees: A memory-based warm starting for real-time MPC. Automatica 2020, 122, 109247. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle swarm optimisation: A historical review up to the current developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Distributed model predictive control with particle swarm optimizer for collision-free trajectory tracking of MWMR formation. Actuators 2023, 12, 127. [Google Scholar] [CrossRef]
- Kim, M.; Lee, M.; Kim, B.; Cha, M. Development of local path planning using selective model predictive control, potential fields, and particle swarm optimization. Robotics 2024, 13, 46. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, P.a.; Wang, L.g.; Wu, J.x.; Lei, M.y.; Zhang, C.w.; Lei, R. PSO-NMPC control strategy based path tracking control of mining LHD (scraper). Sci. Rep. 2024, 14, 28516. [Google Scholar] [CrossRef] [PubMed]
- Ait Dahmad, H.; Ayad, H.; García Cerezo, A.; Mousannif, H. Adaptive model predictive control for 4WD-4WS mobile robot: A multivariate gaussian mixture model-ant colony optimization for robust trajectory tracking and obstacle avoidance. Sensors 2025, 25, 3805. [Google Scholar] [CrossRef] [PubMed]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Nocedal, J.; Wächter, A.; Waltz, R.A. Adaptive barrier update strategies for nonlinear interior methods. SIAM J. Optim. 2009, 19, 1674–1693. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi – A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Computational Intelligence: Concepts to Implementations; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Zuo, Z.; Yang, X.; Li, Z.; Wang, Y.; Han, Q.; Wang, L.; Luo, X. MPC-based cooperative control strategy of path planning and trajectory tracking for intelligent vehicles. IEEE Trans. Intell. Veh. 2021, 6, 513–522. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.M. Formation reconfiguration control with collision avoidance of nonholonomic mobile robots. IEEE Robot. Autom. Lett. 2023, 8, 7905–7912. [Google Scholar] [CrossRef]
- Lee, S.M.; Myung, H. Receding horizon particle swarm optimisation-based formation control with collision avoidance for non-holonomic mobile robots. IET Control Theory Appl. 2015, 9, 2075–2083. [Google Scholar] [CrossRef]
- ROS—Robot Operating System. Available online: https://www.ros.org (accessed on 14 August 2025).



| Parameter Description | Symbol | Value |
|---|---|---|
| Number of particles | M | 50 |
| Maximum generations | 100 | |
| Maximum inertia weight | 0.9 | |
| Minimum inertial weight | 0.4 | |
| Acceleration coefficients | , | 2.0 |
| Parameter Description | Symbol | Value |
|---|---|---|
| Activation threshold | 0.5 | |
| Deactivation threshold | 0.1 | |
| Safe distance | 1.0 m | |
| Maximum linear velocity | 1.5 m/s | |
| Maximum angular velocity | 1.5 rad/s | |
| Sampling interval | 0.1 s | |
| Prediction steps | N | 70 |
| State error weights | Q | diag (0.1, 0.1, 0.01) |
| Control input error weights | R | diag (0.04, 0.04) |
| Terminal state weight | 10 | |
| Potential field weight | 40 | |
| Grid cell size | 1 m × 1 m |
| Scenarios | Conventional IPOPT-Based MPC | Proposed MPC Initialized by IG-PSO |
|---|---|---|
| Scenario 1 | 0/10 | 8/10 |
| Scenario 2 | 0/10 | 10/10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-M. Global-Initialization-Based Model Predictive Control for Mobile Robots Navigating Nonconvex Obstacle Environments. Actuators 2025, 14, 454. https://doi.org/10.3390/act14090454
Lee S-M. Global-Initialization-Based Model Predictive Control for Mobile Robots Navigating Nonconvex Obstacle Environments. Actuators. 2025; 14(9):454. https://doi.org/10.3390/act14090454
Chicago/Turabian StyleLee, Seung-Mok. 2025. "Global-Initialization-Based Model Predictive Control for Mobile Robots Navigating Nonconvex Obstacle Environments" Actuators 14, no. 9: 454. https://doi.org/10.3390/act14090454
APA StyleLee, S.-M. (2025). Global-Initialization-Based Model Predictive Control for Mobile Robots Navigating Nonconvex Obstacle Environments. Actuators, 14(9), 454. https://doi.org/10.3390/act14090454






