Disturbance Observer-Based Robust Force Control for Tendon-Sheath Mechanisms

Abstract

This paper proposes a disturbance observer (DOB)-based robust force control framework for tendon-sheath mechanisms (TSMs) that transmit tension forces from the proximal to the distal end. A detailed physical model of the TSM system, where a motor actuates the tendon and the output corresponds to the contact force at the robot end-effector, is developed. However, the resulting nominal model adopts a simplified representation of friction and involves significant parametric uncertainties due to the inherently complex dynamics of the tendon-sheath structure. By rigorously verifying the well-established robust stability conditions associated with DOB-based control frameworks, it is confirmed that the tendon-sheath transmission system satisfies all required assumptions and stability criteria. Furthermore, the necessary additional conditions can be readily met by appropriately designing the Q-filter, which is comparatively straightforward in practice. This validation supports the theoretical soundness and practical suitability of employing a DOB to effectively estimate and compensate for the system’s inherent parametric uncertainties and external disturbances. Numerical simulations incorporating a discrete-segment tendon model with an advanced friction dynamics formulation demonstrate significant improvements in force tracking accuracy at the tendon’s distal end compared to conventional control schemes without DOB compensation. The results highlight the robustness and effectiveness of the proposed control scheme for tendon-driven robotic systems.

1. Introduction

The design and control of dexterous robotic hands have attracted significant attention due to their essential role in applications such as rehabilitation, industrial automation, and surgical robotics [1,2,3]. Among the various actuation strategies, tendon-sheath mechanisms (TSMs) are widely adopted for their structural flexibility, compactness, and ability to remotely locate actuators, thereby reducing distal mass and enhancing dynamic performance in multi-joint systems [4,5,6,7]. These mechanisms enable the transmission of motion and force from a proximally placed actuator to a distal end-effector through a flexible sheath, making them especially suitable for constrained environments such as minimally invasive surgical tools, soft robots, and continuum manipulators. To address the inherent modeling challenges of TSMs, extensive research has been devoted to developing both analytical and empirical models that capture their complex dynamic behavior [5,6,7,8,9,10,11]. Notably, the foundational works in [8,9] laid the groundwork for modeling tendon-driven robotic systems by characterizing key transmission properties. A primary difficulty in TSM control arises from accurately capturing the nonlinearities introduced by frictional force, tendon elasticity, and the distributed compliance of the sheath. These effects give rise to significant parametric uncertainties and unmodeled dynamics, which hinder precise motion and force control.

To overcome these difficulties, various control methodologies have been explored [12,13], such as proportional–integral–derivative (PID) control [14], adaptive control [15], impedance control [16], neural network-based control [17], and sliding mode control [18]. Specifically, to enhance robustness without incurring excessive control effort, many recent studies have incorporated disturbance observers (DOBs) [19,20,21,22,23,24,25,26] into advanced control frameworks. DOBs offer a simple yet effective means of estimating and compensating for external disturbances in real time, thereby improving tracking performance and disturbance rejection in systems characterized by uncertainty and significant friction [13,27,28]. This approach is particularly valuable in highly uncertain systems such as TSMs, where external disturbances and model uncertainties can severely degrade control performance. Owing to their relatively simple design and strong robustness, DOBs have been widely adopted across various applications, including robotic manipulators [29,30] and precision servomotor control [31]. To further enhance performance, several advanced DOB schemes have been proposed, such as internal model-embedded DOBs [32], filter-embedded DOBs [33], and sliding mode DOBs [34], which extend the capability of conventional DOBs in handling complex disturbances and improving closed-loop stability. For TSMs, DOB-based approaches have been recently applied to tendon-sheath transmission systems [35,36], aiming to compensate for friction-induced effects in tendon-driven robotic hands.

This paper presents a robust and computationally efficient force control framework for tendon-sheath transmission systems by integrating a physically motivated yet simplified friction model with a linear DOB. The nominal model of the TSM for controller design is initially constructed based on the Euler–Eytelwein formula [37], which describes how the tendon tension decreases continuously due to friction as it slides along the curved sheath. Since the Euler–Eytelwein formula accounts only for Coulomb friction, the nominal model inherently neglects certain dynamic effects. In practice, to more accurately capture the behavior of the TSM, the actual plant model must account for the distributed and hysteretic nature of friction along the sheath. This necessitates the use of more advanced dynamic friction models, such as viscous friction, the Dahl model, or the LuGre model [38,39,40,41]. However, the proposed DOB can effectively compensate for the unmodeled dynamics and modeling uncertainties arising from the discrepancy between the nominal and actual plant models. As a result, the proposed scheme mitigates model uncertainties and achieves nominal tracking performance by estimating and rejecting lumped disturbances, including nonlinear friction and transmission errors, without relying on complex controllers. A proportional–integral (PI) controller is employed as the outer-loop controller, designed solely based on nominal model information. The controller structure is not restricted to PI control but only required to stabilize the nominal TSM model, which is shown to be a first-order system. Robust stability is theoretically guaranteed under necessary and sufficient conditions, which are readily satisfied in the TSM system. This is further validated through simulations demonstrating improved force tracking at the distal end.

In conclusion, the main contributions of this paper are threefold. First, it presents a DOB-based force control framework tailored for tendon-sheath transmission systems, which explicitly compensates for nonlinear friction and transmission-induced uncertainties using a physically grounded model and a linear DOB. Second, in contrast to previous works such as [35], which design a DOB for motion control of tendon-driven robotic hands and rely on the small gain theorem, resulting in conservative stability conditions, this approach utilizes the necessary and sufficient robust stability conditions from [24], thereby enabling a less conservative yet theoretically rigorous application of DOB to highly uncertain force control systems. Third, unlike the nonlinear DOB design combined with a sliding mode control used in [36], which may induce chattering and implementation complexity, this method achieves comparable disturbance rejection and tracking performance using a simpler linear DOB structure, improving both practicality and computational efficiency. The effectiveness of the proposed method is validated through detailed simulations, demonstrating improved force tracking and robustness against friction and model uncertainties.

The remainder of this paper is organized as follows: Section 2 presents the physical modeling of the TSM system. Section 3 presents the DOB-based control framework and demonstrates its application to the TSM system, with a focus on analyzing the robust stability conditions. Section 4 provides the simulation setup and results. Finally, Section 5 concludes the paper and outlines future research directions.

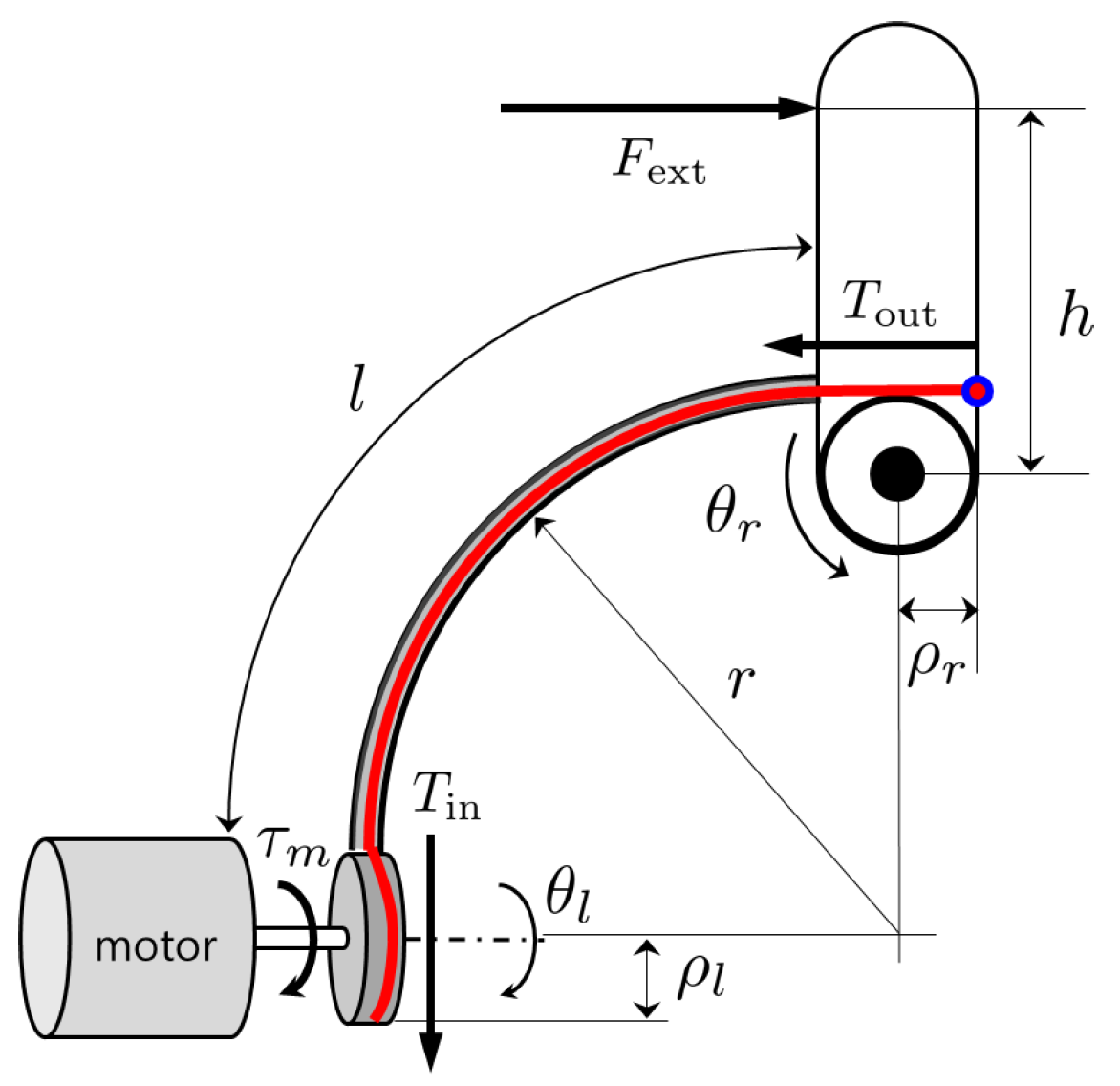
2. Motor-Driven Tendon-Sheath Mechanism

Typically, a TSM is actuated by a motor that generates motion or force at the proximal end, which is then transmitted to the distal end via a tendon cable enclosed within a flexible sheath. Due to the nonlinear friction and backlash effects between the tendon and the sheath, the dynamic behavior of TSMs is highly nonlinear and exhibits hysteresis. These effects become more pronounced with curved sheath routing, long transmission paths, or changes in external loading conditions. Although accurate modeling of the system dynamics is difficult and often impractical, it remains essential for understanding the system behavior and enabling effective control. Therefore, the characteristics of a motor-driven TSM model are analyzed in this section.

2.1. Motor-Driven Actuation of Tendon-Sheath Transmission Systems

To understand the tendon-sheath transmission system, consider a single-joint robotic arm actuated by a TSM, where the tendon is driven by an electric motor, as illustrated in Figure 1. A DC motor generates torque ${\tau }_m$, which is converted into the input tension force $T_{\mathrm{in}}$ applied at the proximal end of the tendon. The generated tension is transmitted through the TSM, resulting in an output tension $T_{\mathrm{out}}$ at the distal end, which in turn actuates the robot link. This output tension is ultimately transformed into an external contact force $F_{\mathrm{ext}}$ at the end-effector of the robotic arm, which interacts with the environment through contact. The symbols r, ${\rho }_l$, ${\rho }_r$, l, and h denote the radius of the tendon-sheath trajectory, the radius of the pulley on the motor’s load side, the radius of the joint pulley on the robot side, the length of the tendon, and the length of the robot arm link, respectively.

We now derive the dynamics of the DC motor system. Let ${\theta }_l$ denote the final angular displacement at the load side of the motor, i.e., after the output of the gearbox (or reducer), representing the effective rotational position transmitted to the tendon; let $i_a$ be the armature current and $v_m$ the input voltage. The relevant motor parameters are defined in

Table 1. Description of motor parameters.

Parameter	Description
$K_t$	Motor torque constant
$K_e$	Motor back electromotive force (EMF) constant
$R_a$	Motor armature resistance
$L_a$	Motor armature inductance
$n_g$	Total gear ratio
$\eta$	Motor efficiency
$J_m$	Moment of inertia of motor’s rotor, including gear on rotor side
$B_m$	Damping (or viscous friction) coefficient of motor’s rotor side
$J_l$	Moment of inertia of motor’s load, including gear on load side
$B_l$	Damping coefficient of motor’s load side
$J_{tot}$	Total moment of inertia of motor from the load side ($=J_m{n}_g^2+J_l$)
$B_{tot}$	Total damping coefficient of motor from the load side ($=B_m{n}_g^2+B_l$)
${\theta }_m$	Angular displacement of motor’s rotor ($=n_g{\theta }_l$)
${\theta }_l$	Angular displacement of motor’s load side after gearbox ($=\frac{1}{n_g}{\theta }_m$)
${\tau }_m$	Generated torque by motor ($=K_t{i}_a$)
${\tau }_l$	Torque transmitted to the load side from the rotor through the gearbox ($=n_g{\tau }_{l\mathrm{to}m}$)
${\tau }_{l\mathrm{to}m}$	Reaction torque transmitted from the load side to the motor rotor ($=\frac{1}{n_g}{\tau }_l$)
$v_m$	Input voltage of motor
$v_{\mathrm{back}}$	Back EMF voltage induced by motor’s rotation ($=K_e{\dot{\theta }}_m$)

.

With these parameters defined, the motor’s dynamic equations of motion can be derived. The electrical dynamics of the motor, including the back EMF, are described by

$$\begin{array}{c}\hfill L_a{\displaystyle \frac{d{i}_a}{dt}}+R_a{i}_a=v_m-v_{\mathrm{back}}=v_m-K_e{\dot{\theta }}_m.\end{array}$$

Since we have ${\theta }_m=n_g{\theta }_l$ due to the gear ratio $n_g$, we have

$$\begin{array}{c}\hfill L_a{\displaystyle \frac{d{i}_a}{dt}}+R_a{i}_a=v_m-K_e\left(n_g{\dot{\theta }}_l\right).\end{array}$$

(1)

Applying Newton’s second law to the rotational motion of the motor’s rotor and load side yields the following equations of motion:

$$\begin{array}{cc}\hfill J_m\left(n_g{\ddot{\theta }}_l\right)+B_m\left(n_g{\dot{\theta }}_l\right)=J_m{\ddot{\theta }}_m+B_m{\dot{\theta }}_m& =\eta {\tau }_m-{\tau }_{l\mathrm{to}m}=\eta K_t{i}_a-{\displaystyle \frac{1}{n_g}}{\tau }_l,\hfill \\ \hfill J_l{\ddot{\theta }}_l+B_l{\dot{\theta }}_l& ={\tau }_l-{\rho }_l{T}_{\mathrm{in}},\hfill \end{array}$$

where ${\tau }_l$ denotes the torque transmitted from the motor rotor to the load side through the gearbox. By multiplying the first equation by $n_g$ and adding it to the second equation, the two equations can be combined and simplified as follows:

$$\begin{array}{c}\hfill J_{tot}{\ddot{\theta }}_l+B_{tot}{\dot{\theta }}_l=\eta n_g{K}_t{i}_a-{\rho }_l{T}_{\mathrm{in}},\end{array}$$

(2)

where the total inertia and damping referred to the load shaft, are defined as $J_{tot}:=J_m{n}_g^2+J_l$ and $B_{tot}:=B_m{n}_g^2+B_l$, respectively, as noted in [42] (Section 2.3.3) and [43] (Problem A-5-2). Furthermore, considering the dynamics of the robot arm, let ${\theta }_r$ denote the joint angle, $J_r$ the arm’s moment of inertia, and $B_r$ the joint’s viscous friction coefficient. The equation of motion for the robotic arm is given by

$$\begin{array}{c}\hfill J_r{\ddot{\theta }}_r+B_r{\dot{\theta }}_r={\rho }_r{T}_{\mathrm{out}}-h{F}_{\mathrm{ext}}.\end{array}$$

(3)

In addition, based on the characteristics of the TSM derived in Appendix A, the relationship between the input and output tendon tensions is given by

$$\begin{array}{c}\hfill T_{\mathrm{out}}=T_{\mathrm{in}}{e}^{-\lambda },\end{array}$$

(4)

as shown in (A16). Furthermore, the angular displacement relationship between the motor and the robot joint, accounting for tendon elongation, is expressed as

$$\begin{array}{c}\hfill {\rho }_l{\theta }_l-\delta \left(l\right)={\rho }_r{\theta }_r.\end{array}$$

(5)

Here, the tendon elongation at the distal end $\delta \left(l\right)$ is derived from (A12), and the stiffness of the tendon relation in (A19) is rewritten as

$$\begin{array}{c}\hfill T_{\mathrm{out}}-T_0=k_e\left(\delta \left(l\right)-{\xi }_B\right),\end{array}$$

(6)

where $T_0$, ${\xi }_B$, and $k_e$ denote the pretension in the tendon corresponding to zero elongation; the inherent backlash threshold, below which the distal end tension remains unchanged until the total tendon elongation exceeds this value, as defined in (A15); and the effective tendon stiffness, as defined in (A20), respectively.

Finally, by combining Equations (1) through (6), the overall dynamic relationship of the tendon-sheath transmission system actuated by a DC motor is obtained. In this formulation, the motor input voltage $v_m$ serves as the system input, and the external force $F_{\mathrm{ext}}$ generated by the robotic arm is regarded as the system output. It is assumed that the system operates outside the backlash region and that the tendon is sufficiently stiff such that its elongation can be neglected. Furthermore, since the robot moves slowly during the force control task [44] (Chapter 11.5), the joint velocities and accelerations are negligible (i.e., ${\ddot{\theta }}_l\approx 0$, ${\dot{\theta }}_l\approx 0$, ${\ddot{\theta }}_r\approx 0$, and ${\dot{\theta }}_r\approx 0$). During this stall operation, where the motor almost ceases to rotate, overheating may lead to motor damage. To prevent this, we assume that the motor is selected such that its maximum continuous stall torque ${\tau }_{\mathrm{cont}}$, as specified in [44] (Chapter 8.9.1) or [45], is sufficient to generate the required output tension force. Specifically, based on the equations of motion (2) and (4) with ${\ddot{\theta }}_l\approx 0$ and ${\dot{\theta }}_l\approx 0$, it is required that

$${\tau }_{\mathrm{cont}}\gg {\tau }_m=K_t{i}_a={\displaystyle \frac{{\rho }_l{e}^{\lambda }}{\eta n_g}}{T}_{\mathrm{out}}.$$

Under these assumptions, the system simplifies to a first-order linear model described by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & L_a{\displaystyle \frac{d{i}_a}{dt}}+R_a{i}_a=v_m,\hfill \\ \hfill & F_{\mathrm{ext}}={\displaystyle \frac{\eta n_g{\rho }_r{K}_t{e}^{-\lambda }}{{\rho }_{l}h}}{i}_a.\hfill \end{array}\right.\end{array}$$

(7)

Then, the transfer function of the system with input $u=v_m$ and output $y=F_{\mathrm{ext}}$ is given by

$$\begin{array}{c}\hfill P\left(s\right)={\displaystyle \frac{y\left(s\right)}{u\left(s\right)}}={\displaystyle \frac{\frac{\eta n_g{\rho }_r{K}_t{e}^{-\lambda }}{{\rho }_{l}h}}{L_{a}s+R_a}}=:{\displaystyle \frac{{\beta }_0}{{\alpha }_{1}s+{\alpha }_0}},\end{array}$$

(8)

where the parameter ${\beta }_0$ is particularly difficult to identify accurately in practice due to uncertainties in system parameters.

2.2. Modeling Challenges and Uncertainties in Tendon-Sheath Transmission Systems

The final model of the motor-driven tendon-sheath transmission system, given in (7) or (8), is a simplified first-order linear model. Although this model neglects several physical phenomena, omits certain unmodeled dynamics, and includes parameters that are not precisely known, it is used as a nominal model by assigning known or reasonably estimated parameter values:

$$\begin{array}{c}\hfill P_{\mathsf{n}}\left(s\right)={\displaystyle \frac{{\beta }_{\mathsf{n},\mathsf{0}}}{{\alpha }_{\mathsf{n},\mathsf{1}}s+{\alpha }_{\mathsf{n},\mathsf{0}}}}.\end{array}$$

(9)

In conclusion, accurately modeling the actual tendon-sheath transmission system remains a significant challenge. The primary sources of modeling difficulty can be summarized as follows:

(1)

Friction: The friction model employed for the TSM in Appendix A incorporates only Coulomb friction while neglecting other critical components such as viscous damping and the spatially distributed, hysteretic characteristics of friction along the sheath. In particular, the friction coefficient $\mu$ in the tension force derivation (A6) is highly uncertain and difficult to measure accurately. Furthermore, both the local radius of curvature r and the direction indicator $sgn\left(\dot{\xi }\right)$ vary continuously along the tendon path, rendering it infeasible to determine their effective values in practice. These uncertainties contribute to significant variability in the lumped parameter $\lambda$ defined in (A13), which is central to the nominal model (9), and introduce unmodeled friction dynamics that are not captured by the simplified model.

(2)

Stiffness: The effective stiffness $k_e$ in (A19) is a nonlinear function of $\lambda$ and includes parameters that are likewise difficult to identify precisely in practical applications. As a result, the tendon elongation $\delta \left(l\right)$, which is determined by (6), becomes difficult to compute accurately. However, owing to its relatively small influence, the tendon elongation effect is neglected in deriving the final model from the angular relationship (5), and thus, it is not incorporated into the nominal model (9).

(3)

Backlash: As described in (A15), the distal tendon tension remains unchanged until the elongation $\delta \left(l\right)$ exceeds the backlash threshold ${\xi }_B$, even if the proximal input tension increases. Although this nonlinearity is represented in (6), it is omitted in the nominal model (9) under the assumption that the tendon operates outside the backlash region.

3. Disturbance Observer-Based Robust Force Control

This section presents a comprehensive review of the DOB-based control framework, which is widely utilized to enhance robustness against model uncertainties and external disturbances. After establishing the theoretical foundation and key design principles of DOB, these concepts are applied to the motor-driven tendon-sheath force transmission system introduced in (8). This approach enables the development of a robust controller capable of overcoming the significant uncertainties inherent in the TSM dynamics, where the DOB proves to be an effective solution for handling such challenges.

3.1. Review on Disturbance Observer

DOB-based control [20,21,22] is a widely used framework for achieving robust performance in the presence of system uncertainties by estimating and rejecting disturbances in real time. A typical closed-loop configuration employing a DOB is illustrated in Figure 2. In this structure, $P\left(s\right)$ denotes a single-input single-output (SISO), linear time-invariant (LTI) real plant that may involve parametric uncertainties. The transfer function $P_{\mathsf{n}}\left(s\right)$ represents the nominal model of $P\left(s\right)$, which is designed to have the same relative degree as the real plant. The following assumption formally characterizes the level of parametric uncertainty considered in the DOB scheme for both $P\left(s\right)$ and its nominal model $P_{\mathsf{n}}\left(s\right)$.

Assumption 1.

The plant $P\left(s\right)$ and its nominal model $P_{\mathsf{n}}\left(s\right)$ are assumed to belong to a bounded set of rational transfer functions defined as

$$\begin{array}{cc}\hfill \mathcal{P}:=\{& {\displaystyle \frac{{\beta }_{n-\nu }{s}^{n-\nu }+{\beta }_{n-\nu -1}{s}^{n-\nu -1}+\dots +{\beta }_0}{{\alpha }_n{s}^n+{\alpha }_{n-1}{s}^{n-1}+\dots +{\alpha }_0}}|\hfill \\ \hfill & {\alpha }_i\in [{\underline{\alpha }}_i,{\overline{\alpha }}_i],{\beta }_i\in [{\underline{\beta }}_i,{\overline{\beta }}_i],0\notin [{\underline{\alpha }}_n,{\overline{\alpha }}_n],0\notin [{\underline{\beta }}_{n-\nu },{\overline{\beta }}_{n-\nu }]\},\hfill \end{array}$$

(10)

where n and ν are positive integers representing the system order and the relative degree, respectively, satisfying $n\ge \nu$. The coefficients ${\underline{\alpha }}_i$, ${\overline{\alpha }}_i$, ${\underline{\beta }}_i$, and ${\overline{\beta }}_i$ are known real constants that define the admissible ranges of parametric uncertainty in the numerator and denominator polynomials.

The DOB constitutes a two-degree-of-freedom control architecture, in which the outer-loop controller $C\left(s\right)$ and the inner-loop DOB (represented by the shaded block in Figure 2) are designed separately. As will be discussed later, the outer-loop controller $C\left(s\right)$ can be designed independently of the inner-loop component, which consists of an implementable controller constructed based on the nominal model $P_{\mathsf{n}}\left(s\right)$. Within this structure, the Q-filter $Q\left(s\right)$ emerges as a critical design element that significantly influences the robustness and performance of the overall system.

Under the configuration of Figure 2, the output y of the closed-loop system can be expressed in terms of the reference r, external disturbance d, and measurement noise v as

$$y\left(s\right)=T_r\left(s\right)r\left(s\right)+T_d\left(s\right)d\left(s\right)-T_v\left(s\right)v\left(s\right),$$

(11)

where the transfer functions are defined as

$$\begin{array}{cc}\hfill T_r\left(s\right)& :={\displaystyle \frac{P_{\mathsf{n}}\left(s\right)P\left(s\right)C\left(s\right)}{\Delta \left(s\right)}},\hfill \\ \hfill T_d\left(s\right)& :={\displaystyle \frac{P_{\mathsf{n}}\left(s\right)P\left(s\right)(1-Q\left(s\right))}{\Delta \left(s\right)}},\hfill \\ \hfill T_v\left(s\right)& :={\displaystyle \frac{P\left(s\right)(Q\left(s\right)+P_{\mathsf{n}}\left(s\right)C\left(s\right))}{\Delta \left(s\right)}},\hfill \end{array}$$

with the common denominator of

$$\begin{array}{cc}\hfill \Delta \left(s\right)& :=P_{\mathsf{n}}\left(s\right)(1+P\left(s\right)C\left(s\right))+Q\left(s\right)(P\left(s\right)-P_{\mathsf{n}}\left(s\right)).\hfill \end{array}$$

(12)

Moreover, the sensitivity function $S_{\mathrm{DOB}}\left(s\right)$ and the complementary sensitivity function $T_{\mathrm{DOB}}\left(s\right)$ of the inner-loop DOB [25,26] are derived as

$$\begin{array}{cc}\hfill S_{\mathrm{DOB}}\left(s\right)& ={\displaystyle \frac{P_{\mathsf{n}}\left(s\right)(1-Q\left(s\right))}{P_{\mathsf{n}}\left(s\right)(1-Q\left(s\right))+P\left(s\right)Q\left(s\right)}},\hfill \\ \hfill T_{\mathrm{DOB}}\left(s\right)& ={\displaystyle \frac{P\left(s\right)Q\left(s\right)}{P_{\mathsf{n}}\left(s\right)(1-Q\left(s\right))+P\left(s\right)Q\left(s\right)}},\hfill \end{array}$$

where $S_{\mathrm{DOB}}\left(s\right)=1-Q\left(s\right)$ and $T_{\mathrm{DOB}}\left(s\right)=Q\left(s\right)$ hold when the actual plant exactly matches the nominal model (i.e., $P\left(s\right)=P_{\mathsf{n}}\left(s\right)$). When the Q-filter is designed such that $Q\left(j\omega \right)\approx 1$ in the low-frequency range, the sensitivity function approaches zero, $S_{\mathrm{DOB}}\left(j\omega \right)\approx 0$, and we have a significant simplification of the closed-loop transfer functions from (11) as follows:

$$T_r\left(j\omega \right)\approx {\displaystyle \frac{P_{\mathsf{n}}\left(j\omega \right)C\left(j\omega \right)}{1+P_{\mathsf{n}}\left(j\omega \right)C\left(j\omega \right)}},T_d\left(j\omega \right)\approx 0,T_v\left(j\omega \right)\approx 1.$$

Note that these simplifications are particularly valid in the low-frequency region, where external disturbances are most dominant and measurement noise is negligible in the same frequency range (i.e., $v\left(j\omega \right)\approx 0$). Under these conditions, the system output becomes

$$y\left(j\omega \right)\approx {\displaystyle \frac{P_{\mathsf{n}}\left(j\omega \right)C\left(j\omega \right)}{1+P_{\mathsf{n}}\left(j\omega \right)C\left(j\omega \right)}}r\left(j\omega \right)=:y_{\mathsf{n}}\left(j\omega \right).$$

Here, $y_{\mathsf{n}}$ denotes the output of the nominal closed-loop system, where the shaded block of the DOB configuration in Figure 2 is simply replaced with the nominal plant model $P_{\mathsf{n}}\left(s\right)$, assuming no external disturbance. This result illustrates the key feature of the DOB, known as nominal performance recovery, wherein the actual output closely approximates the nominal response despite the presence of plant uncertainties and external disturbances.

To achieve nominal performance recovery, the Q-filter $Q\left(s\right)$, which is a key component in the DOB architecture, is typically designed as a proper and stable low-pass filter such that $Q\left(j\omega \right)\approx 1$ in the low-frequency range, as previously discussed. A commonly adopted structure for the Q-filter is given by

$$\begin{array}{c}\hfill Q(s;\tau )={\displaystyle \frac{c_{n_q-{\nu }_q}{\left(\tau s\right)}^{n_q-{\nu }_q}+c_{n_q-{\nu }_q-1}{\left(\tau s\right)}^{n_q-{\nu }_q-1}+\dots +c_0}{{\left(\tau s\right)}^{n_q}+a_{n_q-1}{\left(\tau s\right)}^{n_q-1}+\dots +a_1\left(\tau s\right)+a_0}},\end{array}$$

(13)

where the time constant $\tau >0$ is inversely proportional to the filter’s bandwidth. To ensure the implementability of $P_{\mathsf{n}}^{-1}Q\left(s\right)$ in the DOB configuration shown in Figure 2, the relative degree ${\nu }_q$ of the Q-filter must satisfy ${\nu }_q\ge \nu$, where $\nu$ is the relative degree of the nominal model in Assumption 1. Furthermore, the condition $a_0=c_0\ne 0$ is imposed to guarantee unity DC gain.

However, the nominal performance recovery property holds only if the overall closed-loop system remains internally stable despite the presence of plant uncertainty. Accordingly, the design of the Q-filter $Q(s;\tau )$ to ensure robust internal stability has been a primary focus of DOB research [24]. To establish rigorous stability conditions, the components of the DOB system are often represented in terms of coprime polynomial factorizations:

$$\begin{array}{c}\hfill P\left(s\right)={\displaystyle \frac{N\left(s\right)}{D\left(s\right)}},P_{\mathsf{n}}\left(s\right)={\displaystyle \frac{N_{\mathsf{n}}\left(s\right)}{D_{\mathsf{n}}\left(s\right)}},C\left(s\right)={\displaystyle \frac{N_C\left(s\right)}{D_C\left(s\right)}},Q(s;\tau )={\displaystyle \frac{N_Q(s;\tau )}{D_Q(s;\tau )}}.\end{array}$$

(14)

With this coprime factorization, the characteristic polynomial of the DOB-controlled system can be derived to assess its internal stability, which in turn provides a basis for the systematic design of the Q-filter and outer-loop controller in Figure 2. From the common denominator of the transfer functions in (12), the closed-loop characteristic polynomial can be expressed as

$$\begin{array}{cc}\hfill \delta (s;\tau ):=& \left(D\left(s\right)D_C\left(s\right)+N\left(s\right)N_C\left(s\right)\right)N_{\mathsf{n}}\left(s\right)D_Q\left(s\right)\hfill \\ \hfill & +N_Q\left(s\right)D_C\left(s\right)\left(N\left(s\right)D_{\mathsf{n}}\left(s\right)-N_{\mathsf{n}}\left(s\right)D\left(s\right)\right)\hfill \\ \hfill =& \left(D_{\mathsf{n}}\left(s\right)D_C\left(s\right)N_Q\left(s\right)+N_{\mathsf{n}}\left(s\right)N_C\left(s\right)D_Q\left(s\right)\right)N\left(s\right)\hfill \\ \hfill & +D\left(s\right)D_C\left(s\right)N_{\mathsf{n}}\left(s\right)(D_Q\left(s\right)-N_Q\left(s\right)).\hfill \end{array}$$

(15)

It is shown in [24] that as $\tau \to 0$, the roots of the characteristic equation $\delta (s;\tau )=0$ split into two disjoint groups: one corresponding to the slow dynamics and the other to the fast dynamics governed by the Q-filter. These are characterized by the following two polynomials:

$$\begin{array}{cc}\hfill p_{\mathsf{s}}\left(s\right)& :=\left(D_{\mathsf{n}}\left(s\right)D_C\left(s\right)+N_{\mathsf{n}}\left(s\right)N_C\left(s\right)\right)N\left(s\right),\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill p_{\mathsf{f}}\left(s\right)& :=D_Q(s;1)+\left(\underset{s\to \infty }{lim}{\displaystyle \frac{P\left(s\right)}{P_{\mathsf{n}}\left(s\right)}}-1\right)N_Q(s;1).\hfill \end{array}$$

(16b)

Using this decomposition, the following robust stability condition is obtained.

Theorem 1

([24] (Theorem 3)). Under Assumption 1, there exists a constant ${\tau }^{*}>0$ such that for all $0<\tau \le {\tau }^{*}$, the DOB-based closed-loop system in Figure 2 is robustly internally stable if the following are satisfied:

(1) 

The polynomial $p_{\mathsf{s}}\left(s\right)$ is stable for all $P\left(s\right)\in \mathcal{P}$.

(2) 

The polynomial $p_{\mathsf{f}}\left(s\right)$ is stable for all $P\left(s\right)\in \mathcal{P}$.

Equivalently, these conditions can be stated as follows:

(1a) 

The nominal closed-loop system ${\displaystyle \frac{P_{\mathsf{n}}\left(s\right)C\left(s\right)}{1+P_{\mathsf{n}}\left(s\right)C\left(s\right)}}$ is stable.

(1b) 

The plant $P\left(s\right)$ is the minimum phase for all $P\left(s\right)\in \mathcal{P}$.

(2) 

The polynomial $p_{\mathsf{f}}\left(s\right)$ is stable for all $P\left(s\right)\in \mathcal{P}$.

This result implies that once the outer-loop controller $C\left(s\right)$ is selected to stabilize the nominal plant model $P_{\mathsf{n}}\left(s\right)$ and the actual plant $P\left(s\right)$ is a minimum phase system; it is always possible to design a Q-filter of the form (13) that guarantees the robust internal stability of the entire system. Specifically, the coefficients of the numerator and denominator of $Q(s;1)$ (i.e., with the time constant $\tau$ fixed to one) can be chosen such that the polynomial $p_{\mathsf{f}}\left(s\right)$ is stable, after which the time constant $\tau$ can be selected sufficiently small to satisfy $\tau \le {\tau }^{*}$. The detailed design procedure is provided in [24] (Section 2.3), where root locus techniques are utilized.

3.2. Application of Disturbance Observer to Tendon Transmission System and Design of Q-Filter

The DOB framework, as outlined in Section 3.1, is particularly well-suited for systems characterized by structured parametric uncertainties, as specified in Assumption 1. The TSM, whose force transmission dynamics have been thoroughly examined in Section 2, exhibits precisely such characteristics, making it a strong candidate for the application of DOB-based control techniques. The dynamic behavior of the TSM described in (8), with the motor voltage $v_m$ as the input and the distal end force $F_{\mathrm{ext}}$ as the output, can be rewritten as

$$P\left(s\right)={\displaystyle \frac{\frac{\eta n_g{\rho }_r{K}_t{e}^{-\lambda }}{{\rho }_{l}h}}{L_{a}s+R_a}}={\displaystyle \frac{{\beta }_0}{{\alpha }_{1}s+{\alpha }_0}},$$

(17)

where ${\alpha }_1=L_a$, ${\alpha }_0=R_a$, and ${\beta }_0={\displaystyle \frac{\eta n_g{\rho }_r{K}_t{e}^{-\lambda }}{{\rho }_{l}h}}$ are parameters determined by the physical characteristics of the motor actuated TSM system. In practice, the denominator coefficients ${\alpha }_1$ and ${\alpha }_0$ can be relatively accurately identified based on the electrical specifications of the motor components used in the system design, although their exact values are not perfectly known. In contrast, the numerator coefficient ${\beta }_0$ is subject to considerable uncertainty, as it depends on factors such as the motor efficiency $\eta$, the friction-related term $\lambda$ in (A13), the end-effector contact point h, and other system properties that are difficult to measure directly. As a result, precise identification of the plant $P\left(s\right)$ is generally infeasible in real-world applications.

Nonetheless, the structure of the TSM dynamics satisfies several key prerequisites (namely, Assumption 1 and the stability conditions in Theorem 1) required for DOB design:

(1)

System structure of $\mathcal{P}$: The transfer function $P\left(s\right)$ in (17) is a strictly proper first-order LTI system of relative degree one, which conforms to the admissible class $\mathcal{P}$ defined in Assumption 1. In other words, the system has a fixed order $n=1$ and a relative degree $\nu =1$, both of which are explicitly defined.

(2)

Coefficient bounds in $\mathcal{P}$: All coefficients ${\alpha }_1$, ${\alpha }_0$, and ${\beta }_0$ lie within known bounds due to physical constraints and manufacturing tolerances, although they are highly uncertain, and the corresponding bounds $[{\underline{\alpha }}_i,{\overline{\alpha }}_i]$ and $[{\underline{\beta }}_i,{\overline{\beta }}_i]$ may be relatively large. Additionally, the denominator’s leading coefficient ${\alpha }_1=L_a>0$ is inherently positive, as dictated by the fundamental properties of inductance in electrical circuits. Similarly, the numerator’s leading coefficient ${\beta }_0={\displaystyle \frac{\eta n_g{\rho }_r{K}_t{e}^{-\lambda }}{{\rho }_{l}h}}>0$ is also positive, as each constituent parameter, namely, $\eta$, $n_g$, $K_t$, $e^{-\lambda }$, ${\rho }_l$, ${\rho }_r$, and h, is strictly positive by definition. This ensures that the leading coefficient conditions $0\notin [{\underline{\alpha }}_n,{\overline{\alpha }}_n]$ and $0\notin [{\underline{\beta }}_{n-\nu },{\overline{\beta }}_{n-\nu }]$ in Assumption 1 are satisfied.

(3)

Minimum phase property of $P\left(s\right)\in \mathcal{P}$: Since $P\left(s\right)$ contains no zeros, and hence no right-half plane zeros, it satisfies the minimum phase condition (1b) in Theorem 1.

(4)

Stabilizability of the nominal plant $P_{\mathsf{n}}\left(s\right)$ by an outer-loop controller $C\left(s\right)$: An outer-loop controller $C\left(s\right)$ that stabilizes the nominal model $P_{\mathsf{n}}\left(s\right)$ can be readily designed to satisfy the nominal stability condition (1a) in Theorem 1. For instance, a simple proportional-integral (PI) controller of the form

$$\begin{array}{c}\hfill C\left(s\right)=k_P+{\displaystyle \frac{k_I}{s}}\end{array}$$

(18)

can stabilize the first-order nominal plant $P_{\mathsf{n}}\left(s\right)={\displaystyle \frac{{\beta }_{\mathsf{n},\mathsf{0}}}{{\alpha }_{\mathsf{n},\mathsf{1}}s+{\alpha }_{\mathsf{n},\mathsf{0}}}}$, as the resulting closed-loop transfer function is given by

$${\displaystyle \frac{P_{\mathsf{n}}\left(s\right)C\left(s\right)}{1+P_{\mathsf{n}}\left(s\right)C\left(s\right)}}={\displaystyle \frac{{\beta }_{\mathsf{n},\mathsf{0}}{k}_{P}s+{\beta }_{\mathsf{n},\mathsf{0}}{k}_I}{{\alpha }_{\mathsf{n},\mathsf{1}}{s}^2+({\alpha }_{\mathsf{n},\mathsf{0}}+{\beta }_{\mathsf{n},\mathsf{0}}{k}_P)s+{\beta }_{\mathsf{n},\mathsf{0}}{k}_I}},$$

which can easily be made a stable second-order system with appropriately chosen gains $k_P$ and $k_I$.

So far, the TSM transmission force control system not only fits within the theoretical DOB framework but also serves as a practical and well-structured platform for DOB implementation. The only remaining requirement is the satisfaction of condition (2) in Theorem 1, which concerns the selection of the Q-filter coefficients. Specifically, the Q-filter must be designed such that the polynomial $p_{\mathsf{f}}\left(s\right)$ is stable for all $P\left(s\right)\in \mathcal{P}$. The following presents a systematic guideline for selecting the Q-filter coefficients to satisfy this condition. First, we consider the Q-filter in the form of (13). Given that the required relative degree satisfies ${\nu }_q\ge \nu =1$, the simplest admissible choice is ${\nu }_q=1$, which, for simplicity, leads to the corresponding denominator degree $n_q=1$ for $D_Q(s;\tau )$. To ensure unity DC gain, the coefficients must satisfy $a_0=c_0\ne 0$. With these selections, the Q-filter takes the form

$$\begin{array}{c}\hfill Q(s;\tau )={\displaystyle \frac{N_Q(s;\tau )}{D_Q(s;\tau )}}={\displaystyle \frac{a_0}{\tau s+a_0}}.\end{array}$$

Accordingly, from (16b), the polynomial $p_{\mathsf{f}}\left(s\right)$ becomes

$$\begin{array}{c}\hfill p_{\mathsf{f}}\left(s\right)=s+\left(\underset{s\to \infty }{lim}{\displaystyle \frac{P\left(s\right)}{P_{\mathsf{n}}\left(s\right)}}\right)a_0.\end{array}$$

(19)

It then follows, perhaps unexpectedly, that any positive value $a_0>0$ ensures the stability of $p_{\mathsf{f}}\left(s\right)$. This is because, as established by the leading coefficient condition discussed earlier, the limit ${lim}_{s\to \infty }{\displaystyle \frac{P\left(s\right)}{P_{\mathsf{n}}\left(s\right)}}$ remains strictly positive for all $P\left(s\right)\in \mathcal{P}$. Therefore, we adopt the simplest choice $a_0=1$ for convenience, yielding the final form of the Q-filter as

$$\begin{array}{c}\hfill Q(s;\tau )={\displaystyle \frac{1}{\tau s+1}}.\end{array}$$

(20)

As a final design consideration, the time constant $\tau >0$ should be selected to be sufficiently small to achieve effective disturbance rejection while preserving robust stability, as required in Theorem 1.

4. Simulation Results

This section presents simulation results using a realistic and detailed model of the tendon-sheath transmission system. To evaluate the performance of the proposed DOB-based controller, the actual plant $P\left(s\right)$ is constructed by incorporating various physical effects that were neglected in the nominal system modeling of Section 2, including a more accurate friction model, tendon elongation, and backlash. Specifically, instead of the simple Coulomb friction model, the Dahl model [39,40] is employed, which captures the hysteretic behavior of friction by modeling its dependence on displacement history. Furthermore, viscous damping and spring stiffness are also introduced to account for the effects of tendon elongation and backlash. Based on the framework illustrated in Figure 1, the simulation model of the tendon is constructed to facilitate realistic numerical simulations, with reference to the methods presented in [5,8,9]. As shown in Figure 3, the tendon is modeled as a chain of f equal-length segments, each with mass $m_i=m$, and the segments have been interconnected by linear springs with stiffness $k_i=k$ and dampers characterized by a viscous damping coefficient $b_i=b$.

From the force equilibrium, the dynamics of the tendon model are described by

$$\left\{\begin{array}{cc}\hfill & {\dot{x}}_i=v_i,\hfill \\ & {\dot{v}}_i={\displaystyle \frac{1}{m}}\left(b(v_{i+1}-2v_i+v_{i-1})+k(x_{i+1}-2x_i+x_{i-1})-F_{d,i}\right),\hfill \\ & {\dot{\mu }}_{d,i}=\sigma \left(v_i-{\displaystyle \frac{{\mu }_{d,i}}{{\mu }_c}}\left|v_i\right|\right),\hfill \end{array}\right.\mathrm{for}i=2,\dots ,f-1,$$

(21)

where the state variables $x_i$, $v_i$, and ${\mu }_{d,i}$ represent the position, velocity, and Dahl model-based internal friction state of the i-th segment, respectively. In contrast, ${\mu }_c$ denotes the Coulomb friction coefficient, which corresponds to the saturated value of the internal friction variable ${\mu }_{d,i}$ in the Dahl model. Furthermore, the friction force $F_{d,i}$ and the tension force $T_i$ are computed as

$$\left\{\begin{array}{cc}\hfill F_{d,i}& ={\mu }_{d,i}{N}_i\hfill \\ \hfill & ={\mu }_{d,i}\left((k(x_i-x_{i-1})-T_{\mathrm{pre}}){\displaystyle \frac{\varphi }{2}}+(k(x_{i+1}-x_i)-T_{\mathrm{pre}}){\displaystyle \frac{\varphi }{2}}\right)\hfill \\ \hfill & ={\mu }_{d,i}{\displaystyle \frac{\varphi }{2}}\left(k(x_{i+1}-x_{i-1})-2T_{\mathrm{pre}}\right)\hfill \\ \hfill & ={\displaystyle \frac{{\mu }_{d,i}l}{2rf}}\left(k\left(x_{i+1}-x_{i-1}-{\displaystyle \frac{2l}{f}}\right)\right),\hfill \\ \hfill T_i& =k\left(x_{i+1}-x_i\right)-T_{\mathrm{pre}}\hfill \\ \hfill & =k\left(x_{i+1}-x_i-{\displaystyle \frac{l}{f}}\right),\hfill \end{array}\right.\mathrm{for}i=2,\dots ,f-1,$$

(22)

where f, l, r, $\varphi (=\frac{l}{rf})$, and $T_{\mathrm{pre}}(=k\frac{l}{f})$ represent the total number of segments, the overall tendon length, the radius of the tendon route, the angular span of a single segment, and the inherent pretension in the tendon segment induced by its length, respectively. The parameter $\sigma$ represents the rest stiffness, i.e., the slope of the friction force–deflection curve at $F_{d,i}=0$. Note that the Equations in (21) and (22) apply only for interior segments with $i=2,\dots ,f-1$. The first ($i=1$) and the last ($i=f$) require special treatment due to boundary conditions. For the first segment, the equations become

$$\left\{\begin{array}{cc}\hfill & {\dot{x}}_i=v_i,\hfill \\ \hfill & {\dot{v}}_i={\displaystyle \frac{1}{m}}\left(b(v_{i+1}-v_i)+k\left(x_{i+1}-x_i-{\displaystyle \frac{l}{f}}\right)-T_{\mathrm{in}}-F_{d,i}\right),\hfill \\ \hfill & {\dot{\mu }}_{d,i}=\sigma \left(v_i-{\displaystyle \frac{{\mu }_{d,i}}{{\mu }_c}}\left|v_i\right|\right),\hfill \\ \hfill & F_{d,i}={\displaystyle \frac{{\mu }_{d,i}l}{2rf}}\left(k\left(x_{i+1}-x_i-{\displaystyle \frac{l}{f}}\right)+T_{\mathrm{in}}\right),\hfill \\ \hfill & T_i=k\left(x_{i+1}-x_i-{\displaystyle \frac{l}{f}}\right),\hfill \end{array}\right.\mathrm{for}i=1.$$

(23)

Similarly, for the last segment, the equations are given by

$$\left\{\begin{array}{cc}\hfill & {\dot{x}}_i=v_i,\hfill \\ \hfill & {\dot{v}}_i={\displaystyle \frac{1}{m}}\left(b(0-2v_i+v_{i-1})+k(l-2x_i+x_{i-1})-F_{d,i}\right),\hfill \\ \hfill & {\dot{\mu }}_{d,i}=\sigma \left(v_i-{\displaystyle \frac{{\mu }_{d,i}}{{\mu }_c}}\left|v_i\right|\right),\hfill \\ \hfill & F_{d,i}={\displaystyle \frac{{\mu }_{d,i}l}{2rf}}\left(k\left(l-x_{i-1}-{\displaystyle \frac{2l}{f}}\right)\right),\hfill \\ \hfill & T_{\mathrm{out}}=k\left(l-x_i-{\displaystyle \frac{l}{f}}\right),\hfill \end{array}\right.\mathrm{for}i=f.$$

(24)

The equations of motion given in (21)–(24) are used to represent the actual TSM dynamics in the numerical simulations, where those discrete tendon segments are actuated by a DC motor as shown in Figure 1. All parameters related to the TSM are summarized in

Table 2. Tendon-sheath mechanism parameters used in simulation study.

Parameter	Description	Real Value	Nominal Value	Unit
E	Young’s modulus	$200\times {10}^9$	$200\times {10}^9$	$\mathrm{Pa}$
A	Cross-sectional area	$1\times {10}^{-6}$	$1\times {10}^{-6}$	${\mathrm{m}}^2$
l	Free length of the tendon	$0.2$	$0.2$	$\mathrm{m}$
r	Radius of the tendon route	$0.4/\pi$	$0.1$	$\mathrm{m}$
f	Number of segments	20	20	−
m	Mass of one segment with length $\frac{l}{f}$	$8\times {10}^{-5}$	$8\times {10}^{-5}$	$\mathrm{k}\mathrm{g}$
k	Stiffness of one segment ($=\frac{EA}{l/f}$)	$2\times {10}^7$	$2\times {10}^7$	$\mathrm{N}/\mathrm{m}$
b	Damping coefficient	$8\times {10}^{-4}$	$8\times {10}^{-4}$	$\mathrm{N}/(\mathrm{m}/\mathrm{s})$
$\sigma$	Rest stiffness in Dahl model	$2\times {10}^7$	$2\times {10}^7$	−
${\mu }_c$	Friction coefficient in Coulomb model	$0.15$	$0.18$	−
$\lambda$	Friction related parameter in (A13)	$0.2356$	$0.36$	−
$T_{\mathrm{pre}}$	Pretension of single segment ($=k\frac{l}{f}$)	$2\times {10}^5$	$2\times {10}^5$	$\mathrm{N}$
${\rho }_l$	Radius of the pulley on motor side	$0.01$	$0.01$	$\mathrm{m}$
${\rho }_r$	Radius of the pulley on robot side	$0.01$	$0.01$	$\mathrm{m}$
h	Length of the robot link contact point	$0.05$	$0.045$	$\mathrm{m}$

, while the motor parameters are listed in

Table 3. Motor parameters used in simulation study.

Parameter	Description	Real Value	Nominal Value	Unit
$K_t$	Motor torque constant	$7.68\times {10}^{-3}$	$7\times {10}^{-3}$	$\mathrm{N}\mathrm{m}/\mathrm{A}$
$K_e$	Motor back EMF constant	$7.68\times {10}^{-3}$	$7\times {10}^{-3}$	$\mathrm{V}/(\mathrm{rad}/\mathrm{s})$
$R_a$	Motor armature resistance	$2.6$	3	$\Omega$
$L_a$	Motor armature inductance	$0.18$	$0.2$	$\mathrm{m}\mathrm{H}$
$n_g$	Total gear ratio	70	70	−
$\eta$	Motor efficiency	$0.621$	$0.5$	−
$J_{tot}$	Total moment of inertia	$2.18\times {10}^{-3}$	$2\times {10}^{-3}$	$\mathrm{k}\mathrm{g}{\mathrm{m}}^2$
$B_{tot}$	Total damping coefficient	$1.5\times {10}^{-3}$	$1\times {10}^{-3}$	$\mathrm{N}\mathrm{m}/(\mathrm{rad}/\mathrm{s})$

. By combining the motor and robot dynamics described in (1)–(3) with the tendon-sheath transmission model described in (21)–(24), the complete system is modeled as a real plant $P\left(s\right)$ in the DOB-based control framework. The corresponding nominal model $P_{\mathsf{n}}\left(s\right)$ in (9) is obtained by substituting the nominal parameter values from Table 2 and Table 3 into the first-order transfer function defined in (8). The nominal model $P_{\mathsf{n}}\left(s\right)$ is then used to design the outer-loop controller $C\left(s\right)$. As discussed in Section 3.2, a simple PI controller (18) is sufficient to stabilize the nominal model and achieve satisfactory tracking performance, with control gains provided in

Table 4. Control gains and parameters used in simulation study.

Parameter	Description	Value
$k_P$	Proportional gain	$0.1$
$k_I$	Integral gain	1000
$\tau$	Q-filter time constant	$0.001$

. The final design component of the DOB is the Q-filter. As described in Section 3.2, the filter structure (20) is specified as a first-order low-pass filter with relative degree one. Thus, the only remaining tuning parameter is the time constant $\tau$, which should be chosen sufficiently small, as suggested by Theorem 1. In this study, $\tau =0.001$ is selected, as shown in Table 4, and this choice is found to effectively attenuate disturbances, as demonstrated in the simulation results in Figure 4.

Finally, Figure 4 presents the simulation results comparing the performance of the proposed DOB-based control scheme with that of a conventional PI controller without disturbance compensation. Subplots (a)–(d) illustrate the case without DOB, whereas subplots (e)–(h) show the corresponding results when the DOB is applied. In particular, subplots (a) and (e) display the reference force $r\left(t\right)$ and the actual output force $F_{\mathrm{ext}}\left(t\right)$, where the DOB-based controller exhibits significantly improved tracking performance. Subplots (b) and (f) show the control input $u\left(t\right)$, with subplot (f) also including the estimated disturbance $\widehat{d}\left(t\right)$, thereby demonstrating the DOB’s ability to reconstruct and effectively reject lumped disturbances. Subplots (c) and (g) compare the internal tension forces $T_i\left(t\right)$ in selected tendon segments. Among the total $f=20$ tendon segments, four representative segments have been selected for visualization. As shown in subplots (g), the tension generally decreases from the proximal end ($T_{\mathrm{in}}$) to the distal end ($T_{\mathrm{out}}$) due to the cumulative effect of distributed friction. However, depending on the direction of motion, local increases in tension may occur, especially in the case without DOB compensation, where friction forces are not adequately handled. Subplots (d) and (h) show the corresponding friction forces $F_{d,i}\left(t\right)$, where the DOB-based controller results in smoother force transitions and reduced fluctuations. These findings confirm that the proposed DOB-based control scheme effectively mitigates the adverse effects of friction and transmission uncertainties, thereby improving the output force accuracy and enhancing the overall robustness of the system.

5. Conclusions

This paper presented a DOB-based control framework for tendon-sheath transmission systems characterized by uncertain friction and tension-induced elongations. The TSM system, where a motor drives the tendon and the resulting output is the contact force between the robot end-effector and the environment, was carefully modeled to capture key physical characteristics. The resulting model revealed substantial parametric uncertainties arising from the complex and nonlinear dynamics of the tendon-sheath structure. However, an analysis based on established robust stability conditions for DOB-based control confirmed that the required assumptions are satisfied and that the remaining stability conditions can be readily fulfilled through appropriate Q-filter design, thereby validating the applicability of the DOB framework to the TSM system. A DOB-based PI control scheme was subsequently designed to estimate and compensate for both parametric uncertainties and unmodeled dynamics, including nonlinear friction forces and transmission errors inherent in the TSM system. Under certain assumptions, including the use of a simple Coulomb friction model and the neglect of tendon elongation effects, the nominal model of the motor-driven tendon-sheath transmission system was derived as a simple first-order linear system. To more accurately reflect the hysteretic transmission behavior that critically affects control performance, a more realistic plant model was developed for simulation studies. This model incorporates a chain of discrete segments to represent the tendon, along with a friction dynamics model that combines the Dahl formulation with additional viscous friction. The simulation results demonstrated that the proposed approach significantly enhances force tracking accuracy at the distal end of the tendon compared to conventional methods without DOB compensation. These findings suggest that the DOB-based compensation strategy offers a promising and robust solution for improving control performance in tendon-driven robotic systems. Future work will focus on extending the proposed method to handle bidirectional tendon motion; more complex routing configurations; multi-joint tendon-driven robots; and time-varying external loads. Another important direction is the experimental validation on actual robotic hands. Such practical implementation may pose challenges, including sensor noise and time delays. To address these issues, the proposed control framework can be extended to incorporate noise-reduction DOB structures [46], which have been shown to effectively attenuate measurement noise while maintaining disturbance rejection performance.