DNN-Augmented Kinematically Decoupled Three-DoF Origami Parallel Robot for High-Precision Heave and Tilt Control
Abstract
1. Introduction
2. Impact of Parasitic Motion in Precision-Dependent Applications
- Pointing and Satellite Tracking Systems: Precise angular alignment is critical for effective satellite communication. Parasitic motion introduces alignment errors, potentially causing signal attenuation or loss.
- Satellite Thrust Generators: Accurate thrust vectoring ensures correct orbital maneuvers. Parasitic-induced misalignment may cause off-axis thrust, resulting in incorrect maneuvers and increased collision risks.
- High-Precision Machining Systems: CNC and ultra-precision machining demand accurate tool paths. Parasitic motion leads to surface defects, dimensional inaccuracies, and potential damage to tools or workpieces.
- Coordinate Measuring Machines (CMMs): Accurate probe positioning is vital for geometric assessments. Parasitic motion compromises measurement integrity, leading to erroneous evaluations and product rejections.
- Interactive and Reconfigurable Surfaces: Adaptive interfaces and tactile displays rely on continuous, uniform responses. Parasitic motion disrupts continuity, adversely affecting responsiveness and user experience.
- Haptic VR Controllers: Realistic tactile feedback in virtual environments demands precise motion control. Parasitic motion causes discrepancies between visual and haptic cues, diminishing user immersion and realism.
- Sun Tracking Mechanisms: Optimal solar energy capture necessitates accurate tracking of the sun’s position. Parasitic misalignments reduce exposure, diminishing overall energy efficiency.
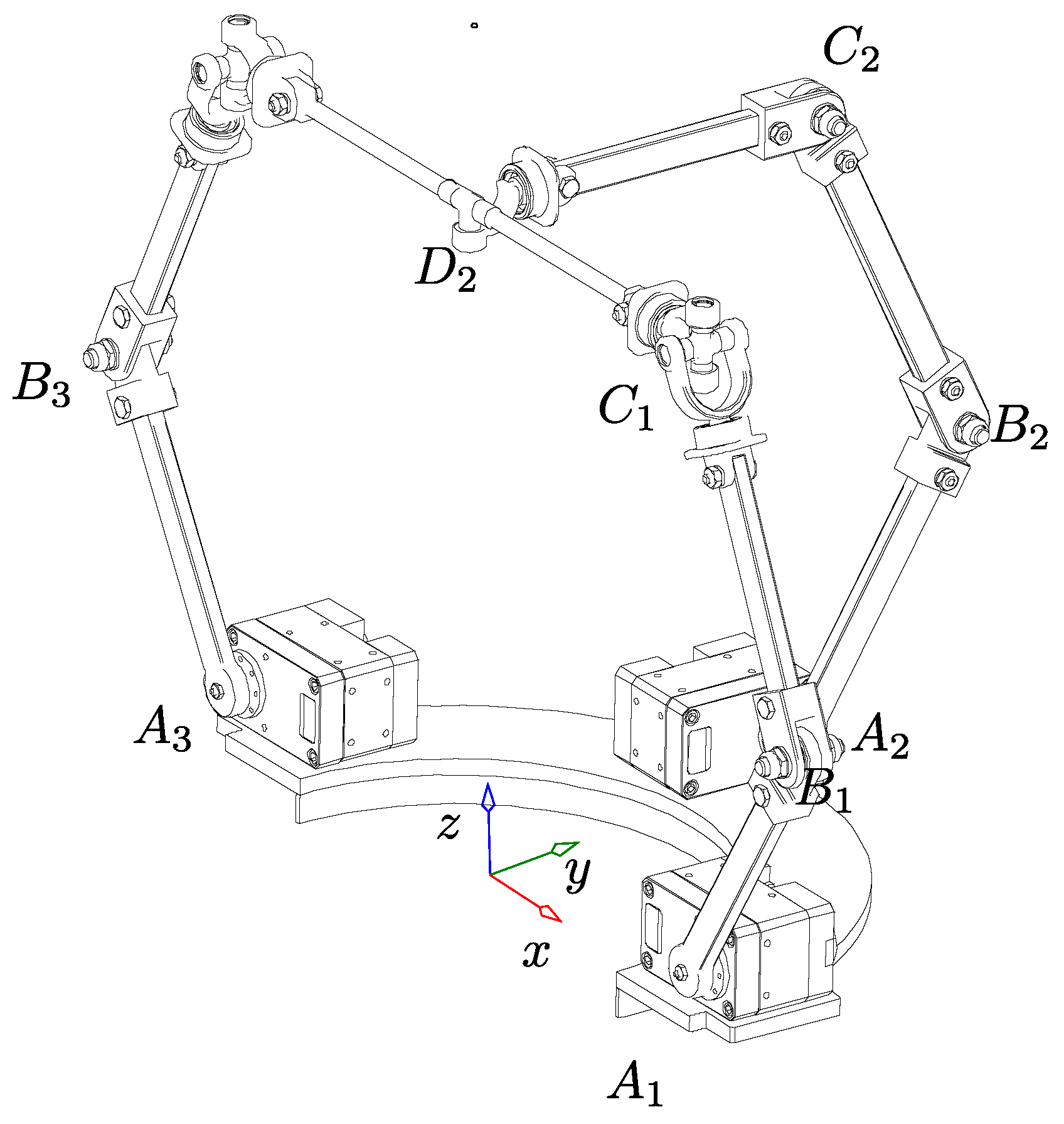
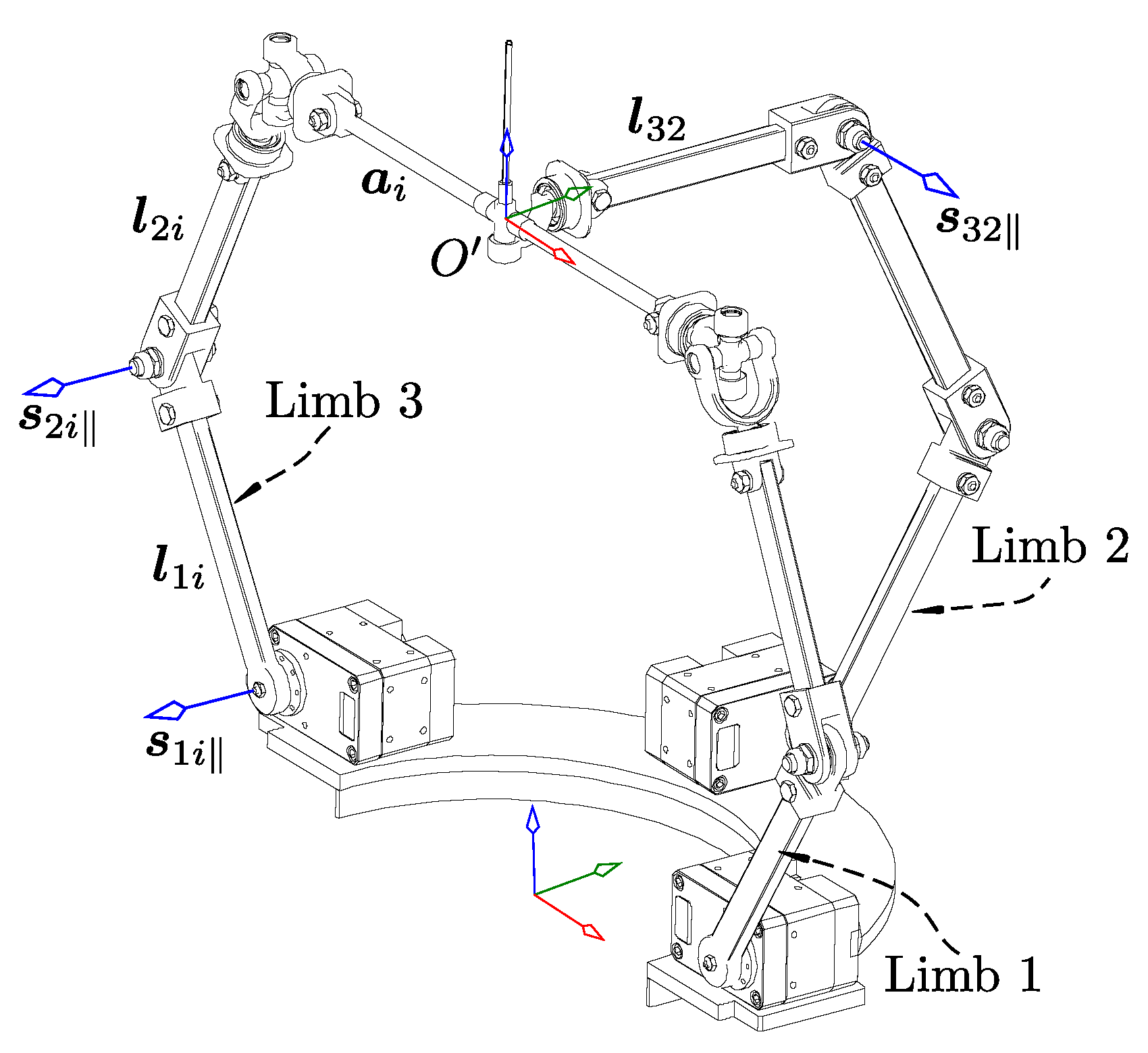
3. Kinematic Architecture of the Robot and Position Information
3.1. Main Kinematic Features of the Robot
3.1.1. Non-Parasitic Motion
3.1.2. Simple to Manufacture and Control
3.1.3. Compactness
3.1.4. Partially Decoupled Motion
3.1.5. Mechanically Constrained Pivoted Motion
4. Rate Kinematics with the Restriction Space
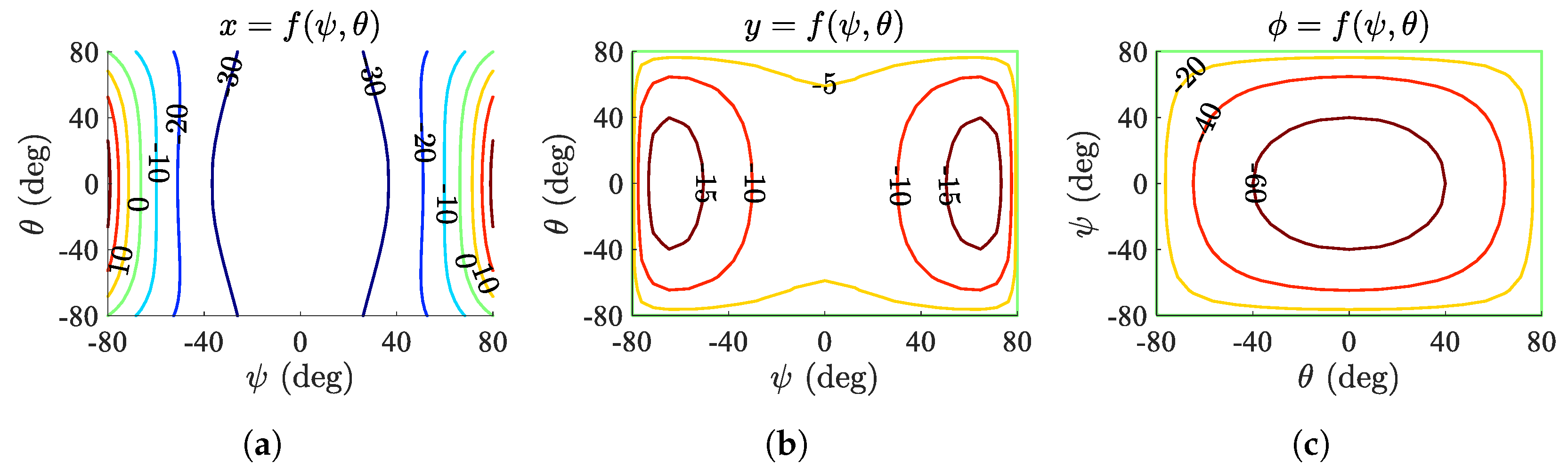
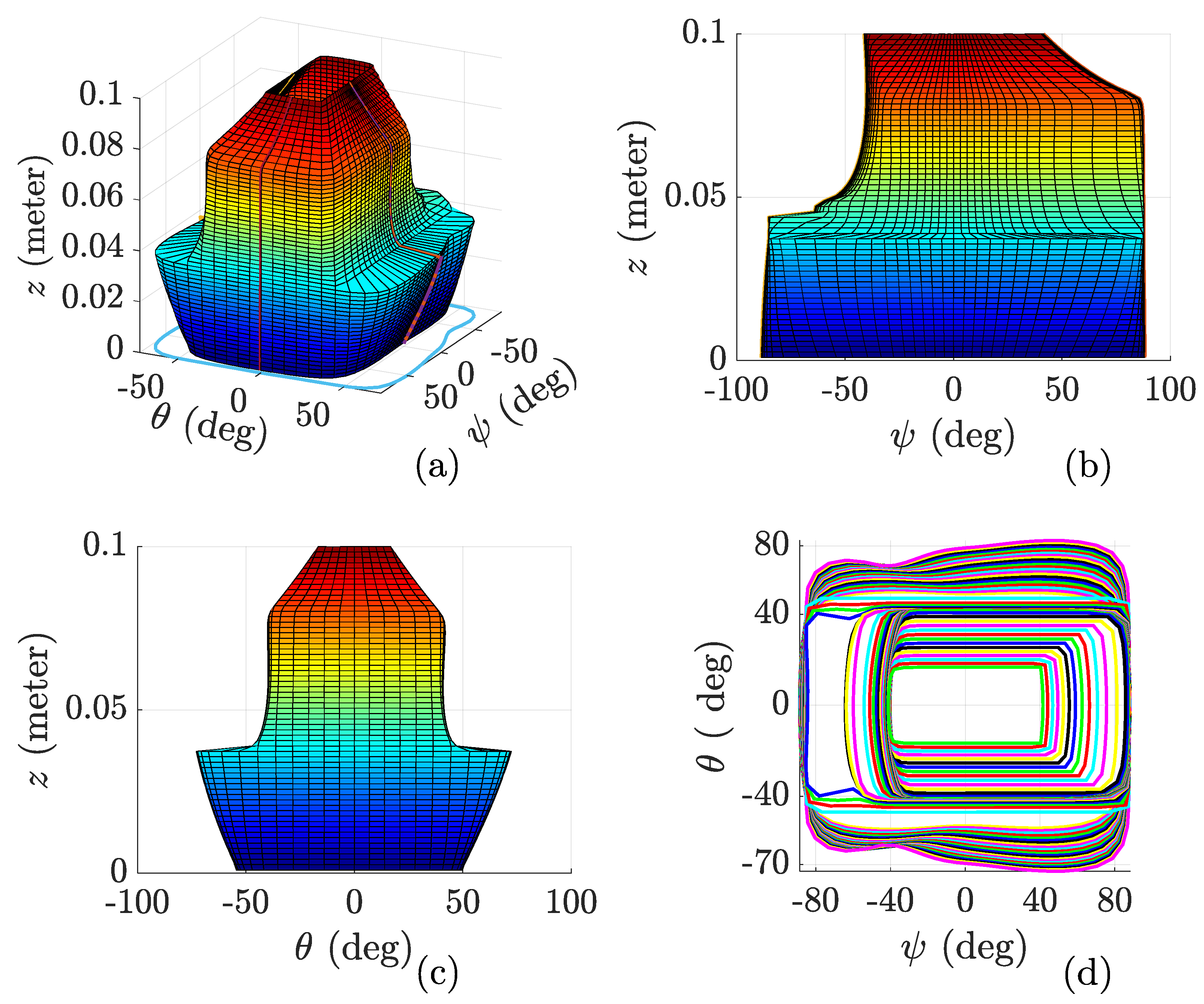
5. Optimization of Parasitic Motion
5.1. Cost Function Formulation
5.2. Comparison with Previous Robots
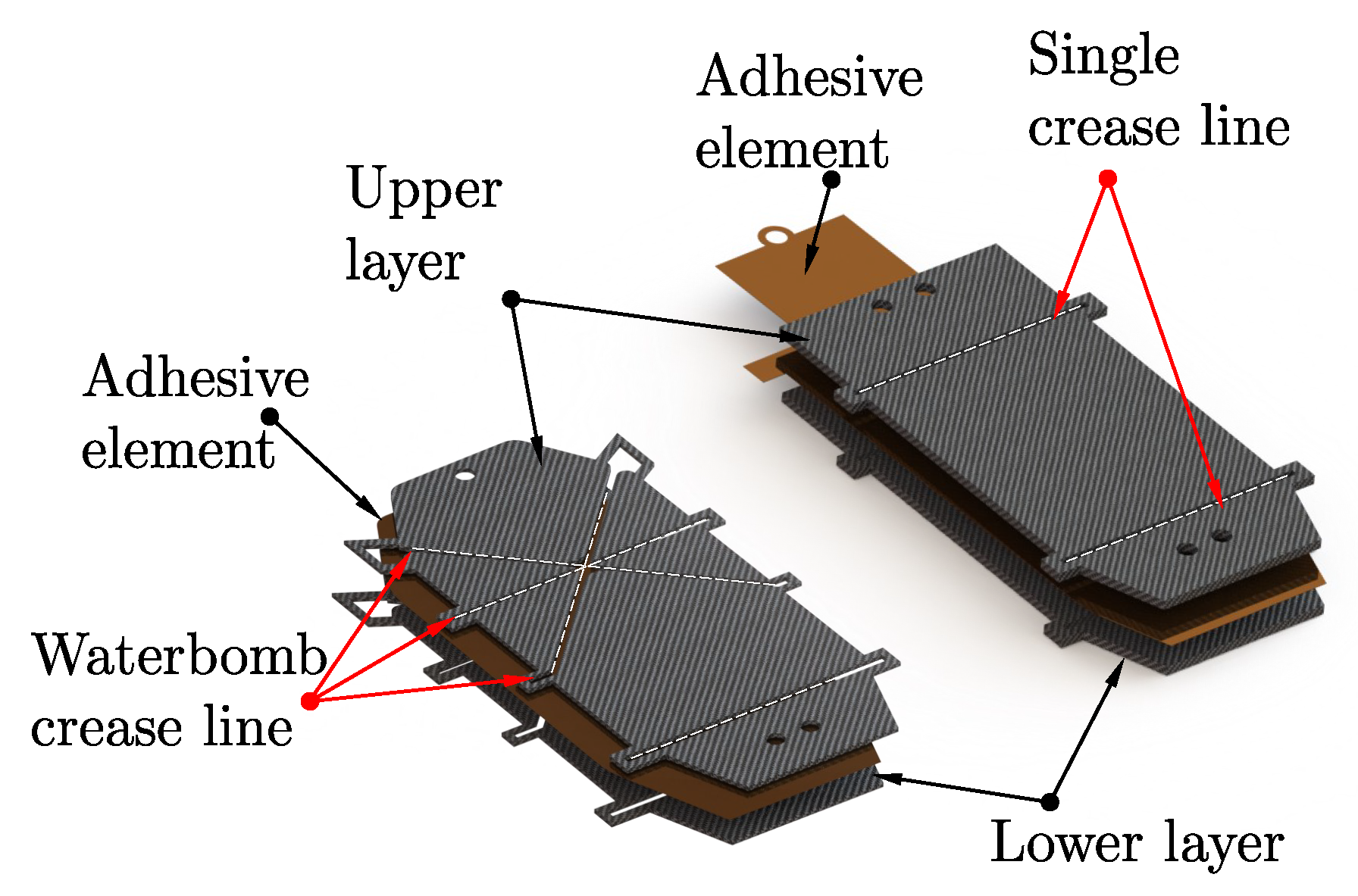
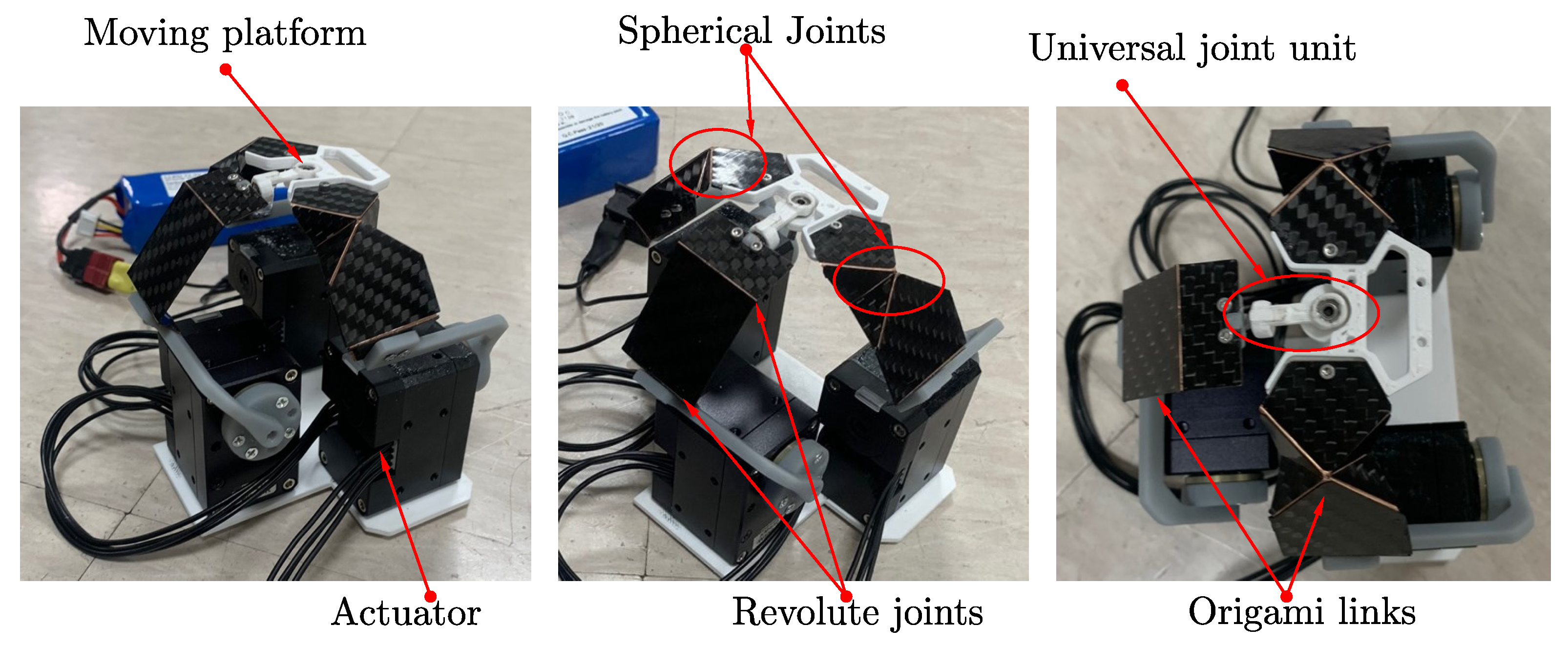
6. Design, Manufacturing, and Control
6.1. Design and Manufacturing
6.2. Hardware Design and Implementation
Transformation to an Origami-Based Parallel Robot
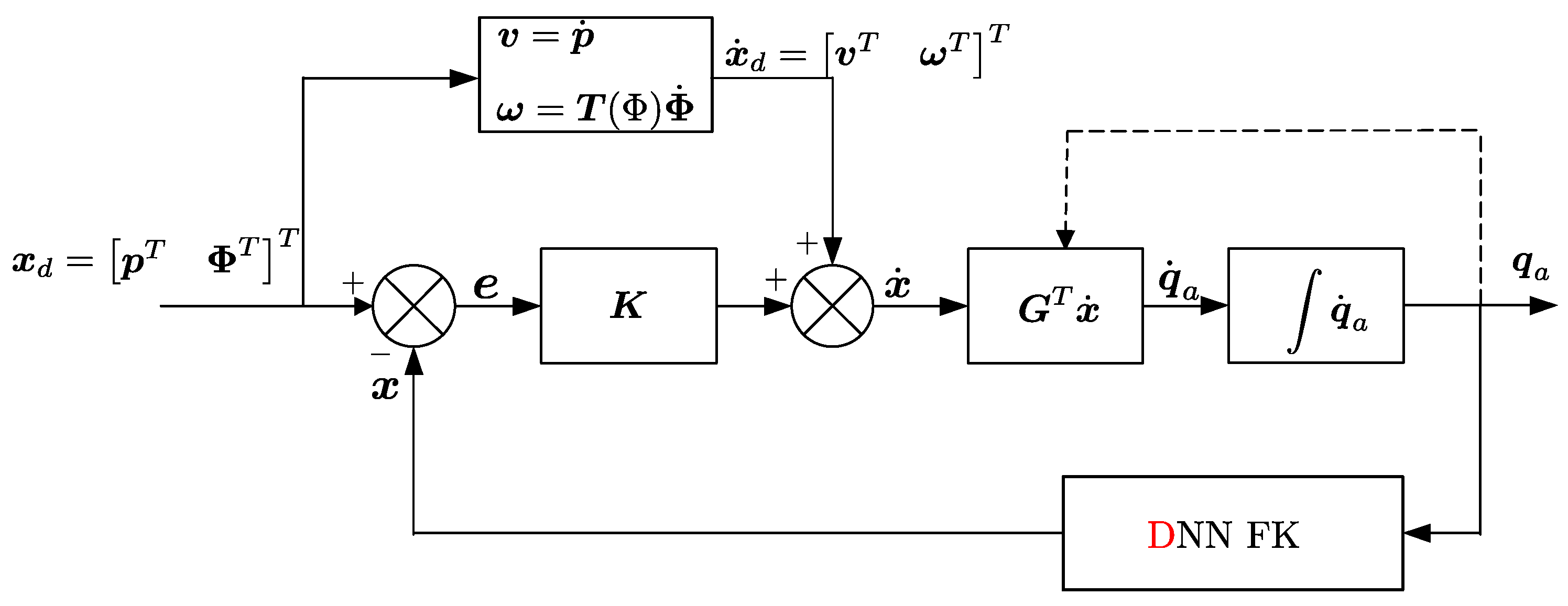
6.3. DNN-Blended Control Scheme
- Robust feedback: a Cartesian gain matrix ensures asymptotic error convergence and disturbance rejection.
- Adaptive compensation: a feedforward DNN approximates nonlinear FK under flexural and geometric uncertainties.
| Algorithm 1 Hybrid DNN-blended control loop | |
| ▹ DNN FK estimate |
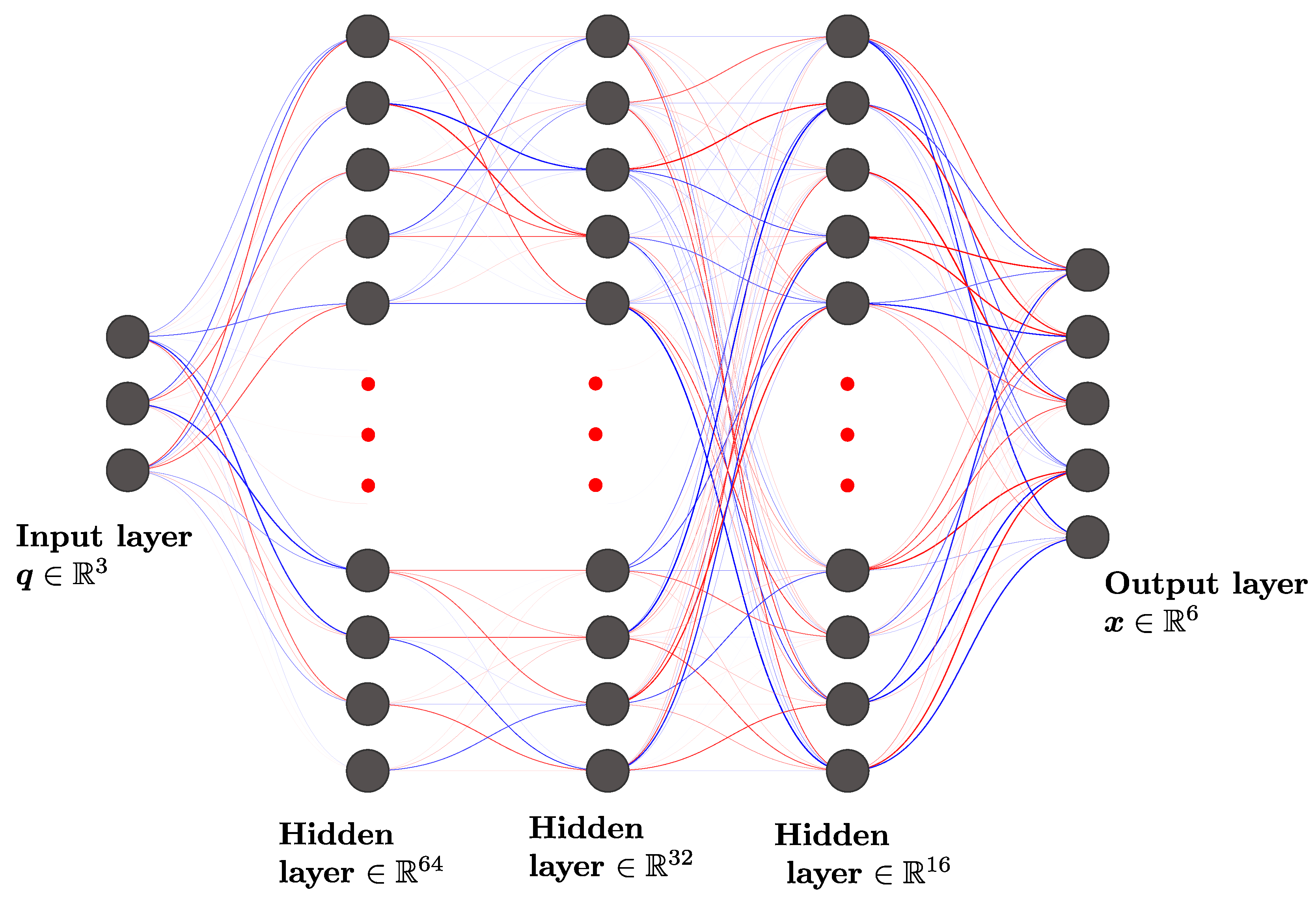
6.4. Deep Learning for State Estimation
6.4.1. Network Architecture
6.4.2. Offline Training Algorithm
| Algorithm 2 Offline DNN training procedure |
|
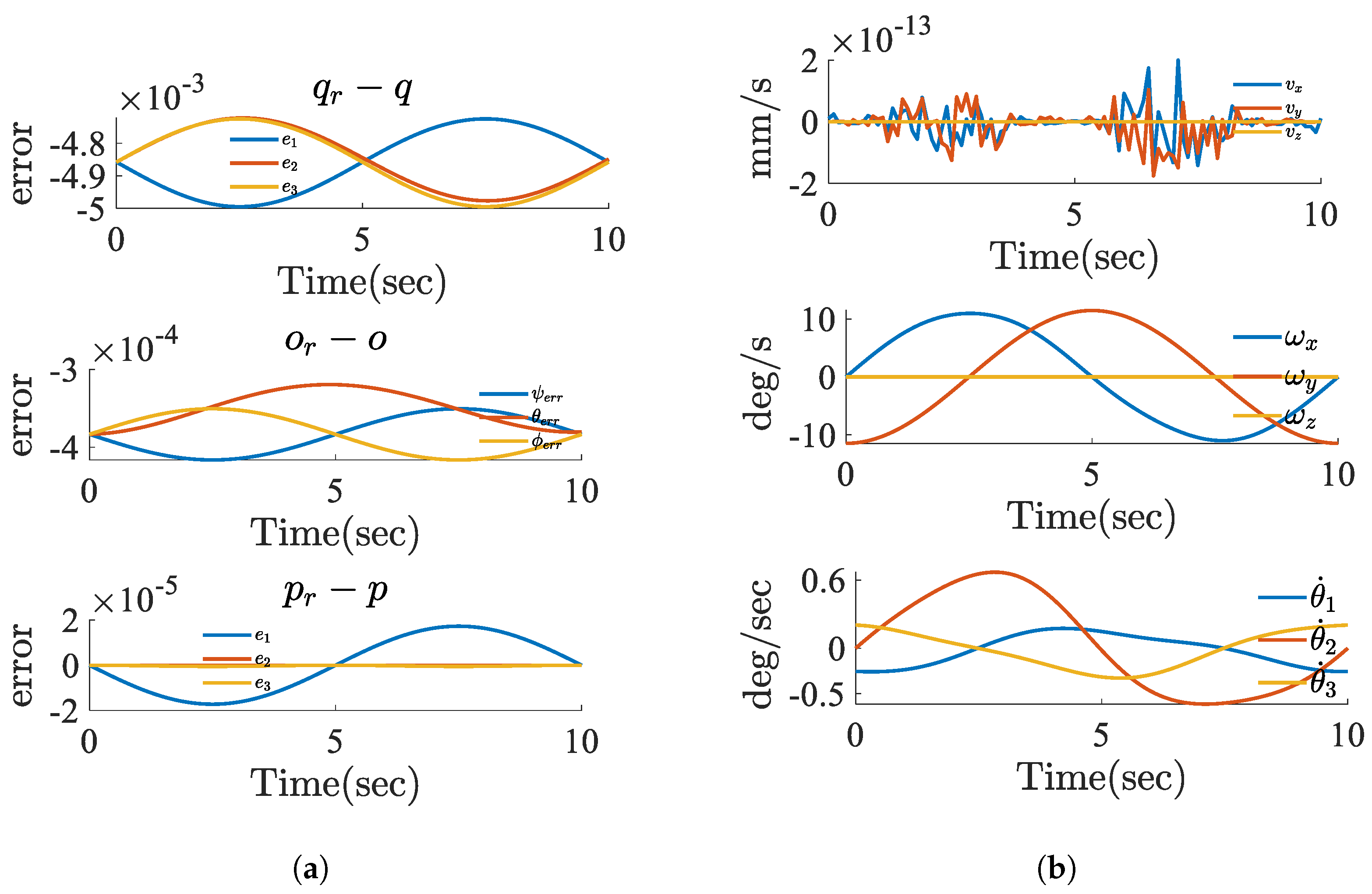
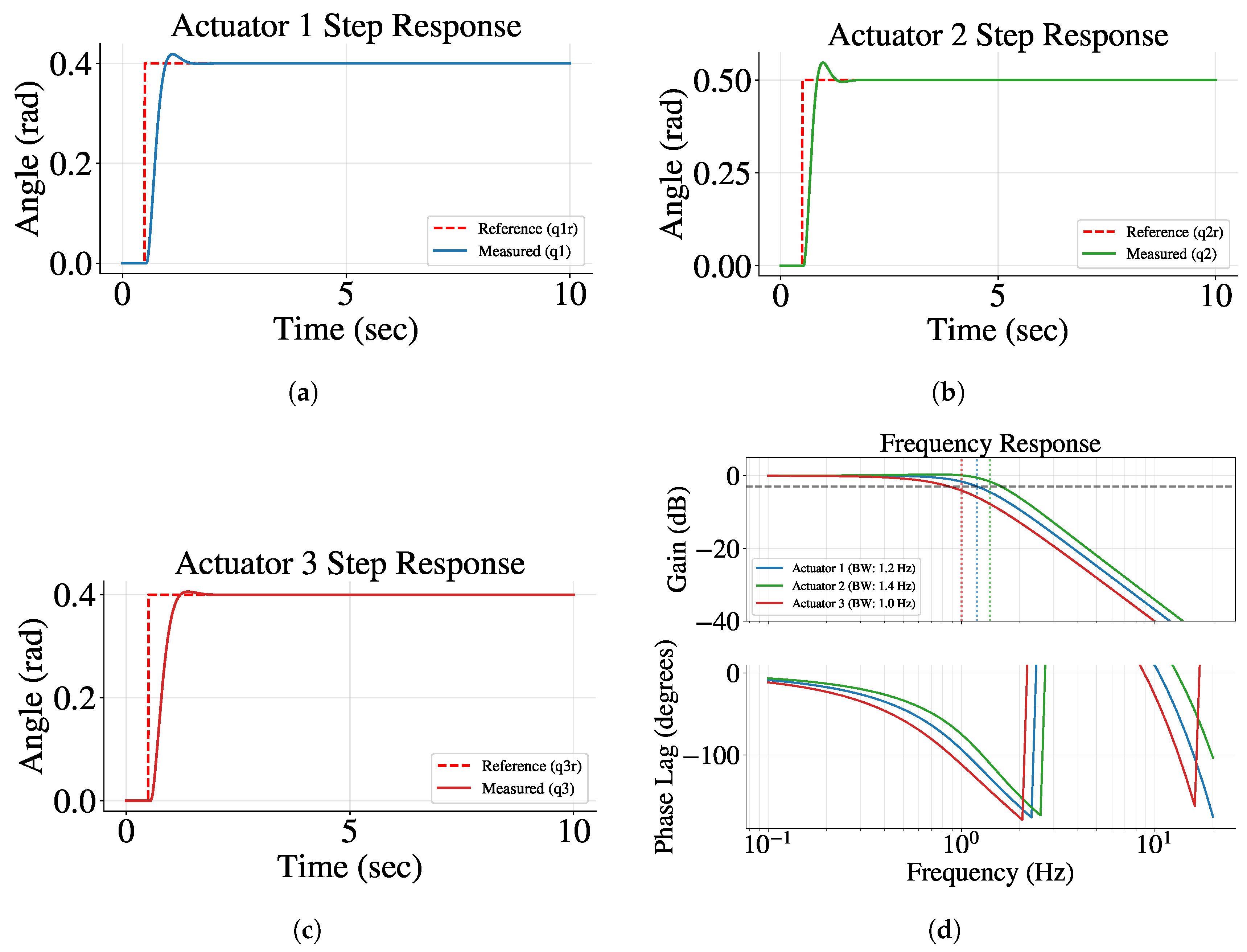
7. Simulation and Experimental Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Solution to the Composite Joint Angles
Appendix B. Derivation of the Actuated Joint Wrench Moment Vector
Appendix C. Lie Group-Based Synthesis of the PR
Appendix D. Nomenclature
| Symbol | Description |
|---|---|
| Mathematical Symbols | |
| Orientation angles (Euler angles for roll, pitch, and yaw) | |
| R | Rotation matrix of the moving platform |
| Angular offset of limb i from the x-axis (e.g., ) | |
| Length of lower links (identical across limbs) | |
| Length of upper links (identical across limbs) | |
| Radius of the fixed base plate | |
| Radius of the moving platform | |
| O | Fixed reference frame |
| Moving reference frame attached to the platform | |
| Direction vector of joint j in limb i | |
| Position vector from to joint center (spherical/universal) | |
| Position vector from O to base actuator center | |
| Rotation matrices about , , and z-axes | |
| Translation matrix along the x-axis | |
| Active joint velocity vector | |
| Task-space velocity twist () | |
| Constraint and motion wrench matrices | |
| Screw representation of joint j in limb i () | |
| Linear velocity components | |
| Angular velocity components | |
| Design parameter vector () | |
| Determinant of the Jacobian (singularity condition) | |
| Abbreviations | |
| DoF | Degrees of Freedom |
| PR | Parallel Robot |
| DNN | Deep Neural Network |
| IT2R/1T2R | One Translation + Two Rotational Motions |
| RRS | Revolute–Revolute–Spherical Limb |
| RRRU | Revolute–Revolute–Revolute–Universal Limb |
| CNC | Computer Numerical Control |
| CMM | Coordinate Measuring Machine |
| VR | Virtual Reality |
| MIS | Minimally Invasive Surgery |
| FK | Forward Kinematics |
| IRK | Inverse-Rate Kinematics |
| R | Revolute Joint |
| P | Prismatic Joint |
| S | Spherical Joint |
| U | Universal Joint |
| BW | Bandwidth (Control Systems) |
References
- Taunyazov, T.; Rubagotti, M.; Shintemirov, A. Constrained Orientation Control of a Spherical Parallel Manipulator via Online Convex Optimization. IEEE/ASME Trans. Mechatronics 2018, 23, 252–261. [Google Scholar] [CrossRef]
- Kuo, C.H.; Dai, J.S.; Dasgupta, P. Kinematic design considerations for minimally invasive surgical robots: An overview. Int. J. Med. Robot. Comput. Assist. Surg. 2012, 8, 127–145. [Google Scholar] [CrossRef] [PubMed]
- Nouaille, L.; Laribi, M.A.; Nelson, C.A.; Zeghloul, S.; Poisson, G. Review of Kinematics for Minimally Invasive Surgery and Tele-Echography Robots. J. Med. Devices 2017, 11, 040802. [Google Scholar] [CrossRef]
- Machinery.co.uk. Ecospeed Celebrated at Starrag Event—A New Model is Launched and Machine Reliability is Praised. 2016. Available online: https://starragtornos.com/media/memi-20160915-e.pdf (accessed on 12 May 2025).
- Howell, P.E.d.W. Articulated Tool Head. U.S. Patent US6431802B1, 13 August 2002. [Google Scholar]
- Salerno, M.; Paik, J.; Mintchev, S. Ori-Pixel, a Multi-DoFs Origami Pixel for Modular Reconfigurable Surfaces. IEEE Robot. Autom. Lett. 2020, 5, 6988–6995. [Google Scholar] [CrossRef]
- Canfield, S.L.; Reinholtz, C.F. Development of the Carpal Robotic Wrist; Springer: Berlin/Heidelberg, Germany, 1998; pp. 423–434. [Google Scholar] [CrossRef]
- Bazman, M.; Yilmaz, N.; Tumerdem, U. An Articulated Robotic Forceps Design with a Parallel Wrist-Gripper Mechanism and Parasitic Motion Compensation. J. Mech. Des. 2022, 144, 063303. [Google Scholar] [CrossRef]
- Carretero, J.A.; Podhorodeski, R.P.; Nahon, M.A.; Gosselin, C.M. Kinematic analysis and optimization of a new three degree-of-freedom spatial parallel manipulator. J. Mech. Des. Trans. ASME 2000, 122, 17–24. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Chen, Q.; Wu, C.; Hu, X. Parasitic motion comparison of 3-PRS parallel mechanism with different limb arrangements. Robot. Comput.-Integr. Manuf. 2011, 27, 389–396. [Google Scholar] [CrossRef]
- Nigatu, H.; Choi, Y.H.; Kim, D. Analysis of parasitic motion with the constraint embedded Jacobian for a 3-PRS parallel manipulator. Mech. Mach. Theory 2021, 164, 104409. [Google Scholar] [CrossRef]
- Li, Q.; Hervé, J.M. 1T2R Parallel Mechanisms Without Parasitic Motion. IEEE Trans. Robot. 2010, 26, 401–410. [Google Scholar] [CrossRef]
- Yaşır, A.; Kiper, G.; Dede, M.C. Kinematic design of a non-parasitic 2R1T parallel mechanism with remote center of motion to be used in minimally invasive surgery applications. Mech. Mach. Theory 2020, 153, 104013. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, Z.; Chai, X.; Li, Q. Kinematic Analysis of a 3-Axis Parallel Manipulator: The P3. Adv. Mech. Eng. 2013, 5, 589156. [Google Scholar] [CrossRef]
- Kang, L.; Yi, B.J. Design of Two Foldable Mechanisms Without Parasitic Motion. IEEE Robot. Autom. Lett. 2016, 1, 930–937. [Google Scholar] [CrossRef]
- Lin, R.; Guo, W.; Gao, F. On Parasitic Motion of Parallel Mechanisms. In Proceedings of the Volume 5B: 40th Mechanisms and Robotics Conference. American Society of Mechanical Engineers, Charlotte, NC, USA, 21–24 August 2016; Volume 5B-2016, pp. 1–13. [Google Scholar] [CrossRef]
- Nigatu, H.; Kim, D. Optimization of 3-DoF Manipulators’ Parasitic Motion with the Instantaneous Restriction Space-Based Analytic Coupling Relation. Appl. Sci. 2021, 11, 4690. [Google Scholar] [CrossRef]
- Nigatu, H. Constraint-Embedded Velocity Analysis of Lower-DoF Parallel Manipulators to Remove Parasitic Motion. Ph.D. Dissertation, UST, Daejeon, Republic of Korea, 2021. [Google Scholar]
- Seo, J.; Shim, S.; Park, H.; Baek, J.; Cho, J.H.; Kim, N.H. Development of Robot-Assisted Untact Swab Sampling System for Upper Respiratory Disease. Appl. Sci. 2020, 10, 7707. [Google Scholar] [CrossRef]
- Kim, D. Kinematic Analysis of Spartial Parallel Manipulators Analytic Approach with the Restriction Space. Ph.D. Dissertation, Pohang University of Science and Technology, Pohang, Republic of Korea, 2001. [Google Scholar]
- Kim, D.; Chung, W.K. Analytic Formulation of Reciprocal Screws and Its Application to Nonredundant Robot Manipulators. J. Mech. Des. 2003, 125, 158–164. [Google Scholar] [CrossRef]
- Nigatu, H.; Ho Choi, Y.; Kim, D. On the Structural Constraint and Motion of 3-PRS Parallel Kinematic Machines. In Proceedings of the Volume 8A: 45th Mechanisms and Robotics Conference (MR), American Society of Mechanical Engineers, Virtual, 17–19 August 2021; Volume 8A-2021. [Google Scholar] [CrossRef]
- Lipkin, H.; Duffy, J. The Elliptic Polarity of Screws. J. Mech. Transm. Autom. Des. 1985, 107, 377–386. [Google Scholar] [CrossRef]
- Hanna, B.H.; Lund, J.M.; Lang, R.J.; Magleby, S.P.; Howell, L.L. Waterbomb base: A symmetric single-vertex bistable origami mechanism. Smart Mater. Struct. 2014, 23, 094009. [Google Scholar] [CrossRef]
- Herve, J.M. The Lie group of rigid body displacements, a fundamental tool for mechanism design. Mech. Mach. Theory 1999, 34, 719–730. [Google Scholar] [CrossRef]
- Li, Q.; Hervé, J.M.; Huang, P. Type Synthesis of a Special Family of Remote Center-of-Motion Parallel Manipulators with Fixed Linear Actuators for Minimally Invasive Surgery. J. Mech. Robot. 2017, 9, 031012. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Nigatu, H.; Wang, Z.; Huang, Y. DNN-Augmented Kinematically Decoupled Three-DoF Origami Parallel Robot for High-Precision Heave and Tilt Control. Actuators 2025, 14, 291. https://doi.org/10.3390/act14060291
Shi G, Nigatu H, Wang Z, Huang Y. DNN-Augmented Kinematically Decoupled Three-DoF Origami Parallel Robot for High-Precision Heave and Tilt Control. Actuators. 2025; 14(6):291. https://doi.org/10.3390/act14060291
Chicago/Turabian StyleShi, Gaokun, Hassen Nigatu, Zhijian Wang, and Yongsheng Huang. 2025. "DNN-Augmented Kinematically Decoupled Three-DoF Origami Parallel Robot for High-Precision Heave and Tilt Control" Actuators 14, no. 6: 291. https://doi.org/10.3390/act14060291
APA StyleShi, G., Nigatu, H., Wang, Z., & Huang, Y. (2025). DNN-Augmented Kinematically Decoupled Three-DoF Origami Parallel Robot for High-Precision Heave and Tilt Control. Actuators, 14(6), 291. https://doi.org/10.3390/act14060291






