The Influence of Axial-Bearing Position of Active Magnetic Suspension Flywheel Energy Storage System on Vibration Characteristics of Flywheel Rotor
Abstract
1. Introduction
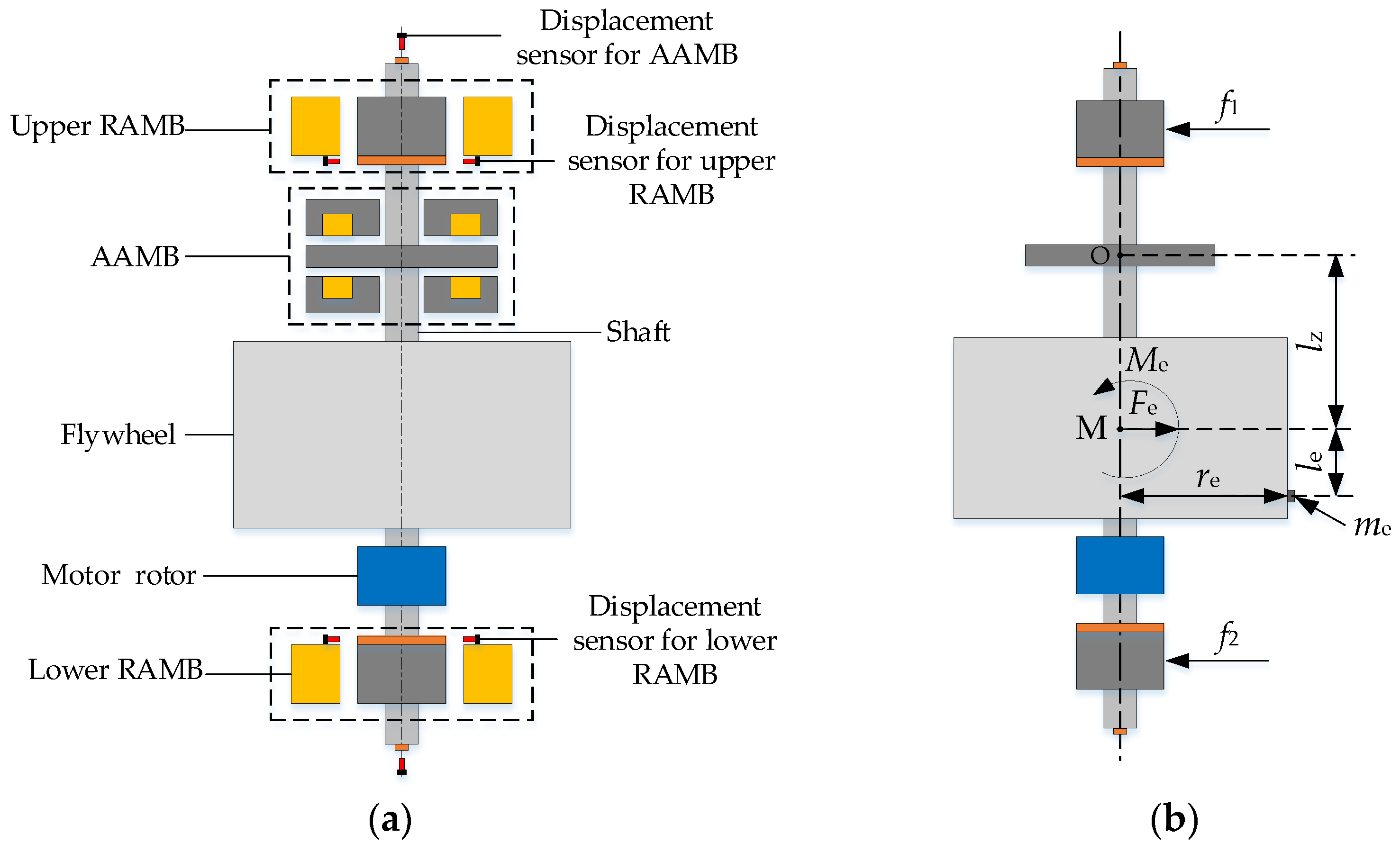
2. Description and Analysis of the Problem
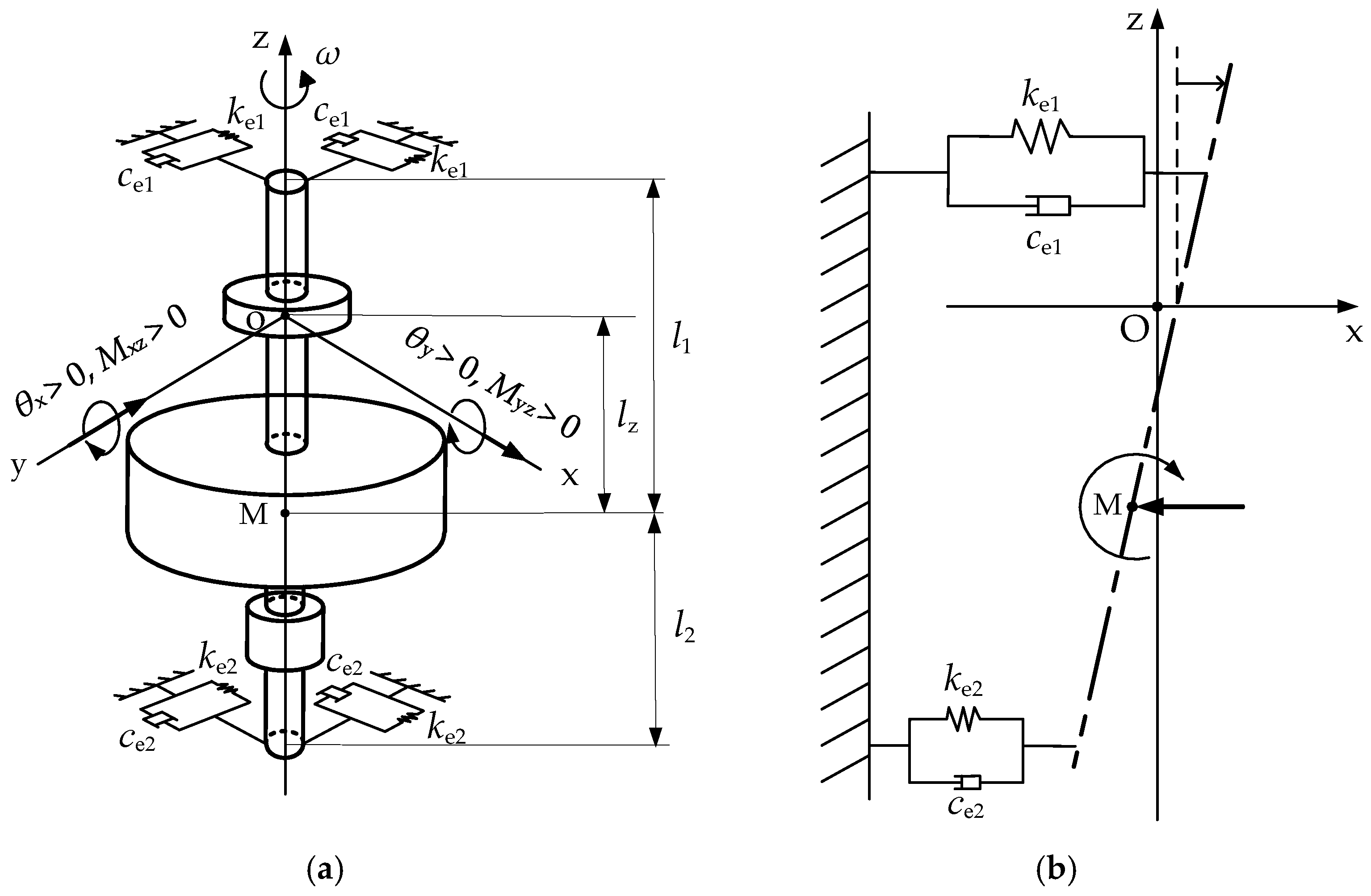
3. Theoretical Modeling
3.1. Equivalent Dynamic Stiffness and Damping of the Electromagnetic Force of Radial Active Magnetic Bearing
3.1.1. Linearization of the Electromagnetic Force of Radial Active Magnetic Bearing
3.1.2. Calculation of the Equivalent Dynamic Stiffness and Damping of Radial Active Magnetic Bearing
3.2. Dynamic Mathematical Model of Rigid Flywheel Rotor Considering the Position of Axial Active Magnetic Bearing
4. Influence of the Axial Active Magnetic Bearing Position on the Characteristic Frequency and Critical Speed of Flywheel Rotor
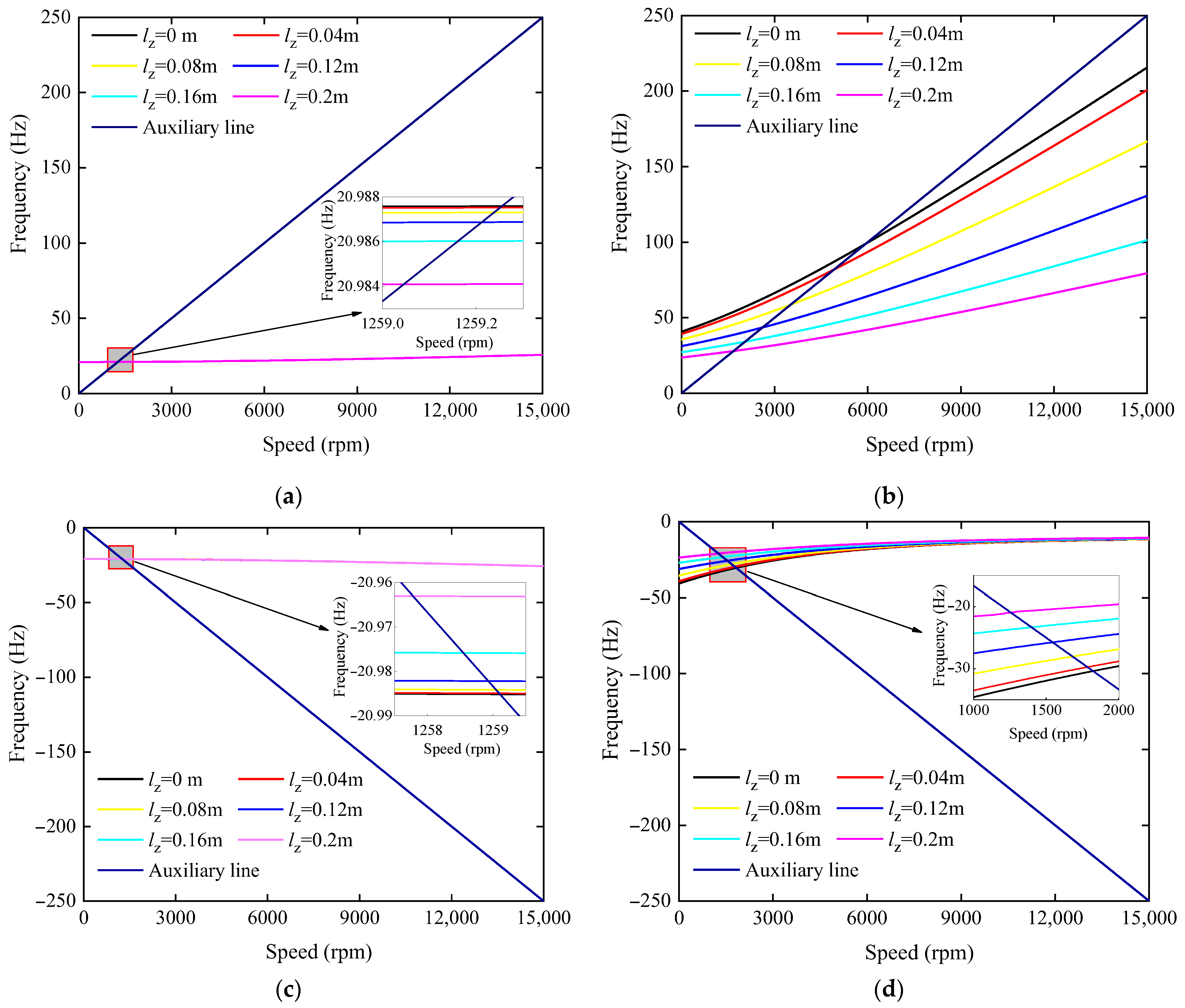
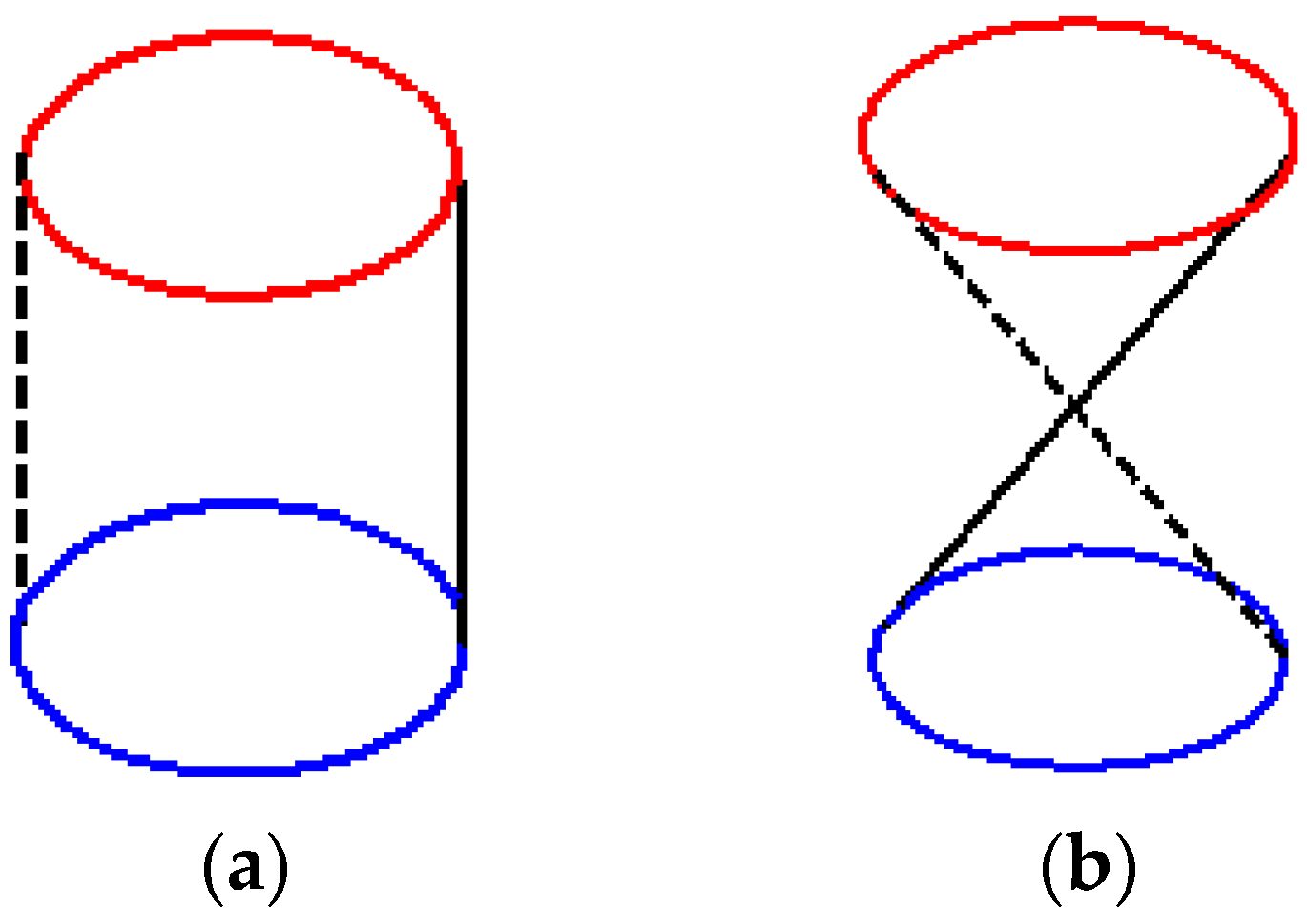
4.1. Solution and Analysis of the Characteristic Frequency of Flywheel Rotor
4.2. The Variation Rule of the Critical Speed of Flywheel Rotor with the Offset Ratio of Axial-Bearing Position
5. Influence of the Axial-Bearing Position on the Mass Unbalance Response of Flywheel Rotor
5.1. Solution and Analysis of the Mass Unbalance Response for Flywheel Rotor
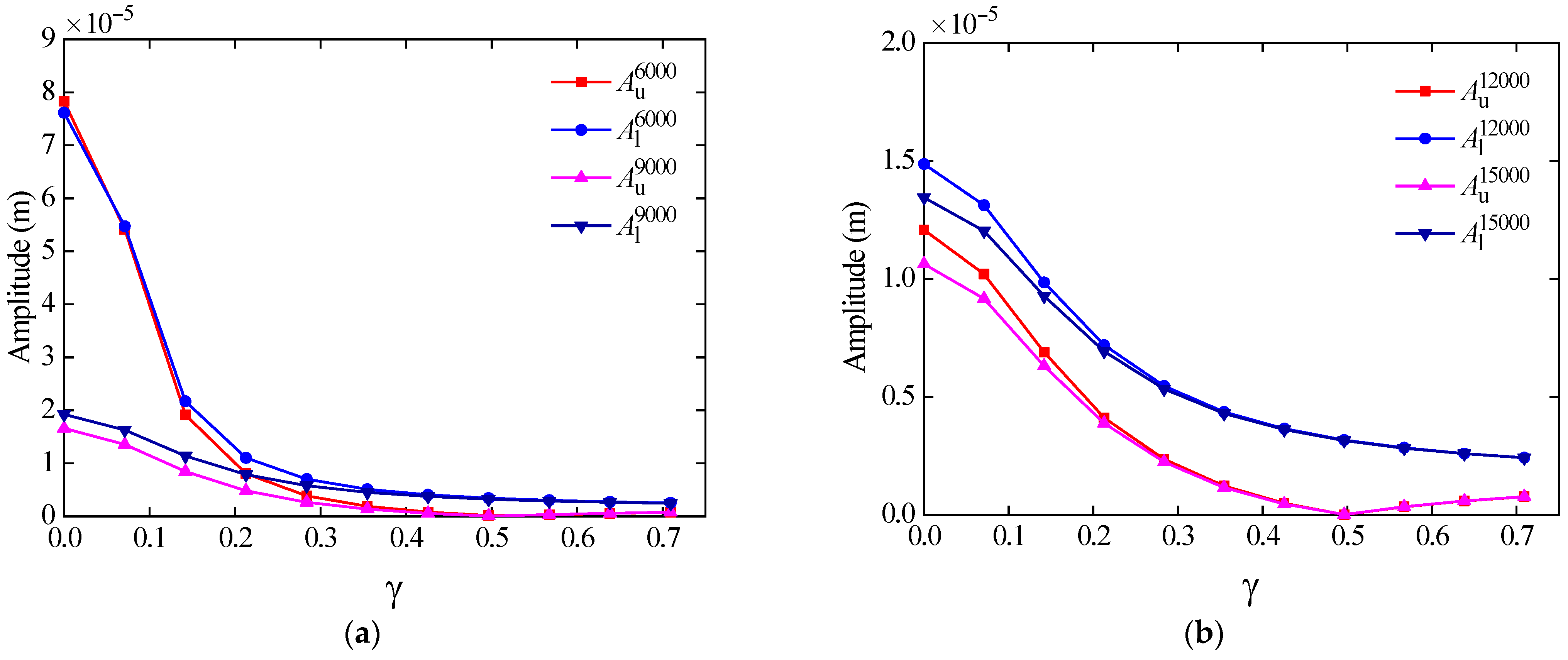
5.2. The Variation Rule of the Mass Unbalance Response of Flywheel Rotor with the Position Offset Ratio of Axial Active Magnetic Bearing
6. Experiment
6.1. The Process of Experiment
6.2. Analysis of Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Qi, X.; Zhang, K.; Wang, G.; Fu, Z.; Dong, Y. Technology of Magnetic Flywheel Energy Storage. In Proceedings of the International Conference on Manufacturing Science and Materials Engineering (ICMSEM 2011), Shanghai, China, 14–15 October 2011. [Google Scholar]
- Tziovani, L.; Hadjidemetriou, L.; Charalampous, C.; Tziakouri, M.; Timotheou, S. Energy Management and Control of a Flywheel Storage System for Peak Shaving Applications. IEEE Trans. Smart Grid 2021, 12, 4195–4207. [Google Scholar] [CrossRef]
- Hopf, T.; Richter, M.; Schüßler, B.; Rinderknecht, S. Control Strategies for Highly Gyroscopic Outer Rotors with Diametral Enlargement in Active Magnetic Bearings. Actuators 2022, 11, 91. [Google Scholar] [CrossRef]
- Rupp, A.; Baier, H.; Mertiny, P.; Secanell, M. Analysis of a flywheel energy storage system for light rail transit. Energy 2016, 107, 625–638. [Google Scholar] [CrossRef]
- Venturini, S.; Cavallaro, S.P.; Vigliani, A. Windage loss characterisation for flywheel energy storage system: Model and experimental validation. Energy 2024, 307, 132641. [Google Scholar] [CrossRef]
- Wang, H.C.; Du, Z.M. Dynamic analysis for the energy storage flywheel system. J. Mech. Sci. Technol. 2016, 30, 4825–4831. [Google Scholar] [CrossRef]
- Liu, S.G.; Jiang, J. Technical Evolution of Advanced Flywheel Energy Storage System. In Proceedings of the 38th Chinese Control Conference, Guangzhou, China, 27–30 July 2019. [Google Scholar]
- Yuan, Y.; Sun, Y.; Xiang, Q. Design and Analysis of a Magnetic Bearings with Three Degrees of Freedom. Chin. J. Mech. Eng. 2019, 32, 3. [Google Scholar] [CrossRef]
- Amiryar, M.E.; Pullen, K.R. A Review of Flywheel Energy Storage System Technologies and Their Applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, G.; Qiu, Q.; Zhang, D.; Sun, X.; Wang, Y.; Liu, Y.; Feng, W.; Li, W.; Ai, L. Electromagnetic and Rotational Characteristics of a Superconducting Flywheel Energy Storage System Utilizing a Radial-Type High-Temperature Superconducting Bearing. J. Supercond. Nov. Magn. 2019, 32, 1605–1616. [Google Scholar] [CrossRef]
- Bonisoli, E.; Venturini, S.; Cavallaro, S.P. Nonlinear characterisation of a rotor on passive magnetic supports. Int. J. Mech. Control 2022, 23, 121–128. [Google Scholar]
- Tang, W.B.; Xiao, L.Y.; Ai, L.W.; Miao, S.; Wang, D.Y.; Han, R.L.; Fan, Z.M. A Novel Axial High-Temperature Superconducting Magnetic Bearing With Simple Structure and Large Suspension Force. IEEE Trans. Appl. Supercond. 2023, 33, 4601811. [Google Scholar] [CrossRef]
- Matsuda, K.; Kanemitsu, Y.; Kijimoto, S. Optimal number of stator poles for compact active radial magnetic bearings. IEEE Trans. Magn. 2023, 43, 3420–3427. [Google Scholar] [CrossRef]
- Li, Q.; Hu, Y.; Wu, H. Structure Design and Optimization of the Radial Magnetic Bearing. Actuators 2023, 12, 27. [Google Scholar] [CrossRef]
- Anantachaisilp, P.; Lin, Z. Fractional Order PID Control of Rotor Suspension by Active Magnetic Bearings. Actuators 2017, 6, 4. [Google Scholar] [CrossRef]
- Jeon, H.W.; Lee, C.W. Proportional-integral-derivative control of rigid rotor-active magnetic bearing system via eigenvalue assignment for decoupled translational and conical modes. J. Vib. Control 2015, 21, 2372–2393. [Google Scholar] [CrossRef]
- Li, B.L.; Li, Z.; Zhang, P.M.; Zhu, Z.D. Sliding mode active disturbance rejection decoupling control for active magnetic bearings. Electr. Mach. Control 2021, 25, 129–138. [Google Scholar]
- Khayyam, U.; He, B.X.; Hassan, S.U. Active Magnetic Bearing Design and Backstepping-Adaptive Control for High-Speed Rotors. In Proceedings of the 6th International Conference on Electrical Engineering, Control and Robotics (EECR)/3rd International Conference on Intelligent Control and Computing (ICICC), Xiamen, China, 10–12 January 2020. [Google Scholar]
- Ji, J.C.; Hansen, C.H.; Zander, A.C. Nonlinear dynamics of magnetic bearing systems. J. Intell. Mater. Syst. Struct. 2008, 19, 1471–1491. [Google Scholar] [CrossRef]
- Liu, J.N.; Ren, Z.Y.; Wu, S.W.; Tang, Y.L. Theoretical Vibration Analysis on 600 Wh Energy Storage Flywheel Rotor—Active Magnetic Bearing System. Int. J. Rotating Mach. 2013, 2013, 512674. [Google Scholar] [CrossRef]
- Xiang, B.; Wong, W.O. Vibration characteristics analysis of magnetically suspended rotor in flywheel energy storage system. J. Sound Vib. 2019, 444, 235–247. [Google Scholar] [CrossRef]
- Xiang, B.; Wen, T.; Liu, Z. Vibration analysis, measurement and balancing of flywheel rotor suspended by active magnetic bearing. Measurement 2022, 197, 111305. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Liu, J.N.; Han, Y.J.; Teng, W.Q. Modal Analysis on 600 Wh Energy Storage Flywheel Rotor System. Key Eng. Mater. 2014, 572, 521–524. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Huang, T.; Feng, J.J.; Zhou, Y.W. Kinematics analysis of vertical magnetic suspension energy storage flywheel rotor under transient rotational speed. In Proceedings of the 6th International Conference on Computer-Aided Design, Manufacturing, Modeling and Simulation (CDMMS), Busan, Republic of Korea, 14–15 April 2018. [Google Scholar]
- Dagnaes-Hansen, N.A.; Santos, I.F. Permanent magnet thrust bearings for flywheel energy storage system: Analytical, numerical, and experimental comparisons. Proc. IMechE Part C J. Mech. Eng. Sci. 2019, 233, 095440621984395. [Google Scholar] [CrossRef]
- Tang, J.Q.; Xiang, B.A.; Zhang, Y.B. Dynamic characteristics of the rotor in a magnetically suspended control moment gyroscope with active magnetic bearing and passive magnetic bearing. ISA Trans. 2014, 53, 1357–1365. [Google Scholar] [CrossRef]
- Ji, J.C.; Hansen, C.H. Non-linear oscillations of a rotor in active magnetic bearings. J. Sound Vib. 2011, 240, 599–612. [Google Scholar] [CrossRef]
- Kandil, A.; Sayed, M.; Saeed, N.A. On the nonlinear dynamics of constant stiffness coefficiennts 16-pole rotor active magnetic bearings system. Eur. J. Mech. A-Solids 2020, 84, 104051. [Google Scholar] [CrossRef]
- Li, X.J.; Palazzolo, A.; Wang, Z.Y. A Combination 5-DOF Active Magnetic Bearing For Energy Storage Flywheel. IEEE Trans. Transp. Electr. 2021, 7, 2344–2355. [Google Scholar] [CrossRef]
- Gao, H.; Yu, X.H.; Cao, J.N. Linear electromagnetic force and beat phenomenon for maglev flywheel battery. Int. J. Appl. Electromagn. Mech. 2019, 60, 409–421. [Google Scholar] [CrossRef]
- Li, X.; An, J.; Erd, N.; Dietz, D.; Gemeinder, Y.; Binder, A. Design and Manufacture of a High-speed Rotor in a Flywheel Demonstrator. In Proceedings of the 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020. [Google Scholar]
- Li, X.; Dietz, D.; An, J.; Erd, N.; Gemeinder, Y.; Binder, A. Manufacture and Testing of a Magnetically Suspended 0.5-kWh Flywheel Energy Storage System. IEEE Trans. Ind. Appl. 2022, 58, 6152–6162. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Mass (m) | 56 kg |
| Moment of inertia (Jp) | 0.93 kg·m2 |
| Equatorial moment of inertia (Jd) | 1.14 kg·m2 |
| Distance from the upper radial magnetic bearing to the mass-center of the flywheel rotor (l1) | 0.282 m |
| Distance from the lower radial magnetic bearing to the mass-center of the flywheel rotor (l2) | 0.273 m |
| Type | Parameter | Value |
|---|---|---|
| Structure and physical parameters | Cross-sectional area of magnetic pole (S) | 784 mm2 |
| The turns for a pair of magnetic poles (N) | 100 | |
| Unilateral standard air gap (x0) | 0.3 mm | |
| Control parameters | Bias current (I0) | 2.5 A |
| Coefficient of power amplifier (Ka) | 0.5 A/V | |
| Coefficient of displacement sensor (Ks) | 10,000 V/m | |
| Time constant of power amplifier (Ta) | 1 × 10−4 | |
| Time constant of displacement sensor (Ts) | 1 × 10−4 | |
| The time constant of the derivative element (Td) | 1 × 10−4 | |
| Proportional coefficient (Kp) | 2.05 | |
| Integral coefficient (Ki) | 5 × 10−5 | |
| Differential coefficient (Kd) | 5 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, T.; Ren, Z. The Influence of Axial-Bearing Position of Active Magnetic Suspension Flywheel Energy Storage System on Vibration Characteristics of Flywheel Rotor. Actuators 2025, 14, 290. https://doi.org/10.3390/act14060290
Wang L, Li T, Ren Z. The Influence of Axial-Bearing Position of Active Magnetic Suspension Flywheel Energy Storage System on Vibration Characteristics of Flywheel Rotor. Actuators. 2025; 14(6):290. https://doi.org/10.3390/act14060290
Chicago/Turabian StyleWang, Lei, Tielei Li, and Zhengyi Ren. 2025. "The Influence of Axial-Bearing Position of Active Magnetic Suspension Flywheel Energy Storage System on Vibration Characteristics of Flywheel Rotor" Actuators 14, no. 6: 290. https://doi.org/10.3390/act14060290
APA StyleWang, L., Li, T., & Ren, Z. (2025). The Influence of Axial-Bearing Position of Active Magnetic Suspension Flywheel Energy Storage System on Vibration Characteristics of Flywheel Rotor. Actuators, 14(6), 290. https://doi.org/10.3390/act14060290





