Synchronised Control of Multiple Actuators of Wind Turbines
Abstract
1. Introduction
2. Electric Drives for the Actuation of Wind Turbines
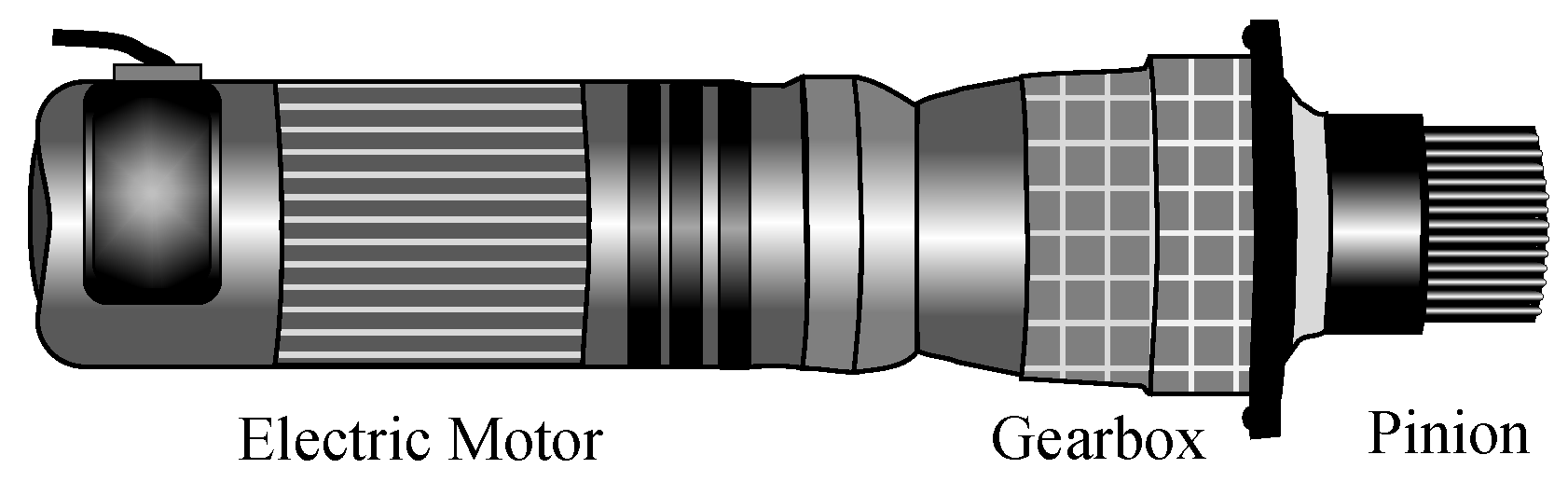
2.1. Introductory Description
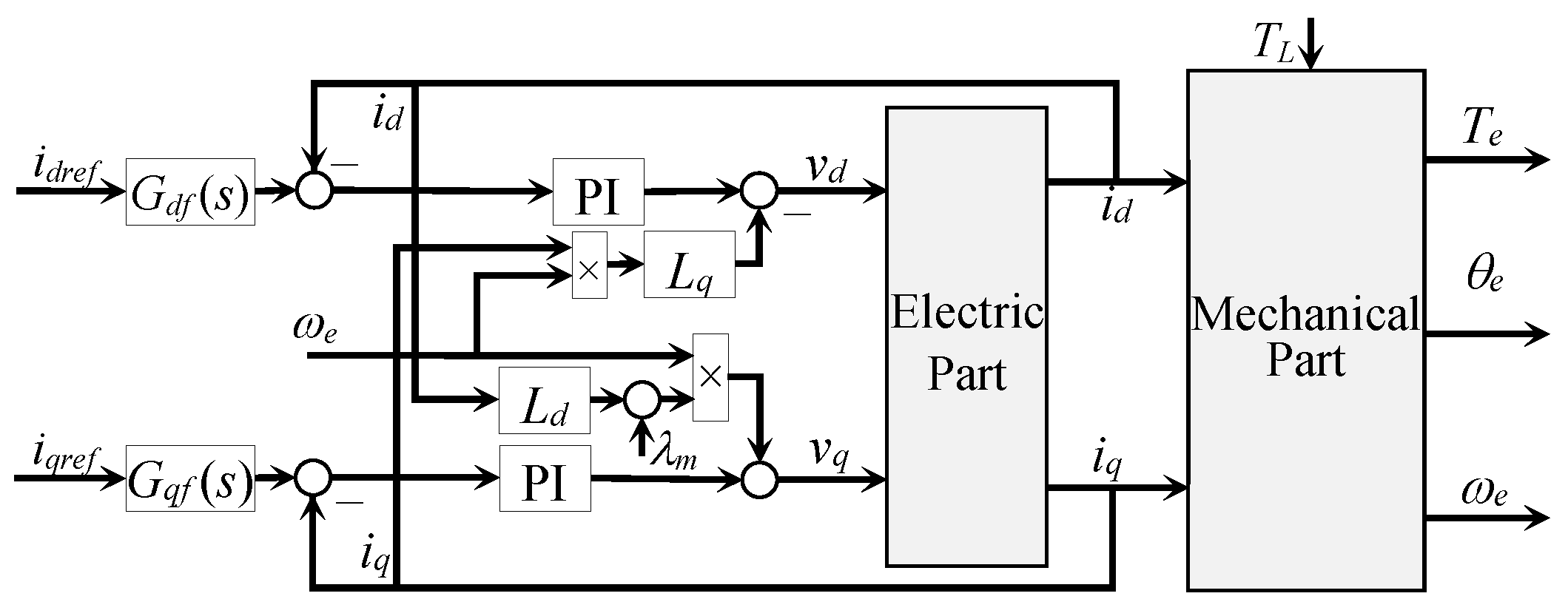
2.2. Modelling of Permanent Magnet Synchronous Motors
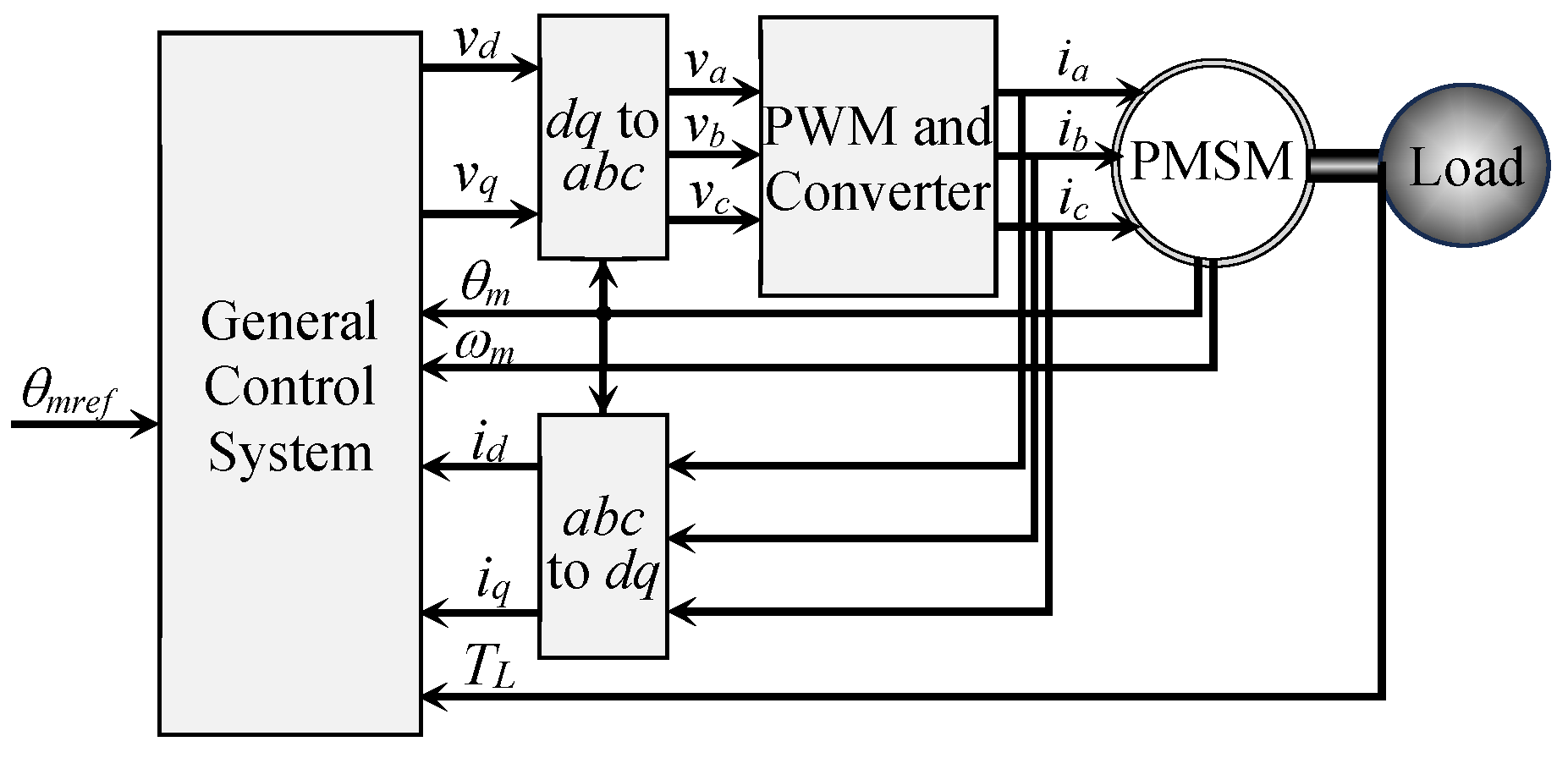
2.3. Control of Permanent Magnet Synchronous Motors
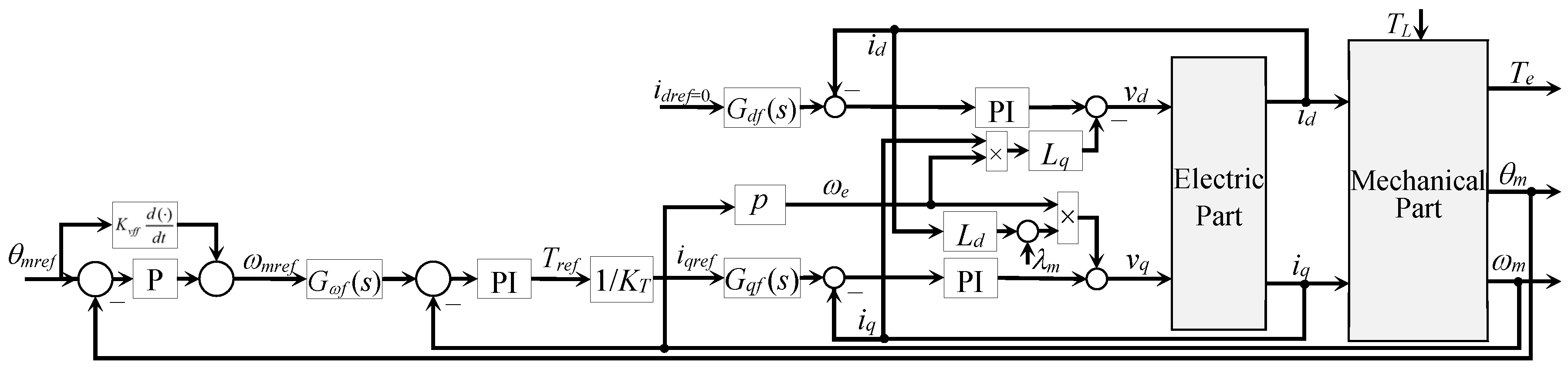
2.3.1. General Control Configuration
2.3.2. Current Control Loops
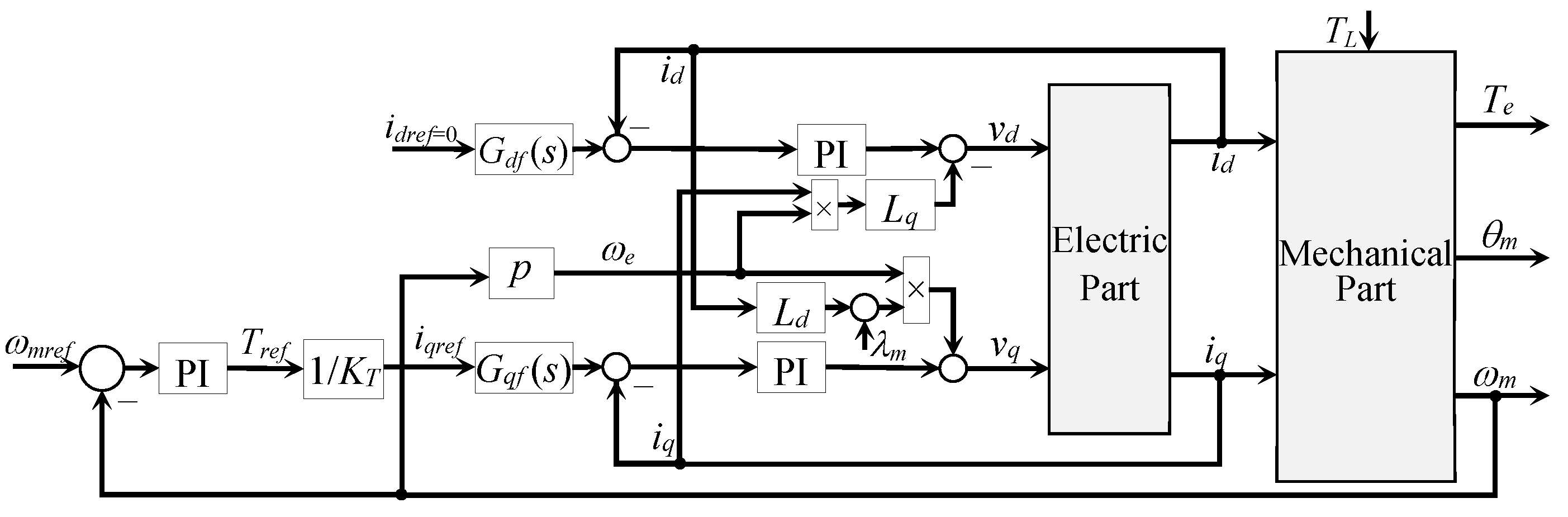
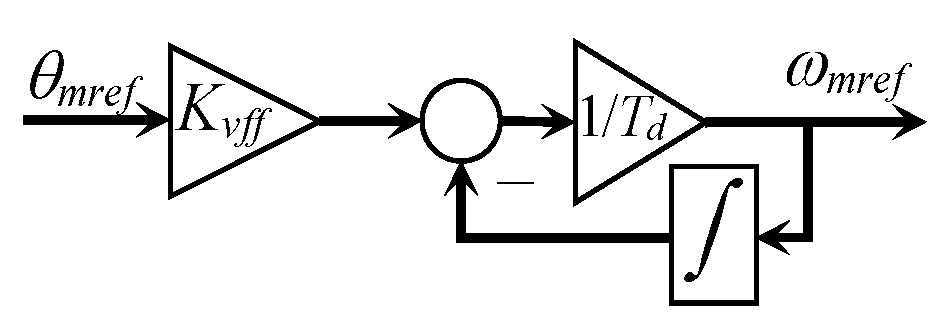
2.3.3. In-Between Speed Control Loop
2.3.4. Position Control Loop
2.3.5. Example of a PMSM Position Control
3. Synchronising Control of Several Systems
3.1. Problem Formulation
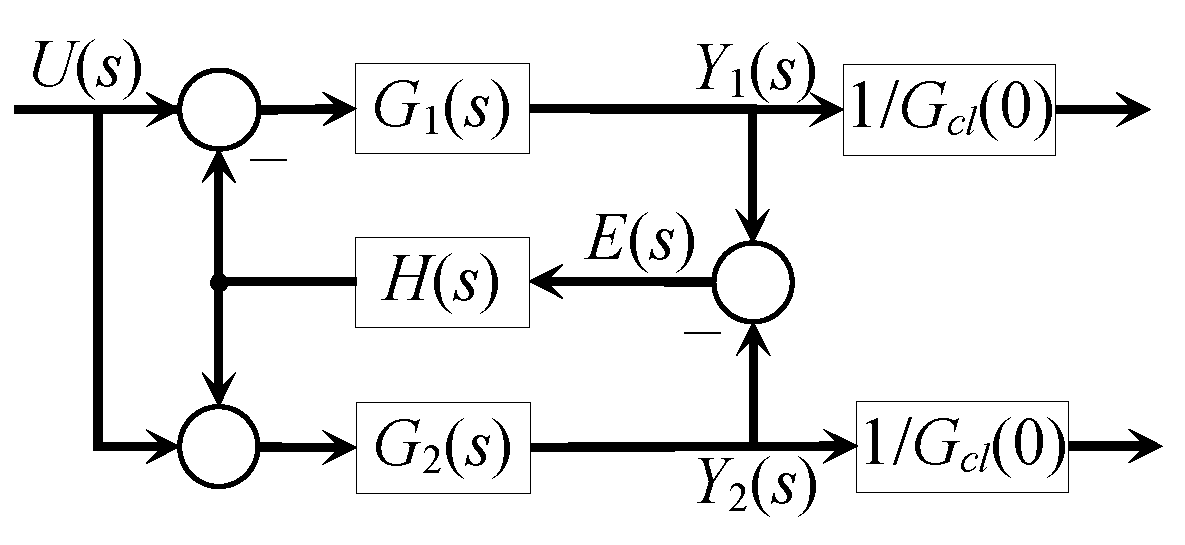
3.2. Two-Systems Case
3.3. Three-Systems Case
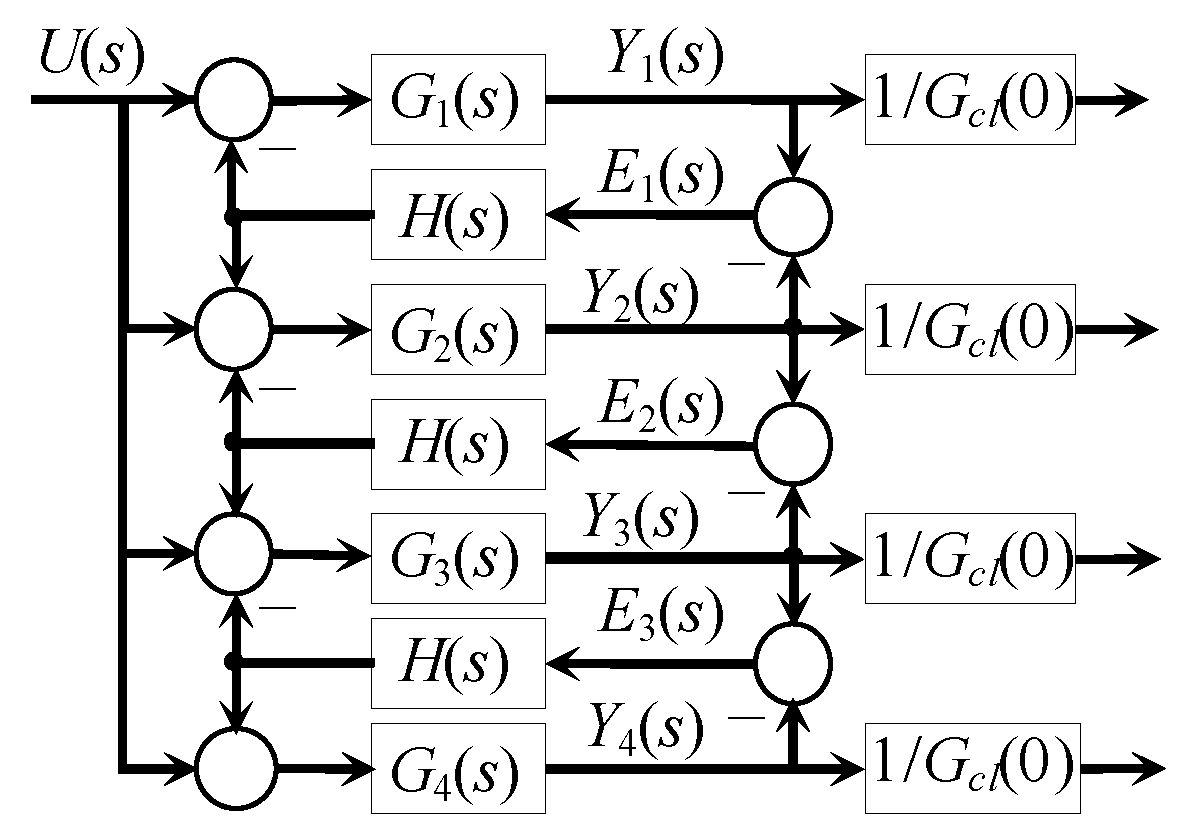
3.4. Example for the Synchronisation of Four Different Systems
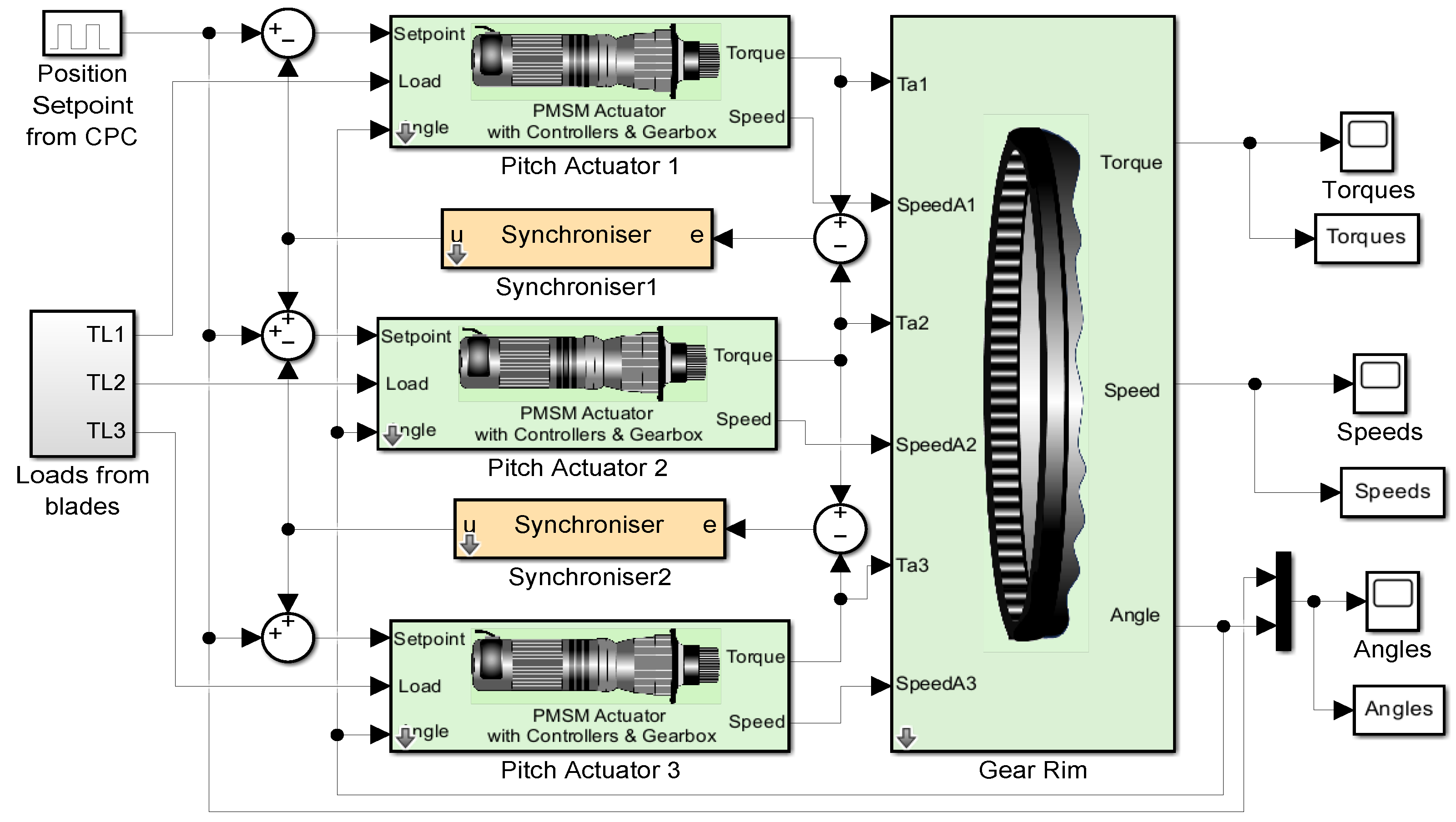
4. Numerical Studies for Pitch Actuators in Wind Turbines
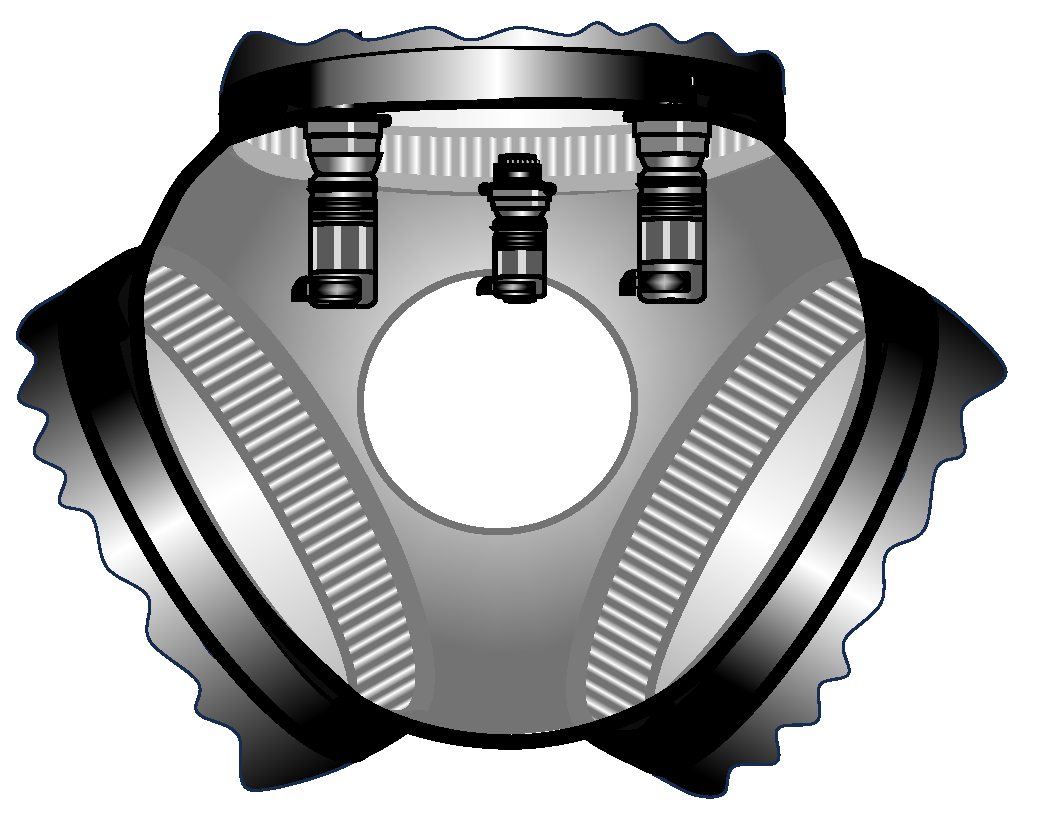
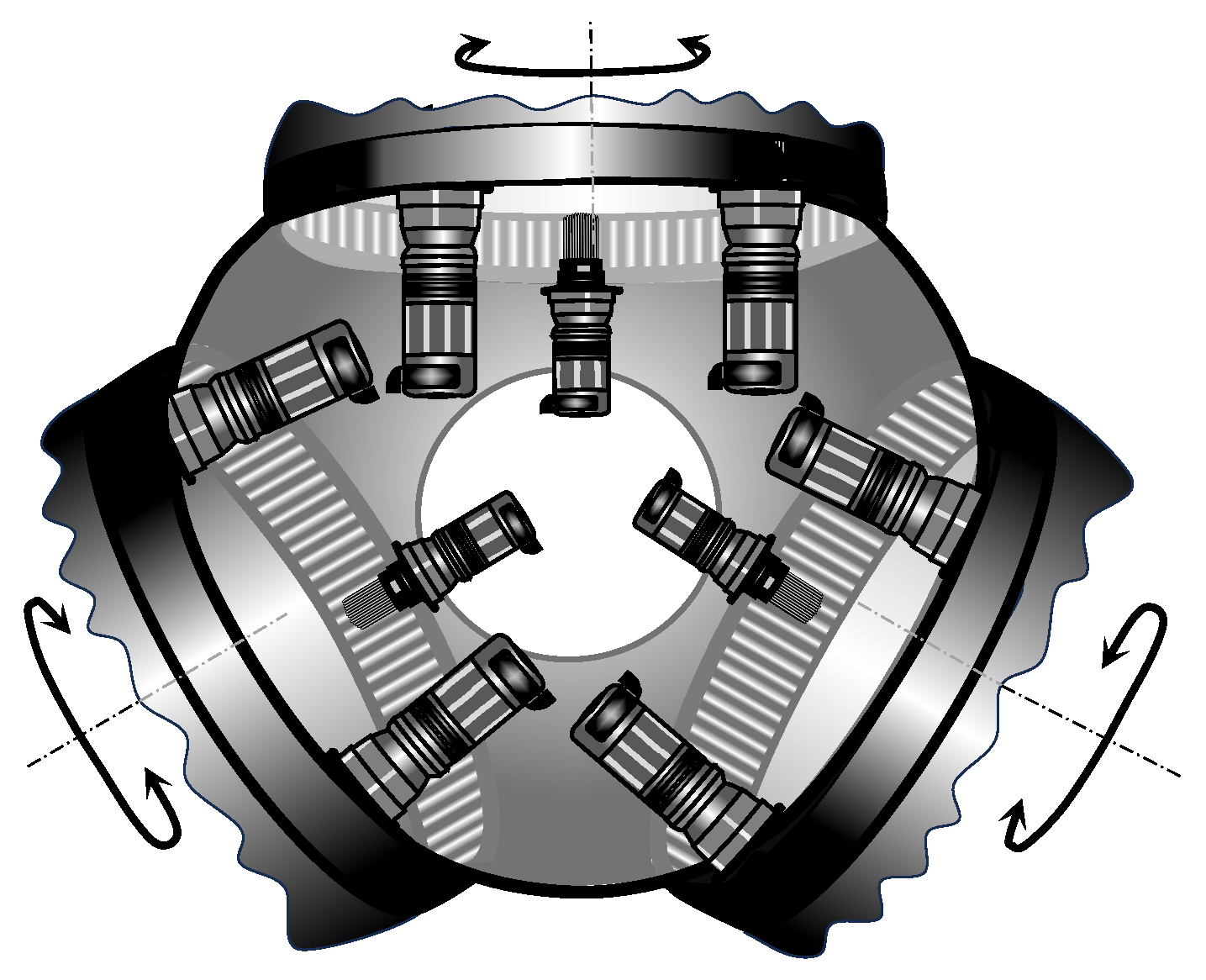
4.1. Pitch Actuator Design and Model Building
4.2. Pitch Actuator Control System Design
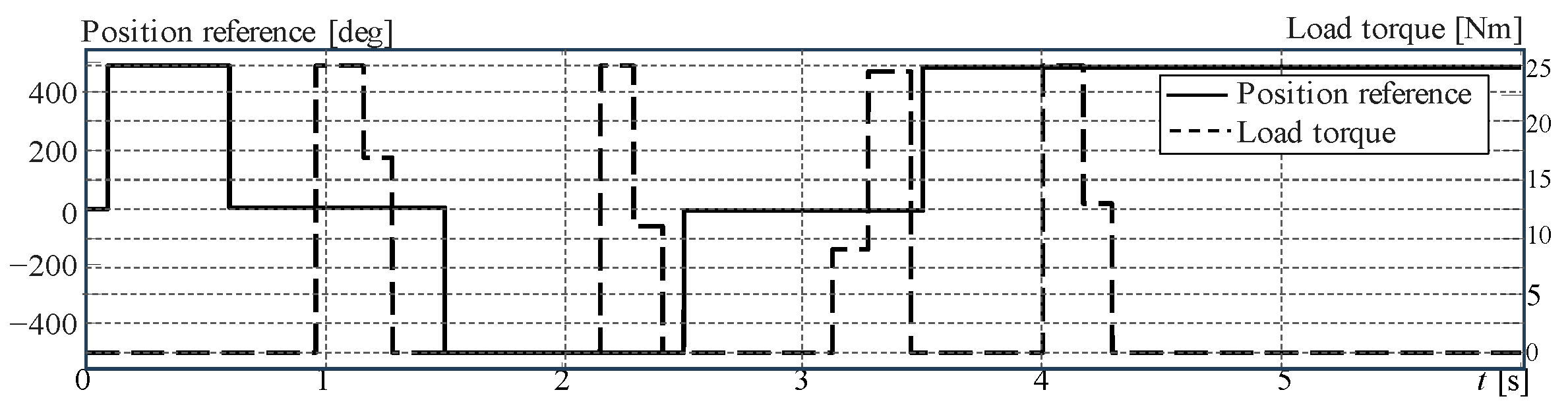
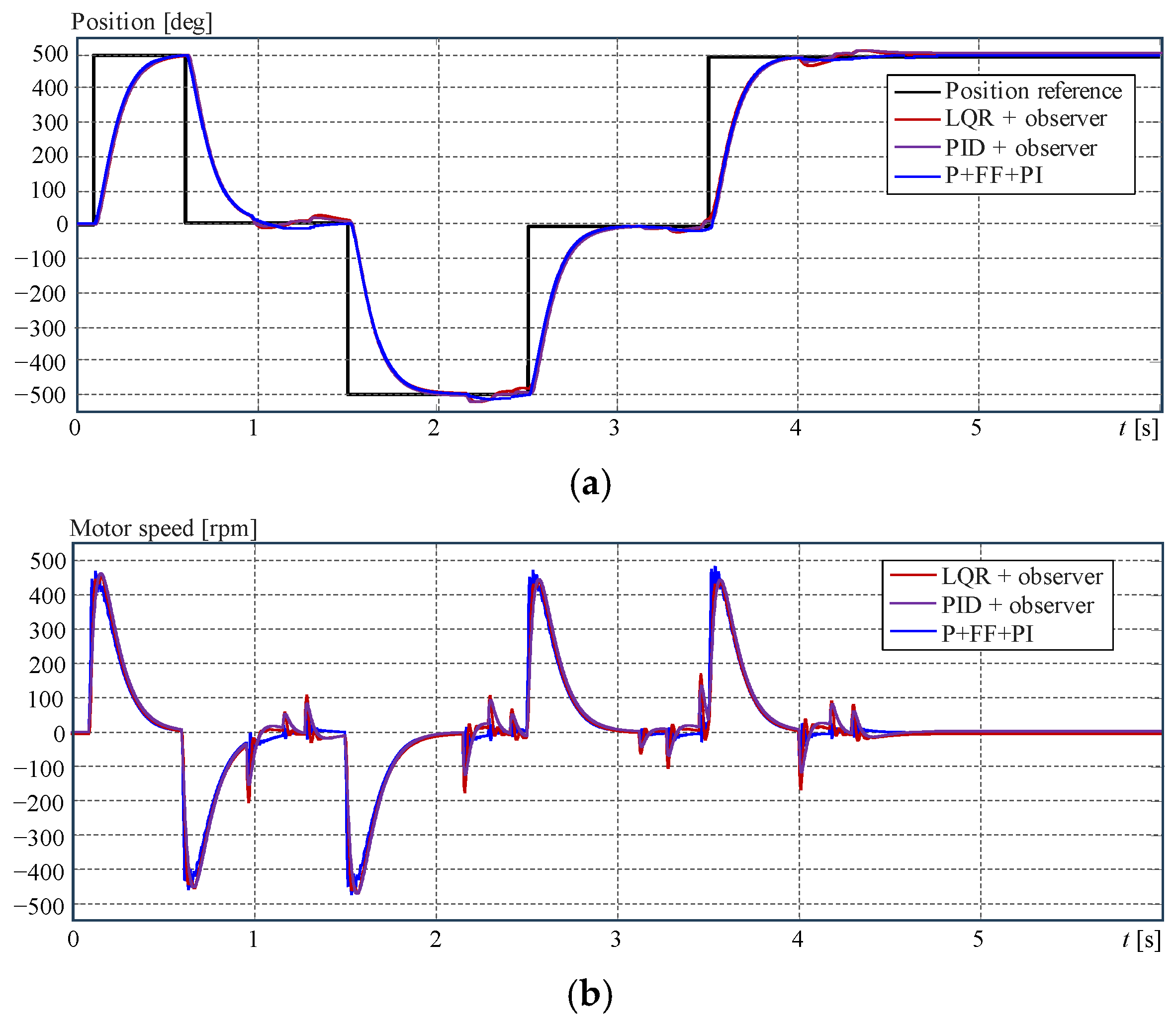
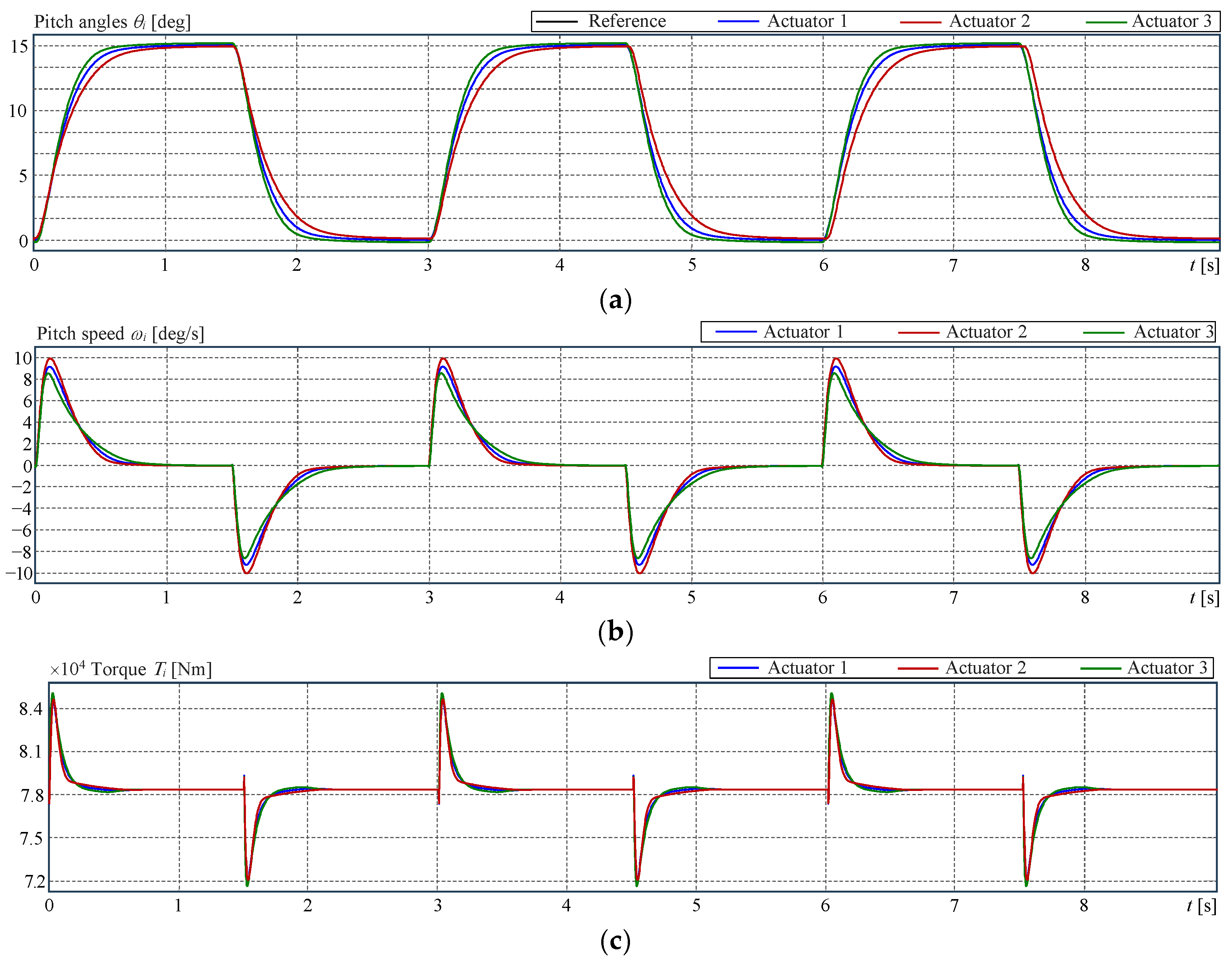
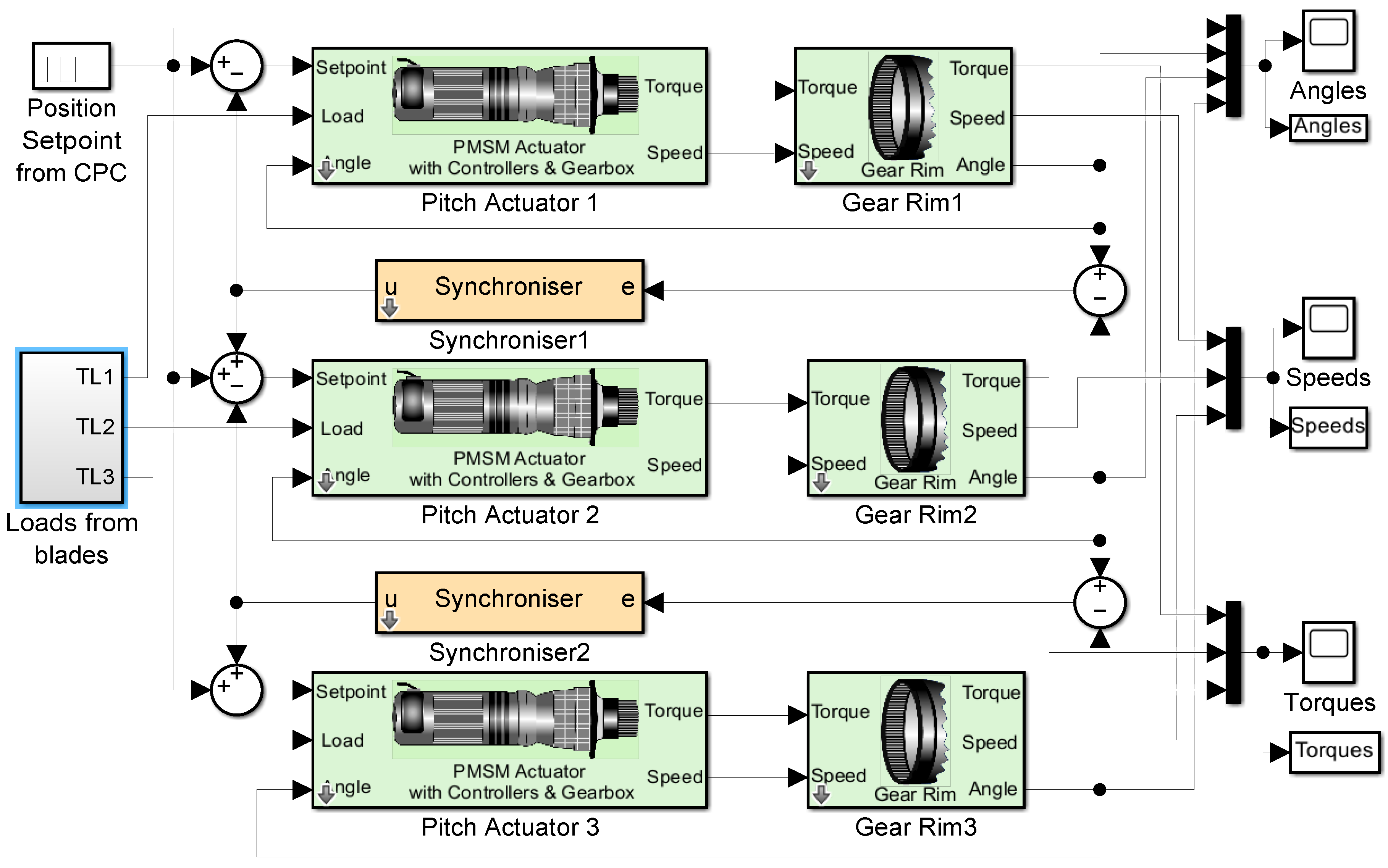
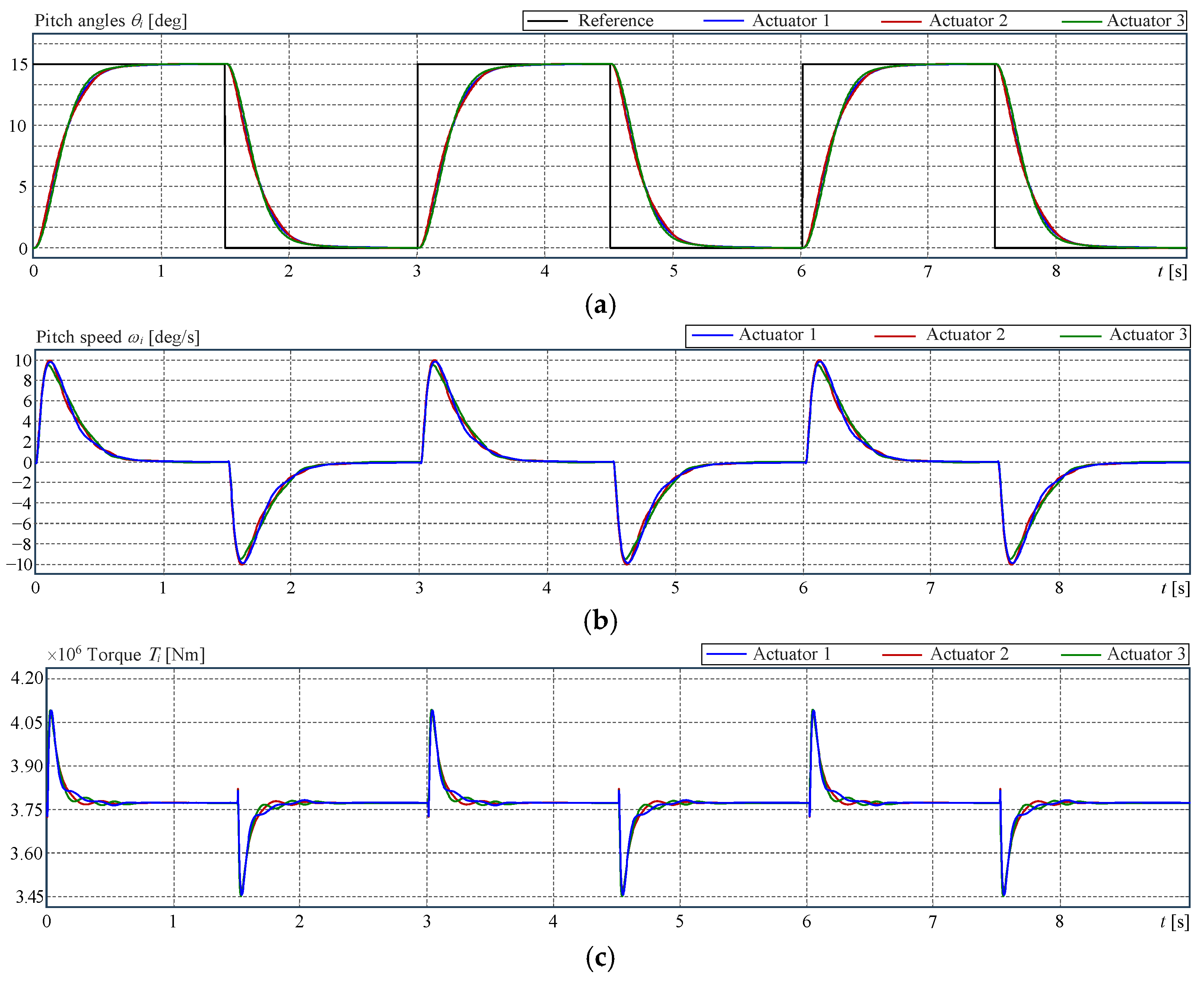
4.3. Example 1: Synchronised Pitch Actuator Control on the Same Blade
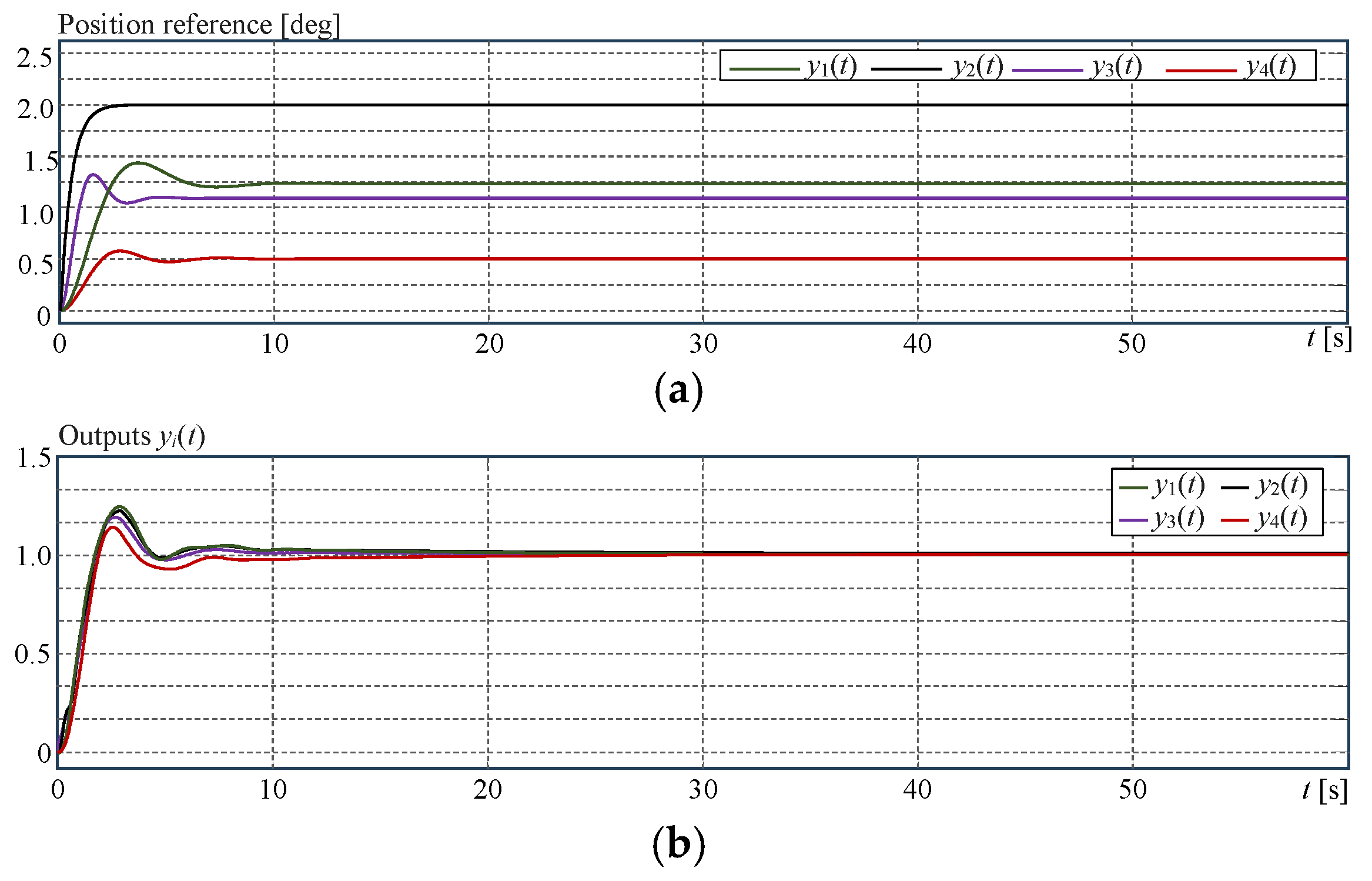
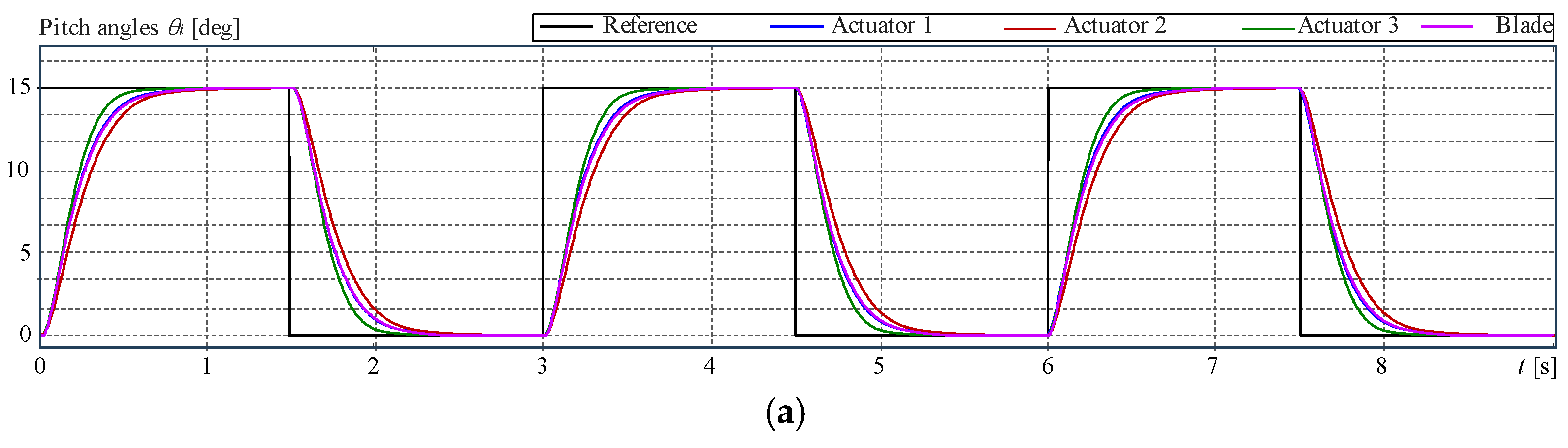
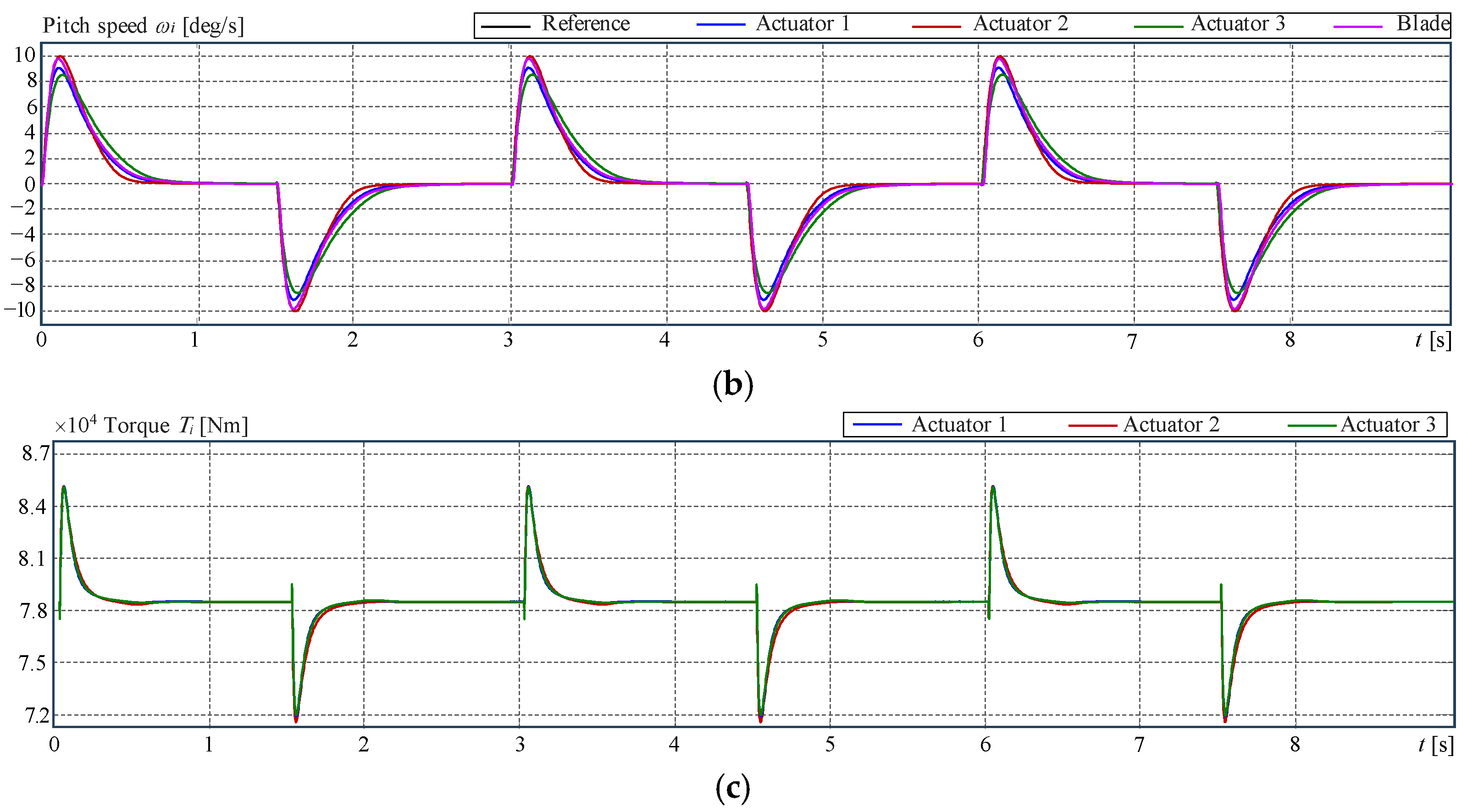
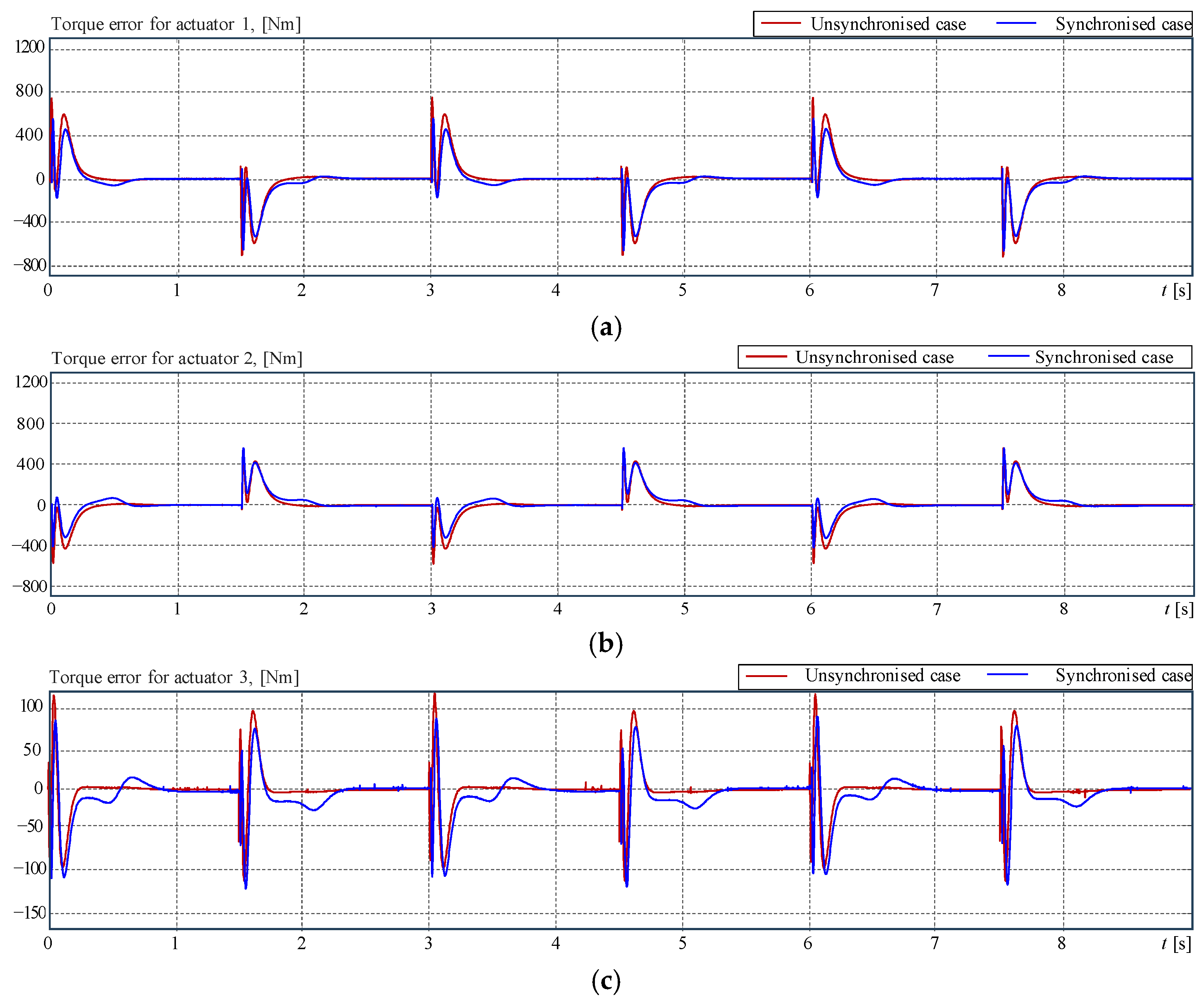
4.4. Example 2: Pitch Actuator Control on Three Different Blades
5. Quantitative Evaluation of the Results
5.1. Context Description for the Assessment of Example 1
5.2. Context Description for the Assessment of Example 2
5.3. Concluding Remarks on the Quantitative Study
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations | |
| CPC | Collective Pitch Control |
| DC | Direct Current |
| LQ, LQR | Linear Quadratic, Linear Quadratic Regulator |
| MOSFET | Metal Oxide Semiconductor Field Effect Transistor |
| PI, PID | Proportional Integral, Proportional Integral Derivative |
| PMSM | Permanent Magnet Synchronous Motor |
| PWM | Pulse-Wide Modulation |
| SVM | Space Vector Modulation |
| Nomenclature | |
| Parameters | |
| ai, bi | Coefficients of denominator and numerator polynomials |
| Bm | Torsional viscous friction of motor shaft, Nm s/rad |
| Jm | Second moment of inertia of the motor, kg m2 |
| Km | Stiffness coefficient of the motor shaft |
| KT | Proportional constant in the equation of electromagnetic torque, Nm/A |
| Kpθ, Kp1, Kp2, Kp3 | Gains of the nonlinear proportional controller |
| Kpd, Kpq, Kpt, Kps | Proportional gains of PI controllers |
| Kid, Kiq, Kit, Kis | Integral gains of PI controllers |
| Kvff | Proportional gain of the derivative feedforward controller |
| Ld Lq | Self-inductances, H |
| n1, n2, n3 | System types of different transfer functions |
| nx, nm | Gearbox and gear rim ratios, -- |
| p | Number of pole pairs, -- |
| rp | Pinion radius, m |
| rb | Blade radius, m |
| Rs | Stator resistance, Ohm |
| Td | Time constant of the derivative feedforward controller |
| Teref | Reference for the electromagnetic torque, Nm |
| TLmax | Maximum load torque, Nm |
| λf | Flux linkage between the rotor and the stator |
| ζd, ζq | Damping ratios for the d- and q-axis |
| τd, τq | Time constants for the d- and q-axis, s |
| ωnd, ωnq | Natural frequencies for the d- and q-axis, rad/s |
| Variables | |
| id, iq | d and q currents, in the dq-reference frame, A |
| idref, iqref | d and q reference currents, in the dq-reference frame, A |
| s | Laplace variable |
| t | Time |
| Te | Electromagnetic torque, Nm |
| TL | Load torque, Nm |
| u | Control variable |
| y | Output variable |
| va, vb, vc | Three-phase input voltages, V |
| vd, vq | d and q input voltages, in the dq-reference frame, V |
| θe, θm, | Electric and mechanical angles, rad |
| ωe, ωm | Electric and mechanical speeds, rad/s |
| θmref, ωmref | Angle and speed references, rad, rad/s |
| Functions | |
| A(s), A1(s), A2(s), A3(s) | Denominators of transfer functions |
| B(s), B1(s), B2(s), B3(s) | Numerators of transfer functions |
| E(s), E1(s), E2(s), E3(s) | Laplace transforms of errors |
| Gs(s), GT(s), G1(s), G2(s), G3(s) | Transfer functions |
| Gdf(s), Gdq(s) | Transfer functions of filters in the d- and q-axis |
| Gder(s) | Transfer function of the derivative feedforward controller |
| H(s) | Transfer function of the synchroniser |
| Q(s), P(s) | Numerator and denominator of controller or synchroniser |
| Id(s), Iq(s), Idref(s), Iqref(s) | Laplace transformed currents and current references |
| U(s), Y(s) | Laplace transformed input and output |
| Ωm(s), Θm(s), Ωmref(s), Θmref(s) | Laplace transformation of ωm, θm, ωmref, and θmref |
References
- Bonfiglioli. Wind Solutions: Product Range. Product Description; Bonfiglioli Riduttori S.p.A.: Bologna, Italy, 2020. [Google Scholar]
- Gambier, A. Pitch control of three bladed large wind energy converters—A Review. Energies 2021, 14, 8083. [Google Scholar] [CrossRef]
- Hu, S.; Ren, X.; Zhao, W. Synchronous control of multi-motor driving servo systems. In Lecture Notes in Electrical Engineering 459; Jia, Y., Du, J., Zhang, W., Eds.; Springer: Singapore, 2017; pp. 611–620. [Google Scholar] [CrossRef]
- Li, M.; Meng, X. Analysis and design of system for multi-motor synchronous control. In Advances in Computer Science, Environment, Ecoinformatics, and Education 217; Lin, S., Huang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 268–273. [Google Scholar] [CrossRef]
- Niu, F.; Sun, K.; Huang, S.; Hu, Y.; Liang, D. A review on multimotor synchronous control methods. IEEE Trans. Transp. Electrif. 2023, 9, 22–33. [Google Scholar] [CrossRef]
- Unbehauen, H.; Vakilzadeh, I. Automatic error elimination between outputs of n identical simple integral plants with different initial conditions. Int. J. Control 1988, 47, 1101–1116. [Google Scholar] [CrossRef]
- Unbehauen, H.; Vakilzadeh, I. Feedforward technique in rendezvous problems for n identical simple-integral plants. Int. J. Syst. Sci. 1992, 23, 2091–2111. [Google Scholar] [CrossRef]
- Vakilzadeh, I.; Unbehauen, H. Tracking performance of ‘n’ integral-plus-time constant plants with ‘one’ controller. Kybernetika 1993, 29, 351–378. [Google Scholar]
- Unbehauen, H.; Vakilzadeh, I. Centralized control of n identical plants. J. Dyn. Syst. Meas. Control 1993, 115, 325–333. [Google Scholar] [CrossRef]
- Unbehauen, H.; Vakilzadeh, I. Synchronization of n non-identical simple-integral plants. Int. J. Control 1989, 50, 543–574. [Google Scholar] [CrossRef]
- Vakilzadeh, I.; Mansour, M. Synchronization of ‘n’ integral-plus-times constant plants with non-identical gain and time constants. Control Theory Adv. Technol. 1989, 5, 569–585. [Google Scholar] [CrossRef]
- Vakilzadeh, I.; Mansour, M. Synchronization of ‘n” integral-plus-double time constant plants with non-identical gain and time constants. J. FrankIm Inst. 1990, 327, 579–593. [Google Scholar] [CrossRef]
- Unbehauen, H.; Vakilzadeh, I. Synchronization of ‘n’ decentralized non-identical plants with integral behavior and two complex poles. Control Theory Adv. Technol. 1994, 10, 385–402. [Google Scholar]
- Vakilzadeh, I.; Unbehauen, H. Four rendezvous problems for n non-identical simple-integral plants. Int. J. Syst. Sci. 1993, 24, 1455–1472. [Google Scholar] [CrossRef]
- Koren, Y. Cross-coupled biaxial computer control for manufacturing systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–271. [Google Scholar] [CrossRef]
- Zhao, D.; Li, C.; Ren, J. Speed synchronization of multiple induction motors with adjacent cross coupling control. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC), Shanghai, China, 15–18 December 2009; pp. 6805–6810. [Google Scholar] [CrossRef]
- Gambier, A. Control of Large Wind Energy Systems; Springer Nature: Basel, Switzerland, 2022. [Google Scholar]
- Bianchi, F.D.; de Battista, H.; Mantz, R.J. Wind Turbine Control Systems; Springer: London, UK, 2007. [Google Scholar]
- Geng, H.; Yang, G. Output power control for variable-speed variable-pitch wind generation systems. IEEE Trans. Energy Convers. 2010, 25, 494–503. [Google Scholar] [CrossRef]
- Fortmann, J. Modeling of Wind Turbines with Doubly Fed Generator System; Springer Vieweg: Wiesbaden, Germany, 2014. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans. Control Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- Esbensen, T.; Sloth, C. Fault Diagnosis and Fault-Tolerant Control of Wind Turbines; Aalborg University: Aalborg, Denmark, 2009. [Google Scholar]
- Sloth, C.; Esbensen, T.; Stoustrup, J. Active and passive fault-tolerant LPV control of wind turbines. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4640–4646. [Google Scholar] [CrossRef]
- Krishnan, R. Electric Motor Drives: Modeling, Analysis & Control; Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Ong, C.-M. Dynamic Simulation of Electric Machinery; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Park, R.H. Two reaction theory of synchronous machines. AIEE Trans. 1929, 48, 716–730. [Google Scholar] [CrossRef]
- Mohan, N. Advanced Electric Drives: Analysis, Control, and Modeling Using MATLAB/Simulink; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wang, L.; Chai, S.; Yoo, D.; Gan, L.; Ng, K. PID and Predictive Control of Electrical Drives and Power Converters Using MATLAB®/Simulink®; John Wiley & Sons: Singapore, 2015. [Google Scholar]
- Wach, P. Dynamics and Control of Electrical Drives; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Vukosavić, S.N. Digital Control of Electrical Drives; Springer Science + Business Media, LLC.: New York, NY, USA, 2007. [Google Scholar]
- Melkebeek, J.A. Electrical Machines and Drives: Fundamentals and Advanced Modelling; Springer Nature: Cham, Switzerland, 2018. [Google Scholar]
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Carpiuc, S.; Villegas, C. Real–time position control in permanent magnet synchronous machine drives. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications, Riga, Latvia, 17–21 September 2018; pp. P.1–P.8. [Google Scholar]
- Leonhard, W. Control of Electrical Drives, 3rd ed.; Springer: Heidelberg, Germany, 2001. [Google Scholar]
- Saafan, M.M.; Haikal, A.Y.; Saraya, S.F.; Areed, F.F.G. Artificial neural network control of permanent magnet synchronous motors. Int. J. Comput. Appl. 2012, 37, 9–18. [Google Scholar] [CrossRef]
- Wang, C.; Liu, B.; Fan, X.; Yang, P. Rotor position angle control of permanent magnet synchronous motor based on slidingmode extended state observer. Syst. Sci. Control Eng. Open Access J. 2022, 10, 757–766. [Google Scholar] [CrossRef]
- Carpiuc, S. Model–based control and real–time simulation of a four–phase PMSM traction drive. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 2378–2383. [Google Scholar] [CrossRef]
- Kung, Y.-S.; Huang, P.-G. High performance position controller for PMSM drives based on TMS320F2812 DSP. In Proceedings of the IEEE International Conference on Control Applications, Taipei, Taiwan, 2–4 September 2004; pp. 290–295. [Google Scholar] [CrossRef]
- Ko, J.-S.; Han, B.-M. Precision position control of PMSM using neural network disturbance observer and parameter compensator. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 1313–1319. [Google Scholar] [CrossRef]
- Aguilar-Mejia, O.; Popocatl, H.M.; Garcia-Morales, J.M.; Castillo-Ibarra, C.O.; Valderrabano-Gonzalez, A. An efficient neurocontroller position method for PMSM drive system. In Proceedings of the 2022 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 9–11 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Q.; Chang, X.-H. Position IP control of a permanent magnet synchronous motor based on fuzzy neural network. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1081–1086. [Google Scholar] [CrossRef]
- Fertik, H.A.; Ross, C.W. Direct digital control algorithm with anti-windup feature. ISA Trans. 1967, 6, 317–328. [Google Scholar]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Rundqwist, L. Anti-Reset Windup for PID Controllers. Ph.D. Thesis, Lund Institute of Technology, Lund, Sweden, 1991. [Google Scholar]
- Mohan, N. Power Electronics: A First Course; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bose, B.K. Power Electronics and Motor Drives: Advances and Trends; Elsevier Inc.: Burlington, VT, USA, 2006. [Google Scholar]
- Pyrhönen, J.; Hrabovcová, V.; Semken, R.S. Electrical Machine Drives Control: An Introduction; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar]
- Johnson, M.A.; Moradi, M.H. PID Control—New Identification and Design Methods; Springer: London, UK, 2005. [Google Scholar]
- Gürocak, H. Industrial Motion Control: Motor Selection, Drivers, Controller Tuning, Applications; John Wiley & Sons Ltd.: Chichester, UK, 2016. [Google Scholar]
- Åström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Gambier, A.; Nazaruddin, Y. Collective pitch control with active tower damping of a wind turbine by using a nonlinear PID approach. IFAC–Pap. 2018, 51, 238–243. [Google Scholar] [CrossRef]
- Shahruz, S.M.; Schwartz, A.L. Design of optimal nonlinear PI compensators. In Proceedings of the IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 3564–3565. [Google Scholar] [CrossRef]
- Xu, Y.; Hollerbach, J.M.; Ma, D. A nonlinear PD controller for force and contact transient control. IEEE Control Syst. Mag. 1995, 15, 15–21. [Google Scholar] [CrossRef]
- Gambier, A.; Jipp, M. Multi-objective optimal control: An introduction. In Proceedings of the Asian Control Conference, Kaohsiung, Taiwan, 15–18 May 2011; pp. 1084–1089. [Google Scholar]
- Ashuri, T.; Zaaijer, M.B.; Martins, J.R.R.A.; Zhang, J. Multidisciplinary design optimization of large wind turbines—Technical, economic, and design challenges. Energy Convers. Manag. 2016, 123, 56–70. [Google Scholar] [CrossRef]
- Gambier, A. Multiobjective optimal control of wind turbines: A survey on methods and recommendations for the implementation. Energies 2022, 15, 567. [Google Scholar] [CrossRef]

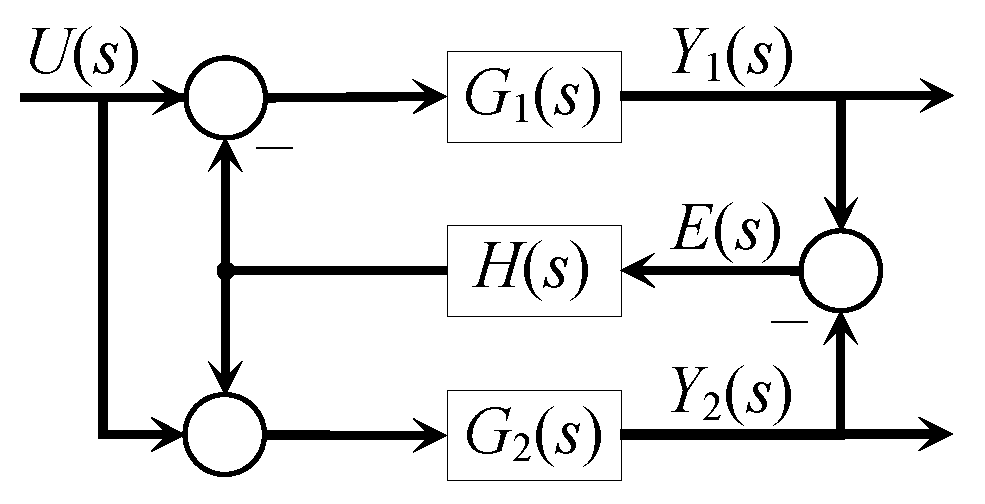


| Parameters | Actuator 1 | Actuator 2 | Actuator 3 |
|---|---|---|---|
| Ld, Lq | 3.4740 × 10−6 H | 3.3003 × 10−6 H | 5.2110 × 10−6 H |
| Rs | 0.2176 Ω | 0.2067 Ω | 0.3263 Ω |
| λf | 0.4459 Wb | 0.4301 Wb | 0.4816 Wb |
| Bm | 0.2969 Nm s/rad | 0.3821 Nm s/rad | 0.1528 Nm s/rad |
| Jm | 1.6134 kg m2 | 1.5327 kg m2 | 1.6457 kg m2 |
| Steady-state speed | 3216.48 rpm | 3486.5 rpm | 3286.98 rpm |
| Parameters | Actuator 1 | Actuator 2 | Actuator 3 |
|---|---|---|---|
| Current controllers | Kpd = 4.4173 | Kpd = 3.9551 | Kpd = 4.3940 |
| Kid = 8.6107 | Kid = 9.1312 | Kid = 7.9113 | |
| Kpq = 0.0143 | Kpq = 0.0099 | Kpq = 0.0211 | |
| Kiq = 0.7001 | Kiq = 0.6906 | Kiq = 0.6798 | |
| Speed controllers | Kpt = 0.9383 | Kpt = 0.9364 | Kpt = 0.8508 |
| Kit = 0.1245 | Kit = 0.1241 | Kit = 0.1214 | |
| Position controllers | Kp1 = 0.0604 | Kp1 = 0.0043 | Kp1 = 0.0421 |
| Kp2 = 4.5104 | Kp2 = 5.0911 | Kp2 = 3.9110 | |
| Kp3 = 2.0000 | Kp3 = 2.0000 | Kp3 = 2.0000 |
| Example 1 (Torque Synchronisation) | Example 2 (Angle Synchronisation) | |||||
|---|---|---|---|---|---|---|
| Actuator 1 | Actuator 2 | Actuator 3 | Actuator 1 | Actuator 2 | Actuator 3 | |
| Unsynchronised control | 1.485 | 1.362 | 1.365 | 1.003 | 6.328 | 7.151 |
| Synchronised control | 1.419 | 1.137 | 1.244 | 0.940 | 0.590 | 1.622 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gambier, A. Synchronised Control of Multiple Actuators of Wind Turbines. Actuators 2025, 14, 264. https://doi.org/10.3390/act14060264
Gambier A. Synchronised Control of Multiple Actuators of Wind Turbines. Actuators. 2025; 14(6):264. https://doi.org/10.3390/act14060264
Chicago/Turabian StyleGambier, Adrian. 2025. "Synchronised Control of Multiple Actuators of Wind Turbines" Actuators 14, no. 6: 264. https://doi.org/10.3390/act14060264
APA StyleGambier, A. (2025). Synchronised Control of Multiple Actuators of Wind Turbines. Actuators, 14(6), 264. https://doi.org/10.3390/act14060264






