Improved Non-Singular Fast Terminal Sliding Mode Control with Hysteresis Compensation for Piezo-Driven Fast Steering Mirrors
Abstract
1. Introduction
- Hysteresis compensation: A feedforward compensation strategy based on the P-I inverse hysteresis model is proposed to mitigate nonlinear hysteresis effects, enhancing control accuracy and system performance.
- Disturbance and uncertainty estimation: The integration of an ESO allows for the real-time estimation of system uncertainties and external disturbances, improving robustness and adaptability under varying operating conditions.
- Improved control strategy: An improved non-singular fast terminal sliding mode control strategy is proposed, which incorporates a terminal sliding mode surface and an improved adaptive reaching law. This design ensures finite-time convergence while enhancing dynamic performance and significantly improving disturbance rejection capabilities.
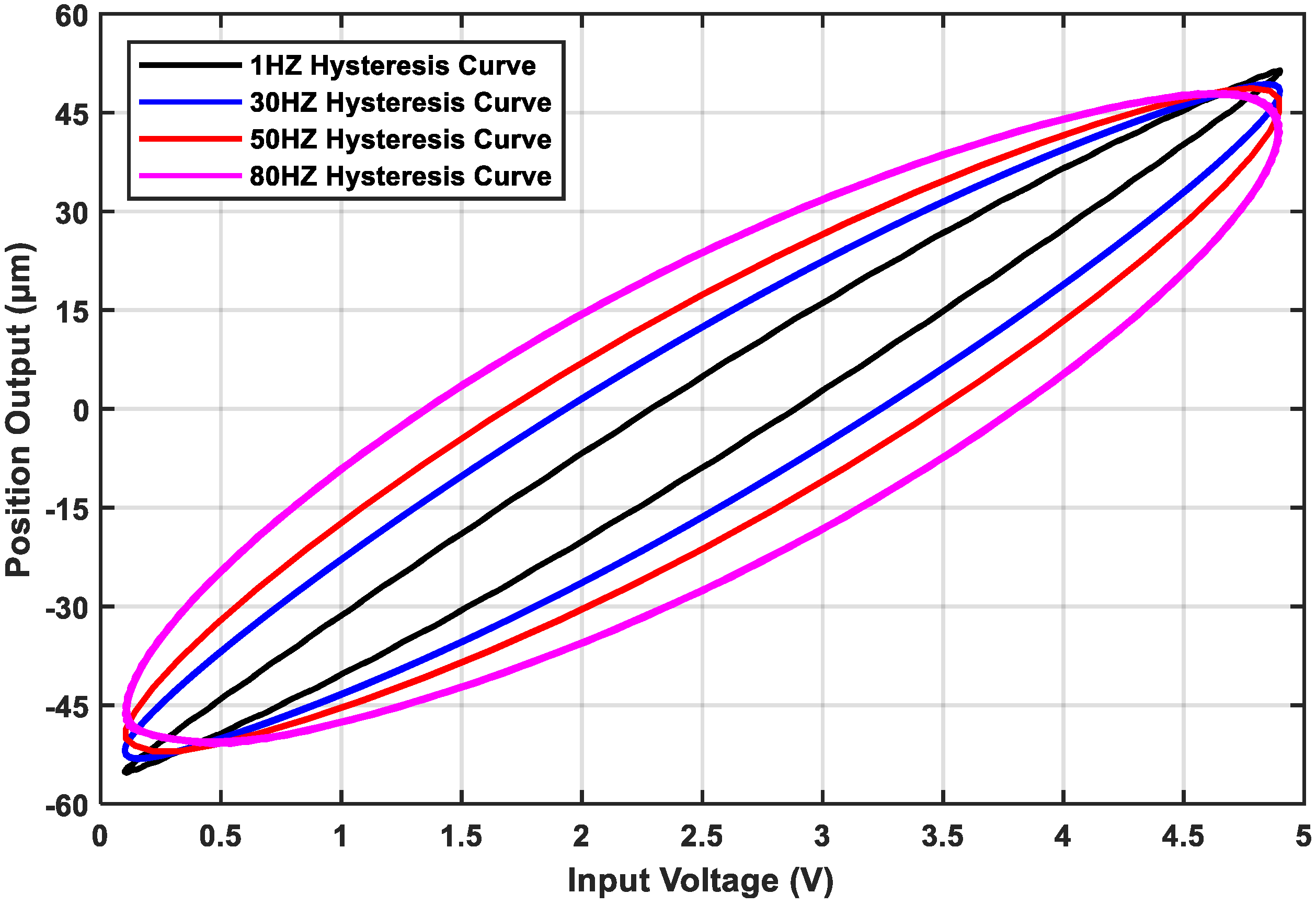
2. System Hysteresis Model
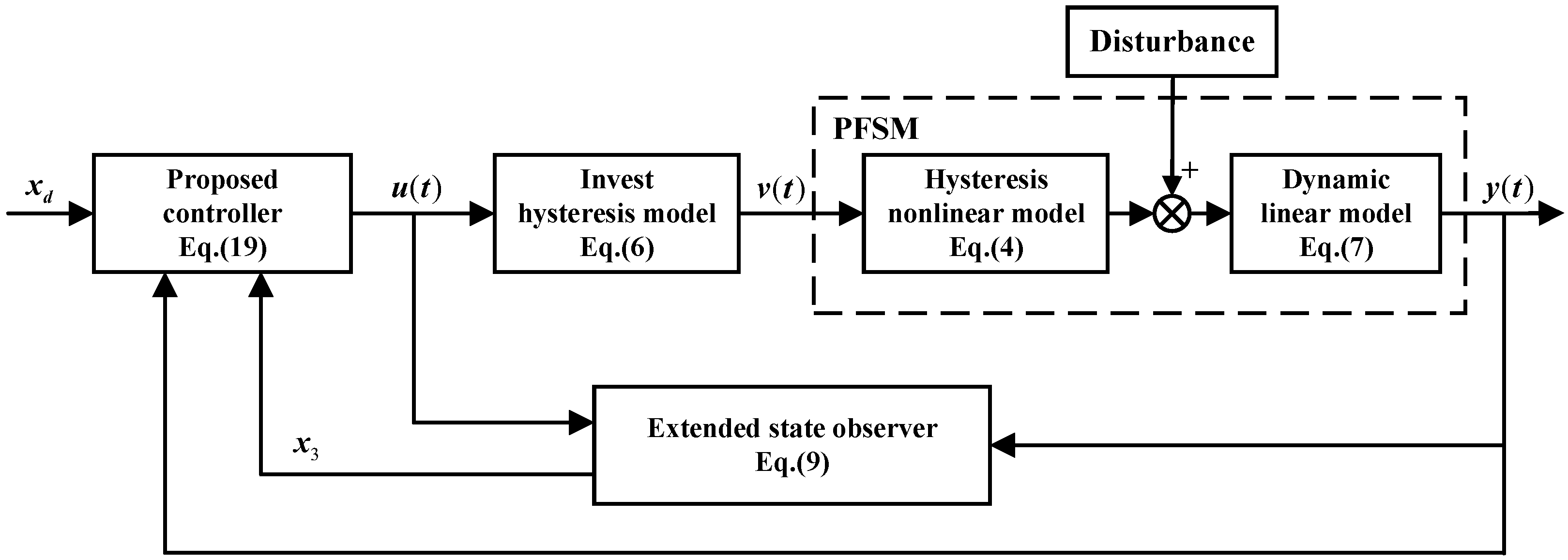
3. Controller Design and Analysis
3.1. Hysteresis Compensation
3.2. Extended State Observer
3.3. Sliding Mode Controller
3.4. Stability Analysis
4. Experimental Verification
4.1. Experimental Setup
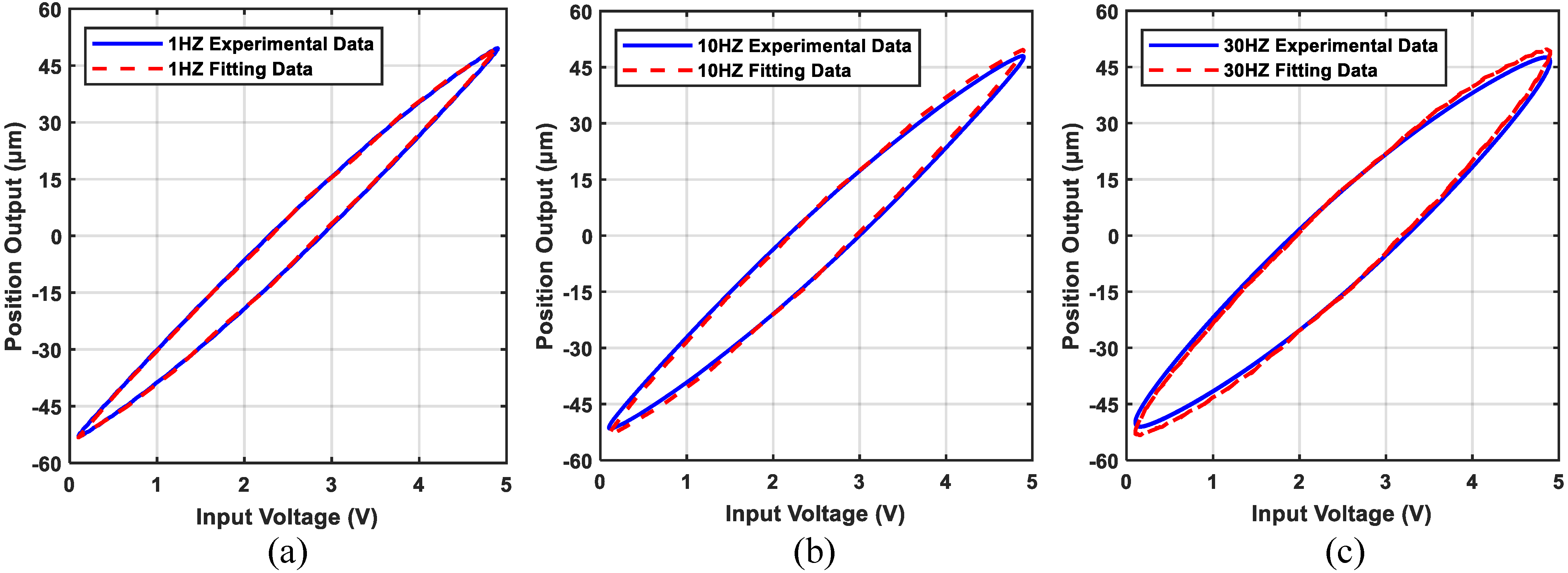
4.2. Model Parameter Identification
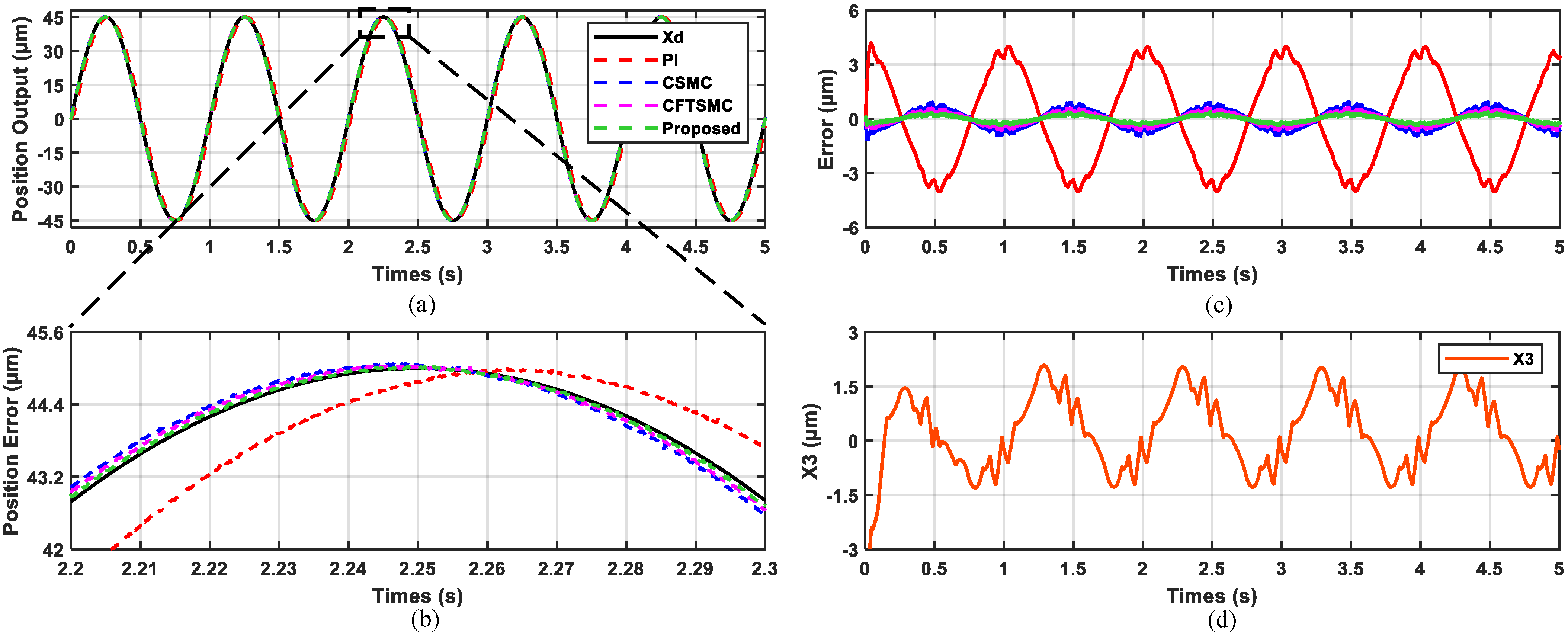
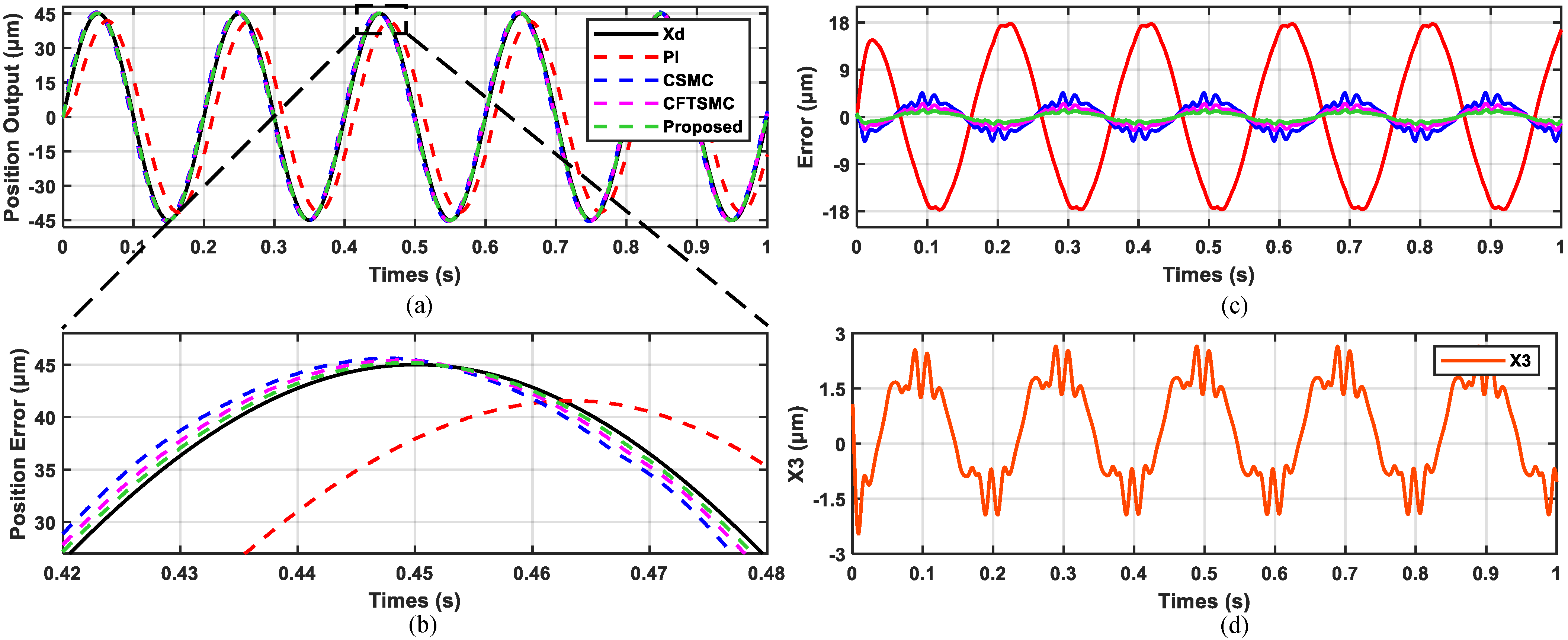
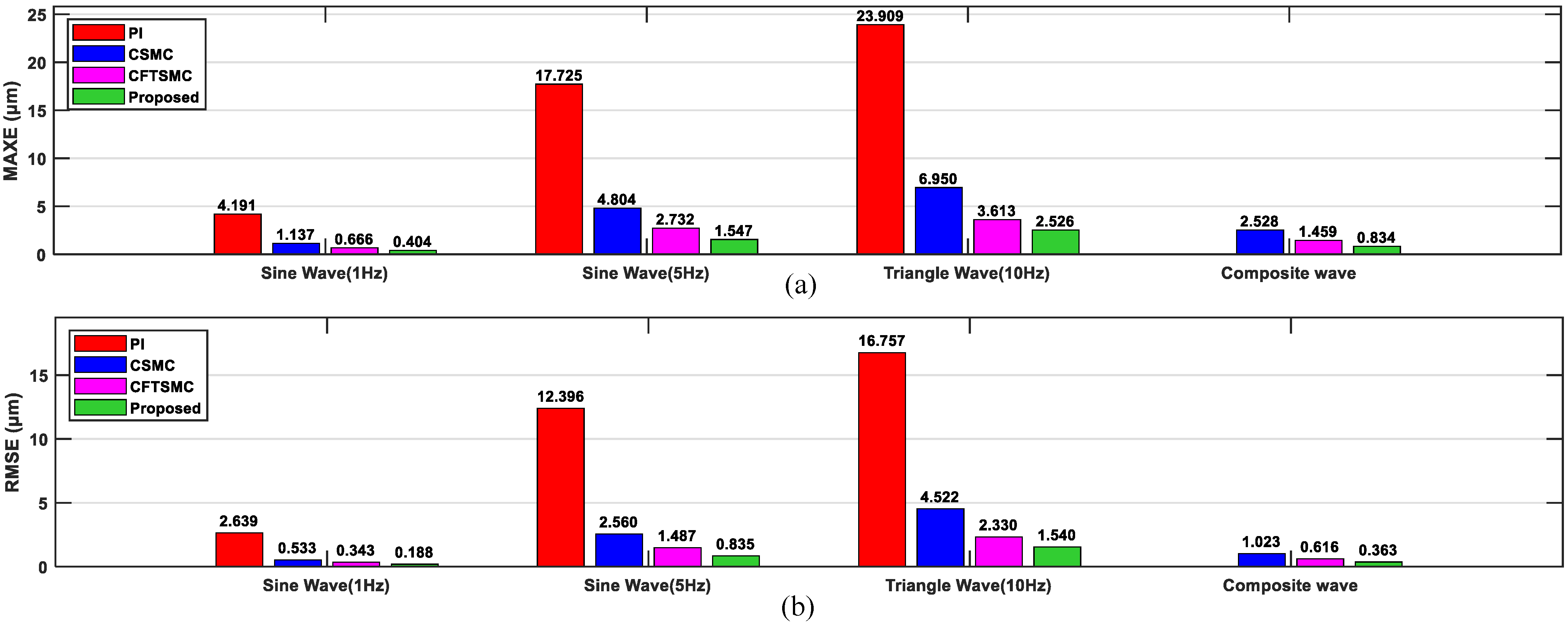
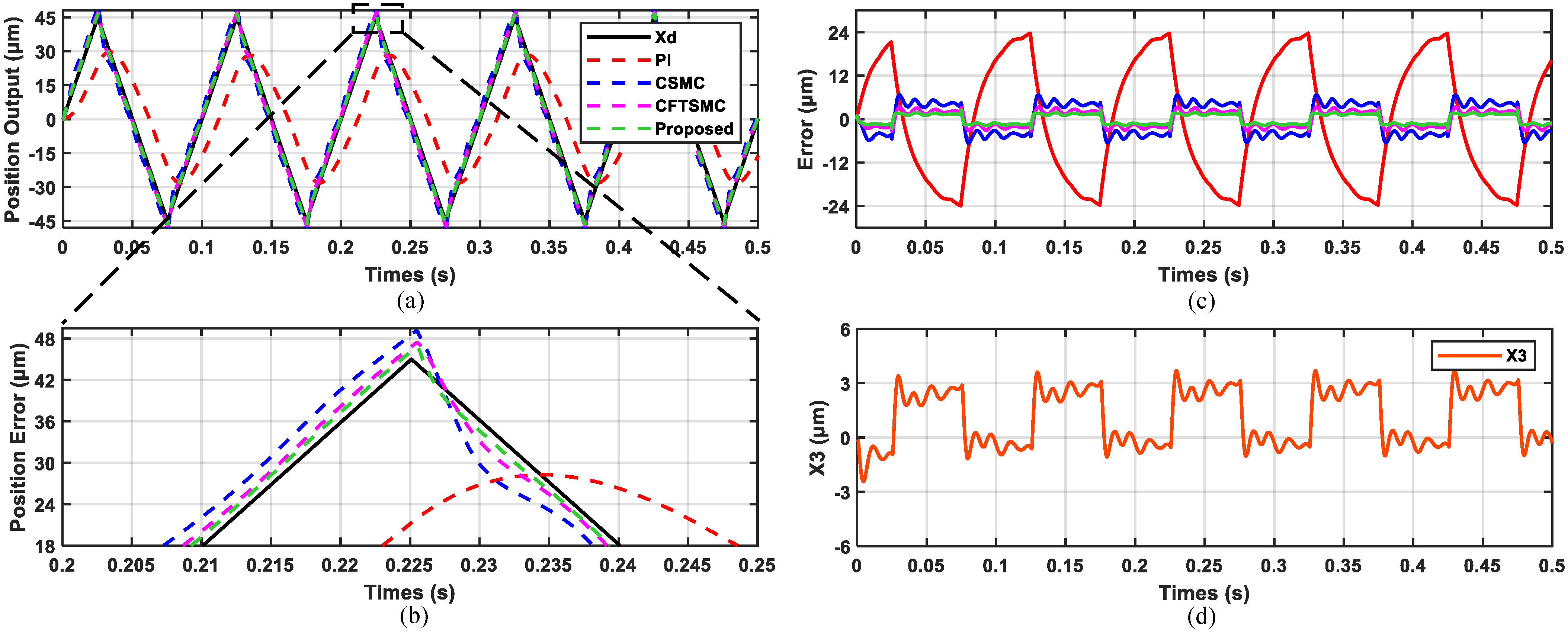
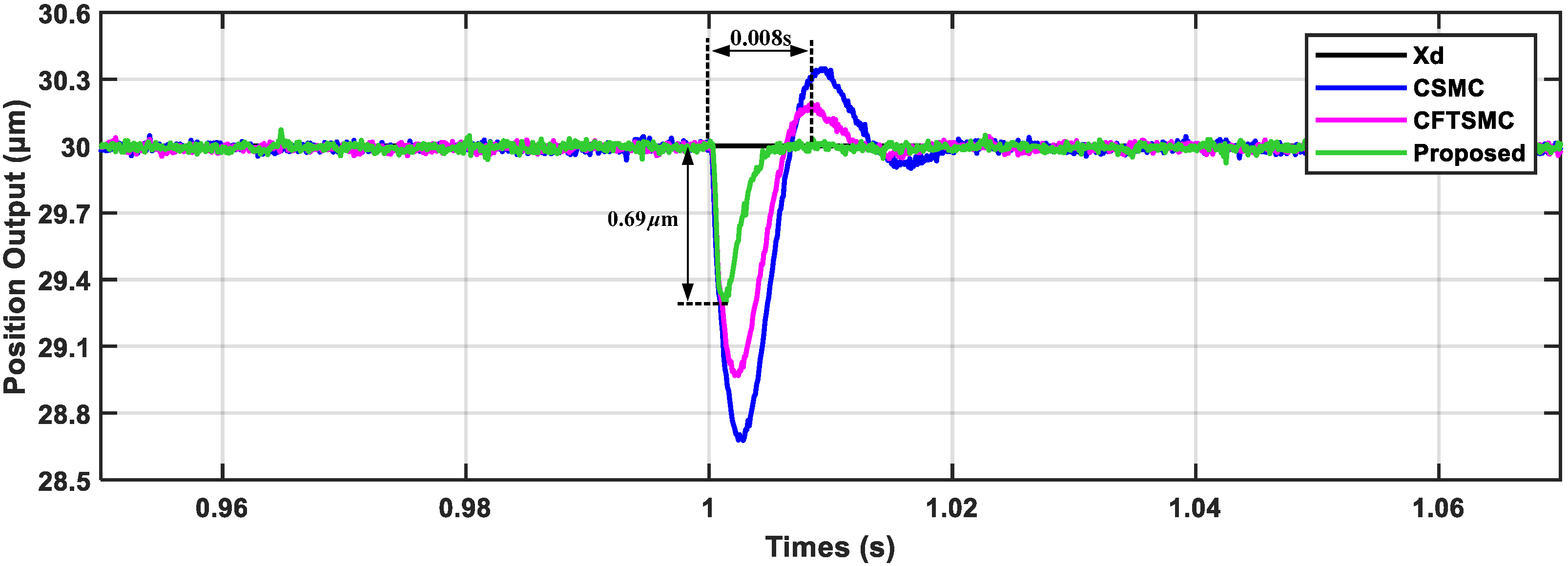
4.3. Real-Time Tracking Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, J.; Nishida, R.; Shinshi, T. Design and precision tracking control of a high-bandwidth fast steering mirror for laser beam machining. Precis. Eng. 2022, 73, 128–139. [Google Scholar] [CrossRef]
- Li, Z.; Li, L.; Zhang, J.; Feng, W. System modeling and sliding mode control of fast steering mirror for space laser communication. Mech. Syst. Signal Process. 2024, 211, 111206. [Google Scholar] [CrossRef]
- Wang, G.; Rao, C. Adaptive control of piezoelectric fast steering mirror for high precision tracking application. Smart Mater. Struct. 2015, 24, 035019. [Google Scholar] [CrossRef]
- Qi, C.; Lin, J.; Wu, Y.; Gao, F. A Wiener Model Identification for Creep and Vibration Linear and Hysteresis Nonlinear Dynamics of Piezoelectric Actuator. IEEE Sens. J. 2021, 21, 27570–27581. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhou, S.; Zhang, Z.; Xiao, Z.; Hong, C.; Chen, X.; Zeng, L.; Li, X. Piezo-actuated smart mechatronic systems: Nonlinear modeling, identification, and control. Mech. Syst. Signal Process. 2024, 221, 111715. [Google Scholar] [CrossRef]
- Mohammadzaheri, M.; Al-Sulti, S.; Ghodsi, M.; Soltani, P. Charge Estimation of Piezoelectric Actuators: A Comparative Study. Energies 2023, 16, 3982. [Google Scholar] [CrossRef]
- Yang, C.; Youcef-Toumi, K. Principle, implementation, and applications of charge control for piezo-actuated nanopositioners: A comprehensive review. Mech. Syst. Signal Process. 2022, 171, 108885. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Jian, Y.; Huang, D.; Liu, J.; Min, D. High-Precision Tracking of Piezoelectric Actuator Using Iterative Learning Control and Direct Inverse Compensation of Hysteresis. IEEE Trans. Ind. Electron. 2019, 66, 368–377. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, Y.; Su, M. Modeling of hysteresis in piezoelectric actuators using neural networks. Mech. Syst. Signal Process. 2009, 23, 2699–2711. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Al Saaideh, M.; Rakotondrabe, M. On hysteresis modeling of a piezoelectric precise positioning system under variable temperature. Mech. Syst. Signal Process. 2020, 145, 106880. [Google Scholar] [CrossRef]
- Dong, Y.; Hu, H.; Wang, H. Identification and experimental assessment of two-input Preisach model for coupling hysteresis in piezoelectric stack actuators. Sensors Actuators A Phys. 2014, 220, 92–100. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Z.; Li, D. Fractional order neural sliding mode control based on the FO-Hammerstein model of piezoelectric actuator. ISA Trans. 2023, 142, 515–526. [Google Scholar] [CrossRef]
- Zeng, X.; Nan, F.; Li, T.; Mo, C.; Su, J.; Wei, K.; Zhang, X. Integrating Strain Gauge Feedback with Adaptive Sliding Mode Motion Control for Piezoelectric Nanopositioning Stage. Actuators 2025, 14, 79. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, Y.; Ni, L.; Aphale, S.S. Global fast non-singular terminal sliding-mode control for high-speed nanopositioning. ISA Trans. 2023, 136, 560–570. [Google Scholar] [CrossRef]
- Dong, Q.; Liu, Y.; Zhang, Y.; Gao, S.; Chen, T. Improved ADRC with ILC Control of a CCD-Based Tracking Loop for Fast Steering Mirror System. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Liu, X.; Wang, J.; Lee, C.H.T. A Variable Structure ADRC for Enhanced Disturbance Rejection and Improved Noise Suppression of PMSM Speed System. IEEE Trans. Ind. Electron. 2024, 1–15. [Google Scholar] [CrossRef]
- Nguyen, M.L.; Chen, X. MPC Inspired Dynamical Output Feedback and Adaptive Feedforward Control Applied to Piezo-Actuated Positioning Systems. IEEE Trans. Ind. Electron. 2020, 67, 3921–3931. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Liu, J.; Zuo, Y.; Liu, X.; Wang, H.; Lee, C.H.T. Improved Deadbeat Predictive Current Control of PMSM Drives with Repetitive Control-Based Disturbance Correction Observer. IEEE Trans. Power Electron. 2025, 40, 801–812. [Google Scholar] [CrossRef]
- Yu, X.; Wu, Y.; Zhihong, M. On global stabilization of nonlinear dynamical systems. In Variable Structure Systems, Sliding Mode and Nonlinear Control; Springer: Berlin/Heidelberg, Germany, 2007; pp. 109–122. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Z.; Wang, H.N.; Xiong, T. Fractional order sliding mode control based on single parameter adaptive law for nano-positioning of piezoelectric actuators. Iet Control Theory Appl. 2021, 15, 1422–1437. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Hou, H.; Yu, X.; Xu, L.; Rsetam, K.; Cao, Z. Finite-Time Continuous Terminal Sliding Mode Control of Servo Motor Systems. IEEE Trans. Ind. Electron. 2020, 67, 5647–5656. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Yang, T.; Deng, Y.; Li, H.; Sun, Z.; Cao, H.; Wei, Z. Fast integral terminal sliding mode control with a novel disturbance observer based on iterative learning for speed control of PMSM. ISA Trans. 2023, 134, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Qin, C.; Zhang, Z.; Fang, Q. Adaptive Backstepping Fast Terminal Sliding Mode Control with Estimated Inverse Hysteresis Compensation for Piezoelectric Positioning Stages. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 1186–1190. [Google Scholar] [CrossRef]
- Song, Z.; Wang, L.; Ling, J.; Wang, L.; Duan, J.; Wang, Y.; Chen, B. Time-delay control scheme with adaptive fixed-time convergent super-twisting fractional-order nonsingular terminal sliding mode for piezoelectric displacement amplifier. ISA Trans. 2024, 146, 99–113. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A Composite Sliding Mode Control for SPMSM Drives Based on a New Hybrid Reaching Law with Disturbance Compensation. IEEE Trans. Transp. Electrif. 2021, 7, 1427–1436. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, R.; Wang, L.; Tian, D. Finite-time adaptive sliding mode control for high-precision tracking of piezo-actuated stages. ISA Trans. 2022, 129, 436–445. [Google Scholar] [CrossRef]
- Yang, S.; Wang, W.; Wang, R.; Bao, L.; Wang, D.; Lu, K.; Chen, Z.; Wang, C. An improved dynamic Prandtl–Ishlinskii hysteresis model and a PID-type adaptive sliding mode controller for piezoelectric micro-motion platform. Smart Mater. Struct. 2024, 33, 075029. [Google Scholar] [CrossRef]
- Xu, Q. Precision Motion Control of Piezoelectric Nanopositioning Stage with Chattering-Free Adaptive Sliding Mode Control. IEEE Trans. Autom. Sci. Eng. 2017, 14, 238–248. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y. Modeling and Compensation of Asymmetric Hysteresis Nonlinearity for Piezoceramic Actuators with a Modified Prandtl–Ishlinskii Model. IEEE Trans. Ind. Electron. 2014, 61, 1583–1595. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Li, H.; Wang, J.; Liu, X.; Lee, C.H.T. Improved ADRC with a Cascade Extended State Observer Based on Quasi-Generalized Integrator for PMSM Current Disturbances Attenuation. IEEE Trans. Transp. Electrif. 2024, 10, 2145–2157. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. Acc 2003, 4, 989-4. [Google Scholar]
- Gao, W.; Hung, J. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar] [CrossRef]
- Moulay, E.; Perruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323, 1430–1443. [Google Scholar] [CrossRef]




| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.54 | 1.08 | 1.62 | 2.16 | 2.70 | 3.24 | 3.78 | 4.32 | 4.86 | |
| 14.93 | 2.71 | 3.95 | −2.10 | 4.81 | −1.97 | 2.34 | −0.36 | 2.34 | 21.11 |
| Controller | Parameters |
|---|---|
| PI | , |
| CSMC | , , , |
| CFTSMC | , , , , |
| , , , | |
| Proposed controller | , , , , |
| , , , | |
| , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, E.; Wang, S.; Zhai, C.; Li, W. Improved Non-Singular Fast Terminal Sliding Mode Control with Hysteresis Compensation for Piezo-Driven Fast Steering Mirrors. Actuators 2025, 14, 170. https://doi.org/10.3390/act14040170
Zhong E, Wang S, Zhai C, Li W. Improved Non-Singular Fast Terminal Sliding Mode Control with Hysteresis Compensation for Piezo-Driven Fast Steering Mirrors. Actuators. 2025; 14(4):170. https://doi.org/10.3390/act14040170
Chicago/Turabian StyleZhong, Enfu, Shuai Wang, Chuanlong Zhai, and Wenjie Li. 2025. "Improved Non-Singular Fast Terminal Sliding Mode Control with Hysteresis Compensation for Piezo-Driven Fast Steering Mirrors" Actuators 14, no. 4: 170. https://doi.org/10.3390/act14040170
APA StyleZhong, E., Wang, S., Zhai, C., & Li, W. (2025). Improved Non-Singular Fast Terminal Sliding Mode Control with Hysteresis Compensation for Piezo-Driven Fast Steering Mirrors. Actuators, 14(4), 170. https://doi.org/10.3390/act14040170








