Collision/Obstacle Avoidance Coordination of Multi-Robot Systems: A Survey
Abstract
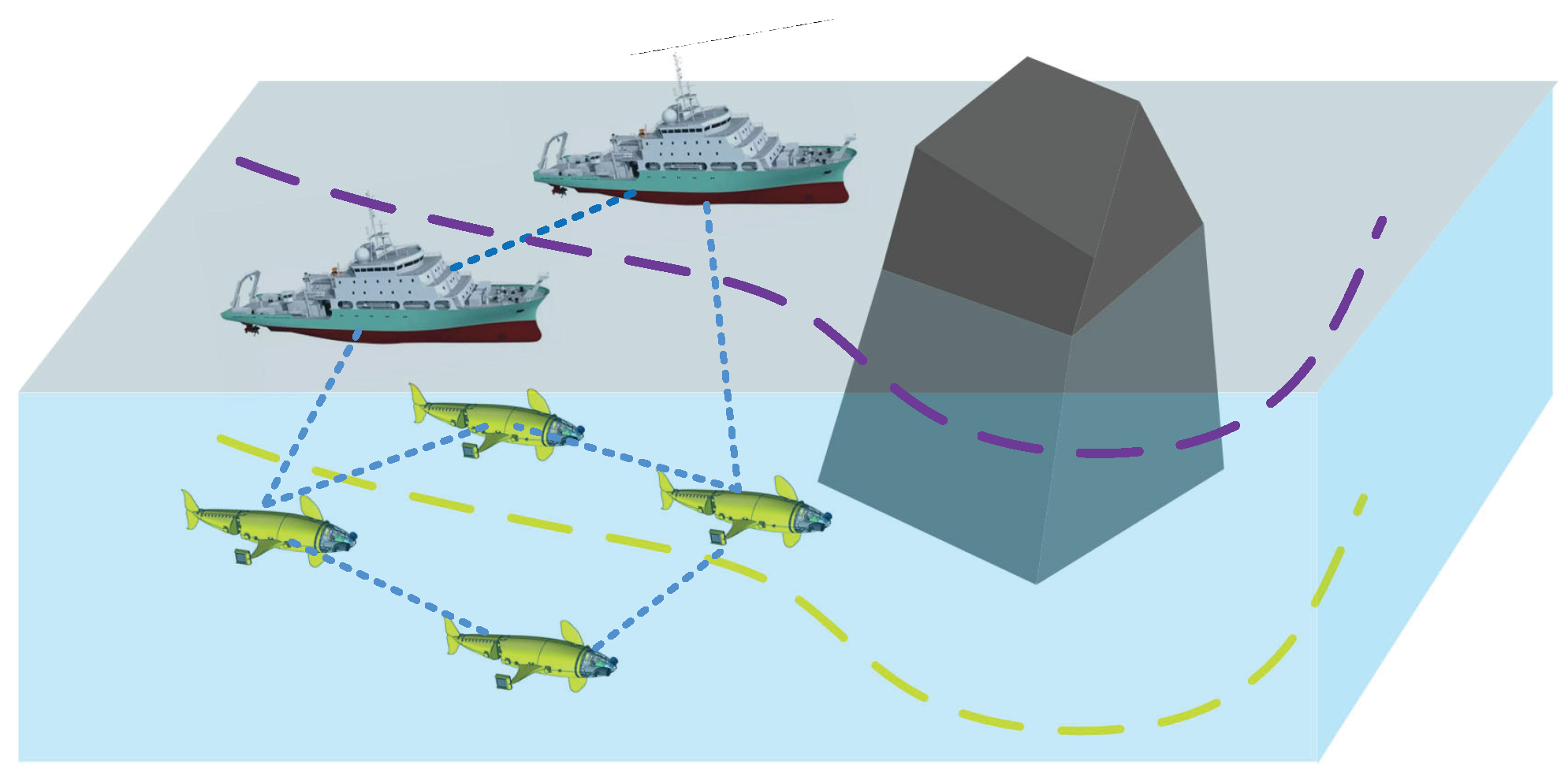
1. Introduction
2. Overview of Collision/Obstacle Avoidance Control Architectures
2.1. Offline Planning
2.2. Receding Horizon Planning
2.3. Reactive Control
2.4. Hybrid Integration Control
3. Overview of Collision/Obstacle Avoidance Control Schemes
3.1. Offline Motion Planner
| Algorithm 1 Local motion planner [51]. |
|
3.2. Model Predictive Control
3.3. Barrier Lyapunov Function
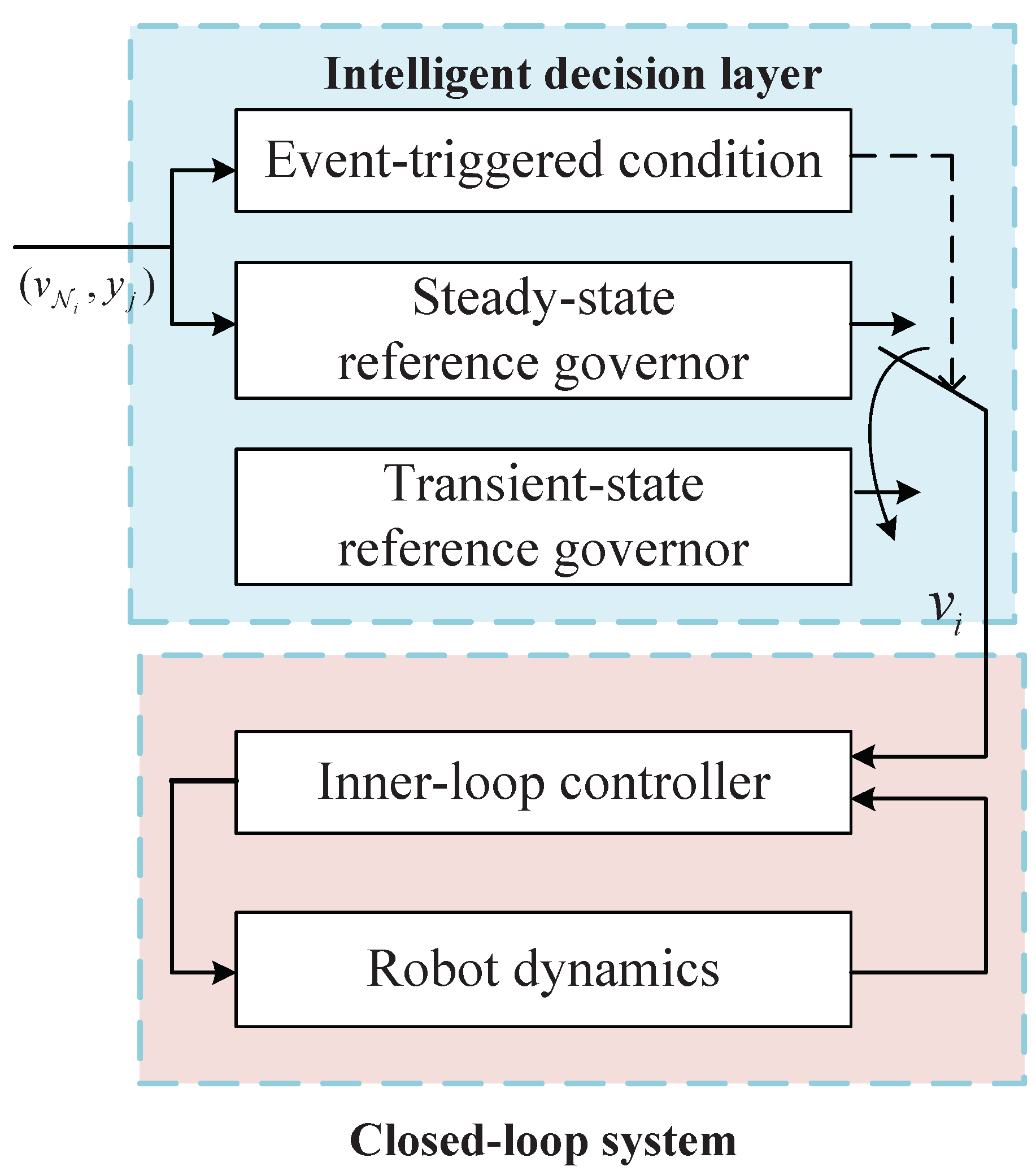
3.4. Reference/Command Governors
3.4.1. Reference Governor for Inter-Robot Collision Avoidance
3.4.2. Command Governor for Collision/Obstacle Avoidance
4. Future Challenges
4.1. Network Constraints
4.1.1. Limited Communications Resources
4.1.2. Malicious Cyber-Attacks
4.2. Deadlock Issue
4.3. Implementation Issues
- Limited actuator forces. As typical mechanical systems, practical robotic systems are usually constrained by various physical constraints, such as limited actuator forces. The tracking performance of robots is usually limited due to physical constraints, which can increase the risk of collisions during extremely fast movements. Therefore, the limited underlying tracking performance should be considered in the design of safety decisions.
- Imprecise actuators and sensors. In practice, sensors and actuators often suffer from measurement errors, nonlinear properties, hysteresis effects, and manufacturing deviations, which result in limited precision of the information acquired by the system and the control performed. These imprecisions make it difficult to ensure the stability and performance of traditional reference governors, thus affecting the control performance. According to the specific task scenario and the selected components, designing plug-and-play reference governors contributes to the flexibility of the system.
- Sensor failures. The failure signals may lead to false detection of obstacles or even to the determination that a collision has already occurred. In such cases, the barrier function tends to infinity, causing the reference governor scheme to be unresolvable or to perform false avoidance behaviors. Therefore, incorporating fault-tolerant schemes to design robust reference governors would be an interesting topic.
- Unknown dynamic environments. Due to computational efficiency constraints, it is difficult for existing motion planning schemes to achieve sufficiently rapid replanning, and thus they are only applicable to static obstacle environments with a priori global information. In the face of complex and unknown dynamic environments, safe decision-making schemes with fast response capabilities are necessary.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, Z.; Ding, N.; Chen, H.; Hu, X.; Zhu, Z.; Fu, X.; Zhang, W.; Zhang, L.; Hazken, S.; Wang, Z.; et al. CCRobot-V: A silkworm-like cooperative cable-climbing robotic system for cable inspection and maintenance. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 164–170. [Google Scholar]
- Sirintuna, D.; Ozdamar, I.; Ajoudani, A. Carrying the uncarriable: A deformation-agnostic and human-cooperative framework for unwieldy objects using multiple robots. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 7497–7503. [Google Scholar]
- Sujit, P.B.; Beard, R. Cooperative path planning for multiple UAVs exploring an unknown region. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 347–352. [Google Scholar]
- Che, W.-W.; Zhang, L.; Deng, C.; Wu, Z.-G. Hierarchical lane-changing control for vehicle platoons in prescribed performance. Automatica 2025, 171, 111972. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, K. Advanced model predictive control framework for autonomous intelligent mechatronic systems: A tutorial overview and perspectives. Annu. Rev. Control 2021, 52, 170–196. [Google Scholar] [CrossRef]
- Chen, F.; Sewlia, M.; Dimarogonas, D.V. Cooperative control of heterogeneous multi-agent systems under spatiotemporal constraints. Annu. Rev. Control 2024, 57, 100946. [Google Scholar] [CrossRef]
- Xiao, W.; Li, A.; Cassandras, C.G.; Belta, C. Toward model-free safety-critical control with humans in the loop. Annu. Rev. Control 2024, 57, 100944. [Google Scholar] [CrossRef]
- Garg, K.; Zhang, S.; So, O.; Dawson, C.; Fan, C. Learning safe control for multi-robot systems: Methods, verification, and open challenges. Annu. Rev. Control 2024, 57, 100948. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. Rrt-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA. IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Sandakalum, T.; Ang, J.M.H. Motion planning for mobile manipulatorsa systematic review. Machines 2022, 10, 97. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, J.; Wan, W. Survey of optimal motion planning. IET Cyber-Syst. Robot. 2019, 1, 13–19. [Google Scholar] [CrossRef]
- Kingston, Z.; Moll, M.; Kavraki, L.E. Sampling-based methods for motion planning with constraints. Annu. Rev. Control Robot. Atonomous Syst. 2018, 1, 159–185. [Google Scholar] [CrossRef]
- Chase Kew, J.; Ichter, B.; Bandari, M.; Lee, T.W.E.; Faust, A. Neural collision clearance estimator for batched motion planning. In Algorithmic Foundations of Robotics XIV; LaValle, S.M., Lin, M., Ojala, T., Shell, D., Yu, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 73–89. [Google Scholar]
- Van Den Berg, J.P.; Overmars, M.H. Roadmap-based motion planning in dynamic environments. IEEE Trans. Robot. 2005, 21, 885–897. [Google Scholar] [CrossRef]
- Peasgood, M.; Clark, C.M.; McPhee, J. A complete and scalable strategy for coordinating multiple robots within roadmaps. IEEE Trans. Robot. 2008, 24, 283–292. [Google Scholar] [CrossRef]
- Kloder, S.; Hutchinson, S. Path planning for permutation-invariant multirobot formations. IEEE Trans. Robot. 2006, 22, 650–665. [Google Scholar] [CrossRef]
- Jiang, C.; Guo, Y. Incorporating control barrier functions in distributed model predictive control for multi-robot coordinated control. IEEE Trans. Control Netw. Syst. 2024, 11, 547–557. [Google Scholar] [CrossRef]
- Wen, G.; Lam, J.; Fu, J.; Wang, S. Distributed MPC-based robust collision avoidance formation navigation of constrained multiple USVs. IEEE Trans. Intell. Veh. 2024, 9, 1804–1816. [Google Scholar] [CrossRef]
- Domahidi, A.; Zgraggen, A.U.; Zeilinger, M.N.; Morari, M.; Jones, C.N. Efficient interior point methods for multistage problems arising in receding horizon control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 668–674. [Google Scholar]
- Richter, S.; Jones, C.N.; Morari, M. Computational complexity certification for real-time MPC with input constraints based on the fast gradient method. IEEE Trans. Autom. Control 2012, 57, 1391–1403. [Google Scholar] [CrossRef]
- Jiang, C. Distributed sampling-based model predictive control via belief propagation for multi-robot formation navigation. IEEE Robot. Autom. Lett. 2024, 9, 3467–3474. [Google Scholar] [CrossRef]
- Abraham, I.; Handa, A.; Ratliff, N.; Lowrey, K.; Murphey, T.D.; Fox, D. Model-based generalization under parameter uncertainty using path integral control. IEEE Robot. Autom. Lett. 2020, 5, 2864–2871. [Google Scholar] [CrossRef]
- Kobilarov, M. Cross-entropy motion planning. Int. J. Robot. Res. 2012, 31, 855–871. [Google Scholar] [CrossRef]
- Williams, G.; Drews, P.; Goldfain, B.; Rehg, J.M.; Theodorou, E.A. Information-theoretic model predictive control: Theory and applications to autonomous driving. IEEE Trans. Robot. 2018, 34, 1603–1622. [Google Scholar] [CrossRef]
- Broek, B.V.D.; Wiegerinck, W.; Kappen, B. Graphical model inference in optimal control of stochastic multi-agent systems. J. Artif. Intell. Res. 2008, 32, 95–122. [Google Scholar] [CrossRef]
- Wan, N.; Gahlawat, A.; Hovakimyan, N.; Theodorou, E.A.; Voulgaris, P.G. Cooperative path integral control for stochastic multi-agent systems. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 1262–1267. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Panagou, D.; Stipanović, D.M.; Voulgaris, P.G. Distributed coordination control for multi-robot networks using Lyapunov-like barrier functions. IEEE Trans. Autom. Control 2016, 61, 617–632. [Google Scholar] [CrossRef]
- Ames, A.D.; Xu, X.; Grizzle, J.W.; Tabuada, P. Control barrier function based quadratic programs for safety critical systems. IEEE Trans. Autom. Control 2017, 62, 3861–3876. [Google Scholar] [CrossRef]
- Wang, L.; Ames, A.D.; Egerstedt, M. Safety barrier certificates for collisions-free multirobot systems. IEEE Trans. Robot. 2017, 33, 661–674. [Google Scholar] [CrossRef]
- Koptev, M.; Figueroa, N.; Billard, A. Reactive collision-free motion generation in joint space via dynamical systems and sampling-based MPC. Int. J. Robot. Res. 2024, 43, 2049–2069. [Google Scholar] [CrossRef]
- Tedesco, F.; Casavola, A.; Garone, E. Distributed command governor strategies for constrained coordination of multi-agent networked systems. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 6005–6010. [Google Scholar]
- Garone, E.; Cairano, S.D.; Kolmanovsky, I. Reference and command governors for systems with constraints: A survey on theory and applications. Automatica 2017, 75, 306–328. [Google Scholar] [CrossRef]
- Hansel, K.; Urain, J.; Peters, J.; Chalvatzaki, G. Hierarchical policy blending as inference for reactive robot control. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 10181–10188. [Google Scholar]
- Rosolia, U.; Singletary, A.; Ames, A.D. Unified multirate control: From low-level actuation to high-level planning. IEEE Trans. Autom. Control 2022, 64, 6627–6640. [Google Scholar] [CrossRef]
- Cui, Y.; Ye, S.; Xu, X.; Sha, H.; Wang, C.; Lin, L.; Liu, Z.; Xiong, R.; Wang, Y. Learning hierarchical graph-based policy for goal-reaching in unknown environments. IEEE Robot. Autom. Lett. 2024, 9, 5655–5662. [Google Scholar] [CrossRef]
- Jin, T.; Di, J.; Wang, X.; Ji, H. Safety barrier certificates for path integral control: Safety-critical control of quadrotors. IEEE Robot. Autom. Lett. 2023, 8, 6006–6012. [Google Scholar] [CrossRef]
- Dahlin, A.; Karayiannidis, Y. Autonomous navigation with convergence guarantees in complex dynamic environments. Automatica 2025, 173, 112026. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Seng, W.L.; Barca, J.C.; Sekercioglu, Y.A. Distributed formation control in cluttered environments. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1387–1392. [Google Scholar]
- Chi, T.; Zhang, C.; Song, Y.; Feng, J. A strategy of multi-robot formation and obstacle avoidance in unknown environment. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 1455–1460. [Google Scholar]
- Wen, G.; Chen, C.P.; Liu, Y.-J. Formation control with obstacle avoidance for a class of stochastic multiagent systems. IEEE Trans. Ind. Electron. 2018, 65, 5847–5855. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots. IEEE Trans. Ind. Electron. 2014, 61, 347–354. [Google Scholar] [CrossRef]
- La, H.M.; Lim, R.; Sheng, W. Multirobot cooperative learning for predator avoidance. IEEE Trans. Control Syst. Technol. 2015, 23, 52–63. [Google Scholar] [CrossRef]
- Bai, C.; Yan, P.; Pan, W.; Guo, J. Learning-based multi-robot formation control with obstacle avoidance. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11811–11822. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, L.; Lam, T.L.; Vijayakumar, S. Task-space decomposed motion planning framework for multi-robot loco-manipulation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8158–8164. [Google Scholar]
- Tang, Q.; Zhang, Y.; Yu, F.; Zhang, J. An obstacle avoidance approach based on system outlined rectangle for cooperative transportation of multiple mobile manipulators. In Proceedings of the 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Shenyang, China, 24–27 August 2018; pp. 533–538. [Google Scholar]
- Roy, D.; Chowdhury, A.; Maitra, M.; Bhattacharya, S. Multi-robot virtual structure switching and formation changing strategy in an unknown occluded environment. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4854–4861. [Google Scholar]
- Alonso-Mora, J.; Knepper, R.; Siegwart, R.; Rus, D. Local motion planning for collaborative multi-robot manipulation of deformable objects. In Proceedings of the in 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5495–5502. [Google Scholar]
- Alonso-Mora, J.; Baker, S.; Rus, D. Multi-robot formation control and object transport in dynamic environments via constrained optimization. Int. J. Robot. Res. 2017, 36, 1000–1021. [Google Scholar] [CrossRef]
- Muskem, K.R.; Rawlings, J.B. Model predictive control with linear models. AIChE J. 1993, 39, 262–287. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K.; Lee, T.H. Applied Predictive Control; Springer: London, UK, 2002. [Google Scholar]
- Christofides, P.D.; Scattolini, R.D.; de la Peña, M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Müller, M.A.; Allgöwer, F. Economic and distributed model predictive control: Recent developments in optimization-based control. SICE J. Control Meas. Syst. Integr. 2017, 10, 39–52. [Google Scholar]
- Ferrari-Trecate, G.; Galbusera, L.; Marciandi, M.P.E.; Scattolini, R. Model predictive control schemes for consensus in multi-agent systems with single-and double-integrator dynamics. IEEE Trans. Autom. Control 2009, 54, 2560–2572. [Google Scholar] [CrossRef]
- Liu, X.; Shi, Y.; Constantinescu, D. Robust distributed model predictive control of constrained dynamically decoupled nonlinear systems: A contraction theory perspective. Syst. Control Lett. 2017, 105, 84–91. [Google Scholar] [CrossRef]
- Franco, E.; Magni, L.; Parisini, T.; Polycarpou, M.M.; Raimondo, D.M. Cooperative constrained control of distributed agents with nonlinear dynamics and delayed information exchange: A stabilizing receding-horizon approach. IEEE Trans. Autom. Control 2008, 53, 324–338. [Google Scholar] [CrossRef]
- Wang, C.; Ong, C.-J. Distributed model predictive control of dynamically decoupled systems with coupled cost. Automatica 2010, 46, 2053–2058. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Robust distributed model predictive control of constrained continuous-time nonlinear systems: A robustness constraint approach. IEEE Trans. Autom. Control 2014, 59, 1673–1678. [Google Scholar] [CrossRef]
- Dai, L.; Cao, Q.; Xia, Y.; Gao, Y. Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance. J. Frankl. Inst. 2017, 354, 2068–2085. [Google Scholar] [CrossRef]
- Wang, P.; Ding, B. Distributed RHC for tracking and formation of nonholonomic multi-vehicle systems. IEEE Trans. Autom. Control 2014, 59, 1439–1453. [Google Scholar] [CrossRef]
- Williams, G.; Aldrich, A.; Theodorou, E.A. Model predictive path integral control: From theory to parallel computation. J. Guid. Control Dyn. 2017, 40, 344–357. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Collisions-free distributed cooperative output regulation of nonlinear multi-agent systems. IEEE Trans. Autom. Control 2024, 69, 8072–8079. [Google Scholar] [CrossRef]
- Verginis, C.K.; Dimarogonas, D.V. Closed-form barrier functions for multi-agent ellipsoidal systems with uncertain lagrangian dynamics. IEEE Control Syst. Lett. 2019, 3, 727–732. [Google Scholar] [CrossRef]
- Arambula Cosio, F.; Padilla Castaẽda, M. Autonomous robot navigationusing adaptive potential fields. Math. Comput. Model. 2004, 40, 1141–1156. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef]
- Kim, J.-O.; Khosla, P.K. Real-time obstacle avoidance using harmonic potential functions. IEEE Trans. Robot. Autom. 1992, 8, 338–349. [Google Scholar] [CrossRef]
- Ge, S.S.; Cui, Y.J. New potential functions for mobile robot path planning. IEEE Trans. Robot. Autom. 2000, 16, 615–620. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, G.-H. Secure adaptive trajectory tracking control for nonlinear robot systems under multiple dynamic obstacles: Safety barrier certificates. IEEE Trans. Ind. Electron. 2022, 69, 11549–11559. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Collisions-free distributed optimal coordination for multiple Euler-Lagrangian systems. IEEE Trans. Autom. Control 2022, 67, 460–467. [Google Scholar] [CrossRef]
- Wang, X.; Ye, D. Finite-time output-feedback formation control for high-order nonlinear multiagent systems with obstacle avoidance. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1878–1888. [Google Scholar] [CrossRef]
- An, L.; Yang, G.H.; Wasly, S. Obstacle avoidance in distributed optimal coordination of multirobot systems: A trajectory planning and tracking strategy. IEEE Trans. Control Netw. Syst. 2024, 11, 1335–1344. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H.; Deng, C.; Wen, C. Event-triggered reference governors for collisions-free leader-following coordination under unreliable communication topologies. IEEE Trans. Autom. Control 2024, 69, 2116–2130. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Tong, S. Observer-based neuro-adaptive optimized control of strict-feedback nonlinear systems with state constraints. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3131–3145. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, W.; Lam, H.-K.; Cao, L. An improved predefined-time adaptive neural control approach for nonlinear multiagent systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6311–6320. [Google Scholar] [CrossRef]
- Do, K.D. Formation tracking control of unicycle-type mobile robots with limited sensing ranges. IEEE Trans. Control Syst. Technol. 2008, 16, 527–538. [Google Scholar] [CrossRef]
- Hu, B.-B.; Zhang, H.-T.; Liu, B.; Ding, J.; Xu, Y.; Luo, C.; Cao, H. Coordinated navigation control of cross-domain unmanned systems via guiding vector fields. IEEE Trans. Control Syst. Technol. 2024, 32, 550–563. [Google Scholar] [CrossRef]
- Carli, R.; Bullo, F.; Zampieri, S. Quantized average consensus via dynamic coding/decoding schemes. Int. J. Robust Nonlinear Control 2010, 20, 156–175. [Google Scholar] [CrossRef]
- Fan, S.; Meng, M.; Fu, Y.; Deng, C. Distributed adaptive tracking control for fuzzy nonlinear MASs under round-robin protocol. IEEE Trans. Fuzzy Syst. 2025, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, C.; Che, W.-W.; An, L. Adaptive backstepping control for nonlinear interconnected systems with prespecified-performance-driven output triggering. Automatica 2023, 154, 111063. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, C.; An, L. Asymptotic tracking control of nonlinear strict-feedback systems with state/output triggering: A homogeneous filtering approach. IEEE Trans. Autom. Control 2024, 69, 6413–6420. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, G.-H. Event-triggered-based adaptive fuzzy finite-time resilient output feedback control for MIMO stochastic nonlinear system subject to deception attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 6534–6547. [Google Scholar] [CrossRef]
- Li, T.; Fu, M.; Xie, L.; Zhang, J.-F. Distributed consensus with limited communication data rate. IEEE Trans. Autom. Control 2011, 56, 279–292. [Google Scholar] [CrossRef]
- You, K.; Xie, L. Network topology and communication data rate for consensusability of discrete-time multi-agent systems. IEEE Trans. Autom. Control 2011, 56, 2262–2275. [Google Scholar] [CrossRef]
- Li, T.; Xie, L. Distributed coordination of multi-agent systems with quantized-observer based encoding-decoding. IEEE Trans. Autom. Control 2012, 57, 3023–3037. [Google Scholar]
- An, L.; Yang, G.-H. Decentralized adaptive fuzzy secure control for nonlinear uncertain interconnected systems against intermittent DoS attacks. IEEE Trans. Cybern. 2019, 49, 827–838. [Google Scholar] [CrossRef]
- Fan, S.; Yue, D.; Yan, H.C.; Xie, X.P.; Deng, C. Resilient cooperative optimization control for fuzzy nonlinear MASs under DoS attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 3903–3913. [Google Scholar] [CrossRef]
- An, L.; Zhao, C.; Zhang, L. Resilient adaptive backstepping tracking control of nonlinear systems without a priori knowledge of DoS attacks. Automatica 2025, 174, 112119. [Google Scholar] [CrossRef]
- Ren, H.; Cheng, Z.; Qin, J.; Lu, R. Deception attacks on event-triggered distributed consensus estimation for nonlinear systems. Automatica 2023, 154, 111100. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Secure state estimation against sparse sensor attacks with adaptive switching mechanism. IEEE Trans. Autom. Control 2018, 63, 2596–2603. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Data-driven coordinated attack policy design based on adaptive L2-gain optimal theory. IEEE Trans. Autom. Control 2018, 63, 1850–1857. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; An, L.; Zhao, C. Collision/Obstacle Avoidance Coordination of Multi-Robot Systems: A Survey. Actuators 2025, 14, 85. https://doi.org/10.3390/act14020085
Yang G, An L, Zhao C. Collision/Obstacle Avoidance Coordination of Multi-Robot Systems: A Survey. Actuators. 2025; 14(2):85. https://doi.org/10.3390/act14020085
Chicago/Turabian StyleYang, Guanghong, Liwei An, and Can Zhao. 2025. "Collision/Obstacle Avoidance Coordination of Multi-Robot Systems: A Survey" Actuators 14, no. 2: 85. https://doi.org/10.3390/act14020085
APA StyleYang, G., An, L., & Zhao, C. (2025). Collision/Obstacle Avoidance Coordination of Multi-Robot Systems: A Survey. Actuators, 14(2), 85. https://doi.org/10.3390/act14020085






