Abstract
Multi-robot systems (MRSs) are widely applied in the fields of joint search and rescue, exploration, and carrying. To achieve cooperative tasks and guarantee physical safety, the robots should avoid inter-robot collisions as well as robot–obstacle collisions. However, the collision/obstacle avoidance task usually conflicts with the given cooperative task, which poses a significant challenge for the achievement of multi-robot cooperative tasks. This paper provides a review of the state-of-the-art results in the collision/obstacle avoidance cooperative control of MRSs. Specifically, the latest developments of collision/obstacle avoidance cooperative control are summarized according to different planning strategies and classified into three categories: (1) offline planning; (2) receding horizon planning; and (3) reactive control. Furthermore, specific design solutions for existing reference/command governors are highlighted to demonstrate the latest research advances. Finally, several challenging issues are discussed to guide future research.
1. Introduction
With the development of automation and intelligent control technologies, the cooperative control of multi-robot systems (MRSs) has gradually emerged. MRSs, with their advantages of flexibility, scalability, and high efficiency, have shown great potential in a variety of fields such as manufacturing, logistics and distribution, environmental monitoring, search, and rescue [1,2,3]. A case is shown in Figure 1. However, with the increase in the number of robots and the complexity of the operating environment, how to ensure that these robots work together safely and efficiently in a limited space has become an urgent technical problem [4].
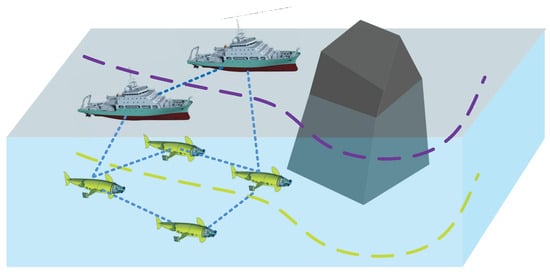
Figure 1.
Case of multi-robot collision/obstacle avoidance coordination.
Collision/obstacle avoidance control is one of the critical techniques for the cooperative control of multi-robot systems. To guarantee the physical safety of robots, the given distances between two robots and between robots and obstacles need to be guaranteed. Different from the obstacle avoidance problem of a single-robot system, the collision/obstacle avoidance control of multi-robot systems should not only consider the safety of individual robots but also the efficiency and coordination of the whole system. In addition, as the number of robots increases, the nonlinearity and uncertainty of the system also increase, which makes the problem of collision avoidance and obstacle avoidance control more complex. In general, there are several approaches to guarantee collision-free operation, including model predictive control, dynamic programming, barrier Lyapunov functions, and control barrier functions. The work in [5] reviews the development and application of model predictive control for autonomous intelligent mechatronic systems. Starting from the conceptual analysis of “mechatronics”, the characteristics of autonomous intelligent mechatronic systems and the design requirements of the control system are analyzed. A current research trend in MRSs is to consider high-level task specifications that go beyond traditional control objectives and take into account the heterogeneous nature of each robot. The work in [6] provides an overview of the control problem for heterogeneous MRSs under spatial and temporal constraints, as well as the challenges and open problems of considering such spatiotemporal constraints. The work in [7] envisions a future direction for a model-free safety control approach using event-triggered control barrier functions. Human interaction can also be naturally incorporated into such a framework. The work in [8] provides a comprehensive review of learning-based design methods for safety control of multi-robot systems.
The main challenges faced by these approaches are their computational complexity, conservatism, and potential infeasibility. Combining these methods and introducing new algorithms that improve existing collision/obstacle avoidance cooperative control methods is critical for rapidly developed autonomous MRSs. Motivated by the above analysis, it is necessary to organize and summarize the latest research contents to help researchers quickly understand and grasp the latest research advances and clarify future research directions. In this paper, we provide a comprehensive overview of the collision/obstacle avoidance coordination problem of multi-robot systems. The paper is organized as follows. In Section 2, we present a categorization of several categories of existing collision/obstacle avoidance schemes. Section 3 presents recent results on collision/obstacle avoidance when it comes to the cooperative control of MRSs. Finally, Section 4 summarizes potential future research topics.
2. Overview of Collision/Obstacle Avoidance Control Architectures
In this section, we provide a brief overview of the control frameworks currently employed to achieve collision/obstacle avoidance, which include offline planning, receding horizon planning, reactive control, and hybrid integration control.
2.1. Offline Planning
The offline planning scheme is a hierarchical approach in which feasible paths are first generated offline and then executed by a high-frequency controller. Specifically, robots need to update the world model by sensing the global world. Based on the constructed world model, the robots will search for the optimal collision-free behaviors in the feasible space by using automated reasoning prior to motion execution so as to achieve the given desired task. Once the optimal planning is generated, it is executed by the controller. It can be considered the dominant paradigm in robotic systems.
There are several sampling-based methods for generating optimal paths in the high-dimensional space of MRSs, such as rapidly exploring random trees, probabilistic roadmaps, and their variants [9,10,11]. Although these methods are applicable to many real-world scenarios, due to the time required to compute the optimal paths, these schemes are mainly applied to environments with a priori environmental configurations [12]. The computation and memory costs of these methods are usually significant [13] and the time to generate optimal paths can vary from seconds to minutes depending on the complexity of the environment and the number of robots [14]. In many investigations on multi-robot motion planning, the formation constraints among robots are not critical. The collaboration is not considered for each robot as it regards the other robots as dynamic obstacles [15,16,17]. However, with tasks becoming more complex, collaboration between multiple robots is inevitable, in particular for formation constraints.
2.2. Receding Horizon Planning
The receding horizon planning scheme involves repeatedly solving a nonlinear optimization problem with a receding horizon, which models the system dynamics and a given desired task as a nonlinear optimization problem with constraints and generates dynamic feasible trajectories online. The model predictive control (MPC) scheme is a classic receding horizon planning scheme, which divides the long-time optimization problem into short-time subproblems and solves the individual subproblems in a receding-level fashion. Due to its online re-planning and the capability to handle state and input constraints, the MPC-based approach is extremely appropriate for solving the collision/obstacle avoidance cooperative control problem of MRSs in complex environments.
To guarantee that the safety constraints are satisfied, various MPC schemes have been designed, such as incorporating the control barrier function and the artificial potential function into the design of the MPC scheme or imposing terminal constraints [18,19]. The computational complexity of the MPC scheme is , where n is the number of parameters determined by the number of states, control inputs, and the time horizon [20,21]. Thus, for robots with a high degree of freedom, these works cannot provide reprogramming at sufficiently rapid rates. Moreover, as the complexity of the cost function (e.g., nonconvexity, local minima) increases, these works may become inefficient or even fail to find a feasible solution. With recent developments in computing hardware, sampling-based methods have been proposed to solve stochastic optimal control problems [22]. This approach utilizes random trajectory samples generated by forward prediction or simulation to synthesize optimal controls and is capable of handling complex dynamics and non-differentiable cost functions. For single-robot obstacle avoidance, recent related works include model prediction path integral control [23], cross-entropy methods [24], and information-theoretic MPC [25]. However, since each robot in the MRS only needs local information, works on the distributed framework for MRS are limited. The scheme in [26] constructs a multi-robot optimal control framework as a graphical model inference that relies on the assumption that each robot can observe the global state of all robots. The scheme in [27] decomposes the multi-robot system into multiple subsystems to compute the joint control of the subsystems, which does not guarantee consensus among the subsystems.
2.3. Reactive Control
In reactive control, the robots can react in real-time using information that is locally sensed in the environment. Since the practical collision processes are extremely rapid, reactive control schemes with sufficiently rapid response times have a wide range of applications.
There are various collision/obstacle avoidance schemes that use the reactive control framework, such as the barrier Lyapunov function (or the artificial potential field approach) [28,29] and the control barrier function [30,31]. The barrier Lyapunov function-based scheme is a gradient-based collision/obstacle avoidance scheme that incorporates the barrier function into the Lyapunov function to derive the collision/obstacle avoidance controller. Integrating the optimization theory, the CBF-based scheme enables the actual control action to be as close as possible to the nominal control action, i.e., minimally invasive control. However, the CBF-based scheme requires solving a quadratic programming problem in each iteration, which reduces scalability in higher dimensions, such as the robot joint space [32]. Compared to the collision/obstacle avoidance scheme that modifies the underlying control loop of the system, the other prevailing scheme is the reference (command) governor [33,34]. The reference governor is an add-on scheme that guarantees that safety constraints are satisfied by modifying the feedforward command signals of the robot whenever necessary. The modular nature of the reference governor allows for a broader range of application scenarios. However, since the reactive control only focuses on the current scenario, as the number of robots increases, the derived solution may plunge into the local minima.
2.4. Hybrid Integration Control
To overcome the drawbacks of the above architectures, it is natural to develop a hybrid control to improve the cooperative performance of MRSs in the real world. In hybrid control, it is desirable to combine the features of local reactive control policies and longer horizon planning schemes [35].
In [36], a hierarchical multi-rate control architecture is proposed. At the highest level, a discrete Markov decision process is utilized to model the system–environment interaction. The constraint set and cost function of the MPC are updated by utilizing a high-level decision strategy, and the trajectory planned by the MPC is then fed into a low-level high-frequency tracking controller with CBF guarantees. For unknown environments, Ref. [37] proposed a hierarchical strategy that consists of a high-level strategy based on deep reinforcement learning and a low-level motion controller dealing with path planning and collision avoidance, which achieves long-horizon non-short-sighted decision-making. In [38], a predictive control strategy combining CBF and model predictive path integral control (MPPI) is proposed, where CBF serves as a safety filter to provide safety guarantees for the derived solution. Due to the limited prediction horizon, the designed scheme may converge to a locally suboptimal solution, which could lead to deadlocks. To provide convergence guarantees, the scheme in [39] combines the motion planner and the predictive controller, which incorporates the favorable convergence of the motion planning technique and the intuitive guarantees of the MPC for the safety constraints.
3. Overview of Collision/Obstacle Avoidance Control Schemes
In this section, we provide an overview for the existing cooperative collision/obstacle avoidance schemes of MRSs.
3.1. Offline Motion Planner
Existing motion planners can be generally categorized into two classes. The first category is to plan each robot individually while satisfying formation constraints and avoiding obstacles [40]. Based on leader–follower and potential function approaches, the work in [41,42,43] achieves the collision/obstacle avoidance formation. The work in [44] proposes a virtual and behavioral structure-based formation control scheme for MRSs. In the introduced approach, each mobile robot can automatically find its position in the formation, and the formation can also be automatically adjusted when the number of mobile robots changes. Adopting the learning-based approach, the works in [45,46] allow each robot to independently adjust its shape to pass through the obstacle region. The work in [47] decomposes the task space (formation and collision/obstacle avoidance) into different convex regions through a global planner. Then, a local planner is designed to plan the configuration. The aforementioned motion planners usually consider collision/obstacle avoidance and formation control separately. However, as collision/obstacle avoidance and formation constraints may conflict in the task space, the desired formation task may not be achieved. In addition, adjusting the weights between them is also a concern.
The second category considers the MRSs as a complete region and guarantees that the whole MRS region is strictly separated from the obstacles by planning the motion scheme. This category simplifies the multi-robot obstacle avoidance problem to a single-robot motion planning problem, where the MRSs can be regarded as a virtual structure of various shapes, such as the virtual rectangular region [48] as well as the time-varying circular region [49]. A constrained optimization approach is proposed in [50,51], in which the robots compute the available formation structures in the maximally convex obstacle-free region in real-time. Consider a group of robots navigating in formation. For each robot , its position at time t is denoted by . Denote by g, q, and s the centroid, direction, and size of the target formation, respectively. To move toward the goal position while avoiding obstacles, the following local planner [51] computes the target formation and the required motions of robots for the given time horizon .
In Algorithm 1, is the position-time obstacle-free workspace, which is computed by the traditional global planning. For the formation f, the optimal configuration is derived by solving the following nonlinear optimization problem:
where is the cost function, (2) contains a constraint for the formation f such that the robots do not collide with the obstacles, and (3) guarantees the inter-robot collision avoidance.
| Algorithm 1 Local motion planner [51]. |
|
However, as the robots are constrained to move within the constructed virtual region, the conservativeness of the design of the obstacle avoidance scheme increases. In contrast to bypassing the obstacle region, for some dense and tiny obstacles, the robot can pass through the obstacle region in a separate form. It is worth noting that although the solution in distributed scenarios faces many constraints, the resulting planning scheme guarantees the convergence of the global cooperative task whenever it is solvable. Moreover, the offline planning algorithm is inherently more developed and easy to implement.
3.2. Model Predictive Control
In recent years, model predictive control has received increasing attention due to its capability to simultaneously handle different constraints and cost functions through optimization-based schemes [52,53]. Compared with offline planning schemes, MPC schemes have significant advantages in dynamic environments, which are able to optimize the control inputs in real-time. The MPC scheme is also capable of handling complex constraints, such as state constraints and environmental changes. According to the implementation form, the MPC schemes can be classified into centralized and distributed MPC. A centralized MPC approach is proposed in [54], where a Lagrangian relaxation method is utilized to convert the nonconvex collision avoidance constraints into a convex semidefinite programming problem. Compared to the centralized MPC, the distributed MPC essentially allocates the computational load to the sub-controller of each robot, which are connected together through wireless network sharing, thus satisfying the real-time safety requirements of MRSs. Comprehensive overviews of this topic are available in recent survey papers [55,56].
Distributed MPC-based control of MRSs has been extensively investigated under different conditions. Taking into account the input constraints of the robots, the work in [57] proposes a distributed MPC scheme and proves that the robots can achieve consensus under mild assumptions. The work in [58] designs a distributed MPC scheme that can handle the exchange delay. Moreover, by employing the small gain theorem and the notion of input-to-state stability, a rigorous stability analysis is presented. The work in [59] proposes a robust tube-based linear MPC scheme where stability and constraints are satisfied via a contractive constraint and set tightening, respectively. The work in [60] proposes a robust nonlinear distributed MPC scheme that guarantees stability and algorithmic feasibility through a robustness constraint that constrains the predicted state trajectories with a monotonically decreasing function. Incorporating input constraints and state constraints into the optimization framework, the work in [61] proposes a collision/obstacle avoidance distributed MPC scheme and guarantees recursive feasibility and closed-loop stability. Taking into account the collision avoidance formation control problem, the work in [62] designs the compatibility constraints that simultaneously guarantee the collision avoidance constraints and the convergence. Consider the multi-robot system with the following nonlinear dynamics:
where and denote the state and control input of robot i, respectively. Then, the optimal safe MPC control sequence can be found with a finite future horizon of T. For each robot i, the relevant MPC optimization formulation [62] is given by
where is the stage cost, is the terminal cost, is the input constraint set, is the state/safe constraint set, and is the terminal constraint, respectively.
The above distributed MPC schemes utilize well-constructed mathematical optimization tools to obtain the solution. The main limitation is that polynomial scaling with respect to the number of parameters in the optimization process can introduce a high computational cost. Therefore, for the high degree of freedom robots, these schemes do not provide sufficiently fast rates of reprogramming. Moreover, as the complexity of the cost function increases (e.g., nonconvexity, local minima), these schemes may become inefficient or even fail to find a feasible solution. In recent years, a novel optimization method that relies on sampling-based exploration of the near-optimal input distribution has received widespread attention. Such an approach is able to deal with complex dynamics and non-trivial cost functions and thus can be acceptable for more general forms of dynamics and task specification. In addition, the randomized forward search in the sampling-based approach renders the algorithm less prone to local minima. The work in [63] presents an MPPI control algorithm based on a generalized significant sampling scheme. Parallel sampling optimization is performed using a graphics processing unit. The work in [22] considers the cooperative control framework of MRSs. Specifically, a distributed framework for sampling-based optimal control is proposed, which defines multi-robot optimal control as probabilistic inference over graphical models and uses belief propagation to implement the inference via distributed computation.
3.3. Barrier Lyapunov Function
The barrier Lyapunov function (BLF) approach has recently been recognized as a powerful tool for addressing the collision/obstacle avoidance problem in MRS coordination by incorporating the barrier function into the traditional Lyapunov function-based controller design. Compared to the MPC scheme, the BLF scheme preserves the traditional controller design approaches, such as the well-known backstepping controller technique. Moreover, the BLF scheme inherits the advantages of traditional controller design in terms of robustness as well as convergence.
Typically, the barrier function can be designed as follows [64]:
where parameter n denotes the orders of the robot system and R denotes the sensing range of the robots. When the other robots or obstacles move into the region with a radius of R from the robot, the robot performs corresponding collision/obstacle avoidance behaviors. Then, the barrier function with respect to constraining the agent i from colliding with the other agents and with the obstacles is defined as follows [64]:
where , denotes the relative distance between robots i and j, and denotes the relative distance between robot i and obstacle .
The design schemes of BLFs can be categorized into additive BLFs as well as multiplicative BLFs. Firstly, the additive BLF can be designed as follows:
The function denotes the original Lyapunov function, which is designed according to the specific cooperative task. The term denotes the barrier function utilized for collision/obstacle avoidance. If inter-robot collisions or collisions between robots and obstacles occur, the term will tend to infinity. Therefore, designing the controller to guarantee the convergence of the BLF can ensure the achievement of the cooperative task as well as collision/obstacle avoidance.
Note that the classical artificial potential function approach also belongs to the BLF scheme. Applying the artificial potential function, the command of each robot is designed as
with
where denotes the attractive force for achieving coordination and denotes the repulsive force for collision/obstacle avoidance. Based on the additive BLF, the work in [29] proposed a set-theoretic formulation that encodes multiple nontrivial control objectives (e.g., collision avoidance and convergence) in terms of a single BLF, yielding gradient-based control solutions. The work in [65] proposes a decentralized control protocol to avoid inter-robot collisions, where the robots consist of three-dimensional ellipsoidal agents obeying second-order uncertain Lagrangian dynamics. However, the artificial potential field method has some inherent limitations—for example, robots may suffer from deadlock phenomena [66]. In such cases, the attractive and repulsive forces will counteract to cause the BLF to fall into a local minimum, which will lead to the failure of the cooperative task of MRSs. Some advances have been made in improving the original potential function methods, such as the virtual force method [67], the harmonic potential method [68], and the improved potential field method [69].
Compared to the additive BLF, a novel multiplicative BLF scheme can guarantee collision/obstacle avoidance and achieve the convergence of the coordination error. Specifically, it is designed as follows:
The case of local minima is avoided by taking the barrier function term as the multiplicative coefficient of the original Lyapunov function . For nonlinear systems with mismatched uncertainties, the design of multiplicative BLFs may render the controller design infeasible [70]. Therefore, the integral multiplicative BLF is designed as follows:
The multiplicative BLF (14) and the integral multiplicative BLF (15) have the same property as the additive BLF (11)—i.e., the BLF (14) and (15) tend to infinity when inter-robot collisions or collisions between robots and obstacles occur (see [70], Lemma 1). It is worth noting that, different from the additive BLF, the multiplicative BLF-induced controller design requires the reference signal to be safe as a pre-condition. Utilizing the integral multiplicative BLF, the work in [71] investigates the distributed collision-free optimal coordination problem for Eulerian–Lagrangian robotic systems. The work in [72] studies the finite-time formation control problem for high-order nonlinear multi-intelligent systems, where obstacle avoidance, unmeasurable states, and deadband inputs are considered. The work in [73] investigates the obstacle avoidance problem in distributed optimal cooperative control by designing a collision-free scheme consisting of an online projection-based trajectory planning scheme and a multiplicative BLF-based distributed backstepping tracking control scheme, which proves that all the robots asymptotically reach the globally optimal position while avoiding collisions with moving obstacles.
3.4. Reference/Command Governors
Reference/command governors [33] are add-on control schemes that enforce the state and control constraints of the pre-stabilized system by modifying the reference, whenever necessary. As an add-on solution, the reference governor and command governor also retain the existing controller schemes, which is attractive to engineers concerned with other demands that are satisfactorily addressed by existing controllers. In this section, we present a reference governor scheme [74] for inter-robot collision avoidance and a command governor scheme [64] for collision/obstacle avoidance, respectively.
3.4.1. Reference Governor for Inter-Robot Collision Avoidance
Consider a team of N heterogeneous agents moving in an n-dimensional Euclidean space, where the dynamics of the ith agent are described by
where denotes the system state and is a smooth function. Further, consider the cooperative formation task, where the desired trajectory of each robot is generated by the following exosystem:
where and are constant matrices. Then, the reference governor scheme is to design a reference signal to regulate the closed-loop system
such that each robot i does not collide with the others and the coordination error converges asymptotically. Note that denotes the predesigned controller which guarantees the tracking error signal is asymptotically stable.
To guarantee the physical safety of the robots, the reference signals should keep a necessary safe distance with tolerance for the tracking error from each other
which guarantees
with denoting the relative distance between robots i and j and denoting the safety threshold. It follows that whether collision avoidance can be achieved depends on the transient tracking performance of the closed-loop system. Accordingly, the reference governor should adjust the reference signal according to the real-time tracking performance of the closed-loop system. For example, a powerful car can perform collision-free maneuvers very close to the other robots, while a less powerful car cannot. Therefore, for robots with poor tracking performance, the decision layer (reference governor) needs to provide a more conservative scheme to strictly guarantee physical safety.
Based on the above analysis, the reference governor is designed depending on whether the tracking error of the robot enters the transient process or not. Define the coordination error variable and the tracking error signal , where X is a matrix satisfying . In the transient-state phase, the distributed reference governor is designed as follows:
where is the output of the high-order filtering of the barrier function. Under the steady-state phase (i.e., ), inter-robot collisions can be avoided after the consensus is reached due to the fact that . Hence, in the design, the barrier function is designed as a gain term. When robots i and j are at risk of collision, term will constrain the consensus error between robots i and j, thus guaranteeing that the system is collision-free. Then, it is assumed that there exist a family of reference dynamics , such that [74]
(i) the closed-loop system is exponentially stable, i.e.,
where is a positive-definite function and is a positive constant.
(ii) for any and if .
In the transient-state phase of the closed-loop system regulated by the reference governor (19), the inter-robot collisions still potentially occur since . To address this issue, we modify (19) with the following event-triggered mechanism
where and denotes the triggering instant. A block diagram of the event-triggered reference governor is shown in Figure 2.
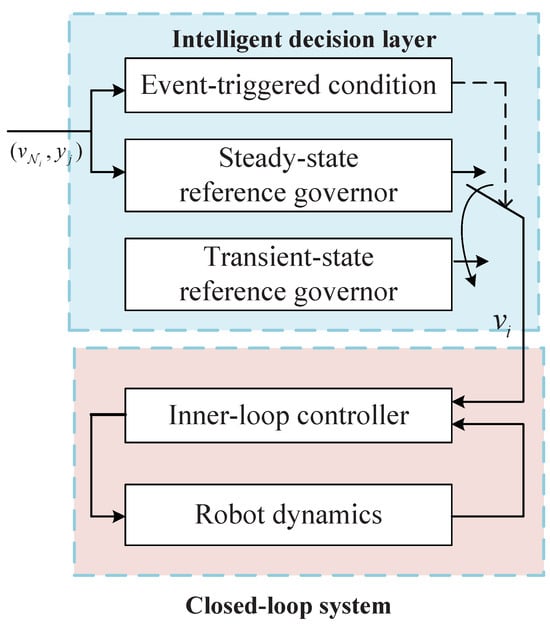
Figure 2.
The framework of reference governor scheme [74].
3.4.2. Command Governor for Collision/Obstacle Avoidance
Consider N heterogeneous nonlinear strict-feedback systems moving on the n-dimensional Euclidean space
Nonlinear strict-feedback system (22) is an important class of nonlinear systems [75,76] that can model many practical systems such as nonholonomic mobile robots [77], unmanned surface vessels [78], and autonomous underwater vehicles.
Consider static elliptical obstacles, i.e.,
To achieve collision/obstacle avoidance, the following assumptions are considered.
Assumption 1.
The reference trajectory is collision-free—i.e., for and , where . Also, there exist two time instants and with such that for any and .
Assumption 2.
The reference trajectory is sufficiently smooth and there exists a positive time-delay value sequence and two positive constants and such that for any .
Assumptions 1 and 2 ensure a feasible solution to the collisions-free scheme. It implies the reference trajectory does not collide with external obstacles—in particular, when only a single agent is allowed to pass through an obstacle, each agent can successively bypass the obstacle along the reference trajectory without colliding with each other. The reference trajectory satisfying Assumptions 1 and 2 can be easily obtained based on the motion planning schemes overviewed in Section 3.1.
To generate a safe command signal, the distributed command governor can be designed as
where , , and and are the high-order filtering of the barrier functions and . For inter-robot collisions, the distributed protocol (14) adopts a similar design to the protocol given in (19). When robots i and j are at risk of collision, the inter-robot consensus error is constrained by the barrier function term . From (14), we can obtain when , thus ensuring the generation of safe command signals. For collisions between robots and obstacles, the collision-free time-delayed command signal is employed. Since the robots need to face different risk scenarios such as no collision risk, inter-robot collision risk, and robot–obstacle collision risk, a convex combinatorial mechanism (14) is designed. The output trajectory in (14) can be rewritten as
where depends on and . This means that trajectory always remains within the generated convex combinatorial space of vectors and , which are collision-free.
The command governor (14) ensures that the generated signal is safe. To ensure that the robots are collision-free, the integral multiplicative BLF is employed to derive the local trajectory tracking controller. Consider the following integral multiplicative BLF:
Applying the traditional backstepping technique, we can obtain the adaptive safety controller.
4. Future Challenges
In the future, there will be numerous practical scenarios where robots will cooperatively perform complex tasks. The development of controllers for collision/obstacle avoidance functions is necessary to guarantee the physical safety of the robots as well as the achievement of tasks in the future. Although the above survey lists numerous approaches that have been proposed and investigated, there are still some challenges in collision/obstacle avoidance control that have not been addressed. Here, we summarize the main challenges.
4.1. Network Constraints
The coordination of MRSs is realized through wireless networks. The introduction of wireless networks also imposes network constraints on MRSs, which mainly include limited communication resources and malicious cyber-attacks. Under network constraints, the cooperative decision-making of MRSs at the command layer will be limited or even destroyed. It is a challenging topic to design decision schemes and control schemes that enable MRSs to make safe decisions under network constraints and thus guarantee the absence of collisions.
4.1.1. Limited Communications Resources
Due to the constraints on communication bandwidth and capacity, only a limited number of bits can be transmitted in the wireless network channel usually [79,80]. Moreover, when a large amount of information interacts frequently through a communication network, it is easy to cause information collision and information retransmission, which in turn leads to communication delay as well as data packet loss. Numerous schemes have been designed to cope with the limited communication resources, such as periodic sampling schemes, event-triggered transmission schemes [81,82,83], and dynamic quantization schemes [84,85,86]. From the results in [81,82,83,84,85,86], it can be obtained that the limited communication resources induce performance degradation of the MRSs in terms of coordination, thus increasing the risk of collisions.
Specifically, constrained by the sampling interval, the design of the consensus gain will be limited, thus the gain term will not be applicable. Moreover, the real-time precise neighbor data will no longer be available. Due to the limited consensus gain and imprecise data interactions, agents i and j are unable to achieve consensus rapidly when faced with the risk of collision, which leads to the occurrence of collision. Therefore, it is a practical challenge to design collision-free schemes under limited communication resources.
4.1.2. Malicious Cyber-Attacks
The introduction of wireless networks also renders MRSs vulnerable to malicious cyber-attacks. Cyber-attacks mainly include Denial-of-Service attacks [87,88,89] as well as false data injection attacks [90,91,92]. Denial-of-Service attacks disrupt the information exchange between robots by blocking the communication links, thus breaking the consensus of the robots at the command layer. False data injection attacks cause robots to receive erroneous information by tampering with or falsifying data. Control decisions based on erroneous data can induce the robot to perform dangerous operations. In the presence of cyber-attacks, MRSs face the dual challenges of communication disruption and information distortion, which make coordination at the command layer more difficult. How to make safe decisions with incomplete and potentially erroneous information poses much higher demands on the design of collision/obstacle avoidance control algorithms.
4.2. Deadlock Issue
Cooperative tasks and collision/obstacle avoidance tasks of MRSs may conflict in the task space. As the number of robots increases, the risk of falling into deadlock increases. In this case, robots achieve collision/obstacle avoidance by not continuing their motion. Although there are various improved schemes to avoid deadlock phenomena by ensuring that the robot is always in motion, such as the consistent perturbation approach, livelock may still exist [31]. This is essentially because the cooperative tasks as well as the collision/obstacle avoidance tasks cannot be handled uniformly in the task space. Therefore, convergence guarantees for cooperative tasks remain an open topic. One possible idea is to improve the robot’s cooperative capabilities by designing the command decision layer that combines collision/obstacle avoidance tasks with cooperative tasks.
4.3. Implementation Issues
There are practical implementation issues that need to be focused on in the collision/obstacle avoidance cooperative control problem of MRSs. These include the following aspects:
- Limited actuator forces. As typical mechanical systems, practical robotic systems are usually constrained by various physical constraints, such as limited actuator forces. The tracking performance of robots is usually limited due to physical constraints, which can increase the risk of collisions during extremely fast movements. Therefore, the limited underlying tracking performance should be considered in the design of safety decisions.
- Imprecise actuators and sensors. In practice, sensors and actuators often suffer from measurement errors, nonlinear properties, hysteresis effects, and manufacturing deviations, which result in limited precision of the information acquired by the system and the control performed. These imprecisions make it difficult to ensure the stability and performance of traditional reference governors, thus affecting the control performance. According to the specific task scenario and the selected components, designing plug-and-play reference governors contributes to the flexibility of the system.
- Sensor failures. The failure signals may lead to false detection of obstacles or even to the determination that a collision has already occurred. In such cases, the barrier function tends to infinity, causing the reference governor scheme to be unresolvable or to perform false avoidance behaviors. Therefore, incorporating fault-tolerant schemes to design robust reference governors would be an interesting topic.
- Unknown dynamic environments. Due to computational efficiency constraints, it is difficult for existing motion planning schemes to achieve sufficiently rapid replanning, and thus they are only applicable to static obstacle environments with a priori global information. In the face of complex and unknown dynamic environments, safe decision-making schemes with fast response capabilities are necessary.
5. Conclusions
This paper provides an overview of cooperative collision/obstacle avoidance control schemes for multi-robot systems, focusing on motion planning, model predictive control, barrier Lyapunov functions, and reference/command governors. The key features of these schemes are discussed, with particular emphasis on the distributed reference/command governor scheme. The design rationale of the reference/command governor is presented, along with a comparison to existing approaches. Finally, the paper discusses future research challenges.
Author Contributions
L.A. was responsible for the Investigation related to the algorithmic framework. C.Z. was responsible for the Methodology related to the collision/obstacle avoidance schemes. G.Y. supervised the entire manuscript and handled the Conceptualization, Writing, Review, and Editing of the entire manuscript. All authors participated in Writing—Original Draft Preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Funds of the National Natural Science Foundation of China (Grant Nos. 62422319, U23A20337 and U1908213); in part by the Provincial Natural Science Foundation of Liaoning (Grant Nos. 2023-MS-069 and 2024-MSBA-44); and by the Research Fund of the State Key Laboratory of Synthetical Automation for Process Industries (Grant No. 2018ZCX03).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zheng, Z.; Ding, N.; Chen, H.; Hu, X.; Zhu, Z.; Fu, X.; Zhang, W.; Zhang, L.; Hazken, S.; Wang, Z.; et al. CCRobot-V: A silkworm-like cooperative cable-climbing robotic system for cable inspection and maintenance. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 164–170. [Google Scholar]
- Sirintuna, D.; Ozdamar, I.; Ajoudani, A. Carrying the uncarriable: A deformation-agnostic and human-cooperative framework for unwieldy objects using multiple robots. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 7497–7503. [Google Scholar]
- Sujit, P.B.; Beard, R. Cooperative path planning for multiple UAVs exploring an unknown region. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 347–352. [Google Scholar]
- Che, W.-W.; Zhang, L.; Deng, C.; Wu, Z.-G. Hierarchical lane-changing control for vehicle platoons in prescribed performance. Automatica 2025, 171, 111972. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, K. Advanced model predictive control framework for autonomous intelligent mechatronic systems: A tutorial overview and perspectives. Annu. Rev. Control 2021, 52, 170–196. [Google Scholar] [CrossRef]
- Chen, F.; Sewlia, M.; Dimarogonas, D.V. Cooperative control of heterogeneous multi-agent systems under spatiotemporal constraints. Annu. Rev. Control 2024, 57, 100946. [Google Scholar] [CrossRef]
- Xiao, W.; Li, A.; Cassandras, C.G.; Belta, C. Toward model-free safety-critical control with humans in the loop. Annu. Rev. Control 2024, 57, 100944. [Google Scholar] [CrossRef]
- Garg, K.; Zhang, S.; So, O.; Dawson, C.; Fan, C. Learning safe control for multi-robot systems: Methods, verification, and open challenges. Annu. Rev. Control 2024, 57, 100948. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. Rrt-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA. IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Sandakalum, T.; Ang, J.M.H. Motion planning for mobile manipulatorsa systematic review. Machines 2022, 10, 97. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, J.; Wan, W. Survey of optimal motion planning. IET Cyber-Syst. Robot. 2019, 1, 13–19. [Google Scholar] [CrossRef]
- Kingston, Z.; Moll, M.; Kavraki, L.E. Sampling-based methods for motion planning with constraints. Annu. Rev. Control Robot. Atonomous Syst. 2018, 1, 159–185. [Google Scholar] [CrossRef]
- Chase Kew, J.; Ichter, B.; Bandari, M.; Lee, T.W.E.; Faust, A. Neural collision clearance estimator for batched motion planning. In Algorithmic Foundations of Robotics XIV; LaValle, S.M., Lin, M., Ojala, T., Shell, D., Yu, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 73–89. [Google Scholar]
- Van Den Berg, J.P.; Overmars, M.H. Roadmap-based motion planning in dynamic environments. IEEE Trans. Robot. 2005, 21, 885–897. [Google Scholar] [CrossRef]
- Peasgood, M.; Clark, C.M.; McPhee, J. A complete and scalable strategy for coordinating multiple robots within roadmaps. IEEE Trans. Robot. 2008, 24, 283–292. [Google Scholar] [CrossRef]
- Kloder, S.; Hutchinson, S. Path planning for permutation-invariant multirobot formations. IEEE Trans. Robot. 2006, 22, 650–665. [Google Scholar] [CrossRef]
- Jiang, C.; Guo, Y. Incorporating control barrier functions in distributed model predictive control for multi-robot coordinated control. IEEE Trans. Control Netw. Syst. 2024, 11, 547–557. [Google Scholar] [CrossRef]
- Wen, G.; Lam, J.; Fu, J.; Wang, S. Distributed MPC-based robust collision avoidance formation navigation of constrained multiple USVs. IEEE Trans. Intell. Veh. 2024, 9, 1804–1816. [Google Scholar] [CrossRef]
- Domahidi, A.; Zgraggen, A.U.; Zeilinger, M.N.; Morari, M.; Jones, C.N. Efficient interior point methods for multistage problems arising in receding horizon control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 668–674. [Google Scholar]
- Richter, S.; Jones, C.N.; Morari, M. Computational complexity certification for real-time MPC with input constraints based on the fast gradient method. IEEE Trans. Autom. Control 2012, 57, 1391–1403. [Google Scholar] [CrossRef]
- Jiang, C. Distributed sampling-based model predictive control via belief propagation for multi-robot formation navigation. IEEE Robot. Autom. Lett. 2024, 9, 3467–3474. [Google Scholar] [CrossRef]
- Abraham, I.; Handa, A.; Ratliff, N.; Lowrey, K.; Murphey, T.D.; Fox, D. Model-based generalization under parameter uncertainty using path integral control. IEEE Robot. Autom. Lett. 2020, 5, 2864–2871. [Google Scholar] [CrossRef]
- Kobilarov, M. Cross-entropy motion planning. Int. J. Robot. Res. 2012, 31, 855–871. [Google Scholar] [CrossRef]
- Williams, G.; Drews, P.; Goldfain, B.; Rehg, J.M.; Theodorou, E.A. Information-theoretic model predictive control: Theory and applications to autonomous driving. IEEE Trans. Robot. 2018, 34, 1603–1622. [Google Scholar] [CrossRef]
- Broek, B.V.D.; Wiegerinck, W.; Kappen, B. Graphical model inference in optimal control of stochastic multi-agent systems. J. Artif. Intell. Res. 2008, 32, 95–122. [Google Scholar] [CrossRef]
- Wan, N.; Gahlawat, A.; Hovakimyan, N.; Theodorou, E.A.; Voulgaris, P.G. Cooperative path integral control for stochastic multi-agent systems. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 1262–1267. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Panagou, D.; Stipanović, D.M.; Voulgaris, P.G. Distributed coordination control for multi-robot networks using Lyapunov-like barrier functions. IEEE Trans. Autom. Control 2016, 61, 617–632. [Google Scholar] [CrossRef]
- Ames, A.D.; Xu, X.; Grizzle, J.W.; Tabuada, P. Control barrier function based quadratic programs for safety critical systems. IEEE Trans. Autom. Control 2017, 62, 3861–3876. [Google Scholar] [CrossRef]
- Wang, L.; Ames, A.D.; Egerstedt, M. Safety barrier certificates for collisions-free multirobot systems. IEEE Trans. Robot. 2017, 33, 661–674. [Google Scholar] [CrossRef]
- Koptev, M.; Figueroa, N.; Billard, A. Reactive collision-free motion generation in joint space via dynamical systems and sampling-based MPC. Int. J. Robot. Res. 2024, 43, 2049–2069. [Google Scholar] [CrossRef]
- Tedesco, F.; Casavola, A.; Garone, E. Distributed command governor strategies for constrained coordination of multi-agent networked systems. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 6005–6010. [Google Scholar]
- Garone, E.; Cairano, S.D.; Kolmanovsky, I. Reference and command governors for systems with constraints: A survey on theory and applications. Automatica 2017, 75, 306–328. [Google Scholar] [CrossRef]
- Hansel, K.; Urain, J.; Peters, J.; Chalvatzaki, G. Hierarchical policy blending as inference for reactive robot control. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 10181–10188. [Google Scholar]
- Rosolia, U.; Singletary, A.; Ames, A.D. Unified multirate control: From low-level actuation to high-level planning. IEEE Trans. Autom. Control 2022, 64, 6627–6640. [Google Scholar] [CrossRef]
- Cui, Y.; Ye, S.; Xu, X.; Sha, H.; Wang, C.; Lin, L.; Liu, Z.; Xiong, R.; Wang, Y. Learning hierarchical graph-based policy for goal-reaching in unknown environments. IEEE Robot. Autom. Lett. 2024, 9, 5655–5662. [Google Scholar] [CrossRef]
- Jin, T.; Di, J.; Wang, X.; Ji, H. Safety barrier certificates for path integral control: Safety-critical control of quadrotors. IEEE Robot. Autom. Lett. 2023, 8, 6006–6012. [Google Scholar] [CrossRef]
- Dahlin, A.; Karayiannidis, Y. Autonomous navigation with convergence guarantees in complex dynamic environments. Automatica 2025, 173, 112026. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Seng, W.L.; Barca, J.C.; Sekercioglu, Y.A. Distributed formation control in cluttered environments. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1387–1392. [Google Scholar]
- Chi, T.; Zhang, C.; Song, Y.; Feng, J. A strategy of multi-robot formation and obstacle avoidance in unknown environment. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 1455–1460. [Google Scholar]
- Wen, G.; Chen, C.P.; Liu, Y.-J. Formation control with obstacle avoidance for a class of stochastic multiagent systems. IEEE Trans. Ind. Electron. 2018, 65, 5847–5855. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots. IEEE Trans. Ind. Electron. 2014, 61, 347–354. [Google Scholar] [CrossRef]
- La, H.M.; Lim, R.; Sheng, W. Multirobot cooperative learning for predator avoidance. IEEE Trans. Control Syst. Technol. 2015, 23, 52–63. [Google Scholar] [CrossRef]
- Bai, C.; Yan, P.; Pan, W.; Guo, J. Learning-based multi-robot formation control with obstacle avoidance. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11811–11822. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, L.; Lam, T.L.; Vijayakumar, S. Task-space decomposed motion planning framework for multi-robot loco-manipulation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8158–8164. [Google Scholar]
- Tang, Q.; Zhang, Y.; Yu, F.; Zhang, J. An obstacle avoidance approach based on system outlined rectangle for cooperative transportation of multiple mobile manipulators. In Proceedings of the 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Shenyang, China, 24–27 August 2018; pp. 533–538. [Google Scholar]
- Roy, D.; Chowdhury, A.; Maitra, M.; Bhattacharya, S. Multi-robot virtual structure switching and formation changing strategy in an unknown occluded environment. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4854–4861. [Google Scholar]
- Alonso-Mora, J.; Knepper, R.; Siegwart, R.; Rus, D. Local motion planning for collaborative multi-robot manipulation of deformable objects. In Proceedings of the in 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5495–5502. [Google Scholar]
- Alonso-Mora, J.; Baker, S.; Rus, D. Multi-robot formation control and object transport in dynamic environments via constrained optimization. Int. J. Robot. Res. 2017, 36, 1000–1021. [Google Scholar] [CrossRef]
- Muskem, K.R.; Rawlings, J.B. Model predictive control with linear models. AIChE J. 1993, 39, 262–287. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K.; Lee, T.H. Applied Predictive Control; Springer: London, UK, 2002. [Google Scholar]
- Christofides, P.D.; Scattolini, R.D.; de la Peña, M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Müller, M.A.; Allgöwer, F. Economic and distributed model predictive control: Recent developments in optimization-based control. SICE J. Control Meas. Syst. Integr. 2017, 10, 39–52. [Google Scholar]
- Ferrari-Trecate, G.; Galbusera, L.; Marciandi, M.P.E.; Scattolini, R. Model predictive control schemes for consensus in multi-agent systems with single-and double-integrator dynamics. IEEE Trans. Autom. Control 2009, 54, 2560–2572. [Google Scholar] [CrossRef]
- Liu, X.; Shi, Y.; Constantinescu, D. Robust distributed model predictive control of constrained dynamically decoupled nonlinear systems: A contraction theory perspective. Syst. Control Lett. 2017, 105, 84–91. [Google Scholar] [CrossRef]
- Franco, E.; Magni, L.; Parisini, T.; Polycarpou, M.M.; Raimondo, D.M. Cooperative constrained control of distributed agents with nonlinear dynamics and delayed information exchange: A stabilizing receding-horizon approach. IEEE Trans. Autom. Control 2008, 53, 324–338. [Google Scholar] [CrossRef]
- Wang, C.; Ong, C.-J. Distributed model predictive control of dynamically decoupled systems with coupled cost. Automatica 2010, 46, 2053–2058. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Robust distributed model predictive control of constrained continuous-time nonlinear systems: A robustness constraint approach. IEEE Trans. Autom. Control 2014, 59, 1673–1678. [Google Scholar] [CrossRef]
- Dai, L.; Cao, Q.; Xia, Y.; Gao, Y. Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance. J. Frankl. Inst. 2017, 354, 2068–2085. [Google Scholar] [CrossRef]
- Wang, P.; Ding, B. Distributed RHC for tracking and formation of nonholonomic multi-vehicle systems. IEEE Trans. Autom. Control 2014, 59, 1439–1453. [Google Scholar] [CrossRef]
- Williams, G.; Aldrich, A.; Theodorou, E.A. Model predictive path integral control: From theory to parallel computation. J. Guid. Control Dyn. 2017, 40, 344–357. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Collisions-free distributed cooperative output regulation of nonlinear multi-agent systems. IEEE Trans. Autom. Control 2024, 69, 8072–8079. [Google Scholar] [CrossRef]
- Verginis, C.K.; Dimarogonas, D.V. Closed-form barrier functions for multi-agent ellipsoidal systems with uncertain lagrangian dynamics. IEEE Control Syst. Lett. 2019, 3, 727–732. [Google Scholar] [CrossRef]
- Arambula Cosio, F.; Padilla Castaẽda, M. Autonomous robot navigationusing adaptive potential fields. Math. Comput. Model. 2004, 40, 1141–1156. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef]
- Kim, J.-O.; Khosla, P.K. Real-time obstacle avoidance using harmonic potential functions. IEEE Trans. Robot. Autom. 1992, 8, 338–349. [Google Scholar] [CrossRef]
- Ge, S.S.; Cui, Y.J. New potential functions for mobile robot path planning. IEEE Trans. Robot. Autom. 2000, 16, 615–620. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, G.-H. Secure adaptive trajectory tracking control for nonlinear robot systems under multiple dynamic obstacles: Safety barrier certificates. IEEE Trans. Ind. Electron. 2022, 69, 11549–11559. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Collisions-free distributed optimal coordination for multiple Euler-Lagrangian systems. IEEE Trans. Autom. Control 2022, 67, 460–467. [Google Scholar] [CrossRef]
- Wang, X.; Ye, D. Finite-time output-feedback formation control for high-order nonlinear multiagent systems with obstacle avoidance. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1878–1888. [Google Scholar] [CrossRef]
- An, L.; Yang, G.H.; Wasly, S. Obstacle avoidance in distributed optimal coordination of multirobot systems: A trajectory planning and tracking strategy. IEEE Trans. Control Netw. Syst. 2024, 11, 1335–1344. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H.; Deng, C.; Wen, C. Event-triggered reference governors for collisions-free leader-following coordination under unreliable communication topologies. IEEE Trans. Autom. Control 2024, 69, 2116–2130. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Tong, S. Observer-based neuro-adaptive optimized control of strict-feedback nonlinear systems with state constraints. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3131–3145. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, W.; Lam, H.-K.; Cao, L. An improved predefined-time adaptive neural control approach for nonlinear multiagent systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6311–6320. [Google Scholar] [CrossRef]
- Do, K.D. Formation tracking control of unicycle-type mobile robots with limited sensing ranges. IEEE Trans. Control Syst. Technol. 2008, 16, 527–538. [Google Scholar] [CrossRef]
- Hu, B.-B.; Zhang, H.-T.; Liu, B.; Ding, J.; Xu, Y.; Luo, C.; Cao, H. Coordinated navigation control of cross-domain unmanned systems via guiding vector fields. IEEE Trans. Control Syst. Technol. 2024, 32, 550–563. [Google Scholar] [CrossRef]
- Carli, R.; Bullo, F.; Zampieri, S. Quantized average consensus via dynamic coding/decoding schemes. Int. J. Robust Nonlinear Control 2010, 20, 156–175. [Google Scholar] [CrossRef]
- Fan, S.; Meng, M.; Fu, Y.; Deng, C. Distributed adaptive tracking control for fuzzy nonlinear MASs under round-robin protocol. IEEE Trans. Fuzzy Syst. 2025, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, C.; Che, W.-W.; An, L. Adaptive backstepping control for nonlinear interconnected systems with prespecified-performance-driven output triggering. Automatica 2023, 154, 111063. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, C.; An, L. Asymptotic tracking control of nonlinear strict-feedback systems with state/output triggering: A homogeneous filtering approach. IEEE Trans. Autom. Control 2024, 69, 6413–6420. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, G.-H. Event-triggered-based adaptive fuzzy finite-time resilient output feedback control for MIMO stochastic nonlinear system subject to deception attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 6534–6547. [Google Scholar] [CrossRef]
- Li, T.; Fu, M.; Xie, L.; Zhang, J.-F. Distributed consensus with limited communication data rate. IEEE Trans. Autom. Control 2011, 56, 279–292. [Google Scholar] [CrossRef]
- You, K.; Xie, L. Network topology and communication data rate for consensusability of discrete-time multi-agent systems. IEEE Trans. Autom. Control 2011, 56, 2262–2275. [Google Scholar] [CrossRef]
- Li, T.; Xie, L. Distributed coordination of multi-agent systems with quantized-observer based encoding-decoding. IEEE Trans. Autom. Control 2012, 57, 3023–3037. [Google Scholar]
- An, L.; Yang, G.-H. Decentralized adaptive fuzzy secure control for nonlinear uncertain interconnected systems against intermittent DoS attacks. IEEE Trans. Cybern. 2019, 49, 827–838. [Google Scholar] [CrossRef]
- Fan, S.; Yue, D.; Yan, H.C.; Xie, X.P.; Deng, C. Resilient cooperative optimization control for fuzzy nonlinear MASs under DoS attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 3903–3913. [Google Scholar] [CrossRef]
- An, L.; Zhao, C.; Zhang, L. Resilient adaptive backstepping tracking control of nonlinear systems without a priori knowledge of DoS attacks. Automatica 2025, 174, 112119. [Google Scholar] [CrossRef]
- Ren, H.; Cheng, Z.; Qin, J.; Lu, R. Deception attacks on event-triggered distributed consensus estimation for nonlinear systems. Automatica 2023, 154, 111100. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Secure state estimation against sparse sensor attacks with adaptive switching mechanism. IEEE Trans. Autom. Control 2018, 63, 2596–2603. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Data-driven coordinated attack policy design based on adaptive L2-gain optimal theory. IEEE Trans. Autom. Control 2018, 63, 1850–1857. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).