Deep Neural Network for Valve Fault Diagnosis Integrating Multivariate Time-Series Sensor Data
Abstract
1. Introduction
- This study targets complex multi-valve systems by constructing experimental apparatuses, collecting data, and proposing diagnostic methods for faults in systems with multiple interconnected valves, in contrast to traditional studies on single valves or simpler systems.
- The proposed method is designed to not only detect the presence of faults but also accurately identify the faulty valve and simultaneously assess fault severities.
- This study aims to predict fault locations and fault severities, enabling flexible diagnostics for fault locations and unseen fault severities.
2. Experimental Setup and Dataset
2.1. Experimental Setup
2.2. Determination of Fault Severity in Valves
2.3. Dataset
3. Methods
3.1. Training Model Based on 1D CNN
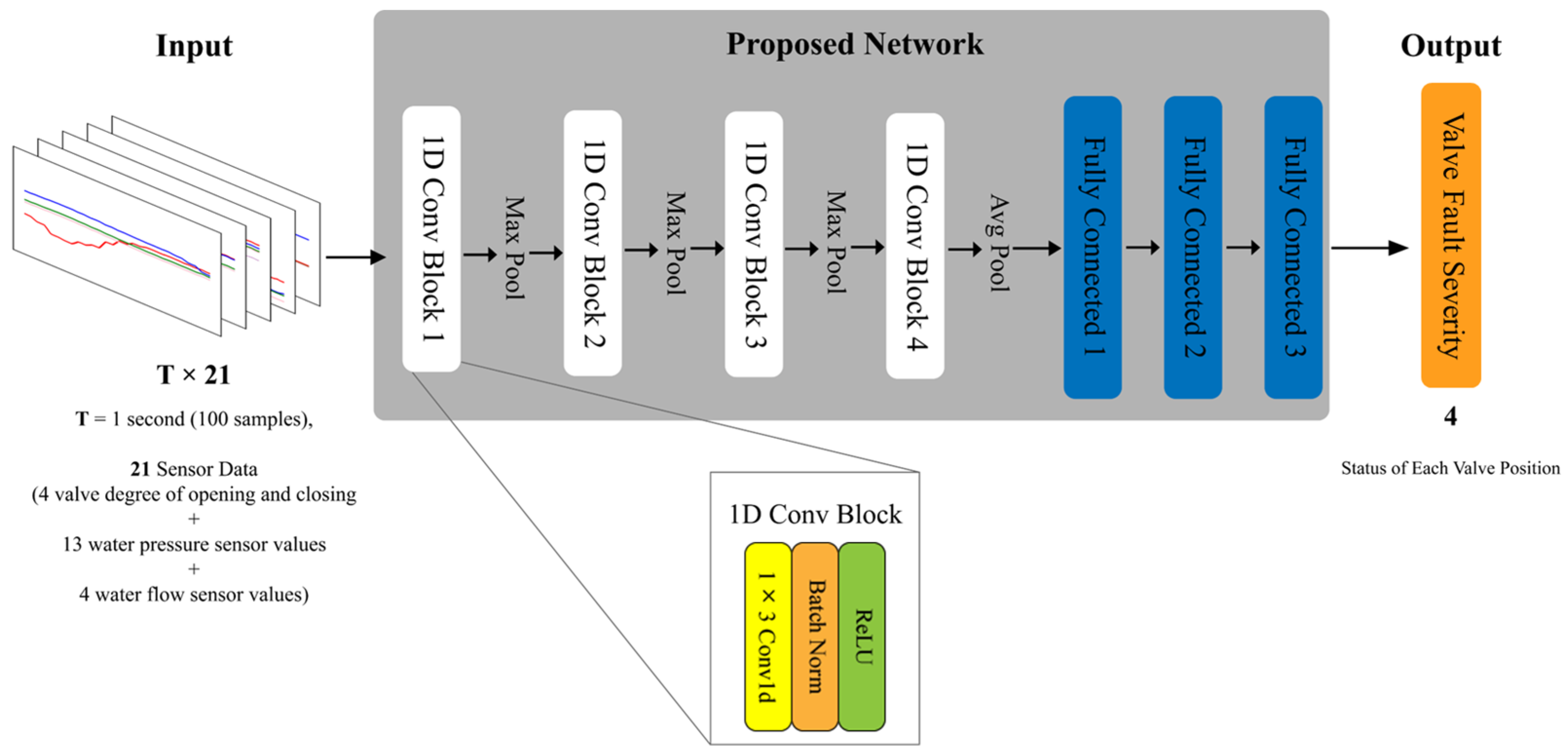
3.1.1. Composition of Input and Output Data
3.1.2. Network Composition
3.1.3. Training Process
3.2. Testing with Trained and Unseen Severities of Valve Faults
4. Experimental Results and Discussion
- Proposed network input composition: This follows the input configuration introduced in the methods section. It consists of the motor rotation values representing the opening and closing amounts of 4 valves, 4 water pressure sensors located at the inlet of each valve, 4 water pressure sensors at the outlet of each valve, a total of 5 water pressure sensors in the main pipe, and a total of 4 flow sensors (a total of 21 input dimensions).
- Input composition 1: It consists of 4 motor values representing the opening and closing amounts of each valve, 4 water pressure sensors at the inlet of each valve, and 4 water pressure sensors at the outlet of each valve (a total of 12 input dimensions).
- Input composition 2: It consists of 4 motor values representing the opening and closing amounts of each valve, and only 4 water pressure sensor values at the inlet of each valve (a total of 8 input dimensions).
- Input composition 3: It consists of 4 motor values representing the opening and closing amounts of each valve, 5 water pressure sensor values located in the main pipe, 4 water pressure sensor values at the inlets of the valves, and 4 water pressure sensor values at the outlets of the valves (a total of 17 input dimensions).
- Input composition 4: It consists of 4 motor values representing the opening and closing amounts of each valve, 5 water pressure sensor values located in the main pipe, and only 4 water pressure sensor values at the outlet of each valve (a total of 13 input dimensions).
- Input composition 5: It consists of 4 motor values indicating the opening and closing amounts of each valve, 5 water pressure sensor values, and 4 flow sensor values (a total of 13 input dimensions).
- Input composition 6: It consists of 4 motor values representing the opening and closing amounts of each valve, and only 4 water pressure sensor values at the outlet of each valve (a total of 8 input dimensions).
- Input composition 7: It consists of 4 motor values representing the opening and closing amounts of each valve, and only 4 flow sensor values (a total of 8 input dimensions).
- Input composition 8: It consists of 4 motor values representing the opening and closing amounts of each valve, 5 water pressure sensor values located in the main pipe, and only 4 water pressure sensor values at the inlet of each valve (a total of 13 input dimensions).
- Input composition 9: It consists of 4 motor values representing the opening and closing amounts of each valve, and only 5 water pressure sensor values located in the main pipe (a total of 9 input dimensions).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, J.; Yu, Y.; Yang, J.; Jia, H. Research on the generalisation method of diesel engine exhaust valve leakage fault diagnosis based on acoustic emission. Measurement 2023, 210, 112560. [Google Scholar] [CrossRef]
- Sim, H.; Ramli, R.; Saifizul, A.; Abdullah, M. Empirical investigation of acoustic emission signals for valve failure identification by using statistical method. Measurement 2014, 58, 165–174. [Google Scholar] [CrossRef]
- Navada, B.R.; Sravani, V.; Venkata, S.K. Enhancing Industrial Valve Diagnostics: Comparison of Two Preprocessing Methods on the Performance of a Stiction Detection Method Using an Artificial Neural Network. Appl. Syst. Innov. 2024, 7, 104. [Google Scholar] [CrossRef]
- Vashishtha, G.; Chauhan, S.; Sehri, M.; Zimroz, R.; Dumond, P.; Kumar, R.; Gupta, M.K. A roadmap to fault diagnosis of industrial machines via machine learning: A brief review. Measurement 2024, 242, 116216. [Google Scholar] [CrossRef]
- Buffa, S.; Fouladfar, M.H.; Franchini, G.; Lozano Gabarre, I.; Andrés Chicote, M. Advanced control and fault detection strategies for district heating and cooling systems—A review. Appl. Sci. 2021, 11, 455. [Google Scholar] [CrossRef]
- Vashishtha, G.; Chauhan, S.; Sehri, M.; Hebda-Sobkowicz, J.; Zimroz, R.; Dumond, P.; Kumar, R. Advancing machine fault diagnosis: A detailed examination of convolutional neural networks. Meas. Sci. Technol. 2024, 36, 022001. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, T.; Zhang, D. Fault Detection of Flow Control Valves Using Online LightGBM and STL Decomposition. Actuators 2024, 13, 222. [Google Scholar] [CrossRef]
- Liang, Q.; Wang, W.; Zhai, Y.; Sun, Y.; Zhang, W. Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim. Actuators 2023, 12, 417. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.; Xie, Y.; Wu, M.; Li, Z.; Mu, W.; Liu, G. Multi-sensor cross-domain fault diagnosis method for leakage of ship pipeline valves. Ocean Eng. 2024, 299, 117211. [Google Scholar] [CrossRef]
- Yin, H.; Xu, H.; Fan, W.; Sun, F. Fault diagnosis of pressure relief valve based on improved deep Residual Shrinking Network. Measurement 2024, 224, 113752. [Google Scholar] [CrossRef]
- Yang, T.; Huang, X.; Zhang, Y.; Li, J.; Zhou, X.; Han, Q. RTCA-Net: A New Framework for Monitoring the Wear Condition of Aero Bearing with a Residual Temporal Network under Special Working Conditions and Its Interpretability. Mathematics 2024, 12, 2687. [Google Scholar] [CrossRef]
- Kumar, P.; Khalid, S.; Kim, H.S. Prognostics and health management of rotating machinery of industrial robot with deep learning applications—A review. Mathematics 2023, 11, 3008. [Google Scholar] [CrossRef]
- Shi, J.; Yi, J.; Ren, Y.; Li, Y.; Zhong, Q.; Tang, H.; Chen, L. Fault diagnosis in a hydraulic directional valve using a two-stage multi-sensor information fusion. Measurement 2021, 179, 109460. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, J.; Chen, Z.; Ma, J.; Li, T. Diagnosisformer: An efficient rolling bearing fault diagnosis method based on improved Transformer. Eng. Appl. Artif. Intell. 2023, 124, 106507. [Google Scholar] [CrossRef]
- Tidriri, K.; Chatti, N.; Verron, S.; Tiplica, T. Bridging data-driven and model-based approaches for process fault diagnosis and health monitoring: A review of researches and future challenges. Annu. Rev. Control 2016, 42, 63–81. [Google Scholar] [CrossRef]
- Sekunda, A.; Niemann, H.; Poulsen, N.K.; Santos, I. Parametric fault diagnosis of an active gas bearing. Int. J. Control Autom. Syst. 2019, 17, 69–84. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, M.; Qian, H.; Liu, L.; Yang, H.; Zhang, Y.; Liu, X.; Xie, Z.; Yang, L.; Zhang, W. A review of valve health diagnosis and assessment: Insights for intelligence maintenance of natural gas pipeline valves in China. Eng. Fail. Anal. 2023, 153, 107581. [Google Scholar] [CrossRef]
- Shlezinger, N.; Whang, J.; Eldar, Y.C.; Dimakis, A.G. Model-based deep learning. Proc. IEEE 2023, 111, 465–499. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Q.; Fang, J.; Lai, Z.; Feng, R.; Wei, J. Active fault-tolerant control for the dual-valve hydraulic system with unknown dead-zone. ISA Trans. 2024, 145, 399–411. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Xu, X.; Shan, H. Model-Based Fault Diagnosis of Actuators in Electronically Controlled Air Suspension System. World Electr. Veh. J. 2022, 13, 219. [Google Scholar] [CrossRef]
- Tian, H.; Li, S.; Gong, Y. Physical Model-based Rapid Quantitative Diagnosis of Solenoid On–Off Valve Spool Stiction Faults. Arab. J. Sci. Eng. 2024, 1–17. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, B.; Chen, W.; Tan, D.; Shen, D. Review of model-based and data-driven approaches for leak detection and location in water distribution systems. Water Supply 2021, 21, 3282–3306. [Google Scholar] [CrossRef]
- Adedeji, K.B.; Hamam, Y.; Abe, B.T.; Abu-Mahfouz, A.M. Towards achieving a reliable leakage detection and localization algorithm for application in water piping networks: An overview. IEEE Access 2017, 5, 20272–20285. [Google Scholar] [CrossRef]
- Chan, T.K.; Chin, C.S.; Zhong, X. Review of current technologies and proposed intelligent methodologies for water distributed network leakage detection. IEEE Access 2018, 6, 78846–78867. [Google Scholar] [CrossRef]
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-based techniques focused on modern industry: An overview. IEEE Trans. Ind. Electron. 2014, 62, 657–667. [Google Scholar] [CrossRef]
- Ma, D.; Liu, Z.; Gao, Q.; Huang, T. Fault diagnosis of a solenoid valve based on multi-feature fusion. Appl. Sci. 2022, 12, 5904. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, L.; Kang, R.; Lan, X. Research on fault diagnosis for reciprocating compressor valve using information entropy and SVM method. J. Loss Prev. Process Ind. 2009, 22, 864–867. [Google Scholar] [CrossRef]
- Xiao, S.; Nie, A.; Zhang, Z.; Liu, S.; Song, M.; Zhang, H. Fault diagnosis of a reciprocating compressor air valve based on deep learning. Appl. Sci. 2020, 10, 6596. [Google Scholar] [CrossRef]
- Guo, F.-Y.; Zhang, Y.-C.; Wang, Y.; Ren, P.-J.; Wang, P. Fault diagnosis of reciprocating compressor valve based on transfer learning convolutional neural network. Math. Probl. Eng. 2021, 2021, 8891424. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Liu, J.; Wu, B.; Hu, Y. Graph features dynamic fusion learning driven by multi-head attention for large rotating machinery fault diagnosis with multi-sensor data. Eng. Appl. Artif. Intell. 2023, 125, 106601. [Google Scholar] [CrossRef]
- Gálvez, A.; Diez-Olivan, A.; Seneviratne, D.; Galar, D. Fault detection and RUL estimation for railway HVAC systems using a hybrid model-based approach. Sustainability 2021, 13, 6828. [Google Scholar] [CrossRef]
- Louen, C.; Ding, S.; Kandler, C. A new framework for remaining useful life estimation using support vector machine classifier. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013; pp. 228–233. [Google Scholar]
- Lim, R.; Mba, D. Fault detection and remaining useful life estimation using switching Kalman filters. In Engineering Asset Management-Systems, Professional Practices and Certification: Proceedings of the 8th World Congress on Engineering Asset Management (WCEAM 2013) & the 3rd International Conference on Utility Management & Safety (ICUMAS); Springer: Cham, Switzerland, 2015; pp. 53–64. [Google Scholar]
- Zhang, K.; Wang, J.; Shi, H.; Zhang, X. A variable working condition rolling bearing fault diagnosis method based on improved triplet loss algorithm. Int. J. Control Autom. Syst. 2023, 21, 1361–1372. [Google Scholar] [CrossRef]
- Alabi, A.; Chiesa, M.; Garlisi, C.; Palmisano, G. Advances in anti-scale magnetic water treatment. Environ. Sci. Water Res. Technol. 2015, 1, 408–425. [Google Scholar] [CrossRef]
- Dayalan, E.; De Moraes, F.; Shadley, J.R.; Rybicki, E.F.; Shirazi, S.A. CO2 corrosion prediction in pipe flow under FeCO3 scale-forming conditions. In Proceedings of the CORROSION 98, San Diego, CA, USA, 22–27 March 1998; p. NACE-98051. [Google Scholar]
- Joshy, N.; Meera, V. Scale control on pipe materials: A review. Green Build. Sustain. Eng. Proc. GBSE 2020, 2019, 421–429. [Google Scholar]
- Shaik, N.B.; Pedapati, S.R.; Dzubir, F.A.B. Remaining useful life prediction of a piping system using artificial neural networks: A case study. Ain Shams Eng. J. 2022, 13, 101535. [Google Scholar] [CrossRef]
- Rezaei, H.; Ryan, B.; Stoianov, I. Pipe failure analysis and impact of dynamic hydraulic conditions in water supply networks. Procedia Eng. 2015, 119, 253–262. [Google Scholar] [CrossRef]
- Cengel, Y.; Cimbala, J. Ebook: Fluid Mechanics Fundamentals and Applications (Si Units); McGraw Hill: New York, NY, USA, 2013. [Google Scholar]
- Allamy, S.; Koerich, A.L. 1D CNN architectures for music genre classification. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 5–7 December 2021; pp. 1–7. [Google Scholar]
- Abrol, V.; Sharma, P. Learning hierarchy aware embedding from raw audio for acoustic scene classification. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 1964–1973. [Google Scholar] [CrossRef]
- Rakhlin, A. Convolutional neural networks for sentence classification. GitHub 2016, 6, 25. [Google Scholar]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Rizvi, S.M.H. Time series deep learning for robust steady-state load parameter estimation using 1D-CNN. Arab. J. Sci. Eng. 2022, 47, 2731–2744. [Google Scholar] [CrossRef]
- Tang, W.; Long, G.; Liu, L.; Zhou, T.; Blumenstein, M.; Jiang, J. Omni-scale cnns: A simple and effective kernel size configuration for time series classification. arXiv 2020, arXiv:2002.10061. [Google Scholar]
- Riedel, H.; Lorenzen, S.R.; Hübler, C. Object-size-driven design of convolutional neural networks: Virtual axle detection based on raw data. Eng. Appl. Artif. Intell. 2025, 141, 109803. [Google Scholar] [CrossRef]
- Krishna, D.; Amrutha, D.; Reddy, S.S.; Acharya, A.; Garapati, P.A.; Triveni, B. Language independent gender identification from raw waveform using multi-scale convolutional neural networks. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 6559–6563. [Google Scholar]
- Khan, A.; Ko, D.-K.; Lim, S.C.; Kim, H.S. Structural vibration-based classification and prediction of delamination in smart composite laminates using deep learning neural network. Compos. Part B Eng. 2019, 161, 586–594. [Google Scholar] [CrossRef]
- Huang, S.; Tang, J.; Dai, J.; Wang, Y. Signal status recognition based on 1DCNN and its feature extraction mechanism analysis. Sensors 2019, 19, 2018. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-W.; Kim, S.-C.; Lim, S.-C. DeepTouch: Enabling touch interaction in underwater environments by learning touch-induced inertial motions. IEEE Sens. J. 2022, 22, 8924–8932. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Cai, X.; Li, D.; Li, F. Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR. Mathematics 2024, 12, 3713. [Google Scholar] [CrossRef]

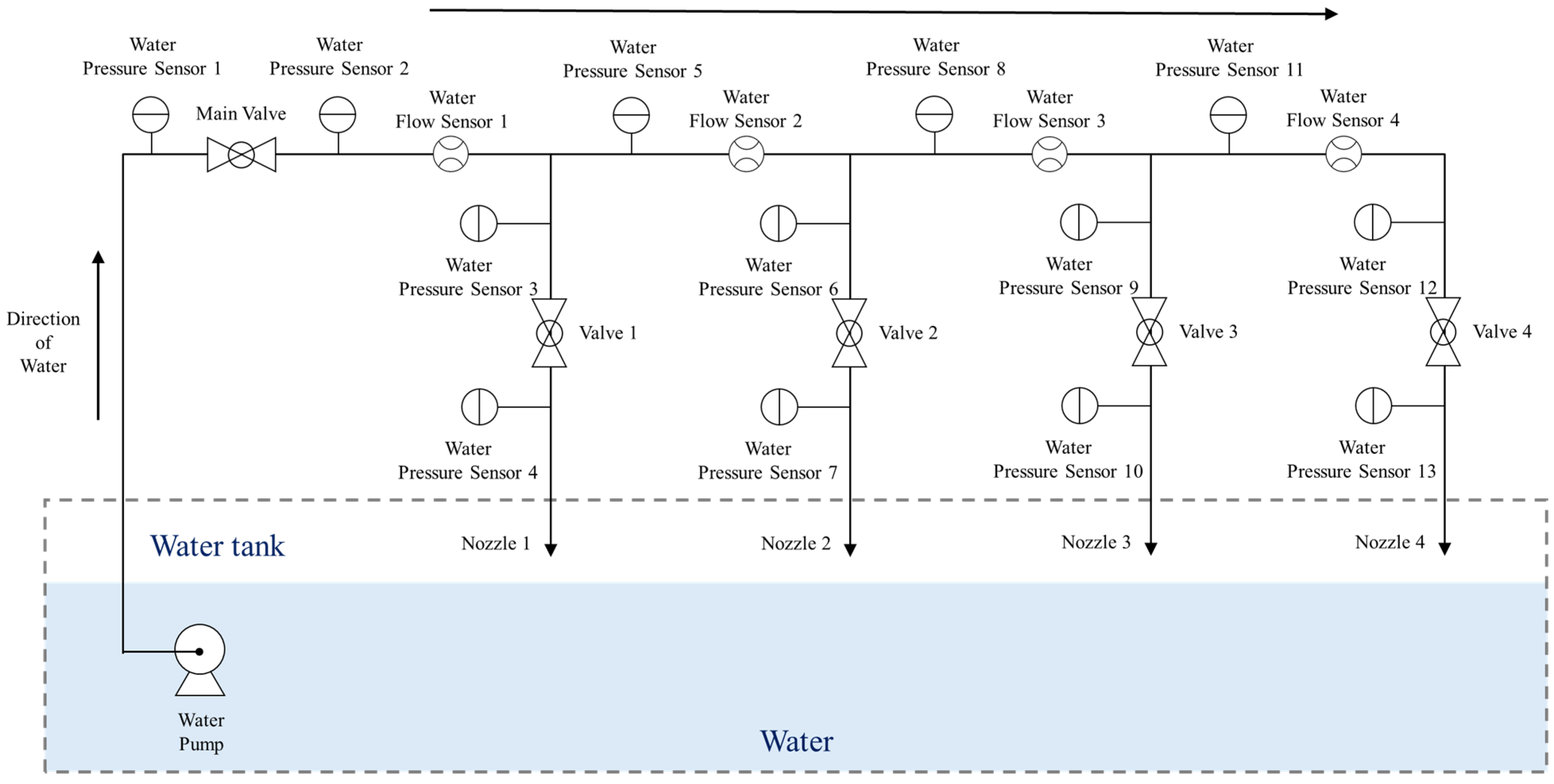




| Fault Severity | Internal Diameter (mm) |
|---|---|
| 0.0 | 7.0 |
| 0.1 | 5.67 |
| 0.2 | 4.33 |
| 0.3 | 3.0 |
| 0.4 | 2.63 |
| 0.5 | 2.25 |
| 0.6 | 1.88 |
| 0.7 | 1.5 |
| 0.8 | 1.0 |
| 0.9 | 0.5 |
| 1.0 | 0.0 |
| Number of Operating Valves | Case (Valve Number) |
|---|---|
| 1 | 4 cases: (1), (2), (3), and (4) |
| 2 | 6 cases: (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), and (3, 4) |
| 3 | 4 cases: (1,2,3), (1,2,4), (1,3,4), and (2,3,4) |
| Fault Severity | Number of Operating Valves | Non-Operating Valve Angle | |
|---|---|---|---|
| Training dataset | 0.0, 0.3, 0.7, 1.0 | 1, 2, 3 | 23°, 35°, 41°, 47°, 59° |
| Testing dataset | 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 | 1, 2, 3 | 29°, 53° |
| Layer Name | Layer Description |
|---|---|
| Input | 21 × 100 Sensor and motor (valve) angle values over 100 time steps |
| Convolution 1, Pooling 1 | Convolution filters 3, Stride 1, Padding 1, Number of filters 512, Batch normalization, ReLU, Max pooling 2, Strides 2 |
| Convolution 2, Pooling 2 | Convolution filters 3, Stride 1, Padding 1, Number of filters 1024, Batch normalization, ReLU, Max pooling 2, Strides 2 |
| Convolution 3, Pooling 3 | Convolution filters 3, Stride 1, Padding 1, Number of filters 2048, Batch normalization, ReLU, Max pooling 2, Strides 2 |
| Convolution 4, Pooling 4 | Convolution filters 3, Stride 1, Padding 1, Number of filters 4096, Batch normalization, ReLU, Average pooling 2, Strides 2 |
| Fully Connected | Input = 24,576, Output = 2048. Batch normalization, Tanh, Input = 2048, Output = 1024, Batch normalization, Tanh, Input = 1024, Output = 4, Batch normalization, ReLU |
| MAE | RMSE | |
|---|---|---|
| Whole case | 0.0306 | 0.0629 |
| Only severities used during training | 0.0024 | 0.0059 |
| Only severities used during testing | 0.0467 | 0.0954 |
| MAE | RMSE | |
|---|---|---|
| Proposed Network (1D Conv + FC) | 0.0306 | 0.0629 |
| LSTM | 0.0434 | 0.0909 |
| RNN | 0.0807 | 0.1176 |
| FC | 0.1171 | 0.2560 |
| SVM | 0.2447 | 0.3550 |
| RF | 0.2145 | 0.3877 |
| MAE | RMSE | |
|---|---|---|
| Proposed network input composition | 0.0306 | 0.0629 |
| Input composition 1 | 0.0329 | 0.0815 |
| Input composition 2 | 0.0359 | 0.0899 |
| Input composition 3 | 0.0380 | 0.1065 |
| Input composition 4 | 0.0385 | 0.3077 |
| Input composition 5 | 0.0442 | 0.1115 |
| Input composition 6 | 0.0478 | 0.1224 |
| Input composition 7 | 0.0579 | 0.1462 |
| Input composition 8 | 0.0640 | 0.1333 |
| Input composition 9 | 0.1288 | 0.3270 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, E.; Yang, J.-H.; Lim, S.-C. Deep Neural Network for Valve Fault Diagnosis Integrating Multivariate Time-Series Sensor Data. Actuators 2025, 14, 70. https://doi.org/10.3390/act14020070
Jeong E, Yang J-H, Lim S-C. Deep Neural Network for Valve Fault Diagnosis Integrating Multivariate Time-Series Sensor Data. Actuators. 2025; 14(2):70. https://doi.org/10.3390/act14020070
Chicago/Turabian StyleJeong, Eugene, Jung-Hwan Yang, and Soo-Chul Lim. 2025. "Deep Neural Network for Valve Fault Diagnosis Integrating Multivariate Time-Series Sensor Data" Actuators 14, no. 2: 70. https://doi.org/10.3390/act14020070
APA StyleJeong, E., Yang, J.-H., & Lim, S.-C. (2025). Deep Neural Network for Valve Fault Diagnosis Integrating Multivariate Time-Series Sensor Data. Actuators, 14(2), 70. https://doi.org/10.3390/act14020070






